Measuring Optical and Mechanical Properties of a Living Cell with Defocusing Microscopy

Abstract

Defocusing microscopy (DM) is a recently developed technique that allows quantitative analysis of membrane surface dynamics of living cells using a simple bright-field optical microscope. According to DM, the contrast of defocused images is proportional to cell surface curvature. Although, until now, this technique was used mainly to determine size and amount of membrane shape fluctuations, such as ruffles and small random membrane fluctuations, in macrophages, its applications on cell biology extend beyond that. We show how DM can be used to measure optical and mechanical properties of a living macrophage, such as cell refractive index n, membrane bending modulus K_c, and effective cell viscosity η for membrane-actin meshwork relaxation. Experimental data collected from defocused images of bone marrow-derived macrophages were used to evaluate these parameters. The obtained values, averaged over several different macrophages, are n = (1.384 ± 0.015), K_c ≈ 3.2 × 10⁻¹⁹ J, and η ≈ 459 Pa·s. We also estimate the amplitude of the small fluctuations to be of the order of 3 nm, which is around the step size of a polymerizing actin filament.

INTRODUCTION

Experimental determination of physical properties of living cells is an important step toward better understanding of several cellular traits, both structural and functional. Knowledge of optical properties like cell refractive index, for instance, may provide indications of local cellular composition and structure, while determination of mechanical properties such as membrane bending modulus and effective cell viscosity for membrane-actin meshwork relaxation can help modeling cellular and intracellular motility processes. In this work, we show how defocusing microscopy (DM), a recently developed technique that allows quantitative analysis of membrane deformations (1,2), can be used to evaluate these parameters. We present our results in two parts.

In the first part of our work, we demonstrate how DM can be used to evaluate the difference Δn between the refractive index of a phase object, such as the ruffles that form over the surface of the plasmatic membrane of adhered macrophages, and the refractive index of the surrounding medium. If the refractive index of the medium is known, the refractive index of the phase object can then be obtained by simple addition.

In the second part, we use DM to characterize quantitatively both the morphology and the dynamics of the small random membrane fluctuations permeating the whole surface of the macrophages (1,3), a common trait shared by many types of living cells (4–6). We improve our previous data on the characteristics of these small fluctuations at 37°C (3), better resolving their correlation length ξ and correcting their root-mean-square (RMS) curvature, previously underestimated due to the larger value of Δn = 0.1 used in the calculations, as compared to the value measured more accurately in the present work. Analysis of the average characteristics presented by this type of fluctuations is expanded, now considering the elastic properties and thermodynamics of lipid bilayers (7–10) and thus allowing evaluation of membrane bending modulus K_c and effective cell viscosity η for membrane-actin meshwork relaxation.

A brief review on how the DM technique works is given in Materials and Methods to familiarize the reader with what is actually measured and how these data can lead to an amplitude resolution of the fluctuations down to the nanometric scale, well below the lateral optical resolution of the microscope.

MATERIALS AND METHODS

Macrophages

Bone marrow-derived macrophages were obtained from C57BL/6 mice following the procedures described by Coelho Neto et al. (3). Samples consisted of single well plates made of Plexiglas and microscope cover glasses, each containing 4–6 × 10⁴ cells on 1 ml of medium (DMEM supplemented with 10% FCS and 0.1% of antibiotics). Before experiments, samples were kept at 37°C, 5% CO₂, for a period of 3–24 h to allow cell adhesion and membrane spreading.

Defocusing microscopy

Defocusing microscopy (1,2) was used to track and analyze membrane deformations that occur normally over the surface of living cells, such as ruffles and small random fluctuations. Unlike phase contrast and DIC microscopy techniques, which measure the thickness and thickness gradient of objects visualized, DM only detects their surface curvature. Since any deformation, artificial or natural, appearing over the membrane of a cell changes the local curvature, it can be detected and quantified by DM through a simple analysis of the contrast patterns appearing in the defocused images, given by

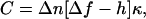(1)

where C is the contrast generated by the curvature κ, Δn is the difference between refractive indexes of the membrane and the surrounding medium, Δf is the defocusing distance, and h is the vertical extension of the deformation.

Equation 1 is a linear expansion in Δf of a more complete expression and is valid typically for 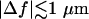(1). For small fluctuations, where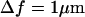 the contrast is proportional to Δf and the curvature. Therefore, the longitudinal (height) resolution in our system is limited by the smallest curvature that can be observed with a defocusing distance of 1 μm. Let us consider a small fluctuation, which excites a single membrane mode of wave vector q. The curvature generated by this mode is κ = q²a, where a is the amplitude of the mode q. Considering the signal/noise ratio for our experimental setup, which allows RMS contrast fluctuations to be measured down to 1%, the smallest curvature κ that can be measured in accordance with Eq. 1, using Δn = 0.05, is κ = 0.2 μm⁻¹. On the other hand, since the lateral resolution ℓ of our microscope is of the order of 0.25 μm, the largest wave vector measurable will be q_max = (π/0.25)μm⁻¹. The height resolution of our system for measuring the average amplitude of small membrane surface fluctuations is then

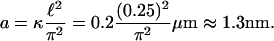(2)

Therefore, DM can achieve amplitude resolution of surface fluctuations down to the nanometric scale, like standard interferometric optical profilers. This is because DM, to be applicable as predicted by our theory, based on coherent optics techniques, light has to be collected under a coherence area. This is usually the case for objectives with high magnification and high numerical aperture, even for illumination with a broadband halogen lamp (1). The surprising result here is that a defocused microscope can work as an optical profiler.

Setup

Experiments were conducted on a Nikon TE300 inverted microscope with oil immersion objective (Nikon Plan APO DIC H, 100×, 1.4 NA; Nikon, Melville, NY). Sample temperature was controlled by heating the objective. Images of single spread macrophages were captured with a CCD camera attached to the microscope and recorded on tape for later digitalization and analysis. A typical defocused image from a spread macrophage is shown in Fig. 1. The defocusing distance was controlled by a motorized stage adapted to move the samples up and down over the objective. Video system pixel gray values captured by the CCD have to be calibrated as a function of the light intensity incident on the samples to translate image contrast to light intensity contrast. Details of the calibration procedure can be found in Agero et al. (2) and Coelho Neto et al. (3).

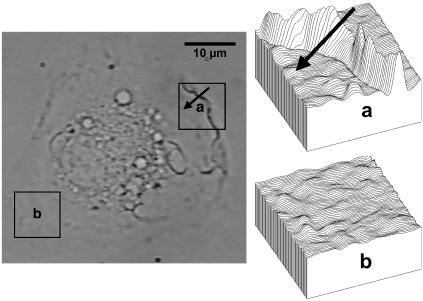
FIGURE 1.

Typical defocused image of a spread macrophage. (a) Detail of the contrast pattern generated by a ruffle. The study of this type of fluctuation is based on the analysis of longitudinal contrast profiles crossing the structure from the border to the center of the cell (arrow). (b) Detail of the contrast pattern generated by the small membrane fluctuations. The study of this type of fluctuation is based on the analysis of the autocorrelation functions for the contrast, calculated pixel by pixel, along a selected area of the image. The defocusing distance is 1 μm.

Measurements

Ruffles, which appear in defocused images as regions of high contrast (Fig. 1 a), were studied while the macrophages were kept at room temperature to slow down their movements, so that each structure would keep reasonably still while the defocusing distance was continuously varied from negative to positive. In each run a ruffle was filmed for ∼5 s at a sampling rate of 30 images per second. The defocusing distance was increased by 0.02 μm per image. At room temperature, ruffles move at ∼(1.0 ± 0.4) μm/min (3), which corresponds to a displacement of <0.1 μm during the whole data acquisition. Therefore, it is reasonable to treat them as still structures during each run. Best results were obtained from structures presenting high contrast levels.

The small random membrane fluctuations, which appear over the whole cell surface (Fig. 1 b), were studied while the macrophages were kept at 37°C. In this type of experiment, the defocusing distance was kept fixed at 1 μm. Typically, each macrophage was filmed for 10 min at a sampling rate of 1.5 images per second.

Image analysis

Recorded images of the macrophages were digitalized as 8-bit grayscale movies and analyzed with the NIH-ImageJ software package (available at http://rsb.info.nih.gov/ij). Images were subjected to two forms of analysis, depending on the type of membrane deformation studied and the parameters under investigation. To evaluate cell refractive index, evolution of the image contrast profile of individual ruffles was followed as a function of the defocusing distance. Evaluation of membrane bending modulus and effective cell viscosity for membrane-actin meshwork relaxation was based on the decay time and the correlation length of the small fluctuations, obtained from temporal and spatial autocorrelation functions for the RMS contrast observed in the defocused images. The autocorrelation functions were obtained directly from the digitalized movies by using ImageJ plug-ins written to calculate their values, pixel by pixel, along a selected area of the membrane (see Appendix B).

RESULTS AND DISCUSSION

Determination of cell refractive index

Ruffles can be described as the structures that appear on sites where the plasmatic membrane is projected vertically from inside the cell by mechanisms involving actin polymerization/reorganization and whose details are not quite established yet (11–13). As sites of significant and sudden increase/decrease in local membrane curvature, ruffles appear in defocused images as regions of high contrast showing mainly two characteristic longitudinal curvature profile types, hyperbolic and Gaussian, each one corresponding to ruffles of specific shape (1,3).

If the shape of the membrane at a given region and time can be reasonably well approximated by a known function h(x, y), such as in the case of a ruffle, the contrast C(x, y) observed at this location due to defocusing can be written as

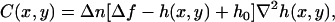(3)

where Δn is the difference between refractive indexes of the cell and the surrounding medium, h(x, y), and h₀ represent the shape and the maximum local height of the membrane relative to the cover glass and Δf is the defocusing distance relative to h₀ (see Appendix A). Although Eq. 3 is valid for any function h(x, y) describing the shape of the membrane, we restrict our analysis to ruffles that best fit the Gaussian profile, since they tend to be the more stable and abundant type of structure present whose shape is well approximated by a known function. Otherwise, we would have to solve Eq. 3 numerically to obtain h(x, y), a cumbersome procedure susceptible to large errors due to baseline-related problems.

According to Eq. 3, the contrast profile generated by a Gaussian ruffle, whose shape can be approximated by

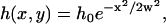(4)

where h₀ corresponds to the maximum ruffle height and w is the width of the structure, is

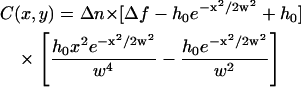(5)

If we plot the expected contrast profile of a Gaussian ruffle, given by Eq. 5, as a function of the position and the defocusing distance, we see that the contrast pattern is gradually inverted as we move from positive to negative defocusing (Fig. 2). Experimental contrast profiles of the same ruffle for negative and positive defocusing amounts confirm these inversions (Fig. 3). In fact, the change in the defocusing distance is the cause of the light-dark inversion usually seen when we are focalizing a thick transparent sample under an optical bright-field microscope. Good results were obtained from structures presenting high contrast levels and which best fit the contrast profile of a Gaussian ruffle.

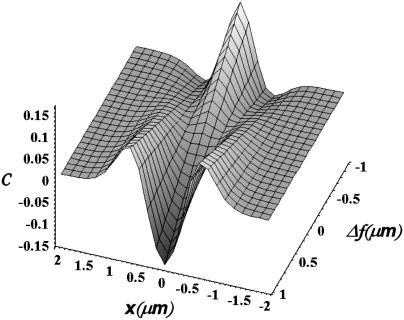
FIGURE 2.

Evolution of the contrast profile for a Gaussian ruffle as a function of the position x and the defocusing distance Δf, according to Eq. 5. As Δf varies from positive to negative values, the contrast profile is gradually inverted, so that positions showing positive contrast (light regions) swap to negative contrast (dark regions) and vice versa. For this example, we used h₀ = 0.5 μm, w = 0.4 μm, and Δn = 0.05.

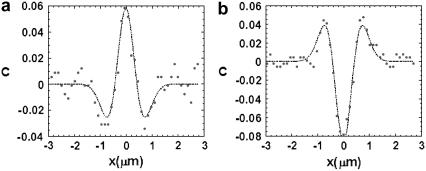
FIGURE 3.

Experimental contrast profiles for a single Gaussian ruffle, at two different defocusing amounts, fit with Eq. 5. (a) Δf = −0.76 μm. Fit values: w = 0.42 μm, h₀Δn = 0.014 μm. (b) Δf = 1.01 μm. Fit values: w = 0.42 μm, h₀Δn = 0.015 μm.

When Δf and Δn are known, Eq. 5 can be used to fit experimental contrast profiles of Gaussian ruffles, so that the values of h₀ and w can be determined (1,3). If, however, only Δf is known, although Δn, h₀, and w can be obtained from a free fit, as shown by Agero et al. (2), w is well defined whereas Δn and h₀ are affected by large uncertainties. To improve the determination of both Δn and h₀, we keep track of the contrast profile of single ruffles while varying the defocusing distance. As already mentioned, the contrast at all points will be gradually inverted as Δf goes from positive to negative values (Figs. 2 and 4). For small defocusing distances, such variation is linear, so that the contrast at any fixed position x will vary with Δf as

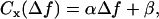(6)

where α and β are constants that depend on h₀, w, and Δn and vary according to the position x fixed in the profile. Using the value of w obtained from the fit of the corresponding contrast profile using Eq. 5, Δn and h₀ will be the only unknown parameters appearing in Eq. 6. This equation can then be used to fit the contrast as a function of the defocusing distance, observed at any point, and determine the individual values of h₀ and Δn.

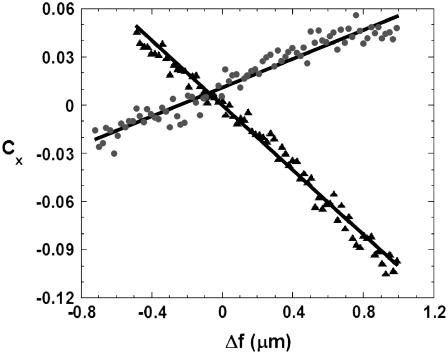
FIGURE 4.

Contrast inversion curve as a function of Δf for the central (▴) and right lateral (•) peaks of a Gaussian ruffle. Using Eqs. 7a and 7b to fit these data, we obtained h₀Δn = (0.0161 ± 0.0002) μm for the central peak and h₀ = (0.31 ± 0.02) μm, Δn = (0.051 ± 0.005) for the right lateral peak. Since both curves belong to the same structure, we can use the value of h₀ obtained from the fit on the lateral peak to obtain Δn = (0.052 ± 0.005) for the central peak. For this ruffle, w = 0.4 μm. The distance between the central and the lateral peaks was 0.7 μm.

Despite the fact that Eq. 6 can be used to fit the contrast inversion at any point, the best choices for a Gaussian ruffle are the central (x = 0) and lateral (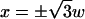) contrast peaks, where the amplitude of the contrast inversion is higher, as can be seen from Fig. 2. At these specific positions, we have

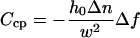(7a)

for the contrast variation at the central peak and

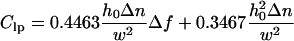(7b)

for the contrast variation at the lateral peaks. Although h₀ and Δn remain coupled in Eq. 7a, they are only partially coupled in Eq. 7b, allowing the individual value of both h₀ and Δn to be well determined for the lateral peaks. Since h₀ must be the same for both lateral and central peaks of the same ruffle, we can use the average value of h₀ obtained from the contrast variation at the two lateral peaks to obtain Δn for the central peak as well. An example of two contrast inversion curves for a single ruffle, evaluated at these positions and fit according to Eqs. 7a and 7b, is shown in Fig. 4.

We analyzed 14 contrast inversion curves (four central peaks and 10 lateral peaks) in eight ruffles of four different macrophages using this approach. The average value obtained was Δn = (0.049 ± 0.015). Using n₀ = (1.3355 ± 0.0003) as the refractive index of the surrounding medium (2), we obtain n = (1.384 ± 0.015) as the average refractive index of living macrophages. This value is consistent with previous measurements made in other cell lines using different approaches (14,15).

Determination of cell mechanical properties

Aside from ruffles, which constitute localized phenomena of relatively large amplitude, the presence of small membrane fluctuations, uniformly distributed over the cell surface as a whole, seems to be a common trait shared by many types of cell lines, including erythrocytes, lymphocytes, fibroblasts, monocytes, cardiomyocytes, and macrophages (1,3–6). As structures of relatively small sizes and small curvatures, when compared to ruffles, the contrast generated by this type of membrane fluctuation is not high enough to allow their characteristics to be obtained directly from a contrast profile. Nevertheless, characterization of these small random membrane fluctuations can be achieved from the analysis of the temporal and spatial autocorrelation functions for the contrast/curvature generated by these structures, calculated point by point (see Appendix B).

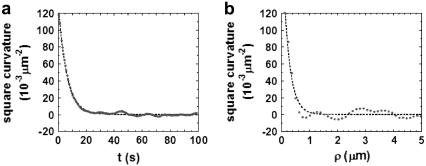
From the relaxation of the temporal and spatial autocorrelation functions, we obtain the decay time τ and the correlation length ξ of these small fluctuations. In both cases, their RMS curvature κ is defined as the square-root of the autocorrelation functions amplitudes. An example of both temporal and spatial autocorrelation functions for the curvature over the surface of a macrophage is shown in Fig. 5.

FIGURE 5.

Typical autocorrelation functions for the curvature over the surface of the plasmatic membrane of a spread macrophage. (a) Temporal autocorrelation function (decay time τ = 6 s, RMS curvature κ = 0.4 μm⁻¹). (b) Spatial autocorrelation function (correlation length ξ = 0.23 μm, RMS curvature κ = 0.5 μm⁻¹).

We analyzed ∼60 autocorrelation functions obtained from 15 different macrophages. The average results are shown in Table 1.

TABLE 1.

Average characteristics of the small membrane fluctuations observed in 15 different macrophages using DM

Decay time τ (s)	Correlation length ξ (μm)	RMS curvature κ (μm−1)
7 ± 2	0.23 ± 0.04	0.5 ± 0.2

The values presented represent the result from the analysis of the relaxation of both temporal and spatial autocorrelation functions for the contrast generated by the small fluctuations.

The average correlation length ξ obtained from this analysis is of the same order of the lateral resolution ℓ of our optical setup, so that ξ represents an upper limit for the correlation length of the small fluctuations. Therefore, all fluctuation modes q that might constitute the whole of these fluctuations must be confined in regions of limited size ξ. Since contrasts measured with DM at any point represent the average contrast at that point, considering the optical resolution limit, all modes with angular wavenumber q higher than q₀ = π/ξ are lost during data acquisition, as the contrasts they generate tend to cancel each other when averaged over a region of size ξ. Therefore, we assume that the decay time τ and the RMS curvature κ obtained from the temporal autocorrelation functions correspond to mode q₀.

Although we are not able to extend our analysis to regions smaller than ξ, studies on similar fluctuations on other cell types (4–6) indicated that these small fluctuations are confined to regions with area ∼0.2 μm², which is compatible with the correlation length obtained from our data. These observations support the fact that the membrane is pinned to the actin meshwork at regular distances, at ∼0.2–0.3 μm, resulting in two-dimensional membrane compartmentalization, as demonstrated by Fujiwara et al. (16), thus confining single small fluctuations.

The height of the fluctuation inside each confinement area, considering only the mode q₀, can be written as h(x, y) = a₀ sin(q₀ x) sin(q₀ y), where a₀ is the amplitude of the fluctuation. Approximating the curvature by κ ≈ ∇²h, we can write 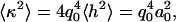from which we obtain the RMS value

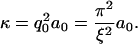(8)

Using the measured values for κ and ξ, we can estimate the amplitude of the small membrane fluctuations to be a₀ = (3 ± 2) nm. This value is slightly below the range of values (10–400 nm) reported for different cell types (4–6), which is likely because we are able to separate-out the small random fluctuations from larger fluctuations as ruffles.

Evaluation of the membrane bending modulus

The amount of energy necessary to bend a membrane in order to generate a curvature κ in a region with area A is (7,9,10)

(9)

where K_c is the bending modulus of the membrane. Applying the equipartition energy theorem to Brownian fluctuations of mode q₀ confined to an area ξ², we rewrite Eq. 9 as

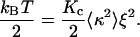(10)

Using the experimental values for κ and ξ from Table 1, obtained for T = 37°C, we can evaluate the bending modulus for the plasmatic membrane of the macrophages in this length scale, obtaining K_c ≈ 3.2 × 10⁻¹⁹ J. This value is consistent with membrane bending modulus of other cells and artificial lipid membranes obtained from different methods, as shown in Table 2. This result can be interpreted based on the Brownian ratchet model of cell motility, proposed by G. Oster and co-workers (17–20). The main assumption of the model is that an actin filament close to the membrane cannot grow unless there is a gap between the filament tip and the membrane, large enough to accommodate new actin monomers. The gap is provided by thermal fluctuations of free portions of the membrane as it moves away from the tip. Before the membrane recedes back, the polymerizing actin filament rapidly fills this gap, thus rectifying the Brownian motion of the membrane. Based on this model of motility, our interpretation of the measurements of the small random surface fluctuations, described previously, is as follows: Our data show that these small fluctuations are confined to linear dimensions of the order of 0.2 μm, where the membrane is pinned to the actin cortex in agreement with the model of Fujiwara et al. (16). These regions of the membrane can fluctuate thermally, thus causing the observed small cell surface fluctuations. In our measurements the amplitude of such small fluctuations, (3 ± 2) nm, is of the order of the size of an actin monomer, (2.7) nm. To determine the bending modulus related to the deformation of the macrophage surface, we used, as shown above, the average area of the confined regions, the mean-square curvature of cell surface fluctuations, measured with defocusing microscopy, and equipartition theorem. The use of the equipartition theorem is justified by the fact that the amplitude of the small surface fluctuations is determined by the thermal motion of free portions of the membrane. The bending modulus obtained (K_c ≈ 3.2 × 10⁻¹⁹ J) is typical of free membranes, supporting the assumptions above.

TABLE 2.

Values of K_c for different cell types obtained from different experimental techniques

Cell type	Method	Kc (10−19 J)	Ref. No.
Artificial vesicles	Micropipette aspiration	0.4–2.5	(27)
Erythrocytes	Phase contrast microphotometry	0.8	(8)
Erythrocytes	Micropipette aspiration	1.8	(28)
Erythrocytes	Reflection interference contrast and phase contrast microscopy	4	(29)
Neutrophils	Micropipette aspiration	15	(30)
Dictyostelium	Reflection interference contrast microscopy	16	(31)
Macrophages	Defocusing microscopy	3.2	This work

Evaluation of the effective cell viscosity for the membrane-actin meshwork relaxation

According to Brochard and Lennon (8), the relaxation dynamics of the mode q of a membrane of bending modulus K_c, subjected to a viscosity η, obeys

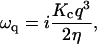(11)

if qd ≫ 1, where d is the local cell thickness. The imaginary oscillation frequency ω_q can be related to the decay time τ_q of the membrane fluctuations by making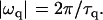 The decay time of the mode q₀ would then be

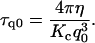(12)

From this equation and the values of τ, q₀, and K_c previously obtained, we can evaluate the effective cell viscosity perceived by the membrane while receding from a fluctuation as η ≈ 459 Pa·s. This value is well within the range of the viscosities obtained for similar cell lines (21–25), as shown in Table 3. As in the previous section, we interpret this result based on the ratchet model. The membrane can move away from the actin cortex by a Brownian fluctuation. Actin filaments grow, impeding the membrane from freely receding back. The relaxation of the fluctuations corresponds then to the relaxation of the composite system (membrane plus actin cortex), whose relaxation time τ we measure. Therefore, in Eq. 12 the bending modulus of the composite system should be used to obtain the actual viscosity. However, we do not know the value of the bending modulus for the composite system, which is expected to be larger than the value obtained for the free membrane. By using, in Eq. 12, the value of the bending modulus for the free membrane, determined in the previous section, we obtain a lower bound (η ≈ 459 Pa·s) for the effective cell viscosity for the membrane-actin meshwork relaxation.

TABLE 3.

Values for the effective cell viscosity η for similar cell lines obtained from different techniques

Cell type	Method	Probe diameter d (μm)	Effective viscosity η (Pa·s)	Ref. No.
Fibroblasts	Electron spin resonance	0.00064	0.0021	(32)
Macrophages	Magnetometry of twisted particles	0.3–0.7	1950	(21)
Macrophages	Magnetometry of twisted particles	0.2	1100	(23)
Fibroblasts	Magnetic bead micro-rheometry	4.5	2000	(24)
Macrophages	Magnetic bead micro-rheometry	1.3	210	(25)
Macrophages	Defocusing microscopy	Not applicable	459	This work

The results shown seem to depend, in some degree, on the size of the probe used. A broader comparison, which also supports this idea, can be found in Valberg and Albertini (21) and Valberg and Feldman (22).

Another interpretation for the relaxation time τ that we observe was proposed recently in a new model of motility, where the dynamics of membrane fluctuations is determined by the diffusion of surface proteins that trigger actin polymerization (26). Our data of the decay time of small fluctuations and velocity of ruffles as a function of temperature (3) were used to support this model. The slow-decay time constant we observe is associated with the diffusion time of membrane proteins. This model successfully predicts the origin and propagation of large fluctuations like ruffles and lamellipodia.

CONCLUDING REMARKS

We have shown how DM can be used to measure the refractive index, the membrane bending modulus, and the effective cell viscosity for the membrane-actin meshwork relaxation in viable macrophages.

Unlike most techniques usually applied to access optical and mechanical parameters of living cells, DM takes advantage of the natural membrane deformations observed in the behavior of these cells, such as membrane ruffles and small membrane fluctuations, generating quantitative data on these structures which can then be used to evaluate such parameters. The technique does not require the cells to be subjected to any kind of special condition during the experiments, like fluid dragging, adhesion/ingestion of physical probes, illumination with harmful wavelengths or immersion in intense magnetic fields, keeping the cells absolutely undisturbed during experiments.

The results obtained with DM give additional support to recent physical models of cell membranes and motility. We show that small surface fluctuations are uncorrelated to distances larger than 0.23 μm, indicating that the cell membrane is compartmentalized, supporting the model of Fujiwara et al. (16). The obtained bending modulus is close to that of a free membrane, giving additional support to ratchet models (17–20). Our results on the decay time of small fluctuations and propagation velocity of ruffles also support a new model, which considers the coupling between membrane proteins that trigger actin polymerization and surface fluctuations (26).

The amount of information obtained from such a simple method, which can be easily implemented in almost any bright-field optical microscope connected to a good image acquisition system, without need for optical filters, phase plates, or special prisms, demonstrates how DM constitutes a powerful and very useful new tool for the study of cell motility and other related topics on cell biology.

APPENDIX A: DEFOCUSING MICROSCOPY—CONVERTING IMAGE CONTRAST TO SURFACE CURVATURE

According to the DM theory (1,2), the contrast generated by a phase object, like the plasmatic membrane of a living cell, whose shape is described by a function h(x, y) relative to the bottom of the sample, is well described by the expression

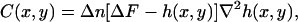(13)

where ΔF (defocusing distance) is the position of the focal plane of the objective relative to the bottom of the sample and Δn is the difference between refractive indexes of the cell and the surrounding medium. The local curvature of the object is approximated by κ ≈ ∇²h(x, y).

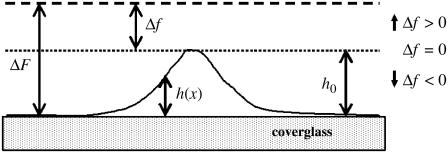
For thin objects (objects for which the depth of field of the microscope is greater than h(x, y) at all points), the defocusing distance is determined as the actual distance from the point where the observed contrast vanishes, which corresponds to the bottom of the sample (ΔF = 0). When, however, the object under analysis cannot be considered thin, the contrast vanishes when ΔF = h(x, y), and not when ΔF = 0. To continue measuring the defocusing distance as the current distance from the point where the contrast vanishes, we move the origin of our reference frame from the bottom of the sample (h = 0) to the top of the structure under analysis (h = h₀). The defocusing distance Δf and the shape of the membrane H(x, y) relative to this new reference frame (Fig. 6) are

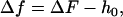(14a)

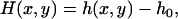(14b)

so that Eq. 13 is now written as

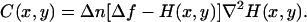(15)

FIGURE 6.

Out-of-scale diagram representing the optical distances involved in a defocused image of a phase object whose shape is described by a function h(x, y). The value ΔF represents the defocusing distance relative to the bottom of the sample, and Δf represents the defocusing distance relative to the top of the structure under analysis. The focal plane is located at the upper dashed line.

In terms of the shape h(x, y) of the object under analysis, Eq 15 takes the form

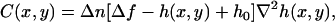(16)

which we used to analyze our data.

APPENDIX B: AUTOCORRELATION FUNCTIONS

The temporal and spatial autocorrelation functions for the curvature κ produced by the small random membrane fluctuations were calculated from the average product of the contrast/curvatures observed at different times and positions. Approximately 10⁵ data points were considered for the calculation of each individual function.

Temporal autocorrelation functions F_t(t) were calculated as the product between the contrast observed at a fixed position ρ at a fixed time t₀ and the contrast observed at the same position at later times, averaged for different starting times t₀ and different positions ρ, so that

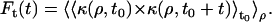(17a)

Spatial autocorrelation functions F_s(ρ) were calculated as the product between the contrast observed at a fixed time t at a fixed position ρ₀ and the contrast observed at the same instant at adjacent positions, apart from the starting point by a distance ρ, averaged for different starting positions and different times, so that

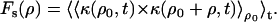(17b)

In both cases, the resulting functions presented a relaxation which could be reasonably well fit by single exponentials, with

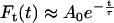(18a)

and

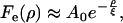(18b)

where A₀ = 〈κ²〉.