A molecular mechanism for osmolyte-induced protein stability

Abstract

Osmolytes are small organic compounds that affect protein stability and are ubiquitous in living systems. In the equilibrium protein folding reaction, unfolded (U) ⇌ native (N), protecting osmolytes push the equilibrium toward N, whereas denaturing osmolytes push the equilibrium toward U. As yet, there is no universal molecular theory that can explain the mechanism by which osmolytes interact with the protein to affect protein stability. Here, we lay the groundwork for such a theory, starting with a key observation: the transfer free energy of protein backbone from water to a water/osmolyte solution, Δg_tr, is negatively correlated with an osmolyte’s fractional polar surface area. Δg_tr measures the degree to which an osmolyte stabilizes a protein. Consequently, a straightforward interpretation of this correlation implies that the interaction between the protein backbone and osmolyte polar groups is more favorable than the corresponding interaction with nonpolar groups. Such an interpretation immediately suggests the existence of a universal mechanism involving osmolyte, backbone, and water. We test this idea by using it to construct a quantitative solvation model in which backbone/solvent interaction energy is a function of interactant polarity, and the number of energetically equivalent ways of realizing a given interaction is a function of interactant surface area. Using this model, calculated Δg_tr values show a strong correlation with measured values (R = 0.99). In addition, the model correctly predicts that protecting/denaturing osmolytes will be preferentially excluded/accumulated around the protein backbone. Taken together, these model-based results rationalize the dominant interactions observed in experimental studies of osmolyte-induced protein stabilization and denaturation.

The equilibrium protein folding reaction, unfolded (U) ⇌ native (N), is not an ordinary chemical reaction because no covalent bonds are made or broken in the interconversion between N and U. Instead, protein denaturation/renaturation is just a reequilibration between the unfolded and folded populations under changed solvent conditions. Accordingly, a thermodynamic description of protein folding can be framed in terms of solvent interactions with the unfolded and native states (1–3).

Osmolytes are small organic compounds that exert a dramatic influence on the protein folding reaction, again without making or breaking covalent bonds. Protecting osmolytes push the folding equilibrium toward N, whereas denaturing osmolytes push the equilibrium toward U. Both types of osmolytes are of utmost significance. Protecting osmolytes are ubiquitous in nature, where they play a vital role in stabilizing intracellular proteins against a wide variety of adverse environmental conditions (4–7). Alternatively, urea, a denaturing osmolyte found naturally in mammalian kidney, has been a key reagent throughout the long history of solvent denaturation studies (3, 8–10).

The solution thermodynamics of protein/osmolyte mixtures has been well characterized in the literature (3, 11–19). In the emerging view (12, 17), protecting osmolytes raise the free energy of the unfolded state, favoring the folded population, whereas denaturing osmolytes lower the free energy of the unfolded state, favoring the unfolded population. Accordingly, protecting/denaturing osmolytes interact unfavorably/favorably with the unfolded state, resulting in preferential depletion/accumulation of osmolyte proximate to the protein surface. Such osmolyte-induced behavior has been well characterized in thermodynamic terms, but thermodynamics is a descriptive science, deliberately devoid of mechanism. As yet, there is no universal theory that can account for the mechanism by which osmolytes interact with the protein to affect stability.

What specific molecular interactions in a protein–osmolyte–water solution stabilize/destabilize the unfolded state of proteins? An important clue comes from recent work showing that the osmolyte effect operates predominantly on the protein backbone, a component common to all residues (11–13). This conclusion was reached by measuring transfer free energies, Δg_tr, of backbone models from water to 1 M osmolyte solutions. Although side chains do play a role, it is primarily the backbone transfer free energy that determines the extent to which osmolytes either stabilize (i.e., Δg_tr > 0) or destabilize (i.e., Δg_tr < 0) the protein relative to an equivalent aqueous solution.

Thus, the backbone Δg_tr value is the key metric for evaluating the relative denaturing/stabilizing strength of different osmolytes. The thermodynamic reference state for this metric is given by interactions of the peptide backbone unit with solvent water. When that backbone unit is transferred from water to an aqueous osmolyte solution, the very presence of a molecule that experiences backbone interactions which differ from corresponding interactions with water either raises (for a protecting osmolyte) or lowers (for a denaturing osmolyte) the Δg_tr value relative to this reference state. Furthermore, given the well defined nature of the two solvent systems, the resultant Δg_tr will arise solely from differences between backbone/water and backbone/water/osmolyte interactions. Any molecular interpretation of osmolyte interactions must be consistent with this experimental reality.

We demonstrate that Δg_tr values for a wide variety of osmolytes are negatively correlated with their fractional polar surface area (SA), f_{polar surface}^osmolyte. The correlation suggests that polar and nonpolar osmolyte surfaces interact with the protein backbone at different energies, and that the extent of interaction is related to interactant SA. Specific instances in the literature are in known agreement with this plausible idea. For example, the polar molecule urea that has long been known to interact favorably with the amide backbone of proteins (20, 21). Also, in a related correlation, Record and colleagues (18) noted that Δg_tr for glycine betaine is proportional to polar SA. To quantify our idea, we develop a simple statistical mechanics backbone solvation model in which the interaction energy depends on interactant polarity, and the interaction degeneracy (i.e., the number of energetically equivalent ways of realizing the interaction) depends on the corresponding interactant SAs. Our goal is to learn whether this minimal model, polar interactions in a statistical mechanical framework, is sufficient to account for the diversity of experimental phenomena associated with protecting and denaturing osmolytes.

Results

Calculations described below were performed by using x-ray structures of eight stabilizing osmolytes [trimethylamine N-oxide (TMAO), betaine, sarcosine, proline, trehalose, sucrose, glycerol, and sorbitol], a destabilizing osmolyte (urea) and a related denaturant (guanidine). The Δg_tr values for these 10 compounds have been measured by two independent methods in all cases except guanidine (11) (Table 1). Comparisons between osmolyte structures and the associated water to osmolyte Δg_tr values (Fig. 1) indicate no evident correlation with either the total osmolyte SA or its polar SA. For example, TMAO and urea (Fig. 1 a and j) have similar total SAs but opposite effects on protein stability. Likewise, sucrose (Fig. 1c), an intermediate stabilizer, has greater polar SA than either TMAO, a strong stabilizer, or urea, a strong denaturant.

Table 1.

Solvent accessible surface areas and Δg_tr values of osmolytes

Osmolyte*	SA+, Å2†	SA−, Å2†	SAo, Å2†	ΣSA, Å2‡	Δgtr, cal/mol§
TMAO	0.0	43.2	168.4	211.6	89 ± 2
Betaine	3.6	82.7	166.7	253.0	65 ± 3
Sucrose	0.0	336.9	137.3	474.2	56 ± 6
Trehalose	0.0	340.6	145.2	485.8	54 ± 8
Sarcosine	24.5	43.3	141.6	209.4	50 ± 2
Sorbitol	0.0	233.6	97.8	331.4	43 ± 7
Proline	24.5	88.9	133.5	246.9	40 ± 8
Glycerol	0.0	142.7	84.1	226.8	22 ± 8
Urea	111.8	51.4	11.6	174.8	−41 ± 2
Guanidine	167.8	0.0	11.6	179.4	−59

*The 10 osmolytes listed in Fig. 1.

^†Osmolyte surface areas in Ų with partial positive, negative, and neutral charge are indicated by SA₊, SA₋, and SA_o, respectively.

^‡Total surface area in Ų = sum of SA₊, SA₋, and SA_o.

^§Δg_tr is the free energy change that accompanies the transfer of a backbone unit from water to a 1 M osmolyte solution. Uncertainty in Δg_tr values is based on two independent measurement techniques (11). Value for guanidine was provided by S. Sarker (personal communication).

Fig. 1.

Molecular structures of osmolytes. Protecting osmolytes are TMAO, betaine, sucrose, trehalose, sarcosine, sorbitol, proline, and glycerol (A–H), and denaturants are urea and guanidine (J–K). Compounds are ordered by their measured Δg_tr values (see Table 1), shown in space-filling representations and color-coded by atom type: oxygen (red), nitrogen (blue), and carbon (green). Water polarity is represented by its surface electrostatic potential (I, Upper), using a color saturation scale that runs from −0.07 (red) to 0.11 (blue) e/Å; white indicates neutral potential. The water surface is partitioned into discrete positive (red), negative (blue), and neutral (white) surfaces (I, Lower) using electrostatic potential cutoffs described in Methods.

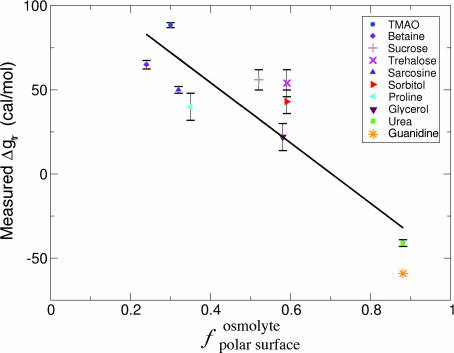
However, there is a clear correlation (R = 0.88) between Δg_tr and f_{polar surface}^osmolyte for these osmolytes (Fig. 2). Specifically, as f_{polar surface}^osmolyte increases, the osmolyte interaction with the protein backbone becomes increasingly favorable (i.e., their Δg_tr value decreases). This correlation suggests that the interaction between the protein backbone and osmolyte polar groups is more favorable than the corresponding interaction with nonpolar groups. Furthermore, the correlation suggests that the probability of interaction scales with interactant SA.

Fig. 2.

The polar fraction of osmolyte surface correlates with measured Δg_tr values. Fractional polar SA, f_{polar surface}^osmolyte, is plotted against Δg_tr values from Table 1 for the 10 osmolytes in Fig. 1. The linear regression line (solid line) has a negative slope with a correlation coefficient of 0.88, indicating that backbone/osmolyte interactions become increasingly favorable as osmolytes become increasingly polar.

A Model for Solvent Interactions with the Protein Backbone.

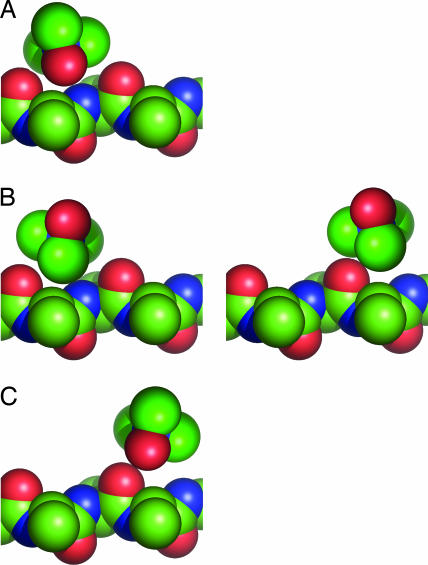
Given the chemical heterogeneity of these osmolytes, what accounts for the observed correlation between f_{polar surface}^osmolyte and Δg_tr? The most direct explanation would be the existence of a universal interaction mechanism. Accordingly, we propose a quantitative model for solvent (water and osmolyte) interactions with backbone polar groups (the amide nitrogen, bearing a partial positive charge, and the carbonyl oxygen, bearing a partial negative charge). Three types of protein/solvent interactions were defined for these two backbone groups: favorable, unfavorable, and neutral, having energies of −1, 1, and 0 kcal/mol, respectively. Favorable interactions occur between polar groups with opposite charges, unfavorable interactions are between polar groups with like charges, and neutral interactions involve nonpolar groups, as illustrated for TMAO in Fig. 3. The backbone amide nitrogen is assigned to have one solvent interaction site, whereas the larger carbonyl oxygen, with its two lone pair electrons, is assigned to have two such sites. However, the overall results do not change appreciably if both backbone groups are treated equivalently (discussed below). Solvent/solvent and backbone/backbone interactions are not included in the model.

Fig. 3.

Illustrating TMAO/backbone interactions. Interactions between an osmolyte, such as TMAO (upper molecule), and the protein backbone (lower structure) can be favorable, neutral, or unfavorable. Favorable interactions are between groups of opposite charge (A), neutral interactions involve at least one nonpolar group (B), and unfavorable interactions are between groups of like charge (C). Atoms are color-coded as in Fig. 1. A large fraction of the TMAO surface is nonpolar, affording more opportunities (i.e., a higher degeneracy) for this osmolyte to realize neutral interactions than either favorable or unfavorable interactions.

A degeneracy term was included to quantify the number of ways of realizing a given backbone/solvent interaction in terms of the area of its available participating interactant surfaces (see Methods). To implement this contribution, polar and nonpolar SAs were calculated for each osmolyte, with polar surface further subdivided into contributions from groups with partial positive (nitrogen) and negative (oxygen) charges (Table 1).

To treat water and osmolytes in a consistent manner, it was also necessary to subdivide a water molecule into polar and nonpolar regions. Although the decomposition of osmolyte surfaces into polar and nonpolar components is uncomplicated, a similar decomposition of water requires a method to evaluate its surface charge distribution. To this end, an ab initio calculation of the water electrostatic potential and electron density was performed, as described in Methods. When this potential is mapped onto a space-filling model (22), distinct regions of positive (blue), negative (red), and neutral (white) charge are apparent (Fig. 1i, top structure). After applying polar and nonpolar cutoff values (see Methods), the water surface is found to have approximately equal regions of positive, negative, neutral charge (37%, 33%, and 29%, respectively; Fig. 1i, lower structure). Although the precise decomposition depends on the chosen electron density and the electrostatic potential threshold (data not shown), our overall results are quite insensitive to this decomposition, as discussed below. Consequently, the total water SA of 30 Ų (the area of a water-sized sphere of radius ≈1.5 Å) was subdivided into three equal-area regions of 10 Ų each.

Comparisons Between Model-Based and Measured Δg_tr Values.

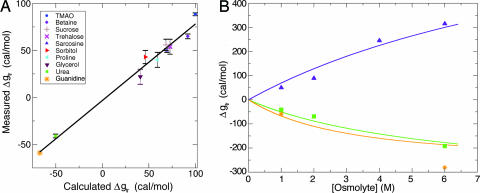
The model was tested by using it to calculate Δg_tr values and comparing them to experimentally measured values. For 1 M osmolyte concentrations, the calculated and measured Δg_tr values are in good agreement (Fig. 4A), with a correlation coefficient of 0.99, a substantial improvement from the corresponding correlation with f_{polar surface}^osmolyte (R = 0.88). Although the slope of the linear regression line is less than unity (slope = 0.81), a slope of 1 with a correlation coefficient of 0.98 can be obtained if interaction energies are set to −1.5, 1.5, and 0 kcal/mol (for favorable, unfavorable, and neutral interactions, respectively). As a further test, Δg_tr values were calculated at osmolyte concentrations beyond 1 M (Fig. 4B, solid lines); these values compare favorably with the corresponding experimental values for sarcosine, urea, and guanidine (Fig. 4B, symbols), those osmolytes for which measurements beyond 1 M are available (13).

Fig. 4.

Comparison between calculated and measured Δg_tr values for osmolytes. (A) Δg_tr values, calculated from the model, are plotted against experimentally determined values from Table 1. Good agreement is apparent. The linear regression line (solid line) is given by Δg_tr^measured = 0.81 Δg_tr^calculated − 3.2, with correlation coefficient 0.99. Data points corresponding to the 10 osmolytes in Fig. 1 are annotated in Inset. (B) Calculated Δg_tr values on higher osmolyte concentrations (>1 M) are plotted against available experimental data for sarcosine (indigo triangles), urea (green squares), and guanidine (orange asterisks). Solid lines were drawn from model-based Δg_tr values, extended beyond 1 M osmolyte concentrations.

The success of the model in predicting Δg_tr values for a diversity of compounds across a range of concentrations is consistent with our hypothesis that interactions between the protein backbone and osmolytes are dominated by their SA and outer-group polarity. Moreover, this conclusion is insensitive to substantial changes in model parameters, as discussed below.

How Robust Are the Calculated Δg_tr Values?

Our model has two adjustable parameters: the polar and nonpolar SAs associated with water, and the interaction energy between solvent and the protein backbone. To assess the sensitivity of calculated Δg_tr values to these parameters, both were varied extensively and Δg_tr values were recalculated.

Positive, negative, and neutral water SAs were simultaneously randomized within a 5- to 15-Ų interval, with solvent interaction energies fixed at their original values. The resulting Δg_tr values remain in good agreement with the measured values (Fig. 6, which is published as supporting information on the PNAS web site); ≈90% of the calculated Δg_tr values have correlation coefficients with measured values that exceed 0.80.

In another test, interaction energies were assigned random values in the range 0.5–5 kcal/mol (multiplied by −1 for favorable interactions), with neutral interaction energy and the polar and nonpolar water SAs held fixed at their original values. The correlation with measured Δg_tr values was recalculated for each new value (Fig. 7, which is published as supporting information on the PNAS web site), and again, model-based and measured Δg_tr values were found to be in good agreement; all correlation coefficients exceed 0.80.

As a final test, the correlation between model-based and measured Δg_tr values was recalculated under the alternative assumption that the backbone carbonyl oxygen provides only one solvent interaction site, not two. Water surface decomposition and interaction energies were held fixed at their original values. Still, model-based and measured Δg_tr values remain highly correlated (Fig. 8, which is published as supporting information on the PNAS web site), although the correlation coefficient is reduced to 0.86.

Preferential Osmolyte Interactions with the Protein Backbone.

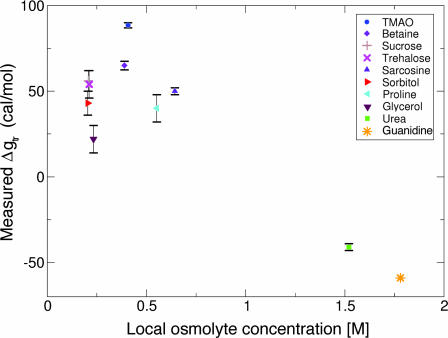
Characteristically, stabilizing/destabilizing osmolytes are preferentially excluded/accumulated at the protein surface, respectively (14, 15, 23). To test this aspect of the model, the local concentration of osmolytes at backbone interaction sites was calculated for a 1 M osmolyte solution (see Methods). As shown in Fig. 5, stabilizing osmolytes are preferentially excluded from backbone polar groups, whereas denaturing osmolytes are preferentially accumulated there. In the model, the molecular basis of these preferential interactions is rooted in solvent/backbone interactions. Stabilizing osmolytes, such as TMAO, are preferentially excluded from the backbone because water is more likely than TMAO to interact favorably with backbone polar groups. Conversely, destabilizing osmolytes, such as urea, are preferentially accumulated near the backbone because they have a stronger propensity to interact with the backbone than water. However, it should be noted that the model does not take nonpolar backbone regions into account, and interactions around these regions can also contribute to the actual local osmolyte concentration.

Fig. 5.

Protecting/denaturing osmolytes are preferentially depleted/accumulated at the protein backbone. Concentration of osmolyte around the backbone in a 1 M osmolyte solution plotted against measured Δg_tr values from Table 1. Data points corresponding to the 10 osmolytes in Fig. 1 are annotated in Inset. The local osmolyte concentration is given by the scaled difference between 〈O_pref〉 and 〈O_bulk〉, described in Methods. It is apparent that the backbone concentration of protecting osmolytes (Δg_tr > 0) is comparatively depleted ([osmolyte] < 1.0 M), whereas that of denaturing osmolytes (Δg_tr < 0) is comparatively enriched ([osmolyte] > 1.0 M).

Discussion

The model presented here establishes a connection between bulk thermodynamic quantities and the molecular interactions that give rise to these quantities. In particular, it was developed to explain the experimentally determined backbone transfer free energies from water to osmolyte in terms of interactions between the protein backbone and water or osmolyte molecules. The model was validated by using it to predict significant, experimentally observed behavior. In addition, the model predicts that the free energy change for folding/unfolding will be linearly dependent on osmolyte concentration or approximately so, and for both protectants and denaturants, consistent with Pace’s linear extrapolation model (9, 10). Our model also correctly predicts m values (dΔg_tr/d[osmolyte]) of opposite sign and approximately equal magnitude for proteins that are either forced to fold by sarcosine or denatured by urea, thereby accounting for the wide range of effects that natural osmolytes can exert on protein stability (12). Finally, Δg_tr values calculated by using the model correlate extremely well with experimental values (R = 0.99), illustrating that the relevant water–osmolyte–backbone energies are captured by the model.

Protein/osmolyte interactions are conspicuously weak, and in such cases, classical binding models are notoriously deficient (24). In particular, urea/backbone interactions would have apparent binding constants slightly greater than unity (K_binding ≈ 1.2) (3), whereas protecting osmolyte/backbone interactions would have apparent binding constants slightly less than unity (K_binding ≈ 0.8). In this weak-binding regime, free energy effects are ostensibly additive because neither type of osmolyte occupies a significant fraction of the backbone surface, so there is essentially no competition for backbone binding sites. Such additivity is observed in experiments (25) and is consistent with the model.

Many previous studies have related SA calculations to thermodynamic quantities associated with protein folding (26–32), motivated by the early observation that the transfer of nonpolar groups from organic to aqueous solvent is accompanied by an anomalous change in heat capacity, ΔCp (33). The observed correlation between ΔCp and nonpolar surface is often interpreted to mean that water around nonpolar surfaces differs structurally and thermodynamically from water in bulk solution (34). In contrast, the model proposed here focuses on solvent interactions with the protein backbone, and SAs are only used here to estimate the binding-competent fraction of interacting molecules.

Several other types of solvent interactions affecting protein stability are neglected in our model, including crowding and excluded volume (35–37), the structure of water in osmolyte solutions (38, 39), side chain/solvent interactions, and binding situations in which a large osmolyte molecule can occlude more than one backbone unit. In addition, the model treats all nitrogens and oxygens as equally polar, an obvious simplification. However, despite such simplicity, the model captures key thermodynamic aspects of osmolyte behavior in a parameter-insensitive fashion. Therefore, it seems likely that the model’s anchoring suppositions, solvent/protein interactions that depend on polarity and SA, are primarily responsible for the osmolyte effect in proteins.

Methods

Atom coordinates for TMAO, betaine, sucrose, trehalose, sarcosine, sorbitol, proline, glycerol, urea, and guanidine were obtained from the HICUP database (40). Their solvent accessible polar and nonpolar SAs were calculated by using PyMOL (41) with a probe radius of 1.4 Å (Table 1). Guanidine differs from other osmolytes investigated here because it is introduced into solution as a salt, guanidinium hydrochloride. To correct for the chloride ion associated with guanidine, a small, negatively charged surface of 30 Ų was added to the guanidine SA, although this addition does not dramatically change its calculated Δg_tr value (these values are −67 and −62 cal/mol with and without chloride ion addition, respectively).

The surface of a water molecule was defined at a threshold electron density of ρ = 0.005, giving a molecular volume of 11.5 ų (approximately the volume of a 1.5-Å sphere). The surface of water was decomposed into polar, nonpolar, and neutral regions by calculating the electrostatic potential and mapping it onto this surface. The thresholds used to delimit polar and nonpolar regions were defined by the boundary where the potential decays to 1/e of its minimum and maximum values, −0.023 and 0.037 e/Å, respectively. The neutral region was then defined as the complement to these two regions. Both the electrostatic potential and the electron density were calculated ab initio by using CPMD (42).

The average energy of the protein backbone in various osmolyte solutions was calculated by using a statistical mechanics model in which the backbone has three interaction sites: one at the amide nitrogen and two at the carbonyl oxygen; these sites are represented by the indices i, j, and k, respectively. At each interaction site, the solvent (either water or osmolyte) can present a positively (+), neutral (o), or negatively charged (−) surface. Accordingly, the indices i, j, and k can take the values +, o, or −, resulting in a total of 3³ = 27 possible microstates. Interactions between the backbone and solvent are assigned energies of −1, 1, and 0 kcal/mol corresponding to interactions between opposite, like, or uncharged groups, respectively. The interaction energies for each site are assumed to be additive and independent. These microstates and their associated energies and degeneracies are enumerated in Table 2.

Table 2.

Solvent interactions with the protein backbone

Interaction site*			Microstate†
N, i	O1, j	O2, k	E, kcal/mol	Ω
+	+	+	−1	Ω+++
+	+	o	0	Ω++o
+	+	−	1	Ω++−
+	o	+	0	Ω+o+
+	o	o	1	Ω+oo
+	o	−	2	Ω+o−
+	−	+	1	Ω+−+
+	−	o	2	Ω+−o
+	−	−	3	Ω+−−
o	+	+	−2	Ωo++
o	+	o	−1	Ωo+o
o	+	−	0	Ωo+−
o	o	+	−1	Ωoo+
o	o	o	0	Ωooo
o	o	−	1	Ωoo−
o	−	+	0	Ωo−+
o	−	o	1	Ωo−o
o	−	−	2	Ωo−−
−	+	+	−3	Ω−++
−	+	o	−2	Ω−+o
−	+	−	−1	Ω−+−
−	o	+	−2	Ω−o+
−	o	o	−1	Ω−oo
−	o	−	0	Ω−o−
−	−	+	−1	Ω−−+
−	−	o	0	Ω−−o
−	−	−	1	Ω−−−

The 27 microstates and their associated energies and degeneracies.

*The single amide nitrogen and two carbonyl oxygen backbone interaction sites are indicated by N, O₁, and O₂, respectively. Solvent interactions with these sites are given by the charge of the interacting solvent surface: positive (+), negative (−), and neutral (o), and i, j, and k indices are varied over the range of values for these interactions.

^†E is the energy of a given microstate, and Ω is its degeneracy.

The degeneracy of a solvent interaction at a particular backbone interaction site reflects the number of energetically equivalent ways of making that interaction. In our model, the degeneracy is given by the water or osmolyte SA that can participate in the interaction. Given that the three backbone interaction sites (i, j, and k) are independent, the total degeneracy (Ω_ijk) of a specific microstate, consisting of a +, o, or − solvent interaction at sites i, j, and k, will be the product of the degeneracies, as represented by their SAs, at individual interaction sites

These SAs will have a contribution from water (SA_w,i, SA_w,j, and SA_w,k) and a contribution from osmolyte (SA_o,i, SA_o,j, and SA_o,k) that depends on the osmolyte concentration. At Y molar:

In the model, +, o, and − water SAs are equal (10 Ų), and the corresponding osmolyte SAs are given in Table 1. The SA calculations treat the activity of water as a constant (i.e., that molarity of water in osmolyte solutions of varying concentration is ≈55.5 M), a plausible approximation at the low cosolvent concentrations used here.

The probability of any given microstate is given by

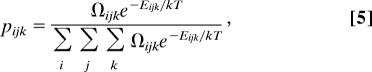where k is Boltzmann’s constant and T is 298.15 K, the temperature at which Δg_tr values were measured experimentally. These probabilities can be used to calculate the average energy of the system

with Δg_tr values given by the difference between the average system energy at 0 and 1 M osmolyte concentrations. The average occupancy of osmolytes on the backbone interaction sites can also be calculated as

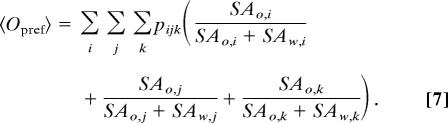This value can be compared with the expected osmolyte occupancy based solely on the bulk solution concentration (i.e., no preferential interactions with the three backbone interaction sites)

The relative difference between 〈O_pref〉 and 〈O_bulk〉 yields a local osmolyte concentration when scaled to molarity.

All numerical calculations were performed in Python (www.python.org).

Abbreviations

TMAO

trimethylamine N-oxide

SA

surface area.