Abstract
Many diverse infectious diseases exhibit seasonal dynamics. Seasonality in disease incidence has been attributed to seasonal changes in pathogen transmission rates, resulting from fluctuations in extrinsic climate factors. Multi-strain infectious diseases with strain-specific seasonal signatures, such as cholera, indicate that a range of seasonal patterns in transmission rates is possible in identical environments. We therefore consider pathogens capable of evolving their ‘seasonal phenotype’, a trait that determines the sensitivity of their transmission rates to environmental variability. We introduce a theoretical framework, based on adaptive dynamics, for predicting the evolution of disease dynamics in seasonal environments. Changes in the seasonality of environmental factors are one important avenue for the effects of climate change on disease. This model also provides a framework for examining these effects on pathogen evolution and associated disease dynamics. An application of this approach gives an explanation for the recent cholera strain replacement in Bangladesh, based on changes in monsoon rainfall patterns.
Keywords: pathogen evolution, seasonal drivers, extrinsic forcing, cholera, disease dynamics, adaptive dynamics
1. Introduction
Seasonal disease fluctuations can be caused by many factors, including seasonally heightened host susceptibility resulting from seasonal stressors, changes in contact rates resulting from school terms in the case of childhood diseases (Fine & Clarkson 1982) and seasonal changes in pathogen transmission rates resulting from climate variation (Spira 1981). When seasonality in disease is owing to seasonal changes in pathogen transmission rates, the isolation of the dominant seasonal drivers becomes a priority for understanding and mitigating the effects of the disease. Linking seasonal variables (e.g. temperature and rainfall) to seasonal fluctuations in pathogen transmission rates and disease incidence is therefore an active area of current research in disease ecology (Glass et al. 1982; Colwell 1996; Bradbury 2003).
The effects of climate change on human and wildlife diseases are inextricably linked to mean trends in climate conditions, as well as to seasonal changes in environmental drivers. Many diseases are expected to increase in range and severity with projected climate changes. The underlying reasons for these responses include increases in pathogen development and transmission rates and the relaxation of pathogen overwintering restrictions that accompany increases in mean global air temperatures (Coakley et al. 1999; Harvell et al. 2002). Changes in the magnitude or the seasonal timing of environmental drivers, however, can be as important as mean trends in affecting disease dynamics and the frequency of disease outbreaks. Many of the significant projected climate changes are expected to be regional in scale (IPCC 2001) and to involve changes in seasonal climatic fluctuations, with the effects of these changes on the host population's health being pathogen-specific and largely unknown.
As the ecological effects of seasonal drivers and climate change become more fully understood, how pathogens adapt to their seasonal environments and to climate change must also be considered (Palumbi 2001). Many pathogens have short generation times and high mutation rates, resulting in an ability to evolve on the time-scale of decades, making this consideration particularly important. Here, we present a theoretical framework that predicts pathogen adaptation to seasonal climate forcing. We then use this model to analyse the evolutionary consequences of climate change on seasonal disease dynamics, where climate change is mediated through changes in seasonal climate patterns. In our examples, we explicitly use seasonal climate patterns and pathogen transmission rates motivated by the effect of rainfall on cholera dynamics in Bangladesh. Supported by calculations of seasonal cholera reproductive rates, these simulations provide an explanation for the recent cholera strain replacement in Bangladesh that invokes decadal changes in monsoon rainfall patterns.
2. The model
(a) Host–pathogen dynamics
We consider a host–pathogen system in which the pathogen is a microparasite that induces temporary immunity in the host, governed by susceptible–infected–recovered–susceptible (SIRS) population dynamics. Many diseases are seasonally driven by multiple extrinsic drivers, but for simplicity, we model just one seasonal driver that affects the transmission rate of the pathogen. The disease dynamics are given by:
| 2.1 |
where S, I and R are the number of individuals who are susceptible, infected and recovered (and immune), respectively. The total host population size is N and is kept constant in this model, with S+I+R=N. The mode of transmission is assumed to be frequency-dependent (de Jong et al. 1995; McCallum et al. 2001). The seasonally fluctuating transmission rate βs depends on the environmental driver P. This dependence can be modelled using a functional relationship, with transmission being highest at a certain value of P, Popt, and progressively lower further away from this value. We use a parabolic function to describe the dependence of transmission on the seasonal driver:
| 2.2 |
where βmax is the maximum transmission of the pathogen, occurring when the seasonal driver has a value of P=Popt. The curvature of the parabola, c, is necessarily negative and quantifies the sensitivity of transmission to P. A pathogen's seasonal phenotype is defined as its transmission rate response to P and is fully specified by βmax and c. A trade-off between climate sensitivity c and maximum transmission rate βmax is assumed, such that a pathogen with a high βmax is more sensitive to climatic fluctuations than a pathogen with a lower βmax. We provide empirical evidence for this trade-off in a later section, with an application of this model to two cholera strains in Matlab, Bangladesh. A continuous range of seasonal strategies is then present that describes a pathogen's response to the environmental driver (figure 1a). The seasonal phenotype's spectrum spans from a seasonal ‘specialist’ pathogen (high maximum transmission rate, high sensitivity to seasonal conditions) to a seasonal ‘generalist’ pathogen (low maximum transmission rate, low sensitivity to seasonal conditions). The strength of the trade-off between climate sensitivity and maximum transmission rate is controlled by a parameter γ, with higher values of γ increasing the strength of the trade-off, as in previous studies (Egas et al. 2004):
| 2.3 |
where βmax(g) and βmax(s) refer to the maximum transmission rates for generalist and specialist strains, respectively, and c(g) and c(s) refer to the transmission sensitivity to P for generalist and specialist strains, respectively. Differences in trade-off strength γ can change the type of phenotypic evolution, a point to which we will return.
Figure 1.
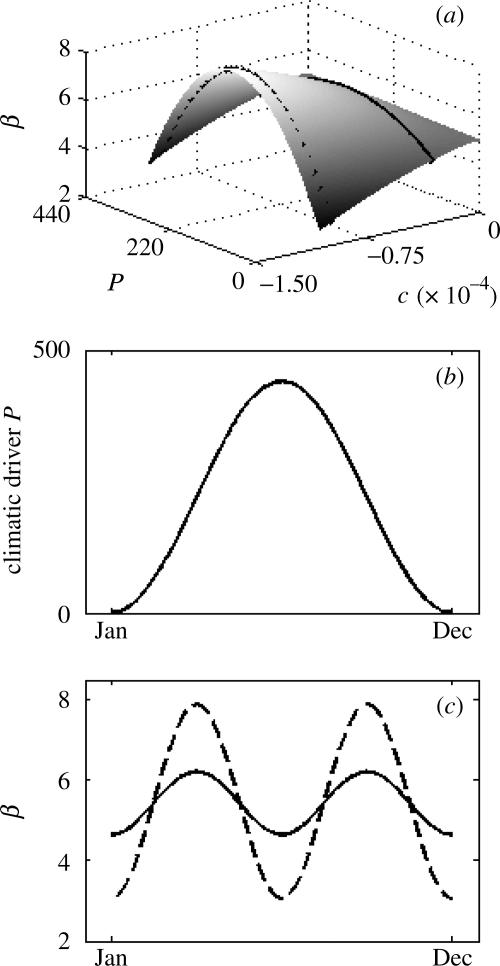
Seasonal forcing of the pathogen transmission rate, β. (a) A pathogen's transmission rate is a function of the climatic conditions it experiences (here, P) and its seasonal phenotype. Strains varying in their seasonal phenotypes are identified by the continuous variable c, which quantifies the degree of sensitivity to seasonal fluctuations (see equation (2.2)). Pathogens with no sensitivity to seasonal variability (c=0) are seasonal generalists, while pathogens with high sensitivity (c<<0) are seasonal specialists. Transmission rate β, for a given climatic condition, is given by equations (2.2) and (2.3), with Popt=220, c(g)=0, c(s)=−1.074×10−4, βmax(g)=5, βmax(s)=8 and γ=0.85. Pathogens with seasonal phenotypes shown in (c) are explicitly marked. (b) Seasonal variability in the extrinsic driver P. According to equation (2.5), P fluctuates seasonally, with Pm=220 and A=220. (c) Seasonal fluctuations in β for two different strains, for the climatic fluctuations shown in (b). The strain with the more generalist seasonal phenotype (c=−3.223×10−5) has lower variability in β (solid line), while the strain with the more specialist phenotype (c=−9.987×10−5) has higher variability (dashed line).
(b) Evolutionary analyses
The adaptation of a pathogen to its seasonally fluctuating environment can now be addressed within the context of this model. We use a game theoretic adaptive dynamics approach to this problem, instead of the R0 maximization technique widely used in addressing pathogen evolution (May & Anderson 1983). The reason for using this alternative approach lies in the limitations of R0 maximization in general (Dieckmann 2002), and more particularly in its use for studying seasonal diseases. An adaptive dynamics framework follows the evolution of a continuous trait through the sequential replacement of resident strains with phenotypically local mutants (Geritz et al. 1998). Several previous studies have used adaptive dynamics or similar approaches to address the evolution of virulence and resistance traits in host–pathogen systems (Boots & Haraguchi 1999; Koella & Doebeli 1999). Here, the specific phenotypic character subject to evolution is the pathogen's sensitivity to seasonal drivers.
Using standard adaptive dynamics notation, the ability of a mutant pathogen y in a host population with a resident pathogen x is given by the invasion fitness f( y, x):
| 2.4 |
where βs(y, P) is the seasonally driven transmission rate of the mutant strain, α(y) is the rate of recovery from an infection with the mutant strain (hereafter just α since the duration of infection does not differ between the strains), and S(x, t)/N is the seasonally varying fraction of susceptible individuals in a host population with resident pathogen x. A positive invasion fitness indicates an ability to invade when rare, whereas a negative invasion fitness indicates an invasion failure (Metz et al. 1992). We can now consider the climatic driver P to vary seasonally according to:
| 2.5 |
with time t measured in years (figure 1b). Given the seasonal fluctuations in the environment and a specification of the transmission response to these seasonal fluctuations, the seasonal transmission fluctuations throughout a year can be evaluated for any of the strains (see figure 1c for two examples). The invasion fitness expression (equation (2.4)) can then be rewritten by substituting the time-varying seasonal variable P (equation (2.5)) into the mutant's seasonal transmission expression (equation (2.2)). Any other seasonal fluctuations of the driver can be similarly substituted. Owing to the time-dependent nature of the invasion fitness expression (equation (2.4)), a general analytical approach for finding evolutionary singular points and their stabilities is intractable except in limited cases, such as when the resident strain is a complete generalist (see Electronic Appendix) or when there is no seasonal variability. The following results therefore rely on numerical simulations.
Several studies have already highlighted the importance of trade-off structure when the evolution of constrained traits is considered (Bowers & White 2002; de Mazancourt & Dieckmann 2004; Egas et al. 2004). Similarly, the structure of the trade-off between maximum transmission rate βmax and transmission sensitivity to climatic fluctuations c in this model, influences the stability of the evolutionary singular points of the pathogen's seasonal phenotype (see Electronic Appendix figure and text). To illustrate the simplest case scenario, we limit our following analyses of pathogen adaptation to climate change with a trade-off structure that results in continuously stable strategies, although similar analyses can be performed for other trade-off structures.
(c) Pathogen adaptation to climate change
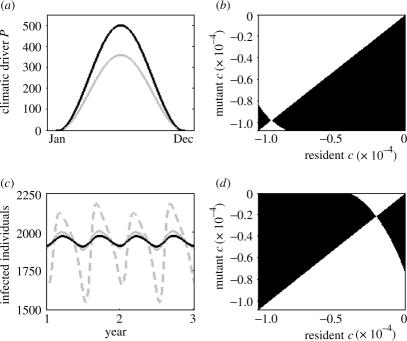
Given seasonal fluctuations in a pathogen's climatic driver and a particular trade-off structure, the presented model can predict the evolution of a pathogen's seasonal phenotype. It can also therefore be used to address the question of how a pathogen's seasonal phenotype will evolve to changes in seasonal climate. Consider P as the extrinsic driver of the disease again, with current seasonal fluctuations shown in figure 2a. A pathogen with specific infection characteristics would evolve a highly specialized seasonal phenotype (figure 2b) in this variable environment. The population dynamics of individuals infected with this continuously stable strain are shown in figure 2c. As the climate changes to projected seasonal fluctuation levels (figure 2a), the dynamics of infected individuals would change on an ecological time-scale, with more extreme seasonality evident in disease cases (figure 2c). However, when the evolution of the pathogen's seasonal phenotype is also considered with the change in climate, the pathogen becomes a more generalist strain (figure 2d). The dynamics of infected individuals after strain adaptation to climate change then more closely reflect the dynamics before the change in seasonal environmental patterns (figure 2c). As this example illustrates, increased climate variability resulting in further deviations away from the optimal environmental conditions for pathogen transmission thereby drives the pathogen to adapt to a more generalist seasonal phenotype.
Figure 2.
Climate change and the evolution of the seasonal phenotype. (a) Current (grey) and projected (black) climatic fluctuation scenarios. Seasonal climatic fluctuations follow equation (2.5), with Pm=180 and A=180 for the current scenario and Pm=250 and A=250 for the projected scenario. For these scenarios, Popt=175. (b) A pairwise invasibility plot (PIP) for the seasonal phenotype for the current climate. (c) Disease dynamics of infected individuals, shown over two full years. Disease dynamics for the current climate scenario are shown in solid grey with the resident strain having the continuously stable seasonal phenotype shown in (b). The annual number of disease cases is 681 752. Disease dynamics for the projected climate scenario are in dashed grey, with this same resident strain. The annual number of disease cases is expected to be 670 897, a decrease of 1.59%. Disease dynamics for the projected scenario are in black, after the strain has evolved to its new continuously stable seasonal phenotype shown in (d). The annual number of disease cases is expected to be 678 852, an increase of 1.19% from the expected disease burden considering only ecological responses of the pathogen (an overall decrease in only 0.43% from the original disease burden before climate change). (d) A PIP for the seasonal phenotype for the projected climate scenario. Invasion fitness values f(y, x) are positive in the black areas and negative in the white areas in both PIPs, and are obtained through numerical simulation of equation (2.4). Trade-off strength γ and both βmax and c values for the specialist and generalist phenotypes are given in figure 1. The epidemiological parameters in these simulations are α=1/7, δ=1/28 and N=10 000, according to the notation of equation (2.1).
Considering pathogen adaptation allows for a further analysis of the influence of pathogen evolution on disease burden. In the example above, increases in the magnitude of the environmental driver during the summertime would be expected to decrease disease incidence by lowering the transmission of the pathogen in the summertime. However, if we allow for pathogen adaptation, it becomes evident that just by considering the ecological effects of climate change, we would underestimate the expected disease burden on the host population (figure 2, legend). The effects of considering pathogen evolution for other seasonal climate change scenarios were also analysed (results not shown). Even when the ecological effect of the considered climate change scenario is to immediately increase disease burden, results indicate that cumulative incidence is greater when pathogen evolution is considered than when only the ecological responses are taken into account.
(d) Climate change and cholera strain replacement in Bangladesh
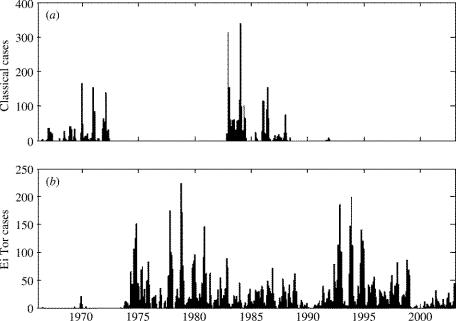
As an application of this seasonal phenotype model, cholera strain replacement in Matlab, Bangladesh is considered. The cholera data were obtained from a surveillance programme by the International Centre for Diarrhoeal Disease Research (ICDDR, B) and consist of monthly symptomatic cases from Matlab, Bangladesh. Cholera is an infectious disease endemic to Bangladesh, caused by the bacterium Vibrio cholerae. Strains within the 01 serogroup of cholera are designated as being either of the Classical or the El Tor biotype. The Classical strain was the dominant pathogenic strain until the 1970s, when the mutant El Tor strain invaded the resident population and replaced the Classical strain (figure 3). Both cholera biotypes exhibit pronounced seasonality in disease incidence, although their seasonal signatures differ from each other (Spira 1981; Glass et al. 1982).
Figure 3.
Monthly cholera cases in Matlab, Bangladesh for the period 1966–2002, illustrating that the classical biotype has been replaced by the El Tor biotype. (a) Time-series of the Classical biotype. (b) Time-series of the El Tor biotype. Although the Classical biotype transiently returned in the mid-1980s (perhaps owing to the large 1982/1983 El Niño event), it is unlikely that another transient comeback will occur: the Classical strain appears absent from the aquatic environment in the Matlab surveillance area (Islam et al. 1994) and was not found in clinical or aquatic isolates sampled from surrounding areas (Zo et al. 2002).
Given that the Classical and El Tor biotypes differ in their seasonal case signatures, we can explore whether seasonal differences in transmission rates might explain this strain replacement. We can approximate the fluctuations in seasonal transmission rates by looking at the biotypes' mean reproductive rates from one month to the next (figure 4a). Seasonal fluctuations in reproductive rates indicate that Classical behaves as a seasonal specialist, while El Tor is more of a seasonal generalist. Maximum transmission occurs in the spring and in the autumn for both biotypes, with Classical having higher maximum transmission than El Tor at both of these points. However, during the summer months of sub-optimal environmental conditions, Classical has much lower transmission than does El Tor.
Figure 4.
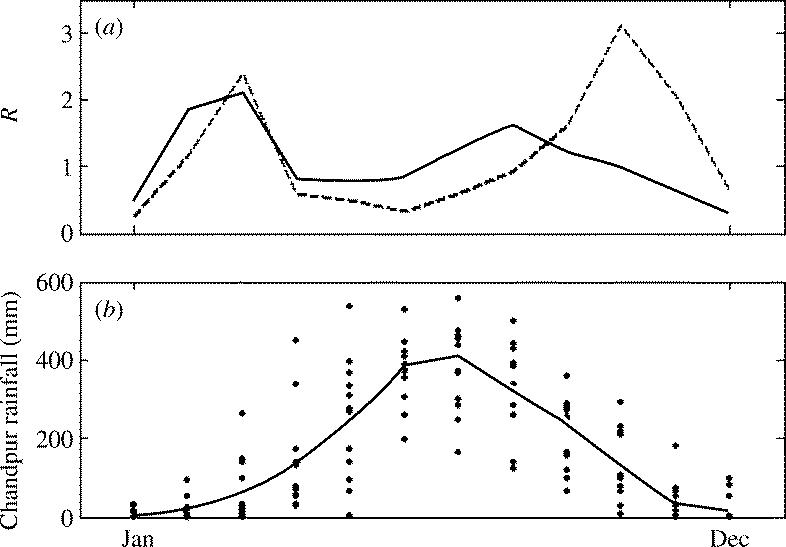
Seasonal reproductive rates and rainfall patterns. (a) Monthly reproductive rates R for the Classical and El Tor biotypes. Reproductive rates were obtained by dividing the next month's number of biotype-specific cholera cases by the current month's case number, and then geometrically averaging between all month-specific data points. Classical reproductive rates are shown in dashed black; El Tor reproductive rates are shown in solid black. Periods of local extinctions were problematic in providing reproductive rates. In the case of a disease fade-out, the reproductive rate was estimated conservatively by 1/(the current month's case number), while recolonizations and consecutive absences of disease cases were excluded from the calculations. Biotype-specific frequencies of summer fade-outs also indicated that Classical reproductive rates were lower in the summer than were El Tor's: temporary Classical fade-outs occurred in nine summers out of the 13 years during which the strain was present, while temporary El Tor fade-outs occurred in only four summers out of the 28 years it was present. (b) Monthly rainfall levels (points) and mean monthly rainfall fluctuations (solid line) at the Chandpur rainfall station, located near Matlab, Bangladesh, averaged over the years 1966–1979. Rainfall data were collected and made available by the United Nations Development Programme/Food and Agriculture Organization of the United Nations (FAO 1988).
Because cholera has a faecal–oral disease transmission route, seasonal changes in climatic factors can affect the transmission rate of the pathogen. Linking fluctuations in transmission rates and reproductive rates directly to climatic drivers is difficult because many factors, such as water salinity and pH, river discharge, rainfall, temperature and plankton abundances, are all candidates for affecting cholera's seasonality (Bouma & Pascual 2001; Sack et al. 2003). Further difficulties in isolating cholera's seasonal drivers arise from the covariation of many of these factors. However, the decrease in cholera cases during the summer months for both biotypes is typically explained as the result of a dilution effect by the monsoon rains and the concurrent reduction in water salinity levels (figure 4a,b; Miller et al. 1984; Pascual et al. 2002).
Climate change over the next 50 years in Bangladesh is projected to affect monsoon rainfall patterns, with pronounced increases in rainfall during the months of July and August (Ahmed & Alam 1999). This trend is already apparent: the quantity of surface water in Matlab is affected by river discharge levels, for which there has been an increasing trend over the period 1975–2000, associated with the increasing trend in rainfall in northeast India (a measure of regional rainfall) over this period (Koelle et al. submitted). With the increased severity of the monsoon rains, the relative fitness of the generalist El Tor biotype over the Classical biotype is enhanced. Recent strain replacement may therefore be owing to the fitness advantage gained by El Tor from changes in rainfall fluctuations.
3. Discussion
We have shown that a pathogen's sensitivity to environmental fluctuations can be considered a phenotypic character trait subject to evolution. Considering the evolution of host–pathogen systems with respect to this trait will improve our ability to forecast disease burden and predict disease dynamics when changes in climate occur. We have shown that increased climatic variability will result in pathogens evolving reduced sensitivity to climate fluctuations. Whether changes in seasonal climate patterns can alter not only the degree of climate sensitivity but also the nature of the evolutionary singular strategy has yet to be determined, with direct implications for evolutionary branching and strain diversity. Alternative evolutionary approaches such as quantitative genetic models (Day & Proulx 2004) may also provide fruitful directions for future research on climate change implications and pathogen evolution, allowing for the merging of ecological and evolutionary time-scales.
An application to cholera indicated that strains may differ in their seasonal phenotypes, and that these differences, together with changes in monsoon patterns, may explain the reversal of competitive dominance of one strain over another. El Tor, a seasonal generalist, seems to gain an advantage over the Classical strain, a seasonal specialist, when monsoon rainfall becomes more extreme. Ecological knowledge about the relative hardiness of the biotypes in the aquatic environment is in agreement with this seasonal phenotype classification of the strains (Spira 1981). El Tor is known to be more resilient to fluctuations in water quantity and quality, as is evident by the less pronounced seasonal variability of its reproductive rates. El Tor's resiliency has an established mechanistic basis: unlike the Classical biotype, it expresses vps (Vibrio polysaccharide) genes responsible for the production of an exopolysaccharide that allows it to form a biofilm on abiotic surfaces, facilitating its environmental persistence (Reidl & Klose 2002). However, the expression of this exopolysaccharide also seems to inhibit intestinal colonization, leading to reduced infectivity and virulence (Watnick et al. 2001). The Classical biotype therefore has a larger chance of infecting a susceptible host, given contact. This molecular difference therefore establishes the trade-off between maximum transmission and sensitivity to climatic fluctuations.
We have illustrated the theoretical model in a largely qualitative application to cholera. Whether the transition from Classical to El Tor is owing to the sign reversal of the strains' invasion fitnesses from the historical period to today's rainfall environment is difficult to assess quantitatively. Although time-series analysis methods exist that fit transmission rates and reconstruct the level of susceptibles in the host population (Koelle & Pascual 2004), the cholera time-series includes interannual variability in disease cases (causing interannual fluctuations in the fraction of susceptibles), climatic forcing at interannual frequencies (affecting transmission rates between years, not simply within years; Koelle et al. submitted), long-term trends, and stochastic extinctions (i.e. fade-outs). These factors make the quantification of the invasion fitnesses difficult. Furthermore, whether interannual disease variability and stochastic extinctions can affect the evolution of the seasonal phenotype has yet to be established; a recent study indicates that when population oscillations become large, the evolutionary behaviour of the system can change, despite a fixed underlying trade-off curve (A. White, personal communication).
We have presented the case of a pathogen evolving its seasonal phenotype, as defined by its degree of seasonal specialization and associated maximum transmission rate. An alternative or complementary strategy may be for a pathogen to evolve Popt, its optimal transmission environment. Whether evolution of this trait is possible and what trade-offs would underlie these changes are open questions. The degree to which evolution of Popt occurs relative to the evolution of climatic sensitivity, c, will likely be affected by the way in which the climate changes, as well as genetic constraints. Pathogens may respond to directional climate change, such as an increase in mean yearly temperatures, by primarily evolving Popt, while they may respond to increased variability in climate by primarily evolving c. In the case of cholera, El Tor may then differ from Classical by not only being more of a generalist, but also by having its maximum transmission at a higher precipitation level. This hypothesis is supported by El Tor's earlier autumn peak in reproduction rate (figure 4a), occurring when precipitation is still moderately high (figure 4b). However, if this were the case, a delay in El Tor reproduction would be expected in the spring, a pattern that we do not see. In fact, while the reduction in transmission rate in the spring has been explained by the onset of the monsoons, the occurrence of the fall peak eludes a complete explanation (Bouma & Pascual 2001). The possibility of El Tor having its maximum transmission at higher water levels is therefore only partly supported.
This model specifically focused on the evolutionary responses of pathogens to seasonal climate changes. Changes in seasonal climate patterns will necessarily also affect host susceptibility and host contact patterns. An understanding of the social dynamics of the host and the plasticity of host behaviours is therefore crucial in accurately predicting disease dynamics. Combining host behavioural changes with pathogen evolution when considering climate change is, therefore, a natural extension to this work.
Acknowledgments
We thank Mobinul Islam for the maintenance of the cholera records and members of the NCEAS Seasonality and Disease working group for discussions and feedback. We also thank two anonymous referees for their helpful suggestions. This work was conducted as part of the Seasonality and Disease Working Group supported by the National Centre for Ecological Analysis and Synthesis, a Centre funded by NSF (grant no. DEB-0072909), the University of California, and the Santa Barbara campus. We also thank University of Michigan's Rackham Graduate Program for a travel grant to KK and a National Oceanic and Atmospheric Administration grant ( Joint Program on Climate Variability and Human Health, with Electric Power Research Institute-National Science Foundation-Environmental Protection Agency-National Aeronautics and Space Administration) to MP.
Supplementary Material
References
- Ahmed A.U, Alam M. Development of climate change scenarios with general circulation models. In: Huq S, Karim Z, Asaduzzaman M, Mahtab F, editors. Vulnerability and adaptation to climate change for Bangladesh. Kluwer Academic Publishers; Dordrecht: 1999. pp. 14–20. [Google Scholar]
- Boots M, Haraguchi Y. The evolution of costly resistance in host–parasite systems. Am. Nat. 1999;153:359–370. doi: 10.1086/303181. [DOI] [PubMed] [Google Scholar]
- Bouma M.J, Pascual M. Seasonal and interannual cycles of endemic cholera in Bengal 1891–1940 in relation to climate and geography. Hydrobiologia. 2001;460:147–156. [Google Scholar]
- Bowers R.G, White A. The adaptive dynamics of Lotka--Volterra systems with trade-offs. Math. Biosci. 2002;175:67–81. doi: 10.1016/s0025-5564(01)00091-8. [DOI] [PubMed] [Google Scholar]
- Bradbury J. Beyond the fire-hazard mentality of medicine: the ecology of infectious diseases. PLoS Biol. 2003;1:148–151. doi: 10.1371/journal.pbio.0000022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coakley S.M, Scherm H, Chakraborty S. Climate change and plant disease management. Annu. Rev. Phytopathol. 1999;37:399–426. doi: 10.1146/annurev.phyto.37.1.399. [DOI] [PubMed] [Google Scholar]
- Colwell R. Global climate and infectious disease: the cholera paradigm. Science. 1996;274:2025–2031. doi: 10.1126/science.274.5295.2025. [DOI] [PubMed] [Google Scholar]
- Day T, Proulx S.R. A general theory for the evolutionary dynamics of virulence. Am. Nat. 2004;163:E40–E63. doi: 10.1086/382548. [DOI] [PubMed] [Google Scholar]
- de Jong M, Diekmann O, Heesterbeek H. How does transmission of infection depend on population size? In: Mollison D, Moffatt H.K, editors. Epidemic models: their structure and relation to data. Cambridge University Press; 1995. pp. 84–94. [Google Scholar]
- de Mazancourt C, Dieckmann U. Trade-off geometries and frequency-dependent selection. Am. Nat. 2004;164:765–778. doi: 10.1086/424762. [DOI] [PubMed] [Google Scholar]
- Dieckmann U. Dynamics of pathogen–host interactions. In: Dieckmann U, Metz J.A.J, Sabelis M.W, Sigmund K, editors. Adaptive dynamics of infectious diseases: in pursuit of virulence management. Cambridge University Press; 2002. pp. 39–59. [Google Scholar]
- Egas M, Dieckmann U, Sabelis M.W. Evolution restricts the coexistence of specialists and generalists: the role of trade-off structure. Am. Nat. 2004;163:518–531. doi: 10.1086/382599. [DOI] [PubMed] [Google Scholar]
- FAO 1988 Land resources appraisal of Bangladesh for agriculture development. Report 3: land resource data base, volume 1:climatic data base United Nations development programme/Food and Agriculture Organization of the United Nations.
- Fine P.E, Clarkson J.A. Measles in England and Wales—I: an analysis of factors underlying seasonal patterns. Int. J. Epidemiol. 1982;11:5–14. doi: 10.1093/ije/11.1.5. [DOI] [PubMed] [Google Scholar]
- Geritz S.A.H, Kisdi E, Meszena G, Metz J.A.J. Evolutionary singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 1998;12:35–57. [Google Scholar]
- Glass R.I, Becker S, Huq S.I, Stoll B.J, Khan M.U, Merson M.H, Lee J.V, Black R.E. Endemic cholera in rural Bangladesh, 1966–1980. Am. J. Epidemiol. 1982;116:959–970. doi: 10.1093/oxfordjournals.aje.a113498. [DOI] [PubMed] [Google Scholar]
- Harvell C.D, Mitchell C.E, Ward J.R, Altizer S, Dobson A.P, Ostfeld R.S, Samuel M.D. Climate warming and disease risks for terrestrial and marine biota. Science. 2002;296:2158–2162. doi: 10.1126/science.1063699. [DOI] [PubMed] [Google Scholar]
- IPCC. Cambridge University Press; 2001. Climate change 2001: the scientific basis. [Google Scholar]
- Islam M.S, Hasan M.K, Miah M.A, Yunus M, Zaman K, Albert M.J. Isolation of Vibrio cholerae O139 synonym Bengal from the aquatic environment in Bangladesh: implications for disease transmission. Appl. Environ. Microbiol. 1994;60:1684–1686. doi: 10.1128/aem.60.5.1684-1686.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koella J.C, Doebeli M. Population dynamics and the evolution of virulence in epidemiological models with discrete host generations. J. Theor. Biol. 1999;198:461–475. doi: 10.1006/jtbi.1999.0925. [DOI] [PubMed] [Google Scholar]
- Koelle K, Pascual M. Disentangling extrinsic from intrinsic factors in disease dynamics: a nonlinear time series approach with an application to cholera. Am. Nat. 2004;163:901–913. doi: 10.1086/420798. [DOI] [PubMed] [Google Scholar]
- Koelle, K., Rodó, X., Pascual, M., Yunus, M. & Mostafa, G. In press. Refractory periods and environmental forcing in cholera dynamics. Nature [DOI] [PubMed]
- May R.M, Anderson R.M. Epidemiology and genetics in the coevolution of parasites and hosts. Proc. R. Soc. B. 1983;219:281–313. doi: 10.1098/rspb.1983.0075. [DOI] [PubMed] [Google Scholar]
- McCallum H, Barlow N, Hone J. How should pathogen transmission be modelled? Trends Ecol. Evol. 2001;16:295–300. doi: 10.1016/s0169-5347(01)02144-9. [DOI] [PubMed] [Google Scholar]
- Metz J.A.J, Nisbet R.M, Geritz S.A.H. How should we define fitness for general ecological scenarios? Trends Ecol. Evol. 1992;7:198–202. doi: 10.1016/0169-5347(92)90073-K. [DOI] [PubMed] [Google Scholar]
- Miller C.J, Drasar B.S, Feachem R.G. Responses of toxigenic Vibrio cholerae 01 to physico-chemical stresses in aquatic environments. J. Hyg. Camb. 1984;93:475–495. doi: 10.1017/s0022172400065074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palumbi S. Humans as the World's greatest evolutionary force. Science. 2001;293:1786–1790. doi: 10.1126/science.293.5536.1786. [DOI] [PubMed] [Google Scholar]
- Pascual M, Bouma M.J, Dobson A.P. Cholera and climate: revisiting the quantitative evidence. Microbes Infect. 2002;4:237–245. doi: 10.1016/s1286-4579(01)01533-7. [DOI] [PubMed] [Google Scholar]
- Reidl J, Klose K.E. Vibrio cholerae and cholera: out of the water and into the host. FEMS Microbiol. Rev. 2002;26:125–139. doi: 10.1111/j.1574-6976.2002.tb00605.x. [DOI] [PubMed] [Google Scholar]
- Sack R.B, et al. A four-year study of the epidemiology of Vibrio cholerae in four rural areas in Bangladesh. J. Infect. Dis. 2003;187:96–101. doi: 10.1086/345865. [DOI] [PubMed] [Google Scholar]
- Spira W.M. Environmental factors in diarrhea transmission: the ecology of Vibrio cholerae 01 and cholera. In: Holme T, Holmgren J, Merson M.H, Mollby R, editors. Acute enteric infections in children: new prospects for treatment and prevention. Elsevier; Amsterdam: 1981. [Google Scholar]
- Watnick P.I, Lauriano C.M, Klose K.E, Croal L, Kolter R. The absence of a flagellum leads to altered colony morphology, biofilm development, and virulence in Vibrio cholerae 0139. Mol. Microbiol. 2001;39:223–235. doi: 10.1046/j.1365-2958.2001.02195.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zo Y, Rivera I.N.G, Russek-Cohen E, Islam M.S, Siddique A.K, Yunus M, Sack R.B, Huq A, Colwell R. Genomic profiles of clinical and environmental isolates of Vibrio cholerae 01 in cholera-endemic areas of Bangladesh. Proc. Natl Acad. Sci. 2002;99:12 409–12 414. doi: 10.1073/pnas.192426499. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.