Quantifying archaeal community autotrophy in the mesopelagic ocean using natural radiocarbon

Abstract

An ammonia-oxidizing, carbon-fixing archaeon, Candidatus “Nitrosopumilus maritimus,” recently was isolated from a salt-water aquarium, definitively confirming that chemoautotrophy exists among the marine archaea. However, in other incubation studies, pelagic archaea also were capable of using organic carbon. It has remained unknown what fraction of the total marine archaeal community is autotrophic in situ. If archaea live primarily as autotrophs in the natural environment, a large ammonia-oxidizing population would play a significant role in marine nitrification. Here we use the natural distribution of radiocarbon in archaeal membrane lipids to quantify the bulk carbon metabolism of archaea at two depths in the subtropical North Pacific gyre. Our compound-specific radiocarbon data show that the archaea in surface waters incorporate modern carbon into their membrane lipids, and archaea at 670 m incorporate carbon that is slightly more isotopically enriched than inorganic carbon at the same depth. An isotopic mass balance model shows that the dominant metabolism at depth indeed is autotrophy (83%), whereas heterotrophic consumption of modern organic carbon accounts for the remainder of archaeal biomass. These results reflect the in situ production of the total community that produces tetraether lipids and are not subject to biases associated with incubation and/or culture experiments. The data suggest either that the marine archaeal community includes both autotrophs and heterotrophs or is a single population with a uniformly mixotrophic metabolism. The metabolic and phylogenetic diversity of the marine archaea warrants further exploration; these organisms may play a major role in the marine cycles of nitrogen and carbon.

Nonthermophilic archaea represent up to 40% of the free-living prokaryotic community in the water column of the world’s oceans (1–6), but until recently there has been limited information about the sources of carbon and energy that fuel these organisms (7–11). The characteristic membrane lipids of planktonic archaea include glycerol dialkyl glycerol tetraethers (GDGTs) (12). These compounds are ubiquitous in marine sediments and ocean water (12–15). The relative abundance of individual GDGTs recovered from sediments is used to reconstruct sea-surface temperatures (16–18). This distribution, known as TEX₈₆, has been shown through experimental manipulation of surface-water mesocosm experiments to respond to changes in incubation temperature (18). In addition, the δ¹³C values of GDGTs display a remarkably constant offset from δ¹³C values of dissolved inorganic carbon (DIC) over a range of settings and geologic time (13, 19–21). The collective metabolic activities of the numerous archaea in the ocean are likely to play a significant role in the cycling of organic carbon (OC) and nutrients, and their membrane lipids show significant utility for paleoceanography. However, neither the metabolic requirements of the natural population of marine archaea nor the mechanisms by which these populations record sea-surface temperature are known.

Chemoautotrophy in the marine archaea first was invoked to explain the stable carbon (δ¹³C) (20, 21) and radiocarbon (Δ¹⁴C) (13) isotopic measurements of GDGT-derived lipids extracted from sediments. Incubation studies subsequently confirmed the presence of autotrophic capacity by demonstrating the uptake of isotopically labeled inorganic carbon directly into archaeal biomass (10, 11). However, other incubation experiments also demonstrated the incorporation of labeled amino acids by archaeal populations (9, 11), suggesting that some archaea are heterotrophic or mixotrophic. Most recently, an ammonia-oxidizing autotrophic crenarchaeon, Candidatus “Nitrosopumilus maritimus,” has been grown in culture (7). In addition, the gene for a subunit of a putative ammonia monooxygenase has been found in diverse locations throughout the ocean and appears to be affiliated with the archaea (8). Oxidation of reduced nitrogen may be highly prevalent or ubiquitous among marine archaea. Although these studies all demonstrate the presence of autotrophic metabolic potential within pelagic marine archaea, it has remained unknown to what extent these results are applicable to the environment. Direct in situ observation of the relative importance of heterotrophy and autotrophy among archaea in the oligotrophic ocean is lacking.

Here, we quantify the proportion of marine archaeal lipid that is synthesized by chemoautotrophic production in mesopelagic waters. These results have important implications for biogeochemical cycles and for development of paleoceanographic proxies. Archaeal chemoautotrophy fueled by oxidation of ammonia would result in a significant contribution to global water-column nitrification. Archaeal biomass also represents a source of recently fixed, but ¹⁴C-depleted, OC below the photic zone and possibly to the sediments.

Results

The Δ¹⁴C value of surface DIC measured at the time of sampling was +71 ± 3‰, and deep DIC was −151 ± 3‰ (Table 1). Two steroidal-lipid fractions were purified from the surface prefilter (>0.5 μm). The most abundant compound in the first fraction was the C₂₇ sterol, cholesterol, and the most abundant compound in the second fraction was a C₂₉Δ⁵ sterol, probably β-sitosterol. The Δ¹⁴C values of the two sterol fractions were +56 ± 9‰ and +69 ± 9‰ (Table 1). Marine sterols have been shown to reflect the ¹⁴C content of surface DIC (22). Sterols are products of phytoplankton and zooplankton (23), and as such they reflect the recent photosynthetic fixation of DIC to particulate OC (POC). Here the Δ¹⁴C values of sterols were measured as control samples to confirm the isotopic composition of freshly produced biomass and to check for measurement biases in our compound-specific analyses. The lower value (+56 ± 9‰) suggests there could be a small amount of older carbon (coeluting, nonsteroidal material) in this sample, because this value is >1σ but <2σ different from the Δ¹⁴C value for DIC; but overall these control samples are consistent with insignificant analytical bias.

Table 1.

Water temperature, values of Δ¹⁴C, sizes of samples, and AMS facility sample numbers

Depth, m; temp., °C	Sample	Δ14C,* ‰	Total error, ‰	Sample size, μg·C	Facility sample nos.†
21; 24.5–27.5	DIC	71	3		OS-46826
	Eukaryotic sterols
	C27 mixed sterols	56	9	43	115347
	C29 mixed sterols	69	9	48	115348
	Archaeal GDGTs
	I, III, IV, and V	77	13	26	17027
	II and VI	84	12	28	17029
670; 6	DIC	−151	3		OS-46825
	Archael GDGTs
	I	−68	65	5.4	16873
		−110	11	30	17022
	II	−72	32	9.6	17023
		−64	13	24	17026
	III	−60	54	6.1	16878
	IV	−127	41	7.6	16883
		−64	32	9.8	17031
	V	n.a.	n.a.	n.a.	n.a.
	VI	98	257	2.8	16861

Italics symbolize samples excluded from the algebraic model. n.a., not available.

*Δ¹⁴C values after correction for combustion blanks and sample processing blanks as described in Supporting Text.

^†AMS facility nos. all refer to University of California, Irvine, except for those beginning with “OS,” which are for National Ocean Sciences Accelerator Mass Spectrometry, and 115347–115348, which are from Lawrence Livermore National Laboratory.

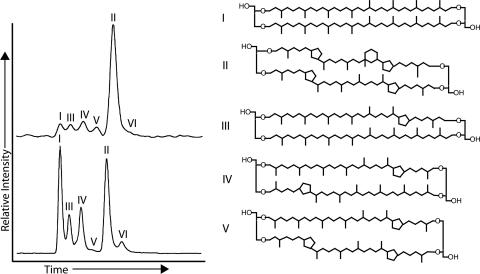
The six different GDGTs typically detected in marine water columns and sediments (12–16) were found in the surface (21 m) and deep (670 m) water samples (Fig. 1; see also Figs. 3 and 4, which are published as supporting information on the PNAS web site). The most significant differences between the two depths are the relative abundances of uncyclized GDGT I and the pentacyclic marine archaeal compound, crenarchaeol (GDGT II). In the surface, GDGT I accounts for 8% and GDGT II for 64% of total archaeal lipids, but in deep water, they are 29% and 36% of the total, respectively (Table 2). In addition, GDGT VI represents an insignificant proportion of the total archaeal lipids in the surface (2%), whereas the least abundant lipid in the deep sample is GDGT V (1%). Two fractions of GDGTs were collected from the surface sample (Figs. 1 and 3); compounds I, III, IV, and V were combined to obtain sufficient carbon for ¹⁴C-accelerator mass spectrometry (AMS) analysis (Δ¹⁴C = +77‰). Likewise, compounds II and VI were collected together as a second fraction (Δ¹⁴C = +84‰). The abundance-weighted average Δ¹⁴C value for the surface GDGTs is +82‰. The difference between the Δ¹⁴C value of surface DIC (+71‰) and the GDGTs is less than the measurement error for the GDGTs.

Fig. 1.

HPLC/atmospheric pressure chemical ionization-MS total ion current chromatograms of GDGTs separated from the surface filter (21 m) (A) and deep filter (670 m) (B) and molecular structures of the GDGT lipids. GDGT VI is a regioisomer of GDGT II (45).

Table 2.

Input for the algebraic model, including relative abundance and isotopic data

Variable	Data source	Modeled parameter	I	III	IV	V	II	VI	Sum
XSi	Meas.		0.08	0.08	0.11	0.06	0.64	0.02	1.0
XDi	Calc.		0.33	0.13	0.18	0.00	0.31	0.06	1.0
XTi	Meas.		0.29	0.12	0.17	0.01	0.36	0.05	1.0
fs	Variable	0.14
XSifS	Calc.		0.01	0.02	0.02	0.01	0.09	0.00	0.14
XDi (1 − fS)	Calc.		0.28	0.11	0.15	0.00	0.27	0.05	0.86
ΔD	Variable	−112
ΔSi	Meas.		77	77	77	n.a.	84	n.a.
ΔTi	Meas.		−110	−60	−64 or −96	n.a.	−64	n.a.
ΔTi	Model result		−104	−94	−95	n.a.	−63	n.a.
Difference*			6	34	31 or 1	n.a.	1	n.a.
AMS 1σ meas. error for ΔTi			11	54	41 or 32	n.a.	13	n.a.

The variables f_S and Δ_D were optimized by iteration. For graphical results of the optimization, see Fig. 5. Values of Δ and errors are in ‰ units. Meas., measurements; Calc., calculated; n.a., not available. Bold indicates model results.

*Difference = |model − measurements|.

Five fractions of GDGTs were collected from the deep sample (Figs. 1 and 4). Values of Δ¹⁴C for individual GDGTs in the deep sample ranged from −127‰ to −60‰ (Table 1). When replicate Δ¹⁴C measurements were available for the same compound, the sample having a larger mass consistently has a more precise measurement than the sample having smaller mass. Therefore, only the values from the larger samples are used for the following analysis and discussion. The abundance-weighted average Δ¹⁴C value of the deep archaeal lipids was −77‰. This average was calculated from 94% of total GDGTs from this depth, because insufficient mass of sample was obtained from GDGTs V and VI to measure accurate Δ¹⁴C values. Both GDGTs V and VI are excluded from further discussion.

Discussion

The values of Δ¹⁴C for surface (21 m) archaeal lipids unambiguously reflect production of biomass from DIC or from freshly produced dissolved OC (DOC; solubilized from fresh POC and used by microbes). In surface waters, it is not possible to distinguish heterotrophy from autotrophy, because the Δ¹⁴C values of the DIC and fresh organic substrates are identical. However, the data do confirm a short residence time and an in situ biosynthetic source for GDGTs obtained from the upper water column. The data also confirm that the GDGTs present in surface waters cannot derive from relict microbial populations or from free lipids entrained during occasional deep mixing events. It is difficult to assess the relative contributions of Group I and II marine archaea to the total surface GDGTs. Because many Euryarchaeota produce diether lipids instead of tetraether lipids, the surface GDGT samples probably underrepresent the contribution of marine Group II Euryarchaeota. However, this bias toward the contribution of Group I Crenarchaeota in the surface sample also makes the comparison between surface and deep samples relevant in the algebraic model discussed below. The deep sample is expected to contain nearly exclusively the lipids of Group I organisms, reflecting the dominance of this population in deeper waters (1, 3 – 6, 11).

There are at least three possible sources of GDGTs that could contribute to the total archaeal lipids found at 670 m: (i) GDGTs that are produced at the surface, either autotrophically or heterotrophically, which subsequently sink in association with the sinking fraction of POC, (ii) in situ autotrophic production in the deep water column, and/or (iii) in situ heterotrophic production in the deep water column.

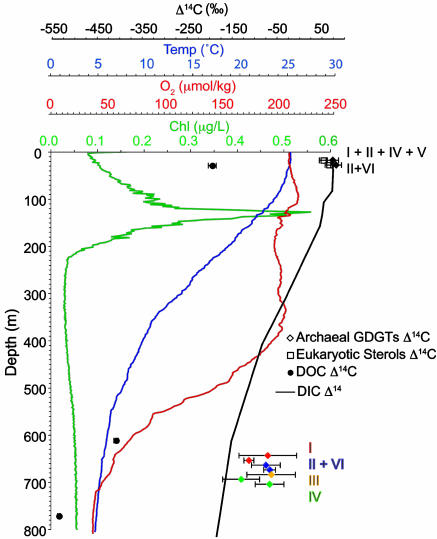
Because the average Δ¹⁴C value of GDGTs at 670 m is −77‰, all of these options can be eliminated as the sole source of GDGTs at this depth. Exclusive production of GDGTs by autotrophy at 670 m would yield Δ¹⁴C_GDGT = −151‰, more negative than all of the observed values (Fig. 2). The Δ¹⁴C values at depth also are not positive enough to derive solely from OC exported from surface waters. The Δ¹⁴C value of sinking POC, which releases organic matter that can be used by microbial heterotrophs, is assumed to be equal to the +71‰ value of surface DIC. In 1987, when there was more bomb-¹⁴C in surface DIC than there is presently, sinking POC collected in nearby sediment traps at 4,800 m and suspended POC at 900 m both had Δ¹⁴C values of approximately +100‰ (24). A decadal residence time for GDGTs within the suspended or sinking POC pools would bias surface-derived GDGTs to more positive Δ¹⁴C values. Therefore, the Δ¹⁴C data suggest the true residence time is much shorter: the surface-derived GDGT I-fraction and GDGT II-fraction both are within 1σ of the present Δ¹⁴C_DIC value; and surface-derived material cannot be the sole source of the deep GDGTs.

Fig. 2.

Water column properties and Δ¹⁴C values for DIC, DOC, sterols, and GDGTs. Chlorophyll, temperature, and dissolved oxygen data are from the Hawaii Ocean Time Series (HOTS) public data collected on May 19, 2004. DOC and DIC Δ¹⁴C data are from refs. 24 and 46. Data points for individual compounds at 670 m have been separated for clarity.

The Δ¹⁴C value of GDGT I provides further evidence that heterotrophic consumption of carbon derived from sinking POC does not contribute a large fraction of the in situ archaeal production at 670 m. This compound shows the largest increase in relative abundance in the deep sample (Fig. 1), indicating the greatest fractional contribution from in situ production at depth, and it has the most negative ¹⁴C-signature. Additionally, because there is no evidence for differential degradation of individual GDGT isomers in oxic sediments (25), presumably this finding also is true in the water column. It suggests the relative compositions and isotopic ratios of these samples would not be affected by degradation taking place in the water column. The GDGTs at 670 m are isotopically and compositionally different from the surface component.

To determine the maximum fraction of the total GDGTs in the deep sample that could be derived from material sinking directly from surface waters, a two end-member mixing model was created. The assumptions were as follows: (i) that GDGTs exported from the surface reach 670 m with the same relative abundance and Δ¹⁴C values as were produced in the surface, and (ii) that all six of the GDGTs produced by archaea in situ at 670 m reflect utilization of the same source of carbon (or the same proportional mixture of multiple sources) having an isotopic value called Δ¹⁴C_D. This value is determined by the model and is not assumed to equal a purely autotrophic value of −151‰. Because incorporation of both isotopically labeled DIC and leucine has been reported for the deep water column (11), we cannot assume a purely autotrophic community metabolism at 670 m. The model also assumes (iii) that none of the individual GDGTs is produced disproportionately by a subset of the archaea that may be expressing a metabolism vastly different in isotopic composition from the mean community metabolism. This assumption can be evaluated by using the model and data below and appears to be valid.

The abundance of ¹⁴C in each GDGT collected from 670 m is the weighted average of two components, specifically

where m represents the molar quantity of carbon and Δ represents the Δ¹⁴C value. The subscript T refers to the total material recovered at 670 m. The subscripts S and D refer to material produced at the surface (S) but that has been exported to 670 m and to material produced in situ at depth (D), respectively. Δ¹⁴C_D therefore becomes Δ_D. The subscript i refers to the ith GDGT (i.e., I, II, III . . .). Thus, the relative abundance of each compound can be expressed in terms of a carbon mole fraction

Substitution for the m terms in Eq. 1 yields

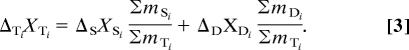From the conservation of mass equations, Σm_Ti = Σm_Si + Σm_Di and f_S ≡ Σm_Si/Σm_Ti, we then obtain

where f_S is the fraction of the total GDGT class collected at depth that was produced and exported from the surface.

Table 2 shows the values of Δ_Ti, X_Ti, Δ_S, and X_Si, which were obtained by laboratory analyses for compounds I–IV. Four equations (one for each of the GDGTs I–IV) thus can be used to obtain values for the two unknowns f_S and Δ_D. The calculations also require values of X_Di. These values depend on the observed values of X_Ti and X_Si and on the modeled variable, f_S. Specifically, from rearrangement and simplification of

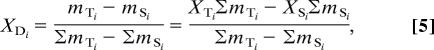we obtain

The model equations 4 and 6 were solved by iteration to determine values of f_S and Δ_D for which predicted values of Δ_Ti differ minimally from observed values of Δ_Ti (Table 2). This approach also allows evaluation of assumption (iii) above: none of the individual compounds, i, generate significantly different values of f_S and Δ_D. The final solution for f_S and Δ_D minimizes the absolute values of the differences between the predicted and observed values of Δ_Ti for compounds I–IV (see Fig. 5, which is published as supporting information on the PNAS web site). The solution reproduces all individual, measured values of Δ_Ti to within the reported 1σ uncertainties of the actual measurements (Table 2). Our approach was similar to previous uses of this algebraic model (26, 27).

We obtained the closest agreement between the model and the individual data points using the pair of values f_S = 0.14 ± 0.07 and Δ_D = −112 ± 28‰. The reported uncertainties reflect the range of values over which agreement was obtained between modeled values and the actual data to within the 2σ measurement precision of the values of Δ_Ti, representing 95% confidence that f_S and Δ_D fall within this range. The model indicates that GDGTs sinking from the surface account for only 14% of the total GDGTs recovered at depth. The remaining 86% result from in situ production by an archaeal community that is using carbon sources having an average Δ¹⁴C value of −112‰.

Therefore, even after removing the contribution of the ¹⁴C-enriched sinking fraction, the GDGTs at 670 m still contain more ¹⁴C than would be expected for a purely autotrophic population. The model does not permit the archaea to live by pure autotrophy at 670 m: Δ_D = −151‰ is not an allowed mathematical solution at any value of f_S. To produce the relatively positive Δ¹⁴C value of −112‰, a portion of the archaeal population appears to be consuming organic material produced recently in surface waters by means of a heterotrophic or mixotrophic metabolism. Either form of heterotrophic activity is likely to contribute GDGTs relatively enriched in ¹⁴C. Heterotrophic production fueled by the consumption of sinking, fresh POC (hydrolyzed to fresh DOC) would result in new production of GDGTs with the relative abundance distribution of the deep sample (X_Di) but with Δ¹⁴C values equal to +71‰. A mixture of 83% autotrophy at 670 m and 17% heterotrophic consumption of surface-derived organic matter is required to explain the Δ_D value of −112‰.

The total mass balance based on the average isotopic endmembers and fractional contributions yields the following estimates: 71 ± 11% of the total archaeal lipids at 670 m are produced autotrophically in the deep water column near 670 m; 15 ± 10% are produced by heterotrophic feeding on modern DOC derived from sinking POC; and 14 ± 7% were produced and exported directly from the surface. Although the latter two components are identical in ¹⁴C-signature, they can be separated because the relative abundance distributions of the GDGTs are markedly different between the surface and deep samples (Fig. 1). The reported uncertainties again represent the 2σ, or 95%, confidence intervals.

The relatively high values of Δ¹⁴C measured throughout this study make it unlikely that the aged, recalcitrant fraction of DOC contributes significantly to archaeal biomass. The Δ¹⁴C value of surface DOC obtained in 1987 was −191 ± 9‰ (24), and because of the dispersal of bomb-¹⁴C, the value of Δ¹⁴C_DOC currently is likely to be an even more negative value. If the surface DOC contains a 1:1 mixture of “fresh” DOC (+71‰) and recalcitrant end-member DOC (approximately −525‰), as suggested in refs. 23 and 28, recalcitrant DOC can contribute no more than 1% of archaeal carbon in surface waters. A similar assumption is plausible for the deep sample. The Δ¹⁴C value of DOC at 598 m in the North Central Pacific is −405 ± 5‰, and at 896 m it is −532 ± 3‰ (Fig. 2 and ref. 24); both are much more negative than any of the values observed here. There is no reason a priori to think that the metabolic pathway of marine archaea would favor utilization of the old, recalcitrant fraction of DOC in deep waters. The total metabolic activity of archaea, including uptake of ¹³C-DIC and free amino acids, appears similar throughout the upper 1,000 m of the water column (11), and the primary trend with depth is a decreasing rate of leucine incorporation, consistent with a relatively greater importance of autotrophy in deeper waters (11). If the marine archaea live primarily as autotrophs (7, 10, 11, 13) but also are using a small amount of OC through mixotrophy or heterotrophy, such activity might be associated with the need to derive energy. In this case, it also would be likely that younger, more labile substrates are being used, possibly associated with the scavenging of reduced N species.

Additionally, if recalcitrant DOC were the source of the negative Δ¹⁴C values, up to 30% of the archaeal carbon would need to derive from this source to explain the values of Δ_Ti (assuming Δ¹⁴C_DOC = −532‰). By using an archaeal cell count of 10^4.1 cells/ml (6), carbon content of 8.4 fg·C·cell⁻¹ (11), average growth rate of 0.02 day⁻¹ (11), and a DOC concentration of 42 μM (24), the archaea would consume the recalcitrant fraction of DOC with a turnover time of ≈2,000 years. This value is a factor of 3 too rapid to be consistent with the ≈6,000-year radiocarbon age that is implied by a value of Δ¹⁴C_DOC = −532‰. Therefore, although it is possible that consumption of old DOC is the explanation for some of the ¹⁴C-depletion found at 670 m, several lines of emerging evidence (7–11, 13), in addition to the data here, suggest that incorporation of isotopically negative DIC is the more likely explanation for the Δ¹⁴C_GDGT values in the deep water column.

Because our model solves for the in situ concentration of GDGTs produced at 670 m, it is possible to compare the distribution of GDGTs in surface and deep samples without including the fraction of the deep sample that is contributed by sinking particles. Experiments using pure cultures show that thermophilic archaea increase the number of cyclopentane units in their membrane lipids in response to temperature or physical agitation (29, 30). Pelagic archaeal lipids show a similar response: the relative distribution of GDGTs III, IV, V, and VI defines the TEX₈₆ index, which has a calibrated relationship to temperature (16). Mesocosm incubations confirm this relationship when carried out at a range of temperatures using surface waters (18). Similarly, our surface sample (21 m) has a TEX₈₆ value of 0.69, corresponding to a calculated TEX₈₆ temperature of 28°C; this value is within the range of actual sea-surface temperature at this location. However, our deep sample (670 m) has a TEX₈₆ value of 0.65 for the modeled fraction produced in situ (X_Di values). This value corresponds to a calculated temperature of 25°C. This value is far from the actual temperature of 6°C at 670 m. Our data are consistent with the suggestion that preferential export of GDGTs associated with surface-derived POC is responsible for the correlation between sea-surface temperature and TEX₈₆ (15, 18); but the data also suggest that GDGTs produced in the deep water column are not regulated by the same processes that control their distribution in surface waters. In the deeper population, the TEX₈₆ value would predict a warm temperature, yet the isotopic data preclude the presence of significant quantities of surface-derived material at 670 m.

Bulk prokaryotic metabolism in the mesopelagic ocean has been characterized as a process fueled by heterotrophic remineralization of organic matter recently produced at the surface (31, 32). In contrast, the definitive demonstration that a marine archaeon is chemoautotrophic (7) could be consistent with prior suggestions that pelagic crenarchaeota might be uniformly autotrophs (e.g., ref. 13). However, our compound-specific Δ¹⁴C measurements of archaeal lipids suggest that the deep archaea are not metabolically monolithic. The results confirm that there may be significant heterogeneity, including heterotrophic (9, 11) and autotrophic (7, 10, 11, 13) pathways, among the total archaea-mediated transformations of carbon in the mesopelagic ocean. Anaplerotic carboxylation reactions masquerade as autotrophy using the approaches applied here. However, typically such reactions are not expected to contribute >5% of cellular carbon (33) and thus would not make a significant impact on the conclusions: the predictions from our mass balance model already have >5% relative uncertainty for the contribution from each endmember. It is not yet known whether there are distinct archaeal groups expressing different pathways of carbon incorporation or whether the deep marine archaea express a uniformly mixotrophic metabolism. Regardless, autotrophy appears to contribute ≈83% of the carbon for the archaea living in the mesopelagic, whereas the remainder comes from heterotrophic consumption of OC.

Herndl et al. (11) calculated that marine archaea produce biomass at a rate of 0.8 Gt·C/year by assuming that all archaea are 100% autotrophic, using an average fixation rate of 0.014 fmol·C·archaeon⁻¹·day⁻¹ (11), and using an abundance of 1.3 × 10²⁸ archaeal cells in the whole ocean (6). The same approach, but considering only the 1.0 × 10²⁸ deep pelagic cells (6), implies that the autotrophic fraction of archaeal biomass below the photic zone is produced at a rate of 0.6 Gt·C/year. However, our model suggests that only 83% of the total community production is autotrophic and therefore that total biomass production by archaea in deep waters is 0.7 Gt·C/year. Although this 0.6–0.7 Gt·C represents only ≈1% of annual marine primary production (50 Gt·C/year), it is of a magnitude significant to the global carbon cycle and is greater than the 0.15 Gt·C/yr that is buried in marine sediments (34). The fraction of buried carbon that is derived from archaeal biomass remains unknown, but it could have the potential to influence the ¹³C (19) and ¹⁴C (13) contents of total sedimentary OC.

Significantly, these estimates of biomass production suggest that the archaea could be quantitatively the major nitrifiers in the ocean. If the archaea are living at the thermodynamic threshold, and assuming average reduction of CO₂ to the level of glucose (ΔG°′ = +478 kJ/mol·C), the oxidation of NH₄⁺ to NO₂⁻ (ΔG°′ = −235 kJ/mol) would require a minimum ratio of N oxidized per C fixed of 2:1. Thus, if archaeal autotrophy is fueled primarily by the oxidation of NH₄⁺, these organisms correspondingly generate ≥1.2 Gt/yr of N as NO₂⁻. This estimate is enough to account for all of global new production, i.e., the nitrification of all of the export flux of N below the photic zone [10–20% of primary production (PP) (35)]. This estimate suggests that the archaea are major participants in an extremely dynamic internal NO₃⁻, NO₂⁻, and NH₄⁺ cycle in the ocean. Given the current uncertainties in the oceanic N budget, including the rates of fixation of N₂, nitrification, conventional NO₃⁻ reduction (denitrification), and anammox, the total supply and demand for NO₂⁻ remains poorly understood. However, if the oxidation of reduced N drives the majority of their autotrophic production, the crenarchaeota must have a major influence on the marine nitrogen cycle.

Methods

Sampling.

The large-volume pumping capacity available at the Natural Energy Laboratory of Hawaii Authority (NELHA) was used to collect particulate organic matter from 104,000 liters of surface seawater (21-m depth) and 208,000 liters of deep seawater (670-m depth). The NELHA station pipeline supplies surface water at 0.6m³/sec and deep water at 0.8 m³/sec through 1-m diameter, high-density polyethylene pipes. Surface-water temperatures vary seasonally between 24 and 28°C and deep-water temperature is consistently 6°C (www.nelha.org/about/facilities.html). Organic matter was collected onto 0.2-μm Pall Supor filters from which lipids were extracted. The surface sample first was prefiltered (0.5-μm Millipore Opticap), although the lipid extracts from both filters subsequently were recombined for separation and analysis of GDGTs to avoid partitioning of the community by size–class. The filtration was performed by using a parallel-flow apparatus, which was fed continuously and directly from the water supply (four filters in parallel for 670-m water; two in parallel for 21-m water). The individual filter cartridges (7 × 25 cm) contained spiral-wound filters of average surface area 4,650 cm² and were housed in stainless steel filter holders connected by Teflon tubing. The flow rate was 4 liters·min⁻¹·filter⁻¹. Filters were kept at the in situ temperatures of the respective water sources, and ≈52,000 liters was passed through each. No significant reduction in flow rate was observed in any of the filters over the duration of the sample collection. Immediately upon recovery, the filters were frozen at −70°C for return to the laboratory.

Lipid Extraction.

Filters were stored at −80°C until being excised by using a combusted hack saw, and all samples were lysed in 1.5 M Na-perchlorate at 4°C for 48 h by using the method of R.L.H. and L.I.A. (unpublished data) after Blair et al. (36). Lysate and filter particles were extracted by using the method of Bligh and Dyer (37); the total lipid extract (TLE) was washed repeatedly against Barnstead Nanopure H₂O; each TLE was concentrated by evaporation under high-purity N₂(g), and the resulting samples were stored at −20°C. TLEs were dried and hydrolyzed in 5% H⁺/MeOH (transesterification) for 4 h at 70°C to cleave polar head-groups; the transesterified products were extracted into CH₂Cl₂ and were dried onto precombusted quartz sand. Each sample was separated into compound-class fractions by SiO₂-gel chromatography (13).

Archaeal Lipids.

Individual compounds were separated by normal phase chromatography and detected between m/z 1,250–1,350 by using HPLC/atmospheric pressure chemical ionization-MS (38, 39). One-minute fractions were collected, and the GDGTs in each fraction were determined by flow injection analysis (FIA), monitoring m/z 350–1,400. For the deep archaeal lipids, the six most abundant compounds were separated into individual samples based on mass and retention time; for the surface samples, the GDGTs with m/z 1,302–1,296 were collected as one fraction, and those with m/z 1,292 were collected as a second fraction. Each subsequent GDGT fraction (six deep and two surface) was purified to remove pigmented impurities by RP-HPLC with an ZORBAX Eclipse XDB-C₈ column (Agilent Technologies, Palo Alto, CA) at 30.0°C (4.6 × 150 mm; 5 μm) with program: 100% solvent A (80% acetonitrile/20% water) to 90% A and 10% ethyl acetate (EtOAc) over 4 min, to 65% A over 10 min, to 31% A over 6 min, to 100% EtOAc over 7 min. One-minute fractions were collected and analyzed by FIA; purity was indicated by the absence of color and the absence of other masses in the total ion chromatograms of the purified compounds (Figs. 3 and 4). The samples were transferred to 9-mm quartz tubes and combusted to CO₂ for AMS analysis (40, 41).

Deep-sample GDGTs I, II, and IV each were collected as two replicates during the second, reverse-phase purification step; these represented one “large” and one “small” sample for each compound. Δ¹⁴C values for all GDGTs were measured at the Keck Carbon Cycle AMS facility at the University of California, Irvine by using the ultra-micro AMS methods of Santos et al. (42). Further methods for the quantification of sample processing blanks and error corrections made to measurements are reported in Supporting Text, which is published as supporting information on the PNAS web site.

Sterols.

Sterols were obtained from the surface sample, >0.5-μm size class fraction only. SiO₂-gel fraction 8 [75% hexane/25% ethyl acetate (13)] was separated isocratically by RP-HPLC by using a Develosil RP-Aqueous C₃₀ column (Phenomenex, Belmont, CA) at 50.0°C (4.6 × 250 mm; 5 μm). Sterols were separated with solvent A (98% methanol/2% water) over 45 min. The column was backflushed with 1:1 solvent A and ethyl acetate. Sterols were detected by atmospheric pressure chemical ionization-MS, monitoring m/z 300–500. The sterols were collected as 1-min fractions; the contents of each vial were determined by flow injection analysis, and the sterols were further purified by RP-HPLC as described above for GDGTs. The composition of the purified sterol fractions was determined by GC/MS (DB5-MS column; methods similar to ref. 13). The two most purely steroidal fractions were combusted, and Δ¹⁴C measurements of the captured CO₂ were made by the AMS facility at Lawrence Livermore National Laboratories.

DIC.

Five hundred-milliliter water samples were collected from the surface and deep Natural Energy Laboratory of Hawaii Authority pipelines according to the World Ocean Circulation Experiment (WOCE) protocol (42) for measurement of Δ¹⁴C_DIC values. The values of Δ¹⁴C_DIC were measured at the National Ocean Sciences Accelerator Mass Spectrometry facility on CO₂ stripped from the water samples (43, 44).

Abbreviations

AMS

accelerator mass spectrometry

DIC

dissolved inorganic carbon

DOC

dissolved OC

GDGT

glycerol dialkyl glycerol tetraether

POC

particulate OC.