Skip to main content
PMC home page
British Journal of Pharmacology logoLink to British Journal of Pharmacology
. 1999 Apr;126(8):1699–1706. doi: 10.1038/sj.bjp.0702477

Mechanism of verapamil block of a neuronal delayed rectifier K channel: active form of the blocker and location of its binding domain

L Catacuzzeno 1, C Trequattrini 1, A Petris 1, F Franciolini 1,*
PMCID: PMC1565955  PMID: 10372811

Abstract

  1. The mechanism of verapamil block of the delayed rectifier K currents (IK(DR)) in chick dorsal root ganglion (DRG) neurons was investigated using the whole-cell patch clamp configuration. In particular we focused on the location of the blocking site, and the active form (neutral or charged) of verapamil using the permanently charged verapamil analogue D890.

  2. Block by D890 displayed similar characteristics to that of verapamil, indicating the same state-dependent nature of block. In contrast with verapamil, D890 was effective only when applied internally, and its block was voltage dependent (136 mV/e-fold change of the on rate). Given that verapamil block is insensitive to voltage (Trequattrini et al., 1998), these observations indicate that verapamil reaches its binding site in the uncharged form, and accesses the binding domain from the cytoplasm.

  3. In external K and saturating verapamil we recorded tail currents that did not decay monotonically but showed an initial increase (hook). As these currents can only be observed if verapamil unblock is significantly voltage dependent, it has been suggested (DeCoursey, 1995) that neutral drug is protonated upon binding. We tested this hypothesis by assessing the voltage dependence of the unblock rate from the hooked tail currents for verapamil and D890.

  4. The voltage dependence of the off rate of D890, but not of verapamil, was well described by adopting the classical Woodhull (1973) model for ionic blockage of Na channels. The voltage dependence of verapamil off rate was consistent with a kinetic scheme where the bound drug can be protonated with rapid equilibrium, and both charged and neutral verapamil can unbind from the site, but with distinct kinetics and voltage dependencies.

Keywords: DRG neurons, delayed rectifier K channel, mechanism of block, verapamil, D890, TEA, patch clamp

Introduction

Voltage-activated K channels and their modulation play a major role in controlling frequency-dependent signalling in excitable cells. Several K channels are blocked by verapamil in a use-dependent manner (see for instance Rampe et al., 1993; Trequattrini et al., 1996), and consequently this compound has received attention as a potential agent in the modulation of anomalous electrical activity of excitable cells such as cardiac arrhytmias or epilepsy (Colatsky et al., 1990; Hondeghem & Snyders, 1990). Previous studies have shown that verapamil induces a dose-dependent decay of IK(DR), without altering its activation kinetics, consistent with a state-dependent mechanism of block in which the drug binds preferentially to the open state of the channel (Pancrazio et al., 1990; Rampe et al., 1993; DeCoursey, 1995; Trequattrini et al., 1998).

Verapamil is a tertiary amine, and in solution is present both as neutral as well as quaternary (charged) compound, with relative fractions depending on the pH. Whereas the neutral form which predominates only at very high pH (pKa=8.6; Retzinger et al., 1986) is highly hydrophobic and can rapidly cross the cell membrane and equilibrate inside, the charged form cannot cross the membrane at any significant rate, and is thus confined to the side of application. These characteristics have led to difficulties in identifying other features of verapamil block, such as the sidedness of action, the active form of the drug and the interpretation of the voltage dependence of block and unblock.

It has been suggested that verapamil crosses the cell membrane in its neutral form, then once inside it protonates, and in this form reaches the blocking site (DeCoursey, 1990; Jacobs & DeCoursey, 1990; Rampe et al., 1993; but see also Pancrazio et al., 1990). This model originated from the small voltage dependency of block found by some authors (Rampe et al., 1993) consistent with a charged molecule acting from the inside. More recently, DeCoursey (1995) however showed that varying the intracellular pH, thus the concentration of the charged form inside the cell, did not, as expected, change the rate of block by external verapamil. Based on this observation, as well as on the very slow recovery upon verapamil washout, he proposed that while charged verapamil can reach the site from the intracellular solution, it can also be accessed by the neutral form via hydrophobic pathways, as originally proposed by Hille (1971) to explain block by local anaesthetics.

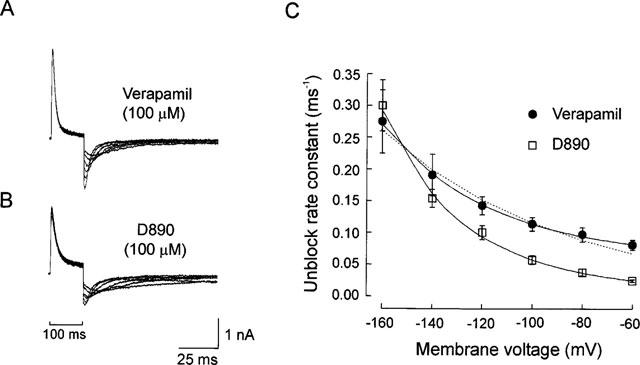
Verapamil block of IK(DR) on chick DRG neurons has been shown to be voltage independent (Trequattrini et al., 1998). The voltage insensitivity in this case was demonstrated by applying dedicated stimulation protocols that would eliminate bias that can easily hamper the assessment of the voltage dependence of state dependent blockers. The nature of the active form could not be ascertained however as no information was available concerning the location of the binding site along the channel pore. Furthermore it has been proposed that once in the site, neutral verapamil is protonated (DeCoursey, 1995). This suggestion was instrumental in explaining the hooked tail currents (currents which did not decrease monotonically but show an initial increase commonly referred as hook; c.f. Figure 5) recorded in presence of verapamil, which can only occur if verapamil off rate is significantly voltage dependent. However in this study the voltage dependence of the off rate of the drug was not tested directly.

Figure 5.

Figure 5

Open in a new tab
Voltage dependence of the unblock rate constants of verapamil and D890. (A) and (B) show hooked tail currents (following a depolarization to +80 mV) at voltages ranging between −60 and −160 mV in presence of 100 μM of either verapamil or D890. In (C) the values of the unblock rate constants, calculated from the decay rate of the tails (see Methods) are plotted as function of voltage. Continuous lines represent the best fit obtained with the following equations (see text for details):
graphic file with name 126-0702477e3.jpg
A regression fit to the data produced values of 0.06±0.0017 ms−1 and 0.00038±0.00007 ms−1 respectively for A and B and 0.0034±0.0004 ms−1 for the koff (0 mV) in D890. k values were 40 for verapamil and 36 for D890. Dashed line represents best fit of data points for verapamil using a simple exponential function similar to that used for D890.

These questions have been addressed here by using the permanently charged and membrane impermeant verapamil analogue D890. This compound, originally used by Affolter & Coronado (1986) to determine the sidedness of block by phenylalkylamines on Ca channels, was also employed by DeCoursey (1995). In addition to resolving these questions, we have used D890 to probe the voltage dependence of D890 block and unblock in order to localize the phenylalkylamine binding site, and to assess whether neutral verapamil is protonated upon binding.

Methods

Preparation

Whole-cell currents were recorded from DRG neurons dissociated from 9–11 day chick embryos (Barde et al., 1980). Ganglia were dissociated into single cells by gentle compression through pipettes with increasingly smaller tip diameters. Dissociated neurones were plated in Petri dishes coated with poly-D-lysine, and used for the experiments after 2–8 h.

Electrophysiology

The whole-cell configuration of the patch-clamp method (Hamill et al., 1981) was used with borosilicate pipettes (Hilgenberg GmbH, Malsfeld, Germany), pulled with a programmable puller (PUL-100; WPI, Sarasota, FL, U.S.A.), whose resistance ranged between 1 and 2 MΩ when filled with standard pipette solutions. In these conditions the access resistance was typically 4–6 MΩ. Normally, 60–80% of the series resistance and cell capacitance was electronically compensated. Currents were amplified with a List EPC-7 amplifier (List Medical, Darmstadt, Germany), and digitized with a 12 bit A/D converter (TL-1, DMA interface; Axon Instruments Inc., Foster City, CA, U.S.A.). The pClamp software package (version 5.6; Axon Instruments Inc.) was routinely used on a Compaq Pentium PC (Compaq Computer Inc., Houston, TX, U.S.A.) for generating the command voltage pulses, recording and archiving the currents, and preliminary analysis of the data. For on-line data collection, current signals were usually filtered at 5–10 kHz and digitized at 20–100 kHz. Data were analysed and plotted by use of MicroCal Origin software (MicroCal Software Inc., Northhampton, MA, U.S.A.) which uses the Levenberg-Marquardt nonlinear least square curve fitting algorithm. Data are expressed as the mean±standard error of the mean (s.e.mean). All experiments were carried out at room temperature (18–22°C).

Solutions

The intracellular (pipette) solution contained (in mM): KCl 145, CaCl2 1, MgCl2 2, EGTA 11, MOPS buffer 2, adjusted to pH 7.3. The bath (extracellular) solution contained (in mM): either NaCl (Na-Physiological Salt Solution, PSS) 140 or KCl (K-PSS) 140, plus CaCl2 5, MgCl2 2, 0.5 Cd, 0.5×10−3 TTX and MOPS buffer 2, adjusted to pH 7.2. The internal solution at pH 6.0 was obtained with citrate buffer. Verapamil and D890 were prepared daily at the final concentration. In experiments using TEA, the equimolar substitution of its Cl salt replaced KCl in the intracellular solution. Verapamil, TEA and TTX were obtained from Sigma (Sigma Chemical Co., St. Louis, MO, U.S.A.). D890 was a kind gift of Dr Martin Traut from Knoll AG, Ludwigshafen, Germany.

Assessment of the unblock rate constant

The off rates of verapamil and D890 were assessed from the hooked tail currents produced upon hyperpolarized voltages in presence of saturating concentrations of the blocker (i.e., concentrations that virtually eliminate the steady-state IK(DR) upon depolarization). The hooked tail currents were modelled using the minimal kinetic scheme describing open-channel block, as follows

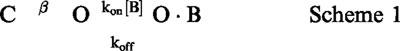graphic file with name 126-0702477e4.jpg

in which the transition to the open state is considered irreversible (α<<β) at the hyperpolarized voltages where hooked tails occur, and the channels are predominantly in the blocked (O·B) state at the beginning of the hyperpolarizing pulse. Based on this kinetic scheme (Scheme 1), the decay phase of the hooked tail current in presence of the blocker can be described by a monoexponential function with a time constant given by the following expression

graphic file with name 126-0702477e1.jpg

The off rate, koff, can be obtained from Equation 1, provided the remaining parameters are known. In particular, τtail was determined from the monoexponential decay of the hooked tail current, and β and kon·[B] were assessed, for the same cell, from the decay rate of the tail current in control conditions, and from the blocker-induced current decay at depolarized voltages.

Results

Blocking features of D890

Internal application of D890 (10–200 μM) via the patch pipette produced an inhibition of IK(DR) the extent of which increased progressively with time after establishing the whole-cell configuration, and stabilized in 10–15 min. The time-dependence of the blocking action of this agent is consistent with pipette diffusion characteristics expected for such a compound (Push & Neher, 1988). The development of the blocking activity of D890 on IK(DR) is shown in Figure 1. D890 altered the conformation of IK(DR), the currents activated to a maximum then decayed exponentially, with time to a small fraction of their peak value. In contrast, no change was recorded in the early activation time course of the current. The kinetics of IK(DR) in presence of D890 is consistent with a state-dependent block, similar to that exerted by verapamil in these neurones (Trequattrini et al., 1996; 1998). Application of D890 to the external side of the membrane at a concentration up to 1 mM was totally ineffective. Even when neurons were incubated for 4–6 h with this concentration of D890, no detectable effect of the drug on the shape of IK(DR) was found. The observation that D890 is effective only when applied internally indicates that the blocking site can be accessed by the drug only from the cytoplasmic side of the membrane.

Figure 1.

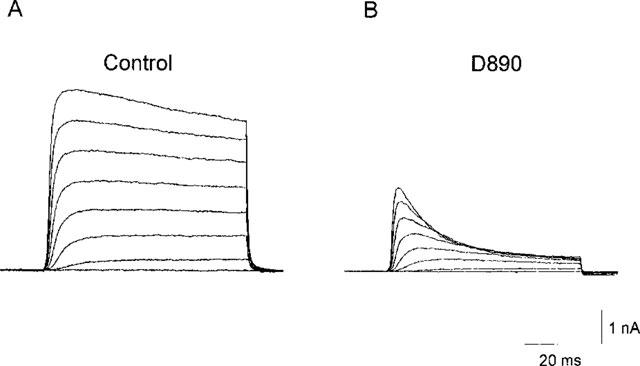
Figure 1

Open in a new tab

Effects of D890 on IK(DR). Families of current evoked by depolarizing pulses from −60 to +80 mV in 20 mV steps (VH=−70 mV) with pipette solution containing 100 μM D890. (A) Current traces recorded immediately after rupture of the patch membrane, when only a negligible fraction of the drug has diffused into the cell. (B) Currents recorded 10 min later, when steady-state of block had been reached. Bath solution, Na-Physiological Salt Solution (PSS).

We further characterized the state dependent nature of D890 block by verifying the dependence of the decay rate of the current on drug concentration (Figure 2). Typical current traces recorded from four different neurons following constant depolarization of +120 mV, and at the blocker concentrations indicated are shown in Figure 2A. Interference from the concurrent inactivation process (the fast component of which develops with a time constant of 200–400 ms in this preparation; Trequattrini et al., 1996), can be neglected when compared with the much faster current decay induced by D890 at the concentrations of 10–200 μM used. Figure 2B shows the effect of D890 concentration on the decay rate of the current, confirming the state dependent block of this analogue. Moreover, the linear dependence resulting from the plot is consistent with a one to one interaction between blocker and channel (molecularity=1). In addition, this plot affords an estimate of the blocker kon from the slope of the line interpolating the experimental data, and koff from the y-intercept, using the relation 1/τb=(kon·[B]+koff) as already described (Swenson, 1981). The kon and koff determined from 14 neurons (3–5 for each concentration) were 0.61±0.03 ms−1 mM−1 and 6.4−10−4±0.0017 ms−1, respectively. Given the high standard error of koff due to its small contribution to the decay rate of the current, this parameter was determined more reliably from the hooked tail currents, where at the potential at which they occur koff and kon are comparable (c.f. Figure 5).

Figure 2.

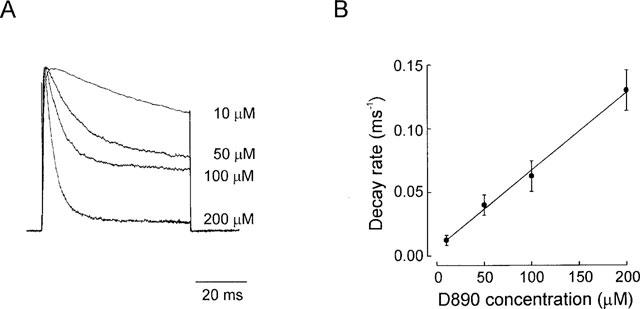
Figure 2

Open in a new tab

Evaluation of the kinetics of block. (A) Typical IK(DR) (normalized) elicited by depolarizing steps to +120 mV (VH=−70 mV) in presence of varying concentrations of D890 in the pipette. (B) The reciprocal of the time constant of the rate of block, obtained by single exponential fit of the decay phase of the current, is plotted against D890 concentration. Data points (each averaged from 3–5 experiments) were well fitted by a linear regression, indicating that block occurs with molecularity of 1.kon and koff, given by the slope and y-intercept of the interpolated line, were 0.61±0.03 ms−1.mM−1 and 6.4×10−4±0.0017 ms−1, respectively. Bath solution, Na-PSS.

Voltage dependence of D890 block

The voltage dependence of block by the permanently charged D890, was investigated to locate the binding site, and assessed from the rate of block at varying voltages, as shown in Figure 3. Experiments were carried out with a stimulation protocol designed to minimize bias that could overestimate the voltage dependence of open channel blockers. For instance, transfer of voltage dependence from the voltage dependent channel activation to the kinetically coupled D890 block that can occur when the kinetics of the two processes are of same order of magnitude. By contrast, when channel activation is significantly faster than block (α>>kon·[B]+koff), the two processes can be considered virtually uncoupled, and the error introduced negligible. For these reasons we assessed the kinetics of block on currents activated with high depolarizing voltages (at which τact<4 ms) to quickly activate virtually all channels, thus uncoupling the activation process from block. These highly depolarized voltages would also make negligible the other possible source of error arising from the shift of the gating equilibrium (French & Shoukimas, 1981).

Figure 3.

Figure 3

Open in a new tab

Voltage dependence of D890 block of IK(DR). (A) IK(DR) obtained by a stimulation protocol consisting of a conditioning depolarizing pulse +120 mV for 15 ms, followed by a test pulse ranging from +120 to +60 mV (VH=−70 mV), with 50 μM D890 in the pipette. (B) The reciprocal of the time constant obtained by single-exponential fits of the currents shown in A is plotted against membrane voltage. Continuous line represents the least-squares fit of the data obtained with the equation 1/τb/V)=kon (0 mv)·[B]·emV/k, where kon (0 mv) is the on block rate at 0 mV, [B] is the blocker concentration, and k is the slope parameter indicating the mV necessary per an e-fold change in the kon value. Fit of the data yielded a value of 0.24 ms−1.mM−1 for kon (0 mV) and 136 mV for k.

The protocol used consisted in applying a fixed, highly depolarized conditioning prepulse (+120 mV, for 15 ms) followed by test pulses at varying voltages (+60, +140 mV). The range of test voltages was then selected to yield time-invariant currents in absence of the blocker to ensure that at the end of the prepulse all channels were fully activated and no deactivation had occurred (c.f. Figure 6 of Trequattrini et al., 1998). The rate of block was assessed at each test voltage in presence of 50 μM of D890 in the internal solution (Figure 3A). D890-induced current decays at varying voltages were well fitted with single exponential functions, and the resulting decay rates, 1/τb, taken as a good approximation of the on rate, were plotted as function of test voltage (Figure 3B). The on rates changed significantly over the voltage range examined, demonstrating that D890 block is voltage-dependent. An e-fold increase of the on rate was obtained with 136 mV depolarization. Similar experiments carried out on five neurons yielded an average value of 132±9 mV per e-fold.

The voltage dependence of block (i.e. the mV/e-fold change of the on and off rate) are not given in terms of the `electric distance' (commonly referred as δ), a parameter that in the Woodhull model (1973) indicates the fraction of the membrane voltage drop occurring at the binding site. Several studies have in fact shown that the voltage dependence of block is not only determined by the position of the binding site along the channel pore, but strongly influenced by the ionic conditions (MacKinnon & Miller, 1988; Spassova & Lu, 1998). Additionally the multi-ion nature of the DRK channel (Trequattrini et al., 1996) where the movement of conducting and blocking ions are coupled does not allow to determine the precise location of the binding site from the voltage-dependence of block (Hille & Schwarz, 1978; Adelman & French, 1978).

The voltage independence of verapamil block previously found in this preparation (Trequattrini et al., 1998), and the present observation that the binding site is located within the membrane electric field would indicate that verapamil blocks IK(DR) in chick DRG neurons in the uncharged form. Taking advantage that verapamil is a weak base (pKa=8.6), and its charged fraction depends on the pH, we confirmed this conclusion by showing that increasing charged verapamil concentration at the binding site by more than 20 fold did not produce significant changes in the block rate as expected if the charged verapamil were the active form (data not shown). This was done by lowering the internal pH from 7.3–6.0, while keeping external pH constant. At the new pH, the corresponding ratio charged/neutral verapamil is ca. 400/1 (compared to ca. 20/1 at pH 7.3). Charged verapamil inside the cell following external application of 100 μM verapamil must increase from 95–2,000 μM, to keep the neutral form (5 μM) in equilibrium with outside.

Verapamil and TEA inhibitions are competitive

TEA block of IK(DR) has been investigated in great detail in terms of mechanism of action (for review see Stanfield, 1983; Hille, 1992), and binding site structure (MacKinnon & Yellen, 1990; Choi et al., 1993). Like verapamil, TEA is an open channel blocker which accesses its binding site from the cytoplasmic face of the membrane in a voltage dependent manner. These similarities led us to test whether verapamil and TEA block display competitive antagonism. Competition for the binding site by the two open channel blockers, or for distinct binding sites allosterically coupled in such a way that binding of either blocker precludes the binding of the other can be described by the following kinetic scheme

graphic file with name 126-0702477e5.jpg

where O is the open state, O·Bver and O.BTEA are respectively the verapamil and TEA blocked states. kon is the on rate for verapamil. Because the steady state block by verapamil is nearly complete (at the concentrations used in the experiment), the unblock rate for verapamil can be neglected. At the highly depolarized voltages used activation is virtually complete and much faster than the rate of verapamil block so that the two processes can be examined separately. Given that TEA on and off rates are much faster than that of verapamil, the kinetic scheme above predicts that the apparent on rate of verapamil block, *kon(ver), will be slowed by the same factor by which the current is reduced. In other words *kon(ver)=kon(ver)·(ITEA/Ictrl).

An intracellular concentration of TEA that would block approximately 2/3 of IK(DR) was applied through the pipette. On applying a saturating concentration of verapamil extracellularly, the time course of verapamil block in presence of internal TEA was markedly slower than that obtained in absence of internal TEA (Figure 4). The experiment shown in Figure 4 was carried out as follows. Cells were permanently bathed in saturating verapamil (100 μM). The patch pipette contained 45 mM TEA, a concentration that previous experiments showed to depress IK(DR) by ca. 2/3 on this preparation (Trequattrini et al., 1996). Immediately after the rupture of the patch membrane, when only a negligible fraction of TEA had diffused from the pipette into the neurone, the first trace (labelled `Verapamil') was recorded upon a depolarizing pulse to +80 mV (VH=−70 mV). After 13 min to allow equilibration of TEA within the cell, the trace labelled `Verapamil+TEA' was recorded. The peak current was reduced to 43% of control (i.e., first trace), but the TEA block of IK(DR), has been scaled to match control peak current to afford direct comparison of current kinetics. A significant decrease of the rate of current decay (from 0.083 to 0.031 ms−1) can be observed. The mean current decay rate obtained in the presence of both verapamil and TEA was 0.038±0.009 (n=3). The decrease by ca. 2/3 of IK(DR) by TEA, and simultaneous similar decrease of *kon(ver) give support to the idea that verapamil and TEA blocks are competitive (Cahalan & Almers, 1979; Choi et al., 1991). We tested this relationship with two other TEA concentrations, and found the rate of current decay to be inversely related to the amount of block according to the model proposed.

Figure 4.

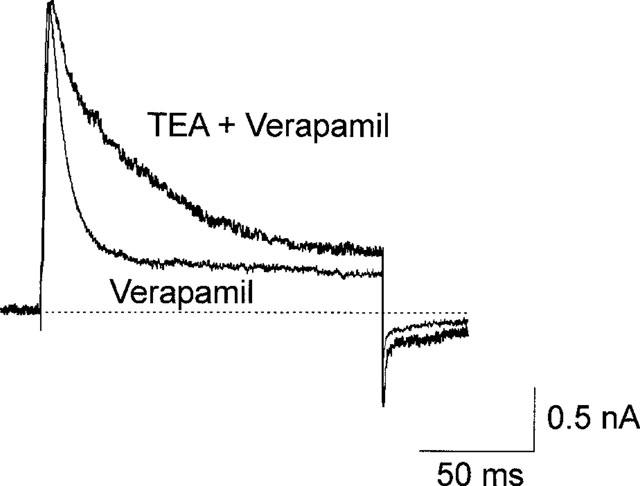
Figure 4

Open in a new tab

Interaction between TEA and verapamil block. Superimposed current traces at +80 mV with 45 mM TEA in the pipette and 100 μM external verapamil, recorded immediately after the rupture of the patch membrane (trace indicated as `Verapamil') and after 13 min (indicated as `TEA+Verapamil'), a time sufficient for the pipette solution to fully equilibrate with the cytoplasm. To afford a better comparison of current decay rates, the `TEA+Verapmil' trace has been scaled (2.3 times) to match the peak current of the `Verapamil' trace. TEA decreases the rate of verapamil-induced current decay from 0.083–0.031 ms−1

Voltage dependence of D890 and verapamil unblock

In high external K-PSS and high concentrations of verapamil or D890 peculiar tail currents were recorded (Figure 5A). This peculiar time course, already observed for verapamil on rat alveolar epithelial cells by DeCoursey (1995) in addition to other open channel blockers (c.f. Armstrong, 1971), was interpreted to result from a marked decrease of the blocker affinity for the site at hyperpolarized voltages. This result would be expected with D890 because of its voltage dependence and permanently charged nature, but not verapamil as our previous results indicate that this blocker binds in the uncharged form only. To clarify this point we assessed the voltage dependence of off rates for the two blockers in the hyperpolarized voltage range (from −60 to −160 mV) where the hooked tail currents occur. The off rates were assessed from the hooked tail currents as described in Methods. Figure 5A and B show families of hooked tail currents obtained at varying hyperpolarized voltages in verapamil and D890, from which the estimate of the unblock rate constants was carried out. Figure 4C plots the unblock rate constants for D890 (n=4) and verapamil (n=5) as function of the hyperpolarizing voltage. The off rates for both blockers are strongly voltage dependent, increasing when the voltage decrease.

We have attempted to fit the data using the classical Woodhull model for the voltage dependence. The result of this analysis is shown in Figure 5. The off rate for D890 varies with voltage as expected for a charged blocker that moves across a region of the channel where a significant voltage drop (36 mV/e-fold) is present. On the contrary, verapamil off rate is poorly fitted by the Woodhull model (dotted line). The verapamil data were however well fitted if unblock, k*off, was modelled as the sum of voltage dependent and voltage independent components, described by the expression

graphic file with name 126-0702477e2.jpg

where k*off=koff+kHoff (c.f. Scheme 3). This expression results from the following kinetic scheme which incorporates verapamil protonation upon binding, an idea originally suggested by DeCoursey (1995).

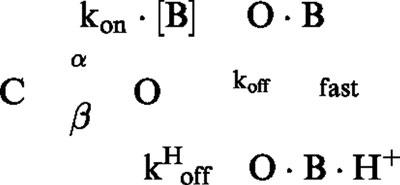graphic file with name 126-0702477e6.jpg

Here the protonation equilibrium between charged and uncharged form of verapamil (O·B·H+ and O·B) is assumed to be very fast. In addition, whilst only uncharged verapamil can bind to the channel, both charged and uncharged molecules can leave the site, although with different rates and voltage dependencies. In this framework, A and B represent the products between the off rates for the uncharged and charged verapamil times their respective fractions. The voltage dependence of the off rate obtained for charged verapamil was 40 mV/e-fold, a value very similar to that found for D890 (36 mV/e-fold; c.f. above). The addition of the O·B·H+ state in Scheme 3 in rapid equilibrium with the O·B state does not prejudize the assessment of the off rates described in Methods.

Discussion

In this study we have investigated the molecular mechanisms underlying verapamil block of the IK(DR) channel. We used the permanently charged, membrane impermeant verapamil analogue D890 to ascertain the location of the binding site, the active form of the drug, and the voltage dependence of the unblock rate.

Location of verapamil binding domain

To address this question, we have investigated the blocking behaviour of D890, and found that akin to verapamil, D890 is an open channel blocker. D890 does not modify the time course of IK(DR) activation, but induces a mono-exponential decay of the current whose time constant is proportional to the blocker concentration. The block on rate determined from D890-induced current decay gave an extrapolated value at 0 mV of 0.24 mM−1 ms−1, compared with verapamil (kon (ver)=0.95 mM−1 ms−1, Trequattrini et al., 1998). Unlike verapamil, D890 was effective only when applied from the intracellular side of the membrane. Extracellular concentrations up to 1 mM did not show any measurable block, indicating that the binding site can be accessed only from the internal side of the membrane.

The voltage dependence of block of the permanently charged D890 assessed at depolarized voltages locates the binding site inside the channel pore. Our previous findings of a lack of voltage dependence of verapamil block (Trequattrini et al., 1998) would then indicate that verapamil is active in neutral form, or at least much more active in this form than the cationic drug so as to produce an unmeasurable voltage dependence. We tested this assumption by lowering the internal pH down to 6.0, which increases the solely intracellular concentration of charged verapamil by more than 20 times. We found that this manouvre did not increase (<10%) significantly the block rate, indicating that the charged form is not significantly active. It should be noticed however that uncertainties may remain regarding the actual internal pH in these experimental conditions, since when internal pH is lowered to 6.0, for the new ratio between charged and neutral verapamil to be reached (400/1, c.f. Results), the buffering system which has to reach the cytoplasm through the pipette, may be unable for diffusion restrictions to keep the nominal internal pH.

Verapamil and TEA binding domains interact

The slowing of the rate of block by verapamil when TEA, a fast open channel blocker, is present (Figure 4), is consistent with competitive antagonism of verapamil by TEA. Slowing occurs because the TEA-blocked IK(DR) channels are in rapid equilibrium with open-unblocked channels, and TEA-blocked channels cannot bind verapamil. When verapamil blocks open-unblocked channels it will not produce the expected rate of decay of the current because as block by verapamil proceeds and the pool of open-unblocked channels decreases TEA-blocked channels rapidly free TEA to maintain the equilibrium. The congruency of the experimental and predicted results based on the competition scheme provides compelling evidence that verapamil and TEA compete for the same site. Alternatively the data would be satisfactorily described if the binding sites for the two drugs are physically distinct (although presumably close), yet binding to either site allosterically distorts the tertiary structure of the protein sufficiently to prevent the other site accepting the blocker.

Does verapamil protonate upon binding?

Upon repolarization after a strong depolarized pulse in presence of external K and high concentrations of verapamil we recorded hooked tail currents. Open channel blockers display this behaviour only if there is significant voltage dependence of their off rate. This result was unexpected since we found verapamil to bind in neutral form. Hooked tails were also observed by DeCoursey (1995) in rat alveolar epithelial cells where verapamil was found to block the IK(DR) in the uncharged form. To explain this result he suggested that, once in the site, verapamil has to be protonated (from the internal solution) to acquire the voltage dependence of unblock and give rise to hooked tail currents.

Using the permanently charged verapamil analogue D890 we tested DeCoursey's suggestion of blocker protonation upon binding by comparing the voltage dependence of the off rate of verapamil and D890 from the hooked tail currents. The test was based on the assumption that protonated (charged) verapamil would give the same voltage dependence as the permanently charged D890. As shown in Figure 5, the off rate of both verapamil and D890 were significantly voltage dependent. However, while the voltage dependence of D890 could be described by the classical Woodhull model, verapamil data could only be fitted with an expression containing a voltage dependent and a voltage independent component. This expression stems from the kinetic scheme shown in Results (Scheme 3) which has as major features that while only neutral verapamil can bind to the channel, both charged and uncharged drug can leave the site, although with different rates (c.f. legend to Figure 5). In addition, protonation of bound verapamil is so fast to be described by the reaction's dissociation constant. In this view, the voltage dependent component is given by the protonated verapamil, whereas the neutral fraction of the blocker will contribute the voltage independent component. The voltage dependencies for the two blockers were instead comparable (36 and 40 mV/e-fold for D890 and verapamil respectively), a result expected for two very closely related molecules with same charge. The marked difference in the voltage dependence of D890 on and off rates (136 vs 36 mV/e-fold respectively) would be interpreted in the classical framework for the voltage dependence of block as due to asymmetry of the energetic barrier the blocker has to overcome in order to reach or leave the blocking site. We have verified however whether the different voltage-dependence could have a different origin, for instance, result from relief of block by external K ions, which could occur at hyperpolarized voltages.

Relief of block has been observed in several K channels following application of K ions on the side of the membrane opposite to where the blocker binds (Bezanilla & Armstrong, 1972; Yellen, 1984; MacKinnon & Miller, 1988). This effect has been modelled as due to electrostatic destabilization brought about by K ions that bind to a site close to where the blocker dwells, and analytically described by an expression where the blocker off rate varies with both K concentration (according to the Langmuir isotherm for the K site occupancy), and voltage (see Equation 3 of MacKinnon & Miller, 1988). This expression (thus the involvement of external K in determining the higher voltage dependence of D890 and protonated verapamil off rate) was however inadequate to fit our data because the voltage dependence of relief of block by K ions that bind to a site along the channel pore should be a saturating function of external K and voltage as saturable is the K site. By contrast, our data are hyperlinear at more negative voltages (Figure 5).

The non-saturating feature of the data would not conflict with Armstrong's original (1971) interpretation of relief of block of long-chain quaternary ammonium (QA) ions by K ions. In this view, external K ions would help dislodging the QA ions by knocking them off the site. That is, occasionally an external K ion has enough kinetic (thermal) energy to enter the blocked channel and push the blocker over its energy barrier for exit. This view is based on the notion that the probability for an external ion to have a high enough energy for knocking off the blocker increases markedly with voltage. This idea of the bombardment of the blocker by external K would have also represented an alternative explanation to verapamil protonation to account for the voltage independence of verapamil on rate vs the significant voltage dependence of the off rate. This view has recently been challenged on the basis of apparent energetic inconsistencies. The movement of ions inside a pore seems to be well described by electrodiffusion equations (Chen & Eisenberg, 1992; 1993). This theory assumes that the ions are in an over-damped environment, where the energy they acquire from the electric field is continuously scattered because of molecular impacts between ions, water molecules and the channel wall. Consequently, the amount of block relief that would be expected by the knock off mechanism would be only a negligible fraction of what is actually observed.

Acknowledgments

We thank Drs Franco Conti and Sandy Harper for their critical comments at varying stages of this work, and Dr Martin Traut from Knoll AG (Ludwigshafen, Germany) for kindly providing us with D890. This work was supported by MURST grant Cofin-97-9705224541.

Abbreviations

EGTA

ethylene glycol-bis(β-aminoethyl ether)-tetraacetic acid

MOPS

morpholinopropanesulphonic acid

TEA

tetraethylammonium chloride

TTX

tetrodotoxin

References

  1. ADELMAN W.J., JR, FRENCH R.J. Blocking of the squid axon potassium channel by external caesium ions. J. Physiol. (Lond). 1978;276:13–25. doi: 10.1113/jphysiol.1978.sp012217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. AFFOLTER H., CORONADO R. Sidedness of reconstituted calcium channels from muscle tranverse tubules as determined by D600 and D890 blockade. Biophys. J. 1986;49:767–771. doi: 10.1016/S0006-3495(86)83703-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. ARMSTRONG C.M. Interaction of tetraethylammonium ion derivatives with the potassium channels of giant axons. J. Gen. Physiol. 1971;58:413–437. doi: 10.1085/jgp.58.4.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. BARDE Y.A., EDGARD D., THOENEN H. Sensory neurons in culture: Changing requirements for survival factors during embryonic development. Proc. Natl. Acad. Sci. U.S.A. 1980;77:1199–1203. doi: 10.1073/pnas.77.2.1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. BEZANILLA F., ARMSTRONG C.M. Negative conductance caused by entry of sodium and cesium into the potassium channels of squid axons. J. Gen. Physiol. 1972;60:588–608. doi: 10.1085/jgp.60.5.588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. CAHALAN M.D., ALMERS W. Interactions between quaternary lidocaine, the sodium channel gates, and tetrodotoxin. Biophys. J. 1979;27:39–56. doi: 10.1016/S0006-3495(79)85201-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. CHEN D.P., EISENBERG R.S. Constant fields and constant gradients in open ionic channels. Biophys. J. 1992;61:1372–1393. doi: 10.1016/S0006-3495(92)81944-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. CHEN D.P., EISENBERG R.S. Flux, coupling, and selectivity in ionic channels of one conformation. Biophys. J. 1993;65:727–746. doi: 10.1016/S0006-3495(93)81099-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. COLATSKY T.J., FOLLMER C.H., STARMER C.F. Channel specificity in antiarrhythmic drug action: mechanism of potassium channel block and its role in suppressing and aggravating cardiac arrhytmias. Circulation. 1990;82:2235–2242. doi: 10.1161/01.cir.82.6.2235. [DOI] [PubMed] [Google Scholar]
  10. CHO K.L., ALDRICH R.W., YELLEN G. Tetraethylammonium-blockade distinguishes two inactivation mechanisms in voltage-activated K channels. Proc. Natl. Acad. Sci. U.S.A. 1991;88:5092–5095. doi: 10.1073/pnas.88.12.5092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. CHOI K.L., MOSSMAN C., AUBE' J., YELLEN G. The internal quaternary ammonium receptor site of Shaker potassium channels. Neuron. 1993;10:533–541. doi: 10.1016/0896-6273(93)90340-w. [DOI] [PubMed] [Google Scholar]
  12. DECOURSEY T.E. Verapamil applied externally blocks open K channels in rat alveolar epithelial cells in the whole-cell configuration by permeating the membrane in uncharged form and blocking from inside the cell in charged form, as revealed by varying the external pH. Biophys. J. 1990;57:51a. [Google Scholar]
  13. DECOURSEY T.E. Mechanism of K+ channel block by Verapamil and related compounds in rat alveolar epithelial cells. J. Gen. Physiol. 1995;106:745–779. doi: 10.1085/jgp.106.4.745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. FRENCH R.J., SHOUKIMAS J.J. Blockage of squid axon potassium conductance by internal tetra-n-alkyammonium of various sizes. Biophys. J. 1981;34:271–291. doi: 10.1016/S0006-3495(81)84849-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. HAMILL O.P., MARTY A., NEHER E., SAKMANN B., SIGWORTH F.J. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free memrbane patches. Pflügers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
  16. HILLE B. The permeability of the sodium channel to organic cations in myelinated nerve. J. Gen. Physiol. 1971;58:599–619. doi: 10.1085/jgp.58.6.599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. HILLE B. Sinauer, Sunderland (MA); 1992. Ion channels of excitable membranes. [Google Scholar]
  18. HILLE B., SCHWARZ W. Potassium channel as multi-ion single-file pores. J. Gen. Physiol. 1978;72:409–442. doi: 10.1085/jgp.72.4.409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. HONDEGHEM L.M., SNYDERS D.J. Class III antiarrhytmic agents have a lot of potential but a long way to go: reduced effectiveness and dangers of reverse use dependence. Circulation. 1990;81:686–690. doi: 10.1161/01.cir.81.2.686. [DOI] [PubMed] [Google Scholar]
  20. JACOBS E.R., DECOURSEY T.E. Mechanisms of potassium channel block in rat alveolar epithelial cells. J. Pharmacol. Exp. Ther. 1990;255:459–472. [PubMed] [Google Scholar]
  21. MACKINNON R., MILLER C. Mechanism of charybdotoxin block of the high-conductance Ca-activated K channel. J. Gen. Physiol. 1988;91:335–349. doi: 10.1085/jgp.91.3.335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. MACKINNON R., YELLEN G. Mutations affecting TEA blockade and ion permeation in voltage-activated K channels. Science. 1990;250:276–279. doi: 10.1126/science.2218530. [DOI] [PubMed] [Google Scholar]
  23. PANCRAZIO J.J., VIGLIONE M.P., KLEIMAN R.J., KIM Y.I. Verapamil-induced blockade of voltage-activated K+ current in small-cell lung cancer cells. J. Pharmacol. Exp. Ther. 1990;257:185–189. [PubMed] [Google Scholar]
  24. PUSH M., NEHER E. Rates of diffusional exchange between small cells and a measuring patch pipette. Pflügers Arch. 1988;411:204–211. doi: 10.1007/BF00582316. [DOI] [PubMed] [Google Scholar]
  25. RAMPE D., WIBLE B., FEDIDA D., DAGE R.C., BROWN A.M. Verapamil blocks a rapidly activating delayed rectifier K channel cloned from human heart. Mol. Pharmacol. 1993;44:642–648. [PubMed] [Google Scholar]
  26. RETZINGER G.S., COHEN I., LAU S.H., KEZDY F.J. Ionization and surface properties of verapamil and several verapamil analogs. J. Pharmacol. Sci. 1986;75:976–982. doi: 10.1002/jps.2600751014. [DOI] [PubMed] [Google Scholar]
  27. SPASSOVA M., LU Z. Coupled ion movement underlies rectification in an inward-rectifier K channel. J. Gen. Physiol. 1998;112:211–221. doi: 10.1085/jgp.112.2.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. STANFIELD P.R. Tetraethylammonium ions and the potassium permeability of excitable cells. Rev. Physiol. Biochem. Pharmacol. 1983;97:1–68. doi: 10.1007/BFb0035345. [DOI] [PubMed] [Google Scholar]
  29. SWENSON R.P., JR Inactivation of potassium current in squid axon by a variety quaternary ammonium ions. J. Gen. Physiol. 1981;77:255–271. doi: 10.1085/jgp.77.3.255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. TREQUATTRINI C., CATACUZZENO L., PETRIS A., FRANCIOLINI F. Verapamil block of the delayed rectifier K+ current in chick embryo dorsal root ganglion neurons. Pflügers Arch. 1998;435:503–510. doi: 10.1007/s004240050545. [DOI] [PubMed] [Google Scholar]
  31. TREQUATTRINI C., PETRIS A., FRANCIOLINI F. Characterization of a neuronal delayed rectifier K current pemeant to Cs and blocked Verapamil. J. Membrane Biol. 1996;154:143–153. doi: 10.1007/s002329900139. [DOI] [PubMed] [Google Scholar]
  32. WOODHULL A.M. Ionic blockade of sodium channel in nerve. J. Gen. Physiol. 1973;61:687–708. doi: 10.1085/jgp.61.6.687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. YELLEN G. Relief of Na block of Ca-activated K channels by external cations. J. Gen. Physiol. 1984;84:187–199. doi: 10.1085/jgp.84.2.187. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from British Journal of Pharmacology are provided here courtesy of The British Pharmacological Society

RESOURCES