Estimating the prevalence of breast cancer using a disease model: data problems and trends

Abstract

Background

Health policy and planning depend on quantitative data of disease epidemiology. However, empirical data are often incomplete or are of questionable validity. Disease models describing the relationship between incidence, prevalence and mortality are used to detect data problems or supplement missing data. Because time trends in the data affect their outcome, we compared the extent to which trends and known data problems affected model outcome for breast cancer.

Methods

We calculated breast cancer prevalence from Dutch incidence and mortality data (the Netherlands Cancer Registry and Statistics Netherlands) and compared this to regionally available prevalence data (Eindhoven Cancer Registry, IKZ). Subsequently, we recalculated the model adjusting for 1) limitations of the prevalence data, 2) a trend in incidence, 3) secondary primaries, and 4) excess mortality due to non-breast cancer deaths.

Results

There was a large discrepancy between calculated and IKZ prevalence, which could be explained for 60% by the limitations of the prevalence data plus the trend in incidence. Secondary primaries and excess mortality had relatively small effects only (explaining 17% and 6%, respectively), leaving a smaller part of the difference unexplained.

Conclusion

IPM models can be useful both for checking data inconsistencies and for supplementing incomplete data, but their results should be interpreted with caution. Unknown data problems and trends may affect the outcome and in the absence of additional data, expert opinion is the only available judge.

Background

Estimates of disease-specific incidence, prevalence and mortality, specified by age and sex, are important information to health care policy and planning. They are essential inputs to cost-effectiveness analyses and burden of disease calculations. Empirical data, however, are often difficult to obtain or are of questionable validity. To remedy some of these data problems, disease models have been developed that describe the relationship between the epidemiological parameters, by exploiting the causal structure of a disease. Incidence, prevalence, mortality models (IPM models) formalise the relationship between the three parameters, using the fact that incidence has to precede prevalence, and that cause-specific mortality can only follow disease. IPM models have been used frequently both to supplement missing data and to study the agreement between different epidemiological data [1-4]. Our previous study supported the formal validity of IPM models, but when the modelling was applied to empirical data on four types of cancer, the model calculations differed to a large extent from the empirical data [5]. For breast cancer the difference was particularly large. It was argued that these discrepancies may indicate inconsistencies in the data, but that they may also be caused by time trends.

When the data for one disease are not in accordance with each other, they are internally inconsistent. Inconsistencies may be caused by differences in the completeness of the data. For example, when more incident cases are missed than deaths, incidence and mortality are inconsistent. Also, inconsistencies may arise when the data were derived from different contexts (e.g. a different region) or measured differently (e.g. varying case-definitions). Applying inconsistent incidence and mortality to an IPM model will result in under- or overestimating prevalence, and thus in discrepancies between model estimations and empirical prevalence data. Time trends, on the other hand, may cause the data to appear inconsistent in a steady state model, while in fact they are not. Because prevalence is the resultant of incident cases from the past, it cannot react instantaneously to changes in incidence and case-fatality, but only with a certain delay. It is possible to account for the effects of time trends in a dynamic model, but this requires additional input data on the nature and size of the trends, which are not available for most diseases. Often, we do not even know whether a trend is present or not, and the researcher faces a dilemma what to do with the discrepancies. Adjusting observed data for apparent inconsistencies that are in fact the consequence of past trends would rather defeat the purpose of IPM models.

For breast cancer in the Netherlands the discrepancy between observed prevalence and prevalence calculated from incidence and mortality was particularly large [5]. Fortunately, for breast cancer several data problems are known, and, in addition, there is a tentative estimate of the trend in incidence. This allowed us to quantify the relative contribution of the trend and several known data problems on the discrepancy and to throw some light upon the researcher's dilemma. Even though prevalence of breast cancer is not a very useful epidemiological measure, it does allow us to illustrate the difficulties in the use of IPM modelling because of the relative abundance of data.

Methods

General approach

We calculated the point-prevalence of breast cancer in the Netherlands and its 95 % confidence interval from national incidence rates and cause-specific mortality rates using the IPM model described by Barendregt et al. [6]. We compared it to regional prevalence data. To determine the separate effects of trends and known data problems we next recalculated the model:

a) incorporating the incompleteness in the prevalence data (see below),

b) adjusting for a trend in incidence,

c) adjusting for double counting of incident women with secondary primaries, and

d) taking excess mortality from non-breast cancer deaths into account.

For point c a single cohort model was used, while for a, b, and d it was necessary to use a multi-cohort model that takes into account both age and calendar time. We estimated the proportion of the difference that was explained by each of the recalculations from the overall differences in the number of prevalent cases using 1993 population figures and summing over all age groups.

IPM model

Our model is based upon the conceptual disease model depicted in Figure 1 and was described in Kruijshaar et al. [5]. Briefly, the model describes a population as being in two states: diseased or susceptible, while transition hazards determine how people move from one state to another. Following an initially disease-free cohort over time and applying the transition hazards, the number of cases can be calculated. Under the important assumption of a steady-state situation, time is equivalent to age. The model then allows the calculation of prevalence at a certain age from the prevalence at the previous age and the transition hazards. By assuming furthermore equal mortality from other causes in cases and susceptibles, prevalence at exact age n can be calculated from incidence and cause-specific mortality probabilities using formula 1a in the Appendix See additional file: 1 [6].

Figure 1.

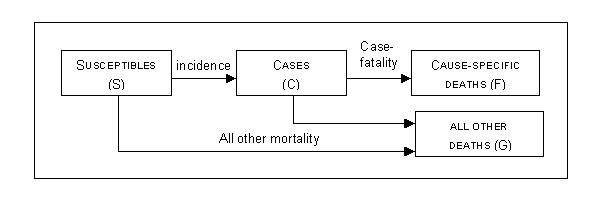
A Markov model for cancers

Baseline calculation

First, we calculated prevalence from national incidence and mortality rates of female breast cancer (ICD-9 code 174) for 1991–1995, averaged by five-year age groups up to 85+. Incidence data obtained from the Netherlands Cancer Registry (NKR) are based on pathology and hospital admission data, and the mortality data from Statistics Netherlands (CBS) on death certificates. To enable comparison with the prevalence data we used incidence rates excluding in-situ tumours. Incidence and mortality rates were first interpolated to one-year age groups using the cubic-spline method and then converted into probabilities (see the Appendix Additional file: 1 for formulas). A 95% confidence interval of the calculated prevalence was obtained by parametric bootstrapping assuming a Poisson distribution for numbers of incident cases and deaths in each age group. The @risk software programme [7] was used to simulate 10000 iterations by Monte Carlo sampling.

The Regional Cancer centre South (IKZ) was the only cancer registry in the Netherlands that has estimated prevalence. The IKZ determined prevalence for a specific part (the core region) of the region South at 1-1-1993 by checking the vital status of all incident cases registered in the region since 1970 against the municipal population administration and the National Death Index. If a person had moved to another municipality in the Netherlands, data from that municipal population administration was used (under Dutch law, registration with the municipal population administration is obligatory within five days of changing address). In case of migration to another country, a case was lost to follow up. In-situ tumours are not included. For more information on these data we refer to Coebergh et al. [8]. A 95% confidence interval around these data (by five-year age group up to 85+) was calculated assuming a binomial distribution (see formula 2 in the Appendix Additional file: 1 ). Point estimates and confidence intervals were interpolated to one-year age groups as described in the Appendix Additional file: 1.

Limitations of the prevalence data

Prevalence registered by the IKZ does not include patients diagnosed before 1970 and is consequently underestimated. To quantify the effect of this, we created a dynamic model, incorporating a parameter y that represents the number of years prior to incidence. Prevalence in the reference year y0, was calculated from prevalence in the 23 years prior to y0 (see Appendix Additional file: 1).

Also, prevalence data refer to a specific region only, whereas the model calculations are based on national input. We showed in our previous study [5], that differences between regional and national incidence and mortality rates hardly affected the calculated prevalence. Therefore, we did not further examine this here.

Trend in incidence

Next, we estimated the effect of a trend of increasing incidence on the calculated prevalence. While incidence increased, the population mortality rate for breast cancer has remained approximately the same in the Netherlands [8-12], thus case-fatality must have declined. Coebergh et al. have estimated the yearly rise in incidence in the region South between 1975 and 1986, to be approximately one percent [13]. The effects of screening are not included in this estimate, as it was not introduced until later, but effects of other types of increased case finding were included – if present.

We estimated the effect using the dynamic model described above, decreasing incidence by one percent for each additional year y prior to the year of reference (see Appendix Additional file: 1). We assumed the trend was present up to 95 years before the year of reference. Sensitivity to the trend was inspected, by applying a 50% higher and lower trend (1.5% and 0.5%) as input values.

Double counting incident women with a secondary primary

The NKR registers the number of incident tumours, whereas prevalence refers to women. Women are thus counted twice, if they have a second primary tumour in their breast (SP). The percentage of SPs by age group were provided for 1991–1995 by the IKZ. We estimated the incidence of women with breast cancer, by subtracting the age-specific proportion SP from the reported incidence rate and recalculated our model.

Excess mortality from non-breast cancer deaths

Breast cancer patients have been shown to be at increased risk of dying from other causes of death [14], although with longer survival (>20 years) they may experience a decreased risk [15]. Cause-specific mortality data thus underestimate the total excess mortality from breast cancer. We adjusted for this estimating excess mortality from duration-specific relative survival data assuming a lognormal survival distribution from breast cancer and a proportion not dying from breast cancer (proportion cured) [16], as described in the Appendix Additional file: 1 (formula 5). Relative survival data, i.e. excess mortality over and above the background mortality, were reported by the IKZ registry for three cohorts (1970–1979, 1980–1986 and 1987–1992) for ages < 70, and > 70 [8]. Because survival improves over time, we used survival probabilities at one, three and five years after incidence of the youngest 1987–1992 cohort. As longer follow-up was not available for this cohort, survival at 10 and 20 years was estimated using the conditional 10 and 20-year survival in the older cohorts. Fitting the lognormal model allowed us to estimate the cumulative probability of excess mortality with time after incidence, from which we calculated the yearly mortality probability (see Appendix Additional file: 1).

We extended our baseline model to include duration (see Appendix Additional file: 1 for the mathematical description): prevalence at age n, d years after incidence was calculated from the prevalence at the previous age and year. Summation across all years d provided age-specific prevalence.

Results

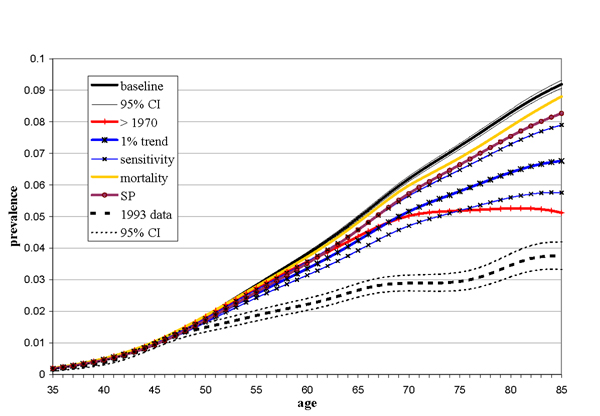
In our baseline calculation we estimated the prevalence of breast cancer from national incidence and cause-specific mortality data. The results of this are shown in black in Figure 2 (solid line), together with the regional data (dotted line), while the total number of calculated prevalent cases and the difference with the IK2 are shown in Table 1. Both the IKZ and calculated prevalence increased exponentially with age to about age 47, but thereafter they started to diverge. The model calculations increased linearly to a prevalence of 9.2 % at age 85, while the IKZ prevalence increased more slowly and levelled off to 3.7 %. At age 55 the calculated prevalence was 1.5 times higher than the data, increasing to 2.5 times at age 85, a difference in total number of cases of 86%. The 95 % confidence interval for the calculated prevalence was narrow, due to the high numbers of breast cancer incidences and deaths. The uncertainty in the prevalence data was larger. From age 48 upward the confidence intervals did not overlap.

Figure 2.

Calculated prevalence and prevalence data of breast cancer by age. Baseline calculation and separate effects of known data problems and trend. Baseline: baseline calculation, 95 % CI: 95 % confidence interval, >1970:excluding incident cases of before 1970, 1% trend: estimating the effect of a secular trend in incidence, sensitivity: 50% sensitivity borders around the effect of the secular trend, SP: adjusting for secondary primaries, mortality: including excess mortality from non-breast cancer deaths.

Table 1.

Comparison of the total number of prevalent cases of breast cancer, estimated in different ways, and 1993 prevalence data.

	Total number of cases estimated	% difference from 1993 data	% of the gap explained
1993 data	123216	0.0	0.0
Baseline	66370	85.6	100.0
Combined	89169	34.4	59.9
>1970	101268	52.6	38.6
1% trend	103943	56.6	33.9
SP	113440	70.9	17.2
mortality	119769	80.5	6.1

Baseline: baseline calculation, combined: adjusting for one-% trend and excluding incident cases of before 1970, >1970: excluding incident cases of before 1970, 1% trend: estimating the effect of a secular trend in incidence, SP: adjusting for secondary primaries, mortality: including excess mortality from non-breast cancer deaths.

Figure 2 and Table 1 also show the effects of the known data problems and trend in incidence (coloured lines). First, excluding cases that became incident more than 23 years before the year of reference had the largest effect and altered the age pattern. Prevalence increased with age more slowly, levelling off to a maximum of 4.4 % at age 78, and declining thereafter. The total number of prevalent cases was 53 % higher than the IKZ prevalence, explaining 39% of the difference between calculated and IKZ prevalence. Second, incorporating a secular trend in incidence in the calculation of prevalence resulted in a lesser increase with age, levelling off after age 70, without reaching a plateau. The secular trend of one percent decreased the discrepancy with 44% (ranging between 49% and 18% for 50% higher and lower estimates of the trend). Third, adjusting for double counting of incident women with a second primary tumour of the breast (SP) had a smaller effect. The percentage of SP did not exceed nine percent for any age group. Subtracting this percentage from the incidence rate explained 17% of the difference. Fourth, taking excess mortality from non-breast cancer deaths into account made a difference of six percent.

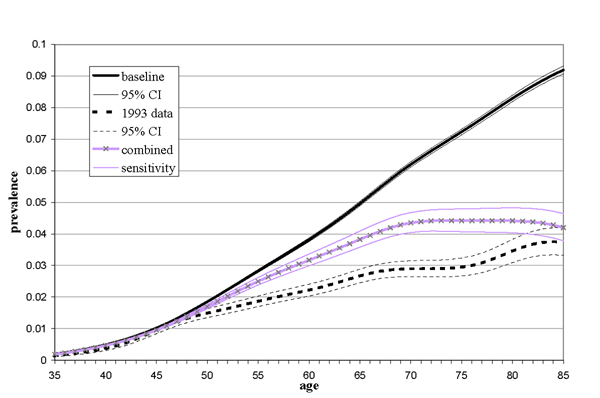
The combined effect of restricting the duration of prevalence and the trends, shown in Figure 3, resulted in a 60% decrease of the difference (ranging between 70% and 50% for a 50% higher or lower trend). At age 85 the calculations touched upon the upper confidence limit of the data.

Figure 3.

Calculated prevalence and prevalence data of breast cancer by age. Baseline calculation and the effect of both the secular trend and restricting prevalence. Baseline: baseline calculation, 95 % CI: 95 % confidence interval, combined: adjusting for one-% trend and excluding incident cases of before 1970, sensitivity: the effect of 50% change in the estimated trend in incidence on the combined adjustment.

Discussion

We quantified the separate effects of known data problems and a trend in incidence on IPM model calculations of breast cancer prevalence, and inspected their influence on the discrepancy between model estimations and prevalence data. Two factors had a major effect on the estimated prevalence: the limitation of the IKZ prevalence data including only incident cases since 1970, and the trend in incidence. Together, they accounted for a major part (60%) of the discrepancy. Still, their combined effect leaves a part of the discrepancy unexplained. The effects of adjusting for double counting of incident women with secondary primaries of the breast and of taking excess mortality from non-breast cancer deaths into account were small. Consequently, the combined effect of all four factors does not explain the entire difference. Either unknown data problems are present contributing to the remaining difference, or we underestimated some of the effects.

The two factors with the largest effects could influence the calculations because prevalence is a stock variable: it contains cases that became incident in the past. The long survival time of breast cancer explains why these two factors can exert such a strong influence. The time lag after which prevalence fully reflects a change in incidence is determined by the rate at which the pool of prevalent cases is replaced by new cases, which, in turn, depends on the survival time. The underestimation of the prevalence data due to its limitation to incident cases after 1970 may be as large as 44 % at age 85, but is lower on average, as the effect increases with age. When the effect is calculated additional to adjusting for the trend in incidence, it is also smaller: 24 % at age 85. In a small part of the IKZ region prevalence can be based upon incidence registration since 1958 [9]. These data are indeed higher than the IKZ data for the larger region indicating the data will improve with longer follow-up in the future.

The estimated trend in incidence and the effect of adjusting for it are subject to some uncertainty for several reasons. First, the one percent trend is an average figure; its magnitude differs with age and calendar year. Second, the regional estimate may deviate somewhat from the national trend. Furthermore, it is a rounded figure. Nevertheless, as the results of the sensitivity analysis showed that increasing or decreasing the trend by 50% altered the percentage explained by a combined effect (of limiting prevalence and the secular trend) by only 10%-points, we expect these three effects to be small. The estimated one percent may also be too low because it does not include the effect of the introduction of screening around 1990 in the Netherlands. We estimated this effect in an additional analysis, increasing the estimated one percent to five percent for the last four years. The additional effect of screening was very small. Finally, we may have overestimated the effect assuming that a one percent trend was present many years before the period for which it was estimated (1975 to 1986). Assuming no trend before 1975 in an extra analysis increased the calculated prevalence by almost 10 % at age 85, but inspection of the incidence rates since 1958 for the smaller part of the IKZ region showed that incidence has increased since 1958 [9]. The effect of assuming no trend before 1960 was negligible.

The effects of adjusting for secondary primaries and excess mortality were only small, but this is not surprising. The proportion of women with a secondary primary in the breast did not exceed nine percent, preventing a much larger change in the calculated prevalence. Also, the relative risk of breast cancer patients to die from other causes of death is not that high, and may even inverse with longer follow-up [14,15].

Thus, although the effect of the trend may be somewhat uncertain, other unknown data problems are likely to cause the remaining difference between calculated and IKZ prevalence. One possible explanation for the remaining deviation could be that when the cancer registries started completeness of incidence was not as high as it is now. As a result the prevalence is underestimated by the IKZ. On the other hand, IKZ prevalence was determined by checking population administrations, which involves matching of the registrations, which is never 100% accurate. Therefore, some deaths may have been missed and individuals inaccurately assumed to be alive, resulting in an overestimation of the IKZ prevalence. How large both counteracting effects are, is difficult to determine. An additional explanation may be found in variation between national and regional all-cause mortality, as the equations in our model are based on the assumption of similar background mortality. A higher background mortality in the IKZ region would decrease the discrepancy, but we expect only a minimal effect as the differences in all-cause mortality will be minor. Additional reasons for overestimating incidence or underestimating mortality (both resulting in overestimating prevalence) are difficult to think of. Cancer incidence data in the Netherlands are reliable with a completeness of 96.2 % around 1990 [17], and probably even higher in the years thereafter. Furthermore, mortality by cause-of-death statistics of the Netherlands are assumed to be reliable and, compared to other European countries, the detection fraction for deaths from cancer is high [18]. The causes of the remaining discrepancy thus remain uncertain.

Conclusions

Even when data are regarded as relatively reliable, as was the case for breast cancer in the Netherlands, data problems may be present. 1993 prevalence data for breast cancer in the IKZ region are underestimated, as they do not include incident cases before 1970. Our analyses show the importance of using IPM modelling to detect data problems. However, we also showed the trend in incidence to have a large effect on the model estimations for breast cancer, complicating the use of IPM models.

IPM models can be useful both for checking for data inconsistencies and for supplementing incomplete data, but in both cases there remains the need for careful interpretation of the results. In the all too common situation where, unlike for breast cancer, no data on the size and nature of trends are available, the effects of trends cannot be estimated. Furthermore, unknown data problems may affect the model estimations in unknown directions. In the absence of additional data the researcher is faced with the dilemma of how to interpret model discrepancies, and expert opinion is the only available judge.

Competing interests

None declared.

Authors contributions

MK carried out the analyses and drafted the manuscript. JB participated in the design of the analyses. LvdP-F provided additional points for analyses. All authors read and approved the final manuscript.