Poxy models and rash decisions

The second-to-last case of smallpox was diagnosed on August 24, 1978, when Janet Parker, a photographer at the University of Birmingham Medical School (Birmingham, U.K.), was admitted to the hospital. She had been infected when a virus escaped from the school’s smallpox laboratory. On September 6th, Professor Henry Bedson, who was responsible for the laboratory, killed himself. Five days later, Janet died in the hospital. Although many people were exposed to her before the diagnosis, Janet infected only her mother (who survived). The incident shows that fears of the accidental release of smallpox are certainly justified. The variola virus is now officially stored at two locations (one in Russia and one in the United States), and there are concerns that covert stocks may also exist. The events of September 11th, 2001, and the deliberate releases of anthrax in the weeks that followed, led many to believe that the chance of a bioterrorist attack with variola had previously been underestimated. In the event of the deliberate or accidental release of smallpox, what should be done? Would isolation of cases suffice to control an outbreak? Would it also be necessary to trace and vaccinate contacts of cases? Under what circumstances would mass vaccination be justified? In this issue of PNAS, Riley and Ferguson use a mathematical model of smallpox transmission to answer these questions (1). Although theirs is not the first simulation model to address such questions, nor even the first explicitly spatial analysis, it is the first carefully parameterized and repeatable study to account for the spread of the disease over a wide area. Fittingly, the analysis focuses on the island associated with not only the most notorious deliberate release of the virus (the British army infamously gave smallpox-contaminated blankets to Native Americans during Pontiac’s Rebellion in 1763) but also, thanks to Edward Jenner a few years later, with the development of the technique that ultimately led to its eradication.

The months after the 2001 anthrax attacks in the United States saw the beginnings of what became a minor epidemic of speculation in the medical and scientific press about the best way to respond to such a hypothetical smallpox attack. In many cases, the speculation was informed (arguably, misinformed) by mathematical models. It is reasonable to assume that some of this work was influential in the U.S. Government’s decision in December 2002 to order smallpox vaccination for military personnel and voluntary vaccination for frontline medical staff. Given the known dangers of the vaccine, this was a controversial decision.

Understandably, for such rapid responses, the quality of the early modeling work was variable (2). Collective eyebrows were raised when the Centers for Disease Control’s model completely neglected contact tracing and forecast 77 trillion cases if the epidemic went unchecked (a consequence of a model that assumed Malthusian growth; real epidemics, of course, slow and then decline as the pool of susceptibles decreases, a process accounted for in almost all standard epidemic models) (3). The RAND Corporation also published an analysis (4) that a subsequent review concluded “had little explanatory or predictive power” (2). Two papers were less easily dismissed. Kaplan et al. (5) presented an analysis appropriate for a large population (10 million were assumed) and compared policies of mass vaccination and ring vaccination (tracing and vaccinating contacts of cases). This work was innovative in that delays in contact tracing and vaccination were explicitly accounted for through a queuing system, but in other respects it was a traditional deterministic model of the kind that has proved useful for approximating the average behavior of epidemics in large populations (6). The analysis indicated that mass vaccination was far superior to ring vaccination. Halloran et al. (7), in contrast, presented a stochastic model of a small idealized community (2,000 inhabitants, four schools, and excellent preschool daycare facilities) and reached a different conclusion. If there was assumed to be no residual immunity to smallpox in the community, a policy of mass vaccination would again be preferred. If residual immunity was important, as recent analysis suggests it should be (8), a targeted policy of contact tracing would be better.

Different diseases may exhibit very different patterns of spatial spread.

A robust debate took place about the validity of these conclusions (7, 9). Halloran et al. argued that, by assuming a population where each case was equally likely to meet and infect each susceptible person (the mass-action formulation, introduced by Ronald Ross 90 years ago), Kaplan et al. had overestimated the likely rate of spread of the virus. Their own model, which aimed at a more realistic characterization of contact patterns, allowed for the fact that cases would tend to cluster in households and other social groupings. The resulting local depletion of susceptibles would slow spread compared with a mass-action model. Kaplan et al. countered that the two model structures, in fact, gave very similar results when their inputs were the same; the major differences in the conclusions resulted from the differing population sizes (9).

Both positions had their merits: people do not mix homogeneously, and mass-action models will tend to overestimate the rate of spread; household and other social structuring will slow epidemics. On the other hand, as Halloran et al. acknowledged, it is not clear how well conclusions based on an analysis of a simulated community of 2,000 people will generalize to a population of tens of millions. However, the whole argument was effectively nullified when Eichner and Dietz (10) published research that convincingly argued that the conclusions of both teams were wrong because both were based on wildly inaccurate biological assumptions. It takes ≈12 days before someone infected with smallpox enters a prodromal period, characterized by a fever indistinguishable from that caused by other common viral diseases. Two to three days later, the characteristic smallpox rash develops. Both research groups had assumed that cases would infect approximately three others during the prodromal period in a fully susceptible population and that little or no transmission would occur after onset of rash. Eichner and Dietz pointed out that not only was this assumption at odds with field observations, it was also incompatible with their analysis of unusually detailed data from a 1967 smallpox epidemic in Nigeria. They demonstrated that, in a fully susceptible population, each case would have infected only ≈0.2 others during the prodromal period (15 times less than the other groups had assumed). Almost all of the transmission occurred after the rash developed. By hugely overestimating infectiousness in the prodromal period, the earlier analyses would have been massively biased against measures based on contact tracing and isolation of those developing fever. Further analysis with the new parameter estimates, and under rather pessimistic assumptions, showed that outbreaks could readily be controlled by contact tracing and case isolation alone (11).

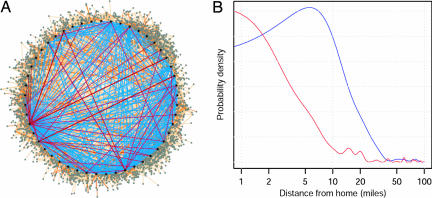
Riley and Ferguson’s model builds on this work and assumes that infectiousness is almost certainly much greater after the rash has developed than before and that cases are far more likely to infect household members than they are to infect other contacts. Social structuring is accounted for using the somewhat abstract concept of peer-group networks (Fig. 1A), but without the earlier limitation of a small population size. Journey-to-work census data are used to estimate the spatial distribution of extrahousehold contacts, and hence the likely rate of geographic dispersal of the disease. Apart from some differences in the interventions assessed, what makes this work unique and particularly impressive is the level of detail in the modeling of social and spatial interactions, the careful parameterization, and the sheer scale of the model.

Fig. 1.

Observed contact pattern data from contact surveys. (A) A peer-group network recorded at Warwick University. Network members are represented by black dots arranged in a circle. Contacts between members represent physical contact (red lines) and conversational nonphysical contact (blue lines). Contacts with individuals outside the peer group (gray dots) are represented by orange lines. (B) Observed spatial distribution of contacts, showing work-based contacts (blue) and physical contacts both in and out of work (red). Both images are based on unpublished data, courtesy of John Edmunds (Health Protection Agency, London, U.K.). The image in A is courtesy of Jonathan Read (Warwick University, Coventry, U.K.).

A major difficulty with this kind of work is the lack of contemporary smallpox data with which to calibrate and assess the model. The authors go a long way toward overcoming this problem by performing a careful sensitivity analysis. Their central findings are that rash-motivated case isolation alone would be able to control an outbreak except under what the authors consider to be the most pessimistic credible scenarios. In the worst case, a policy of ring vaccination (and rapid isolation when contact-traced individuals enter the prodromal period) would also be required. Regional mass vaccination was not found to be an effective policy: any benefits in reducing the duration of the epidemic would be greatly outweighed by deaths caused by the vaccine.

The paper raises some interesting methodological questions. How should human contact patterns be modeled, and how complex do models need to be? The use of journey-to-work data as a proxy for the spatial distribution of potentially infectious contacts is appealing because it is based on an objective and comprehensive data set. As with other approaches, however, it can only be considered a rough approximation to the truth. Different diseases may exhibit very different patterns of spatial spread depending on the mode of transmission. For example, because smallpox transmission requires close contact and because survey data suggest that such contacts tend to be made closer to home than work-based contacts (Fig. 1B), commuting data may overestimate the rate of geographic spread (although the lack of longer-distance travel in commuting data could also lead to the opposite bias). Does any of this matter? A spatial model is needed in this paper because an explicitly spatial intervention is considered, but would a nonspatial model have reached similar conclusions about the other interventions? If so, accurate modeling of spatial spread would, for many purposes, be reduced to a question of academic interest but little practical significance. It is not possible to tell from this paper how much difference space makes to the evaluation of nonspatial interventions (it would be nice to know!), but the comparable conclusions in Eichner’s far-simpler model suggest that it is probably far more important to get the model of the underlying biology right than to accurately account for spatial mixing. If so, this would be a good thing because spatial mixing is far harder to assess, is likely to vary considerably both within and between countries (limiting the generalizability of the conclusions), and may change unpredictably in response to an epidemic.

With hindsight, the U.S. smallpox vaccination policy of 2003 looks misguided. As Riley and Ferguson remind us, the 38,885 voluntary vaccinations during 2003 resulted in three deaths, two permanent disabilities, and 10 life-threatening illnesses. The new analysis adds further weight to the growing evidence that a future smallpox outbreak would be far easier to control than initial analyses suggested.