The galactic cosmic ray ionization rate

Abstract

The chemistry that occurs in the interstellar medium in response to cosmic ray ionization is summarized, and a review of the ionization rates that have been derived from measurements of molecular abundances is presented. The successful detection of large abundances of H₃⁺ in diffuse clouds and the recognition that dissociative recombination of H₃⁺ is fast has led to an upward revision of the derived ionization rates. In dense clouds the molecular abundances are sensitive to the depletion of carbon monoxide, atomic oxygen, nitrogen, water, and metals and the presence of large molecules and grains. Measurements of the relative abundances of deuterated species provide information about the ion removal mechanisms, but uncertainties remain. The models, both of dense and diffuse clouds, that are used to interpret the observations may be seriously inadequate. Nevertheless, it appears that the ionization rates differ in dense and diffuse clouds and in the intercloud medium.

The fractional ionization is a fundamental parameter, distinguishing the different physical regimes that occur in the interstellar medium. Because of the presence of electrons and positive ions the gas dynamics is modified by the coupling to the magnetic field which controls the transfer of angular momentum and the dissipation of turbulence. The fractional ionization determines the strength of the coupling and is a crucial aspect of the evolution of the interstellar gas and the formation of stars and planets. Energetic cosmic rays penetrate planetary atmospheres and create low-altitude ionospheric regions and drive a low-altitude chemistry.

Local regions of ionization are created in the interstellar medium by hot stars and prestellar objects radiating at UV and x-ray wavelengths and are found also in warm regions of the gas subjected to energetic shock waves generated by stellar outflows and supernovae. Cosmic rays are a global source of ionization distributed through the Galaxy. Measurements have been made of the cosmic ray flux at high energies, but at energies below 100 MeV the cosmic rays are excluded from the heliosphere by the solar wind and the total ionization rate cannot be directly determined.

Spitzer and Tomasko (1) used the available data to obtain a probable lower limit of 6.7 × 10⁻¹⁸ s⁻¹ for the ionization rate ζ of hydrogen atoms and from a general consideration of energies released in supernovae estimated a probable upper limit of 1.2 × 10⁻¹⁵ s⁻¹. More recently, Webber (2) used data from the Voyager and Pioneer spacecraft acquired at distances from the Sun out to 60 AU to determine a probable minimum rate of (3–4) × 10⁻¹⁷ s⁻¹ for H atoms. Webber drew attention to the possibility of enhanced rates exceeding 10⁻¹⁶ s⁻¹ near massive stars with strong stellar winds.

Cosmic rays heat the interstellar gas and drive an interstellar chemistry. Following the attribution by Klemperer (3) of an interstellar emission line at 89,188 MHz to the molecular ion HCO⁺, the influence of cosmic rays on the chemistry of dense clouds was discussed by Herbst and Klemperer (4) and Watson (5) and on the chemistry of diffuse clouds by Black and Dalgarno (6). It is applications of chemical models to interpret measurements of interstellar molecular abundances that has yielded the values of ζ in use today.

Dense Clouds

Typical values for the ionization rate in dense gas lie in the range from 1 to 5 × 10⁻¹⁷ s⁻¹ (7–14), depending on the details of the measurements, the physical model, and the chemistry. There may be real variations in the ionizing flux. In some cases, values of ζ as high as 10⁻¹⁵ s⁻¹ have been derived and the enhanced rate tentatively attributed to x-rays from a central source (15). A range of values with an average of (2.8 ± 1.6) × 10⁻¹⁷ s⁻¹ was derived by van der Tak and van Dishoeck (16) from measurements of HCO⁺ in several dense molecular clouds in the direction of massive young stars, but from measurements of H₃⁺ (17) rates in excess of 10⁻¹⁶ s⁻¹ were obtained. A later analysis of the cloud in the direction of the massive star-forming region AFGL 2591 yielded a rate of 5.6 × 10⁻¹⁷ s⁻¹, good to a factor of three (18). There was a discrepancy between the rates derived from HCO⁺ and H₃⁺ that could easily be removed by a modification of the assumed distribution of material in front of the source.

Because of the relative simplicity of the chemistry, the most direct determination of ζ would seem to be from studies of the abundance of H₃⁺ (17, 19, 20). In a cloud of H₂ molecules, cosmic rays ionize H₂ and produce H₂⁺ ions that immediately react with H₂ in a fast ion-molecule process to yield H₃⁺ ions (4, 5, 21). The H₃⁺ ions are removed by proton transfer reactions with the neutral constituents X, where X is any of interstellar CO, O, N₂, H₂O, and HD and D. If k(X) is the rate coefficient for the reaction

then in equilibrium the number density of H₃⁺ is given by (22)

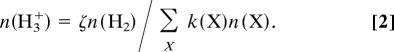The rate coefficient for the reaction with CO

is 1.7 × 10⁻⁹ cm³·s⁻¹ (23). The HCO⁺ ion then undergoes dissociative recombination

HCO⁺ is also removed by H₂O, producing H₃O⁺. The reactions with atomic oxygen,

have a total rate coefficient of 8.0 × 10⁻¹⁰ cm³·s⁻¹ (24). The process initiates an ion-molecule sequence that terminates in H₃O⁺ (4), which in turn leads to OH (22). The observation of H₃O⁺ would be a valuable diagnostic of oxygen depletion (25). The reaction with N₂ is similar to that for CO. It produces N₂H⁺, which can be lost by dissociative recombination,

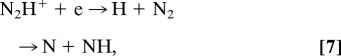and by reaction with CO,

Eq. 2 shows that the abundance of H₃⁺ is a constant, increasing with the ionizing flux and with the amount of depletion of the heavy neutral gas components. For ζ = 5 × 10⁻¹⁷ s⁻¹ and no depletion, n(H₃⁺) = 5 × 10⁻⁵ cm⁻³.

With increasing depletion dissociative recombination

becomes significant. The rate of 9 and 10 was once thought to be negligible. It is now known to be rapid (26), and most of the early estimates of ζ in diffuse clouds are too small. If α is the rate coefficient of 9 and 10 combined, the abundance of H₃⁺ is given by

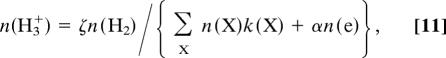where n(e) is the electron number density.

Positive ions X⁺ may also be removed by charge transfer with metal atoms M,

A simple model of the effects of charge transfer was given by Oppenheimer and Dalgarno (27), and more complex studies of its influence on the ionization balance of protoplanetary discs have been carried out by Fromang et al. (28) and by Ilgner and Nelson (29, 30). The ionization source is cosmic rays and x-rays from the parent star (31). If k(M) is the rate coefficient of 12,

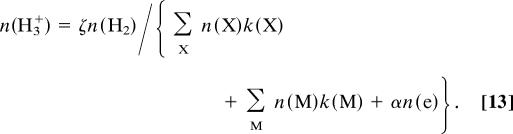The metal ions are unreactive and recombine slowly by radiative recombination and dielectronic recombination,

The molecular ions and the metal ions may also be removed by neutralization on grain surfaces (27, 32).

The ionization balance and the ion distribution may be greatly modified by the presence of large molecules such as the polycyclic aromatic hydrocarbons (PAHs). PAHs are expected to be present in dense interstellar clouds (33). PAHs have ionization potentials of typically 6.5 eV, and charge transfer

will occur for most of the interstellar ions. The PAH⁺ ions will be removed by recombination with electrons and by mutual neutralization with anions PAH⁻,

formed by attachment processes

(34, 35). The equilibrium abundance of H₃⁺ may be written

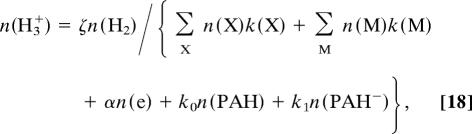where k₀ is the rate coefficient of

and k₁ is the rate coefficient of

Model chemistries of dense clouds appear not to include reactions involving PAHs, presumably on the assumption that any PAH molecules that are present are absorbed onto grains and do not remain in the gas phase. Their influence could be substantial (36). Recombination onto grain surfaces may be still more significant (27, 32). We add n(g)k(g) to the denominator of Eq. 18. Inclusion of any metals or PAHs or grains will increase the inferred ionization rate.

The possible effects of depletion, metals, large molecules, and grains can be assessed by a consideration of the deuteration of molecular ions by fractionation processes. Observations show that the ratio of the abundances of molecular ions such as DCO⁺ to HCO⁺ and neutral molecules such as H₂CO and HDCO is often much enhanced above the cosmic [D/H] ratio. Doubly and triply deuterated isotopologs have also been detected (37). The fractionation is driven by the exothermic reaction (38)

H₂D⁺ is removed by the reverse reaction

and by the same set of reactions that destroyed H₃⁺. We get

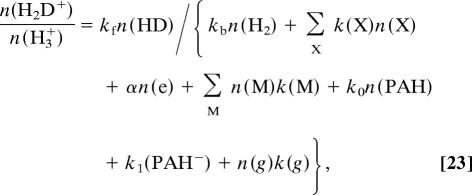where k_f is the rate coefficient of reaction 21, k_b is the rate coefficient of reaction 22, and the other rate coefficients refer to the deuterated analogues of the reactions in the denominator of 18. The forward and backward rate coefficients are related by k_b = k_f exp(−T/T*). A value of T* = 220 K is usually adopted together with a forward rate coefficient of 1.7 × 10⁻⁹ cm³·s⁻¹ (37) although they have been brought into question by measurements of Gerlich and Schlemmer (39). The consequences to interstellar chemistry have been explored by Gerlich, Herbst, and Roueff (40). They appear to indicate a small increase in the ionization rate. The rate coefficients in 23 may be taken equal to those in 17 except for α, which is about half that of H₃⁺ (41). Then it is clear from expressions 18 and 23 that the abundance of H₃⁺ and the ratio of H₂D⁺ to H₃⁺ increase together with the depletion of CO and O and N₂ (22) and provide a powerful probe of star-forming regions. The deuterated ion H₂D⁺ has been detected in a low-mass protostar (42), a prestellar core (43), and circumstellar discs (44). Ceccarelli et al. (44) interpreted the molecular data with a sophisticated chemistry to conclude that ζ = 5 × 10⁻¹⁷ s⁻¹ for the disk source TW Hya and a magnitude lower for DM Tau. The values of ζ are uncertain because they depend on assumptions about depletion and the ratio n(H₂D⁺)/n(H₃⁺) is not known.

Because reactions of H₃⁺ and H₂D⁺ with CO are the principal sources of HCO⁺ and DCO⁺, of which there have been many measurements (7, 45), the ratio of H₂D⁺ to H₃⁺ can be obtained from the ratio of DCO⁺ to HCO⁺. Other ions are also useful, particularly N₂D⁺ and N₂H⁺ (10). Expression 23 is modified by processes involving atomic deuterium. Because of fractionation and the resulting high abundances of deuterated ions there is a large supply of deuterium atoms through dissociative recombination,

The atomic D/H ratio is considerably enhanced over the cosmic ratio and reactions of D atoms,

may contribute to the fractionation when ζ is large (46).

To a close approximation, n(DCO⁺)/n(HCO⁺) = (1/3)n(H₂D⁺)/n(H₃⁺). The measured ratio provides an upper limit to any one of the individual terms in the denominator of Eq. 23. Thus defining the parameter f by the relationship

we may write Eq. 23 in the form

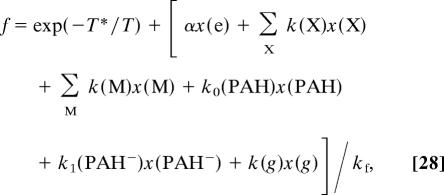where x(Y) is the fractional abundance n(Y)/n(H₂). Then

for any of the neutral atoms and molecules, metals, PAHs, PAH⁻s, or grains. Depending on the physical environment, different terms of f may control the loss of H₃⁺. When one term dominates, f provides an actual measure of the corresponding fractional abundance. Of special importance is the fractional ionization x(e). Estimates for low-mass cloud cores lie between 10⁻⁸ and 10⁻⁶ (47), between 10^−7.5 and 10^−6.5 (7), and between 1.5 × 10⁻⁸ and 7.5 × 10⁻⁸ (11). With modest depletion the rates of removal of H₃⁺ by neutral atoms and molecules, by metals, and possibly by PAH⁻ may be comparable to dissociative recombination. To reproduce the measured fractionation, depletion, often severe, must be invoked in the chemical models. Observations of other molecular species are used to estimate the depletion (47). PAHs are not usually considered explicitly, but their influence is incorporated in the recombination in collisions of ions with grains. (The observations place an upper limit of ≈10⁻⁷ for the fraction of PAHs.) Grain recombination has been explicitly included in models of dense cloud cores (47), protoplanetary discs (48), and completely depleted prestellar cores (49). In reproducing the measured abundances, all models take implicit account of grain recombination. In the absence of dissociation events the chemistry depends not on ζ itself but on the ratio ζ/n(H₂) so that some of the variation in the derived values of ζ may be due to differences in the adopted densities. Some of the variations are probably real. No definitive value for dense clouds emerges from the numerous studies, but it appears that the canonical traditional value of 1 × 10⁻¹⁷ s⁻¹ is too small and 5 × 10⁻¹⁷ s⁻¹, even 1 × 10⁻¹⁶ s⁻¹, may be a more realistic mean value.

Diffuse Molecular Clouds

Values of ζ have been obtained from analyses of the chemical composition of diffuse clouds for which reactions driven by photons play a major role and atomic hydrogen and molecular hydrogen are both present in significant amounts. Diffuse clouds have visual extinctions A_v up to one magnitude or so, and the molecules that have been detected are mostly diatomic species (50). Cosmic rays ionize H and H₂ and produce H⁺ and H₂⁺ at rates, respectively, of ζ(H) s⁻¹ and ζ(H₂) s⁻¹. The ratio of ζ(H₂)/ζ(H) depends on the mixture of H and H₂ in the gas (51), but the conventional assumption that ζ(H₂) = 2ζ(H) is an adequate approximation for most purposes.

The molecules OH and HD are direct probes of the ionization rates (6). H atoms are ionized and the H⁺ ions undergo charge transfer

The rate coefficient is sensitive to temperature (52, 53). If there is little H₂ in the gas, Eq. 30 is followed by its reverse (54). If H₂ is present, O⁺ reacts with H₂ in a sequence that leads to OH and H₂O (4). The sequence can be entered also from the reactions 5 and 6. OH is destroyed by

It is also destroyed by photodissociation by the interstellar radiation field and the cosmic ray-induced radiation (55, 56). Equating the production and loss rates of OH, we may obtain the ionization rate. Hartquist, Black, and Dalgarno (57) reported rates of 1.5 × 10⁻¹⁷ s⁻¹, 2.2 × 10⁻¹⁷ s⁻¹, and 2.5 × 10⁻¹⁶ s⁻¹ for clouds in the direction of ζ Oph, ζ Per, and ο Per, respectively. They suggested that the enhanced rate for ο Per was a reflection of the energetic event that gave rise to the observed motion of the ο Per cloud. Black and Dalgarno (58) had earlier obtained 1.6 × 10⁻¹⁷ s⁻¹ for ζ Oph and Black, Hartquist, and Dalgarno (59) the same value for ζ Per. These values were consistent with values inferred from measurements of HD. HD is made by reactions initiated by the ionization of H₂ and H. Thus

(5, 60), with D⁺ supplied by

is a source of HD as is the dense cloud sequence

(Analysis of the HD abundances yielded a value of 2 × 10⁻⁵ for the cosmic ratio [D/H].) The most comprehensive studies of diffuse clouds were those of van Dishoeck and Black (61) using data on the column densities of CO, OH, C₂, CN, OH, HD, and rotationally excited H₂. They were seeking a value of ζ common to the clouds in front of ζ Oph, ο Per, χ Oph, and ζ Per, and they selected ζ = 5 × 10⁻¹⁷ s⁻¹. These early values were obtained at a time when it was believed dissociative recombination of H₃⁺ was slow. However, van Dishoeck and Black did consider the possibility that it was fast, as we now believe, and they revised the values of ζ upwards to 4 × 10⁻¹⁶ s⁻¹ for ζ Oph, 1–2 × 10⁻¹⁶ s⁻¹ for ζ Per, and 8 × 10⁻¹⁶ s⁻¹ for ο Per. Federman, Weber, and Lambert (62) derived for the ionization rate of H₂, ζ = 4 × 10⁻¹⁷ s⁻¹ for ο Per and 3 × 10⁻¹⁷ s⁻¹ for ζ Per. The different rates stem from the assumptions made about the intensity of the UV photons that dissociate OH and the value of α.

From a consideration of HD abundances resulting from H⁺ and the loss of H⁺ in collisions with grains, Liszt (63) proposed 4 × 10⁻¹⁶ s⁻¹ as a lower limit to the ionization rate of H₂ in diffuse clouds, but he may have underestimated the source from reaction 35. In a major discovery, McCall et al. (26) detected H₃⁺ in the ζ Per cloud. The chemistry is simple. The H⁺ ions are removed by dissociative recombination, which in a diffuse gas is much faster than the other loss processes that complicate the chemistry of dense clouds. Then in equilibrium,

In a diffuse cloud, n(e) ∼ n(C⁺). The absorption measurements yield the column densities N(H₃ ⁺) and N(C⁺), which are integrals of n(H₃⁺) and n(C⁺) along the line of sight. McCall et al. (26) assumed that the density distribution was uniform so that the n(H₃⁺)/n(C⁺) = N(H₃⁺)/N(C⁺). With the assumption that n(H₂) = 250 cm⁻³ throughout the cloud, they obtained ζ = 1.2 × 10⁻¹⁵ s⁻¹. Le Petit, Roueff, and Herbst (64) constructed a more elaborate two-phase model consisting of an extended diffuse region with a density n_H = n(H) + 2n(H₂) = 100 cm⁻³ and a dense edge with n_H = 2 × 10⁴ cm⁻³, and they explored the possible contribution of shocks to the formation of molecules. They reproduced the measured abundances of a wide range of atoms, ions, and molecules to within a factor of three with an ionization rate of 2.5 × 10⁻¹⁶ s⁻¹. The column density N(H₃⁺) was 2.9 × 10¹³ cm⁻² compared with the measured value of 8.0 × 10¹³ cm⁻². Increases in ζ to bring N(H₃⁺) into agreement are constrained by the column density of OH.

H₃⁺ has been detected in the direction of the star Cygnus OB2 No. 12 (20, 65) in what is thought to be diffuse gas. McCall et al. (65) adopted a uniform density model with n(H) = 10 cm⁻³, and they noted that the path length needed to reproduce N(H₃⁺) was extreme. The difficulties encountered in their model would be alleviated by a larger ionization rate of 3 × 10⁻¹⁶ s⁻¹ or more (20). Gredel, Black, and Yan (66) developed a comprehensive model with greater densities in which the ionization is due to x-rays. They obtained agreement with a range of molecular observations with ζ = (0.6–3.0) × 10⁻¹⁶ s⁻¹.

An alternative model was suggested by Cecchi-Pestellini and Dalgarno (67, 68). In their model, clumps of material with a mean density of 100 cm⁻³ and a visual extinction of 1.6 mag are embedded in a tenuous interclump medium. The clumps contain dense cores. The ionizing flux that reproduces the measured H₃⁺ abundance is 6 × 10⁻¹⁷ s⁻¹. Some support for the model is provided by the detection of HCO⁺ (69).

Chemistry of the Intercloud Medium

The density of the intercloud medium is low, and the chemistry is limited to the recombination of cations with electrons, PAHs, and grains if any are present. The electrons are primarily due to photoionization of atoms like carbon, silicon, and iron that have ionization potentials of <13.6 eV and a secondary contribution from cosmic ray ionization of hydrogen and helium. The H⁺ ions and the He⁺ ions reveal their presence by radio recombination lines. Hughes, Thompson, and Colvin (70) gave an estimate of 2 × 10⁻¹⁵ s⁻¹, Shaver (71) reported an upper limit of 2 × 10⁻¹⁶ s⁻¹, and Payne, Salpeter, and Terzian (72) recommended an upper limit of 1.×10⁻¹⁵ s⁻¹ for the ionization rate of H atoms from comparisons of free–free absorption and 21-cm data, but Liszt (63) has argued that taking into account recombination of H⁺ in collisions with PAHs and PAH⁻s and grains will allow an increase in these upper limits. These limits were important because they cast doubt on the validity of the two-phase model of the interstellar medium (73) and perhaps should be reexamined.

Variability of the Ionization Rate

The different estimates of ζ raise the question of its possible variation. The cosmic rays lose energy in ionizing and exciting the gas through which they travel. The corresponding path length R traversed by the cosmic rays is inversely proportional to the gas density. Table 1 lists the range in the form of the column depth of penetration Rn(H₂) cm⁻² for incident energies from 1 to 100 MeV of protons moving along a straight line path (74). The column densities N_H of gas in front of the stars ζ Oph, ζ Per, and ο Per are, respectively, 1.4 × 10²¹, 1.6 × 10²¹, and 1.6 × 10²¹ cm⁻². If the origin of the cosmic rays is external to the clouds, some loss of the low-energy flux of protons may occur. In the case of ο Per there appears to be an enhancement of the cosmic rays. Hartquist and Morfill (75) attributed it to stochastic acceleration in an associated supernova remnant. The possible influence of magnetic fields was noted by Greenberg (76) and further discussed by Nakano and Tademaru (77) and Cesarsky and Volk (78). Hartquist, Doyle, and Dalgarno (79) considered the intercloud cosmic ray ionization rate, taking into account the screening mechanism of Skilling and Strong (80). They calculated intercloud rates 20–100 times the diffuse cloud rates. Padoan and Scalo (81) have developed a comprehensive description of the confinement of cosmic rays by scattering from self-generated Alfven waves, and they predicted that large variations would occur in the cosmic ray intensities in the interstellar medium. They cited the case of ζ Per as an example.

Table 1.

Range of protons R × n(H₂) cm⁻²

Proton energy, MeV	R × n(H2)
1	2.5 × 1020
2	8.8 × 1020
10	1.6 × 1022
20	5.9 × 1022
50	3.2 × 1023
100	1.2 × 1024

In conclusion, considerable uncertainties attend the values of the cosmic ray ionization rates in the interstellar medium, but there are indications that the range could be narrow, lying between 10⁻¹⁶ and 10⁻¹⁵ s⁻¹ from dense cores in molecular clouds to the intercloud medium. The interesting question may be not why are they so different but why are they so similar.

Glossary

Abbreviation:

PAH

polycyclic aromatic hydrocarbon.