Nature designs tough collagen: Explaining the nanostructure of collagen fibrils

Abstract

Collagen is a protein material with superior mechanical properties. It consists of collagen fibrils composed of a staggered array of ultra-long tropocollagen (TC) molecules. Theoretical and molecular modeling suggests that this natural design of collagen fibrils maximizes the strength and provides large energy dissipation during deformation, thus creating a tough and robust material. We find that the mechanics of collagen fibrils can be understood quantitatively in terms of two critical molecular length scales χ_S and χ_R that characterize when (i) deformation changes from homogeneous intermolecular shear to propagation of slip pulses and when (ii) covalent bonds within TC molecules begin to fracture, leading to brittle-like failure. The ratio χ_S/χ_R indicates which mechanism dominates deformation. Our modeling rigorously links the chemical properties of individual TC molecules to the macroscopic mechanical response of fibrils. The results help to explain why collagen fibers found in nature consist of TC molecules with lengths in the proximity of 300 nm and advance the understanding how collagen diseases that change intermolecular adhesion properties influence mechanical properties.

Materials found in nature often feature hierarchical structures ranging from the atomistic and molecular scales to macroscopic scales (1–5). Many biological materials found in living organisms, often protein-based, feature a complex hierarchical design.

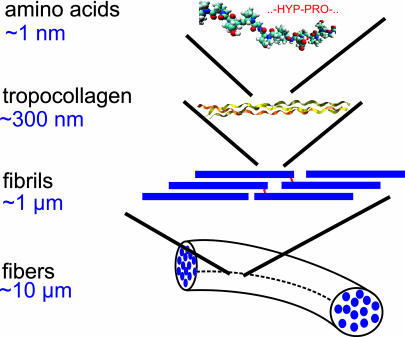
Collagen, the most abundant protein on earth, is a fibrous structural protein with superior mechanical properties, and it provides an intriguing example of a hierarchical biological nanomaterial (4, 6–18). Collagen consists of tropocollagen (TC) molecules that have lengths of L ≈ 280 nm and diameters of ≈1.5 nm, leading to an aspect ratio of ≈190 (6, 7, 9, 18–20). Staggered arrays of TC molecules form fibrils, which arrange to form collagen fibers (Fig. 1).

Fig. 1.

Schematic view of some of the hierarchical features of collagen, ranging from the amino acid sequence level at nanoscale up to the scale of collagen fibers with lengths on the order of 10 μm. Here we focus on the mechanical properties of collagen fibrils consisting of a staggered array of TC molecules.

Collagen plays an important role in many biological tissues, including tendon, bone, teeth, and cartilage (6, 7, 13, 15, 19, 21). Severe mechanical tensile loading of collagen is significant under many physiological conditions, as in joints and in bone (22, 23). Despite significant research effort over the past couple of decades, the geometry and typical length scales found in collagen fibrils, the deformation mechanisms under mechanical load, and, in particular, the relationship between those mechanisms and collegen’s molecular and intermolecular properties, are not well understood. Moreover, the limiting factors of the strength of collagen fibrils and the origins of toughness remain largely unknown.

Some experimental efforts focused on the deformation mechanics of collagen fibril at nanoscale, including the characterization of changes of D-spacing and fibril orientation (18, 20, 24), analyses that featured x-ray diffraction (18) and synchrotron radiation experiments (19). Other experimental studies were focused on the averaged response of arrays of collagen fibrils, considering nanoscale deformation mechanisms (3).

However, most research has been focused on the macroscopic, overall mechanical properties of collagen fibers and scales beyond, for example, of tissues, often without explicitly considering the molecular nanoscale structure (21). Other studies focused on the properties of individual TC molecules without linking to the response of macroscopic materials (7, 9, 10, 25, 26).

To develop a fundamental and quantitative understanding of collagen mechanics, it is critical to develop theoretical models encompassing the mesoscopic scales between the atomistic and macroscopic levels. There exists no model that links the properties of individual molecules with the overall mechanical response of fibrils or fibers, considering the different types of chemical bonding and nanoscale mechanics and geometry. The role of the staggered structure and the reasons for the specific length scales and high aspect ratio of TC molecules remain unexplained.

An improved understanding of the nanomechanics of collagen may help in the development of biomimetic materials or for improved scaffolding materials for tissue engineering applications (27). Diseases such as Ehlers–Danlos (28), osteogenesis imperfecta, Scurvy, or the Caffey disease (29) are caused by defects in the molecular structure of collagen altering the intermolecular and molecular properties due to genetic mutations, which modifies the mechanical behavior of collagen fibrils.

Here we use a hierarchical multiscale modeling scheme based on atomistic and molecular simulation to describe the mechanical properties of collagen under large stretch, leading to permanent deformation or fracture. We show that the key to understanding the mechanics of collagen is to consider the interplay between the mechanics of individual TC molecules with characteristic length scales, the intermolecular chemical interactions, and the mesoscopic properties arising from hundreds of molecules arranged in fibrils. We explore the mechanics of collagen by considering different nanostructural designs, and pay specific attention to the details of molecular and intermolecular properties and their impact on the mechanical properties.

Results and Discussion

Under macroscopic tensile loading of collagen fibrils, the forces are distributed predominantly as tensile load carried by individual and as shear forces between different TC molecules (Fig. 1, fibrils). This model is similar to the shear–tension model suggested for bone (2, 3, 5, 17).

Energetic effects rather than entropic contributions govern the elastic and fracture properties of collagen fibrils and fibers. The fracture strength of individual TC molecules is largely controlled by covalent polypeptide chemistry. The shear strength between two TC molecules is controlled by weak dispersive and hydrogen bond interactions and by some intermolecular covalent cross-links.

Deformation Modes of Collagen Fibrils: Critical Molecular Length Scales.

We first consider a simplistic model of a collagen fibril by focusing on a staggered assembly of two TC molecules (Fig. 2a). The shear resistance between two TC molecules, denoted τ_shear, leads to a contact length-dependent force,

where L_C is the contact length, and F_tens is the applied force in the axial molecular direction, which can alternatively be expressed as tensile stress σ_tens = F_tens/A_c by considering the molecular cross-sectional area A_c. The parameter α describes the fraction of contact length relative to the molecular length, α = L_C/L. Because of the staggered geometry, the shear resistance increases linearly with L, thus F_tens ∼ τ_shearL. This model holds only if shear deformation between the molecules is homogeneous along the axial direction.

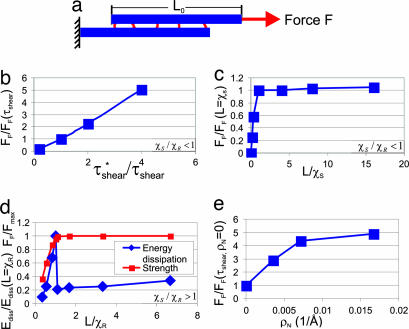
Fig. 2.

Study of a BM assembly of TC molecules. (a) Simplistic model of a collagen fibril used to study the dependence of the BM fibril tensile strength F_F on molecular length and adhesion strength. (b) The variation of F_F due to changes of the adhesion strength [tensile strength normalized by F_F(τ_shear) and adhesion strength normalized by τ_shear, considering fully hydrated TC molecules without cross-links, χ_S/χ_R < 1]. (c) F_F as a function of molecular length [normalized by its maximum value F_F(L/χ_S = 1), for χ_S/χ_R < 1]. At the critical molecular length (L/χ_S = 1), the tensile force saturates, corresponding to a change from homogeneous shear to propagation of slip pulses. (d) The transition from homogeneous shear to brittle-like rupture of TC molecules, depicting F_F and the dissipated energy (both normalized by reference values for χ_S/χ_R > 1). Energy dissipation is maximized when L/χ_R = 1, when the transition from shear to molecular rupture occurs. (e) The effects for variations in cross-link density on the BM fibril strength (normalized by the strength of the cross-link-free BM fibril) for a collagen molecule with a length of 840 Å, assuming a regular distribution of cross-links. The BM fibril strength approaches a finite value for large cross-link densities.

An alternative to homogeneous intermolecular shear is propagation of slip pulses due to localized breaking of intermolecular “bonds.” In the spirit of Griffith’s energy argument describing the onset of fracture, nucleation of slip pulses is controlled by the applied tensile stress σ_R, where

where E is Young’s modulus of an individual TC molecule, and γ relates to the energy required to nucleate a slip pulse.

When σ_tens < σ_R, deformation is controlled by homogeneous shear between TC molecules. However, when σ_tens ≥ σ_R, intermolecular slip pulses are nucleated, which leads to a critical molecular length

For fibrils in which L < χ_S, the predominant deformation mode is homogeneous shear. When L > χ_S, propagation of slip pulses dominates. The strength of the fibril is then independent of L (Eq. 3), approaching τ_shearαχ_S. This concept is somewhat similar to the flaw tolerance length scale proposed for mineral platelets in bone (2).

The length scale χ_S depends on the material parameters and interaction between molecules. If γ assumes very large values, for instance because of high cross-linking density or the effects of solvents (e.g., low water concentration), the tensile forces in each TC molecule (Eq. 1, or F_tens ∼ L) reaches the tensile strength of TC molecules, denoted by F_max, before homogeneous shear or slip pulses are nucleated. (F_max is a material constant that ultimately depends on the molecular structure of the TC molecule, including the influence of the chemical environment, e.g., the presence of enzymes.)

Considering F_tens = F_max leads to a second critical molecular length scale,

This molecular length χ_R characterizes when the transition from molecular shear to brittle-like rupture of individual TC molecules occurs. The response of collagen fibrils to mechanical load changes from shear or glide between TC molecules, to molecular fracture as L increases. For L > χ_R, TC molecules break during deformation, whereas, for L ≤ χ_R, deformation is characterized by homogeneous intermolecular shear.

The integrity of a complete collagen fibril is controlled by the strength of the weakest link. Thus, the interplay of the critical length scales χ_S/χ_R controls the deformation mechanism.

When χ_S/χ_R < 1, slip-pulse nucleation governs at large molecular lengths, whereas, when χ_S/χ_R > 1, fracture of individual TC molecules occurs. In both cases the strength does not increase by making L larger than χ_S or χ_R. The maximum strength of the fibril is reached at L = L_χ = min(χ_R, χ_S), which is true for any arbitrary length L of a TC molecule. For L/L_χ < 1, homogeneous intermolecular slip dominates deformation. For molecules with L > L_χ, either slip pulses or fracture set in, depending on which of the two length scales χ_S or χ_R is smaller. For short TC molecules, the strength of collagen fibrils tends to be small and depends on L_C. When L ≈ L_χ, the maximal tensile strength of fibrils is reached.

Furthermore, choosing L ≈ L_χ leads to maximized energy dissipation during deformation. The work necessary to separate two fibers in contact along a length L_C under macroscopic tensile deformation is

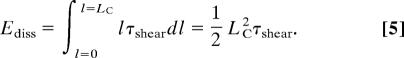Eq. 5 predicts an increase of the dissipated energy with increasing molecule length, therefore favoring long molecules. If χ_R < χ_S, the critical length L_χ constitutes an upper bound for L_C, because molecules rupture before shear deformation sets in. After bond rupture and formation of shorter molecules, E_diss decreases significantly, suggesting that L > L_χ is not favored. Energy dissipation is at a maximum for L ≈ L_χ. If χ_S < χ_R, the dissipated energy can be approximated (assuming L_C > χ_S) by

suggesting that, after a quadratic increase for small molecular lengths, the dissipated energy increases linearly with L_C.

Molecular Modeling of Bimolecular (BM) Assemblies.

All simulations are carried out by using the mesoscopic molecular bead model of collagen. In the spirit of computational experiments (30, 31), we explore how different nanoscale designs and modifications in molecular properties influence the mechanical properties of collagen fibrils.

First, we focus on computational experiments of shearing an assembly of two TC molecules using steered molecular dynamics (see Fig. 2a) (32). The overlap α = 3/4, according to x-ray diffraction analyses of collagen fibrils (18).

This BM model serves as a simplistic representation of the fibril microstructure. (Note that the strength of the BM fibril is reduced compared with a complete collagen fibril.) We use a reference (control) system of fully hydrated, cross-link-free fibril. Full atomistic modeling reveals that F_max ≈ 24 × 10³ pN and τ_shear ≈ 5.55 pN/Å, and χ_R ≈ 436 nm for this case (see the supporting information, which is published on the PNAS web site).

Our objective is to demonstrate the dependence of the deformation mode (intermolecular shear, propagation of slip pulses, or brittle-like rupture) on the TC molecule length and adhesion strength between TC molecules.

Fig. 2b depicts the normalized BM fibril tensile strength for different values of the normalized adhesion strength, τ^*_shear/τ_shear, when χ_S/χ_R < 1. The adhesion strength τ^*_shear = μτ_shear, where 0 < μ < 4.

The results corroborate the predictions made by Eq. 1: The stronger the adhesion between two molecules, the larger the strength of a collagen fibril. Increased adhesion between TC molecules could be due to increased cross-linking density [for example, during aging (33)].

Fig. 2c shows the BM tensile strength as a function of variations of the molecular length L/χ_S and for χ_S/χ_R < 1. In agreement with the considerations reported above, we find a transition in deformation mode from homogeneous shear between two TC molecules to a regime in which slip pulses are nucleated as L is increased. Analysis of the molecular displacement fields shows the existence of slip pulses as proposed theoretically. The strength of the fibril approaches a finite value when L > χ_S.

By considering the point of transition between homogeneous shear and slip pulses, we estimate χ_S^BM ≈ 42 nm. Therefore χ_S/χ_R < 1, indicating that either homogeneous shear or slip pulse propagation dominate deformation.

Fig. 2d depicts the transition from homogeneous shear to brittle-like rupture of TC molecules when χ_S/χ_R >1. This condition is realized by modifying the properties of the mesoscale model to feature lower molecular fracture forces. (r_break is chosen at 14.5 Å, which leads to a smaller value of F_max; thus, χ_R decreases to ≈250 Å.) The plot depicts both the strength of the BM fibril and the dissipated energy. The dissipated energy is maximized when L ≈ χ_R, in agreement with the theoretical model. Repeated fracture of TC molecules results in formation of a large number of smaller TC segments, leading to a reduction in strength.

Fig. 2e depicts how the tensile strength of BM fibrils depends on the cross-linking density. The BM fibril strength increases with larger cross-linking density but starts to saturate for cross-link densities beyond 0.01 Å⁻¹. For larger cross-linking densities, the ratio χ_S/χ_R changes to values larger than one and molecular rupture occurs.

The computational results corroborate the theoretical analysis reported above and confirm the existence of the two length scales and the interplay of dominating deformation modes characterized by the factor χ_S/χ_R.

Molecular Modeling of Mechanical Properties of Larger Collagen Fibrils.

We now model the deformation behavior of a more realistic fibril geometry as shown in Fig. 1 (beside the label “fibril”), by studying the change in mechanical properties due to variations in molecule length L.

Because of the staggered design of collagen fibrils with an axial displacement of ≈25% of the molecular length (18), the contact length between TC molecules in a fibril is proportional to L. The length scales suggested in Eqs. 3 and 4 therefore have major implications on the deformation mechanics of collagen fibrils.

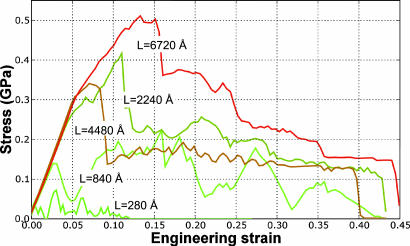
We consider fully hydrated cross-link-free collagen fibrils serving as a model for cross-link-deficient collagen. Fig. 3 shows the stress versus strain response of a collagen fibril for different molecular lengths L. The results suggest that the onset of plastic deformation, the maximum strength, and large-strain mechanics of collagen fibrils depend on the molecular length.

Fig. 3.

Stress versus strain of a collagen fibril for different molecular lengths (model for cross-link-deficient collagen, because no covalent cross-links are present in the collagen fibril). The longer the molecular length, the stronger the fibril. The maximum elastic strength achieved by collagen fibrils approaches ≈0.3 GPa, with the largest stress at ≈0.5 GPa. The onset of intermolecular shear can be recognized by the deviation of the stress–strain behavior from a linear elastic relationship.

Fig. 4a shows the normalized elastic strength of the fibril as a function of molecular length L. The results suggest an increase up to ≈200 nm, then reaching a plateau value of ≈0.3 GPa (results normalized by this value). The elastic uniaxial strains of collagen fibrils reach up to ≈5%. The maximum stress reaches up to 0.5 GPa during plastic deformation.

Fig. 4.

Elastic strength and energy dissipation of the collagen fibril. (a) The critical stress at the onset of plastic shear between TC molecules. An initial regime of linear increase of strength with molecular length is followed by a regime of finite strength at a plateau value. (b) The dissipated energy during deformation per unit volume in a collagen fibril as a function of molecular length normalized by the maximum value. An initial steep increase is followed by a plateau regime, with a local maximum of ≈220 nm. The smooth curve is a fit of a third-order expansion to the simulation data.

The molecular length at which the saturation occurs corresponds to a change in deformation mechanism, from homogeneous shear (L→0) to nucleation of slip pulses (L→∞). The corresponding molecular length provides an estimate for the critical molecular length scale χ_S ≈ 200 nm.

This length scale χ_S is larger in the actual collagen fibril geometry compared with the simplistic BM model [see Molecular Modeling of Bimolecular (BM) Assemblies]. Unlike in the BM case, where loading is applied at the ends of the molecule, in the actual fibril geometry the distribution of shear forces along the molecular axis is more homogeneous. This change in boundary conditions generally favors homogeneous shear over slip-pulse nucleation. Furthermore, nucleation of slip pulses requires bending of the molecule and is therefore energetically more expensive because of geometric confinement due to the lattice-like arrangement in which different molecules are immediately neighboring other molecules (Fig. 1).

We note that χ_R ≈ 436 nm, as described in the previous section (it is a material property of the reference system). Therefore, the ratio χ_S/χ_R < 1, suggesting a competition between slip pulses and homogeneous shear as the molecular length is varied. This result suggests that cross-link-deficient collagen may predominantly undergo intermolecular shear deformation.

Fig. 4b depicts the energy dissipated during deformation per unit volume. We observe a continuous increase with molecule length L, reaching a maximum at a critical molecular length L_χ, then a slight decrease. Energy dissipation increases further at ultra-large molecular lengths beyond 400 nm because of longer shear paths during slip-pulse propagation. The modest increase in energy dissipation for ultra-long molecules may be an inefficient solution, because assembling such ultra-long molecules into regular fibrils is challenging.

Conclusion

Our results suggest that the length of TC molecules and strength of intermolecular interactions plays a significant role in determining the deformation mechanics, explaining some of the structural features of collagen found in nature.

The two length scales χ_S and χ_R provide a quantitative description of the three different deformation mechanisms in collagen fibrils: (i) intermolecular shear, (ii) slip-pulse propagation, and (iii) fracture of individual TC molecules (see Figs. 2–4).

The governing deformation mechanism is controlled by the ratio χ_S/χ_R: Whether molecular fracture (χ_S/χ_R > 1) or slip pulses (χ_S/χ_R < 1) dominate deformation, the strength of the fibril approaches a maximum at L_χ = min (χ_R, χ_S) that cannot be overcome by increasing L. When L ≈ L_χ, tensile forces due to shear are in balance with either the fracture strength of TC molecules (χ_S/χ_R > 1) or with the critical load to nucleate slip pulses (χ_S/χ_R < 1). In either case, the maximum strength of the fibril is reached when L ≈ L_χ, including maximum energy dissipation.

When the length of collagen molecules is close to the critical length scale L_χ, two objectives are satisfied: (i) Under large deformation, TC molecules reach their maximum strength without leading to brittle fracture, and (ii) energy dissipation during deformation is maximized. This concept may explain the typical staggered geometry of collagen fibrils found in experiment with extremely long molecules, leading to large energy dissipation during deformation (Fig. 4).

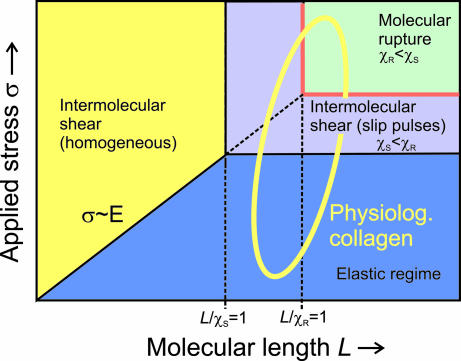
The mechanisms of deformation and their dependence on the molecular design are summarized in a deformation map shown in Fig. 5.

Fig. 5.

Deformation map of collagen fibrils. The mechanical response is controlled by two length scales, χ_S and χ_R. Intermolecular shear governs deformation for small molecular lengths, leading to a relatively small strength of the collagen fibril. For large molecular lengths, either intermolecular slip pulses (χ_S/χ_R < 1) or rupture of individual TC molecules (χ_S/χ_R > 1) dominate. The maximum strength and maximum energy dissipation of the collagen fibril is reached at a critical molecular length scale L_χ that is defined as the minimum χ_S and χ_R. The regime χ_S/χ_R > 1 refers to the case of strong intermolecular interactions (e.g., increased cross-link densities or due to the effects of solvants that effectively increase molecular adhesion). Physiological collagen typically features long molecules with variations in molecular interaction so that either intermolecular shear (e.g., slip pulses) or molecular fracture are expected to dominate.

Slip pulses are nucleated by localized larger shear stresses at the end of the TC molecules. Thus, cross-links at these locations provide a molecular-scale mechanism to prevent slip-pulse nucleation because this leads to an increase of the energy required to nucleate slip pulses and, thus, to a larger value of γ. This increase of γ results in an increase of χ_S due to the scaling law

As a consequence, the ratio χ_S/χ_R increases, making collagen fibrils stronger. Remarkably, this nanoscale distribution of cross-links agrees with the natural collagen design seen in experiment, often showing cross-links at the ends of the TC molecules [reminiscent of crack bridging (23, 34)] (3–5).

Cross-links provide additional strength to the fibrils, in agreement with experiment (33). However, extremely large cross-link densities lead to negative effects because the material is not capable of dissipating much energy during deformation, leading to a brittle collagen that is strong but not tough. Such behavior is observed in dehydrated collagen or in aged collagen featuring higher cross-link density (33). In contrast, decreased cross-linking as it occurs in Ehlers–Danlos V disease (28, 29) leads to a significantly reduced tensile strength of collagen, as χ_S/χ_R < 1. The ratio L/L_χ decreases, resulting in skin and joint hyperextensibility due to extremely weak collagen tissue incapable of dissipating significant energy.

Our model can be used to study different design scenarios. A design with many cross-links and short molecules would lead to a very brittle collagen, even in the hydrated state. Such behavior would be highly disadvantageous under physiological conditions. In contrast, long molecules provide robust material behavior with significant dissipation of energy (Fig. 4). Some experiments (19) support the notion that cross-link-deficient collagen shows wide yield regions and large plastic deformation, as seen in Fig. 4a.

Both elastic strength and energy dissipation approach a finite value for large molecular lengths, making it inefficient to create collagen fibrils with TC molecules much longer than L_χ, which is on the order of a few hundred nanometers (Fig. 4). This length scale agrees somewhat with experimental results of TC molecules with lengths of ≈300 nm (6, 7, 9, 18–20).

Large deformation is a critical physiological condition for collagen-rich tissue. The risk of catastrophic brittle-like failure needs to be minimized to sustain optimal biological function. The nanoscale ultrastructure of collagen may be designed to provide robust material behavior under large deformation by choosing long TC molecules. Robustness is achieved by the design for maximum strength and maximized energy dissipation by shear-like mechanisms. The requirement for maximum energy dissipation (Eqs. 5 and 6) plays a crucial role in determining the optimal molecular length L_χ. The layered design of collagen fibrils plays a vital role in enabling long deformation paths with large dissipative stresses. This is reminiscent of the “sacrificial bond” concept that is known from other protein materials (5).

The properties of collagen are scale-dependent (19). The fracture strength of an individual TC molecule (11.2 GPa) differs from the fracture strength of a collagen fibril (0.5 GPa). Similarly, Young’s modulus of an individual TC molecule is ≈7 GPa, whereas Young’s modulus of a collagen fibrils is smaller, approaching 5 GPa (for L ≈ 224 nm). This decrease of Young’s modulus is in qualitative agreement with experiment (20).

Quantitative theories of the mechanics of collagen have many applications, ranging from the development of new biopolymers to studies in tissue engineering for which collagen is used as a scaffolding material (27). In addition to optimization for mechanical properties, other design objectives, such as biological function, chemical properties, or functional constraints, may be responsible for the structure of collagen. However, the physiological significance of large mechanical deformation of collagen fibers suggests that mechanical properties could indeed be an important design objective.

Materials and Methods

Slip-Pulse Nucleation and Propagation.

This analysis is based on a one-dimensional model of fracture initially proposed by Hellan (35). The model describes a one-dimensional strip of material attached on a substrate that is under tensile loading in the axial direction. At a critical load, the energy released per advancement length of the adhesion front is equal to the energy required to break the bonding between the material strip and the substrate, leading to initiation of failure front. The failure front, corresponding to a dynamic crack tip, propagates at a fraction of the sound velocity, eventually displacing the material permanently in the direction of the applied load.

We apply this model to intermolecular deformation in collagen fibrils. The energy release rate is given by

where E is Young’s modulus of the TC molecule and σ_R is the applied tensile stress. With γ as the energy necessary to nucleate this defect, at the onset of nucleation the condition

needs to be satisfied [similar to the Griffith condition (36)]. The detachment front corresponds to the front of decohesion. Combining Eqs. 8 and 9 and solving for σ_R leads to Eq. 2. Bonds behind the fracture front reform, thus forming a slip pulse. The slip pulse is a region with increased tensile strain in the TC molecule (several nanometers wide).

The existence of slip pulses is not a consequence of the discretization of the mesoscale model. Instead, this theoretical framework is developed based on continuum mechanics, assuming a homogeneous distribution of adhesive interactions along the molecular surface.

Reactive Mesoscopic Model.

We use a reactive mesoscopic model describing TC molecules as a collection of beads interacting according to interparticle multibody potentials. The total energy is

The bending energy is

with k_B relating to the bending stiffness of the molecule. We approximate the nonlinear stress–strain behavior under tensile loading with a bilinear model that has been used successfully in earlier studies of fracture (30, 31) (the function E_T is given by integrating F_T(r) over the radial distance). The force between two particles is

where

In Eq. 13, H(r − r_break) is the Heaviside function H(a), which is defined to be zero for a < 0 and one for a ≥ 0. The parameters k_T⁽⁰⁾ and k_T⁽¹⁾ are the small- and large-deformation spring constants, respectively. The parameter r̃₁ = r₁ − k_T⁽⁰⁾/k_T⁽¹⁾(r₁ − r₀) from force continuity conditions.

Intermolecular interactions are described by a 12:6 Lennard–Jones potential

with σ as the distance, and ε as energy parameter.

The total energy is given by the sum over all pairwise and three-body interactions I = {T, weak}:

The parameters are calculated directly from full atomistic results, without empirical fitting. The parameters of the mesoscopic model are summarized in Table 1 for the reference state of fully hydrated TC molecules (for further details, particularly with regard to how the parameters of the molecular model are determined based on reactive and nonreactive atomistic simulations of individual TC molecules, see the supporting information).

Table 1.

Summary of the parameters used in the mesoscopic molecular model, chosen based on full atomistic modeling of solvated TC molecules (1 kcal·mol⁻¹·Å⁻¹ = 69.479 pN)

Parameters	Value
Equilibrium bead distance r0, Å	14.00
Critical hyperelastic distance r1, Å	18.20
Bond breaking distance rbreak, Å	21.00
Tensile stiffness parameter kT(0), kcal·mol−1·Å−2	17.13
Tensile stiffness parameter kT(1), kcal·mol−1·Å−2	97.66
Cross-link tensile stiffness parameter kXL, kcal·mol−1·Å−2	17.00
Cross-link equilibrium distance rXL, Å	18.00
Cross-link bond breaking distance rbreak,XL, Å	19.80
Equilibrium angle ϕ0, °	180.00
Bending stiffness parameter kB, kcal·mol−1·rad−2	14.98
Dispersive parameter ε, kcal/mol	6.87
Dispersive parameter σ, Å	14.72
Mass of each mesoscale particle, atomic mass units	1,358.7

Intermolecular cross-links are modeled by a harmonic spring, with F_XL(r) = −∂φ_XL(r)/∂r = −H(r − r_break,XL)k_XL(r − r_0,XL). The numerical values are chosen to yield a cross-link strength of ≈2,110 pN (37). We assume an equidistant distribution of N_CL cross-links along L_c. Different choices for N_CL lead to different cross-link densities ρ_N = N_CL/L_c.

We consider a two-dimensional model of collagen fibrils with periodic boundary conditions in the in-plane direction orthogonal to the pulling orientation.

Modeling Procedure.

Simulations are carried out in two steps, (i) relaxation followed by (ii) loading. Relaxation is achieved by slowly heating up the system, then annealing the structure at constant temperature, followed by energy minimization. After relaxation, the structure displays the characteristics of collagen fibrils in agreement with experiment (4, 6–19).

For the simulations with single TC molecules and two TC molecules, we use force boundary conditions in a steered molecular dynamics scheme. For collagen fibrils, we use displacement boundary conditions, continuously displacing particles in the boundary. The simulations are carried out by constantly minimizing the potential energy as the external strain is applied.

We use the virial stress to calculate the stress tensor (38). Further details are provided in the supporting information.

Computing Techniques and Computational Laboratory.

The molecular simulations described here were carried out with an extended version of the LAMMPS MD code (39), compiled with a GNU C++ compiler (LINUX; RedHat, Raleigh, NC) at the Atomistic Mechanics Modeling Laboratory (Massachusetts Institute of Technology). Visualization is done with visual molecular dynamics software (VMD) (40).

Glossary

Abbreviations

TC

tropocollagen

BM

bimolecular.