End-to-end distance distributions and intrachain diffusion constants in unfolded polypeptide chains indicate intramolecular hydrogen bond formation

Abstract

Characterization of the unfolded state is essential for the understanding of the protein folding reaction. We performed time-resolved FRET measurements to gain information on the dimensions and the internal dynamics of unfolded polypeptide chains. Using an approach based on global analysis of data obtained from two different donor–acceptor pairs allowed for the determination of distance distribution functions and diffusion constants between the chromophores. Results on a polypeptide chain consisting of 16 Gly-Ser repeats between the FRET chromophores reveal an increase in the average end-to-end distance from 18.9 to 39.2 Å between 0 and 8 M GdmCl. The increase in chain dimensions is accompanied by an increase in the end-to-end diffusion constant from (3.6 ± 1.0) × 10⁻⁷ cm² s⁻¹ in water to (14.8 ± 2.5) × 10⁻⁷ cm² s⁻¹ in 8 M GdmCl. This finding suggests that intrachain interactions in water exist even in very flexible chains lacking hydrophobic groups, which indicates intramolecular hydrogen bond formation. The interactions are broken upon denaturant binding, which leads to increased chain flexibility and longer average end-to-end distances. This finding implies that rapid collapse of polypeptide chains during refolding of denaturant-unfolded proteins is an intrinsic property of polypeptide chains and can, at least in part, be ascribed to nonspecific intramolecular hydrogen bonding. Despite decreased intrachain diffusion constants, the conformational search is accelerated in the collapsed state because of shorter diffusion distances. The measured distance distribution functions and diffusion constants in combination with Szabo–Schulten–Schulten theory were able to reproduce experimentally determined rate constants for end-to-end loop formation.

Understanding the properties of the unfolded state is a major focus of protein folding studies. The rather harsh and nonphysiological conditions required for populating unfolded states in equilibrium pose a major problem in the characterization of unfolded proteins under physiological conditions. For many proteins, rapid chain compaction in combination with major changes in spectroscopic properties was observed in refolding experiments starting from the denaturant-unfolded state (1–5). It has been discussed whether these rapidly formed compact structures represent the unfolded state under physiological conditions or whether the fast processes are due to the formation of specific folding intermediates separated from the unfolded state by energy barriers (3, 5, 6). Detailed structural information on unfolded proteins under physiological conditions recently became available from studies on natively unfolded proteins (7) and on engineered unstable protein variants (8, 9). For several proteins, compact unfolded states with both specific and nonspecific interactions were directly observed by NMR measurements (10–14). Analysis of the effect of mutations on solvent accessibility changes during folding also revealed the presence of residual structure in unfolded proteins that can be disrupted by side-chain mutations (15). These results from various independent experimental techniques indicate that significant parts of the native structure may already be present in unfolded proteins. This conclusion was supported by theoretical work, which suggested the presence of native-like secondary structure and a large amount of intramolecular hydrogen bonds in unfolded proteins in water (16, 17). Although our understanding of the structural properties of unfolded proteins has recently increased, the contributions from specific interactions, typical for each individual protein sequence, versus contributions from nonspecific side-chain and backbone interactions as a result of general polymer properties of polypeptide chains are still not well understood. Furthermore, only little is known about the dynamic properties of unfolded and partially folded proteins under different solvent conditions.

To gain insight into the structure and dynamics of unfolded proteins, we have recently studied the kinetics of intramolecular loop formation in model polypeptide chains with repetitive amino acid sequences and in sequences derived from natural proteins (18–21). Using intramolecular triplet–triplet energy transfer (TTET) between a donor and an acceptor group, we observed a decreasing rate constant for loop formation, k_c, with increasing denaturant concentration (22). As for protein folding reactions, a linear relationship between lnk_c and the denaturant concentration was found for all investigated polypeptide chains. The effect of guanidinium chloride (GdmCl) and urea on k_c could be dissected into two components. Part of the effect is due to changes in solvent viscosity. The remaining decrease in k_c arises from binding of denaturant molecules to the polypeptide chain and could be quantitatively described by Schellman's weak-binding model (22–24). Because these studies revealed that the properties of unfolded polypeptide chains are drastically changing upon addition of denaturants, we wanted to obtain more detailed information on the structure and dynamics of unfolded chains in different solvents by performing time-resolved (tr) FRET experiments on a long poly(Gly-Ser) chain containing donor and acceptor groups near the ends. These measurements allow for the characterization of general properties of unfolded polypeptide chains in the absence of specific side-chain interactions. Global analysis of results obtained from two different donor–acceptor pairs enabled us to determine end-to-end distance distributions and intrachain diffusion constants between the FRET labels in water and to characterize the effect of denaturants.

Results

FRET Measurements on Flexible Polypeptide Chains.

We have previously used poly(Gly-Ser) chains of different length as a model to investigate the kinetics of loop formation in unfolded polypeptide chains (18, 19, 22). To obtain information on the dimensions and internal dynamics of these chains, we performed FRET measurements. The rate constant, k_T, for FRET between a donor (D) and an acceptor (A) group depends on the properties of the chromophores and on the distance, r, separating them according to (25)

with

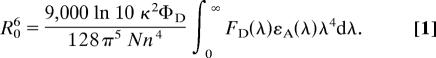τ_D denotes the intrinsic fluorescence lifetime of the donor, and R₀ is the characteristic Förster distance at which a given FRET pair shows 50% transfer efficiency. N is Avogadro's number, n is the refractive index of the medium, and κ² is an orientational term assumed to equal 2/3 for rapidly reorienting fluorophores. Φ_D is the fluorescence quantum yield of the donor, F_D(λ) is the normalized emission of the donor, and ε_A(λ) is the extinction coefficient of the acceptor at wavelength λ. The basic FRET theory has to be extended when unfolded polypeptide chains are studied that represent rapidly interconverting ensembles of different conformations with a distribution of interchromophore distances, p(r), which leads to a distribution of energy transfer efficiencies and to changes in the donor–acceptor distances of individual molecules during the donor lifetime. Haas et al. (26) developed a formalism that treats the effect of conformational heterogeneity and internal dynamics on the population of excited donor molecules in trFRET experiments.

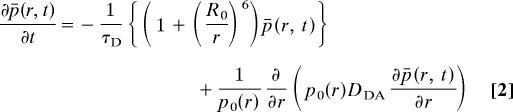with

The first part on the right-hand side in Eq. 2 represents distance-dependent FRET where p̄(r, t) is the time-dependent probability to find an excited donor molecule with an acceptor molecule at distance r and p₀ is the equilibrium distribution of donor–acceptor distances. The second part on the right-hand side represents the effect of diffusion on FRET with D_DA denoting the diffusion constant for motions of the two fluorophores relative to each other.

Eq. 2 shows that FRET measurements on flexible chains with dynamics on the time scale of the donor lifetime provide the chance to obtain information on both the dimensions and the dynamics of a flexible polymer chain. However, p(r) and D_DA cannot be determined from a single FRET experiment because both parameters contribute to the observed FRET efficiency. Several solutions have been proposed to determine both p(r) and D_DA in highly dynamic and flexible systems. Haas et al. (26) and Lakowicz et al. (27) measured FRET in solutions of different solvent viscosity to determine D_DA in peptides of different length. Lakowicz et al. (28) further performed FRET measurements in the presence of different amounts of fluorescence quenchers and globally analyzed the data to obtain p(r). We took a different approach to determining both p(r) and D_DA in unfolded polypeptide chains by using two different donor–acceptor pairs with similar R₀ values but with different donor lifetimes. This allows for a reliable determination of p(r) and D_DA in a global analysis of the data because the diffusional term has a stronger influence on the observed transfer efficiency with increasing donor lifetime.

Spectroscopic Properties of the Fluorophore Systems.

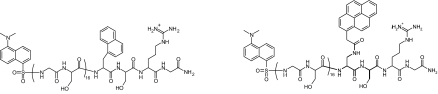
To study the dimensions and dynamics in unfolded model polypeptide chains by global FRET analysis, we synthesized two different peptides, each containing 16 pairs of Gly-Ser between donor and acceptor. Both peptides have the dansyl group as acceptor at the N terminus and either naphthalene or pyrene as donor group introduced C-terminal from the (Gly-Ser)₁₆ stretch (Structure 1). Naphthalene–dansyl and pyrene–dansyl are two well suited donor–acceptor pairs for global FRET analysis because naphthalene and pyrene attached to a poly(Gly-Ser) chain have largely different fluorescence lifetimes in water of (36.9 ± 0.2) ns and (225.5 ± 1.0) ns, respectively (see Tables 1 and 2, which are published as supporting information on the PNAS web site). The R₀ values of the two pairs in water are, however, very similar with (23.3 ± 0.4) Å and (20.5 ± 0.4) Å for naphthalene–dansyl and pyrene–dansyl, respectively, which makes the two pairs sensitive for the same range of donor–acceptor distances. Because we wanted to investigate the effect of denaturants on the chain properties, we additionally determined τ_D and R₀ of the FRET pairs between 0 and 8 M GdmCl. The results show that the two FRET pairs have similar R₀ values but largely differ in their donor fluorescence lifetimes at all GdmCl concentrations (see Tables 1 and 2).

Structure 1.

Structure of the (Gly-Ser)₁₆ peptide labeled with naphthalene/dansyl (Left) and pyrene/dansyl (Right).

Global Analysis of trFRET Measurements.

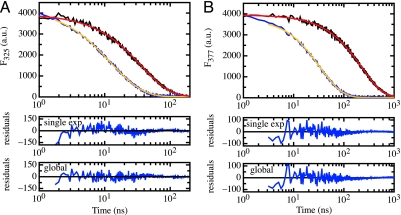
Fig. 1 shows fluorescence decay curves of naphthalene (Fig. 1A) and pyrene (Fig. 1B) attached to the ends of a (Gly-Ser)₁₆ sequence. For both donors, the fluorescence lifetime is decreased in the presence of the dansyl acceptor group indicating energy transfer. The decrease in lifetime is much more pronounced for pyrene, with a 6.8-fold decrease in fluorescence half-life versus a 2.7-fold decrease for naphthalene, although the pyrene–dansyl pair has a slightly smaller R₀ value than the naphthalene–dansyl pair, and thus less energy transfer would be expected for the pyrene–dansyl pair. This observation indicates significant contributions from diffusional processes to the observed FRET efficiency (see Eq. 2) and is in agreement with our earlier results from TTET experiments that revealed end-to-end contact formation on the 50-ns time scale in a (Gly-Ser)₁₆ peptide labeled with xanthone and naphthalene at the ends (19, 22), which is on a time scale similar to the donor lifetimes.

Fig. 1.

Fluorescence decay curves for the different donor-only and donor-acceptor peptides in water. (A) Naphthalene fluorescence decay curves in a naphthalene-only peptide (black) and the (Gly-Ser)₁₆ peptide labeled with naphthalene and dansyl (blue). (B) Fluorescence decay curves of the pyrene-only (black) and pyrene-dansyl (Gly-Ser)₁₆ (blue) peptide. The fluorescence decay curves of the donor-only peptides can be fitted with single-exponential functions with lifetimes (τ_D) of (36.9 ± 0.2) ns (naphthalene) and (225.5 ± 1.0) ns (pyrene). The decay curves of the donors in the presence of the acceptors were fitted globally (red curves) to Eqs. 2 and 3. The residuals show the results from single-exponential and global fits to the donor fluorescence decay curves in the presence of acceptor.

Fluorescence decay curves for both donors in the presence of acceptor are not single-exponential (Fig. 1). A fit of the individual FRET data according to Eq. 2 did not allow the determination of p(r) and D_DA because the observed fluorescence decay curve can be fitted by either close donor–acceptor distances or by rapid diffusion. Only global analysis of the fluorescence decay curves was able to resolve this ambiguity. The analysis used Eq. 2 and global values for p(r) and D_DA in the two peptides, which seems justified because the chromophores are small compared with the chain dimensions. A skewed Gaussian distribution (Eq. 3) was assumed for p(r) (29, 26).

The parameter a determines the width of the distribution, and c = f(a, b) is a normalization constant. The distribution is offset from zero by b. TTET experiments on end-to-end loop formation in the same peptide have previously shown kinetics in the Gaussian chain limit both in water and in the presence of high GdmCl concentrations (19), indicating that this approximation is valid. The global fit yielded the donor–acceptor distribution function shown in Fig. 2A and a D_DA value of (3.6 ± 1.0) × 10⁻⁷ cm² s⁻¹ in water.

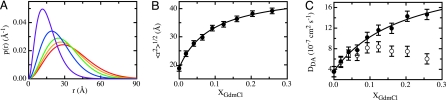
Fig. 2.

Effect of GdmCl on the dimensions and dynamics of the (Gly-Ser)₁₆ chain. (A) Effect of GdmCl on the donor–acceptor distance probability distribution function [p(r)] in the (Gly-Ser)₁₆ peptide. Results for GdmCl concentrations of 0 M (violet), 2.0 M (blue), 4.0 M (green), 6.0 M (orange), and 8.0 M (red) are displayed. (B) rms end-to-end distances, 〈r²〉^1/2, calculated from p(r) curves at GdmCl concentrations between 0 and 8 M. (C) Effect of GdmCl on the donor-to-acceptor diffusion constants (D_DA) obtained from the global analysis (open circles) and on the viscosity-corrected values (filled circles) according to Eq. 5. The solid lines in B and C describe fits to the weak-binding model (Eqs. 4 and 5, respectively).

Effect of GdmCl on Chain Dimensions and Dynamics.

To elucidate the effect of denaturants on the chain properties, we performed FRET measurements in the presence of various GdmCl concentrations. At all GdmCl concentrations, the donor fluorescence showed complex decay curves in the presence of acceptor. With increasing denaturant concentration, the apparent FRET efficiency decreases as indicated by a decreasing effect of the presence of acceptor on the donor lifetime (see Tables 1 and 2). Global analysis of data from the two donor–acceptor pairs revealed that increasing GdmCl concentrations lead to an increase in the average donor–acceptor distance and to a broadening of the distribution function (Fig. 2A). To quantify this behavior, we calculated the rms distance between donor and acceptor, 〈r²〉^1/2, from the p(r) functions (Fig. 2B). In the absence of denaturant, a 〈r²〉^1/2 value of (18.7 ± 1.0) Å is obtained. 〈r²〉^1/2 increases hyperbolically with denaturant concentration and reaches a value of 39.2 Å at 8 M GdmCl. The effect of [GdmCl] on 〈r²〉^1/2 can be quantitatively described by a binding isotherm employing the Schellman model for weak interactions (23, 24), which was also able to describe the effect of denaturants on the rate constant of loop formation (22).

Here, 〈r₀²〉^1/2 denotes 〈r²〉^1/2 in the absence of denaturant and K_ex is an exchange constant on the mole fraction scale (X_D) for replacing water bound to the peptide by GdmCl. γ is a factor that reflects the sensitivity of 〈r²〉^1/2 toward denaturant binding. Fitting the experimentally determined 〈r²〉^1/2 values (Fig. 2B) to Eq. 4 yields 〈r₀²〉^1/2 = (18.9 ± 0.9) Å, K_ex = 12.0 ± 2.7, and γ = 1.46 ± 0.13. This K_ex value is slightly smaller than the value obtained for the effect of GdmCl on the kinetics of loop formation in the same polypeptide chains (K_ex = 27.4 ± 1.5) (22).

A more complex behavior is observed for the effect of GdmCl on D_DA (Fig. 2C). D_DA increases from (3.6 ± 1.0) × 10⁻⁷ cm² s⁻¹ at 0 M GdmCl up to a maximum value of 8.4 × 10⁻⁷ cm² s⁻¹ at 4 M GdmCl (X_D = 0.12). At higher GdmCl concentrations, a slight decrease in D_DA is observed. In our previous studies, we showed that the rate constant for end-to-end loop formation in the (Gly-Ser)₁₆ peptide is inversely proportional to solvent viscosity, η (18, 22). Accordingly, we corrected the values for D_DA at the different GdmCl concentrations using Eq. 5. The viscosity-corrected values (D′_DA) increase hyperbolically with denaturant concentration and reach a value of (14.7 ± 1.0) × 10⁻⁷ cm² s⁻¹ at 8 M GdmCl. The effect of GdmCl can also be described by the weak binding model as follows:

with

where D_DA⁰ represents the value of D_DA in the absence of GdmCl. The fit of the data with Eq. 5 yields D_DA⁰ = (3.7 ± 0.9) × 10⁻⁷ cm² s⁻¹, K_ex = 5.9 ± 4.0, and γ = 5.6 ± 2.3, similar to the exchange constant obtained of the effect of GdmCl on chain dimension.

Discussion

Using Multiple Donor–Acceptor Pairs for FRET Measurements in Flexible Systems.

FRET data from a single donor–acceptor pair do not allow a reliable determination of donor–acceptor distances in unfolded or partially folded polypeptide chains due to contributions from intrachain diffusion. Our results show that this ambiguity can be resolved by performing global analysis of trFRET data obtained with two different donor–acceptor pairs. The global analysis allows for the determination of the donor–acceptor distance distribution function [p(r)] and additionally yields the intrachain diffusion constant between the donor and acceptor (D_DA). The prerequisites for this method are (i) the use of two FRET pairs with similar R₀ values but significantly different donor lifetimes and (ii) chain dynamics on the same time scale as the donor lifetimes. Our earlier results on the kinetics of intrachain loop formation in unfolded polypeptide chains showed that major changes in the donor–acceptor distances occur on the 5- to 50-ns time scale, depending on amino acid sequence and loop length (19, 20). This finding indicates that intrachain diffusion has major effects on the observed FRET efficiency if the donor lifetimes are slower than 1–5 ns.

The effect of chain dynamics on FRET efficiency resolves a paradox reported for unfolded BBL protein, for which an apparent chain compaction was observed in FRET experiments upon increasing the temperature from 280 to 360 K (30). Because the viscosity of water decreases from 1.43 to 0.33 cP (1 P = 0.1 Pa·sec) in this temperature range (31) and intrachain diffusion is inversely dependent on solvent viscosity (18, 22), the contributions from intrachain diffusion to FRET increase significantly with increasing temperature. In the FRET studies on BBL protein, naphthylalanine, which has a fluorescence lifetime on the same time scale as chain dynamics (see Fig. 1A), was used as the donor, which leads to increased transfer efficiencies and thus to apparent chain compaction if the dynamic component is neglected.

Effect of GdmCl on Polypeptide Chain Properties.

Global analysis of FRET data obtained from the two donor–acceptor pairs attached to the ends of a (Gly-Ser)₁₆ chain allowed us to determine both p(r) and D_DA as a function of GdmCl concentration. The results show that GdmCl has major effects on the chain dimensions and dynamics. In the presence of 8 M GdmCl, the 〈r²〉^1/2 value is more than twice as large as it is in the absence of denaturant (Fig. 2B). At the same time, the flexibility of the chain increases as indicated by a 4-fold increase in the diffusion constant between 0 and 8 M GdmCl (Fig. 2C). The effect of GdmCl on 〈r²〉^1/2 and D_DA can be described by Schellman's weak-binding model. The observed effects are not caused by changes in peptide secondary structure as indicated by virtually identical CD spectra in the far-UV region at all denaturant concentrations (see Fig. 4, which is published as supporting information on the PNAS web site). In addition, NMR measurements did not detect any interactions involving the naphthalene moiety (data not shown).

Chain Dimensions at High Denaturant Concentrations.

We compared the average chain dimensions in the (Gly-Ser)₁₆ peptide with data determined for GdmCl-unfolded proteins. A study by Damaschun et al. (32) measured and compiled small-angle x-ray scattering (SAXS) data on 12 proteins unfolded in 6 M GdmCl. They found that the observed radii of gyration, R_g, extrapolated to zero protein concentration scale with the number of residues, N, according to

with values of R_g⁰ = (4.4 ± 0.3) Å and ν = 0.5 ± 0.02. In a recent study, Kohn et al. (33) evaluated SAXS data from 28 proteins unfolded at various protein concentrations and different concentrations of GdmCl. They found values of R_g⁰ = (2.08 ± 0.19) Å and ν = 0.598 ± 0.028. Assuming a Gaussian chain, R_g can be converted to 〈r²〉 with

With the parameters reported by Damaschun et al. (32), this results in 〈r²〉^1/2 = 61.9 Å for a GdmCl-unfolded 33-residue protein, which corresponds to separation of donor and acceptor in our model peptides. This value is significantly larger than the 〈r²〉^1/2 value of (36.4 ± 1.0) Å found for the (Gly-Ser)₁₆ peptide in the presence of 6 M GdmCl. Shorter average end-to-end distances in poly(Gly-Ser) chains are expected because of the high content of glycine residues, which leads to shorter chains compared with natural protein sequences (34, 35). From the data of Kohn et al. (33), a 〈r₀²〉^1/2 value of 41.2 Å is obtained for a 33-residue protein, which seems to be too low when considering the significantly smaller fraction of glycine residues in natural proteins.

We further compared our experimental data with predictions from polymer theory. The use of parameters for the dimensions of polypeptide chains reported by Flory and coworkers (35, 36) yields 〈r₀²〉^1/2 = 37.6 Å for a (Gly-Ser)₁₆ chain when the properties of serine are approximated by alanine (36, 37). Although the validity of the underlying “isolated-pair hypothesis” has recently been shown to be oversimplified (16), this number still provides a useful estimate, which should, however, only apply to Θ conditions where a real polymer chain behaves like an ideal chain and repulsive steric interactions (excluded volume) are exactly compensated by intramolecular attractive forces. To assess the influence of the repulsive steric interactions in the absence of intrachain or solvent interactions, we performed all-atom Monte Carlo simulations of sterically allowed peptide conformations as described in ref. 21. For the (Gly-Ser)₁₆ peptide, the simulations gave a value of (43.9 ± 1.0) Å for 〈r²〉^1/2 between the labels, which is in close agreement with the limiting value of (46.4 ± 1.5) Å of the GdmCl-binding isotherm (Fig. 2B).

Properties of Polypeptide Chains in Water.

The above comparisons show that the dimensions of the (Gly-Ser)₁₆ chain in the presence of high concentrations of denaturant are similar to those predicted for an ideal chain in the absence of intramolecular interactions and to those found for proteins unfolded at high denaturant concentrations. The dimensions of the (Gly-Ser)₁₆ chain are drastically reduced in water because of the formation of intramolecular interactions, which leads to decreased chain flexibility as indicated by the reduced D_DA value. The (Gly-Ser)₁₆ peptide does not contain any hydrophobic side chains except for the fluorescence labels, which were shown to have a broad distance distribution (Fig. 2A). NMR experiments did not detect any interactions between donor and acceptor. In addition, fluorescence anisotropy measurements revealed freely rotating chromophores (see Materials and Methods), and TTET experiments did not show any fast components in the kinetics of loop formation in a (Gly-Ser)₁₆ loop with similar chromophores. Thus, the only possible intrachain interactions in our model chains are hydrogen bonds between backbone amide and backbone carbonyl groups or between backbone carbonyl groups and the serine side chain. Our results indicate that these intramolecular hydrogen bonds are more favorable than hydrogen bonds between the peptide chain and water, which may be due to a favorable solvation free energy of solvent-exposed intramolecular hydrogen bonds, which was recently found to be the major determinant for the stability of alanine-based α-helices (38–40). The presence of intramolecular hydrogen bonds in unfolded proteins has major consequences for the contributions of hydrogen bonds to protein stability. The hydrogen bond inventory discussed by Fersht (41) assumes that each peptide unit in an unfolded chain forms two hydrogen bonds to water, which are broken upon folding, and a single intramolecular hydrogen bond is formed in the native state. Our results suggest that intramolecular hydrogen bonds are formed both in the unfolded and the native state. Folding thus leads to a breakage of nonspecific intramolecular hydrogen bonds, the formation of specific intramolecular hydrogen bonds, and a burial of the majority of hydrogen bonds, which should result in an unfavorable solvation free energy (38).

Our results reveal that formation of intramolecular hydrogen bonds slows down internal chain dynamics and decreases the chain dimensions. This picture is compatible with results from the effect of chain length on the kinetics of loop formation. In the presence of 6 M GdmCl, a persistence length compatible with the predicted value for an ideal chain (35, 36) is observed (19). In water, however, chain stiffness is significantly increased and Gaussian chain behavior was only observed for longer chains with N > 20 (19). The results from our FRET measurements imply that the increased chain stiffness in water is not due to a local chain stiffness but rather reflects an overall loss in flexibility and chain stiffening due to the formation of a network of intramolecular hydrogen bonds. A comparison of the observed chain properties in water with the dynamics of loop formation (19, 22) allows an estimate of the time scale for structural rearrangement of the intramolecular hydrogen bonding network. Because local chain motions and chain stiffness are affected by the intramolecular interactions, their breakage must be slower than local chain motions, which are on the 10-ps time scale for bond rotations. On the other hand, single-exponential kinetics are observed for loop formation, which indicates rapid conformational equilibration of the ensemble of unfolded states (18, 19, 37, 42, 43). These considerations set an upper limit of a few hundred picoseconds on the interconversion of the peptide conformations.

The intramolecular hydrogen bonds are broken upon binding of GdmCl to the peptide chain, which competes for the hydrogen bonding donor and acceptor groups. However, the scaling laws for loop formation derived for Gaussian chains still apply to the experimentally observed kinetics of loop formation in water. This observation indicates that chain compaction due to hydrogen bond formation does not dramatically alter the polymer behavior of an unfolded chain and that the chain can still be approximated as a Gaussian chain, which is in agreement with conclusions from Fitzkee Rose (44) based on simulations of random coil conformations including intramolecular interactions.

Comparison of the Results with Predictions from Szabo–Schulten–Schulten Theory.

Szabo, Schulten, and Schulten (42) developed a theory for treating the dynamics of intramolecular end-to-end contact formation in Gaussian chains (SSS theory). For polymers with only a small fraction of loop conformations in equilibrium and with fast dynamics between different conformations, a single-exponential time constant, τ, for loop formation (42) was predicted, consistent with the kinetics of loop formation observed in TTET experiments (18, 19, 22). SSS theory gives a relationship between τ, p(r), and the diffusion constant (D) between the ends of the polymer.

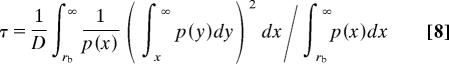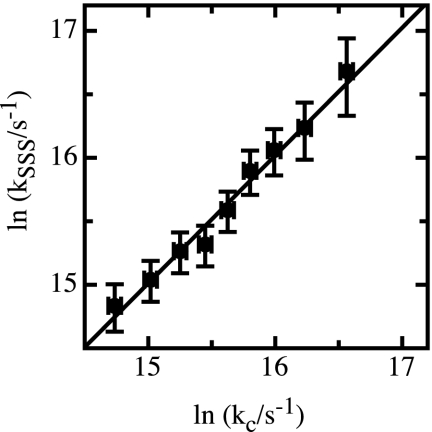
To test SSS theory, we used Eq. 8 with the values for D_DA and p(r) determined in our FRET experiments to calculate rate constants for end-to-end contact formation in the (Gly-Ser)₁₆ peptide (k_SSS = 1/τ). The results were compared with rate constants for loop formation, k_c, measured by TTET (19, 22). The only remaining unknown quantity in Eq. 8 is the value of the reactive boundary, r_b, which designates the distance between two groups required for loop formation. For TTET from xanthone to naphthalene, a bimolecular quenching rate constant of k_q = (4.0 ± 0.2) × 10⁹ M⁻¹ s⁻¹ was determined (20). Comparing this value with diffusion constants for naphthalene and xanthone of (6.5 ± 1.0) × 10⁻⁶ cm² s⁻¹ and (5.6 ± 1.0) × 10⁻⁶ cm² s⁻¹ (45), respectively, yields a reactive boundary of (4.4 ± 0.5) Å for TTET (46), which was used to calculate k_SSS at different GdmCl concentrations. The results showed a linear correlation between the calculated k_SSS values and the experimental k_c values (Fig. 3) with a slope of the correlation plot of 1.00 ± 0.14 (r = 0.99) indicating that SSS theory is able to describe the dynamics of end-to-end loop formation in long unfolded polypeptide chains.

Fig. 3.

Comparison of rate constants for contact formation determined by TTET, k_c, with corresponding rate constants calculated according to SSS theory (k_SSS) using the p(r) and D_DA values determined by FRET experiments. k_SSS was calculated according to Eq. 8 with a value of 4.4 Å for the reactive boundary, r_b. The solid line shows the linear correlation with a slope of 1.00 ± 0.14 (r = 0.99) and an intercept of ln(k_SSS/s⁻¹) = [(−0.1 ± 2.2)].

Implications for the Early Steps in Protein Folding.

The poly(Gly-Ser) chain investigated in our studies serves as a model for an unfolded polypeptide chain that lacks specific side-chain interactions. Comparison of the chain properties in water and in the presence of high concentrations of GdmCl shows drastically reduced chain dimensions in water that are most likely caused by the formation of intramolecular hydrogen bonds. The decrease in chain dimensions accelerates loop formation despite a decreased end-to-end diffusion constant. These results suggest that nonspecific chain compaction can speed up protein folding by accelerating the conformational search on the free-energy landscape for productive side-chain interactions. Because the observed effects of denaturants on chain dimensions and dynamics were obtained in a model chain devoid of side-chain interactions, they likely represent general properties of unfolded polypeptide chains. The results therefore imply that intramolecular hydrogen bond formation has a major contribution to chain compaction early in folding, which is commonly attributed to “hydrophobic collapse.” The results further suggest that rapid structural changes during protein folding do not necessarily indicate the formation of partially folded intermediates. Thus, other methods are required to distinguish between the formation of the defined intermediates and nonspecific chain compaction early in refolding (6, 47).

Materials and Methods

Peptide Synthesis and Purification.

Peptides were synthesized with an amidated C terminus using standard Fmoc chemistry on an Applied Biosystems 433A peptide synthesizer as described in ref. 19, using TentaGel S RAM resin (Rapp Polymere, Tübingen, Germany). Resin-bound peptides were N-terminally labeled with dansyl chloride (Fluka, Buchs, Switzerland). The resin was incubated for 30 min in a solution of 10% (vol/vol) diisopropylethylamine in dimethylformamide containing a 10-fold excess of dansyl chloride. Naphthalene was introduced via Fmoc-1-naphthylalanine (NAla; Bachem, Bubendorf, Switzerland). Pyrene was attached to the side chain of diaminopropionic acid (NovaBiochem, Läufelfingen, Switzerland). The amine side chain of diaminopropionic acid was protected by a methyltrityl group that is selectively cleaved in 2% (vol/vol) TFA in dichloromethane. 1-Pyreneacetic acid (Aldrich, Buchs, Switzerland) was coupled to diaminopropionic acid by using standard Fmoc chemistry. Chemicals were of peptide synthesis or higher grade and were purchased from Fluka or Acros Organics (Basel, Switzerland).

Donor- and acceptor-only peptides consisted of eight Gly-Ser repeats, and the dansyl group was replaced by an acetyl moiety or 1-naphthylalanine was replaced by alanine, respectively. Peptides were purified on an RP-8 HPLC column (Merck, Darmstadt, Germany) (19). Peptides labeled with two fluorophores required a second purification on an RP-8 HPLC column with a mixture of acetonitrile and 50 mM ammonium acetate buffer (pH 6.0). Greater than 95% purity of the peptides was confirmed by analytical HPLC and mass spectrometry.

Spectroscopic Measurements.

Steady-state fluorescence measurements were carried out on an Aminco Bowman series 2 fluorimeter (SLM Aminco). R₀ values were calculated according to Eq. 1. N-acetyl tryptophan amide was used as a standard for determining the quantum yield (Φ_F = 0.144) (48). The donor-only peptides showed low steady-state fluorescence anisotropies of 0.005 ± 0.006 and 0.001 ± 0.014 for naphthalene and pyrene, respectively, which gives rotational correlation times smaller than 0.5 ns. This is much faster than the average fluorescence decay observed in the trFRET measurements and justifies the use of κ² = 2/3 in Eq. 1.

Time-resolved fluorescence measurements were conducted with a time-correlated single-photon counting fluorimeter (FLS900; Edinburgh Instruments, Edinburgh, U.K.) with irradiation at 284 nm by using a H₂ flash lamp with a 1.5-ns pulse width operating at 40 kHz. Fluorescence decay curves were monitored at 325 and 377 nm for naphthalene and pyrene, respectively. Peptide concentrations were 8 μM in 10 mM potassium phosphate buffer (pH 7.0)/0.5% DMSO. GdmCl concentrations were determined by refractive index (49). Samples were degassed and equilibrated at 22.5°C. A mixture of 4 μM acceptor-only and 4 μM donor-only peptide showed no energy transfer, ruling out intermolecular FRET processes.

CD measurements were performed on an Aviv DS62 spectropolarimeter with peptide concentrations between 15 and 150 μM.

Data Analysis.

Data were analyzed with the programs MATLAB (MathWorks, Natick, MA) and pro Fit (QuantumSoft, Zürich, Switzerland). Fluorescence decay curves from the two FRET pairs were fitted globally to the numerical solution of Eqs. 2 and 3 with the global parameters a, b, and D_DA, because even for simple p(r), Eq. 2 does not have an analytical solution. The lifetimes of the two donors in the absence of acceptor were fitted separately at each GdmCl concentration with single-exponential functions (see Tables 1 and 2), and the results were used in the global analysis.

Monte Carlo Simulation of Donor–Acceptor Distance Distribution.

Random conformations for the (Gly-Ser)₁₆ peptide without steric overlap were generated with all-atom hard-sphere model as described in ref. 21. For simulations, xanthone and naphthalene, which have similar size as the FRET pairs used in these studies, were used as donor and acceptor. In total, >60,000 valid conformations without steric clashes were generated.

Glossary

Abbreviations

SSS

Szabo–Schulten–Schulten

trFRET

time-resolved FRET

TTET

triplet–triplet energy transfer.