Model-based analysis of tiling-arrays for ChIP-chip

Abstract

We propose a fast and powerful analysis algorithm, titled Model-based Analysis of Tiling-arrays (MAT), to reliably detect regions enriched by transcription factor chromatin immunoprecipitation (ChIP) on Affymetrix tiling arrays (ChIP-chip). MAT models the baseline probe behavior by considering probe sequence and copy number on each array. It standardizes the probe value through the probe model, eliminating the need for sample normalization. MAT uses an innovative function to score regions for ChIP enrichment, which allows robust P value and false discovery rate calculations. MAT can detect ChIP regions from a single ChIP sample, multiple ChIP samples, or multiple ChIP samples with controls with increasing accuracy. The single-array ChIP region detection feature minimizes the time and monetary costs for laboratories newly adopting ChIP-chip to test their protocols and antibodies and allows established ChIP-chip laboratories to identify samples with questionable quality that might contaminate their data. MAT is developed in open-source Python and is available at http://chip.dfci.harvard.edu/∼wli/MAT. The general framework presented here can be extended to other oligonucleotide microarrays and tiling array platforms.

Identifying the binding sites and regulatory targets of a transcription factor (TF) is crucial to understanding its biological function. Since the first publications on the subject (1–3), chromatin immunoprecipitation (ChIP) coupled with DNA microarray analysis (ChIP-chip) has quickly evolved as a popular technique to study the in vivo targets of DNA-binding proteins at the genome level. Although PCR-based promoter arrays have been successfully used with ChIP-chip to characterize all of the TFs in yeast (4), they are impractical when extended to mammalian genomes. Recently, Affymetrix (Santa Clara, CA), NimbleGen Systems (Madison, WI), and Agilent Technologies (Palo Alto, CA) have developed oligonucleotide arrays that tile all of the nonrepetitive genomic sequences of human and other eukaryotes. The Affymetrix tiling arrays have on average one perfect match (PM) probe for every 35 bp of DNA and an optional mismatch (MM) probe for every PM probe. Although these whole-genome tiling microarrays allow biologists to conduct unbiased genome-wide ChIP-chip experiments, they also generate massive amounts of data, creating a need for effective and efficient analysis algorithms. Our interest in developing such algorithms for Affymetrix whole-genome tiling arrays arises from their low cost and the complex nature of the resulting data.

All methods previously developed to identify regions enriched by ChIP on Affymetrix tiling arrays are based on statistics that compare ChIP array data with one or more control sample. The Mann–Whitney U test is applied to ChIP-chip data by ranking of ChIP and control probe signals within 1-kb sliding windows (5) but does not consider the variability in probe behavior. Other researchers have modeled probe behavior using pooled ChIP-chip data from multiple laboratories and then infer ChIP-enriched states through a hidden Markov model (HMM) (6). Another method applies Welch’s t statistic comparing ChIP and control replicates, calculated for each probe, and then uses a running window average of the t statistics to identify ChIP regions (7). This method becomes unreliable when there are only a few replicates to estimate probe variance. TileMap (8) proposes an empirical Bayes shrinkage improvement by weighting the observed probe variance and pooled variances of all of the probes on the array. TiMAT (http://bdtnp.lbl.gov/TiMAT) first calculates an average fold change between ChIPs and controls for each probe, then uses a sliding-window trimmed mean to find ChIP regions.

In this work, we propose a fast and powerful analysis algorithm, titled Model-based Analysis of Tiling-arrays (MAT), to identify regions enriched by TF ChIP-chip on Affymetrix tiling arrays (see Fig. 1 for a strategy diagram of MAT). Instead of estimating probe behavior from multiple samples, MAT models baseline probe behavior by considering the 25-mer sequence and copy number of all probes on a single tiling array. With a good baseline probe behavior model, MAT can standardize the signals of each probe in each array individually, and detect ChIP regions from a single ChIP sample, multiple ChIP samples, or multiple ChIP samples with controls, with increased accuracy.

Fig. 1.

Strategy diagram for MAT.

Results

We applied MAT to the estrogen receptor (ER) ChIP-chip data (9) on Affymetrix tiling arrays covering chromosome (chr) 21 and 22. This chip set contained A, B, and C arrays, each with ≈300,000 probe pairs (PM and mismatch). Three ChIP-chip replicates (represented as C1, C2, and C3) were hybridized by using MCF7 cells 45 min after ER activation, and three Input control replicates (represented as I1, I2, and I3) were hybridized by using the MCF7 genomic input DNA. We remapped all of the probe sequences to the newest genome assembly (UCSC Hg17), and filtered probes to ensure that no probe is mapped to more than one location in any 1-kb window and that no two probes are mapped to the same genomic location.

Probe Behavior Model Fitting.

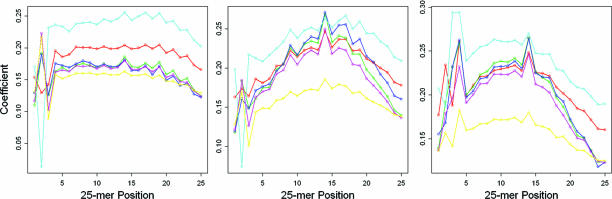
We applied MAT to each array in the data set and estimated the probe behavior model by examining the signal intensity, sequence, and copy number of all probes on an array. Position-specific nucleotides (α and β parameters from Eq. 1) accounted for 28–36% of the variation in the arrays (based on the multiple R² of the model). This model resulted in correlations of 0.53–0.60 between the predicted probe intensities and observed values in five of the six samples. Not only did A, C, G, and T contribute differently to the probe intensity, the position-specific nucleotide coefficients (Fig. 2) indicated that the two or three nucleotides at the two ends and in the middle of the probe tend to have the most variable effects. Including the effect of the squared ACGT counts (γ parameters in Eq. 1), the correlation between model predictions and observations increased to 0.65–0.72 in five of the six samples. Model fitting in I3 only achieved a correlation of 0.49 and multiple R² of 24%. We did not consider this result a failure in our method; rather, based on Fig. 4a, it appeared that less DNA was added to the array; therefore, the noise was higher relative to the signal intensity values.

Fig. 2.

The effect of A (Left), C (Center), and G (Right) at each probe nucleotide position on probe intensity. Plotted are the coefficients estimated from the A array in each of the six samples. C1, red; C2, green; C3, blue; I1, cyan; I2, magenta; I3, yellow.

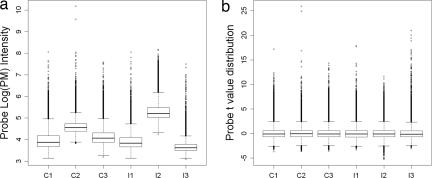
Fig. 4.

Probe value distribution in the A array of the six samples before (a) and after (b) probe standardization.

We found that ≈5% of the probes on the chr21 and chr22 tiling arrays mapped to multiple locations in the genome. These multiple copy number probes gave slightly higher signal than single copy probes with similar sequence and tended to cluster together on the chromosome. This clustering caused regions containing the multiple copy number probes to be falsely identified as ChIP regions (6), unless we adequately accounted for their copy number effect. Although incorporating the copy number effect (δ parameter) did not improve model fitting significantly, it reduced the number of ChIP regions called in the Input triplicates (3I) control sample analysis by 60% at a P value cutoff of 10⁻⁷.

Probe Standardization.

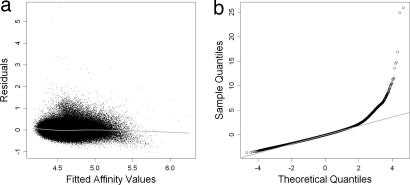
After MAT probe behavior model fitting, the residuals between the model and observation were approximately normally distributed and centered at 0 (Fig. 3a). The residual Q-Q plot (Fig. 3b) showed that the vast majority of probes were on the theoretical quantile, except for a small percentage of probes on the upper tail, which represented DNA enriched during ChIP and PCR amplification and cross-hybridized probes. We divided all of the probes on an array into 100 affinity bins such that each bin contains ≈3,000 probes predicted to have similar intensities. A sample variance was estimated for each bin and used as the variance for all probes in the bin. MAT used the model-predicted intensity and bin variance to standardize every probe on the array according to Eq. 2. Before probe standardization, the probe value distributions in the samples (Fig. 4a) showed a clear need for array-wise normalization. After probe affinity standardization, the resulting t values were well normalized across arrays and samples (Fig. 4b) and thus could be directly compared.

Fig. 3.

Distribution of residuals between MAT model predictions and observed intensities for array A in sample C1. (a) Residuals across model predicted values. The gray line is the Lowess fit. (b) Q–Q plot of the residuals. The gray line is the theoretical normal (0, 1) distribution.

To further confirm that MAT did not need sample normalization, we quantile-normalized (10) all samples before we applied MAT to each array. MAT identified the exact same 77 ChIP regions by using all six samples with or without normalization at a P cutoff of 10⁻⁷, and MATscores were nearly identical except for the highest, which were ≈5–10% lower in the normalized data, resulting in less confident predictions (in terms of P) of these regions.

ChIP Region Detection.

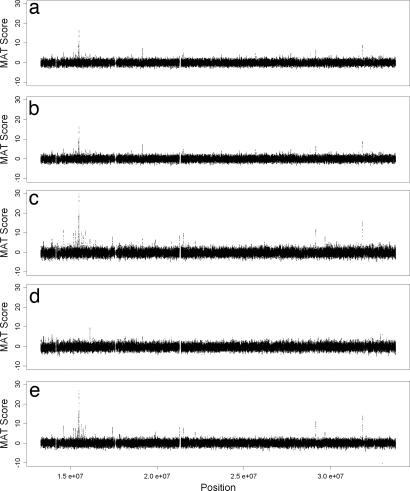
MAT was applied to detect ChIP regions in three different scenarios: single sample, multiple samples (represented as 3C for ChIP triplicates and 3I for Input triplicates), or multiple ChIP samples with input controls (represented as 3C − 3I). When applied to ChIP sample C1, MAT identified many windows with high MATscore (Fig. 5a), most of which were true ChIP regions (detailed method comparison statistics appear below). MAT also scored a few windows high in control sample I1 (Fig. 5b), which were presumably false positives. At a P cutoff of 10⁻⁷, individual ChIP samples produced between 57 and 71 sites, whereas individual Input controls produced between 6 and 12 sites.

Fig. 5.

MATscore of all 600-bp windows across the Affymetrix human chr21/22 tiling A array. Shown are the MATscores calculated by using ChIP sample 1 (C1) (a), Input sample 1 (I1) (b), 3C (c), 3I (d), and all six samples (3C − 3I) (e). The thickness of each horizontal band reflects the variance of the MATscores.

Compared with C1, 3C gave a few more high MATscore windows (Fig. 5c). Although the MATscore distribution in 3C had slightly higher variance than in C1, the high-scoring windows gave much higher MATscores in 3C. This result translated into much more confident predictions for these high-scoring windows. The MATscore distribution from 3I also had slightly higher variance (Fig. 5d). However, most high-scoring windows in I1–I3 either disappeared or gave reduced MATscores in 3I. At a P cutoff of 10⁻⁷, MAT called 81 regions from 3C and only two from 3I. One of these two regions with high MATscores in 3I showed even higher MATscores in 3C and has been validated to be a true ChIP region by quantitative PCR (qPCR). The other region is likely a false positive. These results indicate that at this cutoff, using 3C without controls, MAT had very few false-positive predictions.

When triplicate ChIPs and input controls were combined (3C − 3I), most high-scoring windows retained their MATscores. However, MATscore distribution showed slightly smaller variance compared with 3C, because any cell-specific and probe-specific variations not modeled in Eq. 1 were filtered by subtracting the Inputs. A total of 77 ChIP regions were identified from (3C − 3I) at a P cutoff of 10⁻⁷, of which 68 were in common with the 3C without 3I. So far, 83 regions have been qPCR-validated as ER ChIP regions on chr21/22; 57 sites were previously validated (9); and 26 were validated independently based on ER ChIP-chip data on whole-genome tiling arrays (J.S.C. and M.B., unpublished data). A total of 64 of the 83 qPCR-validated regions were called by MAT at this cutoff. If we lowered the cutoff to 10⁻⁶, MAT called 90 regions, of which 69 were qPCR-validated. At this cutoff, MAT identified 101 regions from 3C and 13 regions from 3I (one of which was even higher in the 3C). The advantage of having controls was demonstrated here because as many as four potential false-positive regions were filtered by subtracting 3I from 3C.

Method Comparisons.

We compared the performance of MAT with that of the HMM (6), TileMap (8), and TiMAT (http://bdtnp.lbl.gov/TiMAT). We did not include the Mann–Whitney U test (5) or Welch t test (7) [both of which only worked with (3C − 3I)] because HMM and TileMap had demonstrated better performance than Mann–Whitney, and TileMap had been shown to work better than Welch’s t test. For the HMM background distribution, a total of 54 ChIP-chip and control samples (5, 9) were used to estimate probe behavior. Quantile normalization was conducted on all six samples for HMM, TileMap, and TiMAT. Default parameters were used for each algorithm to find ChIP regions from all six samples (3C − 3I). Different methods reported different numbers of ChIP regions using default parameters. Because TileMap predicted the fewest ChIP regions, 55 (using the HMM option, its moving average option reported 13 sites), we used the top 50 predictions from each algorithm to compare the performance of the algorithms. The results are summarized in Table 1. We first compared the predictions with the 83 qPCR-validated regions. Among the top 50 predictions from all six samples (3C − 3I), 49 in MAT, 40 in HMM, 45 in TileMap, and 44 in TiMAT were qPCR-validated, respectively. The actual published HMM (9) estimated probe behavior from 76 instead of 54 samples, including some unpublished data. Among the top 50 HMM predictions based on the probe model, 46 were qPCR-validated, and 38 overlapped with the MAT (3C − 3I) predictions. Note that the qPCR-validated regions were biased because they were selected mostly from the HMM and MAT analyses. With this result, we only demonstrated that for (3C − 3I), the top 50 sites predicted by the different methods were comparable.

Table 1.

Percent agreement between the top 50 sites predicted by different analysis algorithms and the 83 qPCR-validated regions and with each other

Analysis method	MAT					HMM					TileMap	TiMAT
	3C − 3I	3C	C1	C2	C3	3C − 3I	3C	C1	C2	C3	3C − 3I	3C − 3I	C1 − I1	C2 − I2	C3 − I3
qPCR	98	94	74	88	92	88 (92)	88	76	74	86	90	88	62	80	72
MAT
3C − 3I
3C	86
C1	68	74
C2	84	88	64
C3	84	90	70	84
HMM
3C − 3I	76	72	58	70	64
3C	74	74	58	74	70	86
C1	62	58				70	72
C2	68	64				76	82	58
C3	74	70				82	82	70	72
TileMap
3C − 3I	78	70	60	72	70	70	70	54	64	66
TiMAT
3C − 3I	84	74	60	76	74	68 (70)	68	60	62	68	84
C1 − I1	58	60				50	52				60	64
C2 − I2	74	64				60	60				74	78	58
C3 − I3	64	54				56	52				66	76	50	60

Values in parentheses are the HMM results when the probe behavior model was estimated from many more samples. Segmental duplication and simple repeat regions were filtered before comparison. (The qPCR regions above were not randomly selected and cannot be used to compare methods; they are included as a quality check to show that the methods above are producing true results.)

We proceeded to compare the different methods when fewer samples were available. TileMap only worked with multiple ChIPs and multiple Inputs. TiMAT could detect ChIP regions from a single ChIP with its corresponding Input. However, the sample-to-sample agreement using TiMAT on paired ChIP and Input samples is not as high as that using MAT on ChIP sample alone. HMM (6) was able to find ChIP regions from single or multiple ChIP samples without controls. Its predictions on C1, C2, C3, and 3C samples were consistent with each other and with (3C − 3I). However, HMM relies on probe behavior estimates from many more samples and could be very sensitive to the number and quality of samples used. Compared with HMM, TileMap, and TiMAT, MAT was able to conduct independent single-sample analysis and showed superior flexibility and consistent accuracy. The MAT analysis on C1, C2, and C3 individual ChIP samples gave concordant results to each other, to the (3C − 3I) result, and to qPCR validations.

The results in Table 1 suggest that MAT yields 68–84% of the ChIP regions from a single ChIP sample as compared with the 3C and 3I controls. This finding is very valuable for laboratories newly adopting ChIP-chip to quickly test and optimize their protocol and antibodies. They could run one ChIP sample on a single array for the different protocols or antibodies and use MAT to make predictions. If a few of the MAT predictions could be qPCR-validated, they could replicate the working protocol or antibody to obtain a comprehensive result. In addition, laboratories familiar with ChIP-chip could still run MAT on each individual ChIP sample and easily identify samples whose results are inconsistent with the other samples and with (3C − 3I). Biologists could choose to ignore the samples of questionable quality from downstream analysis.

Conclusion and Discussion

We propose a fast and powerful algorithm, MAT, for data analysis of ChIP-chip on Affymetrix tiling arrays. By using a simple linear model, MAT estimates the baseline probe behavior based on probe sequence characteristics and genome copy number. By using this baseline model to standardize the probes, MAT is able to filter much of the noise in the data and clarify the true biological signals in the data. This framework could be adapted to fit more sophisticated probe models. For example, we could consider melting temperature, secondary structure, or 23/24-mer cross-hybridization of each probe. Additionally, nonlinear and other modeling approaches could be used to increase the explanatory ability of the model. Because each whole-genome tiling array contains >6 million probes, the overfitting of models with a few hundred parameters is not a concern. For the whole genome tiling arrays, MAT estimates the 81 parameters from randomly selected 400,000 probes instead of from all of the probes on the array to save memory.

It is worth noting that the MAT algorithm presented here is not specific for analyzing ChIP-chip on Affymetrix tiling arrays; however, it is a general method for analyzing data from almost any experiment using Affymetrix tiling microarrays. The approach of MAT for probe sequence modeling, single-chip standardization, can be extended to accommodate analysis of Affymetrix gene expression and SNP arrays and long oligomicroarray platforms.

The current MAT probe model relies heavily on the fact that most of the probes on the array are measuring the nonspecific hybridization. We do not expect that the small percentage of non-null probes will bias the model estimates significantly. In the case that the small percentage of enriched probes did have an effect, a more robust method for parameter estimation (such as median regression or iteratively reweighted least squares) could be used to fit the background model. However, in the case of DNA and histone modification studies, as many as half of the data points could measure true biological signal, and even robust methods would result in a large amount of bias in parameter estimation. In this case, one could first fit the model, identify ChIP regions, and then remove probes in these regions. The model could then be refit and used to identify more ChIP regions.

In most microarray applications, it is necessary to apply array normalization and probe background adjustments to preprocess the resulting data, which is typically a two-step process. The single-array probe standardization procedure presented here is a simultaneous array normalization and background adjustment. The probe background model is fit to each array individually, and then the intensity values are standardized to have the same mean and variance across all probes within all arrays. We have demonstrated here that the method is effective, and it eliminates the need for additional normalization.

MAT is unique in its ability to handle a single ChIP-chip sample, multiple ChIP samples, or experiments with replicate ChIP and control samples. The single chip analysis feature can serve as a quality assessment tool. For laboratories newly adopting the ChIP-chip technology, this feature allows the testing of experimental protocol from a single ChIP sample on a single array (instead of the whole chip set). For laboratories with multiple antibodies against the same TF, this feature enables them to quickly find the antibody that gives the cleanest or strongest target enrichment. For laboratories with a working ChIP-chip protocol and antibody, this feature allows for the examination of individual samples to identify those with questionable quality, which might contaminate the data set. With multiple ChIP samples, MAT can more confidently detect ChIP regions with reduced false discovery rate (FDR). For experiments with multiple ChIP and control samples, MAT has increased sensitivity and specificity and can adjust for possible cell-line–specific anomalies. Finally, MAT can be used to analyze experiments with unbalanced designs (i.e., 3 ChIPs and 1 input control), allowing researchers yet more flexibility for study design, modeling out cell-line–specific anomalies while balancing time and monetary constraints.

The FDR procedure described in MAT controls the FDR among all called regions in the arrays. FDR controls have been incorporated into other ChIP-chip algorithms (8); however, these methods only control probe-wise FDR. To illustrate this distinction, consider the following example. Suppose that there are 20 probes with scores higher than a given cutoff, and also suppose one of these scores is a false positive. Now suppose that the 19 enriched probes are clustered on the chromosome and come from 4 distinct regions. In this hypothetical case, the probe FDR is 0.05, but the region FDR is 0.20. Because regions are usually of interest in tiling array analysis, there is an advantage to controlling for region FDR.

Predicted ChIP regions are sometimes contained in segmental duplication regions; consider, for example, a region that has five segmental duplications in the whole genome, and one copy is bound by the TF with a 6-fold ChIP enrichment. After adjusting for probe copy number, MAT will find this region to be ChIP enriched, and qPCR will likely find a 2-fold enrichment [i.e., (4 × 1 + 1 × 6)/5 = 2]. However, because these segmental duplications are often 99% identical, neither ChIP-chip analysis on tiling arrays (even with control replicates) nor qPCR could distinguish whether it is one copy with 6-fold ChIP-enrichment or all five copies each with a 2-fold ChIP-enrichment. This issue can be problematic for downstream analyses such as finding the genes regulated by a ChIP region. Therefore, MAT will “flag” any ChIP-enriched segmental duplications in the output. Researchers can decide whether to investigate all ChIP regions or only the unique regions in the genome.

Methods

Probe Behavior Model Estimate and Probe Standardization.

The estimation of probe behavior in MAT takes advantage of two characteristics of ChIP-chip data on Affymetrix tiling arrays. First, the majority of probes in a typical ChIP-chip experiment measure primarily nonspecific hybridization. Second, each Affymetrix tiling array contains between 0.3 million and 6 million 25-mer oligonucleotide probes, allowing for an accurate and robust prediction of probe sequence effects. Motivated by the sequence-specific probe behavior models for gene expression microarrays (11, 12), we propose the following tiling array probe affinity model:

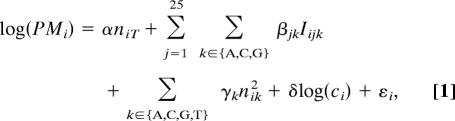where

• PM_i is the PM probe value of probe i;

• n_ik is the nucleotide k count in probe i;

• α is the baseline value (intercept or constant) based on the number of T nucleotides on the probe, e.g., 25α is the baseline when the probe sequence is a run of 25 T nucleotides;

• I_ijk is an indicator function such that I_ijk = 1 if the nucleotide at position j is k in probe i, and I_ijk = 0 otherwise;

• β_jk is the effect of each nucleotide k (except T, which is already modeled in α) at each position j;

• γ_k is the effect of nucleotide count squared;

• c_i is the number of times that the sequence of probe i appears in the genome. Affymetrix tiling array libraries provide the 25-mer sequence of every probe, which we mapped to the non-repeat-masked newest (May 2004) version of the human genome assembly;

• δ is the effect of the log of the probe copy number; and

• ε_i is the probe-specific error term, assumed to follow a normal distribution.

There are 81 parameters in this model, 1 for α, 25 × 3 for β, 4 for γ, and 1 for δ. MAT estimates the parameters by ordinary least squares using all of the probes on a tiling array. Model fitting is applied to each array separately (i.e., each single array in a tiling array chip set) in each ChIP-chip or control sample. After parameter estimation, the model can predict probe the baseline intensity of i, m̂_i, given its probe sequence and copy number. MAT divides the probes on the array into “affinity bins,” each containing a few thousand probes with similar m̂_i. MAT estimates the observed sample variance within each affinity bin and uses it as the probe variance for each probe in the bin. The large number of observations in each affinity bin produce far more stable variance estimates of probe behavior than those derived from multiple samples (6, 8), which may not even be available.

With the probe behavior model, MAT standardizes each probe on each array as follows:

where m̂_i is the baseline intensity predicted by the model based on the sequence and copy number of probe i, and s_{i affinity bin} is the standard deviation of the affinity bin to which probe i belongs. Probes with a high t value are not necessarily all ChIP-enriched, but they exhibit significantly higher values than predicted by the model. The distribution of t values is approximately standard normal, and t values may be compared across experiments without further normalization.

Detect Regions Enriched by TF ChIP-Chip.

We propose a powerful scoring scheme across sliding windows to identify ChIP-enriched regions. Sonication during ChIP procedure shears the DNA to ≈500-bp fragments, and the median length for the predicted ER ChIP regions (6) on chr21 and chr22 that are qPCR-validated is 650 bp (9). Therefore, for our analysis above, MAT considers the 600-bp window surrounding each probe and ignores windows with less than eight probes (however, these parameters are adjustable in the MAT software, so the researcher can find what works best in each case). MAT computes a trimmed mean of all of the t values in the window. The trimmed mean removes the top 10% and bottom 10% of the t values and averages the remaining 80% of the t values. A MATscore is also calculated for each window and assigned to the probe at the center of the window:

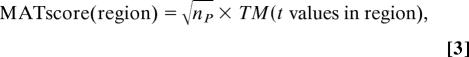where TM is the trimmed-mean of all of the probe t values in the region, and n_p is the number of observation points in the region used to calculate the TM. MATscores are distributed approximately normal and allow different regions to be directly compared, even though they may have different lengths or contain a different number of observations in the region.

MAT can detect regions enriched by TF ChIP-chip in three different scenarios: single sample, multiple replicates, and multiple replicates of ChIP-chips and controls. In a single sample, a MATscore will be calculated from all of the probes within each 600-bp sliding window. The score cutoff to call a ChIP region can be set arbitrarily, determined based on random-sample qPCR validation (5), or based on a P value or FDR (see below for details) cutoff. With multiple replicates, a MATscore will be calculated for each window by pooling all of the probes across all of the replicates. Even though the replicates might have similar trimmed mean t values, having more replicates and more probes in the window will give higher confidence to the prediction. When multiple replicates for the ChIP-chip and controls are all available, the MATscore of each window is calculated as the MATscore of the ChIP replicates subtracted by the MATscore of the control replicates. This process removes any cell-specific variations that are not modeled in Eq. 1 and increases the confidence of ChIP region predictions that are marginally significant from the ChIP-only samples.

In addition, MAT also allows the researcher to divide the MATscore difference (between ChIP and Input) by a region standard deviation estimated from the region’s trimmed t values in the Input controls. This process reduces the scores of regions that are very noisy or where the inputs give inconsistent results. We have found this technique to work well when there are enough t values (>2 Inputs samples) to estimate a good standard deviation. However, for small Input sample size, this estimate is very noisy and thus is not recommended.

To assign a P value to a window, it is necessary to estimate the nonenriched null distribution of the MATscores. To approximate this distribution, we calculate the MATscore for a nonoverlapping set of 600-bp windows that cover the array, starting from the window with the smallest chromosome coordinates and progressively moving across the chromosome in 600-bp increments. Assuming the MATscores to be normally distributed, MAT estimates the variance from windows with MATscores smaller than the median (likely close to zero) and the null distribution to be symmetric about the median.

MAT can also find enriched regions based on a user-specified region FDR. Assuming the null MATscore distribution to be symmetric about the median, for each MATscore cutoff above the median (positive cutoff), the negative MATscore cutoff is defined as the value symmetric to the positive cutoff about the median. After merging nearby probes beyond both MATscore cutoffs, the region FDR can be defined as the ratio of positive over negative regions. MAT can automatically select the proper MATscore cutoff to so that the region FDR is less than or equal to the user-specified FDR value.

Therefore, the user can specify a P value, FDR, or a MATscore cutoff to call ChIP regions. After the initial ChIP regions are called, MAT merges regions that are within 300 bp of each other and assigns them the scores (MATscore and P value) associated with the highest-scoring window in the merged region.

Software Implementation.

MAT is implemented in open source Python and is freely available at http://chip.dfci.harvard.edu/∼wli/MAT. It requires four types of input files. The first three are as follows: the Affymetrix “.cel” files, which contain the signal value of every probe; the “.bpmap” library files, which contain the sequence, locations (on the array and on the genome), and copy number of each probe; the repeat-library file, which contains the chromosome coordinates of RepeatMasker repeats (www.repeatmasker.org), simple repeats (13), and segmental duplications (14). The MAT parameters (including the grouping of the .cel and .bpmap files) are then organized into a user-edited “.tag” (Tiling Array Group) file. MAT returns two types of output file: the “.bar” files, which contain the MATscore for each probe and which can be imported to Affymetrix’s Integrated Genome Browser for visualization; and a “.bed: file with the chromosomal coordinates of all of the ChIP regions with MATscore and repeat (including segmental duplications) flag. MAT can process the tiling arrays on a single Linux computer faster than an Affymetrix scanner can scan these arrays. The strategy diagram is summarized in Fig. 1.

Glossary

Abbreviations

ChIP-chip

ChIP coupled with DNA microarray analysis

chrn

chromosome n

ER

estrogen receptor

FDR

false discovery rate

HMM

hidden Markov model

MAT

Model-based Analysis of Tiling-arrays

PM

perfect match

qPCR

quantitative PCR

TF

transcription factor

3C

ChIP triplicates

3I

Input triplicates

I1–3

Input control replicates 1–3

C1–3

ChIP-chip replicates 1–3.