Autogenous and nonautogenous control of response in a genetic network

Abstract

Feedback-based control methods determine the behavior of cellular systems, an example being autogenous control, the regulation of production of a protein by itself. This control strategy was theoretically shown to be superior to an equivalent but nonautogenously regulated system when based on a repressor. Although some of its advantages were later confirmed with isolated synthetic circuits, the superiority of autogenous control in natural networks remains untested. Here, we use the SOS DNA repair system of Escherichia coli, where autogenous control is part of a single-input module, as a valid model to evaluate the functional advantages and biological implications of this mechanism. We redesign the control of its master regulator, the protein LexA, so that it becomes nonautogenously controlled. We compare both systems by combining high-resolution expression measurements with mathematical modeling. We show that the stronger stability associated with the autogenous regulation prevents false triggering of the response due to transient fluctuations in the inducing signal and that this control also reduces the system recovery time at low DNA damage. Likewise, autoregulation produces responses proportional to the damage signal level. In contrast, bacteria with LexA constitutively expressed induce maximal action even for very low damage levels. This excess in response comes at a cost, because it reduces comparatively the growth rate of these cells. Our results suggest that autogenous control evolved as a strategy to optimally respond to multiple levels of input signal minimizing the costs of the response and highlights reasons why master regulators of single-input modules are mostly autorepressed.

The regulatory complexity of cellular systems is attained by the application of different feedback control strategies. Such mechanisms, even when implemented by simple genetic circuits, are often associated with complex dynamical behaviors, whose complete characterization is necessary to better comprehend fundamental cellular actions. Examples of these schemes are increasingly being discovered by the following two complementary approaches. First, because of the extensive characterization of the molecular constituents of some systems over the years, e.g., the mitogen-activated protein kinase signaling cascade (1) or the network of mediators in the maturation of Xenopus oocytes (2), it is now possible to analyze their control-level properties. Alternatively, studies of large regulatory networks assembled by using genomic data were able to extract recurrent control architectures used in such networks, e.g., control motifs found in the transcriptional network of Escherichia coli (3) or Saccharomyces cerevisiae (4). As a whole, these series of findings are putting forward design principles that resume our understanding of the relationship between structure and dynamics of control mechanisms (5–14), which can be applicable to a wide variety of biological contexts. For instance, the union of various feed-forward loops might be a common feature of programs of cellular differentiation (9, 15). More recently, a combination of fast and slow positive feedback loops were shown to enhance the reliability of cell decisions (16).

The functioning of these control schemes in nonbiological scenarios is commonly associated with optimized system performance (17), optimization that in biological systems has been argued to be a consequence of evolution (13, 18, 19). Thus, one could wonder whether the modification of extant control structures in genetic networks would lead to unoptimized regulation of their corresponding biological responses. Among the many feedback-based methods found in cellular networks, autogenous regulation is probably one of the simplest structures to use for analyzing this issue. Indeed, theoretical comparisons proposed that, when based on a repressor, autogenously regulated systems would exhibit several functional advantages with respect to nonautogenously regulated ones, i.e., they should be generally considered more optimized (20, 21). The development of minimal synthetic circuits confirmed some of these aspects experimentally (22, 23). However, these features were studied in isolated synthetic networks, and thus it remains unknown the extent to which natural networks are found in the precise regime where the superiority of autogenous control becomes effective. Here, we characterize the dynamics of these two control strategies, with all other aspects of the system being equal, and suggest the reasons for their selection in a particular natural regulatory network. Our study also sheds light on why the autoregulation of the master transcriptional factor of a single-input module is generally autorepression (3).

To address these issues, we compared the dynamics of the SOS regulatory network in E. coli under either type of control. The SOS genetic network activates the response to DNA damage in many bacterial organisms. It is composed of a set of genes under synchronized transcriptional regulation of the LexA protein. This master regulator exhibits autogenous control because it represses its own production. DNA damage caused by different agents, e.g., UV radiation, acts as an inducing signal to the system. Exposure to this radiation causes single-stranded DNA (ssDNA), which activates a second core element of the response: the RecA protein. Activated RecA (RecA*) promotes autocleavage of LexA, originating a gradual increase in transcription of the SOS genes. This increase triggers several mechanisms able to repair the damage and hence diminish the concentration of activated RecA. All of these processes ultimately bring LexA back to its original level.

Results

We studied the control strategy of the SOS master regulator by contrasting the natural system with a synthetic one in which LexA production is nonautogenously regulated. In this latter circuit, it was necessary to reproduce the same level of LexA protein as that found in the natural case so that both systems only differ a priori in their control mechanism (Fig. 1 A and B). To this aim, LexA protein was produced under the control of a lactose promoter tightly regulated by the LacI repressor in a lexA(Def) strain. LexA dosage can thus be externally manipulated by induction with isopropyl-β-d-thiogalactopyranoside (IPTG). We obtained cell growth (in terms of optical density; OD) and expression measurements (by using a low-copy reporter plasmid) at high resolution. In this plasmid, GFP is under the control of the lexA promoter. We can in this way measure how LexA concentration evolves as a quantity proportional to the rate of GFP accumulation in both circuits [promoter activity (PA); see Materials and Methods]. Note that whereas this PA is related to the rate of lexA transcription in both systems, this rate is fixed for the IPTG-induced one. Monitoring of LexA dynamics allowed us to characterize quantitatively the differences in the course of the SOS induction associated with the two control strategies.

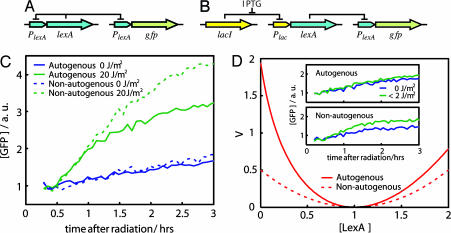
Fig. 1.

Autogenous and nonautogenous control of LexA determines SOS response. (A) Wild-type LexA regulatory circuit plus GFP reporter. (B) Synthetic LexA regulatory circuit plus GFP reporter. (C) SOS dynamics (GFP fluorescence) after UV irradiation in cells with (solid line) or without (dashed line) autogenous regulation. GFP levels without radiation for both cases are shown in blue. (D) Stability potential, V (26, 27), associated with the uninduced LexA state (before UV radiation) for the autogenous (solid line) and nonautogenous (dashed line) circuits. LexA concentrations are in units of uninduced LexA equilibrium such that x_eq = 1. (D Inset) SOS dynamics as in C for a very small UV dose (<2 J/m²) reveals the buffering effect of autogenous control. Reproducibility error of experiments performed on different days was ≈10%.

Stability and Buffering.

We first monitored the response to a fixed dose of UV radiation for both systems. This radiation originates the critical signal (ssDNA) to drive LexA levels from an initially uninduced concentration (before UV) to a lower induced level (after UV) (24). This second concentration represents an equilibrium between degradation, i.e., cleavage, and synthesis (25). As LexA levels diminish, protein production remains fixed in a nonautogenously regulated system, whereas it increases in the presence of feedback control, acting in this latter case as a more effective compensatory force. As a consequence, the balance between production and degradation is achieved at higher LexA levels for the autogenous circuit, and the resulting induced levels are drastically different. This difference is shown in Fig. 1C, where we plotted the dynamics of the reporter GFP for both circuits as a function of time after radiation. A lower induced LexA concentration implies a higher GFP level as repression of GFP production is released.

The previous behavior can be partially understood in terms of the gain in stability of the uninduced steady state of the autogenous circuit. Theoretical results have shown how autoregulation enhances the stability of genetic circuits (20). This feature has been experimentally tested with the use of simple synthetic elements (22). We were interested in observing this effect in a natural network. For this process, a small dose of UV radiation can be considered as an external perturbation experienced by the uninduced steady state of LexA. This perturbation is able to move the protein level out of its equilibrium. The stability σ of each system would then determine the strength of this displacement, i.e., the network strength of response. By considering two simple mathematical models of LexA production, with and without autogenous control, the ratio of stabilities θ = σ_au/σ_na can be shown to be proportional to the PAs of both circuits θ = 2 − α_na/α_au, with α_na being the constant PA of the nonautogenous circuit and α_au the PA in the absence of repressor of the autogenous one (see Materials and Methods). For a strong feedback, α_na/α_au ≪ 1, and the ratio θ reaches its maximum (2-fold). We can estimate the value of this ratio by using of the experimental data on the activity of the promoter (see below for details). The experimental value (θ ≈ 1.8 ± 0.1) is close to the theoretical maximum, which indicates that the autoregulation of the LexA system is fully exploiting this effect. In summary, one could interpret that for low-UV doses, the weaker the stability of the system, the stronger the response. We can further visualize this result by representing the time evolution of LexA concentration as the motion of a heavily damped particle in a potential well (26, 27). The stability of the uninduced LexA state is linked to the curvature of the potential (stronger curvatures implying stronger stability; see Fig. 1D). Finally, the difference in stability is also reflected in the efficient buffering against fluctuations in the inducing signal by the autoregulatory system. We tested this phenomenon by irradiating cells with minimal UV doses (<2 J/m²). An appreciable effect of this radiation is only seen for the nonautogenous system (Fig. 1D Inset).

Recovery Dynamics.

We studied the recovery dynamics of both systems by analyzing their PA. The transition between the induced and uninduced levels of LexA is influenced by both the network intrinsic regulatory dynamics and the repair processes. In this sense, one could envisage two opposite situations. For low damage, activated RecA induces LexA cleavage only for a very short period, because DNA damage is very quickly repaired. The recovery to the uninduced LexA level is mainly determined by the response time of a transcriptional unit whose protein level is out of equilibrium. Both types of control should then differ in their recovery times (23). Alternatively, for larger UV doses, the recovery time is directly related to the repair time. The transition to the uninduced state is mainly driven by the gradual disappearance of the LexA cleavage effect. In this scenario, there should not be a major difference between either type of control.

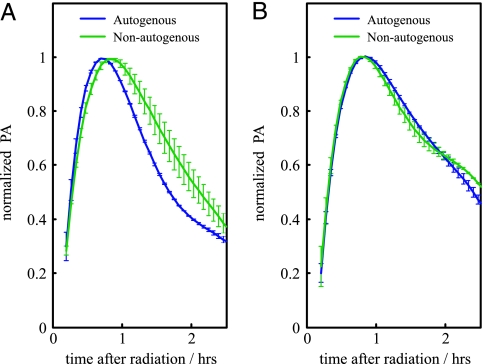
To validate these hypotheses, we computed the PA of each circuit for a given UV dose by taking the derivative of a polynomial fit of the GFP dynamics (we also applied a regression spline algorithm; see Materials and Methods). Maximal PA was different in each system, especially for the low-UV dose (see Discussion). To analyze the turn-on (-off) of the response and to measure recovery time, PAs were normalized by their corresponding maximal value in each situation (9). In Fig. 2, we plot the normalized PA for the autogenously and nonautogenously controlled circuits in a situation of low (Fig. 2A) and high (Fig. 2B) damage. The turn-on transition (uninduced to induced) is very similar for all UV doses and independent of the circuit type. This result is in agreement with previous reports linking this transition to the fast LexA cleavage dynamics (25). However, the turn-off transition (induced to uninduced) determining the recovery time is different. We find that recovery time is smaller for the autogenously regulated circuit at low-UV doses (Fig. 2). We suggest that, in this regime, the repair process is fast enough that the kinetics associated with autogenous control shortens the recovery time of the corresponding circuit. For increasing UV dose, both systems exhibit similar recovery times, which seems to support the initial hypothesis, i.e., that strong DNA damage recovery time is determined by the repair processes.

Fig. 2.

Response dynamics of the SOS system after UV irradiation in terms of normalized PA. (A) PA of the autogenous (blue) and nonautogenous (green) circuits in a regime of low-UV dose (8 J/m²) clearly differs. (B) As in A for a regime of high-UV dose (70 J/m²). In this case, both circuits exhibited very similar recovery times. See text for details.

Range of Response.

Exposure of both circuits to a range of UV doses revealed differences in the proportionality of the SOS response to the intensity of the inducing signal (24, 28). To quantify this phenomenon, cells were given different doses of UV radiation. The nonautogenous system always exhibited an overresponse with respect to the autogenous one. We plotted a comparison of the action of both circuits for low and high damage (Fig. 3 A and B). The relative difference in reaction was revealed to be stronger for low-UV doses.

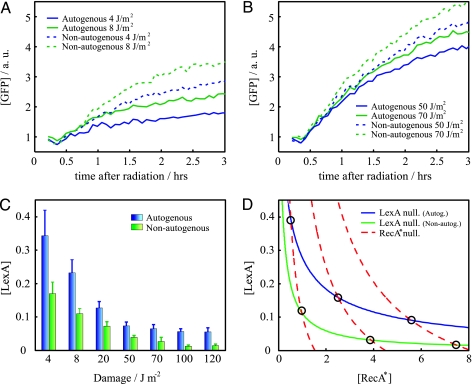
Fig. 3.

SOS response to a wide range of inducing signal. (A and B) SOS dynamics (GFP fluorescence) after UV irradiation in cells with (solid line) or without (dashed line) autogenous regulation in a regime of low (A) or high (B) damage. Overresponse is stronger at low-UV dose. Reproducibility error of experiments performed on different days is ≈10%. (C) Minimal LexA (repressor) concentration as a function of UV dose for the autogenously (blue) and nonautogenously (green) controlled circuits. (D) [LexA]–[RecA*] (activated RecA) phase space. Circles denote equilibrium states. The more proportional response of the autogenous system corresponds to a more gradual decrease of the LexA nullcline as activated RecA increases. Overresponse of the nonautogenous system is here reflected in the distribution of equilibrium states close to minimal [LexA] values. Parameters are as follows: α_au = 6, k = 0.2 (see Materials and Methods), k' = k (36), β = 1.5 (36), δ_x = 1, δ_y = 1, δ_xy = 8, and χ = 0.17, 0.5, 0.9 (corresponding to increasing RecA* nullclines). Protein concentrations are in units of uninduced LexA equilibrium.

The strength of the response is associated with the minimum of LexA concentration, which corresponds to a maximum in PA (see Materials and Methods). In Fig. 3C, we show how this value changes for different UV doses. The ability of the system to exhibit a graded response is clearly lost in the case of nonautogenously regulated LexA. We introduce a simple mathematical model to better understand this behavior (see Materials and Methods). The model describes the dynamics of LexA and activated RecA considering a fixed amount of damage; i.e., we did not include any sort of repair mechanism that decreases damage with time. The equilibrium concentrations of this model correspond to a situation briefly after UV radiation, and thus they denote maximal strength of response (minimal LexA). The difference in response between the autogenous and nonautogenous systems can be understood in terms of the geometry of the associated response curves (nullclines; Fig. 3D) in the phase space (26). These curves depict the equilibrium concentration of LexA (d[LexA]/dt = 0) and activated RecA (d[RecA*]/dt = 0), respectively. We see how the LexA nullcline decreases more gradually as activated RecA increases for the autogenous circuit. This result implies that for this system the equilibrium points, i.e., the intersection with the activated RecA nullcline, are distributed in a wider range of LexA values with respect to the nonautogenous circuit. In this latter case, these states are also shifted to lower LexA levels. The geometry of the nullclines derived from this simple model highlights why larger differences in response are found at low damage.

Differential Growth Rate.

It has been reported that the products of two SOS genes, umuD and umuC, can slow down the cell cycle in E. coli, allowing more time for DNA repair (29). This effect would be particularly important under conditions in which the SOS system is strongly activated. A disproportionate SOS response might thus penalize cell growth, reducing bacterial fitness. We wanted to address the following question: Would the difference in activation between the nonautogenous and autogenous systems be reflected in a differential growth rate under the same damage conditions?

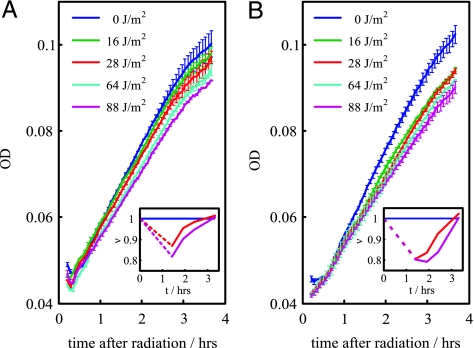
We tested this hypothesis by measuring cell growth in terms of OD. In Fig. 4A, we plot the growth of cells with the autogenously regulated LexA for different UV values. We show how the exposure to increasing levels of UV radiation is reflected in a gradual reduction of the growth rate. This very same feature is observed in cells carrying the nonautogenously regulated LexA (Fig. 4B). However, the overresponse associated with this type of control, in comparison with an equivalent damage situation with autoregulated LexA, comes at a cost, because the relative growth rate of the population is smaller. This cost is more evident at low-UV doses where the dynamical differences between both circuits are more drastic as discussed above.

Fig. 4.

ODs after irradiation. Exposure to increasing UV dose is reflected in a gradual reduction of growth. This reduction in cells carrying the autogenous circuit (A) is smaller than that observed in cells bearing the nonautogenous one (B) for an equivalent damage situation. Thus, the overresponse induced by the nonautogenous control comes at a cost. (Insets) Growth rate (ν) vs. time for intermediate and high UV doses relative to a nonradiated situation (same color code as main images).

Discussion

Biomolecular interactions within cells ultimately decide their physiology. This genetic circuitry resembles in many aspects that found in other nonbiological scenarios, and thus control ideas commonly used in these contexts have been incorporated into the understanding of cellular action (30). These types of studies are contributing to the discovery of a set of feedback-based regulatory strategies in biological systems and to further confirmation of the possible identification of fundamental design principles of cellular control [e.g., robustness (5, 6), noise tolerance (7), programmed temporal order (8, 11), sign-sensitive dynamics (9, 10), ultrasensitivity (12), optimal performance (13), and implementation-dependent dynamics (14)].

To fully understand cellular control mechanisms, it becomes necessary both to characterize their dynamic properties in theoretical terms and to confirm some of these aspects experimentally (21, 31). Although the use of synthetic circuits in isolation is a valid tool for this second goal, and an interesting development by itself from a bioengineering perspective, only by studying these structures as part of natural networks can we completely understand their biological relevance. Here, we characterize one of these strategies, autogenous control, by combining mathematical models and high-resolution expression measurements from living cells. We consider the SOS response network as a valid genetic model for this study and compare its response with or without the presence of this control on its master regulator, the protein LexA.

We first studied how autogenous regulation determines the strength of the SOS response. Under DNA-damage conditions, the concentration of LexA is reduced. This change in LexA levels releases a battery of SOS genes linked to several repair processes leading to the recovery of the system to its uninduced state (24, 32). We followed the course of this response by measuring the dynamics of a GFP reporter protein under the control of the lexA promoter. For a fixed UV dose, the response of the nonautogenous system is larger than that found in the autogenous one, with this difference being more dramatic at low-UV doses. This difference is a direct consequence of the action of the autogenous control, which counterbalances more effectively the degradation of LexA levels induced by the damage. We partially interpreted this result in terms of the stronger stability exhibited by the autogenous system (20, 22). The ratio of stability between both circuits was found to be close to its theoretical maximum, which indicates that this property is being fully exploited in this network. This aspect has an important biological implication, because it acts as a buffering mechanism that prevents unwanted triggering of the response.

The presence of autogenous control has been proposed to provide faster response dynamics in inducible systems regulated by a repressor (20, 21, 23). Here, we were interested in confirming the presence of such speed-up in a natural network. To this aim, we compared the normalized PA of both circuits after exposure to UV radiation. We found that the induction of the response is independent of the type of control and UV dose, because this process is mainly driven by the fast cleavage of the LexA protein, mediated by activated RecA (25). On the contrary, the return from the induced to the uninduced state is circuit dependent. We highlight two different regimes in this case. For low-UV dose, autogenous control does speed up the recovery of the system to the uninduced state, further corroborating the proposed role of this regulation. However, this recovery time equals the nonautogenous case for high-UV doses. We argued that this finding is associated with the longer time required for repair, which, in this regime, determines the recovery time of the system. These two proposed regimes illustrate the relevance of studying simple motifs in their natural context (15). Finally, although we were able to characterize the SOS recovery time by using this type of population-level measurements, it also would be interesting to study how the presence of autogenous control could influence the pattern of activity of the SOS response at the individual cell level (32).

Autogenous control also exhibited a precise fine tuning of the response. We exposed both circuits to a range of UV doses. We showed that the ability of the network to respond proportionally to the level of DNA damage is lost in the nonautogenously controlled system.

All previous discussions contribute to characterize the functional advantages of autogenous regulation in inducible systems controlled by a master repressor. Because induction due to an input signal is associated with repressor elimination, these advantages are specially maximized for low inputs, such as low DNA damage in the case of the SOS system. With sufficiently high inputs, repressor levels are almost emptied with either type of control. This observation suggests that the compensatory mechanisms associated with autogenous regulation lose efficiency, and consequently the difference with respect with nonautogenous control is diminished. When this response comes at a cost for the growth of the bacteria, again as in the SOS system, the precise regulation associated with the autogenous strategy minimizes such a cost. This is likely to be the case for other networks also exhibiting the single-input module motif where overproduction of the set of operons that are controlled by the single transcription factor would amplify response cost (3). Indeed, in these structures, such master transcription elements are generally autorepressed (3).

These results additionally hint at the reasons why the presence of autogenous control could be selected in some genetic networks. Nature environments are rarely constant. Under these fluctuating/variable pressures, the adaptive response originated by the autogenous control mechanism implies the possibility of achieving high fitness in a range of environments. This adaptive response is favored over specialization, e.g., constant strong response in our case, which would likely cause a higher fitness but only in a single scenario (33). Finally, a plausible negative control of these hypotheses is the nonautogenous regulation of the lexA gene recently found in Leptospira interrogans (34). These parasitic bacteria are continuously subjected to strong DNA-damaging host-defense factors. In this environment, the disadvantages caused by the lost of autogenous regulation are compensated for by the need of a continuous pool of repair proteins.

In summary, we have characterized the benefits of autogenous control in a natural network. This control structure acts as an optimal strategy to respond to multiple levels of the input signal, minimizing in this way the costs of the response.

Materials and Methods

Bacterial Strains and Plasmids.

E. coli strains used in this work were JL794 lexA+sulA11Δ(lacIPOZYA)169rpsL31 (35) and its ΔlexA300 derivative, JL2101. Plasmid pSC101-P_lexA::GFP (Kan^R) (36) harbors the gfp gene under the control of the promoter of lexA gene. Plasmid pJWL70 (35) is a pBR322 derivative harboring the lexA gene under the control of the P_lac promoter. Plasmid pBR322 (37) was used as control plasmid lacking lexA. Plasmid pMMB207 (Cm^R) (38) provided the LacI repressor with the P_lacIq promoter. Plasmids pSC101-PlexA::GFP, pBR322, and pMMB207 were introduced by transformation into strain JL794, giving strain FMC110 (autogenous control). Plasmids pSC101-P_lexA::GFP, pJWL70, and pMMB207 were introduced into strain JL2101, giving strain FMC120 (nonautogenous control).

Growth and Expression Measurements.

Parallel cultures of FMC110 and FMC120 (5 ml) were grown overnight in LB medium with kanamycin (50 μg/ml), tetracycline (10 μg/ml), chloramphenicol (60 μg/ml), and IPTG (3 × 10⁻⁵ M) at 37°C with shaking. The preceding IPTG concentration was used to equal the LexA levels of both circuits in absence of damage. These cultures were diluted down to OD₅₉₀ = 0.01 (as measured in a Victor2 multiwell fluorimeter; PerkinElmer, Wellesley, MA) in M9 medium supplemented with 0.1% (wt/vol) casaminoacids, 0.4% (vol/vol) glycerol, 2 mM MgSO₄, 0.1 mM CaCl₂, and 0.05% (wt/vol) vitamin B₁, under the set of conditions initially mentioned. To measure growth and expression, we followed a described protocol (36). Briefly, cultures were grown in the fluorimeter at 37°C with 30 sec of shaking at intervals of 4 min. Cultures were irradiated with a UV lamp (Model VL-6C; Vilbert–Lourmat, Torcy, France) (λ = 254 nm) after reaching OD₅₉₀ = 0.04. The plate was then returned to the fluorimeter, after addition of 100 μl of mineral oil per well to prevent evaporation. A second repeated protocol was implemented that included shaking (2 mm orbital, normal speed, 30 sec), absorbance (OD) measurements (590-nm filter, 0.5 sec), and fluorescence readings (filters 485 nm, 535 nm, 0.5 sec, continuous-wave lamp energy setting 10,000). Time between repeated measurements was 4 min. GFP protein concentration was computed by dividing fluorescence by absorbance measurements. We calculated PA (also see Mathematical Modeling) by first fitting the GFP/OD data to a sixth-order polynomial and then taking the derivative of such curves (36). To avoid possible artefacts due to the polynomial fitting, we used as an alternative a regression spline method. Both methods showed very similar results.

Mathematical Modeling.

We introduced simple mathematical models to study several aspects of the SOS response. These models only incorporate the essential molecular constituents of the SOS network to help compare the behavior of autogenous and nonautogenous control. To understand the difference in stability of the uninduced equilibrium state, we described LexA dynamics in both circuits as dx/dt = Π(x) − δ_xx, with Π(x) = α_au/(1 + x/k), or Π(x) = α_na, for the autogenous (au) and nonautogenous (na) system, respectively (20, 23). Here, α_na is the constant PA of the nonautogenous circuit, α_au is the PA in absence of repressor of the autogenous one, k is the dissociation constant, δ_x is the protein degradation rate, and x denotes LexA concentration. LexA concentration in equilibrium for the nonautogenous system is given by x_eq = α_na/δ_x. Thus, to fulfill the condition of same equilibrium state in both circuits, one gets α_au = α_na(1 + x_eq/k). We can visualize a first-order system dx/dt = F(x) as a heavily damped particle inside a potential well. Under this formalism, F(x) = −dV(x)/dx. Integrating the dynamics of both circuits, we obtain the potentials of Fig. 1D. The stability of the systems is given by the value of the second derivative of this potential with LexA concentration in equilibrium σ = dF(x)/dx|_x=xeq = −d²V(x)/dx²|_x=xeq (26).

One can easily obtain the ratio of stabilities for both systems (θ = σ_au/σ_na) as

This ratio is limited to values ranging from θ = 1 (lack of autogenous control) to θ = 2 (strong autogenous control). Would the presence of delays related to the formation of active repressor modify these stability arguments? This hypothesis could be the case when protein production during delay time (T) was of the order of LexA concentration in steady state (23). For large LexA fluctuations of ≈10% of its equilibrium value, significant effects on stability would be observed for delays of the order of the inverse of the LexA degradation rate, i.e., T ≈ 1/δ_x = τ/ln 2 > 1 h, with LexA half-life τ ≈ 60 min (25). However, delays of the order of only a few minutes are expected in bacterial systems (23).

To analyze how the strength of the response differs for each circuit, we introduced a two-dimensional model describing the dynamics of LexA and activated RecA. The transition from RecA to RecA* is assumed to be in equilibrium, and in this way, RecA* activity becomes proportional to RecA dynamics

Here x and y denote LexA and activated RecA concentrations, respectively; Π(x) is the LexA circuit-dependent PA as before; β is the unactivated RecA PA in the absence of repressor; k' is the dissociation constant of LexA repressor with respect to the RecA promoter region; and δ_x and δ_y are the degradation rates of LexA and activated RecA, respectively. In addition, χ is the ratio of RecA activation that is proportional to DNA damage (ssDNA). This value ranges from 0 (no damage) to 1 (virtually all RecA turns into activated RecA). LexA cleavage is included as a term proportional to LexA and activated RecA concentrations with rate δ_xy (25).

By considering a situation with a fixed χ parameter, we can study the initial course of the response and, in particular, the distribution of induced LexA equilibrium states as a function of the amount of damage. This description is of course an approximation of the more complicated dynamics (39) of the response but corresponds to a realistic scenario in which LexA cleavage dominates such initial dynamics (25). The difference in response for both systems can be analyzed by using the associated response curves (nullclines) in the phase plane (26).

Both systems share the y-equation (Eq. 3), and thus the corresponding activated RecA nullcline (dy/dt = 0),

This equation constitutes a χ-parametric family of curves whose location is displaced toward low activated RecA as damage decreases, collapsing toward the x axis in the absence of damage, β = 0 (note that axes were swapped in Fig. 3 C and D). On the other hand, the LexA nullcline (dx/dt = 0) is different for each system:

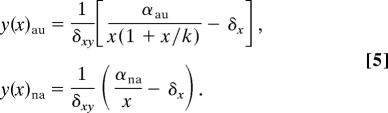Here, the rate between the first terms of the previous equations increases from 1 (same uninduced states) to α_au/α_na when x → 0.

Determination of Parameters.

We specified the effective kinetic parameters of both circuits by computing the corresponding PA, which is proportional to the number of GFP proteins present in the system (36): d[GFP]/dt = α_au/(1 + [LexA]/k) − δ_[GFP][GFP] ≡ Π([LexA]) − δ_[GFP][GFP]. Here the degradation term is mainly due to dilution by cell growth because the GFP used is very stable. We parameterized α_au (the PA in absence of repressor of the autogenous circuit) by using maximal PA values measured under high-UV conditions. We used the data obtained in cells carrying the nonautogenous system, because LexA levels are more effectively emptied in this case. From these values and the relation between both parameters in equilibrium, we find α_na. Finally, by normalizing LexA concentrations by their uninduced value, we derived the magnitude of k in the same units. Specific values used throughout the work are as follows: α_au = (6.0 ± 0.7)α_na, k = 0.20 ± 0.03. Finally, we computed relative repressor concentration dynamics from PA activity as [LexA]/[LexA]_eq = k(α_au/Π(t) − 1). We thus obtained minimal LexA concentrations (Fig. 3C) from maximal PA values for the corresponding strain and damage conditions.

Abbreviations

PA

promoter activity

IPTG

isopropyl-β-d-thiogalactopyranoside