Comparative quantification of health risks: Conceptual framework and methodological issues

Abstract

Reliable and comparable analysis of risks to health is key for preventing disease and injury. Causal attribution of morbidity and mortality to risk factors has traditionally been conducted in the context of methodological traditions of individual risk factors, often in a limited number of settings, restricting comparability.

In this paper, we discuss the conceptual and methodological issues for quantifying the population health effects of individual or groups of risk factors in various levels of causality using knowledge from different scientific disciplines. The issues include: comparing the burden of disease due to the observed exposure distribution in a population with the burden from a hypothetical distribution or series of distributions, rather than a single reference level such as non-exposed; considering the multiple stages in the causal network of interactions among risk factor(s) and disease outcome to allow making inferences about some combinations of risk factors for which epidemiological studies have not been conducted, including the joint effects of multiple risk factors; calculating the health loss due to risk factor(s) as a time-indexed "stream" of disease burden due to a time-indexed "stream" of exposure, including consideration of discounting; and the sources of uncertainty.

Introduction

Detailed description of the level (e.g. rates) and distribution of diseases and injuries, and their causes are important inputs to strategies for improving population health. Data on disease or injury outcomes alone, such as death or hospitalization, tend to focus on the need for palliative or curative services. Reliable and comparable analysis of risks to health, on the other hand, is key for preventing disease and injury. A substantial body of work has focused on the quantification of causes of mortality and more recently burden of disease [1,2]. Analysis of morbidity and mortality due to risk factors, however, has frequently been conducted in the context of methodological traditions of individual risk factors and in a limited number of settings [3-10]. As a result, in most such estimates:

1) Causal attribution of morbidity and mortality to risk factors has been estimated relative to zero or some other constant level of population exposure. This single, constant baseline, although illustrating the total magnitude of the risk, does not provide visions of population health under other alternative exposure distribution scenarios.

2) Intermediate stages and interactions in the causal process have not been considered in the causal attribution calculations. As a result, attributable burden could be calculated only for those risk factor – disease combinations for which epidemiological studies had been conducted (often limited to individual risks).

3) Causal attribution has often taken place using exposure and/or outcome at one point in time or over an arbitrary period of time (for notable exceptions see the works of Manton and colleagues [11-13] and Robins [14-19]). Such "counting" of adverse events (such as death) has not been able to clearly distinguish between those cases that would not have occurred in the absence of the risk factor and those whose occurrence would have been delayed. More generally, this approach is unable to consider the accumulated effects of time-varying exposure to a risk factor – in the form of years of life lost prematurely or lived with disability.

4) The outcome has been morbidity or mortality due to specific disease(s) without conversion to a comparable unit, making comparison among different diseases and/or risk factors difficult.

To allow assessing risk factors in a unified framework while acknowledging risk-factor specific characteristics, the Comparative Risk Assessment (CRA) module of the global burden of disease (GBD) 2000 study is a systematic evaluation of the changes in population health which would result from modifying the population distribution of exposure to a risk factor or a group of risk factors [20]. This unified framework for describing population exposure to risk factors and their consequences for population health is an important step in linking the growing interest in the causal determinants of health across a variety of public health disciplines from natural, physical, and medical sciences to the social sciences and humanities. In particular, in the CRA framework:

1) The burden of disease due to the observed exposure distribution in a population is compared with the burden from a hypothetical distribution or series of distributions, rather than a single reference level such as non-exposed.

2) Multiple stages in the causal network of interactions among risk factor(s) and disease outcome are considered to allow making inferences about combinations of risk factors for which epidemiological studies have not been conducted, including the joint effects of changes in multiple risk factors.

3) The health loss due to risk factor(s) is calculated as a time-indexed "stream" of disease burden due to a time-indexed "stream" of exposure.

4) The burden of disease and injury is converted into a summary measure of population health which allows comparing fatal and non-fatal outcomes, also taking into account severity and duration.

It is important to emphasize that risk assessment, as defined above, is distinct from intervention analysis, whose purpose is estimating the benefits of a given intervention or group of interventions in a specific population and time. Rather, risk assessment aims at mapping alternative population health scenarios with changes in distribution of exposure to risk factors over time, irrespective of whether exposure change is achievable using existing interventions. Therefore, while intervention analysis is a valuable input into cost-effectiveness studies, risk assessment contributes to assessing research and policy options for reducing disease burden by changing population exposure to risk factors. Summary measures of population health (SMPH) and their use in the burden of disease analysis are discussed elsewhere [21,22]. The next three sections of this paper discuss the conceptual basis and methodological issues for the remaining three of the above points. We then discuss the sources and quantification of uncertainty.

Causal Attribution of Summary Measures of Population Health to Risk Factors

Mathers et al. [23] described two traditions for causal attribution of health determinants, outcomes, or states: categorical attribution and counterfactual analysis. In categorical attribution, an event such as death is attributed to a single cause (such as a disease or risk factor) or group of causes according to a defined set of rules (hence 100% of the event is attributed to the single cause or group of causes). The International Classification of Disease system (ICD) attribution of causes of death [24] and attribution of some injuries to alcohol or occupational conditions are examples of categorical attribution. In counterfactual analysis, the contribution of one or a group of diseases, injuries, or risk factors to a summary measure of population health (SMPH) is estimated by comparing the current or future levels of the SMPH with the levels that would be expected under some alternative hypothetical scenario including the absence of or reduction in the disease(s) or risk factor(s) of interest. This hypothetical scenario is referred to as the counterfactual (see Maldonado and Greenland [25] for a discussion of conceptual and methodological issues in use of a counterfactuals).

In theory, causal attribution of an SMPH to risk factors can be done using both categorical and counterfactual approaches. For example, categorical attribution has been used in attribution of diseases and injuries to occupational risk factors in occupational health registries [8] and attribution of motor vehicle accidents to alcohol consumption. In general however, categorical attribution of SMPH to risk factors overlooks the fact that many diseases have multiple causes [26]. The epidemiological literature has commonly used the counterfactual approach for the attribution of a SMPH to a risk factor, and compared mortality or disability under current distribution of exposure to the risk factor to those expected under an alternative exposure scenario.

The dominant counterfactual exposure distribution in these studies has been zero exposure for the whole population (or a fixed non-zero level where zero is not possible such as the case of blood pressure when defined as presence or absence of hypertension). The basic statistic obtained in this approach is the population attributable fraction (PAF) defined as the proportional reduction in disease or death that would occur if exposure to the risk factor were reduced to zero, ceteris paribus [27-35]. As discussed by Greenland and Robins [36], attributable fractions without a time dimension are not able to characterize those cases whose occurrence would have been delayed in the absence of exposure. The authors recommend the use of etiologic fractions with a time dimension to account for this shortcoming. Time-based measures are discussed in more detail below.

The attributable mortality, incidence, or burden of disease due to the risk factor, AB, is then given as AB = PAF × B where B is the total burden of disease from a specific cause or group of causes affected by the risk factor with a relative risk of RR.

The exposed population may itself be divided into multiple categories based on level or length of exposure each with its own relative risk. With multiple (n) exposure categories, the PAF is given by the following generalized form:

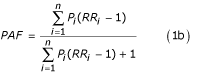
Although choosing zero as the reference exposure may be useful for some purposes, it is a restricting assumption for others. The contribution of a risk factor to disease or death can alternatively be estimated by comparing the burden due to the observed exposure distribution in a population with that from another distribution (rather than a single reference level such as non-exposed) as described by the generalized "potential impact fraction" in Equation 2 [32,37,38].

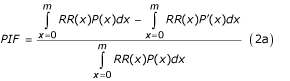
where RR(x) is the relative risk at exposure level x, P(x) is the population distribution of exposure, P' (x) is the counterfactual distribution of exposure, and m the maximum exposure level. The first and second terms in the numerator of Equation (2a) therefore represent the total exposure-weighted risk of mortality or disease in the population under current and counterfactual exposure distributions. The corresponding relationship when exposure is described as a discrete variable with n levels is given by:

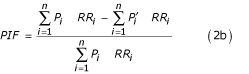
In addition to relaxing the assumption of no-exposure group as the reference, analysis based on a broader range of distributions has the advantage of allowing multiple comparisons with multiple counterfactual scenarios. Equation 2a can be further generalized to consider counterfactual relative risks (i.e. relative risk may depend on other risks, new technology, medical services, etc.). For example the relative risk of injuries as a result of alcohol consumption may depend on road conditions and traffic law enforcement. Similarly, people employed in the same occupation may have different risk of occupational injuries because of different safety measures. Therefore, a more general form of Equation 2a is given by:

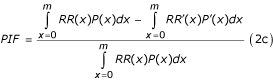
Counterfactual exposure distributions

Various criteria may determine the choice of the counterfactual exposure distributions. Greenland [39] has discussed some of the criteria for the choice of counterfactuals, arguing that the counterfactuals should be limited to operationalizable actions (e.g. anti-smoking campaigns) rather than the effects of removing the outcomes targeted by those actions (e.g. smoking cessation) because in practice, the implementation of counterfactuals for one risk factor or disease, may affect other risks. The solution to Greenland's concern, however, is better analytical techniques for estimating joint risk factor effects, rather than abandoning non-intervention-based counterfactuals which, as argued by Mathers et al. [23], is a limiting view. An understanding of the contributions from risk factors and the benefits of their removal, even in the absence of known interventions, can provide visions of population health attributable to risk factors, and avoidable by their removal. This knowledge of risk factor effects can provide valuable input into public health policies and priorities, as well as research and development (R&D).

Murray and Lopez [20] introduced one taxonomy of counterfactual exposure distributions which, in addition to identifying the size of risk, provides a mapping to policy implementation. These categories include the exposure distributions corresponding to theoretical minimum risk, plausible minimum risk, feasible minimum risk, and cost-effective minimum risk. Theoretical minimum risk is the exposure distribution that would result in the lowest population risk, irrespective of whether currently attainable in practice. Plausible minimum refers to a distribution which is imaginable and feasible is one that has been observed in some population. Finally, cost-effective minimum considers the cost of exposure reduction (through the set of cost-effective interventions) as an additional criterion for choosing the alternative exposure scenario.

In addition to illustrating the total magnitude of disease burden due to a risk factor, theoretical minimum risk distribution (or the current difference between theoretical and plausible or feasible risk levels) can guide R&D resources towards those risk factors for which the mechanisms of reduction (i.e. interventions) are currently underdeveloped. For example, if the reduction in the burden of disease due to improved medical injection safety is high and the methods for risk reduction are well-known so that plausible/feasible and theoretical minima are identical, then current policy may have to be focused on the implementation of such methods. On the other hand, if there are large differences between plausible/feasible and theoretical minima risk levels for blood lipids or body mass index (BMI) [40], then research on reduction methods and their implementation should be encouraged. For this reason the total magnitude of the burden of disease due to a risk factor, as illustrated by the theoretical minimum, provides a tool for considering alternative visions of population health and setting research and implementation priorities.

Biological principles as well as considerations of equity would necessitate that, although the exposure distribution for theoretical minimum risk may depend on age and sex, it should in general be independent of geographical region or population. Exceptions to this are however unavoidable. An example would be the case of alcohol consumption, which in limited quantities and certain patterns, has beneficial effects on cardiovascular mortality, but is always harmful for other diseases such as cancers and accidents [41]. In this case, the composition of the causes of death as well as drinking patterns in a region would determine the theoretical minimum distribution. In a population where cardiovascular diseases are a dominant cause of mortality theoretical minimum may be non-zero with moderate drinking patterns, whereas in a population with binge drinking and large burden from injuries the theoretical minimum would be zero. Feasible and cost-effective distributions, on the other hand, may vary across populations based on the current distribution of the burden of disease and the resources and institutions available for exposure reduction.

The above categories of counterfactual exposure distributions are based on the burden of disease in the population as a whole. Counterfactual exposure distributions may also be considered based on other criteria. For example, a counterfactual distributions based on equity would be one in which the highest exposure group (or the group with highest burden of disease) would be shifted towards low exposure values. Further, such equitable counterfactual distributions for each risk factor may themselves be categorized into theoretical (most equitable), plausible, feasible, and cost-effective as described above. Similarly, a counterfactual distribution which focuses on the most sensitive groups in the population is one that gives additional weight to lowering the exposure of this group. Therefore, by permitting comparison of disease burden under multiple exposure distributions, based on a range of criteria – including, but not limited to, implementation and cost, equity, and research prioritization – relaxing the assumption of constant exposure base-line provides an effective policy and planning tool.

Exposure distribution for theoretical minimum risk

In one taxonomy, risk factors such as those in the GBD project [42] can be broadly classified into categories of physiological, behavioral, environmental, and socio-economic. Some general principles that guide the choice of theoretical minimum distribution for each category are:

1) Physiological risk factors: This group includes those factors that are physiological attributes of humans, such as blood pressure or blood lipids, and at some levels result in increased risk. Since these factors are necessary to sustain life, their "exposure-response" relationship is J-shaped or U-shaped, and the theoretical minimum is non-zero. For such risk factors, the choice of the theoretical minimum needs to be based on empirical evidence from different scientific disciplines. For example, epidemiological research on blood pressure and cholesterol have illustrated a monotonically increasing dose-response relationship for mortality even at low levels of these risk factors [43-46]. But, given the role of these factors in sustaining life, this relationship must flatten and reverse at some level. In the blood pressure and cholesterol assessment, a theoretical minimum distribution with a mean of 115 mmHg for systolic blood pressure and 3.8 mmol/l for total cholesterol (each with a small standard deviation) were used [42]. This distribution corresponds to the lowest levels at which the dose-response relationship has been characterized in meta-analyses of cohort studies [43-46]. Further, these levels of blood pressure and cholesterol are consistent with levels seen in populations which have low cardiovascular disease, such as the Yanomamo Indians [47] and rural populations in China [48,49], Papua New Guinea [47,50], and Africa [51]. Although, meta-analyses of randomized clinical trials have indicated that blood pressure and cholesterol levels may be lowered substantially with no adverse effects [52,53], it is difficult to justify a theoretical minimum lower than those measured in population-based studies, since lower levels in individuals may be caused by factors such as pre-existing diseases. Inferences from evolutionary biology would also support the lower bound on the choice of optimal distribution based on historical survival of populations who are not substantially exposed to factors that raise blood pressure or cholesterol.

2) Behavioral risk factors: the exposure-response relationship for this group of risk factors may be monotonically increasing or J-shaped. For risk factors with a monotonic exposure-response relationship, such as smoking, the theoretical minimum would be zero unless there are physical constraints that make zero risk unattainable. For example in the case of blood transfusion, there may be a lower bound on safety of blood supply process even using the best monitoring technology. With a J-shaped or U-shaped exposure-response relationship, the theoretical minimum would be the turning point of the exposure-response curve. An example of this is alcohol consumption in adult populations with high cardiovascular disease rates, since moderate consumption may result in reduction in coronary heart disease in some age groups [54]. With a J-shaped exposure-response curve, similar to physiological risk factors, empirical evidence would have to be used to determine the theoretical minimum.

Finally, some behavioral risks are expressed as the absence of protective factors such as physical inactivity or low fruit and vegetable intake. In such cases, optimal exposure would be the level at which the benefits of these factors would no longer continue. With a monotonic exposure-response relationship or without detailed knowledge about a possible turning point, the theoretical minimum risk level would have to be chosen based on empirical evidence on the highest theoretically sustainable levels of intake or exposure (for example a purely vegetarian diet or a very active life style).

3) Environmental risk factors: The toxicity of most of the environmental risk factors are monotonically increasing functions of exposure (potentially with some threshold). Therefore, the theoretical minimum for this group would be the lowest physically achievable level of exposure, such as background particulate matter concentration due to dust.

4) Socioeconomic "risk factors": Socioeconomic status and factors – such as income (including levels and distribution) and associated levels of poverty and inequality, education, the existence of social support networks, etc. – are important determinants of health, often through their effects on other risk factors. The effects of each of these factors on health are, however, highly dependent on other socioeconomic variables as well as the policy context, including accessibility and effectiveness of health and welfare systems. For this reason, the theoretical minimum exposure distribution, even if meaningfully defined, is likely to change over time and space depending on a large number of other factors. With this heterogeneity of effects, the effects of socioeconomic variables are best assessed relative to counterfactual distributions defined based on policy and intervention options in specific times and settings, as discussed by Greenland [39].

Risk Quantification Models

Prediction implicitly assumes the use of a conceptual model which infers the value of the variable of interest in a point in time or space based on knowledge from another setting, a different time or another location. Predictive models can be divided along a continuum between aggregate and structural categories. A completely aggregate model uses the previous trend of the variable of interest as the basis for predicting its future value. A structural model, on the other hand, identifies the components – and the relationships among them – of the "system" that determines the variable of interest. It then uses the knowledge of the system for predicting the value of the variable of interest. Most predictive models lie between the two extremes and use a combination of aggregate and structural modeling. At the extreme, a structural model would attempt to use chemical or physical principles as the unit of analysis and modeling. This would of course be currently impossible in studying any system that involves population health.

Consider for example predicting the future population of a city or the future ambient concentration of a pollutant. An aggregate model would extrapolate the historical levels to predict future values. Even in this case the model may include some structural elements. For example, the model may use a specific functional form – linear, exponential, quadratic, or logarithmic – for extrapolation which involves an assumption about the underlying system. A structural model in the case of population prediction would consider the age structure of the population, fertility (which itself may be modeled using data on education and family planning programs), public health variables, and rural-urban migration (which itself can be modeled using economic variables). In the case of air pollution, a structural model may consider demographic variables (themselves modeled as above), the structure of the economy (manufacturing, agriculture, or service), the current manufacturing and transportation technology and effects of R&D on new technology, the demand for private vehicles, the price of energy, and the atmospheric chemistry of pollution. Once again, in both examples the models may include some aggregation of variables by using the historical trends to predict the future values of individual variables in the system, such as funding for family planning or technology R&D.

The comparative advantage of structural and aggregate models lies in the balance between theoretical precision and data requirement. Structural models offer the potential for more robust predictions, especially when the underlying system is complex and highly sensitive to one or more of its components. In such cases, a shift in some of the system variables can introduce large changes in the outcome which may be missed by extrapolation (such as the discovery of antibiotics and infectious disease trends or the change in tuberculosis mortality after the HIV epidemic). Aggregate models, on the other hand, require considerably less knowledge of the system components and the relationships among them. These models can therefore provide more reliable estimates when such information is not available, especially when the system is not very sensitive to its inputs in time intervals that are in the order of the prediction time.

Models for estimation of risk factor outcomes

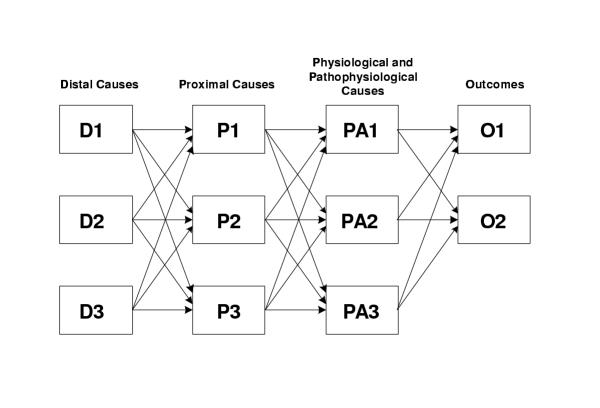
Using the above aggregate – structural taxonomy, it is also possible to classify models that are used to predict changes in death or disease as a result of changes in exposure to underlying risk factor(s). Murray and Lopez [20] described a "causal-web" which includes the various distal (such as socioeconomic), proximal (behavioral or environmental), and physiological and patho-physiological causes of disease, in a structural model shown in Figure 1. While different disciplinary traditions, from social sciences and humanities, to physical, natural, and biomedical sciences have focused on individual components or stages of these relationships, in a single multi-layer causal model with interactions the term "risk factor" can be used for any of the causal determinants of health [23,55]. For example, poverty, location of housing, access to clean water and sanitation, and the existence of a specific parasite in water can all be considered the causes of diarrheal diseases, providing a more complete framework for assessment of interventions and policy options. Similarly, education and occupation, diet, smoking, air pollution, and physical activity, and BMI and blood pressure are some of the risk factors at various levels of causality for cardiovascular diseases.

Figure 1.

A causal-web illustrating various levels of disease causality. Feedbacks from outcomes to preceding layers may also exist. For example, individuals or societies may modify their risk behavior based on health outcomes. The "driving force, pressure, state, exposure, effect" (DPSEE) model of Corvalan et al. [56] does consider the multiple layers of causality. These layers however focus the risk evolution process which is less suitable for multi-risk factor interaction within and between layers. More complete discussions of causality and multiple causes are provided by Yerushalmy and Palmer [55], Evans [57,58], and Rothman and Greenland [26,59].

Compared to a causal-web, Equations 1 and 2 which use relative risk estimates from epidemiological methods such as Cox proportional hazard or other regression models lie further towards aggregate modeling. In general, in such methods, relative risks are estimated so that they incorporate the aggregation of the various underlying relationship (ideally, but not always, controlling for the appropriate confounding variables) without considering intermediate relationships as separate causal stages (the exception is those risk factors whose effects occur through intermediate variables which are themselves a risk factor considered in the study, such as the relationships between CHD and physical inactivity or obesity which are mediated through blood pressure or cholesterol. In such cases, controlling for the intermediate risk factor would result in a bias (towards the null) in the estimation of total hazard when the distal factor is considered alone [60]). On the other hand, if specified and estimated correctly, considering the complete causal pathways which include multiple risk factors will allow making inferences about combinations of risk factors and risk factor levels for which direct epidemiological studies may not be available.

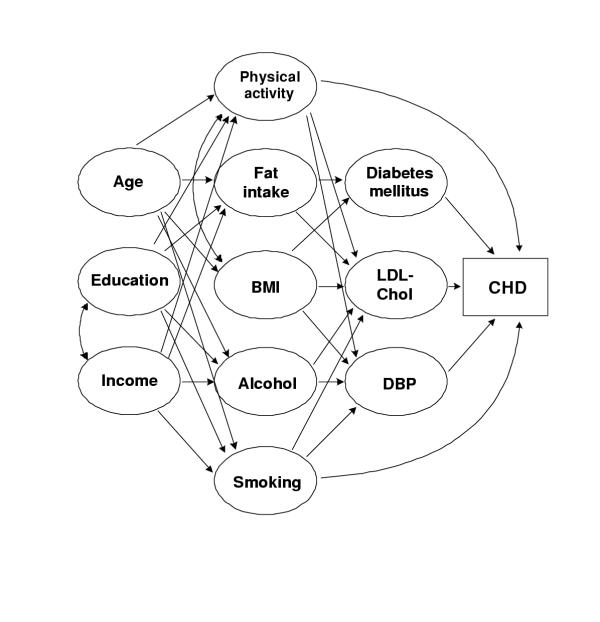
As discussed earlier, the appropriateness of the two approaches to estimation of attributable burden depends on the specific risk factor(s), outcome, and available data. The relationship between smoking and lung cancer has been shown to be highly dependent on smoking patterns and duration which, with appropriate indicators of past smoking [3], can be readily estimated using the relative risk approach of Equations 1 and 2. Consider, on the other hand, the relationship among age, socioeconomic status and occupation, behavioral risk factors (such as smoking, alcohol consumption, diet, physical activity), physiological variables (such as blood pressure and cholesterol level), and coronary heart disease (CHD) shown in the causal diagram of Figure 2.

Figure 2.

A possible causal diagram based on established relationships for estimating the incidence of coronary heart disease (CHD). Other interactions may also be possible.

Given the multiple complex interactions, CHD risk may be best predicted using a structural (causal-web) approach, especially when some risk factors vary simultaneously, such as smoking, alcohol, and diet, requiring joint counterfactual distributions. Using a multi-risk model would also allow considering situations for which direct epidemiological studies may not have been conducted such as the effects of physical activity on those people who have diets different from the study group or those who use medicine to lower blood pressure.

The health effects of global climate change provide another example where a structural approach to risk assessment may be appropriate. Economic activity (including manufacturing, agriculture and forest use, transportation, and domestic energy use) affect the emissions of greenhouse gases (GHG). Changes in precipitation, temperature or rainfall, and other meteorological variables due to atmospheric GHG accumulation alter regional ecology which in turn results in changes in agricultural productivity, quantity and quality of water, dynamics of disease vectors, and other determinants of disease. All these effects are in turn modulated by local economic activities, land-use patterns, and income [61-63]. A model based on the atmospheric physics/chemistry of GHG emissions and accumulation, climate models, plant and vector ecology, and human activity can provide a basis for the prediction of the health effects of climate change (there are no past studies on "climate change" as it is expected to take place in the future. For this reason, the relationship between climate change and health would always be based on a model which relates climate change to meteorological variables (e.g. temperature or rainfall). The relationship between these variables, disease vectors and disease, could then be estimated from past data and vector biology [62,64,65]).

Specifying the causal-web

Assuming for the moment no temporal dimension in the relationship between the different variables in the causal system (temporal aspects are discussed below), each layer of a causal-web may be characterized by the equation:

Xⁿ = ƒ(B(X^n-1, Xⁿ), X^n-1)     (3a)

where Xⁿ is the vector of the variables in the n^th layer of the causal-web (which can be causal or output such as D, P, PA, or O using the notation of Figure 1); ƒ is the functional form connecting the (n - 1)^th layer to the n^th layer; B is a matrix of coefficients for ƒ which itself may be dependent on the variables in the (n - 1)^th and n^th layers (X^n-1 and Xⁿ) (in this case when some of the variables affect not only the other variables in the causal system but also the relationship(s) between variables, they are equivalent to "effect modification" in epidemiological literature [26]. Graphically, in Figure 1 they would be represented as links (arrows) not between two variables but as links from one of the variables (the effect modifier) to another link in the system), as well as time as we discuss below.

If the variables in the nth layer of the causal-web are affected directly by those in the (n-2)^th layer in addition to the (n-1)^th layer, or by variables within the n^th layer itself (see Figure 2 for an example), Equation 3a can be expanded to include these links as well:

Xⁿ = ƒ(B₀(Xⁿ), Xⁿ; B₁ (X^n-1, Xⁿ), X^n-1; B₂(X^n-2, Xⁿ), X^n-2)     (3b)

This can be extended to interactions across multiple causal layers, and in general any variable in the system can be affected by any other one as the concept of causal layer becomes more flexible.

The attributable fraction of disease or mortality due to a single risk factor in the causal-web is then obtained by integrating the outcome (O) over the current (P(x)) and counterfactual (P' (x)) population distributions of exposure, as was done in Equation 2.

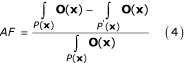
Joint risk factor changes

The attributable fraction relationships described in Equations 1 and 2 are based on individual risk factors. Disease and mortality are however often affected by multiple, and at times correlated, risk factors [26,38]. Estimating the joint effects of multiple distal and proximal risks is particularly important because many factors act through other, intermediate, factors [20,55], or in combination with other factors. It is therefore important to consider how the burden of disease may change with simultaneous variations in multiple risk factors. Considering joint risk factor changes implicitly indicates that the disease causation mechanism involves multiple factors, and is therefore suited to a causal-web framework, with P(x) and P' (x) in Equation 4 being the joint distributions of the vector of risk factors, x. Alternatively, when using Equations 1 or 2, knowledge of the distribution of all relevant risk factors and the relative risk for each risk factor, estimated at the appropriate level of the remaining risk factors is required (in other words the RR(x) in Equations (2a) and (2b) are functions of the other covariates, which we referred to as effect modification earlier. Epidemiological studies that stratify relative risks based on covariates other than age and sex are however very rare). Therefore, in Equation 2a, RR and P may represent joint risks and exposure distributions for multiple risk factors [32]. In this case, the estimates from Equations 2a and 4 may in theory be identical.

Additivity of attributable fraction

Many users of risk assessment desire information characterized by additive decomposition. In other words, they would like to be able to answer what fraction of the disease burden is related to any risk factor or group of risk factors, independent of the changes in other risk factors. As discussed by Mathers et al. [23], additive decomposition is a property of categorical attribution and, in general, not of counterfactual attribution because many diseases are caused by the interaction of multiple risk factors acting simultaneously and therefore can be avoided by eliminating any of these factors [26,55,59]. Consider for example infant and child mortality due to acute respiratory infections (ARI), which is especially high among malnourished children, as a result of exposure to indoor smoke from solid fuels [66,67]. In this case, removal of either risk factor will reduce mortality, some of which can therefore be attributed to both factors. Similarly the risk of mortality due to cardiovascular diseases among some of those who are affected by smoking, low physical activity, and poor diet may be reduced by elimination of any combination of these risk factors. Therefore, counterfactual causal attribution of disease and injury to individual risk factors, does not normally allow additive decomposition and the sum of attributable fractions or burdens for a single disease due to multiple risk factors is theoretically unbounded.

Although epidemiologically unavoidable and conceptually acceptable, the lack of additivity presents additional policy complexity and implies great caution when communicating and interpreting the estimates of attributable fraction and burden. With multiple attribution, the reduction of one risk factor would seem to make other, equally important risk factors, potentially irrelevant from a perspective with limited scope on quantification. At the same time multi-causality offers opportunities to tailor prevention based on availability and cost of interventions. It also necessitates the development of methods to quantify the effects of joint counterfactual distributions for multiple risk factors.

Temporal Dimensions of Risk Factor – Disease Relationship

Both exposure to a risk factor and the health outcomes due to exposure include a time dimension. This can be described by a modified version of Equation 3 in which exposure and outcome as well as the model parameters (B) are dependent on time. In the following two sections we consider the temporal characteristics of exposure and health outcomes.

Temporal characteristics of exposure

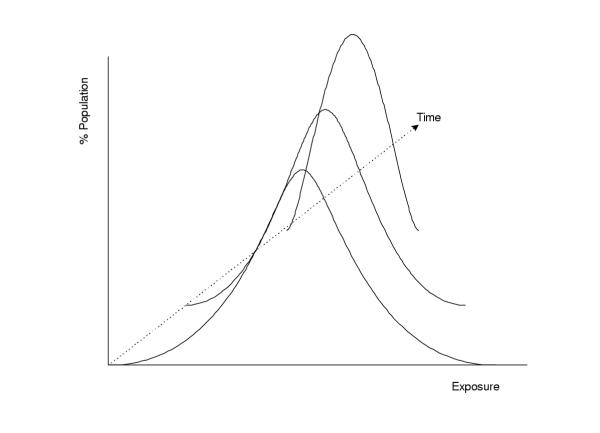
With the exception of acute hazards (e.g. injury risk factors) exposure to a risk factor affects disease over a time period. As a result, the distributional transition between any two exposure distributions includes a temporal dimension as illustrated schematically in Figure 3. The transition path is of little importance if exposure changes over a short time interval, especially relative to the time required for the effect of exposure on disease. Over long time periods, however, there is sufficient time for contributions from the intermediate exposure values and the actual path of transition may be as important as the initial and final distributions in determining the disease burden associated with change in exposure. For example, the effects of reducing the prevalence of smoking or exposure to an occupational carcinogen by half in a population, would be markedly different if the change takes place immediately, gradually over a twenty-year period, or after twenty years. Therefore, the health effects of exposure to many risk factors depend on the complete profile of exposure over time, and may be further accompanied by a time-lag from the period of exposure. Also, for some risk factors there may be complete or partial reversibility, with the role of past exposure gradually declining.

Figure 3.

A (three-dimensional) representation of a time-indexed distributional transition of population exposure to a risk factor, with a decreasing central tendency.

To capture the effects of exposure profiles over time, we begin the analysis by considering the role of temporal dimensions of exposure at the level of individuals (or groups of individuals with similar exposure) before extending the analysis to the whole population. Suppose that at time T the relative risk of a disease, RR, for individuals exposed to a risk factor (compared to the non-exposed group) depends on the complete profile or stream of exposure between time T₀ and T, denoted by x(t), with some lag, L, between exposure and effect. Then, there is some function, ƒ(x), which can be used to describe the contribution of exposure at any point in time between T₀ and T to the relative risk. In mathematical notation:

(The notation 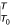denotes "estimated between T₀ and T").

The quantity 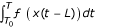is an equivalent exposure between T₀ and T and is dependent on: 1) the profile of exposure (i.e. level of exposure at any point in time) described by x(t); and 2) the contribution of previous exposure to current hazard characterized by ƒ(x), an accumulative risk function. Note that equivalent exposure is an analytical concept and need not be physically realizable. In fact for many risk factors such as carcinogens where the effects are from life-long exposure, the equivalent exposure would be so high that its occurrence at a single instant would be impossible. Further, if there is threshold, M, below which exposure has no effect:

where

This framework can be easily modified to include cases where exposure has different effects below and above threshold by using TRUE(x(t) ≥ M) for the effect above the threshold and TRUE(x(t) <M) for the effect below the threshold. Some potential forms for the accumulative risk function, ƒ(x), are given in Table 1.

Table 1.

Examples of accumulative risk functions

Accumulative Risk Function, ƒ(x)	Interpretation	Relative Risk, RR	Example
	Relative risk depends only on current exposure, with no contribution from past exposure.		Instantaneous poisoning as a result of exposure to high levels of toxic chemicals; injuries or death in accidents due to binge drinking; infection with Hepatitis B or C as a result of an infected injection
ƒ(x) = 1	Relative risk depends on the accumulated exposure (or average exposure if normalized with respect to exposure time), without any effects from the temporal distribution of exposure.		Cancer risk from life-time exposure to carcinogens which have no threshold level
	Relative risk depends on current and past exposures. But the role of past exposure lasts for a limited time, K, and decline as a linear function of time.
ƒ(x) = ea(t-T)	Relative risk depends on current and past exposures. But the role of past exposure decays as an exponential function of time.

For simplicity of notation, in all these cases we assume that: 1) L = 0. Including a lag is straightforward and can be done by replacing t with (t - L) in the corresponding formulas; and 2) there is no threshold for exposure. Including the threshold level is also straightforward using the TRUE (x (t) ≥ X) function. In scenarios 1, 3, and 4, where the effects of past exposure declines over time, risk reversibility can take place if exposure is reduced or removed. In 1 there is immediate risk reversibility; in 3, there is full reversibility after time K; in 4, risk reversibility asymptotically reaches 100%. In scenario 2 there is no risk reversibility and the effects of past exposure remain for an indefinite period.

The above framework can be extended from individuals to populations, by indexing the exposure profile (x(t)) to individuals (i.e. representing the exposure of the i^th individual as x_i(t)) and considering how the distribution of exposure in the population evolves over time (in this manner, the evolution of the exposure distribution is analytically similar to a "random process" in which a probability density function (PDF) describes a random variable which is a function of time. Exposure to a risk factor is not a random variable in the strict sense. But since a time-dependent exposure distribution has an accumulated distribution of 1.0, it has the same representation as a random process). This in turn provides the population distributions of equivalent exposure (current or expected future and counterfactual) which form the basis of calculating attributable fraction (i.e. the terms in the numerator or Equations (2a), (2b), or (4a)).

It is reasonable to assume that if the exposure of one individual is greater than that of another over the whole exposure period (i.e. tracking) [68], the equivalent exposure of the former is also greater than the latter. In other words, the accumulative risk function, ƒ(x), has the following property:

With this property, if the ordering of individuals in the exposure distribution remains unchanged over time (i.e. the rank-order correlation of individual exposures equals 1 between different points in time), the equivalent exposure will also have a distribution with the same ordering of individuals.

The method used by Peto et al. [3] for estimating mortality due to accumulated hazards of smoking implicitly uses such as framework. It is well-known that the accumulated hazards of smoking depend on a number of variables including the age at which smoking began, number of cigarettes smoked per day, and cigarette type. Such data however are extremely rare. To overcome this problem, Peto et al. [3] used smoking impact ratio, SIR, (which uses population lung cancer rates as a marker for accumulated hazard of smoking) to estimate the relative risk for the accumulated smoking exposure in the population. In the above notation:

The temporal profile of exposure for some risk factors may be more easily available than the range of indicators that are needed to estimate the accumulated hazards of smoking. For example, exposure to indoor smoke from solid fuels is likely to remain unchanged as long as household fuel and housing conditions remain the same. Therefore, estimating the effects of long-term exposure may require only knowledge of household fuel, housing, and participation in cooking. Similarly, in the case of blood pressure, it is known that blood pressure follows a predictable age-pattern [69,70], unless severely affected by a changes in social (stress), behavioral (diet or smoking), or medical circumstances. In this case, the usual blood pressure of an individual reflects the history of the person's exposure. On the other hand, the patterns of fruit and vegetable consumption, smoking, or exposure to ambient air pollution may change rapidly in countries with high rates of economic growth and urbanization, requiring more detailed data.

The above discussion is based on two implicit assumptions:

1) It considers the effects of exposure to a single risk factor over time. This approach may be appropriate for some risk factor – disease relationships (e.g. the effects of accumulated exposure to carcinogens with site-specific effects). But the single equivalent exposure cannot characterize other risk factor – disease relationships where risk factor interactions are important over time (e.g. physical activity, BMI, smoking and cardiovascular diseases). Extending this temporal dimension to multiple risk factors requires considering the accumulated effects of the vector of risk factors as well as their interactions. In that case, Equation 5 would be expressed in terms the vector of risk factors of interest. Few epidemiological studies, however, have gathered the data needed for assessing accumulated interactive effects.

2) It considers exposure to each risk factor as an exogenous variable (i.e. intermediate exposure at any time, x(t), is not affected by disease or other risk factors) whose accumulated effect can be captured in single value using the risk accumulation function. For some risk factors, this assumption may not be valid since exposure to behavioral as well as environmental risk factors may be affected by knowledge of their current effects. Individuals may change their diet or activity levels based on knowledge of their weight or blood pressure and governments may introduce regulations based on the level of various contaminants in air or water. Robins [18] discusses this issue in the case of estimating the effects of a dynamic treatment regime whose dose is dependent on symptoms.

Manton et al. [12,71] have relaxed these assumptions using a diffusion model for forecasting cardiovascular disease mortality in the US. In this model, it is the change in the outcome in any time, t, that is modeled as a function of all the other variables in the system (i.e. other risk factors as well as outcomes) and their interactions. Using the notation of Equation 3:

dX(t) = u(X(t), t) dt     (7)

where u(X(t), t) is a drift term whose value depends on the current value of all the variables in the system as well as their interactions (and can be described by a functional form similar to that in Equation 3) (the diffusion model also includes a stochastic component to account for those interactive effects not described by the drift term). Methods for estimation of such models using longitudinal data are discussed by Robins [19,72].

Temporal characteristics of health outcomes

If the outcome variable used in causal attribution of disease and mortality to a risk factor only involves counting of adverse events (such as disease incidence or death), it is not possible to characterize those cases whose occurrence would have been delayed in the absence of the risk factor [16,36,73]. Therefore, this approach is unable to consider the accumulated effects of exposure – in the form of years of life lost prematurely or lived with disability. Parameterizing the above relationships by age (or birth cohort) would allow estimating the effects of exposure to a risk factor not as an event without time dimension but as an event at a certain age and time. More broadly considering the time-indexed stream of health losses due to a risk factor requires using a time-based (and not event-based) SMPH.

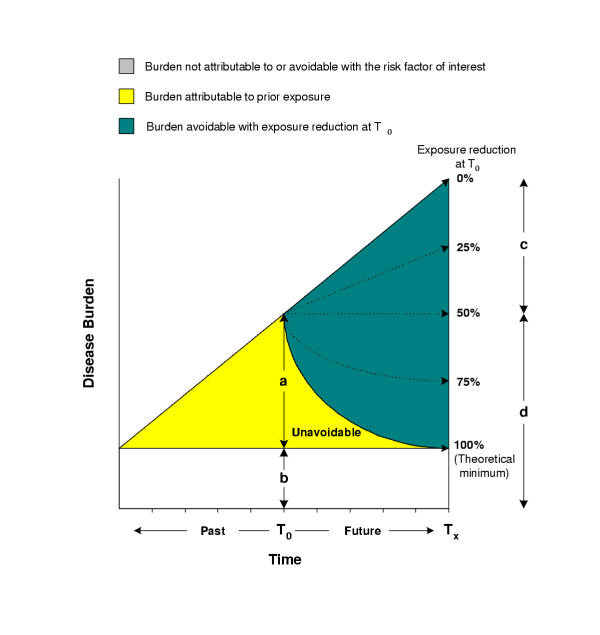
Murray and Lopez [20] have provided an additional temporal distinction for the burden of disease due to a risk factor by introducing the concepts of "attributable" and "avoidable" burden. Attributable burden is defined as the reduction in the current or future burden of disease if the past exposure to a risk factor had been equal to some counterfactual distribution. Avoidable burden is the reduction in the future burden of disease if the current or future exposure to a risk factor are reduced to a counterfactual distribution. Attributable and avoidable burden are shown graphically in Figure 3. While attributable burden is easier to measure and more certain, avoidable burden is more useful for policy purposes. The distinction between attributable and avoidable burden becomes less significant as the time between exposure to risk factor and effects on disease burden decreases, which also makes attributable burden a better predictor of avoidable.

Figure 4 also illustrates a conceptual complexity in defining and estimating avoidable burden. Attributable burden is defined based on the difference between (accumulated) current exposure and a counterfactual. Measuring current exposure, while difficult and uncertain, is conceptually well-defined. Avoidable burden, on the other hand, depends on the expectation of future exposure and counterfactual, with the former being analogous to current exposure. Consider for example a population exposed to rising air pollution or obesity. In this setting, interventions that would maintain pollutant concentrations or body mass index (BMI) at their current levels would result in avoiding disease and mortality; they reduce exposure compared to what it would be in their absence. Therefore, avoidable burden (i.e. how much of future burden can be prevented) by definition requires estimates of future exposure (i.e. how much of future burden there is). Projecting future exposure in turn raises the need to provide a projection framework. To provide visions of public health under various intervention and policy scenarios we suggest the future exposure, with respect to which avoidable burden is estimated, to be the expectation of exposure if the current policy and technological context continued, referred to as "business-as-usual" (BAU) exposure trend. Therefore avoidable burden is the burden of disease averted due to reduction in exposure to a risk factor beyond its expected trends. We emphasize that with this definition, avoidable burden is the difference between two exposure scenarios: the expectation of future trends (BAU) and a reduction with respect to this trend towards theoretical minimum.

Figure 4.

Attributable and avoidable burden. a = disease burden at T₀ attributable to prior exposure. The burden not attributable to risk factor of interest (light area) may be decreasing, constant, or increasing over time. The middle case is shown in the figure. b = disease burden at T₀ not attributable to the risk factor of interest (caused by other factors only). Dashed arrows represent the path of burden after a reduction at T₀. c = disease burden avoidable at T_x with a 50% exposure reduction at T₀. d = remaining disease burden at T_x after a 50% reduction in risk factor.

Cumulative versus snap-shot estimates of attributable and avoidable burden

Although analytically inconsequential, the starting point and the duration of the time interval over which attributable or avoidable burden is reported has important policy implications because reductions in various risk factors may provide health benefits that occur after short or long delays and last for different durations. Consider for example the health benefits of reductions in binge alcohol consumption, smoking, and green house gas (GHG) emissions. Reducing binge drinking would result in immediate health benefits from a drop in alcohol related accidents and injuries (as well as medium and long term benefits from reduction in other diseases). Lowering smoking will have some short and medium-term benefits from reduction of acute respiratory diseases and cardiovascular disease as well as longer term benefits from lowering cancers and chronic obstructive pulmonary disease (COPD). Finally, the benefits of policies that reduce climate change as a result of GHG emissions are likely to be heavily concentrated in the future.

As examples of the duration of health benefits, consider the distribution of a drug that lowers blood pressure or food aid to reduce malnutrition on the one hand, and programs that promote and sustain increased physical activity, the introduction of a new agricultural technology which results in higher food yields, or automotive technology which eliminates the use of leaded gasoline. While the benefits of all interventions may be equally large and important for the current cohort, the former policies have one-time health benefits (unless repeated) while those of the latter are likely to last indefinitely.

The above discussion would motivate reporting the estimates of avoidable burden in multiple ways including both snap-shots (for example annual) and cumulative estimates as well as over short and long time frames. The issue of future estimates and their policy relevance is further complicated by the growing uncertainty in estimates with increasing the length of the estimation interval. Therefore, while it is ideal to increase the prediction horizon, it is important to emphasize that long-term predictions are inherently more uncertain.

Discounting future risk and health effects

Individuals may discount consumption or welfare within their own life span and exhibit a preference for benefits today over future. The theoretical and empirical arguments for and against individual discounting with specific emphasis on health, including the possibility of negative discount rates, are summarized by Murray and Acharya [21,74] and are directly incorporated in calculating a summary measure of population health. In addition to individual discounting and discount rates, policies dealing with risk confront the issue of addressing benefits to different populations across time. As a result these policies must address ethical and analytical dilemmas related to the valuation of current and future health and welfare, in the form of social discount rates [75]. Discounting future risks, benefits, and welfare has been a subject of great debate [76-80], motivating some economists to conclude that "maybe the idea of a unitary decision-maker – like an optimizing individual or a wise and impartial adviser – is not very helpful when it comes to the choice of policies that will have distant-future effects about which one can now know hardly anything. Serious policy choice may then be a different animal, quite unlike individual saving and investment decisions. ... "Responsibility" suggests something less personal" [81].

The arguments for and against discounting of future health and welfare and their validity have been discussed in detail elsewhere [74,82-84]. According to one specific argument, "the disease eradication and health research paradox", not discounting future health would imply investing all of society's health resources in research programs or programs for diseases eradication, which result in an infinite stream of benefits, rather than any programs that improve the health of the current generation. Such an excessive intergenerational "sacrifice" is a particularly powerful argument for discounting of future health (or more precisely for something that resembles discounting as we discuss shortly) [82]. It is important to emphasize that this argument does not claim that future welfare or health is less valuable than current, but rather uses discounting as a tool to avoid excessive sacrifice to the current generation, to the point of investing all resources in an infinite stream of future health. For this reason, Parfit [82] argues that the issue of intergenerational distribution should be considered as an independent criterion, rather than in the form of discounting of future benefits.

Koopmans [85], Dasgupta and Mäler [86], and Dasgupta et al. [87], however, have shown that any preference-ordering defined over the set of well-being paths over time can be represented by a numerical function with an apparently utilitarian form and therefore includes what resembles positive discounting of future well-being (the functional form is 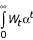where 0 < α < 1 in [85] and 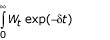where δ > 0 in [86,87] α and δ are the social rate of discount). We emphasize that this notion is simply a consequence of considering the paths of well-being (or temporal distributions), rather than a statement on the value of current or future welfare. With this formulation, Dasgupta and Mäler [86] and Dasgupta et al. [87] consider the implications of the choice of discount rate as a "derived notion", as opposed to a value judgment. Dasgupta and Heal [88] and Solow [89] have shown that if well-being is a result of consumption of an exhaustible resource, zero discount rate would imply investing all available resources for the benefit of future generations, and hence no current consumption. This is because each unit sacrificed by the first generation would yield a finite loss to this generation, but an infinite stream of benefits to future generations [90] which, without discounting, would always be larger than the one-time sacrifice. Although the first generation cannot sacrifice everything (the last unit of sacrifice will have an infinite marginal utility therefore matching the future infinite stream of benefits), the logical conclusion of this situation would be that "given any investment [for future benefits], short of the entire income, a still greater investment would be preferred," [90] or a potentially excessive intergenerational sacrifice [21].

On the other hand, a positive discount rate would imply that in the long run consumption of resources should become zero. In this case, however, the additional requirement that well-being should never fall below a certain threshold would in turn require downward adjustment of the discount rate [91]. The stricter requirement of non-declining consumption and well-being would require a discount rate lower than the productivity of capital [86] (these two additional constraints are external to the economic efficiency arguments as defined by maximizing aggregate welfare. In fact, these additional constrains of minimum acceptable or non-declining welfare result in an "inefficient" outcome in order to achieve better distribution across generations [92]; see Weitzman [93] for another argument for the choice of lower discount rates). Based on these arguments, we suggest discounting of future attributable or avoidable disease burden due to risk factors, but with a low discount rate, to include the welfares of both current and future generations as described above.

Uncertainty

Quantitative risk assessment is always affected by uncertainty about the existence, magnitude, and distribution of risk [94]. Quantitative analysis of uncertainty greatly adds to the applicability of the results because it shows not only the "best-estimate" magnitude and distribution of exposure to a risk factor and resulting burden of disease but also the range of potential outcomes.

Sources of uncertainty in attributable fractions

Population distribution of exposure

Due to complexity and cost, for most risk factors, exposure is measured only in small samples and in a limited number of settings. As we discussed earlier, because a risk factor can be represented in different layers of causality, variables for which data are more readily available can be used as exposure proxies. The use of exposure proxies is sometimes also necessary because epidemiological studies have used such proxies in estimating hazard size. For example, anthropometric variables such as height-for-age or weight-for-age are used as indicators of childhood nutritional status, the presence of clean water sources or sanitary latrines as indicators of faecal-oral transmission of pathogens, concentration of particulate matter as the measure of exposure to the various pollutants in ambient air, and so on. In addition to reduced data requirements, the use of such indirect indicators of exposure (or exposure scenarios [95]) may provide direct mapping to existing interventions. At the same time, these indicators, which are often more distal than actual exposure, do not capture the variability of exposure within each scenario, unless combined with other indicators which affect this variability [96]. For example people using the same water source may experience different levels of faecal-oral transmission of pathogens due to different storage behaviors. Therefore, the use of indirect exposure proxies results in additional uncertainty in exposure characterization.

Even with the choice of exposure proxies, extrapolation of exposure between different populations or age groups is often necessary. Such extrapolation (or spatial prediction) can be based on models as simple as using the average of populations with data for a whole geographical region or more complex prediction models. For example, urban air quality monitoring systems provide data on particulate matter concentrations in some but not all cities in each region. Models to predict ambient concentration based on energy consumption, number of vehicles, and level of industrialization can be used to predict ambient air pollution levels for the cities where data are not available. Similarly, the level of physical (in)activity in a population may be predicted from a model that uses rural-urban population distribution, income, education, distribution in occupational categories, and available transportation modes in each geographical region. Each such extrapolation adds to the uncertainty of exposure distributions.

Finally, as we discussed earlier, for many risk factors, hazards are associated with accumulated effects of sustained exposure. Indicators of accumulated hazard for those risk factors with changing exposure such as smoking, ambient urban air pollution, or body mass index, are needed but not always available. Further, few epidemiological studies have consider the role of temporal profile of exposure on disease (see Peto [97] for an example of an exception). Therefore even if longitudinal data on exposure prevalence were available, they could not always be used together with epidemiological studies that consider a single exposure variable, at the beginning or end of the follow-up period for example. At the same time, if the ordering of individuals in the exposure distribution remains unchanged over time (see above), risk estimates from epidemiological studies with similar ordering may be applicable, but results in an additional source of uncertainty. If exposure is sustained for a longer time in the risk assessment population than in the study population and if the whole exposure period contributes to hazards, this would result in an underestimation of risk (and vice versa). For example, in many cohorts in current epidemiological studies, BMI increased when the subjects were in their twenties or thirties. There is however increasing child and adolescent overweight or obesity in many regions of the world. If this continues into adult life, the hazards may be higher than those subjects in the current study cohorts.

Risk factor – disease relationship

At the most fundamental level, quantifying the hazards associated with exposure to a risk factor requires identifying the diseases and injuries that are caused by a risk factor. The criteria for establishing disease causality have been the subject of interest and debate for over a century [55,57,58,98,99]. Epidemiological studies have successfully provided the basis for establishing causality between some risk factor – disease pairs. For other risk factor – disease combinations, where the measurement of exposure or disease has been difficult or the delay between exposure and health effect is very long, observational or experimental epidemiology has had less success in establishing causality [18,57]. For this reason, epidemiological evidence must often be complemented with inferences from other disciplines such as toxicology, physiology, Parasitology, and increasingly biophysics in establishing disease causation.

Even when causality is established, the magnitude of the hazard due to a risk factor needs to be quantified. Although the statistical issues around establishing causality and estimating the effect size are similar (lack of causality is equivalent to zero excess risk) [18,100], in practice with knowledge from multiple disciplines in establishing causality, it is often the latter that is the source of increased uncertainty in risk assessment. For example, the collectivity of scientific knowledge from disciplines such as economics and behavioral sciences, vector biology, physiology and bio-mechanics, and epidemiology would confirm the possibility that climate change or inequality would increase disease, or whether the relationships between occupational factors or physical inactivity and lower back pain are causal. At the same time, risk assessment would require estimating the hazard magnitude for each of these relationships. Therefore, the complexity of the causal relationship or lack of detailed data would shift the debate from causality to hazard size.

Epidemiological studies that quantify hazards are often conducted in a limited number of settings, with emphasis on estimating the average effect size in the whole study group. While the robustness of relative measures risk has been confirmed for more proximal factors in studies across populations [45,101], their extrapolation is an important source of uncertainty for more distal risks (e.g. childhood sexual abuse) or those whose effects are heterogeneous (e.g. alcohol and injuries versus alcohol and cancer) and has received less attention in epidemiological literature [102]. At least for some risk factors, it is likely that the magnitude of hazard may depend on the levels of other variables (i.e. effect modifiers). Therefore in extrapolating the results of individual epidemiological studies or meta-analyses, the very strength of the original study – applicability to the average person – would be the source of uncertainty if the population to whom the effect size is extrapolated has characteristics which would result in effect modification [103-106]. The role of alcohol drinking patterns on cardiovascular disease risk estimates [41,107] are an example of the importance of considering the modulating effects in risk extrapolation.

Risk factor and disease correlations

Because multiple risks and disease are correlated (e.g. higher malnutrition, unsafe water, sanitation, and hygiene, indoor smoke and childhood mortality in poor rural households in developing countries; higher smoking, BMI, and occupational risks in developed countries [108]), estimating attributable fractions would require stratified (e.g. by other risk factors) prevalence as well as disease data. Lack of stratified data is another source of uncertainty, in general leading to underestimation of effects in the presence of positive risk factor correlation [34].

Characterizing and quantifying uncertainty

Various taxonomies of uncertainty have been used in risk assessment [99] including:

1) classification based on information type such as uncertainty in hazard identification, exposure assessment, exposure-response assessment, as discussed above;

2) classification based on uncertainty type such as randomness, true variability, and bias; and

3) classification based on the approach to handling uncertainty which divides uncertainty into model uncertainty and parameter uncertainty. Parameter uncertainty includes the uncertainty quantifiable using random-variable methods such as uncertainty due to sampling and measurement error. Model uncertainty is due to gaps in scientific theory, measurement technology, and data [99]. It includes uncertainty in the knowledge of causal relationships or of the form of the exposure-response relationship (threshold versus continuous, linear versus non-linear, etc.), the level of bias in measurement, etc. Defined broadly, model uncertainty also includes extrapolation of exposure or hazard from one population to another. Uncertainty in international risk assessment is by far dominated by model uncertainty, which is a result of lack and difficulty of direct studies on exposure, hazard, and background disease burden.

We distinguish between uncertainty – which is due to gaps in knowledge, methods, or data – and variability – which is a real property of the world and itself may be known with certainty or with uncertainty. Variability can nonetheless be a source of uncertainty in the absence of population-specific data on exposure or exposure-response relationship. For many risk factors, data on exposure distribution are available for a limited number of countries or demographic groups. The exposure distribution for other populations are then extrapolated from the available data based on some model. As we discussed earlier, the extrapolation model may be as simple as using the population-weighted average of the existing data or more complex and based on a number of predictors. In such cases, the statistical uncertainty of the estimator (e.g. the 95% confidence interval of the mean or regression coefficients) is an underestimation of true uncertainty in predicted values due to the unexplained variability in the data. More complex models can increase the predictive power and therefore reduce uncertainty but even the most sophisticated models are unlikely to fully explain the variability of the data, hence leaving behind some uncertainty. Variability can also be a source of uncertainty in estimation and extrapolation of exposure-response relationships or relative risks that are measured in a limited number of settings. In the presence of multiple estimates of hazard, it is common to use meta-analytical approaches to obtain an overall estimate. At the same time, the differences between various estimates may reflect true variability in effect size, especially if obtained from different populations, resulting in uncertainty in hazard estimates.

Parameter uncertainty can be readily included in quantitative analysis using random-variable statistical tools [109]. While we have discussed the various sources of uncertainty, the important issue of extrapolation of exposure and hazard using models requires new approaches to quantifying uncertainty in the presence of limited data. Quantitative analysis of model uncertainty by definition would require considering the uncertainty of the models and assumptions used (including assumptions about disease mechanism or data/parameter extrapolation) using tools of Bayesian statistics.

Conclusions

We have described a framework for systematic quantification of the burden of disease due to risk factors which attempts to unify the growing interest in health risks in a number of health, physical, and social sciences. We have discussed the following attributes of the framework along with the corresponding methodological issues that arise in its application:

1) comparing the burden of disease due to the observed exposure distribution in a population with the burden from a hypothetical distribution or series of distributions, rather than a single reference level such as non-exposed;

2) considering the multiple stages of causality and interactions between risk factor(s) and disease outcome to allow making inferences about combinations of risk factors for which epidemiological studies have not been conducted, including the joint effects of changes in multiple risk factors;

3) calculating the health loss due to risk factor(s) as a time-indexed "stream" of disease burden due to a time-indexed "stream" of exposure, including consideration of discounting;

4) describing the sources of uncertainty in the risk assessment process.

For each of the above aspects, we have described the important conceptual and methodological issues and their implications for risk assessment. While this framework provides a means for considering risk factors in different layers of causality, with multiple counterfactuals [42], its application is limited by the availability of data on risk factors and hazards [40]. The availability and form of data on both exposure and hazard are often determined by disciplinary boundaries as well as measurement difficulties. Analysis of selected risks itself illustrates data and monitoring needs for better quantification and intervention of important risk factors, especially more detailed data on exposure, hazard accumulation over time, and heterogeneity of risk factor – disease relationships.

For more effective and affordable implementation of a prevention paradigm, policies, programs, and scientific research should acknowledge and take advantage of the interactive role of major risks to health, across and within causality layers. Despite methodological complexity and empirical difficulties, especially in estimating time-based multi-risk exposures, this framework provides a consistent basis for better information about the causes of disease and injury.

Competing Interests

None declared.

Authors' contributions

CJL Murray and AD Lopez developed the initial CRA framework and M Ezzati further methodological aspects in discussion with other authors. Majid Ezzati drafted the paper, with contributions from other authors.