A theory of cortical responses

Abstract

This article concerns the nature of evoked brain responses and the principles underlying their generation. We start with the premise that the sensory brain has evolved to represent or infer the causes of changes in its sensory inputs. The problem of inference is well formulated in statistical terms. The statistical fundaments of inference may therefore afford important constraints on neuronal implementation. By formulating the original ideas of Helmholtz on perception, in terms of modern-day statistical theories, one arrives at a model of perceptual inference and learning that can explain a remarkable range of neurobiological facts.

It turns out that the problems of inferring the causes of sensory input (perceptual inference) and learning the relationship between input and cause (perceptual learning) can be resolved using exactly the same principle. Specifically, both inference and learning rest on minimizing the brain's free energy, as defined in statistical physics. Furthermore, inference and learning can proceed in a biologically plausible fashion. Cortical responses can be seen as the brain’s attempt to minimize the free energy induced by a stimulus and thereby encode the most likely cause of that stimulus. Similarly, learning emerges from changes in synaptic efficacy that minimize the free energy, averaged over all stimuli encountered. The underlying scheme rests on empirical Bayes and hierarchical models of how sensory input is caused. The use of hierarchical models enables the brain to construct prior expectations in a dynamic and context-sensitive fashion. This scheme provides a principled way to understand many aspects of cortical organization and responses. The aim of this article is to encompass many apparently unrelated anatomical, physiological and psychophysical attributes of the brain within a single theoretical perspective.

In terms of cortical architectures, the theoretical treatment predicts that sensory cortex should be arranged hierarchically, that connections should be reciprocal and that forward and backward connections should show a functional asymmetry (forward connections are driving, whereas backward connections are both driving and modulatory). In terms of synaptic physiology, it predicts associative plasticity and, for dynamic models, spike-timing-dependent plasticity. In terms of electrophysiology, it accounts for classical and extra classical receptive field effects and long-latency or endogenous components of evoked cortical responses. It predicts the attenuation of responses encoding prediction error with perceptual learning and explains many phenomena such as repetition suppression, mismatch negativity (MMN) and the P300 in electroencephalography. In psychophysical terms, it accounts for the behavioural correlates of these physiological phenomena, for example, priming and global precedence. The final focus of this article is on perceptual learning as measured with the MMN and the implications for empirical studies of coupling among cortical areas using evoked sensory responses.

1. Introduction

This article represents an attempt to understand evoked cortical responses in terms of models of perceptual inference and learning. The specific model considered here rests on empirical Bayes, in the context of generative models that are embodied in cortical hierarchies. This model can be regarded as a mathematical formulation of the longstanding notion that ‘our minds should often change the idea of its sensation into that of its judgment, and make one serve only to excite the other’ (Locke 1690). In a similar vein, Helmholtz (1860) distinguishes between perception and sensation. ‘It may often be rather hard to say how much from perceptions as derived from the sense of sight is due directly to sensation, and how much of them, on the other hand, is due to experience and training’ (see Pollen 1999). In short, there is a distinction between percepts, which are the products of recognizing the causes of sensory input and sensation per se. Recognition (i.e. inferring causes from sensation) is the inverse of generating sensory data from their causes. It follows that recognition rests on models, learned through experience, of how sensations are caused. In this article, we will consider hierarchical generative models and how evoked cortical responses can be understood as part of the recognition process. The particular recognition scheme we will focus on is based on empirical Bayes, where prior expectations are abstracted from the sensory data, using a hierarchical model of how those data were caused. The particular implementation of empirical Bayes we consider is predictive coding, where prediction error is used to adjust the state of the generative model until prediction error is minimized and the most likely causes of sensory input have been identified.

Conceptually, empirical Bayes and generative models are related to ‘analysis-by-synthesis’ (Neisser 1967). This approach to perception, drawn from cognitive psychology, involves adapting an internal model of the world to match sensory input and was suggested by Mumford (1992) as a way of understanding hierarchical neuronal processing. The idea is reminiscent of Mackay's epistemological automata (MacKay 1956) which perceive by comparing expected and actual sensory input (Rao 1999). These models emphasize the role of backward connections in mediating predictions of lower level input, based on the activity of higher cortical levels.

Recognition is simply the process of solving an inverse problem by jointly minimizing prediction error at all levels of the cortical hierarchy. The main point of this article is that evoked cortical responses can be understood as transient expressions of prediction error, which index some recognition process. This perspective accommodates many physiological and behavioural phenomena, for example, extra classical RF effects and repetition suppression in unit recordings, the MMN and P300 in ERPs, priming and global precedence effects in psychophysics. Critically, many of these emerge from the same basic principles governing inference with hierarchical generative models.

In a series of previous papers (Friston 2002, 2003), we have described how the brain might use empirical Bayes for perceptual inference. These papers considered other approaches to representational learning as special cases of generative models, starting with supervised learning and ending with empirical Bayes. The latter predicts many architectural features, such as a hierarchical cortical system, prevalent top-down backward influences and functional asymmetries between forward and backward connections seen in the real brain. The focus of previous work was on functional cortical architectures. This paper looks at evoked responses and the relevant empirical findings, in relation to predictions and theoretical constraints afforded by the same theory. This is probably more relevant for experimental studies. We will therefore take a little time to describe recent advances in modelling evoked responses in human cortical systems to show the detailed levels of characterization it is now possible to attain.

(a) Overview

We start by reviewing two principles of brain organization, namely functional specialization and functional integration and how they rest upon the anatomy and physiology of hierarchical cortico-cortical connections. Representational inference and learning from a theoretical or computational perspective is discussed in §2. This section reviews the heuristics behind schemes using the framework of hierarchical generative models and introduces learning based on empirical Bayes that they enable. The key focus of this section is on the functional architectures implied by the model. Representational inference and learning can, in some cases, proceed using only forward connections. However, this is only tenable when processes generating sensory inputs are invertible and independent. Invertibility is precluded by nonlinear interactions among causes of sensory input (e.g. visual occlusion). These interactions create a problem for recognition that can be resolved using generative models. Generative or forward models solve the recognition problem using the a priori distribution of causes. Empirical Bayes allows these priors to be induced by sensory input, using hierarchies of backward and lateral projections that prevail in the real brain. In short, hierarchical models of representational learning are a natural choice for understanding real functional architectures and, critically, confer a necessary role on backward connections. Predictions and empirical findings that arise from the theoretical considerations are reviewed in §5–7. Implications for functional architectures, in terms of how connections are organized, functional asymmetries between forward and backward connections and how they change with learning, are highlighted in §3. Then, §4 moves from infrastructural issues to implications for physiological responses during perceptual inference. It focuses on extra classical RF effects and long-latency responses in electrophysiology. The final sections look at the effect of perceptual learning on evoked responses subtending inference, as indexed by responses to novel or deviant stimuli. We conclude with a demonstration of how plasticity, associated with perceptual learning, can be measured and used to test some key theoretical predictions.

2. Functional specialization and integration

(a) Background

The brain appears to adhere to two fundamental principles of functional organization, integration and specialization. The distinction relates to that between ‘localizationism’ and ‘(dis)connectionism’ that dominated thinking about cortical function in the nineteenth century. Since the early anatomic theories of Gall, the identification of a particular brain region with a specific function has become a central theme in neuroscience and was the motivation for Brodmann's cytoarchitectonic work (Brodmann 1905; see also Kötter & Wanke 2005). Brodmann posited ‘areae anatomicae’ to denote distinct cortical fields that could be recognized using anatomical techniques. His goal was to create a comparative system of organs that comprised these elemental areas, each with a specific function integrated within the system (Brodmann 1909).

Initially, functional localization per se was not easy to demonstrate. For example, a meeting that took place on 4 August 1881 addressed the difficulties of attributing function to a cortical area, given the dependence of cerebral activity on underlying connections (Phillips et al. 1984). This meeting was entitled Localization of function in the cortex cerebri. Although accepting the results of electrical stimulation in dog and monkey cortex, Goltz considered that the excitation method was inconclusive because the behaviours elicited might have originated in related pathways or current could have spread to distant centres. In short, the excitation method could not be used to infer functional localization because localizationism discounted interactions or functional integration among different brain areas. It was proposed that lesion studies could supplement excitation experiments. Ironically, it was observations on patients with brain lesions some years later (see Absher & Benson 1993) that led to the concept of ‘disconnection syndromes’ and the refutation of localizationism as a complete or sufficient explanation of cortical organization. The cortical infrastructure supporting a single function may involve many specialized areas whose union is mediated by functional integration. Functional specialization and integration are not exclusive; they are complementary. Functional specialization is only meaningful in the context of functional integration and vice versa.

(b) Functional specialization and segregation

The functional role, played by any component (e.g. cortical area, subarea, neuronal population or neuron) of the brain is defined largely by its connections. Clearly, this ‘connectivity’ may transcend many scales (e.g. molecular to social). However, here we focus on anatomical connections. Certain patterns of cortical projections are so common that they could amount to rules of cortical connectivity. ‘These rules revolve around one, apparently, overriding strategy that the cerebral cortex uses—that of functional segregation’ (Zeki 1990). Functional segregation demands that cells with common functional properties be grouped together. There are many examples of this grouping (e.g. laminar selectivity, ocular dominance bands and orientation domains in V1). This architectural constraint necessitates both convergence and divergence of cortical connections. Extrinsic connections, between cortical regions, are not continuous but occur in patches or clusters. In some instances, this patchiness has a clear relationship to functional segregation. For example, the secondary visual area V2 has a distinctive cytochrome oxidase architecture, consisting of thick stripes, thin stripes and inter-stripes. When recordings are made in V2, directionally selective (but not wavelength or colour‐selective) cells are found exclusively in the thick stripes. Retrograde (i.e. backward) labelling of cells in V5 is limited to these thick stripes. All the available physiological evidence suggests that V5 is a functionally homogeneous area that is specialized for visual motion. Evidence of this nature supports the idea that patchy connectivity is the anatomical infrastructure that underpins functional segregation and specialization.

(c) The anatomy and physiology of cortico-cortical connections

If specialization depends upon connections, then important organizational principles should be embodied in their anatomy and physiology. Extrinsic connections couple different cortical areas, whereas intrinsic connections are confined to the cortical sheet. There are certain features of cortico-cortical connections that provide strong clues about their functional role. In brief, there appears to be a hierarchical organization that rests upon the distinction between forward and backward connections (Maunsell & Van Essen 1983). The designation of a connection as forward or backward depends primarily on its cortical layers of origin and termination. The important characteristics of cortico-cortical connections are listed below. This list is not exhaustive but serves to introduce some principles that have emerged from empirical studies of visual cortex.

(i) Hierarchical organization

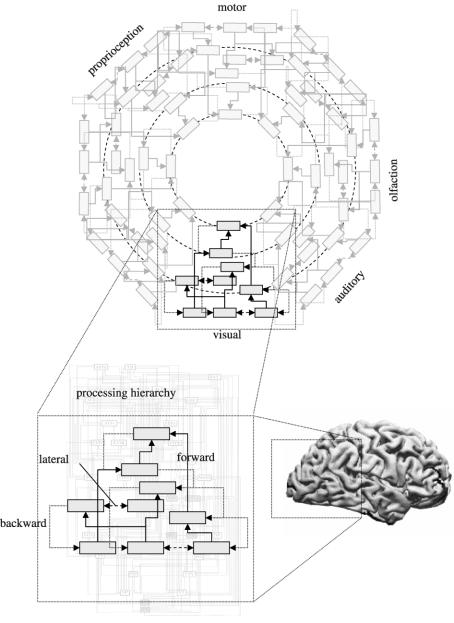
The organization of the visual cortices can be considered as a hierarchy of cortical levels with reciprocal cortico-cortical connections among the constituent cortical areas (Maunsell & Van Essen 1983; Felleman & Van Essen 1991). Forward connections run from lower to higher areas and backward connections from higher to lower. Lateral connections connect regions within a hierarchical level. The notion of a hierarchy depends upon a distinction between extrinsic forward and backward connections (see figure 1).

Figure 1.

Schematic illustrating hierarchical structures in the brain and the distinction between forward, backward and lateral connections. This schematic is inspired by Mesulam's (1998) notion of sensory-fugal processing over ‘a core synaptic hierarchy, which includes the primary sensory, upstream unimodal, downstream unimodal, heteromodal, paralimbic and limbic zones of the cerebral cortex’ (see Mesulam 1998 for more details).

(ii) Reciprocal connections

Although reciprocal, forward and backward connections show a microstructural and functional asymmetry and the terminations of both show laminar specificity. Forward connections (from a low to a high level) have sparse axonal bifurcations and are topographically organized, originating in supragranular layers and terminating largely in layer 4. On the other hand, backward connections show abundant axonal bifurcation and a more diffuse topography, although they can be patchy (Angelucci et al. 2002a,b). Their origins are bilaminar/infragranular and they terminate predominantly in agranular layers (Rockland & Pandya 1979; Salin & Bullier 1995). An important distinction is that backward connections are more divergent. For example, the divergence region of a point in V5 (i.e. the region receiving backward afferents from V5) may include thick and inter-stripes in V2, whereas its convergence region (i.e. the region providing forward afferents to V5) is limited to the thick stripes (Zeki & Shipp 1988). Furthermore, backward connections are more abundant. For example, the ratio of forward efferent connections to backward afferents in the lateral geniculate is about 1 : 10. Another distinction is that backward connections traverse a number of hierarchical levels whereas forward connections are more restricted. For example, there are backward connections from TE and TEO to V1 but no monosynaptic connections from V1 to TE or TEO (Salin & Bullier 1995).

(iii) Functionally asymmetric forward and backward connections

Functionally, reversible inactivation studies (e.g. Sandell & Schiller 1982; Girard & Bullier 1989) and neuroimaging (e.g. Büchel & Friston 1997) suggest that forward connections are driving and always elicit a response, whereas backward connections can be modulatory. In this context, modulatory means backward connections modulate responsiveness to other inputs. At the single cell level, ‘inputs from drivers can be differentiated from those of modulators. The driver can be identified as the transmitter of RF properties; the modulator can be identified as altering the probability of certain aspects of that transmission’ (Sherman & Guillery 1998).

The notion that forward connections are concerned with the promulgation and segregation of sensory information is consistent with: (i) their sparse axonal bifurcation; (ii) patchy axonal terminations; and (iii) topographic projections. In contrast, backward connections are considered to have a role in mediating contextual effects and in the co-ordination of processing channels. This is consistent with: (i) their frequent bifurcation; (ii) diffuse axonal terminations; and (iii) more divergent topography (Salin & Bullier 1995; Crick & Koch 1998). Forward connections mediate their post-synaptic effects through fast AMPA (1.3–2.4 ms decay) and GABA_A (6 ms decay) receptors. Modulatory effects can be mediated by NMDA receptors. NMDA receptors are voltage-sensitive, showing nonlinear and slow dynamics (approximately 50 ms decay). They are found predominantly in supragranular layers where backward connections terminate (Salin & Bullier 1995). These slow time constants again point to a role in mediating contextual effects that are more enduring than phasic sensory-evoked responses. The clearest evidence for the modulatory role of backward connections (that is mediated by ‘slow’ glutamate receptors) comes from corticogeniculate connections. In the cat LGN, cortical feedback is partly mediated by type 1 metabotropic glutamate receptors, which are located exclusively on distal segments of the relay-cell dendrites. Rivadulla et al. (2002) have shown that these backward afferents enhance the excitatory centre of the thalamic RF. ‘Therefore, cortex, by closing this corticofugal loop, is able to increase the gain of its thalamic input within a focal spatial window, selecting key features of the incoming signal.’

Angelucci et al. (2002a,b) used a combination of anatomical and physiological recording methods to determine the spatial scale of intra-areal V1 horizontal connections and inter-areal backward connections to V1. ‘Contrary to common beliefs, these (monosynaptic horizontal) connections cannot fully account for the dimensions of the surround field (of macaque V1 neurons). The spatial scale of feedback circuits from extrastriate cortex to V1 is, instead, commensurate with the full spatial range of centre-surround interactions. Thus these connections could represent an anatomical substrate for contextual modulation and global-to-local integration of visual signals.’

It should be noted that the hierarchical ordering of areas is a matter of debate and may be indeterminate. Based on computational neuroanatomic studies Hilgetag et al. (2000) conclude that the laminar hierarchical constraints presently available in the anatomical literature are ‘insufficient to constrain a unique ordering’ for any of the sensory systems analysed. However, basic hierarchical principles were evident. Indeed, the authors note, ‘All the cortical systems we studied displayed a significant degree of hierarchical organization’ with the visual and somato-motor systems showing an organization that was ‘surprisingly strictly hierarchical’.

In the post-developmental period, synaptic plasticity is an important functional attribute of connections in the brain and is thought to subserve perceptual and procedural learning and memory. This is a large and fascinating field that ranges from molecules to maps (e.g. Buonomano & Merzenich 1998; Martin et al. 2000). Changing the strength of connections between neurons is widely assumed to be the mechanism by which memory traces are encoded and stored in the central nervous system. In its most general form, the synaptic plasticity and memory hypothesis states that, ‘Activity-dependent synaptic plasticity is induced at appropriate synapses during memory formation and is both necessary and sufficient for the information storage underlying the type of memory mediated by the brain area in which that plasticity is observed’ (see Martin et al. 2000 for an evaluation of this hypothesis). A key aspect of this plasticity is that it is generally associative.

(iv) Associative plasticity

Synaptic plasticity may be transient (e.g. short-term potentiation or depression) or enduring (e.g. long-term potentiation or depression) with many different time constants. In contrast to short-term plasticity, long-term changes rely on protein synthesis, synaptic remodelling and infrastructural changes in cell processes (e.g. terminal arbours or dendritic spines) that are mediated by calcium-dependent mechanisms. An important aspect of NMDA receptors, in the induction of long‐term potentiation, is that they confer associativity on changes in connection strength. This is because their voltage-sensitivity allows calcium ions to enter the cell when, and only when, there is conjoint pre-synaptic release of glutamate and sufficient post-synaptic depolarization (i.e. the temporal association of pre- and post-synaptic events). Calcium entry renders the post-synaptic specialization eligible for future potentiation by promoting the formation of synaptic ‘tags’ (e.g. Frey & Morris 1997) and other calcium-dependent intracellular mechanisms.

In summary, the anatomy and physiology of cortico-cortical connections suggest that forward connections are driving and commit cells to a prespecified response given the appropriate pattern of inputs. Backward connections, on the other hand, are less topographic and are in a position to modulate the responses of lower areas. Modulatory effects imply the postsynaptic response evoked by presynaptic input is modulated by, or interacts in a nonlinear way with, another input. This interaction depends on nonlinear synaptic or dendritic mechanisms. Finally, brain connections are not static but are changing at the synaptic level all the time. In many instances, this plasticity is associative. In §3, we describe a theoretical perspective, provided by generative models, that highlights the functional importance of hierarchies, backward connections, nonlinear coupling and associative plasticity.

3. Representational inference and learning

This section introduces learning and inference based on empirical Bayes. A more detailed discussion can be found in Friston (2002, 2003). We will introduce the notion of generative models and a generic scheme for their estimation. This scheme uses expectation maximization (EM; an iterative scheme that estimates conditional expectations and maximum likelihoods of model parameters, in an E- and M-step, respectively). We show that predictive coding can be used to implement EM and, in the context of hierarchical generative models, is sufficient to implement empirical Bayesian inference.

(a) Causes and representations

Here, a representation is taken to be a neuronal response that represents some ‘cause’ in the sensorium. Causes are simply the states of processes generating sensory data. It is not easy to ascribe meaning to these states without appealing to the way that we categorize things, either perceptually or conceptually. Causes may be categorical in nature, such as the identity of a face or the semantic category to which an object belongs. Others may be parametric, such as the position of an object. Even though causes may be difficult to describe they are easy to define operationally. Causes are quantities or states that are necessary to specify the products of a process generating sensory information. For the sake of simplicity, let us frame the problem of representing causes in terms of a deterministic nonlinear function.

$$u=g(v,\theta ),$$ (3.1)

where v is a vector (i.e. a list) of underlying causes in the environment (e.g. the velocity of a particular object, direction of radiant light, etc.), and u represents sensory input; g(v,θ) is a function, that generates inputs from the causes; θ represents the parameters of the generative model. Unlike the causes, they are fixed quantities that have to be learned. We shall see later that the parameters correspond to connection strengths in the brain's model of how inputs are caused. Nonlinearities in equation (3.1) represent interactions among the causes. These can often be viewed as contextual effects, where the expression of a particular cause depends on the context established by another. A ubiquitous example from early visual processing is the occlusion of one object by another. In a linear world, the visual sensation caused by two objects would be a transparent overlay or superposition. Occlusion is a nonlinear phenomenon because the sensory input from one object (occluded) interacts with, or depends on, the other (occluder). This interaction is an example of nonlinear mixing of causes to produce sensory data. At a cognitive level, the cause associated with the word ‘hammer’ will depend on the semantic context (that determines whether the word is a verb or a noun).

The problem the brain has to contend with is to find a function of the inputs that recognizes the underlying causes. To do this, the brain must effectively undo the interactions to disclose contextually invariant causes. In other words, the brain must perform a nonlinear unmixing of causes and context. The key point here is that the nonlinear mixing may not be invertible and that the estimation of causes from input may be fundamentally ill-posed. For example, no amount of unmixing can discern the parts of an object that are occluded by another. The corresponding indeterminacy in probabilistic learning rests on the combinatorial explosion of ways in which stochastic generative models can generate input patterns (Dayan et al. 1995). In what follows, we consider the implications of this problem. Put simply, recognition of causes from sensory data is the inverse of generating data from causes. If the generative model is not invertible then recognition can only proceed if there is an explicit generative model in the brain. This speaks to the importance of backward connections that may embody this model.

(b) Generative models and representational learning

This section introduces the basic framework within which one can understand learning and inference. This framework rests upon generative and recognition models, which are simply functions that map causes to sensory input and vice versa. Generative models afford a generic formulation of representational learning and inference in a supervised or self-supervised context. There are many forms of generative models that range from conventional statistical models (e.g. factor and cluster analysis) and those motivated by Bayesian inference and learning (e.g. Dayan et al. 1995; Hinton et al. 1995). The goal of generative models is ‘to learn representations that are economical to describe but allow the input to be reconstructed accurately’ (Hinton et al. 1995). The distinction between reconstructing inputs and learning efficient representations relates directly to the distinction between inference and learning.

(i) Inference versus learning

Generative models relate unknown causes v and unknown parameters θ, to observed inputs u. The objective is to make inferences about the causes and learn the parameters. Inference may be simply estimating the most likely cause, and is based on estimates of the parameters from learning. A generative model is specified in terms of a prior distribution over the causes p(v;θ) and the generative distribution or likelihood of the inputs given the causes p(u|v;θ). Together, these define the marginal distribution of inputs implied by a generative model

$$p(u;\theta )=\int p(u|v;\theta )p(v;\theta )\text{d}v.$$ (3.2)

The conditional density of the causes, given the inputs, are given by the recognition model, which is defined in terms of the recognition distribution

$$p(v|u;\theta )=\frac{p(u|v;\theta )p(v;\theta )}{p(u;\theta )}.$$ (3.3)

However, as considered above, the generative model may not be inverted easily and it may not be possible to parameterize this recognition distribution. This is crucial because the endpoint of learning is the acquisition of a useful recognition model that can be applied to sensory inputs by the brain. One solution is to posit an approximate recognition or conditional density q(v;u) that is consistent with the generative model and that can be parameterized. Estimating the moments (e.g. expectation) of this density corresponds to inference. Estimating the parameters of the underlying generative model corresponds to learning. This distinction maps directly onto the two steps of EM.

(c) Expectation maximization

Here, we introduce a general scheme for inference and learning using EM (Dempster et al. 1977). To keep things simple, we will assume that we are only interested in the first moment or expectation of q(v;u), which we will denote by ϕ. This is the conditional mean or expected cause. EM is a coordinate ascent scheme that comprises an E-step and an M-step. In the present context, the E-step entails finding the conditional expectation of the causes (i.e. inference), while the M-step identifies the maximum likelihood value of the parameters (i.e. learning). Critically, both adjust the conditional causes and parameters to maximize the same objective function.

(i) The free energy formulation

EM provides a useful procedure for density estimation that has direct connections with statistical mechanics. Both steps of the EM algorithm involve maximizing a function of the densities above that corresponds to the negative free energy in physics.

$$\begin{array}{l}F={\langle L\rangle }_{\text{u}}\hfill \\ L=\text{ln}p(u;\theta )-KL\{q(v;u),p(v|u;\theta )\}.\hfill \end{array}$$ (3.4)

This objective function has two terms. The first is the likelihood of the inputs under the generative model. The second term is the Kullback–Leibler divergence1 between the approximate and true recognition densities. Critically, the second term is always positive, rendering F a lower bound on the expected log likelihood of the inputs. This means maximizing the objective function (i.e. minimizing the free energy) is simply minimizing our surprise about the data. The E-step increases F with respect to the expected cause, ensuring a good approximation to the recognition distribution implied by the parameters θ. This is inference. The M-step changes θ, enabling the generative model to match the input density and corresponds to learning.

$$\begin{array}{l}\text{Inference}(\text{E})\varphi =\underset{\varphi }{\text{max}}F\hfill \\ \text{Learning}(\text{M})\theta =\underset{\theta }{\text{max}}F\hfill \end{array}$$ (3.5)

EM enables exact and approximate maximum likelihood density estimation for a whole variety of generative models that can be specified in terms of prior and generative distributions. Dayan & Abbot (2001) work through a series of didactic examples from cluster analysis to independent component analyses, within this unifying framework. From a neurobiological perspective, the remarkable thing about this formalism is that both inference and learning are driven in exactly the same way, namely to minimize the free energy. This is effectively the same as minimizing surprise about sensory inputs encountered. As we will see below, the implication is that the same simple principle can explain phenomena as wide-ranging as the MMN in evoked electrical brain responses to Hebbian plasticity during perceptual learning.

(d) Predictive coding

In §3(c), we established an objective function that is maximized to enable inference and learning in E- and M-steps, respectively. In this section, we consider how that maximization might be implemented. In particular, we will look at predictive coding, which is based on minimizing prediction error. Prediction error is the difference between the input observed and that predicted by the generative model and inferred causes. We will see that minimizing the free energy is equivalent to minimizing prediction error. Consider any static nonlinear generative model under Gaussian assumptions

$$\begin{array}{l}u=g(v,\theta )+{ϵ}_{\text{u}}\hfill \\ v=v_{\text{p}}+{ϵ}_{\text{p}},\hfill \end{array}$$ (3.6)

where Cov{ϵ_u}=Σ_u is the covariance of any random or stochastic part of the generative process. Priors on the causes are specified in terms of their expectation v_p and covariance Cov{ϵ_p}=Σ_p. This form will be useful in the next section when we generalize to hierarchical models. For simplicity, we will approximate the recognition density with a point mass. From equation (3.4),

$$\begin{array}{l}L=-\frac{1}{2}{\xi }_{\text{u}}^{\text{T}}{\xi }_{\text{u}}-\frac{1}{2}{\xi }_{\text{p}}^{\text{T}}{\xi }_{\text{p}}-\frac{1}{2}\text{ln}\left|{\mathrm{\Sigma }}_{\text{u}}\right|-\frac{1}{2}\text{ln}\left|{\mathrm{\Sigma }}_{\text{p}}\right|\hfill \\ {\xi }_{\text{u}}={\mathrm{\Sigma }}_{\text{u}}^{-1/2}(u-g(\varphi ,\theta ))\hfill \\ {\xi }_{\text{p}}={\mathrm{\Sigma }}_{\text{p}}^{-1/2}(\varphi -v_{\text{p}}).\hfill \end{array}$$ (3.7)

The first term in equation (3.7) is the prediction error that is minimized in predictive coding. The second corresponds to a prior term that constrains or regularizes conditional estimates of the causes. The need for this term stems from the ambiguous or ill-posed nature of recognition discussed above and is a ubiquitous component of inverse solutions.

Predictive coding schemes can be regarded as arising from the distinction between forward and inverse models adopted in machine vision (Ballard et al. 1983; Kawato et al. 1993). Forward models generate inputs from causes (cf. generative models), whereas inverse models approximate the reverse transformation of inputs to causes (cf. recognition models). This distinction embraces the noninvertibility of generating processes and the ill-posed nature of inverse problems. As with all underdetermined inverse problems, the role of constraints is central. In the inverse literature, a priori constraints usually enter in terms of regularized solutions. For example, ‘Descriptions of physical properties of visible surfaces, such as their distance and the presence of edges, must be recovered from the primary image data. Computational vision aims to understand how such descriptions can be obtained from inherently ambiguous and noisy data. A recent development in this field sees early vision as a set of ill-posed problems, which can be solved by the use of regularization methods’ (Poggio et al. 1985). The architectures that emerge from these schemes suggest that ‘Feedforward connections from the lower visual cortical area to the higher visual cortical area provides an approximated inverse model of the imaging process (optics)’. Conversely, ‘…the backprojection connection from the higher area to the lower area provides a forward model of the optics’ (Kawato et al. 1993; see also Harth et al. 1987). This perspective highlights the importance of backward connections and the role of priors in enabling predictive coding schemes.

(i) Predictive coding and Bayes

Predictive coding is a strategy that has some compelling (Bayesian) underpinnings. To finesse the inverse problem posed by noninvertible generative models, constraints or priors are required. These resolve the ill-posed problems that confound recognition based on purely forward architectures. It has long been assumed that sensory units adapt to the statistical properties of the signals to which they are exposed (see Simoncelli & Olshausen 2001 for a review). In fact, the Bayesian framework for perceptual inference has its origins in Helmholtz's notion of perception as unconscious inference. Helmholtz realized that retinal images are ambiguous and that prior knowledge was required to account for perception (Kersten et al. 2004). Kersten et al. (2004) provide an excellent review of object perception as Bayesian inference and ask a fundamental question, ‘Where do the priors come from. Without direct input, how does image-independent knowledge of the world get put into the visual system?’ In §3(e), we answer this question and show how empirical Bayes allows priors to be learned and induced online during inference.

(e) Cortical hierarchies and empirical Bayes

The problem with fully Bayesian inference is that the brain cannot construct the prior expectation and variability, v_p and Σ_p, de novo. They have to be learned and also adapted to the current experiential context. This is a solved problem in statistics and calls for empirical Bayes, in which priors are estimated from data. Empirical Bayes harnesses the hierarchical structure of a generative model, treating the estimates at one level as priors on the subordinate level (Efron & Morris 1973). This provides a natural framework within which to treat cortical hierarchies in the brain, each level providing constraints on the level below. This approach models the world as a hierarchy of systems where supraordinate causes induce and moderate changes in subordinate causes. These priors offer contextual guidance towards the most likely cause of the input. Note that predictions at higher levels are subject to the same constraints, only the highest level, if there is one in the brain, is unconstrained. If the brain has evolved to recapitulate the causal structure of its environment, in terms of its sensory infrastructures, it is possible that our visual cortices reflect the hierarchical causal structure of our environment.

Next, we introduce hierarchical models and extend the parameterization of the ensuing generative model to cover priors. This means that the constraints, required by predictive coding and regularized solutions to inverse problems, are now absorbed into the learning scheme and are estimated in exactly the same way as the parameters. These extra parameters encode the variability or precision of the causes and are referred to as hyperparameters in the classical covariance component literature. Hyperparameters are updated in the M-step and are treated in exactly the same way as the parameters.

(i) Hierarchical models

Consider any level i in a hierarchy whose causes v_i are elicited by causes in the level above v_i+1. The hierarchical form of the generative model is

$$\begin{array}{l}u=g_1(v_2,{\theta }_1)+{ϵ}_1\hfill \\ v_2=g_2(v_3,{\theta }_2)+{ϵ}_2\hfill \\ v_3=\dots ,\hfill \end{array}$$ (3.8)

with u=v₁ (cf. equation (3.6)). Technically, these models fall into the class of conditionally independent hierarchical models when the stochastic terms are independent (Kass & Steffey 1989). These models are also called parametric empirical Bayes (PEB) models because the obvious interpretation of the higher-level densities as priors led to the development of PEB methodology (Efron & Morris 1973). Often, in statistics, these hierarchical models comprise just two levels, which is a useful way to specify simple shrinkage priors on the parameters of single-level models. We will assume the stochastic terms are Gaussian with covariance Σ_i=Σ(λ_i). Therefore, v_i+1, θ_i and λ_i parameterize the means and covariances of the likelihood at each level.

$$p(v_i|v_{i+1};\theta )=N(g_i(v_{i+1},{\theta }_i),{\mathrm{\Sigma }}_i).$$ (3.9)

This likelihood also plays the role of a prior on v_i at the level below, where it is jointly maximized with the likelihood p(v_i−1|v_i;θ). This is the key to understanding the utility of hierarchical models. By learning the parameters of the generative distribution of level i, one is implicitly learning the parameters of the prior distribution for level i−1. This enables the learning of prior densities.

The hierarchical nature of these models lends an important context-sensitivity to recognition densities not found in single-level models. The key point here is that high-level causes v_i+1 determine the prior expectation of causes v_i in the subordinate level. This can completely change the distributions p(v_i|v_i+1;θ), upon which inference in based, in an input and context-dependent way.

(ii) Implementation

The biological plausibility of empirical Bayes in the brain can be established fairly simply. To do this, a hierarchical scheme is described in some detail. A more thorough account, including simulations of various neurobiological and psychophysical phenomena, will appear in future publications. For the moment, we will address neuronal implementation at a purely theoretical level, using the framework above.

For simplicity, we will again assume deterministic recognition. In this setting, with conditional independence, the objective function is

$$\begin{array}{l}L=-\frac{1}{2}{\xi }_1^{\text{T}}{\xi }_1-\frac{1}{2}{\xi }_2^{\text{T}}{\xi }_2-\cdots -\frac{1}{2}\text{ln}\left|{\mathrm{\Sigma }}_1\right|-\frac{1}{2}\text{ln}\left|{\mathrm{\Sigma }}_2\right|-\cdots \hfill \\ {\xi }_i={\varphi }_i-g_i({\varphi }_{i+1},{\theta }_i)-{\lambda }_i{\xi }_i={(1+{\lambda }_i)}^{-1}({\varphi }_i-g_i({\varphi }_{i+1},{\theta }_i))\hfill \end{array}$$ (3.10)

(cf. equation (3.7)). Here, ${\mathrm{\Sigma }}_i^{1/2}=1+{\lambda }_i$. In neuronal models, the prediction error is encoded by the activities of units denoted by ξ_i. These error units receive a prediction from units in the level above2 via backward connections and lateral influences from the representational units ϕ_i being predicted. Horizontal interactions among the error units serve to decorrelate them (cf. Foldiak 1990), where the symmetric lateral connection strengths λ_i hyperparameterize the covariances of the errors Σ_i, which are the prior covariances for level i−1.

The estimators ϕ_i and parameters perform a gradient ascent on the objective function

$$\begin{array}{l}\text{E}:{\dot{\varphi }}_{i+1}=\frac{\partial F}{\partial {\varphi }_{i+1}}=-\frac{\partial {\xi }_i^{\text{T}}}{\partial {\varphi }_{i+1}}{\xi }_i-\frac{\partial {\xi }_{i+1}^{\text{T}}}{\partial {\varphi }_{i+1}}{\xi }_{i+1}\hfill \\ \text{M}:\begin{array}{l}{\dot{\theta }}_i=\frac{\partial F}{\partial {\theta }_i}=-{\langle \frac{\partial {\xi }_i^{\text{T}}}{\partial {\theta }_i}\xi \rangle }_{\text{u}}\hfill \\ {\dot{\lambda }}_i=\frac{\partial F}{\partial {\lambda }_i}=-{\langle \frac{\partial {\xi }_i^{\text{T}}}{\partial {\lambda }_i}\xi \rangle }_{\text{u}}-{(1+{\lambda }_i)}^{-1}.\hfill \end{array}\hfill \end{array}$$ (3.11)

Inferences mediated by the E-step rest on changes in the representational units, mediated by forward connections from error units in the level below and lateral interaction with error units within the same level. Similarly, prediction error is constructed by comparing the activity of representational units, within the same level, to their predicted activity conveyed by backward connections.

This is the simplest version of a very general learning algorithm. It is general in the sense that it does not require the parameters of either the generative or the prior distributions. It can learn noninvertible, nonlinear generative models and encompasses complicated hierarchical processes. Furthermore, each of the learning components has a relatively simple neuronal interpretation (see below).

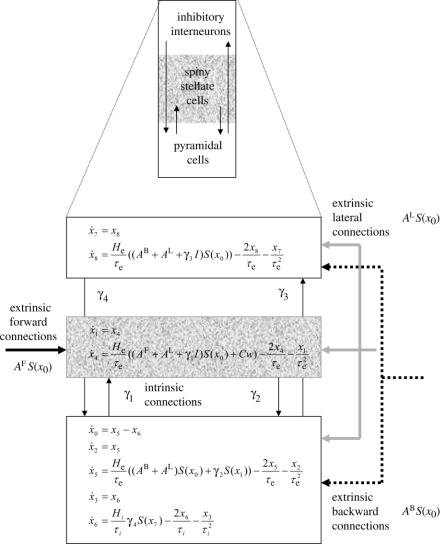
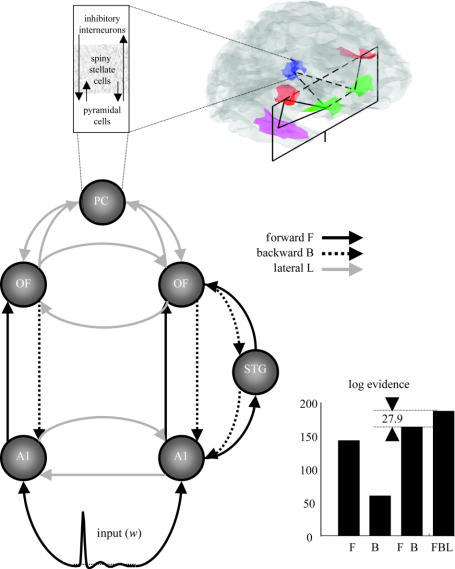
4. Implications for cortical infrastructure and plasticity

(a) Cortical connectivity

The scheme implied by equation (3.11) has four clear implications or predictions about the functional architectures required for its implementation. We now review these in relation to cortical organization in the brain. A schematic summarizing these points is provided in figure 2. In short, we arrive at exactly the same four points presented at the end of §2(c).

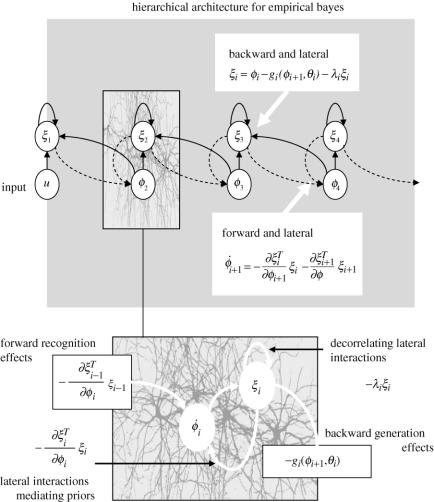
Figure 2.

Upper panel: schematic depicting a hierarchical predictive coding architecture. Here, hierarchical arrangements within the model serve to provide predictions or priors to representations in the level below. The upper circles represent error units and the lower circles functional subpopulations encoding the conditional expectation of causes. These expectations change to minimize both the discrepancy between their predicted value and the mismatch incurred by their prediction of the level below. These two constraints correspond to prior and likelihood terms, respectively (see main text). Lower panel: a more detailed depiction of the influences on representational and error units.

(i) Hierarchical organization

Hierarchical models enable empirical Bayesian estimation of prior densities and provide a plausible model for sensory inputs. Models that do not show conditional independence (e.g. those used by connectionist and infomax schemes) depend on prior constraints for unique inference and do not invoke a hierarchical cortical organization. The useful thing about the architecture in figure 2 is that the responses of units at the ith level ϕ_i depend only on the error at the current level and the immediately preceding level. Similarly, the error units ξ_i are only connected to representational units in the current level and the level above. This hierarchical organization follows from conditional independence and is important because it permits a biologically plausible implementation, where the connections driving inference run only between neighbouring levels.

(ii) Reciprocal connections

In the hierarchical scheme, the dynamics of representational units ϕ_i+1 are subject to two, locally available, influences. A likelihood or recognition term mediated by forward afferents from the error units in the level below and an empirical prior conveyed by error units in the same level. Critically, the influences of the error units in both levels are mediated by linear connections with strengths that are exactly the same as the (negative) reciprocal connections from ϕ_i+1 to ξ_i and ξ_i+1. Mathematically, from equation (3.11),

$$\begin{array}{l}\frac{\partial {\dot{\varphi }}_{i+1}}{\partial {\xi }_i}=-\frac{\partial {\xi }_i^{\text{T}}}{\partial {\varphi }_{i+1}}\hfill \\ \frac{\partial {\dot{\varphi }}_{i+1}}{\partial {\xi }_{i+1}}=-\frac{\partial {\xi }_{i+1}^{\text{T}}}{\partial {\varphi }_{i+1}}.\hfill \end{array}$$ (4.1)

Functionally, forward and lateral connections are reciprocated, where backward connections generate predictions of lower-level responses. Forward connections allow prediction error to drive representational units in supraordinate levels. Within each level, lateral connections mediate the influence of error units on the predicting units and intrinsic connections λ_i among the error units decorrelate them, allowing competition among prior expectations with different precisions (precision is the inverse of variance). In short, lateral, forwards and backward connections are all reciprocal, consistent with anatomical observations.

(iii) Functionally asymmetric forward and backward connections

Although the connections are reciprocal, the functional attributes of forward and backward influences are different. The top-down influences of units ϕ_i+1 on error units in the lower level ξ_i instantiate the forward model ${\xi }_i={\varphi }_i-g_i({\varphi }_{i+1},{\theta }_i)-{\lambda }_i{\xi }_i$. These can be nonlinear, where each unit in the higher level may modulate or interact with the influence of others, according to the nonlinearities in g_i(ϕ_i+1,θ_i). In contrast, the bottom-up influences of units in lower levels do not interact when producing changes at the higher level, because according to equation (3.11), their effects are linearly separable. This is a key observation because the empirical evidence, reviewed in the previous section, suggests that backward connections are in a position to interact (e.g. through NMDA receptors expressed predominantly in supragranular layers in receipt of backward connections). Forward connections are not. In summary, nonlinearities, in the way sensory inputs are produced, necessitate nonlinear interactions in the generative model that are mediated by backward connections but do not require forward connections to be modulatory.

(iv) Associative plasticity

Changes in the parameters correspond to plasticity in the sense that the parameters control the strength of backward and lateral connections. The backward connections parameterize the prior expectations and the lateral connections hyperparameterize the prior covariances. Together, they parameterize the Gaussian densities that constitute the priors (and likelihoods) of the model. The plasticity implied can be seen more clearly with an explicit model. For example, let $g_i(v_{i+1},{\theta }_i)={\theta }_i{v}_{i+1}$. In this instance,

$$\begin{array}{l}{\dot{\theta }}_i={(1+{\lambda }_i)}^{-1}{\langle {\xi }_i{\varphi }_{i+1}^{\text{T}}\rangle }_{\text{u}}\hfill \\ {\dot{\lambda }}_i={(1+{\lambda }_i)}^{-1}({\langle {\xi }_i{\xi }_i^{\text{T}}\rangle }_{\text{u}}-1).\hfill \end{array}$$ (4.2)

This is simply Hebbian or associative plasticity, where the connection strengths change in proportion to the product of pre- and postsynaptic activity, for example, $\langle {\xi }_i{\varphi }_{i+1}^{\text{T}}\rangle$. An intuition about equation (4.2) is obtained by considering the conditions under which the expected change in parameters is zero (i.e. after learning). For the backward connections, this implies there is no component of prediction error that can be explained by estimates at the higher level $\langle {\xi }_i{\varphi }_{i+1}^{\text{T}}\rangle =0$. The lateral connections stop changing when the prediction error has been whitened $\langle {\xi }_i{\xi }_i^{\text{T}}\rangle =1$.

It is evident that the predictions of the theoretical analysis coincide almost exactly with the empirical aspects of functional architectures in visual cortices highlighted in the §2(c) (hierarchical organization, reciprocity, functional asymmetry and associative plasticity). Although somewhat contrived, it is pleasing that purely theoretical considerations and neurobiological empiricism converge so precisely.

(b) Functional organization

In short, representational inference and learning lends itself naturally to a hierarchical treatment, which considers the brain as an empirical Bayesian device. The dynamics of the units or populations are driven to minimize error at all levels of the cortical hierarchy and implicitly render themselves posterior modes (i.e. most likely values) of the causes given the data. In contrast to supervised learning, hierarchical prediction does not require any desired output. Unlike information theoretic approaches, they do not assume independent causes. In contrast to regularized inverse solutions (e.g. in machine vision) they do not depend on a priori constraints. These emerge spontaneously as empirical priors from higher levels.

The overall scheme implied by equation (3.11) sits comfortably with the hypothesis (Mumford 1992) that:

on the role of the reciprocal, topographic pathways between two cortical areas, one often a ‘higher’ area dealing with more abstract information about the world, the other ‘lower’, dealing with more concrete data. The higher area attempts to fit its abstractions to the data it receives from lower areas by sending back to them from its deep pyramidal cells a template reconstruction best fitting the lower level view. The lower area attempts to reconcile the reconstruction of its view that it receives from higher areas with what it knows, sending back from its superficial pyramidal cells the features in its data which are not predicted by the higher area. The whole calculation is done with all areas working simultaneously, but with order imposed by synchronous activity in the various top-down, bottom-up loops.

We have tried to show that this sort of hierarchical prediction can be implemented in brain-like architectures using mechanisms that are biologically plausible.

(i) Backward or feedback connections?

There is something slightly counterintuitive about generative models in the brain. In this view, cortical hierarchies are trying to generate sensory data from high-level causes. This means the causal structure of the world is embodied in the backward connections. Forward connections simply provide feedback by conveying prediction error to higher levels. In short, forward connections are the feedback connections. This is why we have been careful not to ascribe a functional label like feedback to backward connections. Perceptual inference emerges from mutually informed top-down and bottom processes that enable sensation to constrain perception. This self-organizing process is distributed throughout the hierarchy. Similar perspectives have emerged in cognitive neuroscience on the basis of psychophysical findings. For example, reverse hierarchy theory distinguishes between early explicit perception and implicit low level vision, where ‘our initial conscious percept—vision at a glance—matches a high-level, generalized, categorical scene interpretation, identifying “forest before trees” (Hochstein & Ahissar 2002)’.

(c) Dynamic models and prospective coding

Hitherto, we have framed things in terms of static hierarchical models. Dynamic models require a simple extension of equation (3.8) to include hidden states x_i that serve to remember past causes v_i of sensory inputs:

$$\begin{array}{l}u=g_1(x_1,v_2,{\theta }_1)+{ϵ}_1\hfill \\ {\dot{x}}_1=f_1(x_1,v_2,{\theta }_1)\hfill \\ v_2=g_2(x_2,v_3,{\theta }_2)+{ϵ}_2\hfill \\ {\dot{x}}_2=f_2(x_2,v_3,{\theta }_2)\hfill \\ v_3=\dots \hfill \end{array}$$ (4.3)

In a subsequent paper, describing DEM for hierarchical dynamic models, we will show that it is necessary to minimize the prediction errors and their temporal derivatives. However, the form of the objective function and the ensuing E- and M-steps remains the same. This means the conclusions above hold in a dynamic setting, with some interesting generalizations.

When the generative model is dynamic (i.e. is effectively a convolution operator) the E-step, subtending inference, is more complicated and rests on a generalization of equation (3.11) to cover dynamic systems

$$\text{E}:\dot{\varphi }{(t)}_i=\frac{\partial L(t+\tau )}{\partial {\dot{\varphi }}_i}=\frac{\partial L(t)}{\partial {\dot{\varphi }}_i}+\tau \frac{\partial L(t)}{\partial {\varphi }_i}+\frac{\tau }{2}\frac{\partial \dot{L}(t)}{\partial {\varphi }_i}+\cdots$$ (4.4)

In DEM, the aim is not to find the most likely cause of the sensory input but to encode the evolution of causes in terms of conditional trajectories. For static models, equation (4.4) reduces to equation (3.11), which can be regarded as a special case when there are no dynamics and the trajectory becomes a single point. The dynamic version of the E-step is based on the objective function evaluated prospectively at some point τ in the future and can be understood as a gradient ascent on the objective function and all its higher derivatives (see the second line of equation (4.4)). This prospective aspect of DEM lends it some interesting properties. Among these is the nature of the plasticity. Because the associative terms involve prospective prediction errors, synaptic changes occur when presynaptic activity is high and post-synaptic activity is increasing. This has an interesting connection with STDP, where increases in efficacy rely on postsynaptic responses occurring shortly after presynaptic inputs. In this instance, at peak presynaptic input, the postsynaptic response will be rising, to peak a short time later. The DEM scheme offers a principled explanation for this aspect of plasticity that can be related to other perspectives on its functional role. For example, Kepecs et al. (2002) note that the temporal asymmetry implicit in STDP may underlie learning and review some of the common themes from a range of findings in the framework of predictive coding (see also Fuhrmann et al. 2002).

Generative models of a dynamic sort confer a temporal continuity and prospective aspect on representational inference that is evident in empirical studies. As noted by Mehta (2001) ‘a critical task of the nervous system is to learn causal relationships between stimuli to anticipate events in the future’. Both the inference and learning about the states of the environment, in terms of trajectories, enables this anticipatory aspect. Mehta (2001) reviews findings from hippocampal electrophysiology, in which spatial RFs can show large and rapid anticipatory changes in their firing characteristics, which are discussed in the context of predictive coding (see also Rainer et al. 1999 for a discussion of prospective coding for objects in the context delayed paired associate tasks).

It would be premature to go into the details of DEM here. We anticipate communicating several articles covering the above themes in the near future. However, there are a number of complementary approaches to learning in the context of dynamic models that are already in the literature. For example, the seminal paper of Rao & Ballard (1999) uses Kalman filtering and a hierarchical hidden Markov model to provide a functional interpretation of many extra classical RF effects (see below). Particularly relevant here is the discussion of hierarchical Bayesian inference in the visual cortex by Lee & Mumford (2003). These authors consider particle filtering and Bayesian-belief propagation (algorithms from machine learning) that might model the cortical computations implicit in hierarchical Bayesian inference and review the neurophysiological evidence that supports their plausibility. Irrespective of the particular algorithm employed by the brain for empirical (i.e. hierarchical) Bayes, they each provide predictions about the physiology of cortical responses. These predictions are the subject of §5 below.

5. Implications for cortical physiology

The empirical Bayes perspective on perceptual inference suggests that the role of backward connections is to provide contextual guidance to lower levels through a prediction of the lower level's inputs. When this prediction is incomplete or incompatible with the lower areas input, a prediction error is generated that engenders changes in the area above until reconciliation. When (and only when) the bottom-up driving inputs are in accord with top-down predictions, error is suppressed and a consensus between the prediction and the actual input is established. Given this conceptual model, a stimulus-related response can be decomposed into two components corresponding to the transients evoked in two functional subpopulations of units. The first representational subpopulation encodes the conditional expectation of perceptual causes ϕ. The second encodes prediction error ξ. Responses will be evoked in both, with the error units of one level exciting appropriate representational units through forward connections and the representational unit suppressing error units through backward connections (see figure 2). As inference converges, high-level representations are expressed as the late component of evoked responses with a concomitant suppression of error signal in lower areas.

In short, within the model, activity in the cortical hierarchy self-organizes to minimize its free energy though minimizing prediction error. Is this sufficient to account for classical RFs and functional segregation seen in cortical hierarchies, such as the visual system?

(a) Classical receptive fields

The answer to the above question is yes. We have shown previously that minimizing the free energy is equivalent to maximizing the mutual information between sensory inputs and neuronal activity encoding their underlying causes (Friston 2003). There have been many compelling developments in theoretical neurobiology that have used information theory (e.g. Barlow 1961; Optican & Richmond 1987; Oja 1989; Foldiak 1990; Linsker 1990; Tovee et al. 1993; Tononi et al. 1994). Many appeal to the principle of maximum information transfer (e.g. Atick & Redlich 1990; Linsker 1990; Bell & Sejnowski 1995). This principle has proven extremely powerful in predicting many of the basic RF properties of cells involved in early visual processing (e.g. Atick & Redlich 1990; Olshausen & Field 1996). This principle represents a formal statement of the common sense notion that neuronal dynamics in sensory systems should reflect, efficiently, what is going on in the environment (Barlow 1961).

There are many examples where minimizing the free energy produces very realistic RFs, a very compelling example can be found in Olshausen & Field (1996). An example from our own work, which goes beyond single RFs, concerns the selectivity profile of units in V2. In Friston (2000), we used the infomax principle (Linsker 1990) to optimize the spatio temporal RFs of simple integrate and fire units exposed to moving natural scenes. We examined the response profiles in terms of selectivity to orientation, speed, direction and wavelength. The units showed two principal axes of selectivity. The first partitioned cells into those with wavelength selectivity and those without. Within the latter, the main axis was between units with direction selectivity and those without. This pattern of selectivity fits nicely with the characteristic response profiles of units in the thin, thick and inter stripes of V2. See figure 3 for examples of the ensuing RFs, shown in the context of the functional architecture of visual processing pathways described in Zeki (1993).

Figure 3.

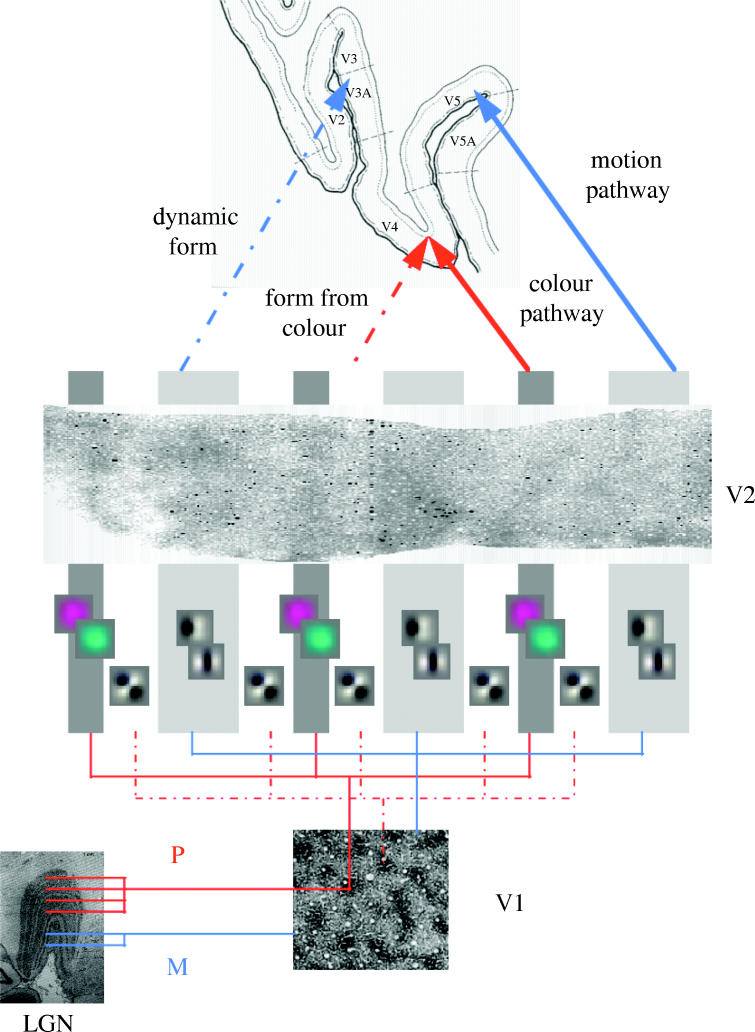
Schematic adapted from Zeki (1993) summarizing the functional segregation of processing pathways and the relationship of simulated RFs to the stripe structures in V2. LGN, lateral geniculate nucleus; P, parvocellular pathway; M, magnocellular pathway. These RFs were obtained by minimizing the free energy of a model neuronal system when exposed to moving natural scenes. See Friston (2000) for details.

(b) Extra classical receptive fields

Classical models (e.g. classical RFs) assume that evoked responses will be expressed invariably in the same units or neuronal populations, irrespective of context. However, real neuronal responses are not invariant but depend upon the context in which they are evoked. For example, visual cortical units have dynamic RFs that can change from moment to moment. A useful synthesis that highlights the anatomical substrates of context-dependent responses can be found in Angelucci et al. (2002a,b). The key conclusion is that ‘feedback from extrastriate cortex (possibly together with overlap or inter-digitation of coactive lateral connectional fields within V1) can provide a large and stimulus-specific surround modulatory field. The stimulus specificity of the interactions between the centre and surround fields, may be due to the orderly, matching structure and different scales of intra-areal and feedback projection excitatory pathways.’

Extra classical effects are commonplace and are generally understood in terms of the modulation of RF properties by backward and lateral afferents. There is clear evidence that horizontal connections in visual cortex are modulatory in nature (Hirsch & Gilbert 1991), speaking to an interaction between the functional segregation implicit in the columnar architecture of V1 and activity in remote populations. These observations suggest that lateral and backwards interactions may convey contextual information that shapes the responses of any neuron to its inputs (e.g. Kay & Phillips 1996; Phillips & Singer 1997) to confer the ability to make conditional inferences about sensory input.

The most detailed and compelling analysis of extra classical effects in the context of hierarchical models and predictive coding is presented in Rao & Ballard (1999). These authors exposed a hierarchical network of model neurons using a predictive coding scheme to natural images. The neurons developed simple-cell-like RFs. In addition, a subpopulation of error units showed a variety of extra classical RF effects suggesting that ‘non-classical surround effects in the visual cortex may also result from cortico-cortical feedback as a consequence of the visual system using an efficient hierarchical strategy for encoding natural images.’ One nonclassical feature on which the authors focus is end stopping. Visual neurons that respond optimally to line segments of a particular length are abundant in supragranular layers and have the curious property of end stopping or end inhibition. Vigorous responses to optimally oriented line segments are attenuated or eliminated when the line extends beyond the classical RF. The explanation for this effect is simple, because the hierarchy was trained on natural images, containing long line segments, the input caused by short segments could not be predicted and error responses could not be suppressed. This example makes a fundamental point, which we will take up further below. The selective response of these units does not mean they have learned to encode short line segments. Their responses reflect the fact that short line segments have not been encountered before and represent an unexpected visual input, given the context established by input beyond the classical RF. In short, their response signals a violation of statistical regularities that have been learned.

If these models are right, interruption of backward connections should disinhibit the response of supragranular error units that are normally suppressed by extra classical stimuli. Rao & Ballard (1999) cite inactivation studies of high-level visual cortex in anaesthetized monkeys, in which disinhibition of responses to surround stimuli is observed in lower areas (Hupe et al. 1998). Furthermore, removal of feedback from V1 and V2 to the LGN reduces the end stopping of LGN cells (Murphy & Sillito 1987).

(c) Long-latency evoked responses

In addition to explaining the form of classical RFs, the temporal form of evoked transients is consistent with empirical (hierarchical) Bayes. This is aptly summarized by Lee & Mumford (2003): ‘Recent electrophysiological recordings from early visual neurons in awake behaving monkeys reveal that there are many levels of complexity in the information processing of the early visual cortex, as seen in the long latency responses of its neurons. These new findings suggest that activity in the early visual cortex is tightly coupled and highly interactive with the rest of the visual system.’ Long-latency responses are used to motivate hierarchical Bayesian inference in which ‘the recurrent feedforward/feedback loops in the cortex serve to integrate top-down contextual priors and bottom-up observations so as to implement concurrent probabilistic inference.’

The prevalence of long-latency responses in unit recordings is mirrored in similar late components of ERPs recorded noninvasively. The cortical hierarchy in figure 2 comprises a chain of coupled oscillators. The response of these systems to sensory perturbation conforms to a damped oscillation, emulating a succession of late components. Functionally, the activity of error units at any one level reflect states that have yet to be explained by higher-level representations and will wax and wane as higher-level causes are selected and refined. The ensuing transient provides a compelling model for the form of ERPs, which look very much like damped oscillation in the alpha (10 Hz) range. In some instances, specific components of ERPs can be identified with specific causes, For example, the N170, a negative wave about 170 ms after stimulus onset, is elicited by face stimuli relative to non-face stimuli. In the following, we focus on examples of late components. We will not ascribe these components to representational or error subpopulations because their respective dynamics are tightly coupled. The theme we highlight is that late components reflect inference about supraordinate or global causes at higher levels in the hierarchy.

(i) Examples from neurophysiology

This subsection considers evidence for hierarchical processing in terms of single-cell responses to visual stimuli in the temporal cortex of behaving monkeys. If perceptual inference rests on a hierarchical generative model, then predictions that depend on the high-order attributes of a stimulus must be conferred by top-down influences. Consequently, one might expect to see the emergence of selectivity for high-level attributes after the initial visual response (although delays vary greatly, it typically takes about 10 ms for spike volleys to propagate from one cortical area to another and about 100 ms to reach prefrontal areas). This delay in the emergence of selectivity is precisely what one sees empirically. For example, Sugase et al. (1999) recorded neurons in macaque temporal cortex during the presentation of faces and objects. The faces were either human or monkey faces and were categorized in terms of identity (whose face it was) and expression (happy, angry, etc.): ‘Single neurones conveyed two different scales of facial information in their firing patterns, starting at different latencies. Global information, categorizing stimuli as monkey faces, human faces or shapes, was conveyed in the earliest part of the responses. Fine information about identity or expression was conveyed later’ starting, on average, about 50 ms after face-selective responses. These observations speak to a temporal dissociation in the encoding of stimulus category, facial identity and expression that is a natural consequence of hierarchically distributed processing.

A similar late emergence of selectivity is seen in motion processing. A critical aspect of visual processing is the integration of local motion signals generated by moving objects. This process is complicated by the fact that local velocity measurements can differ depending on contour orientation and spatial position. Specifically, any local motion detector can measure only the component of motion perpendicular to a contour that extends beyond its field of view (Pack & Born 2001). This aperture problem is particularly relevant to direction-selective neurons early in the visual pathways, where small RFs permit only a limited view of a moving object. Pack & Born (2001) have shown ‘that neurons in the middle temporal visual area (known as MT or V5) of the macaque brain reveal a dynamic solution to the aperture problem. MT neurons initially respond primarily to the component of motion perpendicular to a contour's orientation, but over a period of approximately 60 ms the responses gradually shift to encode the true stimulus direction, regardless of orientation’.

Finally, it is interesting to note that extra classical RF effects in supragranular V1 units are often manifest 80–100 ms after stimulus onset, ‘suggesting that feedback from higher areas may be involved in mediating these effects’ (Rao & Ballard 1999).

(ii) Examples from electrophysiology

In the discussion of extra classical RF effects above, we established that evoked responses, expressed 100 ms or so after stimulus onset, could be understood in terms of a failure to suppress prediction error when the local information in the classical RF was incongruent with global context established by the surround. Exactly the same phenomena can be observed in ERPs evoked by the processing of compound stimuli that have local and global attributes (e.g. an ensemble of L‐ shaped stimuli, arranged to form an H). For example, Han & He (2003) have shown that incongruency between global and local letters enlarged the posterior N2, a component of visually evoked responses occurring about 200 ms after stimulus onset. This sort of result may be the electrophysiological correlate of the global precedence effect expressed behaviourally. The global precedence effect refers to a speeded behavioural response to a global attribute relative to local attributes and the slowing of local responses by incongruent global information (Han & He 2003).

(iii) Examples from neuroimaging

Although neuroimaging has a poor temporal resolution, the notion that V1 responses evoked by compound stimuli can be suppressed by congruent global information can be tested easily. Murray et al. (2002) used MRI to measure responses in V1 and a higher object processing area, the lateral occipital complex, to visual elements that were either grouped into objects or arranged randomly. They ‘observed significant activity increases in the lateral occipital complex and concurrent reductions of activity in primary visual cortex when elements formed coherent shapes, suggesting that activity in early visual areas is reduced as a result of grouping processes performed in higher areas. These findings are consistent with predictive coding models of vision that postulate that inferences of high-level areas are subtracted from incoming sensory information in lower areas through cortical feedback.’

Our own work in this area uses coherent motion subtended by sparse dots that cannot fall within the same classical RF of V1 neurons. As predicted, the V1 response to coherent, relative to incoherent, stimuli was significantly reduced (Harrison et al. 2004). This is a clear indication that error suppression is mediated by backward connections because only higher cortical areas have RFs that were sufficiently large to encompass more than one dot.

(d) Shut up or stop gossiping?

In summary, a component of evoked responses can be understood as the transient expression of prediction error that is suppressed quickly by predictions from higher cortical areas. This suppression may be compromised if the stimulus has not been learned previously or is incongruent with the global context in which it appears. Kersten et al. (2004) introduce two heuristics concerning the reduction of early visual responses to coherent or predictable stimuli. High-level areas may explain away the sensory input and tell the lower levels to ‘shut up’. Alternatively, high-level areas might sharpen the responses of early areas by reducing activity that is inconsistent with the high-level interpretation; that is, high-level areas tell competing representations in lower areas to ‘stop gossiping’. In fact, the empirical Bayes framework accommodates both heuristics. High-level predictions explain away prediction error and tell the error units to ‘shut up’. Concurrently, units encoding the causes of sensory input are selected by lateral interactions, with the error units, that mediate empirical priors. This selection stops the gossiping. The conceptual tension, between the two heuristics, is resolved by positing two functionally distinct subpopulations, encoding the conditional expectations of perceptual causes and the prediction error respectively.

In §6, we turn to the implication of error suppression for responses evoked during perceptual learning and their electrophysiological correlates.

6. Implications for sensory learning and ERPs

In §5, we introduced the notion that evoked response components in sensory cortex encode a transient prediction error that is rapidly suppressed by predictions mediated by backward connections. If the stimulus is novel or inconsistent with its context, then this suppression is compromised. An example of this might be extra classical effects expressed 100 ms or so after stimulus onset. In the following, we consider responses to novel or deviant stimuli as measured with ERPs. This may be important for empirical studies because ERPs can be acquired noninvasively and can be used to study humans in both a basic and clinical context.

(a) Perceptual learning and long-latency responses

The E-step in our empirical Bayes scheme provides a model for the dynamics of evoked transients in terms of the responses of representational and error units. Representational learning in the M-step models plasticity in backward and lateral connections to enable more efficient inference using the same objective function. This means that perceptual learning should progressively reduce free energy or prediction error on successive exposures to the same stimulus. For simple or elemental stimuli, this should be expressed fairly soon after stimulus onset; for high-order attributes of compound stimuli, later components should be suppressed. This suppression of responses to repeated stimuli is exactly what one observes empirically and is referred to as repetition suppression (Desimone 1996). This phenomenon is ubiquitous and can be observed using many different sorts of measurements. An example is shown in figure 4, which details reduced activation in the fusiform region to repeated faces, relative to new faces using fMRI (see Henson et al. 2000 for details).

Figure 4.

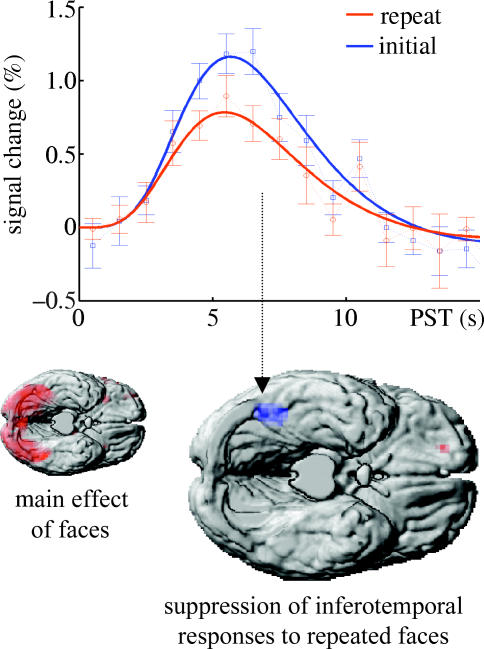
Repetition suppression as measured with fMRI in normal subjects. Top panel: estimated hemodynamic responses to the presentation of faces that were (red), and were not (blue), seen previously during the scanning session. These estimates were based on a linear convolution model of fMRI responses in the most significant voxel in the corresponding statistical parametric map. Lower panel: statistical parametric maps, overlaid on a cortical rendering of a single subject, showing areas that responded to all faces (left) and the region showing significant repetition suppression. For details, see Henson et al. (2000).

In §5, we presented empirical examples where coherence or congruency was used to control the predictability of stimuli. Below, we look at examples where rapid sensory and perceptual learning renders some stimuli more familiar than others do. The behavioural correlate of repetition effects is priming (cf. global precedence for congruency effects). The example we focus on is the MMN elicited with simple stimuli. However, there are many other examples in electrophysiology, such as the P300.

(b) MMN and perceptual learning

The MMN is a negative component of the ERP elicited by any perceptible change in some repetitive aspect of auditory stimulation. The MMN can be seen in the absence of attention and is generally thought to reflect pre-attentive processing in the temporal and frontal system (Näätänen 2003). The MMN is elicited by stimulus change at about 100–200 ms after the stimulus, and is presumed to reflect an automatic comparison of stimuli to sensory memory representations encoding the repetitive aspects of auditory inputs. This prevailing theory assumes that there are distinct change-specific neurons in auditory cortex that generate the MMN. The alternative view is that preceding stimuli adapt feature-specific neurons. In this adaptation hypothesis, the N1 response is delayed and suppressed on exposure to repeated stimuli giving rise to the MMN. The N1 is a negative electrical response to stimuli peaking at about 100 ms. The problem for the adaptation hypothesis is that the sources of the N1 and MMN are, apparently, different (Jääskeläinen et al. 2004).

Neither the change-specific neuron nor the intrinsic adaptation hypotheses are consistent with the theoretical framework established above. The empirical Bayes scheme would suggest that a component of the N1 response, corresponding to prediction error, is suppressed more efficiently after learning-related plasticity in backward and lateral connections. This suppression would be specific for the repeated aspects of the stimuli and would be a selective suppression of prediction error. Recall that error suppression (i.e. minimization of free energy) is the motivation for plasticity in the M-step. This repetition suppression hypothesis suggests the MMN is simply the attenuation of the N1. Fortunately, the apparent dislocation of N1 and MMN sources has been resolved recently: Jääskeläinen et al. (2004) show that the MMN results from differential suppression of anterior and posterior auditory N1 sources by preceding stimuli. This alters the centre of gravity of the N1 source, creating a specious difference between N1 and MMN loci when estimated using dipole equivalents.

In summary, both the E-step and M-step try to minimize free energy; the E-step does so during perceptual synthesis on a time-scale of milliseconds and the M-step does so during perceptual learning over seconds or longer. If the N1 is an index of prediction error (i.e. free energy), then the N1, evoked by the first in a train of repeated stimuli, will decrease with each subsequent stimulus. This decrease discloses the MMN evoked by a new (oddball) stimulus. In this view, the MMN is subtended by a positivity that increases with the number of standard. Recent advances in the MMN paradigm that use a ‘roving’ paradigm show exactly this (see Baldeweg et al. 2004; see also figure 5).

Figure 5.

Schematic using empirical results reported in Baldeweg et al. (2004) relating the MMN to a predictive error suppression during perceptual learning. The idea is that perceptual synthesis (E-step) minimizes prediction error ‘online’ to terminate an early negativity, while perceptual learning (M-step) attenuates its expression over repeated exposures (solid black bars). The magnitude of MMN increases with number N of standards in each ‘roving’ stimulus train. This may be due to the suppression of an N1-like component over repeated presentation of the standards (dotted lines) that reveals the MMN.

(i) MMN and plasticity

The suppression hypothesis for the MMN rests on plasticity in backward and lateral connections to enable the minimization of prediction error. The adaptation hypothesis does not. If the suppression hypothesis is correct, then the MMN should be attenuated when plasticity is compromised pharmacologically. This is precisely what happens. Umbricht et al. (2000) show that ketamine significantly decreases the MMN amplitude, to both pitch and duration, by about 20%. Ketamine is a non competitive NMDA receptor antagonist. NMDA receptors play a key role in short‐ and long-term plasticity as mentioned in §2(c).

The mechanistic link between plasticity and the MMN provided by perceptual learning based on empirical Bayes is important because a number of neuropsychiatric disorders are thought to arise from aberrant cortical plasticity. Two interesting examples are dyslexia and schizophrenia. In dyslexia, the MMN to pitch is attenuated in adults and the degree of attenuation correlates with reading disability. In contrast, in schizophrenia, the MMN to duration is more affected and has been shown to correlate with the expression of negative symptoms (Näätänen et al. 2004). This is potentially important because the disconnection hypothesis for schizophrenia (Friston 1998) rests on abnormal experience-dependent plasticity. From the point of view of this paper, the key pathophysiology of schizophrenia reduces to aberrant representational learning as modelled by the M-step. If the MMN could be used as a quantitative index of perceptual learning, then it would be very useful in schizophrenia research (see also Baldeweg et al. 2002). In §7, we show that the MMN can indeed be explained by changes in connectivity.

7. An empirical epilogue

Although it is pleasing to have a principled explanation for many anatomical and physiological aspects of neuronal systems, the question can be asked, is this explanation empirically useful? We conclude by showing that recent advances in the DCM of evoked responses now afford measures of connectivity among cortical sources that can be used to quantify theoretical predictions about perceptual learning. These measures may provide mechanistic insights into putative functional disconnection syndromes, such as dyslexia and schizophrenia. The advances in data analysis are useful because they use exactly the same EM scheme to analyse neurophysiological data as proposed here for the brain's analysis of sensory data.

(a) Dynamic causal modelling with neural mass models

ERPs have been used for decades as electrophysiological correlates of perceptual and cognitive operations. However, the exact neurobiological mechanisms underlying their generation are largely unknown. In the following, we use neuronally plausible models to explain event-related responses. The example used here suggests changes in connectivity are sufficient to explain ERP components. Specifically we will look at late components associated with rare or unexpected events (e.g. the MMN). If the unexpected nature of rare stimuli depends on learning frequent stimuli, then the MMN must be due to plastic changes in connectivity that mediate perceptual learning. If the empirical Bayes model of perception is right, then this learning must involve changes in backward, lateral and forward connections. Below, we test this hypothesis in relation to changes that are restricted to forward connections, using a neural mass model of ERPs and EEG data.

(i) A hierarchical neural mass model

The minimal model we have developed (David et al. 2005) uses the laminar-specific rules outlined in §2(c) and described in Felleman & Van Essen (1991) to assemble a network of coupled sources. These rules are based on a partitioning of the cortical sheet into supra-, infra‐granular layers and granular layer (layer 4). Bottom-up or forward connections originate in agranular layers and terminate in layer 4. Top-down or backward connections target agranular layers. Lateral connections originate in agranular layers and target all layers. These long-range or extrinsic cortico-cortical connections are excitatory and arise from pyramidal cells.

Each region or source is modelled using a neural mass model decribed in David & Friston (2003), based on the model of Jansen & Rit (1995). This model emulates the activity of a cortical area using three neuronal subpopulations, assigned to granular and agranular layers. A population of excitatory pyramidal (output) cells receives inputs from inhibitory and excitatory populations of inter neurons, via intrinsic connections. Within this model, excitatory inter neurons can be regarded as spiny stellate cells found predominantly in layer 4 and in receipt of forward connections. Excitatory pyramidal cells and inhibitory inter neurons will be considered to occupy agranular layers and receive backward and lateral inputs (see figure 6).

Figure 6.

This schematic shows the state equations describing the dynamics of one source. Each source is modelled with three subpopulations (pyramidal, spiny stellate and inhibitory inter neurons) as described in Jansen & Rit (1995) and David & Friston (2003). These have been assigned to granular and agranular cortical layers which receive forward and backward connection, respectively.

To model ERPs, the network receives inputs via input connections. These connections are exactly the same as forward connections and deliver inputs w to the spiny stellate cells in layer 4. In the present context, these are subcortical auditory inputs. The vector C controls the influence of the ith input on each source. The matrices A^F, A^B, A^L encode forward, backward and lateral connections, respectively. The DCM here is specified in terms of the state equations shown in figure 6 and a linear output equation,

$$\begin{array}{l}\dot{x}(t)=f(x,w)\hfill \\ y=L{x}_0+ϵ,\hfill \end{array}$$ (7.1)

where x₀ represents the transmembrane potential of pyramidal cells, and L is a lead field matrix coupling electrical sources to the EEG channels. As an example, the state equation for an inhibitory subpopulation is3

$$\begin{array}{l}{\dot{x}}_7=x_8\hfill \\ {\dot{x}}_8=\frac{H_{\text{e}}}{{\tau }_{\text{e}}}((A^{\text{B}}+A^{\text{L}}+{\gamma }_{3}I)S(x_0))-\frac{2x_8}{{\tau }_{\text{e}}}-\frac{x_7}{{\tau }_{\text{e}}^2}.\hfill \end{array}$$ (7.2)

Within each subpopulation, the evolution of neuronal states rests on two operators. The first transforms the average density of presynaptic inputs into the average postsynaptic membrane potential. This is modelled by a linear transformation with excitatory and inhibitory kernels parameterized by H and τ. H controls the maximum postsynaptic potential and τ represents a lumped rate constant. The second operator S transforms the average potential of each subpopulation into an average firing rate. This is assumed to be instantaneous and is a sigmoid function. Interactions, among the subpopulations, depend on constants γ_1,2,3,4, which control the strength of intrinsic connections and reflect the total number of synapses expressed by each subpopulation. In equation (7.2), the top line expresses the rate of change of voltage as a function of current. The second line specifies how current changes as a function of voltage, current and presynaptic input from extrinsic and intrinsic sources. Having specified the DCM, one can estimate the coupling parameters from empirical data using EM (Friston et al. 2003), using exactly the same minimization of free energy proposed for perceptual learning.

(ii) Perceptual learning and the MMN

We elicited ERPs that exhibited a strong modulation of late components, on comparing responses to frequent and rare stimuli, using an auditory oddball paradigm. Auditory stimuli of between 1000 and 2000 Hz tones with 5 ms rise and fall times and 80 ms duration were presented binaurally. The tones were presented for 15 min, every 2 s in a pseudo random sequence with 2000 Hz tones on 20% of occasions and 1000 Hz tones for 80% of the time (standards). The subject was instructed to keep a mental record of the number of 2000 Hz tones (oddballs). Data were acquired using 128 EEG electrodes with 1000 Hz sample frequency. Before averaging, data were referenced to mean earlobe activity and band-pass filtered between 1 and 30 Hz. Trials showing ocular artefacts and bad channels were removed from further analysis.

Six sources were identified using conventional procedures (David et al. 2005) and used to construct DCMs (see figure 7). To establish evidence for changes in backward and lateral connections beyond changes in forward connections, we employed a Bayesian model selection procedure. This entailed specifying four models that allowed for changes in forward, backward, forward and backward and changes in all connections. These changes in extrinsic connectivity may explain the differences in ERPs elicited by standard relative to oddball stimuli. The models were compared using the negative free energy as an approximation to the log evidence for each model. From equation (3.4), if we assume the approximating conditional density is sufficiently good, then the free energy reduces to the log evidence. In Bayesian model selection of a difference in log evidence of three or more can be considered as very strong evidence for the model with the greater evidence, relative to the one with less. The log evidence for the four models is shown in figure 7. The model with the highest evidence (by a margin of 27.9) is the DCM that allows for learning-related changes in forward, backwards and lateral connections. These results provide clear evidence that changes in backward and lateral connections are needed to explain the observed differences in cortical responses.

Figure 7.

Upper right: transparent views of the cortical surface showing localized sources that entered the DCM. A bilateral extrinsic input acts on primary auditory cortices (red), which project reciprocally to orbito-frontal regions (green). In the right hemisphere, an indirect pathway was specified via a relay in the superior temporal gyrus (magenta). At the highest level, orbito-frontal and left posterior cingulate (blue) cortices were assumed to be laterally and reciprocally connected (broken lines). Lower left: schematic showing the extrinsic connectivity architecture of the DCM used to explain empirical data. Sources were coupled with extrinsic cortico-cortical connections following the rules of Felleman & Van Essen (1991). A1, primary auditory cortex; OF, orbitofrontal cortex; PC, posterior cingulate cortex; STG, superior temporal gyrus (right is on the right and left on the left). The free parameters of this model included extrinsic connection strengths that were adjusted to best explain the observed ERPs. Critically, these parameters allowed for differences in connections between the standard and oddball trials. Lower right: The results of a Bayesian model selection are shown in terms of the log evidence for models allowing changes in forward (F), backward (B), forward and backward (FB) and forward, backward and lateral connections (FBL). There is very strong evidence that both backward and lateral connections change with perceptual learning as predicted theoretically.

These differences can be seen in figure 8 in terms of the responses seen and those predicted by the fourth DCM. The underlying response in each of the six sources is shown in the lower panel. The measured responses over channels have been reduced to the first three (spatial) modes or eigenvectors. The lower panel also shows where changes in connectivity occurred. The numbers by each connection represent the relative strength of the connections during the oddball stimuli relative to the standards. The percentages in brackets are the conditional confidence that these differences are greater than zero (see David et al. 2005 for details of this study). Note that we have not attempted to assign a functional role to the three populations in terms of a predictive coding model, nor have we attempted to interpret the sign of the connection changes. This represents the next step in creating theoretically informed DCMs. At present, all we are demonstrating is that exuberant responses to rare stimuli, which may present a failure to suppress prediction error, can be explained quantitatively by changes in the coupling among cortical sources, which may represent perceptual learning with empirical Bayes.

Figure 8.

Auditory oddball paradigm: DCM results for the FBL model of the previous figure. Upper panel: the data are the projection of the original scalp time-series onto the three first spatial modes or eigenvectors. Note the correspondence between the measured ERPs (thin lines) and those generated by the model (thick lines). Lower panel: the response of each source is shown for the standard (grey) and oddball (black) trials based on the conditional expectation of the DCM parameters. Changes in coupling are shown alongside each connection in terms of the relative strength (oddball to standard). The percentages refer to the conditional confidence this change is non-zero (i.e. a relative strength of more than one). Changes with over 95% confidence are shown as solid lines. A1, primary auditory cortex; OF, orbitofrontal cortex; PC, posterior cingulate cortex; STG, superior temporal gyrus.

In summary, we estimated differences in the strength of connections for rare and frequent stimuli. As expected, we could account for detailed differences in the ERPs by changes in connectivity. These changes were expressed in forward, backward and lateral connections. If this model is a sufficient approximation to the real sources, then these changes are a non-invasive measure of plasticity, mediating perceptual learning in the human brain.

Glossary

DEM

dynamic expectation maximization

DCM

dynamic causal modelling

EM

expectation maximization

ERP

event-related potential

fMRI

functional magnetic resonance imaging

LGN

lateral geniculate nucleus

MMN

mismatch negativity

RF

receptive field

STDP

spike-timing dependent plasticity