Relationships between quantitative and reproductive fitness traits in animals

Abstract

The relationships between quantitative and reproductive fitness traits in animals are of general biological importance for the development of population genetic models and our understanding of evolution, and of great direct economical importance in the breeding of farm animals. Two well investigated quantitative traits—body weight (BW) and litter size (LS)—were chosen as the focus of our review. The genetic relationships between them are reviewed in fishes and several mammalian species. We have focused especially on mice where data are most abundant. In mice, many individual genes influencing these traits have been identified, and numerous quantitative trait loci (QTL) located. The extensive data on both unselected and selected mouse populations, with some characterized for more than 100 generations, allow a thorough investigation of the dynamics of this relationship during the process of selection. Although there is a substantial positive genetic correlation between both traits in unselected populations, caused mainly by the high correlation between BW and ovulation rate, that correlation apparently declines during selection and therefore does not restrict a relatively independent development of both traits. The importance of these findings for overall reproductive fitness and its change during selection is discussed.

1. Introduction

Much progress in genetical research has been made in the last few decades, but achieving greater understanding in some areas is a very slow process. Some statements regarding imperfect understanding of certain aspects of artificial selection and their consequences on reproductive fitness, which were made nearly 40 years ago (e.g. Latter & Robertson 1962) still describe the situation today. Latter & Robertson stated, for example, that several aspects of the response of an equilibrium population to artificial selection for extreme expression of a chosen quantitative character are only partially understood, and that although short and medium term responses can be reasonably well predicted, the theory is still incapable of providing useful predictions of long-term response. This also applies to the prediction of the response in characters other than those directly selected (e.g. reproductive fitness; Bohren et al. 1966). Although negative side effects on reproductive fitness may be expected theoretically as a result of the disturbance of the initial genetic equilibrium, there is no way of predicting the rate of decline in reproductive fitness. Furthermore, there is no clear understanding of the role a decline in fitness may have in generating selection limits or of how individual fitness components may be affected by selection. The relative importance of changes of gene frequencies due to selection and due to inbreeding, and the importance of linkage in this process are also unclear.

We propose that an observational rather than analytical approach is useful for improving our understanding of the phenomenon. We have chosen growth rate or body weight (BW) as an archetypal quantitative trait that has been studied intensely genetically, physiologically and metabolically in model animals, fishes, farm animals and humans. Body weight is continuously distributed, is polygenic in its inheritance, seems to be influenced by a large fraction of the genes in the genome and it is moderately to highly heritable in most species (h² ca 0.30–0.55). As our example of fitness traits, we focus on litter size (in fact, primarily first parity litter size) as a main component of the very complex set of traits defining reproductive fitness. Litter size is measured as an integer but is nevertheless a quantitative character and is assumed to result from an underlying continuous distribution of effects. Its heritability is low in several different species (h²=0.05–0.15). Litter size (LS) and BW are both of immense economic importance in livestock. Hence, for the evaluation of animal breeding systems, information is needed on the extent to which both traits can be manipulated by single or multi-trait selection (Eisen 1978).

The relationship between BW/size and LS, as part of the life-history characteristics of different species, has also attracted considerable attention in evolutionary biology. There is evidence of some evolutionary advantage to females in having a large body size. Darwin (1874) proposed a general explanation that ‘increased size must be in some manner of more importance to the females…and this perhaps is to allow the production of a vast number of ova’. This general hypothesis on the evolution of large body size in females has enjoyed wide support and this ‘fecundity advantage’ model has been used to explain why females grow larger than males in zooplankton, insects, fishes, amphibians, reptiles, birds and other animal species/taxa. More recent studies have shown that Darwin's ‘fecundity advantage hypothesis’ may apply to a limited set of species only and that the demonstration of a positive relationship between maternal size and clutch size is not a sufficient basis from which to infer that natural selection should favour large female body size generally (Shine 1988). Although it is widely agreed that fecundity selection and sexual selection are the major evolutionary forces selecting for larger body size in most organisms, the general view is that selection for large body size is eventually counterbalanced by opposing selective forces, explaining the relative constancy of these traits (Blanckenhorn 2000).

2. How should the relationship between body weight and litter size be investigated?

The ‘interspecific comparison’ approach is common in various scientific disciplines such as comparative physiology, biochemistry, medicine and physiological ecology. One major benefit of this method is that it takes advantage of the large between-species variation. The best known example might be the study of the relationship between mammalian basal metabolic rate (BMR) and BW, which has been the subject of regular investigation for over a century. Since the pioneering work in the 1880s (Rubner 1883) and Kleiber's influential paper in the 1930s (Kleiber 1932), there has been discussion of whether BMR is proportional to surface area (BMR∝BW^2/3), or if an exponent significantly greater than that of Rubner's surface law (three quarters or close to three quarters) should be used (Smil 2000; White & Seymour 2003; Savage et al. 2004). Despite this discussion, the log–log mouse-to-elephant line (Brody 1945; Kleiber 1961) became one of the most important and best known generalizations in bioenergetics. Simply following such an approach here would indicate a negative relationship between BW and LS, since a female mature mouse weighs approximately 35 g and has a LS of around 10 and the female elephant is about 10⁵-fold heavier, but has usually a LS of 1. That conclusion seems contrary to Darwin's fecundity advantage hypothesis and would be misleading, as illustrated later. Comparative interspecies studies have well recognized limitations (Harvey & Pagel 1991), and there is growing evidence that the relationship of LS to BW is different in different taxa and exhibits a positive correlation in small and a negative correlation in bigger mammals (Tuomi 1980). The genetic relationship between both traits seems to be weak, since different mammalian species have developed different life-history characteristics or different strategies for leaving living descendants independently of BW. Two divergent strategies are recognized: the r-strategy and the K-strategy (MacArthur & Wilson 1967), discussed and criticized by Charlesworth (1994, ch. 5). Mice seem to tend towards the r-strategy, whereas elephants exemplify the K-strategy. The r-strategists are short-lived, opportunistic, rapidly maturing and produce many descendants, but do not invest heavily (energy, time, care) in offspring. This results in low offspring survival. The population size is not density regulated, with boom and bust population dynamics. The K-strategists on the other hand are long-lived, late and slow maturing, provide high care for their offspring, have low juvenile mortality and low number of offspring and with population size usually regulated by carrying capacity of the environment (MacArthur & Wilson 1967).

Here we focus on the relationship between LS and BW/size within different species.

3. Relationship between body weight or size and litter size or fecundity in different species

(a) Fishes

In most fishes, males and females are separate individuals, fertilization is external and the very large number of eggs produced by a female (per year=fecundity) are mostly left to develop, hatch and grow without further parental care. There are some departures from this typical life-history strategy (e.g. hermaphrodites, sex changes, internal fertilization, guarding of eggs). Spawning is usually seasonal, can be in batches or as a one-off spawning (Blaxter 1969; Bone et al. 1995). There is a negative relationship between fecundity and egg size, possibly due to the ovary to body size ratio. For example, the ninespine sticklebacks in Puck Bay (Poland) have an average size of 40 mm, and when the fishes are gravid the ovaries are very large, and can fill the body cavity to a considerable extent, displacing the internal organs upwards, and can form approximately 20% of the total female BW (Sokolowska & Skora 2002). As the size of the ovary is limited by female size, females with high egg numbers usually produce smaller eggs and vice versa (Bone et al. 1995). Apart from enormous interspecific differences in fecundity (e.g. Spur dogfish: 2–7 eggs/female/year, Ling: 20–30×10⁶ eggs/female/year) there is also considerable variation within a species and many authors have found that fecundity increases with length or weight over species and within species (for details see Blaxter 1969). In a recent study, the fecundity–length relationship was investigated in 25 kokanee (K) and 48 sockeye (S) populations of salmon (Mcgurk 2000). Different reproductive strategies between the two varieties were found: (i) fecundity was more highly correlated with length for K than S salmon; (ii) K had higher fecundity–length regression slopes and lower intercepts than S salmon and (iii) K salmon populations shared a common fecundity–length regression slope, but S salmon populations did not. It was confirmed that K salmon maintain a constant egg size while increasing egg number with increasing body size, but that S salmon increased both egg number and egg size with increasing body size. Altogether, this shows that body size in fishes might be a physical constraint on ovary size and therefore ovulation rate (OR). The general picture seems also to indicate a large genetic plasticity of the BW–fecundity relationship in fishes, allowing for the development of breed-/variant-specific reproductive strategies.

(b) Dogs

Dogs are remarkable for the very considerable difference in size that exists between the smallest and largest breeds, exceeding that for any domesticated mammalian species. Heavy breeds like the St Bernard, Mastiff and Newfoundland have mature weights of approximately 70 kg, whereas the Papillion, Pekinese and Chihuahua have weights around 1.5–3 kg (Kaiser 1971; Robinson 1973). Only a few studies have investigated the relationship between BW and LS. Data from Swiss dog breeding organizations on 17 106 pups from 2875 litters of nine breeds used in a breed comparison showed a clear positive relationship between shoulder height (SH; range ca 22–70 cm) and average and maximal LS. The correlation between SH and BW was 0.91, which allows SH to be used as a good predictor for BW (Kaiser 1971). The correlation coefficient between SH and LS (calculated from Kaiser's data) is about 0.88 and the regression coefficient is 0.12 pups cm⁻¹ SH. Some breeds deviate substantially from the common regression line. For example, the ‘Appenzeller Sennenhund’ has a SH close to average, but had the highest mean LS (mean of 8.0 pups). Another study based on 76 breeds provided a correlation estimate of 0.71 between BW and LS and predicted an average increase in LS of 0.09 pups kg⁻¹ BW (Robinson 1973). It is of note that the three heaviest breeds deviate considerably from the common regression line, with lower than expected average LS, indicating either a nonlinear relationship and/or reflecting some independence between the traits. Observations on nearly 70 bitches from 37 breeds undergoing ovariohysterectomy, weighing 4.6–65 kg (mean 28 kg) with average weight of the ovaries of 0.3–4.2 g (mean 1.5 g), showed a positive correlation between BW and ovarian weight (0.7; Strom et al. 2001). However, unlike the situation in fishes, BW is probably not a physical constraint on the size of the ovary in dogs and other mammals.

There are no within-breed investigations based on individual data for BW and LS known to the authors. The main conclusion to be drawn in dogs is that the relationship between growth and LS is relatively high and positive, though certain breeds deviate substantially from the across-breed regression line. Body weight is a composite trait and does not reflect body type, and its relationship to the size and function of endocrine organs controlling ovulation remains unknown.

(c) Pigs

Domestication of the wild pig and the subsequent selection to meet humankind's needs of efficient production and lean meat has demonstrated the genetic plasticity of the modern pig (Rothschild & Ruvinsky 1998). Pigs produce 43% of the world's red meat and of particular importance to commercial production has been selection for total growth, especially lean growth, to larger market weights of around 115 kg. This selection has primarily been focused on sire lines, but dam lines selected for increased LS and piglet survival have also undergone considerable selection for leanness and increased growth. One could compare breeds for LS based on the breed's average growth rate or mature size. Generally, wild pigs and minipigs have the smallest mature weight and also have the smallest LS. However, dam line breeds that have smaller mature size than sire breeds have larger LSs than sire line breeds.

Researchers have examined the relationship between growth and reproduction employing four primary approaches. The first approach is to examine reproduction in females that have previously undergone selection for growth or lean growth. A number of such experiments have been recorded, but the selected traits may differ, which causes some difficulty in their interpretation. Kuhlers & Jungst (1992) examined correlated responses in LS traits in a closed Duroc line selected for 200 day weight, and found decreased LS at birth. Correlated responses in LS traits in a landrace line selected for 200 day weight, however, produced relationships that were small, and regression coefficients for reproductive traits that did not differ significantly from zero (Kuhlers & Jungst 1993). Kerr & Cameron (1996) estimated genetic and phenotypic relationships between performance test and reproduction traits, after five generations of divergent selection for daily food intake, lean food conversion and lean growth rate in 865 ad-libitum fed large white pigs. They concluded that selection directed to increase lean growth rate and/or reduce daily food intake may have a negative effect on reproductive performance, even though estimates of the genotypic and environmental correlations between traits were small. A thorough review of the literature (Clutter & Brascamp 1998) concludes, however, that while some studies suggest a small negative relationship between lean growth and reproduction, the estimates of the parameters were often of insufficient accuracy to be conclusive about such a relationship.

A second approach is to select for LS traits and then to measure correlated responses in growth rate. To be useful, however, selection for LS traits must be effective over several generations, and such longer-term studies are more limited. Estany et al. (2002) examined BW and backfat measurements in lines previously divergently selected for five generations and in which LS differences were significant. The high LS line grew faster at the initiation of the trial but significantly slower than the low LS line at the end of five generations of selection. Fat deposition increased significantly in the high line, suggesting that selection for LS could decrease lean growth rate.

A third approach is to obtain field data from pig populations recorded in central record-keeping systems. Lean growth and litter traits in Duroc, Hampshire, landrace and Yorkshire pigs collected in the USA from the national swine registry programme revealed that genetic correlations were generally antagonistic between growth and LS, with the correlations between backfat and LS being the largest (Chen et al. 2003).

Molecular genetics offers a fourth approach to examine the relationship between growth and reproduction. Short et al. (1997) demonstrated that the oestrogen receptor locus has a significant effect on LS in four lines of commercial pigs, with an additive effect of 0.42 on LS. Further examination revealed no significant pleiotropic effects of this gene on growth or backfat.

The conclusions to be drawn in pigs on the relationship between growth, especially lean growth and LS are that the relationship is small and antagonistic. Individual selection of genes with positive effects on LS, but no, or no beneficial effects on lean growth, seems to be an alternative to mass selection for either growth rate or LS.

(d) Sheep

Sheep contribute significantly to world demand for meat. Three primary factors contribute to meat production: (i) the number of breeding ewes, (ii) their reproductive efficiency and (iii) the slaughter weight of lambs marketed. As a consequence, the nature of the genetic relationship between growth and body size with reproductive measures such as LS is paramount to the design of selection programmes in sheep.

A common notion when comparing breeds or individuals that differ in growth potential is that their reproductive rates are the same irrespective of body size. Bradford (2002) suggested this notion may not be true; animals that diverge from the species average in body size are often less reproductively fit. In sheep, there is no general relationship between LS and weight among breeds. Breeds of similar weight, for instance, may differ substantially in fertility (Michels et al. 2000).

The correlation between BW and LS has been assessed fairly extensively in sheep. In a review article, Fogarty (1995) reported a weighted average correlation between live weight and LS of 0.41 (range −0.46 to 0.78). The genetic correlation estimates tended to increase from small and slightly negative values for weights at young ages (e.g. weaning) to moderate and positive values for weights at older ages (e.g. above 14 months of age). Brien (1986) argued that correlation estimates involving weights recorded at or before weaning were unreliable because such weights were strongly influenced by maternal effects. Where maternal effects were explicitly modelled, genetic correlations of LS with weaning weight and post-weaning gain were generally positive, and occasionally significant (e.g. Rao & Notter 2000). The genetic correlation of BW with LS is likely to be small yet positive.

Correlated responses in BW and LS through selection for the alternative trait have been observed. After 30 years of selection for LS or weaning weight (replicated) in lines of Targhee sheep, both trait means increased by approximately 15% (Sakul et al. 1999). Much of the gain in the line selected for LS resulted from screening of base ewes, as reported by Turner (1978) in Australian Merinos. Litter size increased slightly in one weight line and by 15% in the other, suggesting a positive correlated response to selection. However, BW did not increase in the LS line. In all lines, fertility and lamb survivability declined, while mature ewe weights increased in the weight lines, partially offsetting other gains in productivity (Bradford 2002). In Romney ewes selected either for or against prolificacy, the prolific line weighed 2–3 kg more at mating (Meyer & Clarke 1982).

Major genes like the Booroola and Inverdale genes are known for their substantial effects on OR and thereby LS (Amer et al. 1999). However, evidence on the pleiotropic effect of such genes on BW is equivocal, although Texel lambs carrying the Booroola gene had heavier yet fatter carcasses (Visscher et al. 2000).

As a general conclusion, simultaneous increases in LS and growth traits through selection appear possible in sheep. However, the risk of a decline in fertility and lamb survivability, and a likely increase in mature size, may counterbalance such benefits in an overall production system, particularly in dual-purpose and dam breeds.

(e) Rabbits

Commercial rabbit farms use crossbred females and synthetic terminal sires (crosses of two or more breeds designed to combine the desirable traits into one composite breed, which is kept afterwards as purebred). Lines for crossbred females are selected for LS at birth or at weaning, and terminal sires are selected for growth rate. In some cases, mainly in developing countries, where facilities allow selection on one line only, this line is selected for LS and growth rate and additionally for some traits related to maternal ability, such as litter weight at weaning. A complete description of lines used in selection programmes is given by Garreau et al. (2004), who also highlighted the importance of knowledge of the genetic relationships of growth and LS.

The genetic relationship between the traits has been assessed by estimating genetic parameters or by estimating correlated responses to selection for LS. Using different breeds and crosses, early studies found that OR and LS increase with the BW of the doe (Gregory 1932). This was confirmed by studies in the 1950s involving rabbits of breeds with a wide range of BWs (from Hermelin at 1.2 kg to Deutsche Riesen at ca. 6 kg, and also including wild rabbits at ca 1.5 kg), which also suggested a positive relationship between BW and LS. However, certain breeds deviated substantially from such an interbreed regression line (Lüdike-Spannenkrebs 1955). Recently, five medium-sized and three small-sized breeds were compared with a medium-sized control strain (Bolet et al. 2004) and the results indicated that the smallest breeds have the lowest LS. No pattern appears when comparisons are made between breeds, because light and heavy breeds have smaller LS than some medium-weight breeds. Estimates of genetic correlations within breeds given in the literature are inconsistent, and both positive and negative estimates have been reported, possibly depending on the line analysed (Camacho & Baselga 1990). However, estimates obtained using REML with an animal model, thereby avoiding bias produced by selection, show very low correlations between growth traits and LS. For example, Gomez et al. (1998) found a correlation between BW at 60 days and LS of −0.16, and Garreau et al. (2000) reported a correlation between BW at 77 days and LS of +0.10 (no s.e. values were given).

Estimating correlated responses to selection, Rochambeau de et al. (1994) reported a negative correlated response in weight at weaning when lines were selected for LS. García & Baselga (2002) estimated the correlated response to selection for LS on growth traits by using a frozen control population that was thawed to be contemporary with the selected population. They reported no genetic correlation between LS and weight at four or nine weeks of age (weaning and slaughter ages) when the LS in which animals were born was included as a covariate. This covariate, which as expected was negative, was included to avoid the negative maternal effect on growth when rabbits are born in large litters.

The general picture emerging from the experiments is that the genetic relationship among LS and growth traits is low or zero, and that it is less pronounced for later weights (slaughter weight) than for weaning weight.

4. Genetics of the relationship between body weight and litter size in mice as a model species

The laboratory mouse is an important genetic model for the study of growth and reproductive fitness and it has been widely used, both in the study of individual genes and of artificial selection. Mice as a model have great advantages including their short generation interval (ca 4 generations per year), their high reproductive rate, a low cost of animal management, ease of measurement, the ability to control and standardize their environment and the availability of genetically modified or mutated animals. These features along with the extensive knowledge of their genetics, including their genome sequence, have led mice to become an important model for studies of the inheritance of quantitative traits.

Litter size and BW are quantitative characters that have been intensely studied in mice. Single-trait selection studies have been reviewed elsewhere (Roberts 1965a,b; Eisen 1974, 2005; Bünger et al. 2001b). About 20 years ago, the relationship between growth and reproduction in mammals was reviewed (Brien 1986), especially in mice. In the last decade or so there has been great progress in mapping quantitative trait loci (QTL) and identifying specific genes for BW (for reviews see Corva & Medrano 2001; Brockmann & Bevova 2002). Fewer QTL have been mapped for fertility traits (LS, OR; Kirkpatrick et al. 1998; Brunsch et al. 1999; Spearow et al. 1999; Peripato et al. 2004) and maternal performance and offspring survival (Peripato et al. 2002). Interestingly, there seems to be some overlap between QTLs affecting both LS and mature weight (Kirkpatrick et al. 1998).

While the main focus has been on the mouse as a model for livestock breeding, mice are now also used as a model for the genetics of human reproduction. Laboratory strains of mice, including selection lines are also increasingly used as model organisms in evolutionary physiology (Carter et al. 1999).

(a) Body weight and litter size in unselected mice

Although there is variation between mouse strains, the general pattern is that an unselected female mouse weighs at mating (usually at 9–11 weeks) about 30 g (phenotypic standard deviation (s_p)=2.6 g) and gives birth to approximately 12 pups (s_p=2.7 pups; see figure 1 for details). Estimates of the genetic parameters for both traits in such an unselected control or base population have been provided. For example, Eisen (1978) reported h²_BW of 0.42±0.02, h²_LS0 of 0.17±0.04 (where LS0 is LS at birth) and r_g of 0.63±0.14, from which one can expect a positive correlated response in LS0 when selection is on BW and vice versa. This situation is illustrated in figure 1. It is of note that, assuming a normal distribution for both traits, one can expect that 99% of females in this example population will have BWs within a range of 23.3–36.7 g and a LS from 5.0 to 19.0 pups, since 99% of animals are in the range of the mean±2.58 times the phenotypic standard deviation (s_p).

Figure 1.

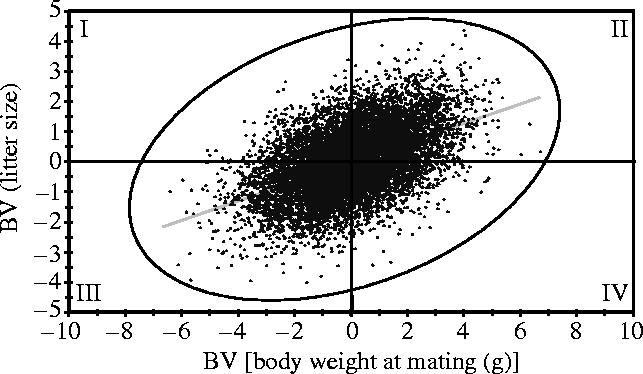
Genetic relationship (simulated data) between body weight at mating (BWM) and litter size at birth (LS0). The simulation used approximate values based on realized and base population estimates: h²_BWM=0.42; h²_LS0=0.17; r_g=0.5 (all from Eisen 1978) and s_p²_BWM=6.88 g²; s_p²_LS0=7.12 pups² (own estimates based on 880 observations from 10 generations of an unselected control line with litter size standardization: DU-Ks, Dummerstorf) with means of 30.7 g and 12.1 pups, resp.). For the simulation, 10 000 random breeding values (BV) of the two variables (BWM, LS0), normally distributed with means and s_g for BW and LS0 (0; 1.70 g) and (0; 1.10 pups), respectively and correlated with r_g=0.5 Mathematica version 4.1 (Wolfram Research Europe Ltd, Oxfordshire 0X29 8RY, UK) were used. Genetic regression coefficients: LS on BW=0.32 pups g⁻¹; BW on LS=0.77 g pup⁻¹.

However, numerous selection experiments have shown that selection can take the mean of a trait far beyond the range of variation seen in the base population. Selection for an index combining LS and litter weight, or for LS alone, increased mean LS to 19 (Renne et al. 1998) or even 22 pups (Holt et al. 2004), and selection for growth provided responses of 3–17 phenotypic standard deviations, producing animals diverging up to sixfold in weight (Bünger et al. 2001b; Hill & Bünger 2004). Animals with such extreme BW do not occur in the base population. After a few generations there is no overlap between a control and a selection line in their BW range (e.g. fig. 6.11 in Hill & Bünger 2004). Therefore, it seems important to investigate the relationships between BW and LS also in long-term selected lines as changes can be expected.

(b) Correlated effects of growth selection on litter size (first parity, sexually mature females)

One of the pioneering selection experiments for high BW showed a positive correlated response in LS (MacArthur 1944) and this has been confirmed amply by later experiments, reviewed by Roberts (1965b, 1979) and Eisen (1974). We will therefore refer to and summarize here later experiments only. Selection for low growth usually resulted in reductions of LS, whereas selection for high growth in almost all of 20 experiments was associated with an increase in LS. There are a few noteworthy exceptions: (i) Bradford (1971) did not observe changes in LS after selecting for BW gain (BWG from day 21 to 42), but found an increase in OR; (ii) in populations of small size selected for BWG 21–42d there was also no correlated response in LS, probably due to inbreeding effects (Eisen et al. 1973, 1974, 1975); and (iii) in another experiment, where selection successfully increased BW at day 42 over eight generations, a total drop in LS by 3.8 pups was observed in a line in which no standardization of the rearing LS was applied (Bünger et al. 1992). Collectively, these experiments show that the interpretation of changes in first parity LS in response to selection for increased growth is not straightforward. First, fertility traits are susceptible to inbreeding depression, which can be quite substantial because most selection experiments are based on limited population sizes. Second, there are complicated relationships between BW and LS through maternal effects (figure 2). Path diagrams between LS of the mother (LS_M), BW of the daughter (BW_D) and the LS of the daughter (LS_D), without (scenario A; Falconer 1955) and with (scenario B; Eisen 1970) standardization of the rearing LS, showed a higher regression coefficient between LS of the mother and that of her daughter when LS was standardized. The reason is the negative relationship between the LS in which an animal is born and its own BW at mating in scenario A, whereas there is no relationship (b=0.04 g pup⁻¹, n.s.) in scenario B. In both cases there was a similar positive relationship between BW_D and LS_D. This highlights the importance of LS standardization (or possibly cross fostering) for the outcome of a selection experiment and explains why selection on high BW can also be accompanied by a substantially decreased LS, as reported in the experiment mentioned above (Bünger et al. 1992). These authors report a non-significant regression coefficient between the LS of the mother and offspring BW42 (b=0.05 g pup⁻¹) in a control kept in scenario B, but b=−0.75 g pup⁻¹ for male BW42 and b=−0.53 g pup⁻¹ for female BW42 in scenario A. Under these conditions, the selected/heaviest animals always came from very small litters and selection was mainly in quadrant IV of figure 1, resulting in heavier animals with smaller LS.

Figure 2.

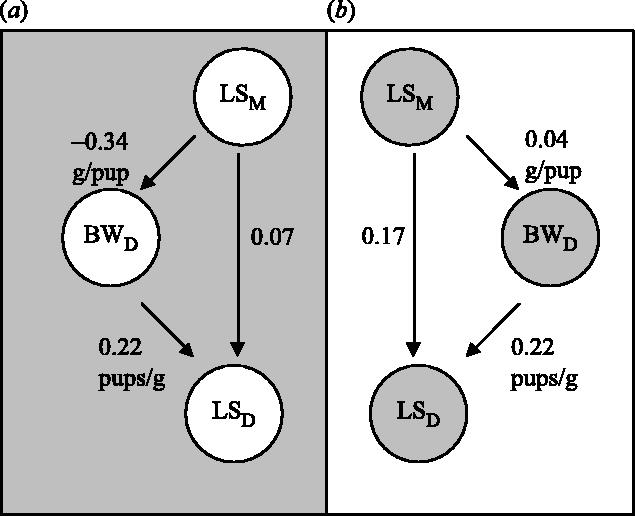
Path diagram and standardized partial regression coefficients between LS of the mother (LS_M), BW of the daughter (BW_D) and the LS of the daughter (LS_D), (a) without (Falconer 1955) and (b) with (Eisen 1970) standardization of the rearing LS.

As can be expected from the correlated response in LS from growth selection described above, estimates of the genetic correlation vary but are usually positive and quite high. Estimates in unselected control or in base populations were 0.89 (Rahnefeld et al. 1966), 0.58 (Hanrahan & Eisen 1974) and 0.63 (Eisen 1978), and realized genetic correlations were mostly of similar size: 0.60, 0.65 (Doolittle et al. 1972), 0.82, 0.25 (Wilson 1973), 0.27 (Bakker et al. 1974), 0.35 (Eisen 1975) and 0.52 (Eisen 1978). Eisen (1978) applied index selection to select against the genetic correlation; that is, selecting for high BW and low LS in one line and for low BW and high LS in another line (selecting in quadrants IV and I in figure 1). Although the observed responses (especially in LS) deviated from the expected results, the experiment showed that both traits can be shifted in the desired direction, indicating some independence.

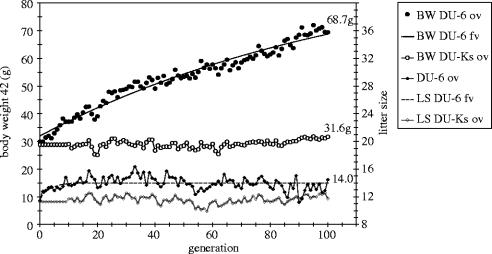
There is also substantial variation in the magnitude and duration of the correlated responses. Whereas MacArthur (1944) and Falconer (1955) observed a correlated response only in the first five or six generations, Rahnefeld et al. (1966) reported a correlated response over 29 generations with no substantial deviation from linearity, resulting in a total increase of LS of approximately three pups. The long-term growth selection in Dummerstorf (figure 3) illustrates the development of direct response in BW and the correlated response in LS0. The estimated half-lives (time when half of the total selection response is reached) for BW and LS were 78 and 2.4 generations, respectively, indicating that most of the correlated response is observed early, in which LS increased in DU-6 from 11.7 to 14 pups. The control (DU-Ks) and the selection lines were maintained such that inbreeding would accumulate at a similar rate in both lines, so the decrease in LS in the period from about 80 to 100 generations is presumably not due to inbreeding, unless there is a line by inbreeding interaction. From this perspective, it is obvious that an initial positive genetic correlation between BW and LS decreases to close to 0, indicating that the two traits can become uncorrelated in high growth lines. This is supported by other experimental evidence, in which it has been shown that continued selection may cause realized genetic correlations to be reduced and even to change sign (Eisen 1974). This author reported a positive genetic correlation between BW gain from 21 to 42d (BWG 21–42) and LS in generations (G) 0–14 (r_g=0.35±0.06), but not in G15–27 (r_g=0.03±0.2). It can be assumed that there is initially a number of segregating loci with positive pleiotropy for BW and LS and that these loci may approach fixation for the desirable alleles, explaining the decrease of the genetic correlation.

Figure 3.

Body weight and litter size in lines DU-6 (selected on BW 42) and DU-Ks (unselected control line). The selection experiment is described in detail elsewhere (Bünger et al. 1983, 1998, 2001a). A modified exponential model (Bünger & Herrendörfer 1994) was fitted to the generations means. ov, observed values; fv, fitted values.

A genetic correlation coefficient is a statistical estimate that can result from different biological causes (pleiotropy, linkage or drift) and it is important to identify (if possible) the cause of the correlation as each has different implications. If the genetic correlation is based on pleiotropic effects of certain genes, it would mean that these genes are involved in the physiological regulation of both trait complexes as discussed by Brien (1986). If loose linkage is responsible for the genetic correlation, one would expect that the association will disappear as a consequence of recombination events. Close linkage and pleiotropy are difficult to distinguish based on the degree of correspondence between the recently known approximate genomic locations of QTLs for LS and BW. This situation will not change until further finemapping has substantially narrowed the intervals or, more ideally, identified the causal molecular genetic polymorphisms. Compared with the vast amount of QTL for growth traits (reviewed by Corva et al. 2001; Brockmann & Bevova 2002), there are only a few studies on fertility traits in mice available (Kirkpatrick et al. 1998; Spearow et al. 1999; Peripato et al. 2002, 2004; Rocha et al. 2004). Whereas the papers by Peripato et al. highlighted the importance of epistasis as a substantial component of the genetic architecture of litter size and other fertility traits, the two other experiments (Kirkpatrick et al. 1998; Rocha et al. 2004) found strong overlaps of some growth QTL and litter size QTL, indicating pleiotropic or linked QTL for growth and fertility, which corresponds very well with the observed genetic correlations. The greatest difficulty in distinguishing pleiotropy and linkage is due to the relatively imprecise QTL localization achieved to date and due to a lack of the understanding of a common physiological basis between both trait complexes. The most recent and comprehensive presentation and discussion of congruencies between growth and fertility QTL can be found in the paper by Rocha et al. (2004).

To elucidate the importance of drift on variation in direct and indirect selection responses, replication of selection lines has been employed (e.g. Falconer 1973; LaSalle et al. 1974). A similar approach is to look at the BW versus LS relationship in several divergent growth lines selected in different laboratories, but measured in the same environment. This has become possible, because several mouse lines, selected generally for divergence in growth traits, were introduced about 10 years ago into the Edinburgh laboratory (Bünger et al. 2001a). Their female BW values at 70d and LS are plotted in figure 4 and there is a positive relation between both traits. Correlation and regression coefficients calculated from generation means, based on approximately 2100 and 5500 observations in total for LS and BW, are r=0.84 and b=0.10 pups g⁻¹, respectively (figure 4).

Figure 4.

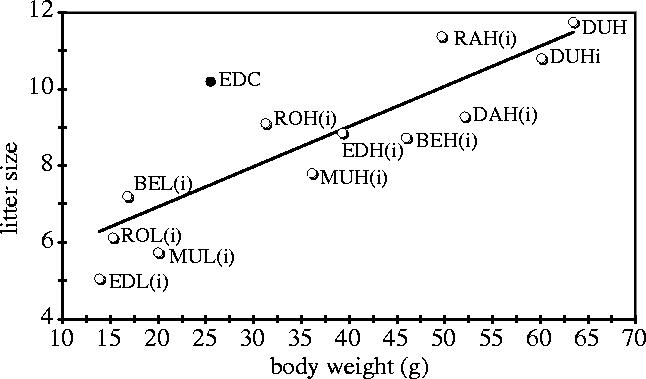
Relationship between female body weight at 70d and litter size based on divergently selected growth lines and an unselected control line (EDC). The means pooled over G4 to 14 are presented. Line description and experimental details are given elsewhere (Bünger et al. 2001b). An ‘i’ indicates inbred, and if shown in brackets, the value comprises data before inbreeding by full-sib matings and from the early inbreeding generations. As there are no obvious inbreeding effects, data from both periods have been pooled. It is of note that inbreeding has accumulated in all selection lines during the selection, but inbreeding in EDC is negligible as it was recently developed from a cross of several control lines.

(c) Inbreeding effects

It is of note that inbreeding, which accumulated during the periods of intense or later relaxed selection in the selection lines, possibly has a strong effect on LS because the difference between the high lines and the outbred control (EDC) is relatively small. For example, the inbreeding coefficient in the DUH and DUHi line is expected to be well over 70%. Using a recent estimate of inbreeding depression of −0.72 pups per 10% inbreeding (Holt 2004) one could expect LS to be about five pups higher if inbreeding were eliminated, which would increase the LS to a level of approximately 16 pups in figure 4. Furthermore, there are obvious deviations from the common regression line, indicating line-specific relationships, as if the ‘RAH are smaller than expected for their LS’ and ‘EDL is still larger than expected for their LS’. In addition, there is no indication of a nonlinear relation in these data although they comprise a very wide BW range (the smallest (EDL) being 13.8 g and the heaviest (DUH) being 63.4 g).

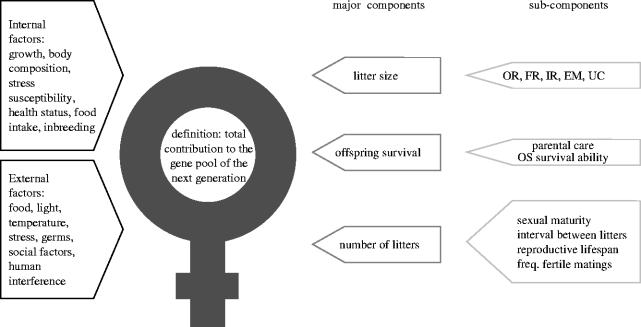
(d) First parity litter size, its components and importance for the reproductive fitness

First parity LS is an important part of the size of all litters in the lifetime of a female, or in other words, her total reproductive output or reproductive fitness, and is itself the result of several sub-components (figure 5). It is usually assumed that the number of corpora lutea determines the maximum number of young born, although there are cases in pigs where the number of embryos exceeded the OR, implicating the presence of monozygotic twinning (Ashworth et al. 1990). However, studies in mice based on DNA fingerprinting showed that this is a very rare event (McLaren et al. 1995) and therefore OR generally sets an upper limit for number of pups born. Ovulation rate is largely influenced by gonadotropins, steroid hormones, growth factors, prostaglandins, and other factors that act and interact to control follicular growth, maturation, and ovulation (Spearow et al. 1999). The fertilization rate, the implantation rate, the embryonic mortality and the uterine capacity are also of importance (figure 5).

Figure 5.

Components of female reproductive fitness (adapted from Bünger 1979). OR, ovulation rate; FR, fertilization rate; IR, implantation rate; EM, embryonic mortality; UC, uterine capacity; OS, offspring.

To characterize the relationship between BW at mating (BWM) and OR or LF (number of live foetuses), the results of two growth-selection experiments involving seven lines (four high, two control and one low growth lines) with a larger range in BW were plotted (figure 6). It is of note that LF is usually measured at 18d post coitum, which differs only slightly from LS because of very late prenatal and perinatal losses. This figure shows that (i) the relationship between BW and OR seems to be nonlinear, (ii) the correlation between OR and BW is higher than between LS and BW, and (iii) both curves diverge with increasing BW, indicating a higher prenatal mortality with increasing BW or OR. An inbreeding effect on these results cannot be totally dismissed here, but seems of minor importance since the ED lines were selected for a short time only (< 10G) and the DU-lines were in generation 45 (G45) without any obvious inbreeding depression (figure 3).

Figure 6.

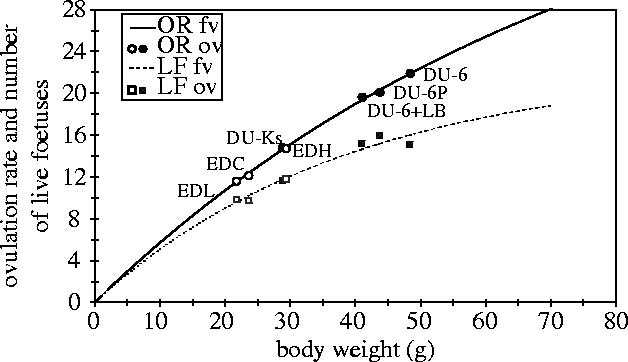
Relationship between female body weight and ovulation rate (OR) and number of live foetuses (LF). White symbols: females from G9 and 10 from an Edinburgh selection experiment with selection on high and low lean amount (EDH, EDL, EDC=control, formerly P-lines; Brien et al. 1984). Black symbols: females from 3 growth selected lines (DU-6+LB, DU-6P, DU-6) and an unselected control line (DU-Ks), 60 females per line, G45) from the Dummerstorf growth-selection experiment (Bünger et al. 1994, 1998, data on OR and LF were taken from an unpublished research report by Bünger et al. 1987).

In figure 7, similar results as in figure 6 are illustrated regarding nonlinearity and higher prenatal mortality with increasing BW or OR, but based on a wider set of lines and including additional line crosses. The relationship between BW and OR or LF in females mated to males from other lines (outbred embryos) was similar to that in females mated to males from the same line (inbred embryos). Therefore, they were not differently marked in figure 7. If the females themselves were crossbred and were mated to crossbred males, their OR apparently does not deviate from a common regression curve; however, the number of LF (especially at a higher BW) was higher than expected from a common nonlinear regression and therefore a specific curve was fitted for them (figure 7, curve in the middle). This indicates that the BW to OR relationship is not affected by inbreeding and that the OR of females can be well predicted from their BW. It also shows that a part of the divergence between the OR and LF curves (perinatal mortality) is due to inbreeding in the mothers, as LF is lower in inbred females. In both outbred and purebred females there is an increased divergence between OR and LF for higher BW, indicating higher prenatal mortality with increasing BW. This amounts at a BW of 70 g, for example, to prenatal mortalities of 46 and 22% in purebred and outcrossed females, respectively.

Figure 7.

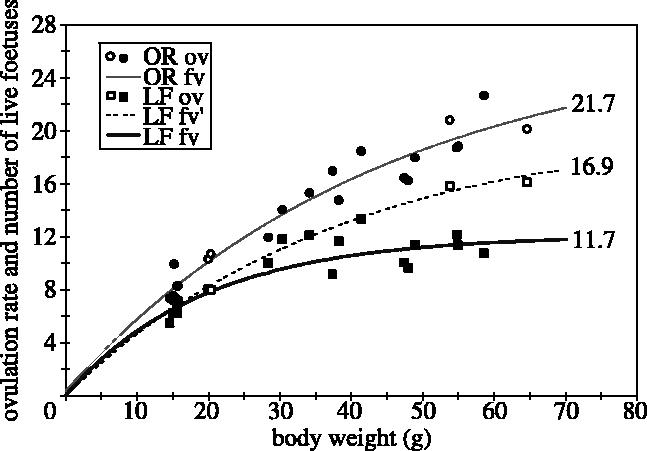
Relationship between body weight at mating and OR and number of life foetuses (LF) based on the same lines as in figure 4 (G15 and 16), one-way (OWC) and two-way line crosses (TWC) and a control line. OWC: purebred females mated to males of other lines ((H(igh) by H, H by L(ow) and L by L to remove inbreeding from the embryos/foetuses; one-way cross). TWC: (open symbols): matings of F and M derived from OWC with their specific regression line (dashed line). ov and fv: observed values and function values. Experimental details and data were given elsewhere (Wahlroos 2002; Wahlroos et al. 2002).

Body weight is a complex composite trait composed of the carcass tissues of muscle and fat, skeleton and organs. Each of these body components can be differentially affected by selection for growth (recently reviewed by Bünger & Hill 2005). Without detailed phenotypic measurements of these traits, it remains unclear which of the body compartments, for example, fat and non-fat tissue in a simple two-compartment model, are actually primarily associated via pleiotropy or close linkage with the fertility traits (OR and LS). It is known that the selection lines described above differ substantially in several aspects of body composition (Bünger et al. 2001a), especially in their fat content. Therefore, some of the variation around the common regression line and some variation in estimated genetic correlations between BW and LS or OR, given in the literature, could possibly be explained by variation in body composition and conformation, but this has not been investigated yet. The future use of high-throughput in vivo scanning methods like computer tomography or similar technologies (e.g. Bünger & Hill 2005) might facilitate such experiments, which could dissect further the BW versus fertility relationships and their genetical basis.

(e) Correlated effects of litter size selection on body weight

There are fewer experiments of selection on LS compared with selection on growth (reviewed by Joakimsen & Baker 1977) but, as expected from the previous section, the correlated change in BW usually follows the direction of selection in LS, and there is substantial variation in magnitude and duration. This seems to be affected by the same complex relationships of mother LS with daughter BW and LS (figure 2), implying that a standardization of the rearing LS has a substantial effect on the correlated response. This could explain why there were only small correlated effects in BW when selection was on high LS without standardization (Bakker et al. 1978). Although LS increased considerably by 5.8 pups, the correlated effect in BW was negligible. This means that selection was on females that realized high LS without an increase in BW (selection in quadrant I; figure 1). Experiments undertaken with standardized LS, on the other hand, usually result in a substantial increase in LS and in a correlated response in BW (Eisen 1978). This author concluded that the LS standardization avoids the masking of the expression of pleiotropic loci influencing both traits.

Two very long-term selection experiments were carried out, one (experiment 1) without LS standardization (Dummerstorf, Germany; Schüler 1982; Renne et al. 1998; Langhammer & Renne submitted), and the other (experiment 2) with LS standardization (Ås, Norway; Joakimsen & Baker 1977; Vangen 1993; Holt et al. 2004). In experiment 1, selection occurred for more than 130 generations (G) using an index combining LS0 and litter weight (LW0) at birth (I=1.6 LS0+LW0). The responses in LS and BW are presented by pooling the generations means for one of the two Dummerstorf fertility lines (FL2) over the latest (G126 to G131) generations (table 1, left; Langhammer & Renne submitted). The second experiment (experiment 2), in which selection was based on high LS0, was run for over 110G (table 1, right; Holt et al. 2004). In experiment 1, LS and BW increased both significantly by 7.4 pups (64%) and 4.1 g (13%), respectively. The correlated effect on BW is relatively small, indicating that selection favoured females from quadrant 1 (figure 1). In experiment 2 with LS standardization, both traits were substantially increased. LS and BW were higher by 10.3 pups (91%) and by 13 g (39%), respectively. In this experiment most of the animals were probably selected from quadrant 2, according to the genetic correlation of both traits.

Table 1.

Litter size at birth (LS0), body weight at mating (BWM), ovulation rate (OR) in two fertility lines (FL2: Dummerstorf, on the left; H, Ås, on the right) and the unselected controls

	FL 2			C			FL2–C	FL 2/C	H			C			H–C	H/C
	n	m	s.d.	n	m	s.d.	n	m	s.d.	n	m	s.d.
LS0	402	18.9	3.6	1118	11.5	2.5	7.4	1.64	107	21.6	4.1	104	11.3	4.2	10.3	1.91
BWM	411	34.9	2.8	1191	30.8	3.1	4.1	1.13	53	46.1	2.8	54	33.1	3.0	13.0	1.39
OR	—	—	—	—	—	—	—	—	98	32.7	3.9	84	16.3	3.8	16.4	2.0
LS21	337	11.4	3.4	1073	10.3	2.4	1.1	1.11	—	—	—	—	—	—	—	—

Data for FL2 and C pooled over generations 126–131 and 127–132, respectively. Data for H from generations 110–112; further explanation in text. Matings in exp. 1 and 2 at 9 and 10 weeks, respectively.

Rough estimates of the realized genetic regression of LS on BW from these two experiments are 1.8 (experiment 1) and 0.79 pups g⁻¹ BW (experiment 2), which are much higher than values (0.31 or 0.34 pups g⁻¹) reported by Eisen (1978) or the realized genetic regression of OR on BW (b=0.4 ova g⁻¹) found by Land (1970). These findings probably reflect in experiment 1 the selection in scenario A, which favours rather ‘normal sized’ females with high LS (figure 2); from the direct response in LS and the coefficient of regression given by Eisen (1978), one would expect in FL2 a BW of approximately 54 g, but in actuality, females are just 35 g. Another cause for these overestimated values might be that the genetic correlation has decreased, as described in the previous section during growth selection. This could be responsible for a further direct response in LS without associated increase in BW, as the realized BW in experiment 2 is 46 g, compared with an expected BW of approximately 65 g.

Two other aspects are of note. First experiment 2 indicates that the selection response in LS was mainly due to an increased OR (+16, 100%) with a small difference in prenatal mortality (H: 34% versus C: 31%). Again, from the high-control difference in BW (13 g) and assuming a genetic regression of LS on BW (b=0.32 pups g⁻¹, figure 1; Eisen 1978) or OR on BW (b=0.4 ova g⁻¹; Land 1970), one would only expect increases in LS of 4.2 and 5.2 pups, indicating that base populations estimates are not useful for the prediction of direct and correlated response in the longer term. Second, data on LS at weaning from experiment 1 show that the difference in FL2 versus C diminishes drastically at weaning from 7.4 to 1.1 pups, indicating the high postnatal/preweaning losses in FL2 (table 1). An estimate for postnatal or preweaning losses cannot be obtained from experiment 2 because the LS was standardized to eight pups at birth. There are several possible explanations for the high losses in experiment 1. Essentially, females selected in experiment 1 (scenario A) are characterized by a high OR with a nearly constant prenatal mortality, but there is no selection pressure for high LS21 or for high preweaning survival, and possibly even the contrary applies. According to the relationships in figure 1, females would need to grow bigger to yield a larger LS. However, because of the negative relationship between LS_M and BW_D in scenario A (figure 2), a female will be retarded when born and raised in a large litter, unless postnatal losses are so high that the LS is ‘standardizing itself’; such appears to be the situation seen in FL2. In other words, selection without standardizing LS may place selection pressure on high postnatal losses to reach the selection goal—an increase in LS0. Recently, partial standardized regression coefficients were calculated for FL2 and the control using data from generations 126 to 131/132 (Langhammer & Renne submitted), as shown in figure 2. Interestingly, the LS_M versus BW_D coefficient was 0.04 g pup⁻¹ (n.s.) in FL2 and −0.2 g pup⁻¹ in the control, supporting the former findings, and the BW_D versus LS_D coefficients were 0.15 and 0.3 pups g⁻¹ in FL2 and the control, respectively, similar to the values given in figure 2.

(f) Litter size and reproductive fitness

The available space does not permit discussion of the effects of selection for BW or LS on the total reproductive fitness of females (figure 5) and on that of males, although there are a few studies on mice published on this subject. For example, a lifetime study on the Dummerstorf fertility lines (experiment 1) showed that the direct selection response in first parity LS is counterbalanced by antagonistic effects on life expectancy, the length of reproductive life and the total number of pups born (Schüler & Bünger 1982). The decreased preweaning survivability (table 1) removes most of the benefit of an increased LS at birth before weaning.

5. Conclusions

(a) Body weight and litter size in different species

A comparison of highly divergent strains/breeds/variants in several species (fishes, dogs, rabbits, sheep, pigs, mice) suggests a positive relationship between body size or weight and LS or fecundity. However, there are a number of deviations from such a general pattern, indicating a substantial genetic plasticity allowing for the development of breed-/variant-specific reproductive strategies and relationships. In breeds of farm animals that have undergone selection there seems to be only a weak positive, zero or even a negative genetic relationship between BW and LS. Given the reduction in size of the initially positive genetic correlation between these traits in mice with selection, one can assume that a positive correlation might also have originally existed in farm animals at the beginning of domestication. However, during domestication and with intense selection, the correlation has been reduced by a rapid fixation of loci having positive pleiotropic effects on both traits.

(b) Body weight and ovulation rate in model animals

Mouse experiments have shown that the genetic correlation between BW and OR seems to be stronger and tends to hold over a wider BW range than that between BW and LS. It also seems not to be affected by a slow accumulation of inbreeding, whereas inbreeding reduces the number of live foetuses, which can be regarded as an approximate in-utero measure for LS. Thus BW is a better predictor of OR, and suggests there are loci having pleiotropic effects on both traits. These effects on growth regulation and OR are perhaps mediated hormonally, an issue that is discussed in detail elsewhere (Brien 1986). Another possibility is that some genes contributing to large BW will also increase the size of the ovary and anterior pituitary gland, which could mean more hormone secretion and therefore a higher OR as discussed by Roberts (1979). The close relationship between BW and OR could also explain the fact that h²_OR (closer to the h²_BW) is usually much higher than h²_LS (e.g. h²_OR=0.36±0.04 versus h²_LS=0.11±0.05; Remus 1979). An overlap of some QTL affecting LS and BW (e.g. Kirkpatrick et al. 1998) might indicate loci affecting primarily OR and BW. In general, this implies that prenatal mortality increases with higher BW, since OR is anticipated to increase with BW, whereas the genetic correlation with LS tends towards zero. However, it has been shown that the genetic relationship between OR and BW can also break down during selection allowing for relative independent development, as seen in the long-term in fertility-selected mice, especially when selected without LS standardization (experiment 1) and when extreme values are reached (experiment 2).

(c) Litter size as an indicator of reproductive fitness

Reproductive fitness in females is a very complex trait and its components (figure 5) can be affected by selection in different ways. To extrapolate from observations on one of its components, for instance, LS at first parity in females, to the total fitness can be very misleading and must be avoided until the relationships between all the different components of the fitness are fully explored. Quantifying the total reproductive output of a female throughout its lifetime is both time and laboratory space consuming (even with the comparatively short lifespan in mice, a study requires approximately 2–3 years). However, since such studies can be carried out in mice under standardized laboratory conditions and since divergent selection lines of mice are indeed available, such studies should be more intensely used to systematically explore the effects of artificial selection for extreme expression of quantitative characters on the complex trait reproductive fitness.