Artificial selection and maintenance of genetic variance in the global dairy cow population

Abstract

Genetic improvement of dairy cows, which has increased the milk yield of cows in the UK by 1200 kg per lactation in 12 years, is an excellent example of the application of quantitative genetics to agriculture. The most important traits of dairy cattle are expressed only in females, but the main opportunity for selection is in males. Despite this, genetic improvement was achieved by the invention of a new statistical methodology, called ‘best linear unbiased prediction’ to estimate the breeding value of bulls. Intense selection of the best bulls, combined with the worldwide use of these bulls through artificial insemination and frozen semen, has created a global population and caused concern that the genetic variation available in the future will be reduced. Maintenance of genetic variation and long-term genetic gains would be aided by rational payment systems, use of crossbreeding where profitable, inclusion of all economically important traits in the breeding objective, recognition of genotype by environment interactions and the use of selection algorithms that balance estimated breeding value against the average relationship among the selected animals. Fortunately, all of these things are happening to some degree.

1. Introduction

Most of the traits of economic importance in livestock production, including dairy cattle, are quantitative traits, implying that traits are affected by many genes, along with environmental effects. Not surprisingly therefore, quantitative genetics has made an important contribution to the genetic improvement of cattle.

The traits of most importance in dairy cows, such as milk yield, are only observable in females, but the main opportunity for selection is in the choice of males. Therefore, it is not easy to genetically improve milk yield by the obvious strategy of selecting high producers and, as a result, the rates of genetic improvement were low until the 1970s. In fact, dairy cattle have other disadvantages from the point of view of the geneticist. Not only are most traits sex limited, but herd sizes were traditionally small, the reproductive rate of cows is low and the generation interval is long. Considering these disadvantages, it is a triumph of quantitative genetics that rates of genetic improvement in dairy cattle are now about 1% of the mean per year and comparable with far more favourable species such as wheat. Figure 1 shows the genetic trend in milk yield in the UK for both bulls and cows.

Figure 1.

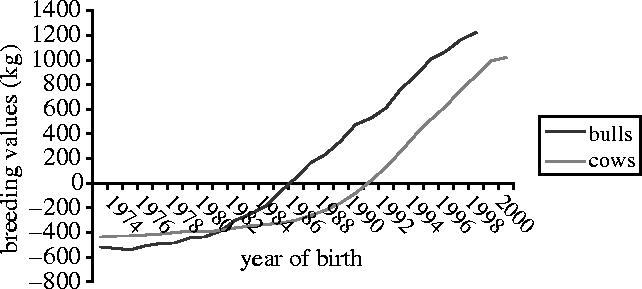
Genetic trend in milk yield (kg) for bulls and cows. (G. Swanson, personal communication).

This success of genetic improvement programmes for dairy cattle relies on three technologies. Since 1900, the milk yields of cows have been systematically recorded on a large proportion of dairy herds for the purposes of management and genetic improvement. Since 1950, artificial insemination (AI), combined with the use of frozen semen, has allowed bulls to be used in multiple herds and even across the globe. Since 1970, the statistical technique best linear unbiased prediction (BLUP) has been used to estimate the genetic merit or breeding value of bulls and cows, which has allowed the bulls and cows with the best genetics to be selected to produce the next generation.

Estimated breeding values (EBVs) are typically calculated within each country, using only that country's data. However, subject to quarantine laws, live cattle, embryos and especially frozen semen can be moved from one country to another and an international trade in semen has existed for years. Once dairy farmers became used to selecting bulls based on EBVs, they wanted to compare bulls from different countries. To accommodate this, the BLUP statistical machinery was further developed, and now bulls from 27 countries have EBVs calculated at the International Bull Evaluation Service (INTERBULL) in Sweden, combining information from each of these countries.

As a result of the use of international EBVs and international sale of semen, it became possible for the same few bulls to be widely used throughout all major dairy countries in the developed world. This caused alarm that the genetic diversity of the world dairy cattle population may be declining rapidly and led to research into the optimum method to select cattle to maximize genetic gain while maintaining genetic variation.

In this review, we consider the development of the statistical methods that drive the calculation of national and international EBVs and the design of breeding programmes that maintain genetic variation while using these EBVs to achieve genetic improvement.

2. Methods for national genetic evaluation of dairy cattle

The aim of predicting the breeding value or genetic merit of dairy bulls has been the catalyst for great statistical innovation. Techniques now widely used in statistics, such as BLUP (Henderson 1948; Henderson 1973), were originally developed to help dairy farmers select bulls. When considering the development of this technology, a theme emerges, in that the development of most statistical methodology for genetic evaluation has been motivated by limitations in the practical use of the available EBVs. Ingenuity by statisticians overcame these deficiencies, often by employing the rapidly increasing computer power. This cycle tends to be self-perpetuating because the removal of perceived weaknesses leads to greater use, greater genetic gain and the uncovering of new deficiencies. This cycle is illustrated in the history of the genetic evaluation systems below.

(a) Contemporary comparisons

Since the introduction of organized milk recording and AI, dairy cattle breeders have looked for tools to help them improve the genetic merit of their animals. The major difficulty in the use of phenotypic records of milk yield and other traits for selection is to distinguish the genetic value from the effect of environmental factors. Initially, bulls were evaluated by comparing the milk yield of their daughters with that of the cow's dam, but this is an inefficient way to use the data and did not adequately account for the environmental differences between herds and seasons. Overcoming this deficiency was a major reason for the development of the method called ‘contemporary comparisons’ (CCs; Robertson & Rendel 1954). In this method, the performance of daughters of a bull are compared with the performance of contemporaries of these daughters (i.e. cows of the same age) milking in the same herd, at the same time under the same conditions.

An assumption of the CC method was that all herds were of the same genetic merit. This may have been an acceptable approximation at first, but as selection on CCs caused genetic improvement, differences between herds and between years in genetic merit became greater. Various approximate methods were used to overcome this deficiency. Their aim was always to estimate how much of the differences in average milk production between herds was genetic and how much was environmental. For instance, improved contemporary comparisons (ICCs) (Milk Marketing Board 1974) were calculated for bulls using a regressed least-squares method, which took account of the estimated genetic merit of the sires of the contemporaries. However, it was the development of BLUP that largely overcame this problem.

BLUP built on an earlier method called the ‘selection index’, which is a method of estimating the genetic merit of an animal from measurements on the animal itself or its relatives (Hazel 1943). It is essentially a multiple regression equation. Selection index procedures have desirable statistical properties but assume that the adjustments for environmental factors (e.g. contemporary group) are known without error. This is rarely the case. In 1948, C.R. Henderson suggested replacing selection index techniques by BLUP (Henderson 1948).

(b) Best linear unbiased predictor

The milk yield of a cow (y_ij) can be described by a simple statistical model:

$$y_{ij}=h_i+s_j+e_{ij}$$ (2.1)

where h_i is the fixed effect of her contemporary group, s_j is the random effect of her sire and e_ij is a random error.

The s and e effects are assumed to be normally distributed with known variances. Estimating the h effects is complicated by the effect of the sires on the performance of their daughters that produced their records in these herds, and vice versa. In principle, the h effects could be estimated by generalized least squares, but this requires the inverse of a matrix the same size as the number of cows. Currently, this is not possible for a dataset comprising all the cows in a country and was certainly not possible with the computers of 1950. With known (or good estimates of) h, the milk yields could be corrected for them and sire effects estimated by the selection index method.

Henderson made several discoveries. The first was that by solving a set of so-called ‘mixed-model’ equations, he could get the same estimates for sire effects as by estimating the h effects using generalized least squares, and then using these estimated h effects to correct the y records and estimate s by selection index methodology. However, the mixed-model equations were only of the order of the number of sires, not the number of cows.

Henderson also showed that the sire estimates he obtained were the ‘best’ (i.e. had the lowest prediction error variance) in the class of linear, unbiased estimators. He meant unbiased in the classical sense, in that the fixed effect estimates were unbiased. In the simple model stated above, this simply means that the mean of all ŝ=mean of all s=0. However, the BLUP estimates have another property that is sometimes called ‘unbiased’ and is always very useful. This derives from the regression nature of BLUP estimates and it is E(s|ŝ)=ŝ. That is, if you consider a large group of bulls whose EBV calculated by BLUP is +100, then the true breeding value of some of these bulls will be greater than 100 and some will be less than 100, but the mean true breeding value of the group will be 100. To achieve this property, BLUP EBVs are ‘regressed back towards the population average’ compared with a least-squares estimate that treats s as a fixed effect.

The early sire models assumed that sires were unrelated and mated at random to dams sampled from the same population. These assumptions are clearly unrealistic, and in 1975, Henderson suggested an extension to the simple sire model that used relationships between sires to increase the accuracy of sire evaluations (Henderson 1975).

Initially, BLUP sire models, as described above, were used to predict the genetic merit of bulls but they did not generate evaluations of cows. Typically, EBVs for cows were calculated using selection index methods. For instance, cow genetic indices (CGIs), based on up to five lactations and including a herd genetic level to allow comparisons across herds, were introduced in the UK in 1981 (Hill & Swanson 1983). The CGI was a selection index that included the genetic merit of the sire, the CGI of the dam and the cow's own milk records.

A sire model, ignoring any relationships between sires, assumes that neither selection nor inbreeding has taken place and genetic means and variances are constant, and including relationships between sires only partly accounts for selection among sires. To address these deficiencies, sire models have largely been replaced with a statistical model called an ‘animal model’. In an animal model, the statistical model (2.1) described above, is replaced by

$$Y_{ij}=h_i+a_{ij}+e_{ij},$$

where the a_ij are the breeding values of individual cows and the correlations between them are described by a matrix of relationships (the additive genetic relationship matrix, or A matrix), which assigns animals to their parentage and is twice the matrix of kinship coefficients. Use of the relationship matrix can account for changes in genetic means and variances resulting from selection and inbreeding. Currently, most countries use an animal model BLUP procedure in their national evaluation systems for a number of livestock species, including dairy cattle, beef cattle and sheep.

Although BLUP was first widely used as a selection tool for animal breeders, its usefulness has now been extended to the analyses of many quantitative traits in diverse populations. BLUP is routinely used to predict future performance of many crops (Xiang & Li 2001; Yan et al. 2002) including fruit trees (De Souza et al. 2000) and BLUP has greatly enhanced our understanding of natural populations (Merila et al. 2001; Kruuk 2004).

(c) Direct analysis of testday milk yields

Dairy cattle production traits are traditionally expressed as 305 day lactation yields, where the 305 day yield is calculated from up to 10 daily measurements (testday records) taken at approximately 30 day intervals.

Genetic evaluation systems based on 305 day milk yield take no account of circumstances affecting individual testday yields (e.g. extreme weather conditions or medical treatment), and assume that all tests are equally affected by any management treatment. There is no opportunity to include information on events that may occur during the course of the lactation (e.g. pregnancy) and part lactation information must be projected to 305 day yield before inclusion.

Therefore, it is logical to use the yields on individual testdays as the data for the statistical analysis instead of the derived lactation yield. The system used in Australia has done this since 1983 (Jones & Goddard 1990). Like so many other improvements to the method of calculating EBVs, full use of testday data requires increased computational power.

(d) Multiple trait models

The selection of animals as parents of the next generation is usually based on more than one trait. For example, most dairy cattle profit indexes include milk yield and composition, longevity and health (Juga et al. 1999; Pederson et al. 2002). The optimum method of evaluating animals is a multiple trait analysis, which takes into account the phenotypic and genetic associations between the traits. Henderson & Quaas (1976) were first to employ a multiple trait BLUP procedure.

Advantages of multiple trait analysis include an increase in the accuracy of the evaluations and the ability to include traits on which selection has been based and so reduce bias. The increase in accuracy of EBVs is greatest when availability of phenotypic measurements is limited for one trait but a correlated trait has been recorded. For instance, length of herdlife is unknown on cows that are still alive but they can have records on conformation traits that are correlated with herdlife.

Multiple trait BLUP is useful in another context as well. Sometimes, what appears at first as a single trait turns out to be multiple traits. For instance, milk yield late in lactation is not genetically the same trait as milk yield early in lactation although the two are highly correlated. If some cows have milk yield recorded only in early lactation, then only a multiple trait analysis (treating early and late lactation yield as different but correlated traits) will correctly predict their milk yield in late lactation.

(e) Random regression models applied to dairy production

If, as is typical, milk yields are recorded on one day per month, then the division of the lactation into early and late seems arbitrary. Random regression models, first proposed as being suitable for the evaluation of testday yields by Schaeffer & Dekkers (1994), provide a more realistic model. They assume that the shape of each cow's lactation can be modelled by a smooth curve and that the parameters of that curve show genetic variation. This means that the variation in shape is smooth with no arbitrary changes from early to late lactation.

The random regression testday model includes a fixed regression to describe the general shape of the lactation curve and individual cow regression coefficients (treated as random effects with known variance) to allow variation from this curve for individual animals. Many parametric curves have been proposed as models for the lactation curve (Guo & Swalve 1997). Legendre polynomials evaluated at time t, conventionally defined in the range −1≤t≤+1 and orthogonal within this range, are a flexible choice, widely used to model both the overall fixed curve and the random deviations from this curve.

Fixed curves can vary depending on many factors, e.g. the parity of the animal, the age at calving, month of calving, and variation in contemporary group (i.e. herd testday) effects across time can also be accommodated. In the UK model, the contemporary group effect is allowed to depend linearly on days in milk, with an intercept and slope for each of milk, fat and protein. Variation in intercept and slope is treated as fixed between herds and random within herds.

3. International evaluation of dairy cattle

(a) Background

Increased across-country trade in semen, embryos and livestock, primarily to improve production, has resulted in a need for breeders to have a tool that will allow them to accurately compare animals both within and across countries. Different countries use different scales to measure traits, and may measure slightly different traits. For example, when assessing the conformation of dairy cows, some countries measure ‘foot angle’, defined as the angle of the front of the hoof to the ground, whereas others use ‘heel depth’, which is the height of the heel from the ground. Furthermore, genetic variances and heritabilities may differ across countries. INTERBULL was set up in 1983 as a non-profit making organization with a remit to promote the development and standardization of international genetic evaluations for dairy cattle. At present, INTERBULL deals exclusively in bull EBVs.

(b) Multiple across-country evaluations

To compare bulls in different countries, a combined analysis of all the raw data from different countries might be desirable, but has not been considered practical. In order to mimic an international BLUP without the use of raw data, Schaeffer (1994) proposed a multi-trait linear model approach, which uses as data the average yield of a bull's daughters corrected for fixed effects in each country (so-called daughter yield deviations; DYDs). Milk yield in each country is treated as a different trait; genetic correlations between these traits describe differences between countries and are used in the linear model to generate for each bull an EBV for each country. This model allows animals to rank differently in each country to reflect any genotype by environment interaction.

Because genetic evaluation methods vary between countries, and DYDs are often difficult to estimate, Banos et al. (1993) suggested employing deregressed bull EBVs rather than DYDs. National BLUP procedures regress bull EBVs back to the mean, depending on the amount of information in the EBV, so as they stand, the bull EBVs cannot be used directly as data in the multiple across-country evaluations (MACE) analysis. Deregressed EBVs are calculated from national EBVs (Fikse et al. 1995) and use the relationship matrix between sires to remove the contribution of male relatives to bull EBVs leaving only the contribution from daughters.

(c) Genotype by environment interaction (G×E)

In a multiple trait approach, genetic correlations between the traits must be estimated before breeding values are predicted. For the MACE procedure, several factors can cause estimates of genetic correlations between milk yield to be less than 1.0, including differences in trait definition, environment, management practices, and differences in national evaluation systems. For the MACE system, the estimation of these correlations presents some problems. With so many countries (traits) participating, the computing resources required are huge. In addition, for some traits, there are tenuous genetic links across countries, particularly in the evaluation of the specialist breeds. To get the best estimates of correlations between the countries, well connected subsets of the sires are used. The definition of ‘well connected’ can vary depending on the breed and traits being evaluated, but would typically include bulls that have proofs in more than one country, plus bulls that are members of full-sib groups with proofs in more than one country (Klei & Weigel 1998).

If the genetic correlation between milk yields in two countries is 1.0, then the correlation between EBVs calculated independently in the two countries should be r₁*r₂, where r_i=correlation between the EBVs from country i and the true breeding value (called the ‘accuracy’ of the EBV). Therefore, if the observed correlation between EBVs from different countries is less than predicted from their accuracies, then the genetic correlation between the two countries is estimated to be less than 1.0. Because any failure of the assumptions of the statistical model used to calculate EBVs tends to cause them to be less accurate than their computed accuracies, there is a natural tendency for estimated genetic correlations to be less than 1.0. Although the method of estimating genetic correlations is more complicated than this over-simplified description, the same bias occurs. This may explain the observation that the estimated genetic correlation between many countries with very similar dairying environments (e.g. Holland and Germany) is about 0.95. However, correlations lower than this probably represent real G×E. The lowest correlation (about 0.8) is between countries that rely heavily on grazing to feed the cows, and countries that do not. Whether this G×E is caused by the grass diet specifically, or whether it is simply a reflection of the lower nutritional status usually provided by grazing, is unknown.

It is known (Hayes et al. 2003) that the genetic correlation between herds with high and low production within a country is about 0.8. (This difference in production is mostly caused by differences in the level of nutrition.) However, recently, we (Hayes et al. 2004) found that data from low-producing US herds did not predict performance in Australian herds any better than data from all US herds. This suggests that reranking of sires between Australia and USA is not simply due to the lower production level in Australia, but could be partly due to other environmental differences such as use of grazing.

(d) Bull breeding value prediction

In 1994, INTERBULL started to offer a MACE service for production traits. Originally, only four countries submitted data, but the following year, 10 countries participated. MACE evaluations for conformation traits followed, and longevity, direct and maternal calving ease and direct and maternal stillbirth are the latest traits to be included. Bull evaluations were originally restricted to the Holstein, as this breed has the best connections across countries. In 2004, INTERBULL provided breeding values for Ayrshire, Jersey, Guernsey, Brown Swiss and Holstein bulls. International breeding values for milk, fat and protein yield are produced for around 80 000 Holstein bulls, and more than 72 000 Holstein bulls obtain breeding values for a wide selection of conformation traits. Even for a (numerically) small breed such as the Guernsey, 800 bulls have international production breeding values and around 600 of these also have conformation evaluations.

Research is underway on the possibility of providing an across-country evaluation for female fertility and currently, more than 25 countries participate for production, 21 for conformation and 12 for udder health. It is now possible for a dairy farmer in, say, the Czech Republic, to consult a list of EBVs that rank virtually all the Holstein bulls available in the world for the predicted profitability of their daughters in the Czech Republic. This is despite the fact that most of these bulls have no daughters in the Czech Republic.

(e) Using phenotypic records in international evaluations

Currently, international genetic evaluations allow the comparison of bulls across countries, but not of cows. In addition, the pedigree information on the bulls is restricted to his sire, maternal grandsire and the genetic group of the maternal granddam. The bull's dam and her ancestors are ignored. To address these limitations, a global animal model using lactation or testday data from participating countries is under investigation (Canavesi et al. 2001). However, many concerns have been raised. How does one handle such a large dataset? What is the best method of parameter estimation? How should fixed effects be defined? Political concerns about making national evaluations redundant and keeping all countries involved in the decision-making process have meant that progress has been slow, but currently the Nordic countries merge their production data (Pederson et al. 2001) for a joint evaluation, as do Austria and Germany.

(f) Borderless evaluation

G×E exists within a country as well as between countries. For instance, the genetic correlation between milk yield in high- and low-producing herds is typically 0.8 to 0.9. It seems probable that genetic correlations between some herds within a country could be less than that between similar countries. Lohuis & Dekkers (1998) first proposed grouping herds based on similarities between them, irrespective of their country borders. Weigel & Rekaya (1999) analysed 4.6 million lactation records from eight countries and five US regions, clustering herds based on 13 variables including herd size, average age at first calving, latitude and altitude. Five clusters were sufficient, each containing herds from 5 to 11 countries or regions. Genetic correlations between three of these clusters were high (0.96–0.97) and all correlations were greater than 0.80. Zwald et al. (2003) expanded the analysis to encompass more than 16 million first lactation-production records from 17 countries. Herds were clustered into seven groups, reducing the number of traits from 17 to 7. However, there is no guarantee that the herds within a cluster have genetic correlations with each other of 1.0. For instance, herds in Poland and in Australia have a similar production level but the genetic correlation between these two countries is only 0.85 (INTERBULL).

Borderless evaluations yield different EBVs for each cluster group, rather than each country, and depending on environmental and management differences within a country, borderless evaluations could yield different EBVs for different herds within a country. MACE assumes that environments are similar within a country and differ between countries, so that the number of traits equals the number of countries. Borderless evaluations are appealing because this assumption is no longer employed and the number of traits is taken as the (reduced) number of environments or clusters. Whether breeding companies and users of breeding indexes would be happy with borderless evaluations is unclear, but certainly within country estimates of environmental sensitivity are being sought by breeding companies, so that they can target their bulls to the appropriate environment. Before borderless evaluations could be implemented, we need to show that herds within a proposed cluster have a genetic correlation of nearly 1.0.

(g) Effects of selection

In the UK, breed substitution has taken place over the last 30 years and what was predominantly a Friesian dairy cattle population is now, on average, 90% North American Holstein (figure 2).

Figure 2.

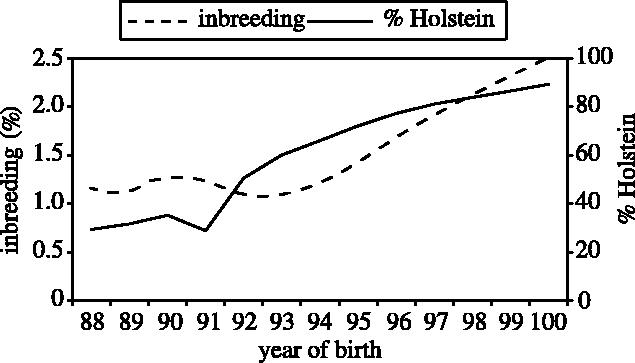
Average proportion of inbreeding and proportion of Holstein in dairy cattle from 1988 to 2000. (From Wall et al. in press.)

Economics has forced breeders to select heavily for production traits and milk yield per cow has increased in all major dairying countries (figure 1). Negative genetic correlations between milk yield, fertility and disease resistance mean that selection for yield has led to a decrease in fertility and health, and worldwide, fertility and lameness problems have become more frequent (Haile-Mariam et al. 2004). More complete selection objectives and EBVs for fertility and disease traits are now halting this trend, so that the genetic trend for fertility and health is fortunately not continuing downwards.

Inbreeding results from the mating of related individuals and is also increasing (figure 2). Inbreeding in the UK currently stands at around 3% and is rising at 0.17% per year. Although inbreeding is not currently considered a problem, if it continues to rise at the same rate, then it will become a real problem in the future (Wall et al. in press). Inbreeding has three undesirable effects. It causes inbreeding depression (including an increase in the incidence of abnormalities caused by recessive alleles), loss of genetic variance and random drift in the population mean.

Inbreeding depression reduces the value of many traits, particularly those related to reproduction and US research estimates an economic loss of £8 per cow lifetime per 1% increase in inbreeding (Smith et al. 1998). Although this loss is undesirable, it is only a small part of the economic gains from improvements in breeding value that result from selection of bulls and cows with the highest EBV for traits of interest.

The same information on dairy bulls is available to all farmers worldwide, and the vast majority select for milk production and other dairy production traits. Consequently, the genetic variation in the global dairy cattle population is being reduced through selection and inbreeding. This is now a major concern for breeders of dairy cattle and maintaining genetic variation in the global dairy population has become important to the survival of the industry.

4. Maintenance of genetic variation

(a) The theory: genetic variation in quantitative traits

The forces controlling genetic variation at genes affecting quantitative traits are the same as for other genes—mutation, selection, migration and drift caused by finite population size. The amount of variation that mutation adds to typical quantitative traits each generation is surprisingly high. Lynch & Walsh (1998), summarizing experiments in model species, concluded that the mutation variance (V_m) is typically about 0.001V_e per generation, where V_e=environmental variance. Under a neutral model with only mutation and drift operating, an equilibrium is reached where genetic variance V_g=2N_eV_m, where N_e=effective population size. In cattle today, even in highly selected breeds such as Holstein, the heterozygosity in intronic regions of the genome is approximately 0.0005, implying a N_e in the past of the order of 10⁴. The neutral model with this N_e predicts that V_g will be 10V_e, or h²=0.9, which is clearly not the case. Presumably, natural selection operates to eliminate some of the variation caused by mutation. If all mutations that affect the quantitative trait were subject to a selection coefficient of 0.001 and N_e=500, then this would produce heritabilities in the observed range of 0.2–0.5. However, in practice, selection coefficients probably vary widely and it has proven difficult to find a model that fits the observations well (Zhang et al. 2002). Nevertheless, theory and observation suggest that normal amounts of genetic variance for quantitative traits can be maintained by N_e<1000.

When humans practice artificial selection in livestock breeds, favourable alleles increase in frequency. As they reach fixation, one would expect the genetic variance for the traits under selection to decline. However, experience does not support this expectation. In selection experiments with N_e of about 20, response to selection usually declines and a plateau may be reached, although sometimes there is still genetic variation remaining. The probable explanation for this is that some alleles that are favoured by artificial selection decrease fitness, and so natural selection is balancing the artificial selection (Hill 2000). When N_e>100, the selection response seems to continue linearly for as long as the experiment (e.g. Dudley 1977; Bunger et al. 1990). In broiler chickens, heritability for growth has remained at approximately 0.3, despite nearly 50 years of intense selection (Hill 1998). Even under a neutral model, many genes show extreme (close to 0 or 1) gene frequency. For those favourable alleles at low frequency, selection increases genetic variance as it drives their frequency towards 0.5. For a time, this balances the loss in variance caused by favourable alleles at other genes increasing in frequency from 0.5 towards 1.0, so that total genetic variance does not decline. If, prior to the start of artificial selection, natural selection was acting to drive down the frequency of some alleles favourable for artificial selection, then they will contribute to maintaining the variance for even longer than under a neutral model. However, eventually, variance would decline, but this may be prevented if mutation adds enough new favourable alleles to the population (Hill 1982).

The long-term response to selection depends on the rate at which new favourable mutations occur in the population and the probability that a new mutant is fixed, and so is very dependant on N_e (Hill 2000). In theory, if N_e is large enough, the long-term response is linear and if N_e is larger than this, then rate of response could accelerate (Wei et al. 1996). In selection experiments in Drosophila, Weber (1990) found that selection response was greater with a population of 1000 than one of 200. With a larger N_e, more mutations occur and so there will be more mutations that are favourable for the trait but not too unfavourable for fitness.

In summary, a simple model of selection–mutation–drift can give a reasonable fit to experimental data (Zhang et al. 2004), but this should not disguise the fact that we do not fully understand the maintenance of genetic variance under either natural or artificial selection and that the true situation is undoubtedly more complex than the simple models used above. With this qualification, it appears that N_e=1000 is desirable for the long-term maintenance of genetic variation in quantitative traits.

This general theory of the maintenance of genetic variation is, of course, relevant to cattle, but it is also important to consider the specific history of domestic cattle.

(b) The history: domestication and evolution of cattle

Cattle were domesticated from two different subspecies—Bos indicus in India and Bos taurus in the Middle East—about 10 000 years ago. These subspecies had separated approximately 0.5 Mya (Loftus et al. 1994; MacHugh et al. 1997; Hassanin & Ropiquet in press) and so were different owing both to isolation and presumably different selection pressures. Thus, at the time of domestication, the genetic variation in cattle consisted of the genetic variation within a population, described in §4a, and the variation between B. indicus and B. taurus. However, dairy cattle in temperate parts of the world are almost entirely B. taurus and we will restrict this discussion to B. taurus dairy cattle.

Although European cattle appear to originate from one domestication event in the Middle East (Troy et al. 2001), this did not involve a severe bottleneck, as indicated by the level of DNA sequence variation found even within a modern breed such as Holstein.

Bos taurus cattle spread out from the Middle East to Europe, Africa and north Asia and populations in different places diverged due to genetic isolation and different selection pressures. However, isolation by distance may not have been strong because humans moved cattle between regions (e.g. the introduction of B. indicus cattle into Africa; MacHugh et al. 1997), which limited the genetic drift between localities.

From about 1800, breed societies with closed herdbooks started to form. This decreased or eliminated the flow of genes between populations that were regarded as different breeds. In addition, in some cases, the N_e in the early formation of the breed was very small (e.g. Hereford and Shorthorn). Based on heterozygosity at microsatellite loci, this breed formation process has slightly reduced genetic variance in European breeds compared with cattle in Africa and India (MacHugh et al. 1997). The amount of inbreeding that has occurred in the divergence of several European breeds is about 0.2 based on blood group and protein polymorphisms (Kidd et al. 1974).

This loss of genetic variation caused by closed herdbooks has been exacerbated by modern breeding programmes, especially in the last 30 years. The Holstein and Jersey breeds in USA have rates of inbreeding of 0.2% per year (Thompson et al. 2000a,b) corresponding to an N_e of 50. This has come about because of the adoption by cattle owners of two technologies. First, methods for estimating the genetic merit of cattle, outlined in §2, have led to intense selection for high profit and, second, reproductive technology has allowed individual bulls and, to a small extent cows, to contribute many genes to the next generation. Movement of cattle between countries and focus on similar breeding objectives have meant the selection of the same cattle everywhere. Consequently, the N_e of the global Holstein population became too low.

(c) The current situation: genetic diversity in dairy cattle today

Considerable genetic variation continues to exist both between breeds and within breeds. However, both sources of variation have declined.

(i) Variation between breeds

A high proportion of dairy cattle in developed countries are now Holstein. This is attributable to the replacement of other breeds by the ‘black and white’ breed and the large-scale migration of Holstein genes from the USA into other black and white populations (e.g. figure 1 for the UK). Three factors caused these changes:

1. it became known world wide that Holsteins gave higher milk yields than most breeds;

2. dairy farmers’ breeding objectives world wide became more focused on income from sale of milk; and

3. technology existed to import Holsteins from USA into other countries.

Thus, although it has decreased genetic diversity, the dominant position of the Holstein today can be regarded as a largely rational response by cattle owners.

(ii) Variation within breeds

In theory, variation within the major dairy breeds is expected to decline for two reasons. First, intense selection for milk yield and other traits might drive the favourable alleles to fixation. It is difficult to compare the genetic variance for milk yield between cattle in say 1950 and 2000, but there is no evidence that it has indeed decreased. As discussed in §4a, selection does not seem to exhaust genetic variation except in very small effective populations.

Second, low N_e causes inbreeding and loss of genetic variation. Estimates of current N_e in Holsteins and Jerseys are about 50–100, but this low N_e has not existed for long, so the mean inbreeding is only about 0.04 relative to a base of 1960 (Thompson et al. 2000a,b). Thus, the loss of genetic variance due to recent inbreeding is not great.

In summary, some genetic variation in dairy cattle has been lost due to restricted N_e, possibly in the initial domestication of cattle, but mainly in the formation of closed breeds and in modern breeding programme. The current N_e of 50 in the US Holstein is less than required to maximize long-term genetic improvement, but it is a recent phenomenon so little genetic variance has been lost to date. Conversely, some genetic variation is preserved by the existence of other dairy breeds, although the temperate dairy cow population is dominated by the Holstein breed.

(d) The future: optimum policy

Many reasons have been advanced for the conservation of genetic variation in livestock—economic, societal, aesthetic and moral. We will take an economic view. The benefit in having a large variation in cattle today is that it will probably lead to more profitable cattle in the future (through choice of breed, selection within breed and less inbreeding depression) and less risk of less profitable cattle (through unfavourable, random genetic drift).

Genetic variation can be conserved in two different ways. It can be maintained within the commercial livestock population or it can be maintained in a population that is not used for commercial livestock production. Among the second group of methods for genetic conservation, semen from a wide range of bulls can be stored in liquid nitrogen so cheaply that there is no excuse for not using this method. However, in our view, this semen is unlikely ever to contribute substantially to the genetic composition of future populations of dairy cows in developed countries (Hill 2000). This storage of frozen semen represents a cheap insurance policy that one does not expect to need.

This implies that genetic variation, if it is to be useful, must be conserved in commercial cattle populations. However, it is undesirable and unrealistic to expect cattle owners to practice policies for genetic conservation, unless these policies maximize their current and future profit. Therefore, we wish to find policies that maximize profit after taking account of the effects of genetic variation on future profit. These policies should address conservation of variation both between and within breeds.

Rational payment systems (e.g. payment for the meat value of cull animals) and better knowledge of breed differences might, in some cases, decrease the dominance of the Holstein breed. For instance, breed differences in fertility, disease resistance and feed conversion have not always been known or used when choosing the Holstein over other breeds. In New Zealand, an across-breed genetic evaluation for profit indicates that, under their conditions, Jerseys are at least as profitable as Holsteins (Montgomerie 2004). Conversely, work in the UK shows that Holsteins are the most profitable breed for use in both conventional and organic systems (S. Brotherstone, unpublished data).

Crossbred dairy cattle benefit from heterosis in many traits contributing to profit, and for two breeds of similar profit, it is probably that crosses between them are more profitable than either. It is surprising that crossbreeding has not been used more in dairy cattle. Use of crossbreeding automatically leads to a demand for cattle of more than one breed. Therefore, we suggest that more rational use of crossbreeding will in the long-term support the conservation of a variety of breeds. In New Zealand, for instance, crossbreds make up 35% of the dairy cows (Montgomerie 2004). Note, however, that in countries like the UK, where the yield (and subsequent profit) of Holsteins exceeds the yield of other breeds, crossbreeding has few commercial benefits.

When carrying out genetic improvement within a breed, there is an unavoidable conflict between the desire to maximize the intensity of selection by using as few animals as possible as parents of the next generation and the desire to maintain a high N_e. Therefore, a compromise must be reached. Breeding programmes designed by maximizing net present value (by discounting future profit to a present-day value) lead to very intense selection and rates of inbreeding of about 1% per generation (Goddard & Smith 1989; Goddard 1992). However, when a breeding programme for the whole world is considered, a higher N_e may be optimum. This comes about because breeding objectives differ slightly between countries, there are small G×E and future changes in breeding objectives diminish the gains from selection but are unlikely to diminish the losses causes by inbreeding (Goddard 1992).

The research to find the optimum design for a breeding programme described above, assumes that the optimum of some parameter (e.g. number of sires selected per year) is calculated before the start of the breeding programme and remains the same each year thereafter. This has been referred to as a ‘strategic decision’ (Kinghorn & Shepherd 1994) or a ‘static design’ (Goddard & Howarth 1994). An alternative, more flexible approach, called ‘tactical’ (Kinghorn & Shepherd 1994) or ‘dynamic’ (Goddard & Howarth 1994), uses the information available at the time each selection decision is made to arrive at the optimum decision. This leads to an algorithm for selecting animals based on their EBVs and their relationship to each other. The aim of the algorithm is to maximize the mean EBV of the selected animals (g) while minimizing the mean relationship among them (‘A’, which includes the relationship of an animal to itself), because it is this mean relationship that determines the long-term inbreeding in the population. This can be done by maximizing g−bA where b is the cost of inbreeding (Wray & Goddard 1994), or by maximizing g while restricting the rate of inbreeding (Meuwissen 1997). The two approaches lead to the same outcome in the sense that for any value of b that is used in the first method, there is a rate of inbreeding in the second method that leads to the same selection decisions. These methods can substantially reduce the rate of inbreeding while losing little selection response. Software to do the calculations is now used by several breeding companies.

However, this method is not ideal for use by a breeding company because it assumes a closed breeding programme. In practice, a breeding company has access to the whole world population of a breed such as Holstein. Therefore, the average relationship among the bulls it selects may predict neither the future inbreeding rate of the population they service nor the profit of the company from sale of semen. Despite this, breeding companies, acting to maximize their own profit, still have an incentive to limit inbreeding because farmers will not want to buy semen that will produce highly inbred calves and so breeding companies do not want to breed such bulls.

Both the strategic and tactical approaches described above assume that there is a person with the power to implement such decisions. This may be the case for an individual farm or breeding company, but it is not the case for, say, the world Holstein population. The extent to which individuals making decisions that maximize their own profit will lead to a near optimum outcome for a national or world population of cattle is unknown. However, the argument in the previous paragraph shows that it is possible.

The likelihood that a near optimum outcome is reached is increased if G×E are taken into account when EBVs are calculated. If it is assumed that the ranking of bulls for milk yield is the same in all countries, then all countries will tend to select the same bulls as sires of the next generation and N_e will be low. However, even genetic correlations between milk yield in different countries as high as 0.9 result in different bulls being selected in different countries, and hence increase N_e (Goddard 1992). Thus, it is important that small, but real G×E are not ignored. Similarly, recognizing the differences in economic weights between different farmers or countries increases the diversity of bulls selected. Recognition of differences in breeding objectives and G×E can lead to the maintenance of different breeds or independent sublines within a breed. This helps to preserve genetic variation because the same alleles are unlikely to be lost in all sublines.

Even with optimum policies to maintain genetic variation, intense selection for dairy traits will probably lead to a loss of fitness through selection of alleles that decrease fitness and through inbreeding depression. The loss of fitness caused by selection in the medium to long term may be greater than predicted from genetic correlations in the base population because new mutations that selection favours are probably detrimental to fitness. Decline in fitness-related traits can be prevented by selection on an index that includes these traits and this is now the practice in many developed countries (Veerkamp et al. 2002).

5. Conclusion

The application of quantitative genetics to dairy cattle breeding has resulted in a considerable increase in milk production and a reduction in the cost of production of milk and dairy products. This has been based on innovations in mixed-model statistics that are now used widely outside genetics. Dairy farmers can now select bulls based on EBVs that compare bulls from most developed countries in the world. Consequently, there has been a worldwide tendency for dairy farmers to select related Holstein bulls and for the effective population size of breeds such as the Holstein to decrease to around 50. However, breeding programmes in most countries have now included a wide range of traits other than milk yield (e.g. fertility and health), and genetic variation is being maintained by the existence of breeds other than Holstein, and by the development of sublines within the Holstein that are each selected for a different breeding objective.