Skip to main content
PMC home page
Philosophical Transactions of the Royal Society B: Biological Sciences logoLink to Philosophical Transactions of the Royal Society B: Biological Sciences
. 2005 Oct 24;360(1463):2085–2094. doi: 10.1098/rstb.2005.1740

Quantification of physical and biological uncertainty in the simulation of the yield of a tropical crop using present-day and doubled CO2 climates

AJ Challinor 1,2,*, TR Wheeler 2, JM Slingo 1, D Hemming 3
PMCID: PMC1569570  PMID: 16433095

Abstract

The impacts of climate change on crop productivity are often assessed using simulations from a numerical climate model as an input to a crop simulation model. The precision of these predictions reflects the uncertainty in both models. We examined how uncertainty in a climate (HadAM3) and crop General Large-Area Model (GLAM) for annual crops model affects the mean and standard deviation of crop yield simulations in present and doubled carbon dioxide (CO2) climates by perturbation of parameters in each model. The climate sensitivity parameter (λ, the equilibrium response of global mean surface temperature to doubled CO2) was used to define the control climate. Observed 1966–1989 mean yields of groundnut (Arachis hypogaea L.) in India were simulated well by the crop model using the control climate and climates with values of λ near the control value.

The simulations were used to measure the contribution to uncertainty of key crop and climate model parameters. The standard deviation of yield was more affected by perturbation of climate parameters than crop model parameters in both the present-day and doubled CO2 climates. Climate uncertainty was higher in the doubled CO2 climate than in the present-day climate. Crop transpiration efficiency was key to crop model uncertainty in both present-day and doubled CO2 climates. The response of crop development to mean temperature contributed little uncertainty in the present-day simulations but was among the largest contributors under doubled CO2. The ensemble methods used here to quantify physical and biological uncertainty offer a method to improve model estimates of the impacts of climate change.

Keywords: crop yield, climate change, model uncertainty, high temperature stress, crop simulation models

1. Introduction

Global food production is expected to change considerably due to climate change over the coming century (Parry et al. 2004). Assessments of the impacts of climate change on the productivity of crops employ crop models to predict crop yields under scenarios of climate change that are provided from general circulation models (GCMs). Often, predictions of the impact of climate on crop yields will vary according to which GCM and/or crop model is used. For example, Matthews & Wassmann (2003) predicted rice productivity across Asia under doubled current atmospheric carbon dioxide (CO2) concentrations using two crop models and three GCMs. The magnitude of yield changes that were predicted differed between the crop models, and the sign of the yield change was affected by the GCM scenario. The reasons for such differences among crop and climate model predictions need to be investigated further in order to improve our assessment of the impacts of climate change.

Uncertainty in climate change impacts assessments comes from a number of sources. Future emissions of greenhouse gases must be estimated, and the response of both the atmosphere and the impact in question have associated uncertainties. There is no consensus in the literature to date on how best to quantify these uncertainties. In the case of agricultural yield, the range of values across sites and/or climate change scenarios is often used (e.g. IPCC 2001a; Tubiello et al. 2002; Trnka et al. 2004). As a result of the differences in methods, uncertainty ranges are not directly comparable. Different studies take account of different uncertainties. For example, Reilly & Schimmelpfennig (1999) projected changes of −98 to +16% for maize in Africa (range across sites and climate scenarios); Jones & Thornton (2003) projected a change of −17% for maize in Zimbabwe. In addition, the large range of possible crops and locations means that the number of directly comparable studies is small. Hence, any consensus from the literature on likely future agricultural yield is being reached by random sampling of the many uncertainties.

This study is a first step towards quantifying the uncertainty in agricultural yield projections by looking at the fundamental biological and physical processes involved. The methods used are consistent with the recommendations of Katz (2002): assessing uncertainty of individual model components separately, and applying uncertainty analysis to simpler impacts models in order that the mechanisms by which uncertainty propagates can begin to be understood.

(a) Physical, biological and anthropogenic uncertainty

Physical uncertainty, for given levels of greenhouse gas and aerosol emissions, comes from a number of sources (IPCC 2001b). First, imperfect knowledge of the impact of emissions on the radiation balance means that the extra heat input to the atmosphere is not known precisely. It is not only atmospheric composition that plays a role; but changing land use will also impact the radiative budget. Second, there is a range of plausible atmospheric responses to the change in radiative forcing. Estimates of this range are constrained by limited computer resources. This is most evident in the relatively coarse spatial resolution of GCMs.

Anthropogenic uncertainty is the result of imperfect knowledge of crop management decisions such as the choice of crop and variety, irrigation and fertilizer application and planting date. For example, improvements in yields over time due to the release of new varieties usually results in a monotonically increasing trend in yield. As with all management-related factors, this may vary in both space and time (e.g. Kulkarni & Pandit 1988; Moss & Shonkwiler 1993). Despite these uncertainties it is still possible to simulate yields with some accuracy using observed large-area gridded data (e.g. Challinor et al. 2004).

Biological uncertainty results from the range of plausible responses of the crop to the climate. It is not only climate over the season that has an impact on crop growth and development; the statistics and timing of the weather within the season are also crucial (e.g. Wright et al. 1991; Wheeler et al. 2000). The uncertainties associated with the simulation of these processes depend upon the spatial scale of the investigation (e.g. Hansen & Jones 2000). For example, the impact of terrain slope may be small when averaged over large areas, but considerable at smaller scales. Even over large areas, the relationship between crop yield and climate is complex and can change over time: Challinor et al. (2005b) found that the relationship between June and September rainfall and groundnut yield for a 0.5° grid cell in Andhra Pradesh, India, changed between the periods 1966–1977 and 1978–1989; the correlation coefficient increased from −0.13 to +0.58.

There is also a direct response of the crop to increased carbon dioxide. A review of 18 crop species under controlled environments (Kimball & Idso 1983) suggested that water use efficiency may double with a doubling of CO2. Based on controlled environment studies of groundnut (Stronach et al. 1994; Clifford et al. 2000), transpiration efficiency for doubled CO2 could increase by between 24 and 100%. Controlled environment experiments also show that changes in water use under doubled CO2 at the canopy level are of the order of 10–30% for C3 crops (e.g. Allen Jr et al. 2003; Kimball & Idso 1983), with the greater reductions being associated with greater increases in transpiration efficiency. Free-air CO2 enrichment (FACE) experiments (see e.g. Ainsworth & Long 2005) have shown that in a field environment, the reduction in water use may be nearer to 3–7% (Kimball et al. 2002). These experiments inform the simulation of the CO2 fertilization effect (e.g. Tubiello & Ewert 2002). The modelling study of Ewert et al. (2002) assumed a linear reduction in crop transpiration up to 10% at doubled CO2.

Simulation models provide a tool for the quantification of variables and their associated uncertainty. The uncertainty in the response of the atmosphere to a doubling of CO2 has been assessed by comparing the results of different GCMs (IPCC 2001b) and by varying parameters within a single GCM (Murphy et al. 2004). Hence, uncertainty due to both model structure and model inputs can be assessed. There are fewer examples of this type of comparison within the crop modelling literature, perhaps because there is already significant uncertainty in the climate change scenarios used as inputs. Mearns et al. (1999) found significant differences in the response of two process-based crop models to a doubling of CO2.

(b) Scope of this study

This study focuses principally on the bio-physical uncertainty in estimates of groundnut (i.e. peanut; Arachis hypogaea L.) yield with CO2 at both present-day levels and at double present-day levels. A single GCM and a single process-based large-area crop model are used to estimate the uncertainty in yield simulation in both of these climates. The response of yield to a doubling of CO2, and its associated uncertainty, is also examined. The uncertainty due to model formulation is not treated, since the focus is on the uncertainty due to the range of plausible parameter values in both the crop and the climate models. Parameters are varied one at a time, so that interactions between parameters, which are likely to be nonlinear, are not considered. Similarly, interactions between crop and climate model uncertainties are not examined; rather, this is a first estimate of the relative magnitude of the crop and climate modelling uncertainties. Further studies with multiple parameter perturbations are planned.

In order for the yields resulting from the parameter perturbations to be directly comparable, the range of parameter values used should be directly comparable. For the crop model, this was achieved using an objective model performance statistic, based on crop yield, to define the parameter perturbations. A similar method is not possible in the climate model case for three reasons: (i) the computational expense of climate models limits the number of simulations, (ii) comparison with observations is hampered by limited data availability on the grid scale of the climate model and (iii) there are many output variables (rainfall, temperature, humidity) of interest, so that a relative importance would have to be given to each. Hence, in the climate model case expert opinion has been sought as to the likely maximum and minimum realistic parameter values (Murphy et al. 2004). While the methods used for the two models are not identical, they are comparable, since they both aim to produce the best possible estimates of the upper and lower limits on parameter values. However, it is worth noting that the comparisons of crop and climate model uncertainty in this study are contingent on the choice of parameter perturbations.

In one case only, multiple parameter perturbations were carried out: two sets of parameters describing the response of the crop to high temperature stress were used with each climate ensemble member. This enabled the assessment, in each climate, of the importance of the sensitivity of the crop to high temperature stress. Also note that some crop model parameters, and their ranges, were changed from the present-day values in order to reflect the impact of doubled CO2 on physiology. The crop and climate model parameter perturbations are described in detail in §2b.

The study region encompasses the major groundnut-growing areas of India. It was chosen because the same study region has been successfully used in previous studies (see §2a). Climates across the region vary: water-limited environments in southern and northwestern parts contrast with eastern regions, where groundnut yield is much less limited by water (Challinor et al. 2003).

2. Method: quantification of physical and biological uncertainty

(a) Modelling methods

(i) The general large-area model for annual crops

The general large-area model for annual crops (GLAM; Challinor et al. 2004) has been designed specifically for use within a combined crop and climate forecasting system; it capitalizes on the predictability suggested by large-area relationships between climate and crop yield (Challinor et al. 2003). GLAM is a process-based model that is easily adaptable to most annual crops. The model operates on a daily timestep using 20 crop-specific parameters and five additional parameters, which vary spatially. Three of these additional parameters describe the soil hydrological properties and the other two relate to the yield gap and the planting window. Temperature, radiation, rainfall and humidity are used to simulate yields at a given technology level; increases in yield due to the mean impact of improvements in crop variety and management techniques are not simulated. The planting date is determined by the model as the first day within a defined planting window in which the soil moisture exceeds a specified threshold.

GLAM has successfully been used to simulate groundnut yield in India using observed gridded data (Challinor et al. 2004), reanalysis data (Challinor et al. 2005b) and probabilistic seasonal hindcast output from GCMs (Challinor et al. 2005a). The soil data for these studies, and for the current study, come from FAO/UNESCO (1974) and the data on planting dates from Reddy (1988). The planting window was given a broad width of one month, with crisis sowing being simulated once this period has passed. The planting window was not changed for the doubled CO2 simulations; the vast majority of changes in simulated planting date (mean and standard deviation) between the two climates were less than 6 days, much smaller than the planting window itself.

GLAM uses a yield gap parameter (YGP) which acts on the maximum rate of change of leaf area index. This is a simple method of simulating the impact of pests, diseases and non-optimal management on the crop. YGP is also the parameter used for calibration and it can correct for climate bias (Challinor et al. 2005a). To the extent that it can account for bias in the input rainfall, it can also account for bias in available soil water, and hence bias in the soils parameterization.

The crop model has also been integrated with a land–surface model and the results have shown skill in reproducing the interannual variability of groundnut yield in India and other parts of the tropics (Osborne 2005).

(ii) Climate simulations

The climate simulations used are those of Murphy et al. (2004). In that study, HadAM3 was coupled to a mixed layer ocean and equilibrium present-day and doubled CO2 simulations were carried out. For both of these cases parameters were varied one at a time, relative to the standard (control) set of parameters. The 29 parameters chosen for this represent key sub-grid physical processes as either logical switches, variable coefficients or thresholds. Parameters were varied one at a time with a minimum and maximum value being used for variable coefficients. These values were chosen by seeking expert opinion (see §1b). This procedure resulted in 53 perturbed physics simulations for both present-day and doubled CO2 climates. The climate sensitivity parameter (λ), defined as the equilibrium response of global mean surface temperature to doubled CO2, was calculated for each pair (present-day and doubled CO2) of simulations.

Data retrieval and transfer limitations meant that at the time of the study there were only a 12 of the 53 simulations available. From these 12, four were chosen such that a broad range of values of λ was represented. The chosen simulations perturbed parameters from the large-scale cloud, sea-ice or convection schemes (table 1). A histogram of the values of λ from all 53 simulations is presented in figure 1. The control simulation (C) was chosen to have a value of λ within the most populated interval of this histogram. The simulations designated λ1 and λ2 have values that are close to the control, and λ3 was chosen as a more extreme and less probable value.

Table 1.

The climate simulations used in this study (Murphy et al. 2004). The GCM parameters shown were perturbed, resulting in different values of the climate sensitivity parameter, λ.

simulation name parameter λ (°C)
C sea ice albedo 3.60±0.05
λ1 cloud droplet to rain conversion rate 2.91±0.06
λ2 ice fall speed 4.10±0.05
λ3 entrainment rate coefficient 6.98±0.04
Open in a new tab
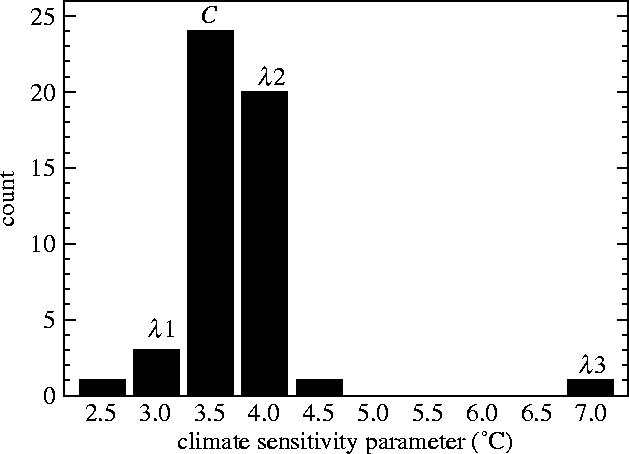
Figure 1.

Figure 1

Open in a new tab

Histogram of the values of the climate sensitivity parameter (λ) resulting from the 53 climate ensemble members. Labels show the location of the simulations used in this study: the control simulation (C) and three perturbations (λ1–λ3).

(b) Choice of crop model parameters

(i) Crop model calibration

The yield data for calibration of the model came from the district-level database of agricultural returns compiled by the International Crops Research Institute for the Semi-Arid Tropics (ICRISAT), Patancheru, India. Districts range in size from less than 1 to 46 800 km2, although there are only two districts which are less than 690 km2 in area. The average of all district sizes is 8300 km2. The yield time-series (1966–1989) for each individual district were linearly detrended to 1966 levels, in order to remove the influence of improved varieties and management methods. Yield data were then upscaled to the crop model grid using an area-weighted mean by assuming that the area under cultivation is spread evenly throughout each district.

The calibration procedure varied YGP in steps of 0.05 between 0.05 and 1, as for previous studies (e.g. Challinor et al. 2005a). Optimal values were defined as those which minimized the difference between the simulated 20 year mean yield at that site and the observed 1966–1989 mean yields described above. This procedure was carried for each of the simulations with the non-perturbed set of crop model parameters (λ1, λ2, λ3 and C) in the present-day climate. In this way the impact of climate biases was minimized (see §2a).

(ii) Perturbation of crop model parameters in the present-day climate

The perturbation of parameters for GLAM used similar methods to those for the climate simulations: parameters were varied one at a time to either a minimum or a maximum value, so that an ensemble of realizations of yield was produced. The parameters chosen were those that previous studies showed to have a large impact on yield when varied within the ranges determined by independent observations (see Challinor et al. 2004). The list of parameters, which is presented in table 2, was chosen to give a broad representation of uncertainty in the response of the crop to climate (i.e. response to mean and high temperatures, radiation and water) and in the representation of crop physiology itself.

Table 2.

GLAM parameter perturbations for the simulations of present-day climate.

parameter units impact non-perturbed perturbation
rate of change of harvest index day−1 biomass partitioning 0.007 0.001
extinction coefficient — available radiation 0.55a 0.17
optimum temperature °C development; response to mean temperature 28.0 1.8
transpiration efficiency Pa response of biomass to water 1.51a 0.47
high temperature stress parameters — response to temperature extremes no response TOL or SEN
Open in a new tab

The three sets of runs carried out for each parameter used the non-perturbed value and the non-perturbed value plus, and minus, the perturbation.

a

Indicates that non-perturbed values differ from those of Challinor et al. (2004). In both cases these differences are less than or equal to 10%. The TOL and SEN parameter sets, representing tolerant and sensitive varieties, respectively, are taken directly from Challinor et al. (in press).

Perturbed parameter values were determined using the simulations of Challinor et al. (2005b). As part of that study GLAM parameter values were calculated which minimized root mean square error for time-series of groundnut yield across India. These values vary spatially and it is the standard deviation of that variability, added to and subtracted from the mean that forms the perturbed parameter values for the present-day climate simulations. All of the perturbations fall within observational constraints (see Challinor et al. 2004). The non-perturbed parameter values are those of Challinor et al. (2004) except where noted otherwise.

(iii) Perturbation of crop model parameters in the doubled CO2 climate

The same perturbations as in the present-day climate were used for the doubled CO2 climate, with one exception: the transpiration efficiency (TE) was changed in order to simulate the direct response of the crop to increased CO2 levels. Associated changes in water use were also made. The two GLAM additional parameter perturbations used in the doubled CO2 simulations (referred to as standard and high-TE) are listed in table 3. The parameter values given are derived from the studies reviewed in §1a. The reduction in transpiration was implemented via a reduction of the calibrated present-day climate maximum transpiration rate (0.3 cm day−1; Challinor et al. 2004). Use of this parameter ensures that the reduction in transpiration of water-stressed crops is less than that on well watered crops, as is seen in observations (Kimball et al. 2002).

Table 3.

GLAM parameters used in the doubled CO2 simulations.

parameter units impact standard high-TE
transpiration efficiency Pa water use efficiency 1.87 3.02
max. transpiration rate cm day−1 absolute water use 0.285 0.210
Open in a new tab

Either the standard or high-TE parameter set was used. The additional parameters and ranges listed in table 2 were also used for these simulations.

The chosen parameter values reported in table 3 correspond to a change in transpiration efficiency from the calibrated present-day non-perturbed climate value (table 2), of +24 and +100%. The maximum transpiration rates chosen for each of these values were 5 and 30% less than the present-day climate value, respectively (table 3). This ensures physiological consistency between these two parameters by excluding the combinations where transpiration efficiency and maximum transpiration rate are both high.

The indirect impact of CO2 concentration changes is simulated by GLAM through the usual pathways: changes in temperature, rainfall, humidity and radiation will affect the crop simulations (Challinor et al. 2004). The high temperature stress parameterization for GLAM (Challinor et al. in press) simulates the impact on pod-set, and subsequently yield, of high temperatures during the period when the crop is flowering. This parameterization was designed with climate change in mind, since high temperature stress events are likely to be more frequent in future climates (Wheeler et al. 2000). The use of varieties which are either tolerant (TOL) or sensitive (SEN) to heat stress (table 2) can be thought of either as representing uncertainty in the response of the crop to these events, or as potential adaptive choices for farmers.

(c) Analysis methods

The perturbations to physical and biological parameters in present-day and doubled CO2 climates described above allow a preliminary assessment of contributions to uncertainty in yield simulation. Using the present-day climate simulations, differences between crop yields from perturbed and control runs indicate which bio-physical parameters currently contribute most to uncertainty. A similar analysis using only doubled CO2 simulations indicates whether or not these contributions are likely to change. Finally, differences between the control present-day simulation and doubled CO2 simulations provide estimates of the climate change signal.

Yield simulations where the crop failed to meet its thermal time requirement (see §2a) were omitted from all analyses. This leads to the removal in some cases of one grid cell in the north of the domain.

Four statistics were used to summarize the uncertainty associated with crop and climate model parameters (§3b). Two of these are based on the difference in mean yield between the control simulation and that of the other simulations. The remaining two are based on percentage differences in the standard deviation of yield. For each of these two cases the variability across grid cells was quantified in two ways, both chosen to minimize sensitivity to extreme values: first, the median value is a measure of spatially systematic differences between simulations; second, the inter-quartile range (IQR) is a measure of the non-systematic differences (i.e. the spatial variability of the response to the parameter perturbation). All four statistics produce one value per parameter perturbation.

3. Results

(a) Calibration and simulation in present-day climate

The calibration procedure (§2b) resulted in values of YGP that were broadly similar across the control, λ1 and λ2 simulations, with λ3 showing greater differences. For λ1, seven out of 35 grid cells had values that differed from those of the control simulation by more than 0.05. For λ2, this figure was 10, and for λ3 was 17. In addition, the values were on the whole greater in magnitude in the λ3 case: the majority were greater than 0.5.

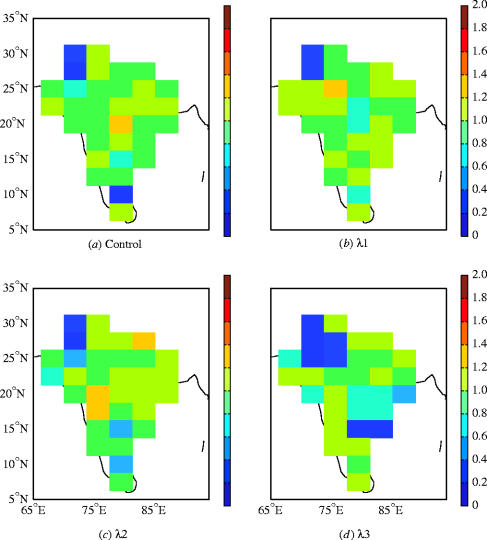
Figure 2 shows the level of agreement between the four simulations with non-perturbed crop model parameters and the observed mean yield. Results are presented only for grid cells where there is a minimum total of 20 district-level observations contributing to the observed mean yield. This avoids the fitting of YGP to give apparently accurate simulations based only on a few data points. It results in the omission of the eastern-most grid cell. The λ3 simulation has a notably higher error in the simulation of mean yield than the other three simulations. The high error in the two grid cells in the northwest in all four runs is due to low seasonal precipitation totals (less than 140 mm in all cases).

Figure 2.

Figure 2

Open in a new tab

Twenty year mean of the simulated yields for the four present-day climate perturbations, normalized by the observed values.

Given the ability of GLAM to simulate groundnut yield in India using observed gridded data (Challinor et al. 2004), the relatively poor performance of λ3 suggests that, at least for parts of India, this climate is less consistent than the other three climates with observed groundnut cultivation in India.

(b) Quantification of uncertainty

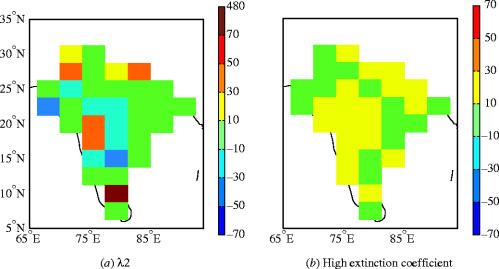
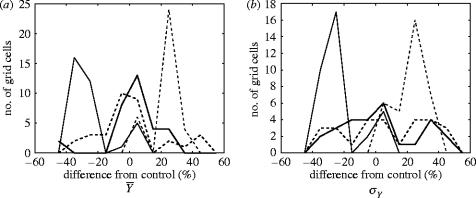
The results presented in this section use percentage differences between perturbed parameter simulations and control simulations, as described in §2c. A map of differences in mean yields for one climate model perturbation and one crop model perturbation is presented in figure 3. The relative importance of the two perturbations for mean yield varies spatially. Figure 4 shows frequency plots, sampled across space, of the differences in the present-day mean and standard deviation of yield for two further crop parameter perturbations and two climate model perturbations. The crop model parameter perturbations have a more narrow and displaced curve, indicating a more spatially systematic impact on yield (this can also be seen in figure 3).

Figure 3.

Figure 3

Open in a new tab

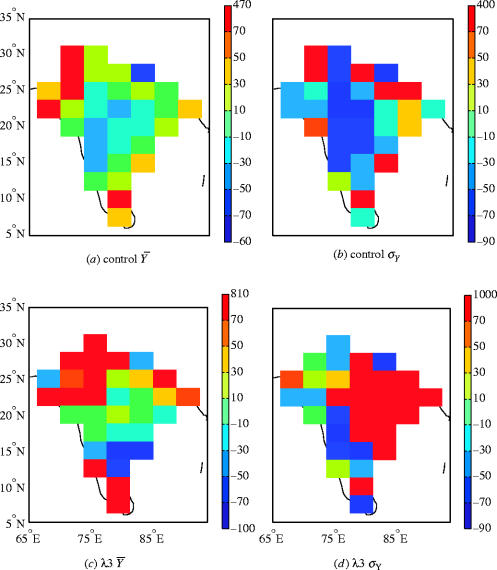
Percentage difference in mean yield between the control present-day simulation (C) and two perturbed present-day simulations.

Figure 4.

Figure 4

Open in a new tab

Frequency plots of the percentage difference in two yield statistics between the control present-day simulation (C) and four perturbed present-day simulations. Two simulations (thin lines) are for perturbed transpiration efficiency. The remaining two simulations are for perturbed climate: the thick solid line is λ1 and the thick dashed line is λ2.

Table 4 summarizes the statistics of the remaining frequency plots (not shown) for the present-day climate. The crop parameter perturbations tend to have lower IQR than the climate parameter perturbations, indicating, as in figure 4, that any impact on yield is relatively systematic across space. This distinction is less clear in the case of mean yield (Y¯) if λ3 is excluded from the analysis. The magnitude of the systematic impact on mean yield (as measured by the median difference Y¯ in across grid cells) is greater for some crop parameters than it is across climate perturbations. For standard deviation in yield (σY) this is not the case, although transpiration efficiency and extinction coefficient do contribute significant uncertainty. In all cases, the climate uncertainty is greater for σY than for Y¯ and it is reduced if λ3 is excluded from the analysis.

Table 4.

Statistics of the percentage difference in the present-day climate between the perturbed-parameter simulations and the control simulation.

median inter-quartile range
variable Y¯ σY Y¯ σY
rate of change of harvest index −14 and 14 −14 and 14 0 and 0 0 and 0
extinction coefficient −24 and 17 −27 and 19 19 and 18 17 and 18
optimal temperature −1 and 6 0 and 2 3 and 20 4 and 24
transpiration efficiency −30 and 26 −28 and 24 2 and 5 7 and 13
λ1, λ2, λ3 −11 to 5 5 to 46 14 to 49 48 to 284
λ1, λ2 −2 and 5 5 and 18 14 and19 48 and 54
Open in a new tab

The median and the inter-quartile range across grid cells are shown for both the 20 year mean yield (Y¯) and the standard deviation over that period (σY).

Table 5 presents the equivalent results for the doubled CO2 climate. These results are broadly similar to those of the present-day climate with some notable exceptions: optimal temperature is more important in determining the distribution of yield over both time and space (i.e. the IQR and median for both σY and Y¯ increase considerably for this parameter). Transpiration efficiency is more important in determining the variability in σY and Y¯ across space (i.e. the IQR is higher). Finally, the uncertainty associated with climate simulation is higher in this climate than in the present-day climate for all four statistics.

Table 5.

Statistics of the percentage difference in the doubled CO2 climate between the perturbed-parameter simulations and the control simulation.

median inter-quartile range
variable Y¯ σY Y¯ σY
rate of change of harvest index −14 and 14 −14 and 14 0 and 0 0 and 0
extinction coefficient −22 and 13 −23 and 13 17 and 20 22 and 24
optimal temperature −19 and 43 −19 and 60 23 and 24 55 and 62
transpiration efficiency 25 24 13 39
λ1, λ2, λ3 −2 to 23 −22 to 58 25 to 66 40 to 438
λ1, λ2 −2 and 6 −22 and 34 25 and 31 40 and 70
Open in a new tab

The median and the inter-quartile range across grid cells are shown for both the 20 year mean yield (Y¯) and the standard deviation over that period (σY).

(c) Yield changes under doubled CO2

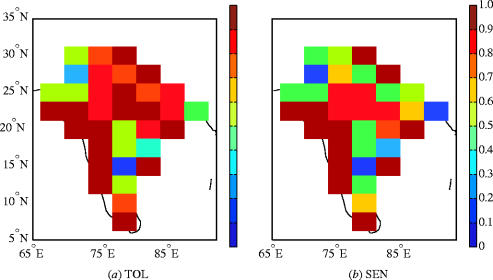
In all four present-day climate simulations, there is very little incidence of high temperature stress (see §2b): all four simulations show less than four grid cells with more than 1 year where pod-set is less than 60% (the value below which yield is affected in the TOL case). For the doubled CO2 case, this figure rises in all four simulations. For the C, λ1 and λ2 this increase is modest: 2–5 grid cells are affected. However, in λ3, most grid cells become affected, and the mean percentage of pods setting becomes seriously reduced. Figure 5 shows the extent of this reduction for both a SEN and TOL groundnut variety. Most of India is affected, although less area is affected in the TOL case than in the SEN case. The magnitude of the impact is greater for SEN than for TOL, showing the increased vulnerability of yield to high temperature stress when this type of variety is used.

Figure 5.

Figure 5

Open in a new tab

The 20 year mean of the percentage of setting pods for the two simulated heat tolerance characteristics, (a) tolerant and (b) sensitive, in the doubled CO2 λ3 simulations.

Figure 6 presents the impact of the doubled CO2 climate on the mean and standard deviation of yield for both the control and the λ3 simulations. The difference between these two cases is marked; in particular, the sign of the change in standard deviation is different over large parts of India. Among the reasons for this might be the increase in the standard deviation of precipitation over most of India in λ3. The corresponding changes in the control case are much less marked. A detailed analysis of causality is beyond the scope of this study.

Figure 6.

Figure 6

Open in a new tab

Percentage changes in the statistics of yield between the present-day control simulation and doubled CO2 climates for two of the parameter perturbations.

A great deal of analysis of the impact of doubling CO2 could be carried out using the simulations in this study. For the purposes of this paper, further analysis is restricted to some general observations. Changes in mean yield from present-day values in the λ1 and λ2 simulations are broadly similar to the control case. Changes in the standard deviation of yield are higher in λ2 than in the control. The increase in transpiration efficiency in the high-TE simulation compensates for the reduction in yields seen over central India in the control case (figure 6), resulting in little change in mean yield in that region. Finally, the choice of optimal temperature, noted in §3b as being critical for the doubled CO2 climate, has an impact comparable to the choice of climate (λ3 or control).

4. Discussion and conclusions

The results presented above highlight the importance of uncertainty when estimating the response of both the mean and variability of crop yield to doubled CO2. The relative importance of the contributions of crop and climate model uncertainties can vary spatially (figure 3). The contribution of climate uncertainty, particularly to the uncertainty in the estimation of yield variability, can be considerable. Also, the contribution of climate uncertainty was shown to be higher in the double CO2 climate than in the present-day climate (tables 4 and 5). The impact of the more extreme, less probable, response to CO2 (λ3) on the standard deviation of yield is large, and acts through two mechanisms: climate variability (figure 6) and high temperature stress (figure 5). The impact of climate uncertainty is smaller when this climate simulation is excluded from the analysis.

The importance of further constraining some of the GLAM parameters in present-day and doubled CO2 climates has also emerged from this study. The transpiration efficiency is the principal source of uncertainty in the present-day climate, while the temperature increases associated with doubled CO2 make the determination of optimal temperature important in that climate. This has relevance beyond that of crop yield simulation using this particular crop model: an understanding of the response of crop duration to increasing temperature is important in any yield impact assessment. The magnitude of the CO2 fertilization effect (mediated in GLAM via the transpiration efficiency) is also important under doubled CO2, and can make the difference between yield increases and yield decreases (§3c). Further experiments under realistic field conditions (e.g. FACE) are needed in order to constrain estimates of CO2 fertilization (see Long et al. 2005).

Ensemble methods such as those used in this study provide a way to quantify physical and biological uncertainty. The methods can be extended to quantify anthropogenic uncertainty and/or look at adaptation strategies, by examining the use of different crops and management techniques (see also Dessai & Hulme 2004). More rigorous probabilistic results can be obtained by using larger ensembles. Also, the observational constraints on the parameter perturbations can be accounted for by comparing the resulting climate and crop quantities (yield, specific leaf area, biomass) to observations. There is already evidence to suggest that the probabilistic nature of climate forecasting on seasonal time-scales can be exploited to provide useful information on crop productivity (e.g. Hansen & Indeje 2004; Cantelaube & Terres 2005; Challinor et al. 2005a; Marletto et al. 2005). Accepting and quantifying the uncertainty associated with climate change may bring similar skill, and has the further advantage of identifying key sources of uncertainty. These methods clearly have the potential to improve vastly on the single-scenario methods commonly used to identify climate change impacts. Application of these methods to other impacts and/or climate models would help to build a sound consensus on the uncertainty associated with climate change impacts.

Acknowledgments

The authors wish to thank Richard Betts and the QUMP team at the Hadley Centre, UK, and Jo Brown at the University of Reading.

Footnotes

One contribution of 17 to a Discussion Meeting Issue ‘Food crops in a changing climate’.

References

  1. Ainsworth E.A, Long S.P. What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. New Phytol. 2005;165:351–372. doi: 10.1111/j.1469-8137.2004.01224.x. doi:10.1111/j.1469-8137.2004.01224.x [DOI] [PubMed] [Google Scholar]
  2. Allen L.H, Jr, Pan D, Boote K.J, Pickering N.B, Jones J.W. Carbon dioxide and temperature effects on evapotranspiration and water use efficiency of soybean. Agron. J. 2003;95:1071–1081. [Google Scholar]
  3. Cantelaube P, Terres J.M. Use of seasonal weather forecasts in crop yield modelling. Tellus. 2005;57A 476–487. [Google Scholar]
  4. Challinor A.J, Slingo J.M, Wheeler T.R, Craufurd P.Q, Grimes D.I.F. Towards a combined seasonal weather and crop productivity forecasting system: determination of the spatial correlation scale. J. Appl. Meteorol. 2003;42:175–192. doi:10.1175/1520-0450(2003)042<0175:TACSWA>2.0.CO;2 [Google Scholar]
  5. Challinor A.J, Wheeler T.R, Slingo J.M, Craufurd P.Q, Grimes D.I.F. Design and optimisation of a large-area process-based model for annual crops. Agric. Forest Meteorol. 2004;124:99–120. doi:10.1016/j.agrformet.2004.01.002 [Google Scholar]
  6. Challinor A.J, Slingo J.M, Wheeler T.R, Doblas-Reyes F.J. Probabilistic hindcasts of crop yield over western India. Tellus. 2005a;57A:498–512. [Google Scholar]
  7. Challinor A.J, Wheeler T.R, Slingo J.M, Craufurd P.Q, Grimes D.I.F. Simulation of crop yields using the era40 re-analysis: limits to skill and non-stationarity in weather–yield relationships. J. Appl. Meteorol. 2005b;44:516–531. doi:10.1175/JAM2212.1 [Google Scholar]
  8. Challinor, A. J., Wheeler, T. R. & Slingo, J. M. In press. Simulation of the impact of high temperature stress on the yield of an annual crop. Agric. Forest Meteorol
  9. Clifford S.C, Stronach I.M, Black C.R, Singleton-Jones P.R, Azam-Ali S.N, Crout N.M.J. Effects of elevated CO2, drought and temperature on the water relations and gas exchange of groundnut (Arachis hypogaea) stands grown in controlled environment glasshouses. Physiol. Plantarum. 2000;110:78–88. doi:10.1034/j.1399-3054.2000.110111.x [Google Scholar]
  10. Dessai S, Hulme M. Does climate adaptation policy need probabilities? Climate Policy. 2004;4:107–128. [Google Scholar]
  11. Ewert F, et al. Effects of elevated CO2 and drought on wheat: testing crop simulation models for different experimental and climatic conditions. Agric. Ecosyst. Environ. 2002;93:249–266. doi:10.1016/S0167-8809(01)00352-8 [Google Scholar]
  12. FAO/UNESCO. 1974 FAO/UNESCO soil map of the world, 1:5,000,000, ten volumes.
  13. Hansen J.W, Indeje M. Linking dynamic seasonal climate forecasts with crop simulation for maize yield prediction in semi-arid kenya. Agric. Forest Meteorol. 2004;125:143–157. doi:10.1016/j.agrformet.2004.02.006 [Google Scholar]
  14. Hansen J.W, Jones J.W. Scaling-up crop models for climatic variability applications. Agric. Syst. 2000;65:43–72. doi:10.1016/S0308-521X(00)00025-1 [Google Scholar]
  15. IPCC . Contribution of working group II to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press; Cambridge, MA: 2001a. Climate change 2001: impacts, adaptation, and vulnerability. pp 1032. [Google Scholar]
  16. IPCC . Contribution of working group I to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press; Cambridge, MA: 2001b. Climate change 2001: the scientific basis. pp 881. [Google Scholar]
  17. Jones P.G, Thornton P.K. The potential impacts of climate change on maize production in Africa and Latin America in 2055. Global Environ. Change—Hum. Policy Dimensions. 2003;13:51–59. [Google Scholar]
  18. Katz R.W. Techniques for estimating uncertainty in climate change scenarios and impact studies. Climate Res. 2002;20:167–185. [Google Scholar]
  19. Kimball B.A, Idso S.B. Increasing atmospheric CO2: effects on crop yield, water use and climate. Agric. Water Manag. 1983;7:55–72. doi:10.1016/0378-3774(83)90075-6 [Google Scholar]
  20. Kimball B.A, Kobayashi K, Bindi M. Responses of agricultural crops to free-air CO2 enrichment. Adv. Agron. 2002;77:293–368. [PubMed] [Google Scholar]
  21. Kulkarni B.S, Pandit S.N.N. A discrete step in the technology trend for sorghum yields in parbhani, India. Agric. Forest Meteorol. 1988;42:156–165. doi:10.1016/0168-1923(88)90074-3 [Google Scholar]
  22. Long S.P, Ainsworth E.A, Leakey A, Morgan P.B. Global food insecurity. Treatment of major food crops to elevated carbon dioxide and ozone under large-scale fully open-air conditions suggest models may seriously over-estimate future yields. Phil. Trans. R. Soc. B. 2005;360:2011–2020. doi: 10.1098/rstb.2005.1749. doi:10.1098/rstb.2005.1749 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Marletto V, Zinoni F, Criscuolo L, Fontana G, Marchesi S, Morgillo A, Soetendael M.V, Ceotto E, Andersen U. Evaluation of downscaled DEMETER multi-model ensemble seasonal hindcasts in a Northern Italy location by means of a model of wheat growth and soil water balance. Tellus. 2005;57A:488–497. [Google Scholar]
  24. Matthews R.B, Wassmann R. Modelling the impacts of climate change and methane emission reductions on rice production: a review. Eur. J. Agron. 2003;19:573–598. doi:10.1016/S1161-0301(03)00005-4 [Google Scholar]
  25. Mearns L.O, Mavromatis T, Tsvetsinskaya E. Comparative response of EPIC and CERES crop models to high and low spatial resolution climate change scenarios. J. Geophys. Res. 1999;104:6623–6646. doi:10.1029/1998JD200061 [Google Scholar]
  26. Moss C.B, Shonkwiler S. Estimating yield distributions with a stochastic trend and nonnormal errors. Am. J. Agric. Econ. 1993;75:1056–1062. [Google Scholar]
  27. Murphy J.M, Sexton D.M.H, Barnett D.N, Jones G.S, Webb M.J, Collins M, Stainforth D.A. Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature. 2004;430:768–772. doi: 10.1038/nature02771. doi:10.1038/nature02771 [DOI] [PubMed] [Google Scholar]
  28. Osborne, T. M. 2005 Towards an integrated approach to simulating crop–climate interactions. Ph.D. thesis, University of Reading.
  29. Parry M.L, Rosenzweig C, Iglesias A, Livermore M, Fischer G. Effects of climate change on global food production under SRES emissions and socio-economic scenarios. Global Environ. Change—Hum. Policy Dimensions. 2004;14:53–67. [Google Scholar]
  30. Reddy P.S, editor. Groundnut. Indian Council of Agricultural Research; Krishi Anusandhan Bhavan, Pusa, New Delhi, India: 1988. [Google Scholar]
  31. Reilly J.M, Schimmelpfennig D. Agricultural impact assessment, vulnerability, and the scope for adaptation. Climatic Change. 1999;43:745–788. doi:10.1023/A:1005553518621 [Google Scholar]
  32. Stronach I.M, Clifford S.C, Mohamed A.D, Singleton-Jones P.R, Azam-Ali S.N, Crout N.M.J. The effects of elevated carbon dioxide temperature and soil moisture on the water use of stands of groundnut (Arachis hypogaea L.) J. Exp. Bot. 1994;280:1633–1638. [Google Scholar]
  33. Trnka M, Dubrovsky M, Semerádová D, Žalud Z. Projections of uncertainties in climate change scenarios into expected winter wheat yields. Theor. Appl. Climatol. 2004;77:229–249. doi:10.1007/s00704-004-0035-x [Google Scholar]
  34. Tubiello F.N, Ewert F. Simulating the effects of elevated CO2 on crops: approaches and applications for climate change. Eur. J. Agron. 2002;18:57–74. doi:10.1016/S1161-0301(02)00097-7 [Google Scholar]
  35. Tubiello F.N, Rosenzweig C, Goldberg R.A, Jagtap S, Jones J.W. Effects of climate change on US crop production: simulation results using two different GCM scenarios. Part I. Wheat, potato, maize, and citrus. Climate Res. 2002;20:259–270. [Google Scholar]
  36. Wheeler T.R, Craufurd P.Q, Ellis R.H, Porter J.R, Prasad P.V.V. Temperature variability and the annual yield of crops. Agric. Ecosyst. Environ. 2000;82:159–167. doi:10.1016/S0167-8809(00)00224-3 [Google Scholar]
  37. Wright G.C, Hubick K.T, Farquahar G.D. Physiological analysis of peanut cultivar response to timing and duration of drought stress. Aust. J. Agric. Res. 1991;42:453–470. doi:10.1071/AR9910453 [Google Scholar]

Articles from Philosophical Transactions of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES