Sexual conflict over mating and fertilization: an overview

Abstract

Sexual conflict is a conflict between the evolutionary interests of individuals of the two sexes. The sexes can have different trait optima but this need not imply conflict if their optima can be attained simultaneously. Conflict requires an interaction between males and females (e.g. mating or parental care), such that the optimal outcomes for each sex cannot be achieved simultaneously. It is important to distinguish between battleground models, which define the parameter space for conflict and resolution models, which seek solutions for how conflicts are resolved. Overt behavioural conflict may or may not be manifest at resolution. Following Fisherian principles, an immediate (i.e. direct) benefit to a male that has a direct cost to his female partner can have an indirect benefit to the female via her male progeny. Female resistance to mating has been claimed to represent concurrence rather than conflict, due to female benefits via sons (males with low mating advantage are screened out by resistance). However, the weight of current evidence (both theoretical and empirical) supports sexual conflict for many cases. I review (i) conflicts over mate quality, encounters between males and females of genetically diverged subpopulations, mating rate and inbreeding, (ii) the special features of postcopulatory sexual conflict and (iii) some general features of importance for conflict resolution.

1. Introduction

There is currently controversy about definitions of sexual conflict, what it is, and how important it is in adaptation (e.g. Pizzari & Snook 2003; Zeh & Zeh 2003, Cordero & Eberhard 2003; Eberhard & Cordero 2003; Chapman et al. 2003a,b, Cameron et al. 2003, 2004; Arnqvist 2004; Arnqvist & Rowe 2005). While the definitions and views expressed here are my own, it is important that sexual conflict has a common philosophical and semantic base with other forms of conflict in evolutionary biology, and I have had this in mind in writing this review.

Sexual conflict is a conflict between the evolutionary interests of individuals of the two sexes (Parker 1979). A ‘conflict of evolutionary interests’ is equivalent to a potential to generate sexually antagonistic selection (see Lessells 2006). This may or may not result in overt behavioural conflict between males and females, depending on the form of the conflict and on how the evolutionary conflict is resolved. In terms of what we actually observe, it is theoretically possible either for one sex to win and the other to lose, or for some intermediate compromise.

Sexual conflict results ultimately from the fact that reproductive partners are genetically different (Lessells 1999); a mutation in one partner will not be present in the other, unless they are sibs in which case the probability of sharing the mutant allele is still below 1.0. Owing to their different genetic interests, for a given trait the two sexes may have different optima (yielding highest fitness prospects). Having different optima for certain character traits need not involve a conflict of interest between the sexes, provided the two optima can be achieved simultaneously (e.g. by sex limitation). For instance, sexual selection often operates to increase male size relative to female size. There is no obvious conflict of interest between the sexes, provided that the two optima can be achieved simultaneously, because the fitness of one partner is independent of the strategy played by the other partner. Conflict requires some interaction or common activity between males and female (such as mating or parental investment (PI)) which generates the constraint that the ideal optima for each sex cannot be achieved simultaneously (e.g. only one outcome is possible). Here, an individual's fitness is both a function of its own strategy and its partner's strategy.

The mean fitness of each sex must be equal in sexually reproducing species with a sex ratio of 1.0. Nevertheless, an individual with a mutant trait that increases its direct fitness in an interaction involving sexual conflict will, by definition, decrease the fitness of an individual of the opposite sex with which it interacts. If the trait spreads, counter selection may generate retaliatory changes in the other sex.

Sexual selection is a selective force defined by Darwin (1871) arising from competition between members of one sex for the other sex. Sexual conflict is not equivalent to sexual selection, it is a form of evolutionary conflict that may, or may not, be generated by sexual selection. For instance, male–male competition may lead to suites of male adaptations (e.g. relating to mate-searching) that have no influence on female fitness. Like parent–offspring conflict or sib conflict, sexual conflict is a potential for generating selective processes, not the selective process itself. The selective pressures it generates may become part of, or modify, the action of sexual selection. Thus, sexual conflict is not equivalent to ‘sexually antagonistic coevolution’, though this may be a product of it.

This distinction is important: we first need to define over what parameter space conflict can occur (i.e. to define the ‘battleground’, sensu Godfray 1995), and to distinguish this clearly from the question of how conflict may be resolved. Confusion can often arise from failure to distinguish between ‘battleground’ and ‘resolution’ models. Resolution models typically require many assumptions about strategic possibilities and trade offs, and typically generate a rich diversity of results. Battleground models typically make few assumptions about individual strategies, and serve to show over what parameter space conflict can occur.

Sexual selection arises ultimately from anisogamy, and a primitive form of sexual conflict may have occurred during the early evolution of anisogamy (Parker et al. 1972), such that early ova (proto-ova) might profit by fusing with other proto-ova rather than with proto-sperm (Parker 1978). The intensity of sexual selection relates to relative PI (Trivers 1972), operational sex ratio (OSR; Emlen & Oring 1977) or potential rates of reproduction (Clutton-Brock & Vincent 1991).

Though sexual conflict has experienced a dramatic resurgence of interest over the past decade (Pizzari & Snook 2003), it is not a new paradigm. Early notions of sexual conflict are implicit in Darwin (1871). It came into focus in the 1970s during the behavioural ecology revolution (Parker 2006): discussions of male–female conflict can, for example, be found in Parker (1970a, 1979), Downhower & Armitage (1971), Trivers (1972), Dawkins (1976) and Dawkins & Krebs (1979). The resurgence of interest in sexual conflict in the 1990s appeared to have occurred to some extent independently of insights from the 1970s, which may account for some of the current confusion.

Cordero & Eberhard (2003) claim that a new, narrower vision of sexual conflict is represented by female choice in which females evolve resistance rather than attraction to males (e.g. Gavrilets et al. 2001). Though its newness can be questioned (Chapman et al. 2003b), the minimization by females of costs arising from male interests certainly forms one of the consequences of sexual conflict. But sexual conflict is present in all forms of female choice involving the rejection of some males, whether rejection occurs because they are not attractive enough or because of the costs they impose. Eberhard & Cordero (2003) correctly state: ‘Inconsistent use of old, broad definitions, and new, narrow definitions has plagued recent literature on sexual conflict.’ My feeling is that it is best to retain the simple broad definition given above, and to recognize that it applies to many different biological circumstances.

My early theoretical analyses of sexual conflict (Parker 1979, but mainly completed by 1976) were little cited until interest in the topic resurged within the last decade (Arnqvist & Rowe 2005). This paper clarifies some of its conclusions, and reviews some of the many recent developments relating to it.

2. Genetics of sexual conflict

The phenotypic definition of sexual conflict can be interpreted in terms of gene action, and at the level of nuclear genes can be inter-locus or intra-locus (Chapman & Partridge 1996; Rice & Holland 1997; Parker & Partridge 1998). Cytoplasmic genetic elements are maternally inherited and require a different logic (Zeh 2004).

(a) Intra-locus conflict

Autosomal allelic variation at a locus can affect a trait in both sexes. With different optima in males and females, this may initially impose constraints on sexual dimorphism. Thus, if locus S determines body size, alleles at S could be claimed to generate conflict if the sexes have different size optima. If sex-limited gene expression can be achieved at S, to enable the size optimum to be attained in each sex, no conflict of evolutionary interest need exist between male and female phenotypes. Much may depend, however, on how quickly sex limited expression at S can be achieved (e.g. Rice 1984): initially, there will be selection towards alleles relating to the weighted mean effect of size on fitness across the two sexes, which might generate secondary adaptations and polymorphisms before the two sex-limited optima can be achieved (Rice & Chippindale 2001). For sexually antagonistic alleles occurring on the sex chromosomes, the sex linkage can allow expression to be limited to sexual phenotype. Rice (1984) thus suggested that sexually antagonistic alleles, whether intra- or inter-locus (since sex limitation may not be immediate at mutation), should accumulate on the sex chromosomes, and there is some evidence for this (Gibson et al. 2002).

More complex forms of intra-locus conflict can arise. Trivers (1974) first stressed that there can be different optima for PI between parents and their offspring. Explicit genetic models of a locus (C) determining the PI taken by each offspring showed that (unless special conditions prevail; Parker 1985; Lessells & Parker 1999) an allele at C causing an offspring to take more from its mother would be constrained (in how much PI it took) if inherited from its mother, but unconstrained if inherited from its father (Parker & Macnair 1978; Macnair & Parker 1978). There is conflict between parental male and female interests for what the offspring should take from the mother, resulting in intra-locus conflict between alleles at C. We (Macnair & Parker 1978) explicitly assumed that the allele favoured at C would be related to its mean effect (half from each parent). However, genomic imprinting allows the expression of an allele to differ, depending on whether it is inherited from the male or the female parent: it is a mechanism allowing expression to be ‘parentally sex-limited’. Moore & Haig (1991) and Haig (1992) linked this sexual conflict over the PI that offspring should take with genomic imprinting, and highlighted a new possibility: intra-locus sexual conflict expressed via offspring. Haig (1997) has called such alleles ‘parentally antagonistic’.

(b) Inter-locus conflict

Conflict can involve adaptations arising through expression between loci. Imagine two sex-limited loci: M expressed in males, F in females. Suppose that M prescribes ‘in situation X, attempt to mate’ and F prescribes ‘in situation X, attempt to resist mating’, where mating and not mating are respectively the optimal responses of males and females in situation X. There will be inter-locus conflict: any mutant allele at M or F allowing cost-free achievement of the optimal outcome for the male or female will spread. Most of the present review is about inter-locus conflict; plausibly many biological interactions between phenotypes fall into this category.

3. Male–female conflict in nature

The two major forms of sexual conflict relate to mating/fertilization and PI. But there are also several more traits over which sexual conflict can occur, e.g. conflicts over limited resources, infanticide (Trivers 1972; Hrdy 1977), mate cannibalism (Parker 1979).

Mating conflicts relate to asymmetries between the sexes in the benefits of mating versus its costs, which may be significant. They may be precopulatory, i.e. concerning mating decisions (Trivers 1972; Dawkins 1976; Parker 1979), or postcopulatory, i.e. concerning sperm use (Thornhill & Alcock 1983; Eberhard 1996). Typically, in mating or fertilization conflicts it pays a female not to mate with (or to use sperm from) the male, while it pays the male to mate and fertilize her eggs. Paternity choice may or may not be important for the female. If it is, it will normally involve conflict about fertilization.

PI involves conflict between parents concerning how much PI each should give (Trivers 1972; Maynard Smith 1977). If one parent gives more, the other can potentially increase its reproductive success at no cost to itself. There can also be a parental conflict as to how much PI a progeny should take from its mother (Haig 1992, 1997).

The present review concerns conflicts over mating and fertilization; the literature search was concluded in April 2005.

4. Male harm to females: collateral or adaptive?

Lessells (2006) stresses the need to distinguish between ‘harm’ (costly damage arising from antagonistic manipulation) and the fitness cost (which she terms ‘conflict load’) that an individual suffers when the value of the trait over which there is conflict is moved away from its optimum. The present section concerns the former.

Damage to females commonly arises as the collateral result of manipulative male traits. Examples include seminal toxins that reduce female receptivity or enhance oviposition and plugs that prevent females from remating (reviewed in Simmons 2001). These have been termed ‘pleiotropic harm’ by Morrow et al. (2003a) to differentiate them from ‘adaptive harm’, where the inflicted damage per se induces some immediate change in female behaviour or reproductive allocation that benefits the male. ‘Collateral’ may be a better term than ‘pleiotropic’ since the harm itself is actually pleiotropic in both cases (Lessells 2006). Harm can also arise from collateral effects of intra-sexual selection, rather than from manipulative traits in sexual conflict. Traits conferring a male mating advantage may have incidental costs to females (Parker 1979), e.g. the deleterious effects to females of male–male combat during pairing (Parker 1970b) or toxins that harm previously stored sperm (reviewed in Simmons 2001). In this form of harm, the collateral damage can be the selective force that creates sexual conflict.

Adaptive harm may explain (i) sexual coercion by punishment or harassment (Clutton-Brock & Parker 1995a,b), (ii) mating damage that makes it disadvantageous for females to mate again (Constantz 1984; Johnstone & Keller 2000), or (iii) changes in life history pattern (Michiels 1998; Lessells 1999, 2005). Lessells's (2005) life history model allowed continuous variation in male and female strategies and always generated of some level of adaptive harm: damage could even ‘provoke’ females into semelparity (see also §8a(ii)).

Despite the fact that penile spines (e.g. Stockley 2002) and harmful seminal toxins (see Simmons 2001) look seductively like candidates for adaptive harm, there is little direct evidence yet to rule out collateral harm. In experiments on three insect species, Morrow et al. (2003a) found no evidence that females respond to being harmed in a way that gives harming males a selective advantage over benign males, as required by the adaptive harm hypothesis. Harmed females remated sooner (consistent with Lessells's model, but inconsistent with Johnstone & Keller's) and showed either no change or a reduction in oviposition rate (inconsistent with both models). Similarly, Hosken et al. (2003) argued that collateral harm was more likely in the fly Sepsis cynipsea, where males inflict damage during mating (Blanckenhorn et al. 2002).

5. Can there be sexual conflict if the male and female share common progeny?

Sexual conflict is just one form of conflict between interacting phenotypes; phenotype-limited gene expression allows different strategies to interact antagonistically (Parker 1982). However, unlike conflicts between non-reproducing individuals, with sexual conflict genomes may mix at fertilization to produce common progeny. Can this shared interest remove the conflict?

A similar question applies in parent–offspring conflict (and initially generated claims that such a conflict could not exist). During the spread of an allele for selfishness in offspring, genes for manipulation by offspring bring a direct benefit to the individual as an offspring, but an indirect cost to the same individual as an adult because its own offspring are more likely than an average offspring in the population to carry the manipulation allele. Put another way, linkage disequilibrium between alleles at offspring manipulation and parental resistance loci creates indirect selection on each locus through direct selection on the other locus.

To answer this question, consider Fisher's (1930) now famous model for female choice of males. A beneficial trait spreads initially by natural selection, and females choosing males that have the trait are favoured because they produce progeny with the trait (now called ‘good genes’ choice). A gene causing females to prefer males carrying the trait spreads at an initially increasing rate as the male trait spreads, because of positive feedback due to the increasing mating advantage of trait through the increasing preference (called ‘Fisher's runaway’ process). If the trait is some form of mating advantage, it will typically be sex limited, but females can still benefit through their sons (the ‘sons effect’; now often ‘sexy sons’). The sons effect represents the accounting that we have to do to include the component of reproductive success (an indirect benefit) that the female gets because she has sexy sons who are chosen by (or can otherwise mate more readily with) other females. This component results from the linkage disequilibrium (positive covariance) between the trait and female preference; it may or may not lead to runaway. A final part of the Fisher process occurs if the preference pushes the male trait to a level where it becomes disadvantageous in terms of natural selection (e.g. reduced survivorship due to sexual advertisement). It is important to differentiate between ‘good genes’, ‘sons effect’, and ‘runaway’ as essentially different components in Fisher's process. Good genes would spread anyway, with or without the female preference. The sons effect can allow a trait to spread simply because females are more likely to mate with males that possess it, even if neutral or disadvantageous through natural selection. Runaway is the positive feedback process that can lead to escalating increases in the trait and preference, due to positive covariance (Lande 1981) between the male trait and the female preference genes.

Can the sons effect apply if the male trait harms the female and reduces her lifetime reproductive success? This is the subject much current debate (e.g. see Cameron et al. 2003). I analysed female interests relating to a potential mating with a male with a mating advantage that harms the female at the time of mating (Parker 1979). I sought to establish, when the male trait is rare, whether the indirect benefits due to the sons effect could offset the direct effects of the harm. When the male trait is rare, any effect of runaway is weak, and we can determine whether the harm is in female interests (and hence should be preferred) or against female interests (and hence resisted): the analysis defined the conflict battleground (not its resolution). I envisaged collateral harm, but its conclusions should also apply to adaptive harm.

Consider a rare dominant autosomal allele A at a sex-limited locus expressed in males giving a mating advantage against null allele a. Aa (or AA) male genotypes gain B times as many matings as aa males, but impose harm of cost C on females, so that (1−C) progeny are produced after each mating compared to each progeny produced after a mating with an aa male. At a locus expressed in females, will an allele for acceptance of harmful males be favoured? If it is, there is no sexual conflict because it pays females to accept the harm to gain sons with the mating advantage. If not, there is sexual conflict, and an allele favouring rejection of a harmful male will be favoured.

Suppose the female has m matings (and broods) per lifetime, and that a proportion p of broods that are progeny of non-harming (aa) males also sustain the cost C inflicted by a harming male. When A is rare, there is conflict if the value of B satisfies

$$\frac{4pC(m-1)+\mu C+1}{{(1-C)}^2}>B>\frac{1}{(1-C)}.$$ (5.1)

The first inequality gives the condition for the harmful trait to be beneficial to the female, and the second gives that for the trait to be beneficial to the male. The female's threshold for B (where costs and benefits are exactly balanced) always exceeds the male's, and thresholds are closest if only the progeny of the harmful male are affected (p=0), when

$$\frac{\mu C+1}{{(1-C)}^2}>B>\frac{1}{(1-C)}$$ (5.2)

(Parker 1979), where μ=3.

If mating advantage B is constant with respect to gene frequency, the male threshold is independent of the genetic mechanism or the gene frequency and obeys the phenotypic rule that the fitness of the harmful mutant must be greater than that of the wild type males, i.e. B(1−C)>1.

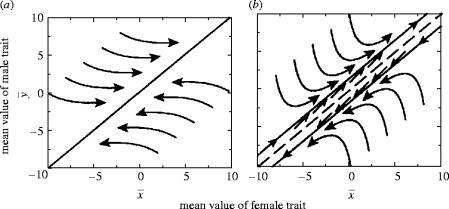
However, the female threshold depends critically on (i) the genetic mechanism for the harmful allele (Parker 1979; Andrés & Morrow 2003) and (ii) on its gene frequency (Parker 1979). Andrés & Morrow (2003) extended the above analysis to the case of sex linked genes for the harmful male trait, and showed that for Y-linkage, μ=1, giving a lower female threshold; for X-linkage, μ=7, giving a higher female threshold; and for Z-linkage, μ=3, giving the same female threshold as for the autosomal case (see figure 1). Parker (1979) showed that there would always be conflict if the dominant allele A has spread to fixation. As the frequency f of allele A increases, the curve A (for an autosomal dominant) becomes steeper, and when f=1, the curve runs straight up the y-axis. As a result, even if the initial state is in the concurrence zone, at some point in the fixation of the male trait, females must be forced into selection for resistance.

Figure 1.

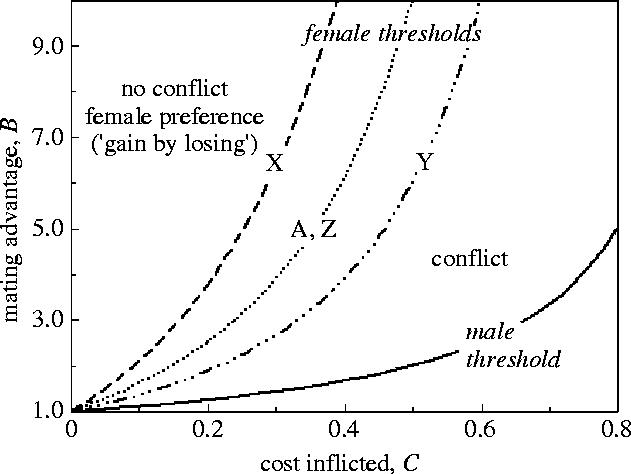
Conflict and Fisher's sons effect under different genetic mechanisms. Conflict concerns a mutant male with a rare gene that confers a male mating advantage, but has a harmful effect on the female that he mates with (see text) that affects only their joint progeny (p=0; see text). The mating advantage is advantageous to males if B lies above the lower curve. The three upper curves are the thresholds for B above which it will pay the female to mate with males with the trait (at lower B, it pays the female to resist). Conflict occurs when B lies between the male and female thresholds. The dominant autosomal case (A) is taken from Parker (1979). The sex linkage (Y, X and Z-linked) cases are plotted from the equations in Andrés & Morrow (2003) with p=0, after correcting a typographical error in their equations (10.1) and (10.2).

So if the male allele fixes before there can be counter selection at the female locus, there will always be conflict. Further, if the harmful allele is recessive, the male trait cannot be of advantage to the female when rare: in this case, there is again always conflict (Parker 1979).

In summary, coupling of male and female interests through the sons effect shows that sexual conflict cannot be assumed without elucidation of costs and benefits (Parker 1979; Cordero & Eberhard 2003; Eberhard & Cordero 2003; Córdoba-Aguilar & Contreras-Garduño 2003). Figure 1 shows that are three zones:

1. where the male trait is disadvantageous to both sexes and will not spread;

2. the sexual conflict zone—where the trait is advantageous to males but disadvantageous to females (sexually antagonistic coevolution may occur between the traits at the male locus to increase B, and those at the female locus to avoid mating with harmful males and/or to diminish harmful effects);

3. the concurrence zone—where the trait is advantageous to both sexes (selection favours both the harmful trait in males and female traits to accept or prefer males with the trait).

Note that the model asks the question whether female acceptance or rejection will spread when the harmful trait in males is relatively rare: it does not include Fisher's runaway, which only occurs if the trait is favourable to the female. Thus, if we are the concurrence zone (iii), runaway may accelerate fixation of the harmful trait, while simultaneously increasing benefits through the sons effect as female preference for the harmful trait increases in the population. If we are in the conflict zone (ii), we would expect sexually antagonistic coevolution at the female locus (for reduction of conflict load by rejection of males with the trait and/or for reduction of its harmful effects), unless a maladaptive preference gene in females can by chance drift to a sufficiently high level.

The above arguments assume nuclear gene transmission. Cytoplasmic genetic elements are exclusively transferred through mothers. Owing to this strict maternal inheritance, cytoplasmic genetic elements may suffer the direct costs of male manipulation but can receive no indirect benefits from the production of sexy sons. Zeh (2004) has thus concluded that there will be perpetual sexual conflict between nuclear genes coding for male manipulation and cytoplasmic genetic elements that promote female resistance, because there can be no sons effect to offset the direct costs of male harm.

6. Conflict or concurrence?

Section 5 showed that the sons effect may or may or may not be strong enough to bring about concurrence rather than conflict. Most literature on sexual conflict assumes selection to be operating in the sexual conflict zone, both at a general level (e.g. Chapman et al. 2003a,b), and at the level of specific, harmful, male adaptations (e.g. Crudgington & Siva-Jothy 2000; Stockley 2002), and evidence that there has been female counter adaptation to such adaptations is sometimes available (e.g. Reinhardt et al. 2003; Morrow & Arnqvist 2003; Wigby & Chapman 2004).

The alternative view, expressed particularly by Eberhard and co-workers (Cordero & Eberhard 2003; Eberhard & Cordero 2003; Eberhard 2004, 2005) is that most adaptation can be explained by concurrence: selectively allowing males to win may ensure that the female gains indirect benefits through sons—females can effectively ‘gain by losing’ (Eberhard 2005). Thus, for instance, Eberhard (2002) argues that apparent female resistance against male persistence might represent a form of ‘screening’ where poor quality males (with low mating advantage) are rejected and high quality males eventually accepted. While this cannot be ruled out without due cost/benefit accounting for given cases, varying degrees of resistance would be a prediction from the evolutionarily stable strategy (ESS) conflict resolution models (e.g. see §8a).

The term ‘gain by losing’ must be qualified. Eberhard (2005) uses it in the context of gaining indirect benefits via sexy sons. Females may ‘gain by losing’ without the sons effect. It can be in female interests to acquiesce to mating simply because the direct costs of resistance are greater than the costs of allowing mating (Parker 1970a, Arnqvist 1989).

But while a harmful allele can spread within a population and still be in the interests of both sexes (i.e. it is in the concurrence zone, figure 1), the conditions for the initial spread of harmful dominant genes in figure 1 are the most optimistic for that conclusion (Parker 1979). They assume that harm is restricted to just one of the female's m clutches: the conflict zone increases if more of the female's reproductive success is affected, since her direct costs are increased. They also show that there is a large zone where conflict will apply, and if indirect genetic benefits are relatively weak (Møller & Alatalo 1999), ‘agreement’ can occur only if the cost imposed by males is small (Parker 1979; Andrés & Morrow 2003).

Indirect benefits to females preferring males with harmful traits are diluted because they arise only through sons, whereas direct costs to females are undiluted. More specifically, Cameron et al. (2003) used a genetic covariance argument to show that the indirect benefits scale by a factor less than the direct effects (see also Kirkpatrick & Barton 1997). Further, while there is no certainty that the biology of sexual conflict need follow the assumptions of the current equilibrium models, indirect effects via sons in such models are neutral at the equilibria (see also Kirkpatrick 1985, 1988; Gavrilets et al. 2001, Cameron et al. 2003) though they can affect the position of the equilibria (Kokko et al. 2003). Thus, the argument that indirect benefits via sons are generally expected to be a weak force in the face of direct selection to avoid the trait is probably often justified (Parker 1979; Cameron et al. 2003; Chapman et al. 2003a,b) but this view is strongly contested (Cordero & Eberhard 2003; Eberhard & Cordero 2003; Eberhard 2004, 2005). Eberhard (1985) proposed and has consistently argued (e.g. Eberhard 2001) that most of male genital adaptation represents the product of Fisherian sexual selection through copulatory courtship processes, and interprets evidence for genital evolution in this light (Eberhard 1996, 2004), i.e. essentially as the result of cooperative adaptive processes between the sexes. The alternative view that much of genital evolution arises through sexual selection processes involving sexual conflict is equally strongly argued (e.g. Arnqvist 1998; Arnqvist & Rowe 2002). A review is given by Hosken & Stockley (2004).

This controversy cannot be fully resolved for particular adaptations without detailed assessment of all costs and benefits, including measurement of indirect effects via sons, which are rarely measured (but see Wedell & Tregenza 1999). So far only Orteiza et al. (2005), in an elegant test using Drosophila, have clearly shown that indirect benefits via sons are insufficient to account for indirect costs to females of (i) seminal fluid and mating and (ii) persistent male courtship behaviour, suggesting that they represent cases of conflict rather than concurrence. The theoretical arguments also currently favour conflict (see Cameron et al. 2003), but here perhaps history urges caution (Andersson 1994; Eberhard & Cordero 2003). Plausibly, some cases represent conflict and others concurrence; this can only be established empirically.

7. Sexual conflict and female choice: equilibrium models

Many models include Fisher's sons effect to predict how female choice should stabilize in terms of population states. They do not attempt to analyse how the mating decision conflict is resolved (i.e. what happens when the male encountered is unacceptable to the female), but instead make assumptions about this in order to deduce how female choice and male traits will evolve, and the characteristics of the population state at equilibrium.

Thus, since Lande's (1981) pioneering approach, analyses of Fisherian choice have tended to be equilibrium models that make assumptions about the genetic variance available and the probability that a given female will mate with a given male. These typically generate lines of equilibria between the male trait and the female preference (similar to that in figure 3a), but the system may collapse to zero female preference and male trait expression if there are costs of the preference (reviewed in Day 2000), though this need not always be so (Day 2000). The distinction between choice for good genes (where females gain increased fitness through beneficial genes in males) and what is termed ‘Fisherian’ sexual selection (where the sexual advertisement proceeds beyond the optimum set by natural selection) may be spurious, since the sons effect must be included in all aspects of female choice, making the two a continuum (Kokko 2001; Kokko et al. 2002). Thus, males that are attractive but have reduced viability are still cases of good genes, if, when the son's effect is included, the net gain to the female by choosing them is positive. Conceptually at least, as we have seen in §6, the same applies when a male advantage inflicts direct harm as long as the net gain to the female by choosing harmful males is positive.

Figure 3.

Dynamics of mean trait values in Gavrilets (2000) model. (a) Costs of sexual conflict are low. Depending on where mean trait values start (above or below the line of equilibria), the trajectory is towards the line of equilibria at $\overline{y}=\overline{x}$, at which the trait values become static. (b) Costs of sexual conflict are high. Points along line $\overline{y}=\overline{x}$ are now unstable equilibria. Direction of changes again shown by arrows; coevolutionary chase occurs along the continuous lines. Reproduced with permission of S. Gavrilets and Nature Publishing Group (http://www.nature.com).

What happens in equilibrium models when female choice is modelled as avoidance of less harmful males rather than a preference of more attractive ones? There are clear parallels (e.g. Getty 1999). Indiscriminate mating has high costs that could be reduced by increased female choice (Holland & Rice 1998). Gavrilets et al. (2001) studied female choice (by resistance) in a quantitative genetics model for sexual conflict over mating rate, in which females have a specified probability of mating which is a function of the males ‘harm ‘level’, and showed that a wide range of conditions could generate costly female choice and exaggerated male harm traits, leading to a stable equilibrium, or more rarely, a stable limit cycle. In a modification of a previous model (Kokko et al. 2002), Kokko et al. (2003) modelled costly female effort to ‘screen’ males. At equilibrium females show higher preference (resistance) than they would if they minimized the direct costs of mating, because of the sons effect due to the mating advantage of their fathers.

In an equilibrium model designed explicitly to test whether indirect benefits can generate preference rather than rejection, Kokko (2005) allowed a male trait (dominance or coerciveness) to improve a male's mating success. Resistance by females reduces male benefits from being dominant, while female preference enhances the benefits gained by dominant males. In keeping with previous analyses, females may evolve to resist costly mating attempts as a counterstrategy to male traits, particularly if male dominance is environmentally determined (and hence devoid of sons effect) rather than genetically determined. However, indirect benefits are also predicted to influence female mating behaviour, and if sufficiently strong, could produce female preferences for males that harm them, confirming the conclusion that concurrence cannot always be dismissed (Parker 1979; Eberhard & Cordero 2003).

Moore & Pizzari (2005) propose a new approach to sexual conflict evolutionary dynamics based on theoretical quantitative genetics of interacting phenotypes: the phenotype of one sex is seen as a genetically influenced evolving trait as well as the (evolving) social environment in which the other sex evolves.

Note that models of Fisherian choice (as well as Red Queen and mutual mate choice, §8) could be termed ‘partial resolution’ models (they resolve the evolutionary or population dynamics of choice given certain assumptions about what happens when a male and female meet, but not the mating decision conflict in given male female encounters). Most assume either probabilistic mating preferences, or that mating occurs only when in the interests of both partners (i.e. they do not resolve the mating decision conflict). Individual mating decisions under sexual conflict (i.e. where mating benefits one partner but not the other) are not analysed strategically (i.e. by allowing male and female players to employ various strategies to shift the trait towards their own optimum) by game theory as in ESS models (§8).

Mating biases need not imply active mate choice by females; they can arise as artefacts of other processes (e.g. sexual advertisement competitions involving passive attraction of females; Andersson 1982; Parker 1982). Friberg & Arnqvist's (2003) experiments suggest that male courtship in Drosophila melanogaster is costly to females per se, and that apparent female preference for large males is, at least in part, a by-product of sexual conflict over mating rate.

The models outlined in the following sections consider resolution outcomes for inter-locus conflict between two sex-limited loci, but for simplicity often omit indirect benefits due to the sons effect.

8. Resolution models: ESS and red queen

Though the distinction is somewhat arbitrary, approaches to conflict resolution can be categorized into two types: ESS (Maynard Smith 1982) models and ‘Red Queen’ models of coevolution involving endless change through evolutionary time (van Valen 1973). ESS models examine evolutionary stability at the level of strategic adaptation of individuals in competitive interactions, but typically say little about evolutionary (or population) dynamics. They usually ignore genetics and assume that individual phenotypes perform various ‘strategies’ (the ‘phenotypic gambit’; Grafen 1984). They rely on a game-theory approach and seek a strategy which, when fixed in the population, cannot be invaded by any rare mutant strategy (Maynard Smith 1982). The rules of each game are precisely specified: these include the possible strategy sets and the payoffs arising from interactions of different strategies at different frequencies in the population, using plausible assumptions about the biological trade-offs and constraints. Such models may yield continuous change if there is no continuously stable ESS (e.g. Parker 1979, 1983a).

In contrast, the Red Queen approach assumes that there can always be new counterstrategies to existing strategies (the rules of the game constantly change). Red Queen models of sexual conflict make certain assumptions about genetics (e.g. Gavrilets & Waxman 2002) and/or trait distributions (e.g. Gavrilets 2000), and since new strategies can arise that can beat former strategies, continuous coevolution of male and female strategies is allowed, and is often generated. As in models of mate choice outlined in §7, there is usually less strategic specification of what individuals might actually do in competitive interactions, but more focus on evolutionary dynamics and population states (they are partial resolution models). However, it should be stressed that these differences are not really an intrinsic property of the two sorts of model (ESS versus Red Queen); rather, they are a reflection of how modeller's have set them up. Red Queen models also contain certain constraints, and may lead to equilibria under some conditions (e.g. Gavrilets 2000; Gavrilets & Waxman 2002).

(a) ESS approaches

Most ESS models applicable to sexual conflict are reviewed elsewhere (Clutton-Brock & Parker 1995a) and will be covered only briefly here. They are asymmetric games, since the value of winning and the costs involved in competing will differ for males and females. The asymmetric war of attrition and the arms race (opponent independent costs) game were originated for sexual conflict and first approached by simulation (Parker 1979), then later developed analytically for animal contests (Hammerstein & Parker 1982; Parker 1983a), and finally reapplied to sexual conflict (Clutton-Brock & Parker 1985a).

Several game theory models are relevant to resolution; but their application to sexual conflict has sometimes been by conjecture rather than formal analysis (e.g. Clutton Brock & Parker 1995a). Some models concern behavioural strategies, others relate to arms races in which strategies are morphological or physiological investments and winning relates to escalating armament beyond that of the opponent's arms level. Real mating conflicts must in reality consist of both behavioural games and arms races, and a recent behavioural model (Härdling et al. 2001) includes an arms race element.

(i) Behavioural models

The asymmetric war of attrition

Individuals meet in one-off (i.e. unrepeated) dyadic interactions, and gain information about differences in their fighting abilities and values of winning before the contest. In a war of attrition, contestants compete by costly persistence—the winner is the individual who persists longer in the contest, the choice of persistence times occurring before the contest begins (Maynard Smith 1974). Harassment contests (e.g. where males persistently attempt mating while females resist) may be asymmetric wars of attrition (Parker 1979; Hammerstein & Parker 1982; Clutton-Brock & Parker 1995a,b). At the ESS there may be some persistence and rejection, depending on mistakes in assessing self's and opponent's values of winning (opportunity cost difference between winning and losing) and contest costs (related to fighting ability or some other ‘power’ component). Although in a given context one sex will tend to win, it will not always do so and contests may occasionally be protracted. Where V_m and V_f are respectively the male and female's values of winning, and c_m and c_f the rates at which their costs accrue during a contest, the winning role (likely most often to win, though there may or may not be some harassment first) is occupied by the opponent with the higher value for V_i/c_i. High asymmetries in value of V and c typically generate short contests, with outcomes usually related to sex; low asymmetries give long average contest durations where outcomes are weakly correlated with sex.

Sequential assessment game

This model is also for one-off dyadic interactions, and again related to male persistence and female resistance. Opponents have little information about asymmetries in values of winning and fighting abilities (or some other power component) before a contest, and information is gained during the contest itself (Maynard Smith & Parker 1976). The most advanced version is the sequential assessment game (Enquist & Leimar 1983, 1987). Each contestant's estimate of relative fighting ability becomes more accurate with successive rounds in the contest (the sample size increases). The predictions are similar to the asymmetric war of attrition: if V_m and V_f are the male and female values of winning and c_m and c_f the average contest costs per round, the opponent most likely to win is that with the higher value for V_i/c_i. High asymmetries in value of V or c generate short contests, with outcomes usually specified by sex; reducing these asymmetries generates long contests that have outcomes poorly specified by sex.

The punishment game

This game with discrete strategies and multiple rounds was intended for repeated dyadic contests in social groups (Clutton-Brock & Parker 1995a,b), where one individual is more powerful than the other. Suppose that dominant males cannot enforce mating, but are more powerful than females (which cannot effectively retaliate). Under conditions of sexual conflict, females could cooperate and allow mating, or be non-cooperative and resist. Males could either play punish (if a female does not cooperate) or non-punish. Learning is involved: in the first rounds, the female fails to cooperate but may learn to cooperate. There are two ESSs: punishing males and cooperative females, or non-punishing males and non-cooperative females. For large power asymmetries, the ESS is more likely to be that the weaker party loses, by coercion (Clutton-Brock & Parker 1995a,b).

Härdling's et al.'s model

Härdling et al. (2001) analysed a general conflict resolution model for agonistic encounters (it can be also be used to investigate arms races), and discuss its relation to sexual conflict. Across a continuous range of outcomes x, males and females have different optima (x_m, x_f). The interaction is asymmetric, so that one party has greater ‘control’ (or power). Both parties can ‘invest’ k in a behavioural ‘arms race’ and shift the outcome in its preferred direction and (as in the arms race model below) the opponent with more power wins the interaction. As the optima (x_m, x_f) differ, k increases, and the ESS is achieved at some intermediate compromise x^* between x_m and x_f. Although costly behaviours are necessary for the compromise to evolve, there may be no costs at the ESS. In the version featured, Härdling et al. assumed explicitly that contest costs are proportional to k_i(x_m−x_f), i.e. to the arms level multiplied by the difference in values of x chosen. So no costs of armament or behavioural interaction are felt at the ESS (they occur only if males and females choose different values for x). This version of their model is therefore best seen as a behavioural model, rather than a true arms race model.

(ii) Arms race models

Arms race or opponent-independent costs game

A strategy is a ‘choice’ (over evolutionary time) of a morphological or physiological arms level (Parker 1979). The contestant with the higher arms level wins. Armament has a cost that increases with arms level, but there are no significant contest costs as in the behavioural models (hence ‘opponent-independent costs’ game). Values of winning (V) and costs of increases in armament (c) are assumed to be asymmetric (figure 2), since they will differ for males and females. Thus, suppose that arms levels are balanced so that the outcome of the conflict interaction is random. If (during evolution) the female's arms level increases by marginal cost c_f, then to balance this, the male's arms level must increase by marginal cost c_m (slopes of the lines, figure 2): ‘power’ relates to the inequality between c_f and c_m. Early versions of this game (Parker 1979) assumed a strategy to prescribe an armament level exactly, and failed to generate any ESS (reviewed by Parker 1983a). Cycling of arms levels (‘unresolvable evolutionary chases’; Parker 1979) occurs as follows (figure 2): suppose that females have a low arms level, then any mutant male with an arms level just sufficient to win will be favoured and will fixate (the best strategy is to play an arms level marginally higher than females). This in turn is beaten by a similar female retaliation, and arms escalation proceeds to a maximum defined by the sex with the lower V_i/c_i (value of winning)/(contest cost rate) value, at which point the sex with the higher V_i/c_i can still increase and receive positive payoffs (i.e male in figure 2). At some point, the cost that individuals of one sex (i.e. female in figure 2) would have to pay for the arms level that would beat the other sex becomes higher than the benefit of winning. This sex is then selected to reduce its armaments to zero, because its net fitness is higher by losing, but not paying any costs, than by paying the level of costs that are necessary to win. The other sex is then selected to reduce its level of armaments to just above zero, because it still wins but pays much smaller costs. And the cycle then repeats (figure 2).

Figure 2.

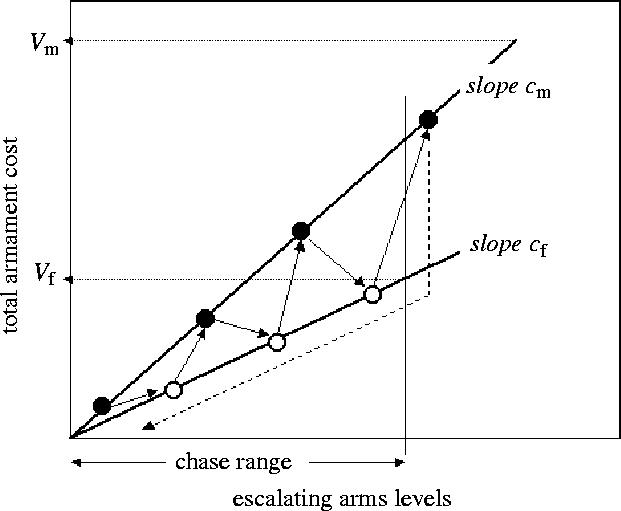
The evolutionary chase in the sexual arms race model (Parker 1979). Total arms costs are plotted against arms levels for the two sexes: at a given point on the x-axis, the total arms for each sex are exactly balanced so that the chances of winning the conflict are random, otherwise the sex with the higher arms level wins. In this example, the value of winning for females (V_f) is lower than that for males (V_m), and the slope of the total costs with escalating arms levels is lower for females (slope c_f) than for males (slope c_m). If females start at a low arms level, males can win by a slightly greater level, which females can then outbid, and so on. As arms levels escalate, females would first reach the point where their total arms costs equal their value of winning: males can still outbid them and achieve a positive payoff. At this point females do better to reduce their arms to zero, which allows males also to reduce to a very low level. The cycle then begins again.

Arms races with probabilistic outcomes

A simple change to the model may radically alter the solution (Parker 1983a; see also Maynard Smith 1982): an ESS can occur if sufficient variation (‘noise’) surrounds an arms level (e.g. due to growth, or random environmental effects). If (say) males pay an armament cost K, and their arms level realized, R, is not fixed (as in the model just described), but drawn from a probability distribution p_M(R). Females pay J, with arms are drawn from p_F(R). Where an ESS exists, it depends on the form of p(R). With two classes of opponents (e.g. males, females), it is suggested (Parker 1983a,b, Clutton-Brock & Parker 1995a) that at the ESS (i) males pay cost K^*, and females J^*, and have overlapping ESS arms distributions—males, $p_{\text{M}}^{*}$(R); females, $p_{\text{F}}^{*}$(R); and that (ii) the opponent with the higher V_i/c_i has the higher mean arms level (and hence winning more often) though this remains to be proven analytically.

Härdling (1999) investigated the arms race (opponent-independent costs) game for symmetric conflicts such as male–male contests. Following Parker (1983a), the probability of winning was probabilistic (rather than all or nothing, as in Parker 1979), increasing as the arms level of the opponent with the higher arms level exceeds that of his opponent. Härdling showed that there was convergence to an ESS level of armament if arms costs increased faster than linearly; with slowly increasing costs, cyclically fluctuating arms levels occurred. Linear costs generated neutrally stable cycles. In a rather specific extension of this model to the asymmetric sexual conflict case where the armament traits are investments in male or female ‘aggressiveness’, Härdling et al. (1999) found that ‘male win’ or ‘female win’ outcomes were possible, with only the sex with most to lose investing in aggressive armament. If arms levels show escalating costs, a stable ESS pair of arms levels can occur (rather as predicted by Clutton-Brock & Parker (1995a) for the sexual arms race game with environmental variation in arms levels) and conflicts should be most costly when payoffs are symmetric.

Härdling & Smith (2005) stress that arms costs will limit arms races; this is the reason that the cycles in the original arms race game occurred across the zone of positive payoffs for the limiting opponent (i.e. the opponent with the lower value for V/c, see figure 2). Härdling & Smith (2005) analyse a specific version of the Härdling et al. (2001; see §8a(i)) model where arms costs can lead to population extinction (see also Kokko & Brooks 2003). Their model predicts a compromise with small conflict costs for the population if costs are in addition determined by the extent of overt behavioural conflict between the sexes, in which case the ESS can be for stable relatively low arms levels (see §8a(i)). They point out that many sexual conflicts may go unseen because the ‘costs of disturbing the compromise for each sex outweigh the benefits of improving the situation’, generating an apparently harmonious compromise solution.

Adaptive harm models

Two of the adaptive harm models (see §4) are forms of arms races. In Johnstone & Keller's (2000) model, male harm to females can be varied continuously, and can be adaptive because it may reduce the chance that his mate will copulate again (females mate either once or twice before oviposition). Their game theoretical model showed that harm (toxicity) as a means of inhibiting remating is stable over a wide range of conditions, though other selective pressures may (under some conditions) account for its initial evolution. Toxin transfer should be more common (and more harmful) in species with a last-male mating advantage; it is also most likely where costs to females are strongly accelerating. Lessells (2005) modelled adaptive harm more extensively, as a stochastic dynamic game in which males have a continuous choice of harm that they inflict on females, and females a continuous choice of oviposition rate, and a choice of whether or not to remate. Some level of harm (which has the sole immediate effect of reducing female survival rate) is always an ESS, and non-damaging populations can always be invaded by damaging male mutants. Male harm to females evolves because it is in female interests to increase oviposition rate (which is beneficial to males), and despite its effect on remating interval (which either remains constant, or decreases against male interests).

(b) Red Queen approaches

Rice & Holland (1997), Rice (1998), and Holland & Rice (1998) have also proposed that sexual conflict can drive endless coevolutionary chases (‘chase-away’; Holland & Rice 1998) between male and female strategies. Especially rapid evolution occurs in reproductive tracts (Eberhard 1985, 1996) and in some gamete proteins (e.g. Palumbi & Metz 1991)—Rice and Holland argue that these may relate to chases arising from fertilization conflicts. Continuous new mutation allows existing strategies of the opposite sex to be beaten, in turn promoting the opportunity for new counterstrategies, hence the Red Queen analogy. In pioneering selection experiments on Drosophila, Rice (1996) prevented females from coevolving with males, which were allowed to adapt to the static female genotype. The resultant male adaptation markedly reduced the static females’ survival. Holland & Rice (1999) demonstrated that males from lines under enforced monogamy (eliminating sexual conflict) were less harmful to referent females, and monogamous-line females died faster than control-line females after mating to control-line males. These effects were due to reduced virulence in males in the monogamous lines, which also evolved higher mean fitness (offspring per female), probably as a result of reduction in conflict costs (Holland & Rice 1999). Although these results do not confirm that sexual conflict in natural Drosophila populations results in Red Queen dynamics, they are very important in demonstrating that the expected changes predicted through selection occur in response to changes in sexual conflict.

Other analyses also suggest male–female coevolution. In a meta-analysis of water strider mating systems, Arnqvist & Rowe (2002) found evidence for antagonistic coevolution in relative abilities of male and female to control premating struggle outcomes. Mating rate is high in species where males have a relative advantage, and low where females have a relative advantage. Their analyses found no consistent evolutionary tendency towards or away from male or female relative advantage.

Gavrilets's (2000) now famous formal model of Red Queen sexual conflict specifies individual payoffs in relation to traits and population states, but has the Red Queen property that strategies can continuously change. He considered a population with Gaussian distributions for two sex-limited quantitative traits, x for males (or sperm) and y for females (or eggs). The probability that that a given x and y are compatible (i.e. mate or fuse) was determined by a quadratic function giving a maximum value of 1.0 when x=y. Mating probability is maximal when the absolute difference between the traits is zero, and falls off to either side as the absolute difference increases. Female fitness initially increases as the number of compatible mates increases, then declines because of adverse costs of multiple mating. In contrast, male fitness is maximized by having the highest probability of mating (i.e. there is sexual conflict over mating rate, §10b). The male's optimal solution is to match the mean trait value for the female (i.e. for $\overline{y}=\overline{x}$) and the female's optimum differs by some fixed amount depending on conditions; the difference represents the battleground. There were two dynamical solutions. Where sexual conflict (strictly, the female fitness reduction for mating with all males) is low, males win (figure 3a): trait matching evolves to a line of equilibria with $\overline{y}=\overline{x}$ (as in models of female choice, Lande 1981). If sexual conflict is higher, neither sex wins: a chase occurs in which $\overline{x}$ and $\overline{y}$ simultaneously increase or decrease, depending on the starting conditions (figure 3b).

Gavrilets & Waxman (2002) relaxed the assumption of Gaussian distributions for traits x and y, instead using an explicit genetic model (sexual haploid population with two multi-allelic loci for x and y). This showed that, in addition to the coevolutionary chase (characterized by low genetic variation), sexual conflict over mating rate can generate two other solutions, depending on conditions. In one, females diversify into separate groups, ‘trapping’ males in the middle. In the other, males diversify in response to female diversification, so that reproductive clusters of isolated genotypes form sympatrically.

Rosenthal & Servedio (1999) distinguished between two components of female resistance (preference): the female's threshold for acceptance (mating threshold), and her sensitivity to the male trait (persistence). Gavrilets's (2000) model assumed that the female's probability of mating is of fixed shape (her ‘sensitivity’ is fixed), and only her mating threshold (the 0.5 mating probability value) changed in evolutionary time. In a major development of Gavrilets's model, Rowe et al. (2005) used an essentially game-theoretic (ESS) approach in which the male persistence trait (P), the female's mating threshold T, and the form of the female's mating probability function (its sensitivity S) could change strategically, and added an underlying natural selection component to each coevolutionary feature (P, T and S each has an intermediate, naturally selected optimum). Allowing female sensitivity to vary strategically much reduces the range over which coevolutionary chases occur. The strength of natural selection acting on female sensitivity determines the extent to which female (=population) fitness is depressed by antagonistic coevolution. Coevolutionary chases are likely only when natural selection is strong, and population fitness can be strongly reduced. Female indifference (insensitivity to the male trait), with little reduction in population fitness, is favoured when natural selection is weak. This has some similarity to the finding that the original sexual arms race model without environmental variation in arms level yields coevolutionary chase (Parker 1979), while sufficient environmental variation in arms level (equivalent to ‘insensitivity’) generates a stable ESS solution (Parker 1983a,b; see §8a(ii)).

Moore & Pizzari's (2005) approach using theoretical quantitative genetics may also generate Red Queen processes. They envisaged evolution of multiple traits, rather than exaggeration of the same traits, with cycles of novel male traits and novel female responses continually evolving. They proposed that this will be likely if, when a new male strategy is successful in counteracting a successful female response to male manipulation, selection on the original response and manipulation is reduced, and outlined a plausible series of adaptations and counter-adaptations in the reproductive biology of the cockroach, Nauphoeta cinerea (see also Moore & Moore 1999; Moore et al. 2001).

9. General principles determining outcomes

This section attempts to generalize the features that will be important in determining the outcome of mating conflicts. Depending on the assumptions about costs and benefits and how male and female strategies interact, almost all forms of outcome are possible, including stable ‘one sex wins, other loses’ solutions, stable intermediate compromises and continuous evolutionary chases. Empiricists can be guided only by assessing the relevance of the assumptions of given models to the constraints apparent in their study system, and by the question they wish to answer.

The two features that determine qualitatively where the outcome is most likely to polarize in the conflict battleground are ‘power’ and ‘value of winning’ (Parker 1979; Clutton-Brock & Parker 1995a,b; Parker & Partridge 1998).

The power component relates to asymmetries between the sexes in costs of competing, e.g. the different rates c at which costs accrue in persistence contests, the costs of enforcing victory in arms races (slopes c_m, c_f in figure 2), or relative abilities to inflict punishment. All things equal, the sex with the higher power has better prospects. Costs are not easy to predict; even if males are much larger than females, it may be less costly for females to prevent mating than for males to achieve it against relatively uncostly resistance (but see Magurran 1998). For example, where the males lack a penis, it may be difficult to transfer sperm to the female tract unless the female cooperates. Nevertheless, enforced copulation appears to occur (e.g. Thornhill 1980), and need not be characterized by overt resistance (Shine et al. 2003). Inability to transfer sperm by force need not imply that the female must generally occupy the winning role: persistent harassment by males is likely to impede females in various deleterious ways, and she may gain by avoiding such costs (Parker 1970a).

Value of winning in general relates to opportunity cost: it is the fitness difference between mating and not mating, or V of the above models. V is likely to be greater for the male: he is often assumed to gain offspring if fertilization occurs, but nothing if it does not (i.e. the missed opportunity value is zero). For the female, V depends on features such as the difference in offspring fitness due to the present male versus another of possibly higher quality, or to remating costs if she already contains sperm. Note that opportunity cost V in mating conflicts will be altered by the outcome of postcopulatory conflict (§13).

Ultimately, the ratio of value of winning to contest costs, V_i/c_i, may be the best predictor of the balance of the outcome, with the sex having higher V_i/c_i under stronger selection to win and most likely favoured at resolution, or adapting faster in evolutionary chases. Since power increases with 1/c_i, this rule is equivalent to the balance being in favour of the opponent in role i, with the higher value for the product of power (1/c_i) and value of winning (V_i), i.e. to the inequality V_i/c_i>V_j/c_j (Parker 1974a, Hammerstein & Parker 1982). For instance, in a war of attrition lasting time t, the opponent in role i can still achieve a positive payoff at the point where j (even if it wins) will exceed its ‘fitness budget for fighting’ (V_j=tc_j), whereas j cannot (Parker 1974a). In the arms race model (Parker 1979), chases in arms levels occur across the zone defined by the lower ratio (V_j/c_j; figure 2).

The potential for mutation may also be important. Since the sex ratio is approximately unity in most species, any mutation imbalance favouring the commoner sex is likely to be marginal. For gametes this is not so, and sperm may have a much greater mutation potential, either due to the higher number of spermatogonia than oogonia, or if there is haploid expression, due directly sperm versus ovum numbers (Parker 1978). This may form an important difference between mating conflict and fertilization conflict (§13).

10. Precopulatory conflict: mating decisions

The previous sections have discussed sexual conflicts very generally. This section examines some specific mating decision conflicts, and some approaches to defining the battleground for each one. In one case (mate quality threshold conflicts), partial resolution solutions are discussed.

There are three possibilities (Parker 1979, 1983b) in an encounter between male and female: (i) it pays both to mate; (ii) it pays neither to mate; (iii) mating conflict—mating is advantageous for one but not for the other: males usually occupy the role in which mating is favourable, and females the role in which it is unfavourable; roles may (atypically) be reversed if there is sex role reversal in PI. Mating decision conflicts occur in various contexts: mate quality, incest, matings between sibling species, etc. Parker (1979) identified the thresholds at which these three possible outcomes would occur, defining the zone of conditions for mating conflict to occur (the battleground). It will be greatest where the male PI is zero.

A time-based logic for male and female activity has been used to model the effect of variable PI, originating with Parker (1979). Each sex takes a (search) time S to acquire a mate, and a time G taken to mate, care for offspring, and replenish spent gametes (figure 4). Clutton-Brock & Parker (1992) termed these ‘time in’ (S) and ‘time out’ (G) of the mating pool, respectively S_m and G_m for males, and S_f and G_f for females. This logic has been used in various forms by several authors (e.g. Hubbell & Johnson 1987; Clutton-Brock & Parker 1992; Parker & Simmons 1996; Parker & Partridge 1998; Kokko & Johnstone 2002). The ratio of times in (G_m/G_f) relates to relative PI (sensu Trivers 1972), and the ratio of times out S_m/S_f (linked with sex ratio) relates to OSR (sensu Emlen & Oring 1977).

Figure 4.

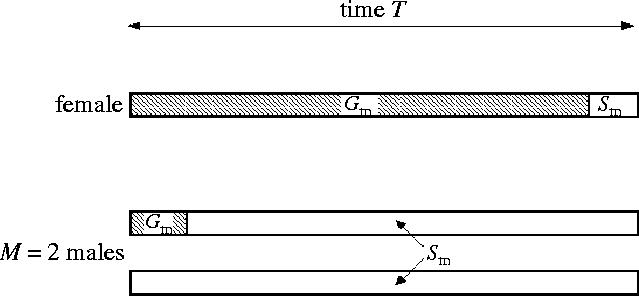
Time in (for males S_m; for females S_f) and time out (for males G_m; for females G_f) of the mating pool for the typical case where male PI is small relative to female PI (G_m<G_f). In this example, the adult sex ratio is M=2 males per female, so in time T (one cycle of reproduction for the female) one male will mate and then spend time out G_m replenishing gametes. Thus, the average time in per male is given as S_m for the two males, after equation (10.1). Modified from Clutton-Brock & Parker (1992) and Parker & Simmons (1996).

For the simple case in which each female mates once per reproductive cycle (i.e. avoiding complexities such as ‘collateral investment’ sensu Parker & Simmons 1996), if the total reproductive cycle of duration for a female is T time units,

$$S_{\text{f}}+G_{\text{f}}=T=(S_{\text{m}}+G_{\text{m}})/M,$$ (10.1)

where the adult sex ratio is M males to each female (figure 4). Viewing G_f, G_mas constants, male search time S_m=MT−G_m, and so increases with MT. The searching male density is proportional to S_m/MT=λ, and so Clutton-Brock & Parker (1992) took the female's search time as inversely proportional to this, i.e. S_f=B/λ, where B is a constant relating to the ‘aptitude for encounter’: the lower B, the more quickly the sexes meet.

(a) Mate quality thresholds

Mate choice is a vast and much studied area in biology (see Andersson 1994; Jennions & Petrie 1997). Optimal mate choice models began with a model for a fixed threshold decision rule (Parker 1979), and a ‘best of n’ sampling process (Janetos 1980). I used a marginal value rule to deduce the battleground for mate quality conflict by comparing what would each sex should do if all individuals of the other sex are willing to mate (Parker 1979, 1983a,b); if one sex is indiscriminate this gives the optimal mate choice rule for the other sex. Thus, we start with random mating and ask what rule would a mutant with optimal mate choice show in this population. For mutual mate choice (both sexes choosy) this defines the zone of conflict for, not the resolution of, mate quality decisions. For sex j, the optimal acceptance threshold is a threshold quality of a given sex i, $Q_i^{*}$: if $Q_i>Q_i^{*}$, j should mate, if $Q_i<Q_i^{*}$, j should reject. Owing to PI disparity, the optimal acceptance threshold for females viewing males, $Q_{\text{m}}^{*}$, is generally much higher than the threshold,$Q_{\text{f}}^{*}$, for males viewing females: the female's search costs are typically trivial compared to the male's, favouring much higher choosiness (figure 5). In many cases it will be optimal for males not to be choosy at all, especially if there is trivial male PI and little variance in female quality (Parker 1979, 1983b). Choosiness is increased by (1) high variance in mate quality of the opposite sex; (2) high ‘aptitude for encounter’ (the physical property relating to encounter rates in a species); (3) high relative PI. These conclusions have been confirmed by more advanced recent analyses (e.g. Kokko & Johnstone 2002).

Figure 5.

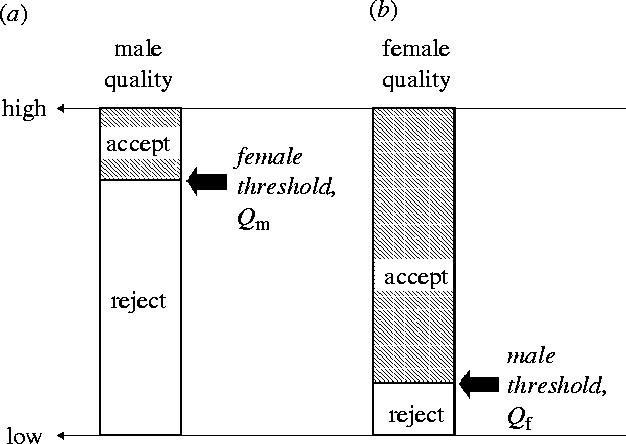
Ideal acceptance thresholds for the two sexes in encounters under random search. Owing to the typical difference in PI, ranking males from highest to lowest quality typically generates a much higher ideal female acceptance threshold for (a) male quality than the corresponding ideal threshold for males when (b) females are ranked for quality. In many cases, males should accept all females, even those of lowest quality.

Assuming the typical case of $Q_{\text{m}}^{*}>Q_{\text{f}}^{*}$, the zone of conflict (encounters between a male of quality Q_m, and female of quality Q_f for which $Q_{\text{m}}^{*}>Q_{\text{m}}$, $Q_{\text{f}}>Q_{\text{f}}^{*}$) increases with increasing relative disparity in PI. For it to be in male interests to reject females at all requires non-trivial male PI, and/or high enough variance in female quality, otherwise all females are acceptable to males ($Q_{\text{f}\min }\ge Q_{\text{f}}^{*}$).

This outlines the battleground for mate quality decisions, but resolution of this mating conflict is a complex problem unless it pays only one sex (typically females) to be choosy (e.g. Parker 1979; Janetos 1980; Real 1990). For the case where both sexes should be choosy, assuming that mating only occurs between ‘consenting’ males and females (i.e. for whom it pays both to mate), I suggested that this would lead to an imperfect pattern of assortative pairing for quality over certain quality ranges (Parker 1983b). Subsequent formal models of mutual mate choice have used similar assumptions about outcomes (usually based on ‘consent’; sometimes allowing error) and have also generated broadly assortative pairing for quality (e.g. McNamara & Collins 1990; Crowley et al. 1991; Real 1991; Johnstone et al. 1996; Johnstone 1997; Kokko & Johnstone 2002). The problem is related to the game theory of human mate choice (Bergstrom & Real 2000). Johnstone (1997) modelled dynamics of mate choice over the reproductive season, showing that choosiness may decrease as the season progresses (i.e. as search costs increase). These approaches represent only partial resolution solutions (as in the Fisherian mate choice analyses), since though the models may solve some strategic problems (e.g. what constitutes a satisfactory mate), they make fixed assumptions (rather than a strategic analysis) concerning mating decision outcomes (mating under conflict is usually assumed to occur with fixed probabilities, or only if beneficial to both parties).

In nature, mutual mate choice exists (e.g. Kraak & Bakker 1998), but is relatively uncommon. It will usually not pay males with low PI to be choosy, especially if there is low variance in female quality (Parker 1979, 1983b; Kokko & Johnstone 2002). Kokko & Johnstone (2002) point out that evolving choosiness in one sex increases the search costs of the other sex, which in turn becomes more choosy and more competitive, causing sexual strategies to diverge, making it even less likely that mutual mate choice will evolve unless the relative PI of the sexes is comparable.

(b) Female already mated: mating rate optima

Mating can be costly to females through time/energy waste (e.g. Parker 1970a), predation risk (e.g. Rowe 1994), disease or parasite transmission risks, or through harm inflicted during or as a result of mating (see §4). So it may pay females not to remate if their supply of acceptable sperm is sufficient to ensure fertility (Parker 1970c, 1984). Females of many species do resist males after one mating, at least until sperm becomes depleted, but many (possibly most) mate multiply, despite not being sperm depleted. The benefits to females of multiple mating may be considerable (e.g. see reviews of Arnqvist & Nilsson 2000; Jennions & Petrie 2000; Zeh & Zeh 2003). In a detailed meta-analysis comparing multiple and single mating groups of insects, Arnqvist & Nilsson (2000) showed that multiple mating generally decreases female longevity when mating involves no direct nutritional benefits; without such effects, female longevity is more or less independent of multiple mating, but egg production is notably increased. In both groups, females generally benefited from more than one mating (partly due to the need to replenish sperm stores), but overall the results strongly supported the conclusion of an intermediate optimum for female mating rate. Nuptial feeding of females by males in insects may itself have an origin related to sexual conflict (e.g. Thornhill 1976; Parker & Simmons 1989; Arnqvist & Nilsson 2000). In contrast, it will generally (but not always) pay males to attempt mating if progeny can be gained.

Thus, female fitness is often argued to be maximized by mating at an intermediate rate that is lower than for males (e.g. Parker 1970c, 1979; Rowe et al. 1994; Rice 1996; Holland & Rice 1998; Arnqvist & Nilsson 2000; Gavrilets et al. 2001), and this has been an assumption of many sexual conflict models. In practice, it is difficult to determine whether female mating rates in nature are optimal for the female, or whether they are higher in accordance with (or towards) male interests.

There have been several attempts to evaluate costs and benefits of multiple mating for females. For example, Arnqvist (1989) attempted to measure the costs and benefits of multiple mating (i.e. before sperm depletion) to female waterstriders, Gerris odontogaster. While there were appreciable costs (reduced mobility, increased predation risk and time/energy costs), no significant genetic benefits could be detected. The mating pattern therefore appeared to be enforced by males at the female's expense. In the yellow dung fly, Scatophaga stercoraria, females mate before each egg batch is laid, despite usually having enough sperm from one mating to fertilize the next successive four batches of eggs (Parker 1970a). Recent evidence suggests that multiple matings are costly to the female in this species (Martin et al. 2004). The male guards the female from other males during oviposition (a paternity assurance mechanism), and it is in female interests to accept what may be a superfluous mating in order to gain the benefits of reduced harassment during oviposition due to the male's postcopulatory guarding phase after mating: this yields an average net time gain of about 50 min (Parker 1970a). Similarly, Arnqvist (1989) proposed that females might minimize the costs of harassment by allowing superfluous matings and gaining postcopulatory guarding by males in the water strider, G. odontogaster.

For some species, it has been suggested that two alternative fitness peaks may be observed, with females minimizing costs by mating at low rates and maximizing benefits by mating at high rates (Wedell et al. 2002a,b). Female fitness may be minimized (rather than maximized) at an intermediate mating rate in the bean weevil, Callosobruchus maculatus (Arnqvist et al. 2005). Such situations may help to explain both intra- and interspecific variation in mating rate (Wedell et al. 2002a,b; Arnqvist et al. 2005).

Conflict over remating sometimes has fascinating consequences. Anucleate (non-fertilizing) apyrene sperm represent some 90% of the ejaculate in many Leidoptera, and there is evidence that they may represent a cheap ‘filler’ (less costly than the fertilizing eupyrene sperm) to delay the onset of remating by females, allowing the male to fertilize more eggs before sperm competition from the next male to mate (Cook & Wedell 1999). Apyrene sperm numbers stored at the time of remating has a genetic component and is negatively correlated with female remating tendency; no such relationship is found for fertilizing sperm (Wedell 2001).

(c) Inbreeding conflict

That inbreeding commonly has adverse effects on progeny viability and other components of fitness is well documented (Keller & Waller 2002). Owing to relative PI disparities between the sexes, inbreeding will have asymmetric consequences for the two sexes (Dawkins 1976) that may lead to sexual conflict (Parker 1979). There can also be disadvantages in extreme outcrossing, leading to the prediction that selection will favour ‘optimal outcrossing’ (Bateson 1983) for which there is some evidence from mate choice experiments (Bateson 1982). Postcopulatory responses are also possible: females may skew paternity in sib mating (e.g. Stockley 1999), and there may be coevolution between expenditure on ejaculates and ejaculate manipulation responses in sib matings (Pizzari et al. 2004).

Kokko & Ots (submitted) stress that, despite being well documented (Parker 1979; Bateson 1983; Waser et al. 1986; Waller 1993; Lehmann & Perrin 2003), the point has been largely ignored that if there are no adverse effects of inbreeding, mating with kin increases an individual's inclusive fitness. The argument goes back to Fisher (1941) in the context of selfing. Whether or not it pays to mate with a relative depends on the costs of inbreeding depression.

Suppose that a female produces n offspring. Consider a sister's decision whether to accept a mating from a brother (with whom she has relatedness r). If there are no opportunity costs to her brother (mating is cost free—he does not miss other mating opportunities by mating with his sister) then by sib mating, she gains a further rn copies of an allele determining mating with the brother. Thus, sib mating has an a priori benefit by a factor (1+r). With a cost ∂ of inbreeding (inbred offspring have fitness (1−∂) relative to 1 for outbred offspring) she does better to sib-mate if $(1+r)(1-\partial )n>n$, i.e. if $\partial <r/(1+r)$ (Waser et al. 1986; Lehmann & Perrin 2003, Kokko & Ots submitted). For the case of full sibs, r=0.5, and so it will be favourable to mate with her brother provided that ∂<1/3 (Parker 1979).

From the male's perspective, he gains $(1+r)(1-\partial )n$ offspring by sib-mating versus rn offspring by not mating, if this allows his sister to outbreed (assuming that she can do so immediately without costly searching). So if this mating has no cost in terms of missed alternative matings, it pays him to mate if $\partial >1(1+r)$, which for full sibs gives ∂<2/3 (Parker 1979). Thus, it is in his interests to accept a much higher level of inbreeding costs, ∂, than his sister.

However, suppose that mating with an immediately available sister has a significant opportunity cost. For example, if a male makes a significant PI each time he mates, he could instead use his PI to produce outcrossed offspring. Parker (1979) modelled this as an opportunity cost cn progeny: if c is 1.0, the male loses all n progeny from an alternative outcross by choosing to mate with his sister; if c=0, sib mating is cost free. Following the usual logic, sib-mating pays for the male if $(1+r)(1-\partial )n-rn>cn$. For the female, sib-mating requires that $(1+r)(1-\partial )n-rcn>n$, since she loses the rcn offspring that her brother would have produced by outcrossing. The battleground for this sexual conflict is

$$(1-c)/(1+r)>\partial >r(1-c)/(1+r),$$ (10.2)

i.e. the male should mate if $\partial <(1-c)/(1+r)$, and the female if $\partial <r(1-c)/(1+r)$. For full sibs, r=0.5, c=0, giving 2/3>∂>1/3 (Parker 1979). As c increases (e.g. increased male PI), the acceptable cost of inbreeding decreases for both sexes—and inbreeding is unfavourable for both if c=1.0, where a male loses an outbred offspring for every offspring gained via his sister (see figure 6, for full sibs).

Figure 6.

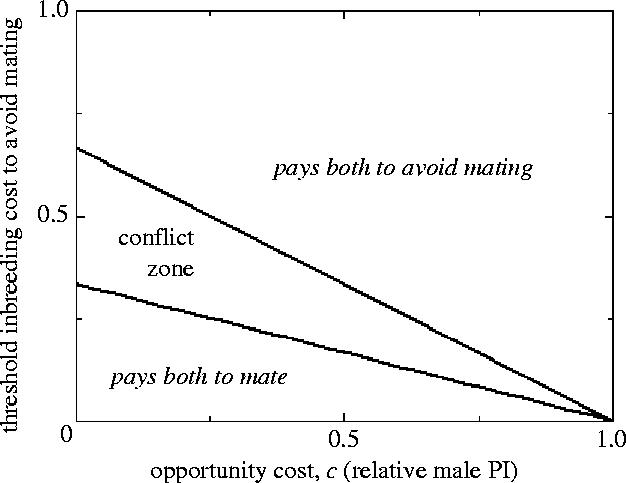
Conflict thresholds for inbreeding in relation to opportunity costs, c, for male's mating (see text). The female should mate if the inbreeding cost, ∂, is less than the lower line, and the male should mate if the costs are lower than the upper line; the zone of conflict lies between the two lines.

The above arguments are made in terms of sib mating, but apply to any mating between relatives, where r defines the probability that the male and female share the allele for the sex limited mating decision). This approach implies that where males have high relative PI, there may be no paradox in incest avoidance even if ∂ is very small.

However, while serving as a heuristic outline, it is clear that this analysis generally underestimates the tolerance thresholds for the two sexes. It simplistically assumes very high aptitude for encounter: the sex with the higher investment has no significant search costs. Kokko & Ots (submitted) give a more advanced analysis using based on ‘time in’ and ‘time out’ logic (§10, figure 4). They distinguish between ‘simultaneous choice’ (an immediate choice between related and unrelated partners) and ‘sequential choice’ (where partners are encountered one at a time). Sequential choice can generate much higher inbreeding tolerance than simultaneous choice, though it will be least when the relative PI of the sexes is similar and the time out is low relative to the time in (as suggested by the simple model above). Inbreeding tolerance is often larger than ∂=1/3 for full-sib mating, particularly if mate choice is sequential rather than simultaneous, and under some conditions can exceed 2/3. The effect of continuous change in sex roles between the sexes is actually quite complex: there is a drop in tolerance for both sexes when times out are equal (as suggested by figure 6 for equal roles with c=1.0), but this is not linear and tolerance is not zero when times out are equal, and may be high under sequential choice because of search costs for alternative mates.

Kokko & Ots (submitted) suggest that in nature incest may be commoner than thought; kin preferences in a mating context may often not be reported simply because authors do not expect to find them. They suggest that it may be profitable to view inbreeding tolerance as an adaptation, rather than a last resort after it has proven impossible to finding any other mate.

Waser et al. (1986) suggested that inbreeding costs are higher for females if they supply more PI than males; this should mean that females tend to disperse, rather than males. In formal models allowing kin recognition, Lehmann & Perrin (2003) proposed that if ∂ is sufficiently high, females do best by avoiding inbreeding and choosing to mate with immigrants, hence enforcing male dispersal. If ∂ is low, females do best by mating with relatives, favouring male philopatry.

In nature, ∂ values can be high but their assessment is complex (see Keller & Waller 2002, who use ∂ in a different sense from that used here). The likely value for full sib mating is between 0.15 and 0.25 (Keller & Waller 2002), making it advantageous to both sexes to mate if mating has zero opportunity costs to males (Parker 1979; Lehmann & Perrin 2003; Kokko & Ots submitted). However, though ∂ may sometimes perhaps exceed 1/3, it is probably much rarer for it to exceed 2/3, suggesting that inbreeding conflict may occur in nature.

The same model can be applied to conflict between males and females over cryptic sperm use (see §12). Suppose that two males have inseminated a female: one is related to her and the other unrelated. Consider the ‘decision’ of the ejaculate of the related male. It is already present in the female tract and has no opportunity costs (c=0)—it either fertilizes her eggs or dies. It pays these sperm to fertilize their sister's n eggs if $(1+r)(1-\partial )n>rn$, and it pays the sister to use her relative's sperm rather than those of the non-relative if $(1+r)(1-\partial )n>n$. Thus, inbreeding conflict over fertilization occurs if $1/(1+r)>\partial >r/(1+r)$. This c=0 case of equation (10.1) is the most interesting situation, since the sexes will both favour inbreeding if ∂ is low (below 1/3 for full sibs), but also shows the greatest zone of conflict, i.e. 2/3>∂>1/3 (see figure 6).

(d) Mating conflict in encounters between genetically divergent subpopulations

If a species is differentiated into local ecotypes, sexual conflict could have important effects in determining whether gene flow does or does not decrease, and hence whether speciation occurs. Suppose that allopatric separation has led to genetic divergence between subpopulations A and B. Parker (1979) examined the battleground for conflict for the case where the two populations meet infrequently at the boundary of their niches, or geographic ranges. Parker & Partridge (1998) refined this model, and added a model for more frequent meetings. Their analysis was a version of the mate quality decision model above, and asked whether it pays an individual of type A to mate with an individual of type B, to define the conflict battleground for this special case.

Owing to ecological separation, hybrid AB progeny are assumed to have lower fitness (1−d) than either AA, BB progeny (relative fitness=1.0). When an A male meets a B female, we can define their two acceptance thresholds for d:

1. if d>d_f (the female acceptance threshold), the B female should reject male A;

2. if d>d_m (the male acceptance threshold), the A male should reject female B.

Typically, d_m>d_f, so that there can be a zone of mating conflict (if d_m>d>d_f) where it pays the male to attempt to mate and the female to reject.

These thresholds are strongly influenced by the ratio of times out of the mating pool for each sex(G_m/G_f, related to relative PI; figure 4). Typically, G_f>G_m, so that G_m/G_f<1. Figure 7 gives an example of acceptance thresholds for the case where meetings between A and B occur with very low frequency. There is an equal sex ratio M=1, and the aptitude for encounter (§10) is B/G_f=0.01. Conflict occurs if d lies between the continuous curves: above d_m it pays neither A nor B to mate, and below d_f both should mate. With typical PI relations (G_m/G_f small), females require a much lower d before it pays them to mate, but as relative male PI increases, the zone of conflict decreases, so that by G_m≈G_f, it disappears. Sex role reversal reverses the conflict thresholds, as expected (Parker & Partridge 1998). The dotted curve d_x shows the hybrid disadvantage at which the intensity of selection on females to resist equals that on males to persist; below this, males are more strongly selected to persist and above this, females are more strongly selected to resist.

Figure 7.

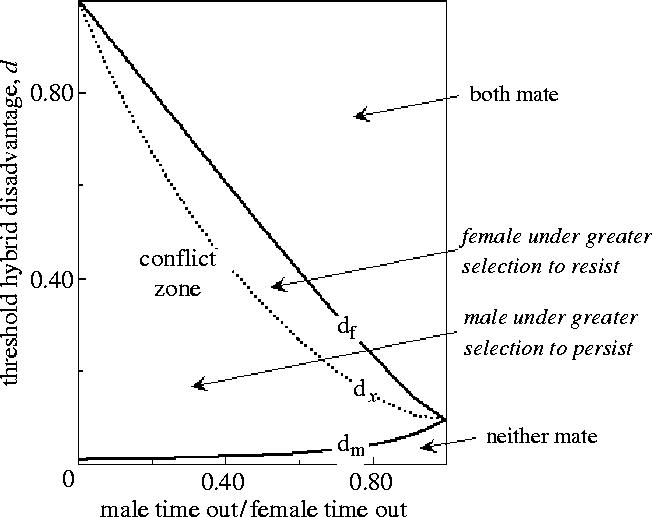
Thresholds of hybrid disadvantage (d_m for males, upper curve; and d_f for females, lower curve) at which it pays to switch decision from mating (below curve) to not mating (above curve), plotted against the ratio of ‘times out’, (G_m/G_f), in rare meetings between a male of sibling species A and a female of sibling species B. The sexes are in conflict at values for d between lines d_m and d_f (see text). Below the female threshold d_f, both sexes favour mating and above the male threshold d_m neither favours mating. The dotted curve d_x shows the hybrid disadvantage at which the intensity of selection on females to resist equals than on males to persist. Calculated from the models of Parker & Partridge (1998); modified from Parker (1979). The adult sex ratio (males/females) is M=1.0, and the aptitude for encounter is moderately high B/G_f=0.01).

The main effect of increasing the frequency of encounters between A and B populations (Parker & Partridge 1998) is that the d_x curve does not converge towards d_m at G_m/G_f=0: it starts at an intermediate value, increasing the range over which the intensity of selection is greater for the female to resist. Thresholds d_m and d_f are relatively insensitive to this change in the model. However, it must be noted that the model is a phenotypic one. If AB matings are common, the approach becomes less adequate: genetics has to be taken into account because individuals are not pure A or B, but a mix of each.

11. Sexual conflict and speciation

The last model has implications for speciation. The idea that sexual selection by female choice will increase speciation probability (and hence species richness) goes back ultimately to Darwin (1871; see also Fisher 1930; Lande 1981). The classical view of reinforcement of isolation due to individuals avoiding heterospecific matings (e.g. see reviews of Panhuis et al. 2001; Schluter 2001; Turelli et al. 2001) suggests that reproductive isolation will occur fastest in small, isolated populations (Lande 1981; Martin & Hosken 2003). It has also been suggested that sexual selection may be a force generating the genetic divergence necessary for speciation (West-Eberhard 1983). By promoting female preferences and coevolutionary male counterstrategies, sexual conflict is seen as generating a high potential for speciation: in the past decade interest has focussed on the potential influence of sexual conflict as ‘an engine of speciation’ (Rice 1996; Rice & Holland 1997; 1998). Formal models of coevolutionary dynamics under sexual conflict (Gavrilets 2000; Gavrilets & Waxman 2002; see §8b) support these ideas. In Gavrilets's model (2000), where conditions lead to equilibria (figure 3a), points along the line of equilibrium are neutral so that if populations are isolated, allopatric genetic divergence may occur by drift along the line. Where they lead to coevolutionary chases (figure 3b), allopatric populations can diverge rapidly and simultaneously by selection in different directions, supporting the notion that sexual conflict drives speciation. In Gavrilets & Waxman's model (2002), in addition to the coevolutionary chase (characterized by low genetic variation), sexual conflict over mating rate can lead to two other solutions, depending on conditions. In one, females diversify into separate groups, ‘trapping’ males in the middle (at which state where reproductive success is reduced). In the other, males diversify in response to female diversification, so that reproductive clusters of isolated genotypes form sympatrically.

The ‘engine of speciation’ theory allows rapid evolutionary change and suggests that divergence should occur faster in larger, denser, populations. Some evidence for this is provided by Martin & Hosken's (2003) experiments on the fly, S. cynipsea: in replicate populations controlled for different levels of sexual conflict, more dense populations with more sexual conflict diverged more (measured by copulation frequency and female resistance) than small populations with relaxed conflict.

Thus, sexual selection and sexual conflict are argued both to generate the diversity necessary for speciation, and also to act as a reinforcement of pre-existing divergence. The isolation reinforcement argument either (i) ignores male interests, or (ii) assumes that males are under less intense selection to avoid outcrossing (whereas, in fact, they will not generally be selected to avoid outcrossing), or (iii) assumes that females will win sexual conflicts. We (Parker & Partridge 1998; see also Parker 1974b, 1979) argued that females (typically, but not always) tend to act as a force favouring speciation by restricting gene flow (resulting in many species per range; low genetic variation per species), while males typically act as a force resisting speciation by promoting gene flow (resulting in few species per range; high genetic variation per species). Magurran (1998) expressed a similar view, supporting it with empirical data from Trinidadian guppies, Poecilia reticulata. Guppy populations show rapid divergence due to variation in predation pressures, and female choice appears to reinforce these divergences. However, there is no evidence for species isolation: despite the fact that females are much larger than males, males may be able to circumvent female choice by sneak mating, promoting gene flow. So we get different predictions if males tend to win the conflict from the case where females tend to win (Parker & Partridge 1998): predictions about sexual conflict and speciation should be ‘outcome moderated’.

Table 1 compares the radically different predictions for species richness expected from the two theories. The outcome moderated theory predicts increased species richness when (i) females win under high sexual conflict, or (ii) if there is monandry such that it pays both sexes to be choosy, restricting their matings to similar ecotypes. Under the engine of speciation theory, increased species richness is expected in high sexual conflict (polyandry) and low species richness with low sexual conflict (monandry).

Table 1.

Predictions of ‘outcome moderated’ and ‘engine of speciation’ theories for the effects of sexual conflict on species richness.

theory	potential for sexual conflict	mating pattern	prediction for species richness
‘outcome moderated’ (Parker & Partridge 1998)	high	male wins: polyandry	decreased; males promote gene flow
high	female wins: monandry	increased; females restrict gene flow
low	monandry	increased; both sexes restrict gene flow
‘engine of speciation’ (e.g. Gavrilets 2000)	high	polyandry	increased; high speciation potential
low	monandry	decreased; low speciation potential

Results of phylogenetic analyses of species richness in relation to measures of sexual selection are highly equivocal (table 2). The earliest results on birds (Barraclough et al. 1995; Mitra et al. 1996; Møller & Cuervo 1998; Owens et al. 1999) gave positive correlations between species richness and various precopulatory measures of sexual selection/sexual conflict (but see Price 1998). Insect studies using measures related to postcopulatory sexual conflict appeared to support the same conclusion (Arnqvist et al. 2000; Katzourakis et al. 2001). However, all the more recent studies have given negative results (Gage et al. 2002; Morrow et al. 2003b, Ritchie et al. 2005), failing consistently to support either the ‘engine of speciation’ or ‘outcome moderated’ theories (table 2). Morrow et al.'s (2003b) study revisited birds using an improved comparative method: it supported Owens et al. (1999) in finding no relation between species richness and sexual size dimorphism, but conflicted with the earlier bird studies in finding no relation with sexual dichromatism. They suggested that the failure to find an effect might be due to the cancellation of the effect of sexual conflict (in increased speciation) by increased risk of extinction for sexually selected species (Tanaka 1996; Morrow & Pitcher 2003). Gage et al. (2002) and Ritchie et al. (in press) concluded that factors other than sexual selection drove speciation.

Table 2.

Studies of the effects of sexual selection or sexual conflict on species richness.

group	sexual selection measure studied	speciation effect	claim	authority
birds (passerines)	sexual dichromatism	increased species richness	sexual selection drives speciation	Barraclough et al. (1995, 1998)
	sexual dichromatism	no effect		Price (1998) (part of same data set as above)
birds	mating system	increased species richness	sexual selection drives speciation	Mitra et al. (1996)
birds	ornamented versus non-ornamented	increased species richness	sexual selection drives speciation	Møller & Cuervo (1998)
birds	sexual dichromatism	increased species richness	sexual selection drives speciation	Owens et al. (1999)
	sexual dimorphism	no effect
	mating system	no effect
birds	sexual size dimorphism	no effect	increased speciation due to sexual conflict may be countered by increased extinction	Morrow et al. (2003a)
	sexual dichromatism	no effect
	testis size	no effect
insects: Coleoptera, Diptera, Ephemeroptera, Homoptera, Lepidoptera	monandry versus polyandry	increased species richness under polyandry	postcopulatory sexual conflict drives speciation	Arnqvist et al. (2000)
insects: Syrphidae (Diptera)	spermathecal width	increased species richness	postcopulatory sexual conflict drives speciation	Katzourakis et al. (2001)
	testis length	increased species richness
insects: Papuan butterflies	sexual size dimorphism	no effect	species richness may arise through allopatry	Gage et al. (2002)
	mating frequency	no effect
spiders	sexual size dimorphism	no effect	species richness may arise through allopatry	Gage et al. (2002)
mammals	sexual size dimorphism	no effect	species richness may arise through allopatry	Gage et al. (2002)
	testis size	no effect
fish: Goodeinae	sexual size dimorphism	no effect	species richness may arise primarily through allopatry and ecological divergence	Ritchie et al. (2005)

Resolution of sexual conflict over mating decisions will depend on a number of biological features (see §8). Based on the balance of power, Parker & Partridge (1998) speculated that ‘male win’ solutions may be more likely when males are larger than females, and vice versa, predicting low species richness for sexual size dimorphism with males bigger, and high species richness when females are bigger. No support for this prediction has so far been found (see table 2); size alone may be a poor predictor of conflict resolution (e.g. guppies; Magurran 1998).

12. Special features of postcopulatory conflict

If a mating conflict results in sperm being transferred to the female, it cannot be concluded that the male has won the conflict: evidence is growing that in some species, females have mechanisms to control fertilization. This section outlines some of the special features of postcopulatory conflict.

In species where the male leaves the female after copulation, direct postcopulatory behavioural or morphological interactions between the sexes are impossible. Nevertheless, sexual selection (and sexual conflict) can continue after mating. Sexual selection continues as intrasexual competition between ejaculates from different males for fertilization opportunities with the ova (sperm competition, Parker 1970c), and as intersexual selection where females may bias paternity of offspring by physically manipulating ejaculates or by operating sperm selection (Eberhard 1996), often called cryptic female choice (Thornhill 1983; Thornhill & Alcock 1983; Eberhard 1996). The consequences of sperm competition and some of the sexual conflicts it causes have been well documented (most recently by Stockley 1997; Birkhead & Møller 1998; Simmons 2001; Birkhead & Pizzari 2002). An excellent review of the issues for the Drosophila system is given by Singh et al. (2002).

Various population genetic models of sperm competition, beginning with Prout & Bundgaard (1977), investigate equilibria and dynamics of alleles generating differences in sperm competitive ability, mainly centred on Drosophila. Prout & Clark (1996) added antagonistic pleiotropic effects on female fecundity of different alleles for offence and defence in male sperm competitive abilities (see also Clark 2002), which may be a mechanism maintaining variation at genes affecting sperm competitive ability. These models do not analyse the fate of alleles at loci allowing female counter-adaptation (but see Curtsinger 1991; Keller & Reeve 1995). Similarly, many ‘sperm competition game’ models have looked for ESS sperm allocations in the absence of female influences (reviewed in Parker 1998; Wedell et al. 2002a,b).

Interest in cryptic female choice has developed more recently: experimental evidence towards the end of the 1990s was sparse and often inadequate (Birkhead 1998; Simmons 2001). It is notoriously difficult to establish whether cryptic female choice is occurring, a topic that has involved heated debate (Birkhead 1998; Eberhard 2000; Kempenaers et al. 2000; Pitnick & Brown 2000; Birkhead 2000). Evidence is now becoming more adequate (e.g. Zeh & Zeh 2003), especially in relation to genetic incompatibility avoidance (Zeh & Zeh 1996, 1997). It is important (Zeh & Zeh 1996, 1997; Ball & Parker 2003, Mays & Hill 2004) to distinguish whether all females choose sperm equivalently using the same index of male quality (or good genes) including the competitive quality of their sperm (the sexually elected sperm hypothesis’, Keller & Reeve 1995; Pizzari & Birkhead 2002), or because of their compatibility with the female genome (Zeh & Zeh 1996, 1997), which will mean that male quality relates to specific male–female interactions and the index of quality varies from female to female. Partners will vary in the extent to which they are genetically compatible for the production of offspring, because of such features as dominance, overdominance, intra- and inter-genomic conflict, mother–foetus interactions and immune system function (Zeh & Zeh 1996, 1997; Tregenza & Wedell 2000). Polyandry, in combination with cryptic female choice may enable females to reduce the risk and/or cost of fertilization due to genetically incompatible sperm. Physiological screening processes in the female reproductive tract are claimed to allow purging of incompatible sperm genotypes. There is mounting experimental evidence for paternity biases that can be interpreted in this way (e.g. Zeh & Zeh 1997; Tregenza & Wedell 2002), though some studies have failed to show any effects (e.g. Fleishman & Sakaluk 2004).

Exactly as with mate quality conflicts, there will be sexual conflict between the female and the male whose ejaculate is being discriminated against by cryptic female choice. Eberhard (1996) gives a detailed review of the biological potential for cryptic female choice. The female superficially appears to have the power advantage: the conflict is enacted in her body, and so it is often argued that the female will control the outcome (Eberhard 1996). However, many morphological and physiological/biochemical possibilities exist for arms races. The potential for cryptic female choice occurs at different levels: (i) ejaculate manipulation where females physically block transfer of certain sperm to the sperm stores, or eject them from her tract (e.g. Davies 1983; Pizzari & Birkhead 2000), or transfer them to a site where they need not be used (e.g. Hellreigel & Ward 1998; Telford & Jennions 1998); (ii) sperm selection where females select against certain sperm, either in the female tract or at the ovum surface (e.g. Zeh & Zeh 1997), (iii) differential reproductive investment where female selectively bias the rate of egg laying or the investment in offspring towards favoured males. It is clear that any demonstration of cryptic female choice requires that an effect is in female interests rather than male interests: for instance the increase in oviposition rate induced by agents in the male accessory gland products in some insects (reviewed in Simmons 2001) is usually seen as being in male interests.

Despite its biological difference from precopulatory conflict, similar general criteria are likely to apply for resolution of postcopulatory conflicts and will again relate to the balance between power and the value of winning.

For ejaculate manipulation, the female must have the power advantage if she can easily eject sperm. However, ejection is unlikely to be total, and may be less easy to achieve if the sperm are deposited far up the female tract (both sperm competition and cryptic female choice may favour increased penis length), or if anatomical mechanisms do not exist upon which a sperm ejection system can be based, as may apply in external fertilizing species. Copulatory plugs and prolonged copulations, in addition to preventing sperm competition (Parker 1970c), might also reduce the probability of sperm ejection. The value of winning is likely to be higher for the male, since this again relies on the all or nothing difference between gaining offspring or not gaining them, whereas for the female it relates to the difference between offspring qualities through use of the present ejaculate versus others. Note however, that the value of winning to the male will be reduced if the female can exercise sperm selection.

For sperm selection, while the usual argument applies that the value of winning is likely to be higher for the male, it is very hard to guess the relative power of each sex. Since the conflict occurs in the female tract in internal fertilizing species, the power advantage seems likely to favour the female. Considerable potential for physiological and biochemical arms races must apply in sperm selection conflicts. The female's greater physical control may be offset at least in part by the male's mutation advantages due to the vast sperm numbers. This may be especially important in external fertilizers, where any power advantage due to the female tract would be lost, and sperm selection must operate at the ovum surface. Here, a mutation advantage may favour sperm, but power may be similar for the sexes unless governed by gamete size (e.g. sperm competition for sperm numbers may force sperm to expend little on defences). Cryptic female choice may therefore be commoner in internal fertilizers.

Formal models of these forms of cryptic female choice are difficult to construct because the mechanisms, costs, and benefits are not sufficiently well known to make well informed assumptions about the trade-offs and constraints. However, Ball & Parker (2003) examined an ESS model where males compete by sperm competition, and females simultaneously exert sperm selection. Competing males produce either favourable ejaculates (producing progeny with high viability) or unfavourable ejaculates (where progeny have lower viability or success). Females can increase the proportion of unfavourable sperm they eliminate, but at increasing cost to fecundity. Males can vary their sperm allocation continuously in both favoured and disfavoured roles, but increasing ejaculate expenditure reduces mating rate. There are two types of game. In the first (the ‘random-roles’ model), each male is favoured with probability, p, and ‘disfavoured’ (discriminated against) with probability (1−p). Male quality depends on the specific female encountered, as would occur with genetic incompatibility (Zeh & Zeh 1996, 1997; Tregenza & Wedell 2000): different males are favoured by different sets of females, but overall each male has equal prospects. In the second (the ‘constant-types’ model), males are unequal in overall prospects—each is either favoured or disfavoured by all females as in selection for good genes (Watson 1998); p is now the population frequency of favoured males.

Figure 8 shows some results for the random roles model (Ball & Parker 2003). Figure 8a shows the change in the female's ESS for selectivity as the relative viability of offspring from the disfavoured male increases from 0 to 1. Her sperm selection strategy is measured as the proportion r of the disfavoured ejaculate that she allows to remain in the tract; r ranges from no selection (r=1.0) to maximum selection (r=0) against the disfavoured sperm. Maximal sperm selection occurs at an intermediate offspring viability. The reason why this is so can be seen from figure 8b, which shows (for the same example) the male's ESS ejaculation expenditures. When in the disfavoured role (lower curve) males avoid sperm expenditure when their offspring are unviable, conserving sperm for ejaculations in the favoured role (upper curve) where their offspring have high viability, and allowing females to relax sperm selection. As offspring viability in the disfavoured role increases, males expend more and the need for sperm selection by females becomes greater. However, as it approaches 1.0, disfavoured males are almost as good as favoured males and so the need for sperm selection is again lost. In this example (figure 8), sperm selection is quite costly to the female—if it is less costly, sperm selection becomes very intense at intermediate offspring viabilities, an intermediate viability zone where there is no ESS. Sperm limitation can stabilize sperm selection (at a high level, i.e. low r) across this zone of offspring viability.

Figure 8.

Sexual conflict resolution in the sperm selection model of Ball & Parker (2003), where male roles are random (see text). (a) Female's sperm selection strategy, measured as the proportion, r, of sperm from the disfavoured male that are left in her tract. Most intense sperm selection occurs at intermediate viabilities of offspring from the disfavoured male (at the minimum of the r curve). (b) Male's ejaculation strategy: upper curve is the number of sperm ejaculated in the favoured role, lower curve is sperm number in the disfavoured role. Modified from Ball & Parker (2003).

In the constant-types model, no relaxation of sperm selection occurs at very low viabilities of disfavoured male progeny—disfavoured males are always disfavoured, and hence have no alternative ejaculations for which to conserve their sperm. There is a no ESS zone across the lowest offspring viabilities; unlike the random roles model, this cannot be stabilized by including sperm limitation (Ball & Parker 2003).

With random roles, males always allocate more sperm in the favoured role (figure 8b). But with constant types, the favoured male type allocates less sperm than the disfavoured type. Ball & Parker (2003) stress that empiricists studying cryptic female choice and sperm allocation patterns therefore need to determine whether sperm selection is applied differently, or consistently, against given males by different females in the same population (this may pose difficulties; see Mays & Hill 2004; Puurtinen et al. 2004). The genetic incompatibility hypothesis would tend to follow the random roles predictions, since given males may be compatible with a given sets of females but incompatible with others.

Some evidence exists that male ejaculation strategies and cryptic female choice coevolve. Pizzari et al. (2004) found that in red jungle fowl (Gallus gallus), males were just as likely to copulate with full-sisters as with an unrelated female (though they appeared to initiate copulation faster with unrelated females). However, females retained more sperm from unrelated males, while males inseminated more sperm into sisters than into unrelated females, suggesting that males have retaliated against cryptic sperm choice by escalating their sperm allocation to sisters. The experiment appears to fit the assumptions of the random roles model, which suggests that more sperm should be ejaculated in the favoured role. However, the Ball & Parker (2003) model did not cover sib mating. Until the costs of inbreeding are ascertained, it is not clear which would be the favoured role: under low inbreeding costs, females should favour the ejaculates of their brothers (see §10c).

13. Postscript

It has been stressed for resolution of family intrafamilial conflicts over PI that its three components (sib-conflict, parent offspring conflict and sexual conflict) must be solved simultaneously to deduce the ESS resolution (Mock & Parker 1997). The same must apply to sexual conflicts over mating and gamete fusion: we must ideally solve the three components (mating decision conflict; ejaculate manipulation conflict (physical); and sperm selection (physiological)) simultaneously in order to establish the ESS paternity outcome. This is critical because the outcome of the final game (if there is no differential investment by females, this will be sperm selection) determines the value of winning for the sperm manipulation game which precedes it, and both therefore influence the value of winning in the precopulatory mating decision: all three games are interdependent (figure 9). This presents a real challenge for both theoreticians and empiricists, since the basic science of the processes involved—especially those that determine relative power of the sexes in each sub-component of the overall conflict (figure 9)—remain obscure and unquantified. So far, for mating and fertilization conflicts we have defined some of the battlegrounds and resolved some of the conflict components separately; much still remains to be done.

Figure 9.

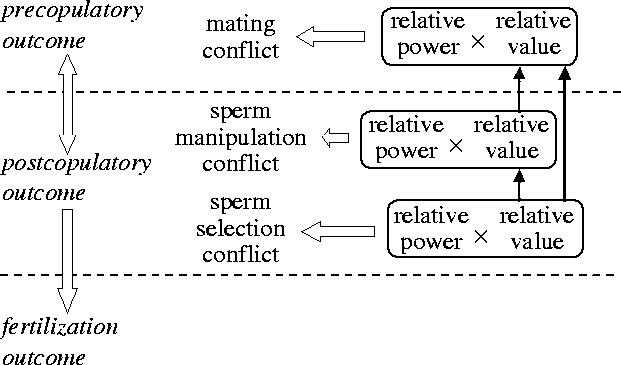
Interactions of subcomponents in mating and fertilization conflicts, which follow the order: mating decision conflict, sperm manipulation conflict, sperm selection conflict (assuming all three can occur). The top arrow on the left indicates the interaction between pre- and postcopulatory conflict: it is bi-directional since postcopulatory conflict occurs only if females lose the precopulatory conflict at least on some occasions (the male mates), and can also lose the postcopulatory conflict on some occasions (otherwise the male would not attempt to mate). Paternity outcome is then determined by the outcome of postcopulatory conflicts (lower left arrow). Arrows on the far right show the backward feedback concerning value of winning between the three sequential games. The fertilization outcome (outcome of sperm selection conflict) determines the value of winning ejaculate manipulation conflict. In turn, the outcome of ejaculate manipulation conflict affects the value of winning mating decision conflict (if ejaculate manipulation does not occur, sperm selection determines the value of winning mating decision conflict directly). Thus, both postcopulatory conflicts feedback towards mating decision conflict: the value of winning in mating conflict is affected by what will happen in postcopulatory conflict. In species where these three subcomponents are present, models of conflict resolution must simultaneously satisfy all three components.