Mapping Quantitative Trait Loci by an Extension of the Haley–Knott Regression Method Using Estimating Equations

Abstract

The Haley–Knott (HK) regression method continues to be a popular approximation to standard interval mapping (IM) of quantitative trait loci (QTL) in experimental crosses. The HK method is favored for its dramatic reduction in computation time compared to the IM method, something that is particularly important in simultaneous searches for multiple interacting QTL. While the HK method often approximates the IM method well in estimating QTL effects and in power to detect QTL, it may perform poorly if, for example, there is strong epistasis between QTL or if QTL are linked. Also, it is well known that the estimation of the residual variance by the HK method is biased. Here, we present an extension of the HK method that uses estimating equations based on both means and variances. For normally distributed phenotypes this estimating equation (EE) method is more efficient than the HK method. Furthermore, computer simulations show that the EE method performs well for very different genetic models and data set structures, including nonnormal phenotype distributions, nonrandom missing data patterns, varying degrees of epistasis, and varying degrees of linkage between QTL. The EE method retains key qualities of the HK method such as computational speed and robustness against nonnormal phenotype distributions, while approximating the IM method better in terms of accuracy and precision of parameter estimates and power to detect QTL.

IN biomedical research, evolutionary biology, and agricultural science alike, it has long been of interest to study the genetic basis of variation in quantitative traits (such as blood pressure, litter size, or crop yield). For this purpose, experimental crosses between inbred lines are widely used; crosses of model organisms can lead to improved understanding of related human diseases, and crosses of inbred animal or plant species can inform breeders of important genomic regions, which may be used in breeding schemes. The genetic variance of a quantitative trait is thought to be controlled by a number of such genomic regions, or quantitative trait loci (QTL), which may interact in intricate ways (see, for example, Falconer and Mackay 1996; Lynch and Walsh 1998).

With the advent of dense genetic marker maps, a lot of effort has been devoted to the development of statistical methods for locating QTL and estimating their effects. The seminal article by Lander and Botstein (1989) introduced the interval-mapping (IM) method, which considers, one at a time, a suite of putative QTL positions along the genome. In the case of a backcross, say, an individual with genotype g = QQ or Qq at the putative QTL is assumed to have phenotype . Since the QTL genotypes will generally not be known, the phenotype distribution given the marker data is a mixture of the two normal distributions. Closed-form expressions for the maximum-likelihood estimators are not available for mixtures of normal distributions. Thus, estimation under the IM method must be done numerically; most commonly a version of the expectation-maximization (EM) algorithm (Dempster et al. 1977) is used.

A key disadvantage to the IM method is long computation time, since the EM algorithm often requires many iterations to converge. Haley and Knott (1992) and Martínez and Curnow (1992) independently developed a simple regression method that usually approximates IM very well and requires much less computation. Again, consider a backcross individual with genotype g = QQ or Qq at the putative QTL. The Haley–Knott (HK) regression method applied to backcross data consists simply of regressing the individuals' phenotypes on the conditional probabilities for having genotypes QQ or Qq at the putative QTL, given the marker data. In other words, an individual with marker data m is assumed to have phenotype . Since we need only to do a simple regression calculation at each putative QTL position, there are great savings in computation time compared to that of the IM method, something that is particularly important when generalizing the methods for multiple-QTL models.

A number of studies have compared the IM and HK methods (Haley and Knott 1992; Xu 1998a,b; Kao 2000), and in many cases the two methods provide almost identical parameter estimates and test statistics. There are, however, important differences; for instance, it is well known that the HK method overestimates the residual variance (Xu 1995; Kao 2000). In general, the total genetic variance may be split into two parts, one part originating from marker genotype variation and one part from variation of QTL genotype given marker genotypes. In the HK method the latter part is contained in the residual variance estimate, sometimes causing overestimation of the residual variance. Also, Kao (2000), in an extensive comparison of the two methods by computer simulations, found that epistasis between QTL and linkage between QTL may lead to large differences in power to detect QTL and efficiency of parameter estimation. One further difference between the IM and HK methods concerns robustness in the presence of nonnormal phenotype distributions. In such cases the IM method may produce large spurious LOD score peaks (Broman 2003; Feenstra and Skovgaard 2004), something that the HK method avoids.

In this study, we develop an extension of the HK method on the basis of estimating equations. In the HK method the conditional mean of an individual's phenotype given marker data, E(y_i | m_i), is specified correctly, but the conditional variance Var(y_i | m_i) is incorrectly assumed to be constant. In the estimating equation (EE) method, we develop joint estimating equations for mean and covariance parameters, on the basis of a coherent specification of both E(y_i | m_i) and Var(y_i | m_i). It has been suggested to overcome the bias of the HK method with an iteratively reweighted least-squares (IRLS) approach using Var(y_i | m_i) to weight observations (Xu 1995, 1998a,b). The IRLS method, however, does not fully utilize information about the mean parameters contained in the conditional variance Var(y_i | m_i) and may be expected to be less efficient than the estimating equation approach taken here.

We explore the performance of the proposed EE method on a number of real and simulated data sets, covering a range of different genetic models and data set structures. Comparison is made with the IM, HK, and IRLS methods with respect to important performance criteria, such as power, robustness, efficiency, bias, and computational speed in implementations. We focus the comparison on situations where either the HK method or the IM method is suspected to perform poorly.

GENETIC MODEL

For simplicity, we consider n individuals from a backcross population, but the results extend easily to other kinds of crosses. Consider m different QTL, indexed by . At any given QTL, the jth say, there are two possible genotypes: Q_jQ_j and Q_jq_j, making the total number of possible QTL genotypes in the population 2^m. The goal of a genetic model is to relate the 2^m possible genotypic values to a set of genetic parameters, such that these parameters are interpretable in terms of main and epistatic effects of the m QTL. We prefer a genetic model using orthogonal contrast scales because it is consistent in the sense that the effect of a QTL is consistently defined whether the genetic model includes one, two, three, or more QTL (Kao and Zeng 2002; Zeng et al. 2005). The relation between the genotypic value G_i of individual i and the genetic parameters can be expressed by

(1)

with

μ the mean genotypic value in the backcross population, a_j the main QTL effects, b_jk and c_jkl the two- and three-locus epistatic effects, and the dots representing fourth- and higher-order epistatic interactions. It is common to include only pairwise interactions between QTL (Kao et al. 1999; Carlborg and Andersson 2002), and the genetic model is then reduced to

(2)

For other kinds of crosses, such as F₂ populations, different contrast scales are needed to achieve orthogonality (Zeng et al. 2005).

STATISTICAL METHODS

A successful statistical model for QTL mapping should relate the phenotypes of individuals to their genotypes at the m putative QTL considered. Many authors describe this relationship using the genetic parameters mentioned above. However, we choose a different parameterization with each of the 2^m mean parameters in the model corresponding to the genotypic value of an m-locus QTL genotype, as this makes for a clearer presentation and comparison of the statistical methods. We emphasize that the two parameterizations are equivalent and demonstrate later in this section how to translate one type of parameter to the other. Assuming independence between individuals and given an m-locus genomic position, the statistical model is given by

(3)

where y_i is the quantitative phenotype; 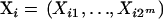is a row vector of length 2^m indicating the multilocus QTL genotype; i.e., one of the X_ig = 1, the rest are zeros; 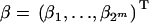is the vector of parameters to be estimated; and e_i is a random error term with an unspecified distribution. The relationship between the model parameters β and the genetic model parameters is important to guide the formulation of relevant hypotheses to test and to interpret the estimates from the final model. Fortunately, estimates of the model parameters are readily translated to genetic parameter estimates; we outline how to do this below.

A key QTL-mapping problem is how to deal with missing genotype data, since the QTL genotypes, X_i, are generally not observed. A number of approaches exist for this; we briefly describe the IM and HK methods and go on to introduce the proposed EE method.

Interval mapping:

The interval-mapping method, pioneered by Lander and Botstein (1989) and generalized to multiple loci by Kao et al. (1999), was the first approach to fully exploit the fact that QTL are located in intervals flanked by genetic markers with observed genotypes. This means that given a genetic marker map and a putative QTL position and assuming a map function, we may calculate p_ig = Pr(g | m_i), the conditional probability of QTL genotype g given the multipoint marker data m_i. The IM method assumes that in Equation 3 and models the phenotypes given the observed marker data as a mixture of normal distributions. The likelihood function for the parameters, β, σ² is

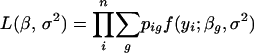(4)

with p_ig defined as above and f(y; β_g, σ²) being the density function of a normal distribution with mean β_g and variance σ².

Haley–Knott regression:

The Haley–Knott regression method deals differently with the missing observations X_ig in the statistical model (3). Although the genotypes X_ig are unobserved, we may calculate their conditional expectations given the marker data. Actually, in the case of backcross populations, E(X_ig | m_i) = p_ig, since the X_ig are indicator variables. The HK method replaces X_ig with E(X_ig | m_i) in the regression (3), which then becomes

(5)

still assuming that . Thus, the likelihood function is

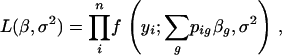(6)

which may be maximized easily by standard regression techniques.

An estimating equation method:

Like the IM and HK methods, the estimating equation method considers the phenotype distribution given the marker data. Initially, we assume that the marginal density function of the phenotype, y_i, given the marker data, m_i for individual i has the general form

(7)

where p_ig is defined as before and f(y | g) is the conditional density function of y given the QTL genotype g. We make no specific assumptions about the f(y | g), provided that these distributions have moments of at least second order. Interval mapping is a special instance of Equation 7 with the f(y | g) being normal distributions. We now obtain the following expressions for the conditional mean and variance of the phenotypes given the marker data

(8)

(9)

where β_g is the mean in f(y | g). In Equation 9, we have partitioned the phenotypic variance into two components; the first component, σ², is assumed to be the same for all individuals and QTL genotypes and may be interpreted as the environmental variance, whereas the second component corresponds to the variance due to uncertainty of QTL genotype given marker data and varies with marker and QTL genotype.

To estimate the β_g-parameters as well as σ², we must find a set of estimating equations for the parameters satisfying the requirement that their expectation equals 0. For simplicity, we further make the assumption in this article that . This resembles the assumption in the HK method that ; we view the method presented here as an extension of the HK method that uses a coherent specification of both E(y_i | m_i) and Var(y_i | m_i) by which the variance reflects the uncertainty about the QTL genotype. We use the resulting score equations as estimating equations for the parameters. It should be emphasized, however, that these score equations may be used perfectly well as estimating equations without assuming normality.

The contribution of a single observation to the negative log-likelihood function for the normal model is

Differentiating this function with respect to the parameters β_g and σ², summing over individuals, and setting the resulting score function equal to 0 yields the estimating equations

(10)

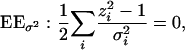(11)

where 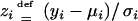and . Note that E(z_i) = 0 and E(z_i²) = 1, confirming that the expectations of the left-hand sides of both Equations 10 and 11 equal 0 as required.

The estimating equations must be solved numerically. To do so, we implemented an algorithm that uses two conditional maximizations in each iteration. First, estimates of β_g are updated by solving Equation 10 while keeping fixed σ² and the β_g's that enter in σ_i and z_i². Second, an updated estimate of σ² is obtained by solving Equation 11 with the β_g's fixed. We iterate until the estimates converge.

Relation to iteratively reweighted least-squares regression:

Xu (1995) first pointed out that the HK method tends to give biased estimates of the residual variance. It was suggested to correct the bias by using Equations 8 and 9 for the conditional mean and variance, respectively, of the phenotypes given full marker data. Xu (1998a,b) further assumed that and claimed to maximize the corresponding likelihood function by the iteratively reweighted least-squares method. In the IRLS method, the variance is written

where i.e., v_i depends both on σ² and on the β_g. In the iterations, updated parameter estimates are obtained by treating the v_i as known weights and performing weighted least-squares regression,

(12)

and

(13)

with V a n × n diagonal matrix of the weights v_i, y the n-vector of phenotype observations, and

(14)

The above two equations correspond to Equations 7 and 8 in Xu (1998b). It may be shown that IRLS iterations using Equations 12 and 13 are (asymptotically) equivalent with using

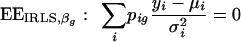(15)

as an estimating equation for β_g and using

(16)

as an estimating equation for σ². These estimating equations are simpler than the ones (Equations 10 and 11) used in the EE method, and intuitively it might be expected that the EE method captures more information about the parameters than the IRLS method. In the appendix, we demonstrate that the EE method is indeed more efficient than the IRLS method under the assumptions used here. Situations where the assumption that is not met are explored by computer simulation in the results.

Estimating genetic parameters:

To illustrate the translation from genetic parameters in the genetic model (1) to mean parameters in the statistical model (3) and vice versa, we consider parameters from a model with three loci in a backcross population.

At each QTL, we index homozygotes by 2 and heterozygotes by 1, e.g., the parameter β₂₁₁ corresponds to QTL genotype Q₁Q₁/Q₂q₂/Q₃q₃. Expressed in matrix notation, the relation between the two types of parameters is

(17)

or β = Sψ, where S is the genetic effect design matrix and ψ is the vector of genetic parameters. Conversely, ψ may be found from β by ψ = S⁻¹β. In the case where there is no three-locus epistasis, i.e., c₁₂₃ = 0, there is a constraint on the parameter vector β in the sense that β₁₁₁ can be expressed as a function of the other seven β_g's. Writing the genetic effect design matrix as

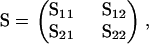where S₁₁ is the top left 7 × 7 submatrix, we may express β₁₁₁ as

where β_|7 is the restriction of β holding the first seven parameters. Evaluating the expression yields β₁₁₁ = β₂₂₂ − β₂₂₁ − β₂₁₂ + β₂₁₁ − β₁₂₂ + β₁₂₁ + β₁₁₂. Obviously, for other models and kinds of crosses different constraints on β apply. These may be found in a similar manner.

RESULTS

We explored the behavior of the IM, HK, IRLS, and EE methods over a range of real and simulated data sets.

As a starting point, we considered the simple situation of detecting a single QTL and estimating its effect. A backcross population was simulated with a single QTL placed at the center of chromosome 1, which had a length of 100 cM and six evenly spaced markers. Progeny sizes of 50, 100, and 200 were considered and the corresponding ranges of additive effects of the QTL (a₁ in Equation 2) were 0.54–3.80, 0.34–2.00, and 0.20–1.00, respectively. In each case, six different values for the additive effect were simulated. Moreover, three different genetic models were used in the simulation setup. First, no other QTL were segregating in the population. Second, a QTL of moderate effect (a₂ = 0.60) was segregating at a position unlinked to chromosome 1. Third, two unlinked but strongly interacting QTL (a₂ = 1.00, a₃ = 1.00, and b₂₃ = 4.00) were segregating at positions unlinked to chromosome 1. The environmental variation was sampled from a standard normal distribution in all cases. Single-locus scans were conducted with all four methods to detect the QTL on chromosome 1. In this simple setup there were only minor differences between the methods for all genetic models, and we therefore summarize the results in text only. Power and precision of locating the QTL were virtually the same for all methods as were mean parameter estimates. In accordance with previous reports (Xu 1995; Kao 2000) the HK method overestimated the residual variance. There was a slight but consistent trend that the lowest standard deviations and mean squared errors on mean parameter estimates were seen with the IM method followed by the EE, IRLS, and HK methods.

Since the differences in the simple simulation setup were only minor, we focus our attention in the following on more complicated situations where either the HK method or the IM method is known to perform poorly.

Nonrandom missing data patterns:

In many cases the costs involved in genotyping an individual for a large collection of genetic markers are much higher than the costs of obtaining the individual's phenotype. In such situations, selective genotyping, where individuals with extreme phenotypes are genotyped much more heavily than intermediate ones, may be an effective strategy for reducing experimental costs without losing much information about the QTL behind the trait of interest (Lander and Botstein 1989; Darvasi and Soller 1992; Sen et al. 2005). It appears, however, that the HK method is particularly sensitive to the special kind of nonrandom missing data that follow from selective genotyping.

Consider, for example, the data set consisting of 250 backcross mice studied for hypertension in Sugiyama et al. (2001). Initially, individuals with extreme phenotypes were genotyped; in regions showing evidence for QTL, all individuals were genotyped and additional markers were added. Further, at some markers only recombinant individuals were genotyped. In 8 of the 19 autosomes, only 46 individuals in each extreme of the phenotype distribution were genotyped; i.e., the middle 158 individuals were not genotyped for any markers on those chromosomes. When those eight chromosomes are scanned with both the IM and the HK methods, the LOD curves produced by the HK method exceed those produced by the IM method, with differences of up to 1 LOD score unit. If, however, the phenotypes of intermediate individuals are discarded, the LOD curves produced by the HK method are virtually indistinguishable from those produced by the IM method for the eight chromosomes considered (results not shown).

To further investigate this behavior of the HK method, we simulated 250 backcross individuals and a single chromosome of length 100 cM with 10 markers and a QTL at position 45 cM explaining 14% of the phenotypic variance. We scanned the simulated chromosome with one-locus versions of the IM, HK, and EE methods in the case where all individuals had complete marker data, but we also considered the case of selective genotyping by letting observations from the 40th to the 60th percentile in phenotype distribution have missing observations for all markers on the chromosome.

Figure 1 shows that discarding marker genotypes for individuals in the middle 20% of the phenotype distribution inflates the HK LOD curve over the whole range of the chromosome compared to using the HK method with all marker data and compared to using the IM method. The inflation is most pronounced at the peak of the LOD curve. The EE method almost completely avoids this problem of inflated LOD curves. In Figure 1, it can be seen that the LOD curves for the EE method are close to the IM curve, both in the case of full marker data and in the case of selective genotyping.

Figure 1.—

A simulation example of QTL mapping with a population of 250 backcross individuals and a single QTL at 45 cM. The right side magnifies the box in the left side. The HK method inflates the LOD curve in the case of selective genotyping. The EE method almost completely avoids inflation of the LOD curve.

A closer look at the HK method explains the phenomenon of inflated LOD curves. The one-locus regression may be written

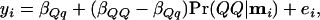where . In Figure 2, regression lines are shown for the position with the largest LOD score. Observations from the middle 20% of individuals are shown as solid dots and other observations as open circles.

Figure 2.—

Haley–Knott regression lines at the position with largest LOD score in a simulated data set. Lines are shown in the case of full marker data (left side, dashed line) and in the case of selective genotyping with missing marker data for the intermediate 20% of individuals (right side, solid line).

In Figure 2, left, full marker data are used. There is indeed a QTL effect, as the regression line is not horizontal. In Figure 2, right, the middle 20% of individuals have missing marker data. Thus, there is no marker information for those individuals about Pr(QQ | m_i) and this probability therefore equals 0.5. Consequently, the points corresponding to the middle 20% of individuals are translocated horizontally to Pr(QQ | m_i) = 0.5, thereby removing positive residuals from the low end of the regression line and negative residuals from the high end, causing the line to become steeper. Furthermore, the points cluster closer around the regression line with selective genotyping, meaning that the likelihood under the alternative is larger. It is, however, unchanged under the null hypothesis of no QTL effect, since the points do not move vertically, and the LOD score is thereby inflated. Also, the steeper slope of the regression line means that the size of the QTL effect is overestimated by the HK method in the case of selective genotyping.

As may be seen from the simulation example in Figure 1, the EE method almost completely avoids this problem, as it weights observations by their inverse variances. Thus, observations with large variance due to uncertainty of QTL genotype [i.e., Pr(QQ | m_i) close to 0.5] have little weight in the likelihood calculation.

Nonnormal phenotype distributions:

In earlier work, we have considered QTL mapping strategies in situations where the phenotype distribution deviates from a normal distribution (Broman 2003; Feenstra and Skovgaard 2004). The IM method can occasionally produce spurious LOD score peaks in regions of low genotypic information (e.g., widely spaced markers), especially if the phenotype distribution deviates markedly from a normal distribution. This is caused by the fact that the IM method models the phenotype distribution as a mixture of two or more normal distributions when a QTL is included in the model, while only using a single normal distribution under the null hypothesis. If the phenotype distribution is not normal, the model including a QTL may fit the data much better than the null model, even if there is no real QTL and no genetic marker information (Feenstra and Skovgaard 2004).

In Feenstra and Skovgaard (2004), we considered models with a single QTL and developed a two-component mixture model that avoids the problem of spurious LOD score peaks. Here, we broaden our view to models with more than one QTL with possible epistatic interactions between loci. It appears that the problem of spurious LOD score peaks gets worse when the IM method is used to map more QTL simultaneously.

Figure 3 shows the results of two-QTL scans of a simulated data set consisting of 80 backcross individuals, five chromosomes of length 140 cM with 12, 12, 8, 6, and 4 markers, respectively, and two epistatically interacting QTL on chromosome 1 at position 45 cM and chromosome 2 at position 5 cM, respectively. In Figure 3A, results for the IM method are shown. It can be seen that the interacting QTL on chromosomes 1 and 2 are detected with high LOD scores. However, there are also large areas in the plot corresponding to combinations of positions on other chromosomes with high LOD scores. These high LOD score areas involve chromosomes with few markers, i.e., little genetic information, strongly suggesting that this is the same kind of artifact as the spurious LOD score peaks seen in one-QTL scans. In this simulation example, the residual variation was normal, but the influence of the two interacting QTL caused the phenotype distribution to be nonnormal, thereby allowing the phenomenon of artificially high LOD scores at other positions.

Figure 3.—

LOD scores for a two-dimensional, two-QTL genome scan of a simulated population of 80 backcross individuals with two interacting QTL on chromosomes 1 and 2. Values below the diagonal correspond to a test of two additively acting QTL vs. none. Values above the diagonal correspond to a test for two-locus epistasis. In the gray-tone scale, the numbers to the right and left correspond to values below and above the diagonal, respectively. (A) Results from the IM method. (B) Results from the EE method.

The HK method is known to be quite robust toward nonnormal phenotype distributions (Rebaï 1997), and both the HK and the EE methods are immune to the artifact of spurious LOD score peaks, since single normal distributions are used both when one or more QTL are included in the model and under the null hypothesis of no QTL effect. Figure 3B shows LOD scores for a two-QTL scan of the same data set by the EE method. The interacting QTL on chromosomes 1 and 2 are detected, but no other combinations of positions show high LOD scores. The HK method gave very similar results to the EE method for these data (results not shown).

Epistasis between QTL:

In an extensive analytical and simulation-based comparison between the IM and HK methods, Kao (2000) found that there may be significant differences between the two methods, especially if QTL interact or are linked. Here, we focus on the situation where two unlinked QTL interact. We use the simulation setup from Table 3 in Kao (2000) and also include the IRLS and EE methods in the comparison. Data were generated from a genetic model with two unlinked epistatic QTL with genetic parameters μ = 0, a₁ = 1, a₂ = 1, and b₁₂ = 1, 2, or 3 (cf. Equation 1). Thus, the strength of epistasis was increased compared to the additive effects of the QTL. Estimates of the genetic parameters, σ², and the broad sense heritability, h² (see, for example, Falconer and Mackay 1996), were recorded as well as likelihood-ratio test (LRT) statistics comparing the full model with a null model of no QTL.

Table 1 displays the simulation results. The means of the estimated main and epistatic effects by the four methods are almost identical and very close to the true values for all three degrees of epistasis. Standard deviations (SDs) and mean square errors (MSEs) are smallest for the IM method, slightly larger for the EE method, and largest for the HK method. The IRLS method resembles the HK method with respect to SDs and MSEs for the main and epistatic effect estimates.

TABLE 1.

Comparison of the IM, HK, IRLS, and EE methods applied to simulated data under different strengths of epistasis

	1:1:1			1:1:2			1:1:3
	Mean	SD	MSE	Mean	SD	MSE	Mean	SD	MSE
μ = 0
IM	0.001	0.061	0.004	0.001	0.070	0.005	0.004	0.086	0.007
HK	0.000	0.063	0.004	0.001	0.074	0.006	0.003	0.091	0.008
IRLS	0.000	0.062	0.004	0.001	0.072	0.005	0.003	0.088	0.008
EE	0.000	0.062	0.004	0.001	0.072	0.005	0.002	0.088	0.008
a1 = 1
IM	0.998	0.136	0.019	0.995	0.164	0.027	1.018	0.181	0.033
HK	1.000	0.155	0.024	0.991	0.185	0.034	1.024	0.220	0.049
IRLS	1.001	0.152	0.023	0.993	0.181	0.033	1.024	0.212	0.046
EE	0.999	0.143	0.021	0.995	0.172	0.030	1.020	0.192	0.037
a2 = 1
IM	1.003	0.145	0.021	1.001	0.157	0.025	0.995	0.178	0.032
HK	1.003	0.160	0.026	1.003	0.178	0.032	1.000	0.215	0.046
IRLS	1.003	0.158	0.025	1.004	0.173	0.030	1.002	0.207	0.043
EE	1.004	0.151	0.023	1.003	0.163	0.027	0.996	0.188	0.035
b12
IM	0.987	0.289	0.084	2.005	0.342	1.128	2.986	0.395	4.101
HK	0.984	0.385	0.149	1.998	0.434	1.185	3.024	0.518	4.364
IRLS	0.984	0.385	0.148	1.997	0.433	1.182	3.024	0.517	4.364
EE	0.990	0.314	0.099	2.002	0.370	1.141	3.014	0.459	4.265
σ2
IM	0.548	0.073	0.006	0.731	0.092	0.009	1.026	0.127	0.018
HK	0.776	0.081	0.052	1.080	0.114	0.122	1.556	0.158	0.268
IRLS	0.560	0.091	0.008	0.751	0.131	0.017	1.035	0.187	0.036
EE	0.543	0.085	0.008	0.728	0.117	0.014	1.009	0.162	0.029
h2 = 0.5
IM	0.511	0.064	0.004	0.511	0.057	0.003	0.514	0.056	0.003
HK	0.426	0.062	0.009	0.414	0.063	0.011	0.416	0.065	0.011
IRLS	0.508	0.083	0.007	0.505	0.088	0.008	0.517	0.092	0.009
EE	0.514	0.075	0.006	0.513	0.074	0.006	0.522	0.075	0.006
LRT
IM	83.0	17.3		80.5	16.2		77.2	15.5
HK	73.6	16.4		65.1	14.7		61.3	14.4
IRLS	80.0	17.2		75.2	16.0		71.7	15.5
EE	80.6	17.2		75.8	16.0		72.3	15.5

For each combination of simulated parameters, 1000 replicates, each with sample size 200, were analyzed with QTL located in the middle of two unlinked 40-cM marker intervals. σ² = 0.5625 for effect 1:1:1; σ² = 0.75 for effect 1:1:2; σ² = 1.0625 for effect 1:1:3. b₁₂ = 1, 2, and 3 for the three effect ratios, respectively. h², the broad sense heritability (proportion of variance explained by QTL).

As in Kao (2000), we find that the most conspicuous difference between the IM and HK methods is the bias of the HK method in the estimation of σ² and h². The EE method does not show this bias and provides almost identical estimates of σ² and h² to those by the IM method (Table 1). The IRLS method also performs very well in this respect.

We note that the results are in good accordance with those from Kao (2000), with one exception. When calculating the genetic variance component, and thereby the heritability for the HK method, Kao (2000) does not use the model that the data were simulated from (Equation 3). Rather, it appears that the modified regression model (Equation 5) is used for calculating the genetic variance. Indeed, when calculating the genetic variance on the basis of Equation 5 we get h²-estimates for the HK method of 0.310, 0.279, and 0.259 for the three levels of epistasis, which are very close to the values 0.302, 0.277, and 0.255 reported by Kao (2000). Thus, while our estimates of h² by the HK method are also clearly biased (Table 1), our findings indicate that the bias in Kao (2000) is exaggerated. In any case, the EE method avoids the bias and approximates the IM method very well for all parameter estimates and with respect to the LRT statistics. In addition, it is superior to the IRLS method, considering the efficiency of the parameter estimates.

Linked QTL:

The most pronounced differences between the IM and HK methods are found when two QTL of opposite effect are linked (Kao 2000). Here we focus on that situation, using the simulation setup from Table 5 in Kao (2000) and also including the EE and IRLS methods in the comparison. Data were generated from a genetic model with two linked QTL of opposite effects without epistasis (μ = 0, a₁ = 1, a₂ = −1, b₁₂ = 0, cf. Equation 1). The two QTL were placed in two neighboring 40-cM intervals and were 10, 20, 30, or 40 cM apart from each other. Haldane's map function was used.

Table 2 shows the simulation results. Again, the means of the estimates of μ, a₁, and a₂ are close to the true values for all four methods, and again the IM method has the lowest MSEs on the paramater estimates, followed by the EE method and then the IRLS and HK methods. Estimates of σ² and h² from the HK method are even more biased than in the epistasis case. Again, the IM, IRLS, and EE methods provide very similar estimates of σ² and h². Like in the epistasis simulations, the results are in good accordance with those reported in Kao (2000) with the exception that the h²-estimates for the HK method are not as dramatically biased as those in Kao (2000).

TABLE 2.

Comparison of the IM, HK, IRLS, and EE methods applied to simulated data under different strengths of linkage

	10 cM		20 cM		30 cM		40 cM
	Mean	MSE	Mean	MSE	Mean	MSE	Mean	MSE
μ = 0
IM	−0.001	0.001	0.002	0.001	0.001	0.002	0.001	0.002
HK	0.000	0.001	0.002	0.002	0.001	0.002	0.001	0.002
IRLS	0.000	0.001	0.002	0.001	0.001	0.002	0.001	0.002
EE	0.000	0.001	0.002	0.001	0.001	0.002	0.001	0.002
a1 = 1
IM	0.961	0.062	0.985	0.014	0.988	0.015	0.996	0.015
HK	1.023	0.218	0.997	0.095	0.985	0.059	1.012	0.038
IRLS	1.023	0.217	0.997	0.095	0.986	0.058	1.013	0.038
EE	0.931	0.167	0.987	0.035	0.989	0.024	1.002	0.019
a2 = –1
IM	−0.962	0.060	−0.985	0.013	−0.987	0.015	−0.993	0.015
HK	−1.026	0.218	−0.997	0.093	−0.986	0.059	−1.010	0.039
IRLS	−1.024	0.215	−0.997	0.093	−0.984	0.058	−1.009	0.039
EE	−0.932	0.166	−0.986	0.034	−0.987	0.024	−0.999	0.020
σ2
IM	0.090	0.000	0.165	0.001	0.225	0.001	0.271	0.002
HK	0.174	0.008	0.305	0.021	0.400	0.032	0.458	0.036
IRLS	0.085	0.003	0.163	0.005	0.229	0.006	0.271	0.005
EE	0.088	0.001	0.16 1	0.002	0.222	0.003	0.267	0.003
h2 = 0.5
IM	0.495	0.004	0.495	0.006	0.498	0.007	0.503	0.007
HK	0.346	0.053	0.347	0.040	0.353	0.033	0.381	0.022
IRLS	0.523	0.088	0.506	0.053	0.492	0.033	0.512	0.021
EE	0.509	0.034	0.505	0.022	0.502	0.014	0.511	0.011
LRT
IM	39.7	15.0	31.4	12.1	35.6	12.3	46.3	13.3
HK	8.0	5.5	14.8	7.8	23.3	10.1	36.5	12.5
IRLS	14.8	10.9	22.9	10.9	31.0	11.5	43.3	13.0
EE	19.7	11.1	25.4	11.2	32.7	11.7	44.3	13.1
LRT1
IM	38.7	15.0	30.0	11.9	32.8	11.9	40.0	12.3
HK	7.0	5.4	13.5	7.6	21.0	9.7	31.2	11.5
IRLS	13.8	10.9	21.5	10.7	28.4	11.1	37.2	12.0
EE	18.7	11.0	24.0	11.0	29.9	11.3	38.0	12.0
LRT2
IM	38.6	15.0	30.0	12.0	32.8	11.9	40.2	12.3
HK	7.0	5.3	13.5	7.6	20.9	9.7	31.4	11.5
IRLS	13.8	10.9	21.5	10.8	28.3	11.1	37.4	12.0
EE	18.6	11.0	24.0	11.0	29.8	11.3	38.2	12.0
Power (%)
IM	99.4		98.1		99.3		99.9
HK	32.8		70.8		92.3		98.8
IRLS	66.1		89.7		98.3		99.5
EE	82.1		94.6		99.2		99.7

For each combination of simulated parameters, 1000 replicates, each with sample size 200, were analyzed with two QTL contributing 50% of the total phenotypic variance. The QTL were located in two neighboring 40-cM marker intervals 10, 20, 30, or 40 cM apart. σ² = 0.091 for distance 10 cM; σ² = 0.165 for distance 20 cM; σ² = 0.226 for distance 30 cM; σ² = 0.275 for distance 40 cM. LRT is the likelihood-ratio test for H₀: a₁ = 0 and a₂ = 0. LRT₁ is the likelihood-ratio test for H₀: a₁ = 0 and a₂ ≠ 0. LRT₂ is the likelihood-ratio test for H₀: a₂ = 0 and a₁ ≠ 0. Power is taken to be the percentage of replicates with LRT₁ > 7.88 and LRT₂ > 7.88. For the LRT quantities, numbers in the MSE columns are standard deviations. h² is the proportion of variance explained by the QTL.

As for the power to detect two QTL, the EE method provides higher LRT statistics and greater power compared to the HK and IRLS methods. When the two QTL are >20 cM apart, the LRT statistics and power results are similar for the IM and EE methods. However, for QTL only 10 cM apart, the LRT statistics from the IM method are more than twice as large as those from the EE method, three times larger than the IRLS statistics, and five or six times larger than those from the HK method (Table 2). This is related to the phenomenon of spurious LOD score peaks that the IM method occasionally shows with nonnormal phenotype distributions. The residual variance used for the simulations when the QTL were only 10 cM apart was small (0.091) compared to the additive effects. This means that phenotype distributions resulting from the simulations bore much closer resemblance to a mixture of three normal distributions (with means −1, 0, and 1 as given by the two-locus additive model) than to one with two normals (corresponding to a one-locus model). Indeed, the two additive QTL were detected with high LRT statistics and high power.

However, this did not come without a price. To investigate the effect on chromosomes unlinked to QTL we simulated a second chromosome with the same marker spacing, but with no QTL on it, while retaining the phenotypes (which are strongly influenced by the QTL on chromosome 1). We then considered positions on this second chromosome that mirrored the positions of the QTL on the first chromosome and calculated LRT statistics for going from a model with two additively acting QTL on the second chromosome to a model with just one QTL (data not shown). Since there were no QTL on this second chromosome, we would expect low LRT statistics. On the contrary, very high LRT statistics were observed for the IM method (the 95th percentile was at 35.5), strongly suggesting that the phenomenon of spurious LOD score peaks had occurred. The HK, IRLS, and EE methods did not show such high LRT statistics on the unlinked chromosome (the 95th percentiles were at 4.2, 6.0, and 3.8, respectively).

Taking a closer look at the LRT statistics for the IRLS method on this second chromosome with no QTL on it revealed another problem. Following Xu (1998a,b) we calculate LRT statistics for the IRLS method using the likelihood based on the assumption that . However, it follows from the appendix that the IRLS method does not give maximum-likelihood estimates corresponding to this likelihood (in contrast to the EE method). Thus, the LRT statistics for the IRLS method are not guaranteed to be nonnegative. In fact, analyzing the second chromosome with no QTL while keeping the phenotypes, which are influenced by the two 10-cM-apart QTL on the first chromosome, yielded negative LRT statistics for the IRLS method in ∼400 of 1000 simulation replicates with the 10th percentile being at −1.2.

In summary, these simulations have shown that the EE method approximates the IM method very well when two loci with opposite effects are closely linked. The EE method avoids the bias shown by the HK method, estimates the parameters more efficiently than the IRLS method, and also avoids problems with artificially high LRT statistics on other chromosomes observed with the IM method and negative LRT statistics seen with the IRLS method.

DISCUSSION

Most quantitative traits are believed to be influenced by multiple QTL that may interact, and it is therefore desirable to model the effect of these QTL simultaneously. This may, however, pose a formidable computational burden even for a moderate number of loci, since the number of possible models increases exponentially with the number of loci considered in the model. These computational problems may be addressed along two main lines of attack.

First, the multidimensional model space may be searched much more efficiently compared to doing an exhaustive grid search. More efficient model search procedures include techniques such as forward selection and backward elimination to search through nested sequences of models (Broman and Speed 2002), randomization algorithms such as Markov chain Monte Carlo (Yi 2004) or a genetic algorithm (Carlborg et al. 2000), and deterministic global optimization algorithms that repetitively divide the search space into smaller parts (Ljungberg et al. 2004).

Second, any model space search procedure will involve fitting the statistical model many times. Thus, a fast and efficient method for estimating model parameters is needed to reduce total computation time. Currently, the HK method is preferred as a fast approximation to the IM method for estimating model parameters. However, the HK method is known to produce biased estimates of the residual variance and to be sensitive to epistasis and linkage between QTL.

We have focused on the latter issue, fitting multilocus QTL models fast and efficiently. An extension of the HK method is proposed and formulated using estimating equations. This EE method involves simultaneously solving estimating equations for both mean and variance parameters. We have compared the IM, HK, IRLS, and EE methods primarily by computer simulation, focusing on situations where either the HK method or the IM method performs poorly.

It is found here that the HK method is sensitive to certain missing data patterns, e.g., as arise from selective genotyping. With such data, the HK LOD curve may be artificially inflated over large stretches of the genome. The EE method alleviates this problem and produces LOD curves very similar to IM LOD curves. Also, the HK method suffers from large bias in the estimation of the residual variance and has lower power to detect QTL than the IM method, especially in situations of epistatically interacting QTL or QTL that are linked (Kao 2000). Here, it is found that the EE method approximates the IM method more closely in cases of epistasis or linked QTL: it produces unbiased estimates of the residual variance, it has smaller standard deviations on the parameter estimates than the HK method, and it has high power to detect even closely linked QTL of opposite effect.

In comparison to the IM method, the EE method has increased robustness toward nonnormal phenotype distributions. The IM method occasionally produces large spurious LOD score peaks in regions with little marker information if the phenotype distribution deviates markedly from a normal distribution (Feenstra and Skovgaard 2004). This artifact is caused by the fact that a mixture distribution with many components always produces a better fit than a mixture with few components. It is found that the problem is aggravated for models with multiple loci. The HK and EE methods are immune to this problem, since single normal distributions are used both for full and for reduced models.

The EE method is not as fast as the HK method, since it involves solving a set of estimating equations numerically. Still, it may provide gains in computational speed compared to the IM method. In full two-locus genome scans, for example, our implementation of the EE method was twice as fast as the IM method in computation time, and we expect additional gains in speed when the code has been further optimized.

We have demonstrated analytically in the appendix that the EE method is more efficient than the HK and IRLS methods under the assumption that . Admittedly, this assumption may often be violated; the residual variation of certain traits may be inherently nonnormal and the effects of major QTL may also cause the phenotype distribution to deviate from normality. It is evident, however, from the simulations investigating epistasis and linkage that the EE method can also be very efficient compared to the HK and IRLS methods in cases where y_i | m_i is clearly not normally distributed. Moreover, the IRLS method may result in negative LRT statistics, something that the EE method avoids.

The estimating equations used by the EE method involve weighted linear combinations of the simple estimating functions y_i − μ_i and (. Under the assumption taken by the HK, EE, and IRLS methods that , it may be shown that the EE method is asymptotically optimal in the sense that any other linear combination of the simple estimating functions gives rise to estimates with a larger asymptotic covariance matrix (Godambe and Heyde 1987). A further development might be to assume a specific distribution of the residuals in Equation 3 and derive optimally weighted combinations of the simple estimating functions on the basis of this distribution. We anticipate that the gain in efficiency compared to the EE method will be minimal and possibly at the expense of greater numerical instability.

Few authors have employed estimating equations for mapping QTL in experimental crosses. Lange and Whittaker (2001) provide a recent exception and develop a generalized estimating equation (GEE) approach for QTL mapping of multiple correlated traits. However, in contrast to the EE method, these authors assume that the variance due to uncertainty of QTL genotype given marker genotype could be ignored. This is the same assumption taken by the HK method, which may lead to problems of inflated LOD curves, biased variance estimates, and low power, as seen here. It might be worthwhile to pursue the estimating equation approach further compared to this presentation. For instance, the EE method, as proposed here, tests hypotheses by likelihood-ratio tests based on a normal model. It would, however, be perfectly possible to still obtain parameter estimates by solving the estimating equations (Equations 10 and 11), but then use, e.g., score-type test statistics for hypothesis testing. This could possibly contribute some extra robustness compared to using the EE method in conjunction with LRT statistics.

In conclusion, the estimating equation method presented here may be used as a fast and efficient approach for mapping multiple QTL. Generally, it performs better than the HK method at approximating the IM method. Importantly, it avoids problems shown by the HK method in situations with special missing data patterns, epistasis, and linked QTL. Furthermore, the EE method is more robust than the IM method toward nonnormal phenotype distributions, and it is computationally faster. These issues become especially important in the analysis of multiple-QTL models.

The EE method was implemented with new functions soon to be incorporated in the QTL mapping software R/qtl (Broman et al. 2003), an add-on package for the general statistical software, R (Ihaka and Gentleman 1996; R Development Core Team 2005).

APPENDIX

To demonstrate that the EE method yields more efficient estimates of the mean parameters, β, than the IRLS method, we take a closer look at the estimating equations. We let G_EE(y; θ) denote the 2^m + 1 vector of estimating functions for the EE method, i.e., G_EE(y; θ) corresponds to the left-hand sides of the estimating equations (Equations 10 and 11). Similarly, G_IRLS(y; θ) denotes the estimating functions for the IRLS method, corresponding to the left-hand sides of Equations 15 and 16.

In general, the asymptotic distribution of an estimator 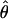that solves a set of estimating equations G(y; θ) = 0 is Gaussian with mean θ and variance of the so-called sandwich form

The information matrix may be found by inverting :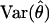

Assuming that (or slightly more generally, that the third and fourth cumulants are zero) the information matrices for the EE and IRLS methods are given by the matrix expressions (derivations not shown)

(A1)

(A2)

where

(i.e., 2^m × n matrices), and (i.e., a 1 × n matrix), and 1_n is the identity vector of length n.

To invert the information matrices, we use the following result about inverting a partitioned square matrix. Let

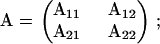then

The submatrix corresponding to may be considered the effective information about the mean parameters, β, since inverting it yields the asymptotic variance on the estimate of β. The effective information matrices for the EE and IRLS methods are

(A3)

(A4)

Consider the difference between the effective information for the two methods:

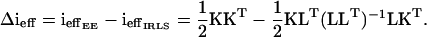By a matrix version of the Cauchy–Schwarz inequality (Marshall and Olkin 1990) it can be seen that Δi_eff is positive definite. Thus, by inverting the effective information matrices we get that is negative definite asymptotically; i.e., the EE method estimates the mean parameters more efficiently than the IRLS method.

We also consider efficiency under the HK method. The closed-form expression for the estimator of β is

with U defined as in Equation 14. The variance of the estimator is

The corresponding effective information about β may be found by inverting this matrix, since the estimator of β is independent of that of σ² under HK regression. This matrix may be written

with M as previously defined and

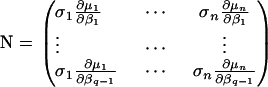Consider now the difference between the effective information for the IRLS method and that for the HK method

Again, it follows from the matrix version of the Cauchy–Schwarz inequality Marshall and Olkin (1990) that is positive definite and consequently that is negative definite asymptotically. Thus the EE method is more efficient than the IRLS method, which in turn is more efficient than the HK method.