Signatures of Demographic History and Natural Selection in the Human Major Histocompatibility Complex Loci

Abstract

Many lines of evidence show that several HLA loci have experienced balancing selection. However, distinguishing among demographic and selective explanations for patterns of variation observed with HLA genes remains a challenge. In this study we address this issue using data from a diverse set of human populations at six classical HLA loci and, employing a comparative genomics approach, contrast results for HLA loci to those for non-HLA markers. Using a variety of analytic methods, we confirm and extend evidence for selection acting on several HLA loci. We find that allele frequency distributions for four of the six HLA loci deviate from neutral expectations and show that this is unlikely to be explained solely by demographic factors. Other features of HLA variation are explained in part by demographic history, including decreased heterozygosity and increased LD for populations at greater distances from Africa and a similar apportionment of genetic variation for HLA loci compared to putatively neutral non-HLA loci. On the basis of contrasts among different HLA loci and between HLA and non-HLA loci, we conclude that HLA loci bear detectable signatures of both natural selection and demographic history.

ANALYSES carried out over the last decade have made it clear that various genes in humans are under natural selection, resulting in patterns of variation that are different from those expected under neutrality (Vallender and Lahn 2004). There are several examples of genes undergoing directional (Romeo et al. 1989; Kidd et al. 2000; Enard et al. 2002), weak purifying (Smirnova et al. 2001), and balancing selection (Bamshad et al. 2002; Wooding et al. 2004). The genes within the human major histocompatibility complex (MHC) that code for glycoproteins involved in peptide presentation, known as the human leukocyte antigen (HLA) loci, play a critical role in the adaptive immune system and are prime examples of loci that have been under natural selection (Hughes and Yeager 1997; Hedrick 1999; Meyer and Thomson 2001). The MHC region in humans lies on chromosome 6 and contains >120 genes, ∼40% of which are related to the immune response (MHC Sequencing Consortium 1999). The HLA genes code for molecules that are responsible for binding peptide fragments of either intracellular origin (in the case of the class I loci, including HLA-A, -B, and -C) or extracellular origin (in the case of class II loci, including DRB1, DQB1, and DPB1). Once exposed on the cell surface, the peptide–HLA complex can stimulate cytotoxic T-cells (in the case of class I molecules) or induce helper T-cells to secrete cytokines, leading to the production of antibodies and stimulation of macrophage activity (in the case of class II molecules).

Even before it was known that HLA molecules bind peptides, Doherty and Zinkernagel (1975) had proposed that the immune response is “MHC restricted,” leading them to suggest that heterozygous individuals would respond to a broader range of parasite antigens and would therefore be selectively favored. Various genetic studies have since been carried out that support the hypothesis that HLA genes have been under balancing selection. As expected for loci under balancing selection, analyses have shown a more even allele frequency distribution than expected under neutrality at HLA loci in various human populations (Hedrick and Thomson 1983; Salamon et al. 1999; Valdes et al. 1999; Tsai and Thomson 2006). These studies revealed considerable heterogeneity among loci with respect to the evidence of selection. For example, while many populations appear to be selected at DQB1, there is less evidence of selection at DRB1 and even less at DPB1. Analyses of the ratio of synonymous to nonsynonymous substitutions revealed an excess of nonsynonymous substitutions at codons involved in peptide binding, consistent with balancing selection upon these codons (Hughes and Nei 1988, 1989). Linkage disequilibrium (LD) analyses in the MHC region have indicated a deviation from neutral expectations, with higher than expected levels of LD (Hedrick and Thomson 1986; Klitz et al. 1992). Results from disequilibrium pattern analysis (Klitz and Thomson 1987; Thomson and Klitz 1987; Williams et al. 2004) and the constrained disequilibrium values method (Robinson et al. 1991a,b; Grote et al. 1998) have identified specific HLA haplotypes that show signs of past selection in specific populations. In addition, assessments of molecular diversity in the MHC indicated that regions of high diversity were centered on the classical class I and II loci, as would be expected if they were targets of a regime of balancing selection (Satta et al. 1998).

Recently, Prugnolle et al. (2005b) examined the correlation between the pathogen richness of different world regions and the amount of HLA heterozygosity, after correcting for the effect of distance of populations from Africa, a factor known to be correlated with heterozygosity. The authors found that a significant positive correlation existed between pathogen richness (especially that of viral origin) and HLA heterozygosity for HLA-A and -B, corroborating a model of pathogen-driven selection in maintaining high levels of diversity at these loci. Finally, numerous examples of associations between HLA alleles and susceptibility or resistance to infectious diseases have been found, demonstrating the importance of these genes in the face of selective agents (Hill 1998; Petzl-Erler 1999).

These studies revealed patterns of variation consistent with a form of balancing selection, but the precise mode of selection has remained unresolved, since the results were compatible with models of heterozygote advantage, frequency-dependent selection, or changes in selective regime over time and/or space (Denniston and Crow 1990; Takahata and Nei 1990; Meyer and Thomson 2001). In this study we use a data set composed of populations from eight broadly defined regions of the world, with sample sizes >40 individuals, to assess the effects of selection upon three HLA class I loci (HLA-A, -B, and -C, surveyed in 20 populations each) and two class II HLA loci (DRB1 and DQB1, surveyed in 17 populations each). Eleven of the populations typed for DRB1 and DQB1 were also surveyed at the class II DPB1 locus.

Given that the null hypothesis of neutral evolution has been tested in several previous studies (reviewed in Hughes and Yeager 1998; Meyer and Thomson 2001), we focus the present analysis on the differences in the effects of selection among human populations, examining in particular the interaction of the proposed selective regimes and the demographic histories of the populations. Specifically, our goals are the following: (1) to test the hypothesis that balancing selection has resulted in reduced interpopulation differentiation, in comparison with that observed for neutral markers; (2) to provide a description of the geographical distribution of HLA alleles and haplotypes, quantifying the number and frequency of alleles restricted to specific geographic regions; (3) to quantify the extent of LD among HLA loci; and (4) to distinguish between the effects of selection and demographic history upon the observed levels of single and multilocus variation.

A major challenge in the interpretation of genetic polymorphism is that natural selection and demographic history can have similar effects upon the data, making it difficult to differentiate between the effects of these processes (Nielsen 2001). In this study we address this issue by comparing the results obtained for HLA to those for non-HLA data sets, which presumably have not been shaped by the same selective processes as the HLA loci and therefore offer information on the demographic history of human populations.

DATA AND METHODS

Data:

Population samples were collected and genotyped by participating laboratories of the 13th International Histocompatibility Workshop (IHW). A variety of PCR-based genotyping methods were used, all of which detect nucleotide variation primarily within exons 2 and 3 (for HLA-A, -B, and -C) and exon 2 (for DRB1, DQB1, and DPB1). These methods fall into four different categories of typing protocols: (1) PCR sequence-specific oligo probe (SSO, SSOP), employed in populations 1, 3, 7, 11, 18, 21–25, and 27 (numbers correspond to names in Table 1); (2) reverse hybridization format PCR–SSOP methods [IHWG reverse line strip (RLS) and Innolipa PCR–SSO systems], employed in populations 4–6, 10–17, 19, 26, and 28–31; (3) sequence-specific primer (SSP) methods (Genovision SSP and Dynal SSP systems), employed in population 8; and (4) sequence-based typing (SBT) methods, employed in populations 2 and 20.

TABLE 1.

Population names, geographic regions, sample sizes, and number of alleles

				Sample size (2n)			No. of alleles (k)
Population	Codea	Region	Abbreviation	A	C	B	A	C	B
Dogon	1	Sub-Saharan Africa	SSA	276	258	276	21	19	31
Kenyan	2	Sub-Saharan Africa	SSA	286	224	286	39	25	46
Shona	3	Sub-Saharan Africa	SSA	450	452	452	30	21	39
Zulu	4	Sub-Saharan Africa	SSA	372	196	402	28	18	33
Czech	5	Europe	EUR	210	210	212	22	22	33
Georgian	6	Europe	EUR	210	214	216	23	24	42
Irish	7	Europe	EUR	1000	1000	1000	22	22	43
Malay	10	Southeast Asia	SEA	248	214	202	24	20	38
Puyuma	12	Southeast Asia	SEA	100	100	100	8	8	11
Saisiat	13	Southeast Asia	SEA	102	102	102	7	9	9
Yami	14	Southeast Asia	SEA	100	100	100	5	7	8
Korean	15	Northeast Asia	NEA	400	400	400	17	21	37
Okinawan	16	Northeast Asia	NEA	210	210	208	11	12	20
Tuva	17	Northeast Asia	NEA	378	348	360	31	25	52
Filipino	19	Oceania	OCE	188	188	188	16	19	35
Ivatan	20	Oceania	OCE	100	100	100	7	10	16
Yuendumu	25	Australia	AUS	382	384	386	10	8	11
Mixe	27	North America	NAM	102	102	102	8	8	12
Yupik	28	North America	NAM	504	298	504	16	17	21
Guarani–Nandewa	31	South America	SAM	104	104	106	12	8	30

Population	Codea	Region	Abbreviation	DRB1	DQB1	DPB1	DRB1	DQB1	DPB1
Shona	3	Sub-Saharan Africa	SSA	458	458	456	26	15	19
Zulu	4	Sub-Saharan Africa	SSA	176	174	174	24	9	14
Czech	5	Europe	EUR	206	212	204	30	13	17
Slovenian	8	Europe	EUR	200	200	200	25	14	15
Kinh	9	Southeast Asia	SEA	204	200	0	24	12	0
Malay	10	Southeast Asia	SEA	108	110	104	20	12	19
Muong	11	Southeast Asia	SEA	166	164	0	17	14	0
East Timorese	18	Oceania	OCE	166	172	172	18	10	9
Moluccan	21	Oceania	OCE	80	92	92	11	9	11
PNG Lowlander	22	Oceania	OCE	160	182	0	5	9	0
Cape York	23	Australia	AUS	198	198	192	22	12	10
Kimberley	24	Australia	AUS	82	82	76	12	6	5
Canoncito	26	North America	NAM	80	80	80	8	6	6
Mixe	27	North America	NAM	102	102	102	9	4	4
Zuni	29	North America	NAM	100	100	100	9	6	4
Central America	30	South America	SAM	100	100	100	11	3	7
Guarani–Nandewa	31	South America	SAM	106	106	0	18	6	0

^aThe population numbers are used to indicate the geographic location of each sample in Figure 1.

Methods 1–3 do not involve the resequencing of HLA genes and are instead based on the genotyping of several polymorphic regions within the gene. A polymorphic region is defined by a stretch of nucleotides that has multiple variants within humans. Each variant within a polymorphic region is defined by a combination of nucleotides and is referred to as a sequence motif. The combination of sequence motifs present is used to determine the pair of alleles in an individual. A large number of sequence motifs are interrogated for each locus: using the IHWG RLS system the number of polymorphic regions (and the number of sequence motifs in parentheses) surveyed in class I was 21 (54) for HLA-A, 23 (81) for HLA-B, and 16 (36) for HLA-C. For class II, the number of polymorphic regions (and the number of sequence motifs) surveyed in exon 2 is between 11 and 15 (35 and 40) for DQB1 and DPB1 (depending on the specific protocol used). For DRB1, a two-tier approach to typing was used in which an initial screening of ∼15 sequence motifs is performed, followed by the separate amplification of the two alleles using primers based on the initial typing. The amplicons from each DRB1 allele are then typed with a panel of probes that interrogates 35 sequence motifs. The combination of motifs found across all polymorphic regions allows for the discrimination of alleles that differ at sites that result in amino acid differences. The set of polymorphic regions surveyed at each locus was defined on the basis of prior knowledge of sequence polymorphism of HLA loci. A large database of sequences from different human populations was available for the design of the SSO probes, including populations from all major geographic regions of the world. Further details on the sampling and ethnographic information for the populations and genotyping methods used, as well as the resolution of ambiguous genotypes and allele calls, are given in Mack et al. (2006). The dbMHC website (http://ncbi.nih.gov/mhc/) contains a listing of the primers and probes used to generate the data for the 13th IHW.

Populations were selected to meet the following criteria: the sample size was 40 or more individuals; there was no significant deviation (P > 0.01) from Hardy–Weinberg proportions (HWP) at any of the loci; genotyping for the population was available for at least one of these two sets of loci, (a) HLA-A, HLA-B, and HLA-C or (b) DRB1 and DQB1 (a subset of populations additionally had genotyping for DPB1); and the HLA genotyping was carried out at high molecular resolution. Using these criteria, we defined a representative data set with indigenous populations from the following eight geographic regions: sub-Saharan Africa (SSA), Europe (EUR), Southeast Asia (SEA), Oceania (OCE), Australia (AUS), Northeast Asia (NEA), North America (NAM), and South America (SAM). Figure 1 provides the location of the samples and Table 1 gives the sample size and the loci typed for each population. Two of the population names refer to geographic regions, rather than an ethnic group. The population listed as Kenyan is composed of a group of unrelated Kenyan women who were enrolled as a control population, in a study of mother-to-child human immunodeficiency virus transmission, when they gave birth in the hospital in Nairobi. The population listed as Central American is composed of Chibchan language-speaking individuals from Costa Rica and Panama.

Figure 1.—

Map of the world showing the location of sampled populations. The numbers identifying populations are given in Table 1.

To place our results on HLA polymorphism in the context of the demographic history of human populations, we analyzed two non-HLA data sets using the same methods as those applied to the HLA data. We refer to these as the Centre d'Etude du Polymorphisme Humain (CEPH) Diversity Panel data (Cann et al. 2002) and the Frisse data (Frisse et al. 2001).

The CEPH Diversity Panel (CDP) data consist of genotypes for 377 microsatellite loci, spread over all 22 autosomes, from 52 populations with an average of 20 individuals per population sample. We compared both the degree of sharing of alleles among populations and the amount of differentiation among populations and regions revealed in subsets of this data set to the values obtained for the HLA loci.

The Frisse data consist of DNA sequences from 10 unlinked noncoding regions, each spanning ∼1 kb, obtained for 15 individuals (30 chromosomes) from each of three populations: 15 Hausa from Yaounde (Cameroon), 15 individuals from central Italy, and 15 Han Chinese from Taiwan. These sequences define haplotypes that we used to address the effects of demographic history upon tests based on allele frequency distributions (e.g., the Ewens–Watterson test of neutrality).

Methods:

Unless otherwise stated, all analyses were carried out using the PyPop software package (Lancaster et al. 2003). Further details on the methods implemented in PyPop (http://www.pypop.org/) are given in Single et al. (2006).

Measures of diversity:

For all loci, we computed the observed heterozygosity (H_obs), defined as the proportion of heterozygotes expected under HWP, for the observed allele frequencies (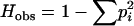). To test whether heterozygosities were significantly different among populations, we performed an analysis of variance on the ranks of heterozygosity values. This technique provided a nonparametric assessment similar to the Kruskal–Wallis test, but allowed for the use of more powerful multiple comparison tests (Connover and Iman 1981).

Deviation from HWP:

We tested for deviation from HWP using the exact test developed by Guo and Thompson (1992). Population samples that deviated from HWP (P < 0.01) at any of the loci were excluded to minimize the impact of possible admixture or genotyping errors, which are known to result in deviations from HWP when heterozygous individuals are erroneously identified as homozygous for one of the alleles.

Deviation from neutrality and population equilibrium:

To test for deviation from neutrality, we used the sample homozygosity, 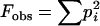(Watterson 1978), as a test statistic. Because deviation from the neutral model can be the result of either natural selection or deviation from population equilibrium, we refer to the hypothesis being tested as “neutrality equilibrium.” Under the null hypothesis of neutrality equilibrium the sampling distribution of the homozygosity statistic (the distribution of F_eq), for samples with the same size and number of alleles in the observed data, was used to assess the significance of the observed sample homozygosity (F_obs). This test was implemented using the algorithm proposed by Slatkin (1994), which uses the Ewens sampling formula (Ewens 1972) to obtain the distribution of F_eq under the null hypothesis. The P-values for the Ewens–Watterson test indicate the proportion of the distribution of F_eq that is smaller than F_obs, providing a one-sided test against the alternative of balancing selection. Fisher's method for combining P-values (Fisher 1970) was used to test for significant deviation for the entire set of results for each locus, where 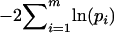has a chi-square distribution with 2m d.f. and m is the number of P-values, p_i, combined.

In addition, we summarized the degree to which sample heterozygosity differs from neutral-equilibrium expectations by using the normalized deviate of the sample heterozygosity: H_ND = (H_obs − H_eq)/SD(H_eq) (Salamon et al. 1999; Garrigan and Hedrick 2003). Positive H_ND-values indicate that sample heterozygosity is higher than that expected under neutrality equilibrium and is in the direction of balancing selection. These H_ND-statistics can be combined to test whether the entire distribution of normalized deviations from equilibrium heterozygosity values for a set of populations is compatible with neutrality equilibrium at a locus. Under the assumption that samples from m different populations are independent, the distribution of the mean H_ND-value over m populations, 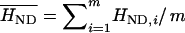, will be asymptotically normal. A two-sided t-test was used to test if the mean H_ND was significantly different from zero.

Haplotype frequency estimation and linkage disequilibrium:

We estimated haplotype frequencies on the basis of genotypic data for all pairs of loci within each of the three subsets of HLA genes [(1) A, B, and C; (2) DRB1 and DQB1; and (3) DRB1, DQB1, and DPB1], using an expectation–maximization algorithm with 50 starting conditions. The permutation distribution of the likelihood-ratio statistic (Slatkin and Excoffier 1996) was used to test the null hypothesis of no genetic association among loci. The inferred haplotypes were used to compute two multiallelic LD measures: W_n (a multiallelic version of the correlation measure; Cramer 1946) and D′ (Hedrick 1987). Each measure summarizes individual LD coefficients, D_ij and D′_ij = D_ij/D_max, respectively, across all pairs of alleles for a set of loci.

The fraction of complementary haplotypes further characterizes the distribution of the individual D′_ij-values. Haplotypes for which D′_ij = 1, the maximum possible value, are referred to as complementary haplotypes (Feldman et al. 1975). For a given locus pair, the complementary fraction (CF) is defined as the proportion of haplotypes that are complementary. This statistic was computed for all haplotypes that were estimated to have at least two copies, as suggested by Slatkin (2000).

Population differentiation and region-specific alleles:

To quantify the differentiation among populations at each locus, we used the analysis of molecular variance (AMOVA) framework (Excoffier et al. 1992). The analyses were implemented using the AMOVA function of the ADE4 package for R (Ihaka and Gentleman 1996). Differentiation among populations and regions was quantified under the assumption that all alleles are equidistant. Populations from AUS were not used in these analyses because there are no populations from this region in the CDP data set, which we used for comparison with the HLA results. Differentiation among pairs of populations at the allele level was quantified using the distance proposed by Reynolds et al. (1983), D = −ln(1 − F_ST), with the F_ST values computed using the analysis of variance framework discussed in Michalakis and Excoffier (1996). The proportion and frequency of region-specific alleles were computed as in Rosenberg et al. (2002) by restricting attention to alleles that were found more than once in the full set of populations.

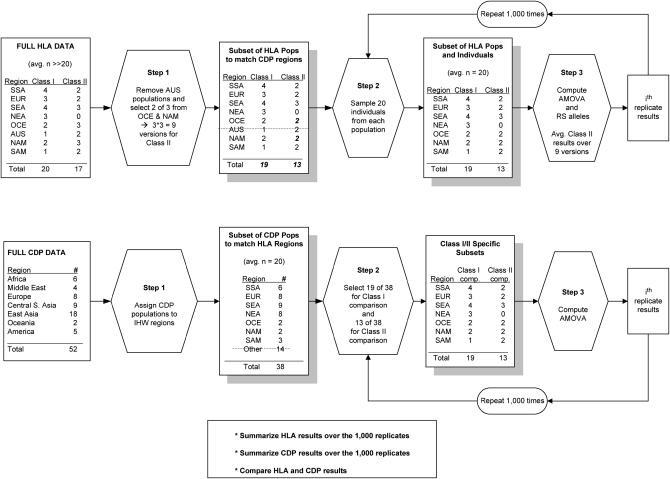
To make the HLA and CDP data sets comparable, we used the resampling approach described below and in Figure 2. First, we identified a set of 38 populations from the 52 CDP populations that could be assigned to the same regions as those used in the analysis of the HLA data. From this collection of 38 populations, we sampled 19 populations to match the HLA class I data set and 13 populations to match the HLA class II data set. The numbers of populations sampled from each region for the comparison with HLA class I (II) data were 4 (2) from SSA, 3 (2) from EUR, 4 (3) from SEA, 2 (2) from OCE, 3 (0) from NEA, 2 (2) from NAM, and 1 (2) from SAM. For the class II comparison, 13 populations were chosen rather than 15, since there were only 2 CDP populations from OCE and NAM. The HLA results were computed separately for each combination of 2 of the 3 populations from OCE and NAM and averaged over these nine possibilities. We accounted for the difference in sample size between the HLA and CDP populations by analyzing subsamples of size n = 20 from the HLA data, which is the average size of the CDP population samples. Population differentiation and region-specific allele statistics were computed in each resampled CDP data set and in each replicate set of subsampled populations for the HLA data. The above procedure was repeated 1000 times, allowing the computation of empirical 95% confidence intervals.

Figure 2.—

Steps taken to make CDP and HLA data sets comparable.

RESULTS

Polymorphism within populations:

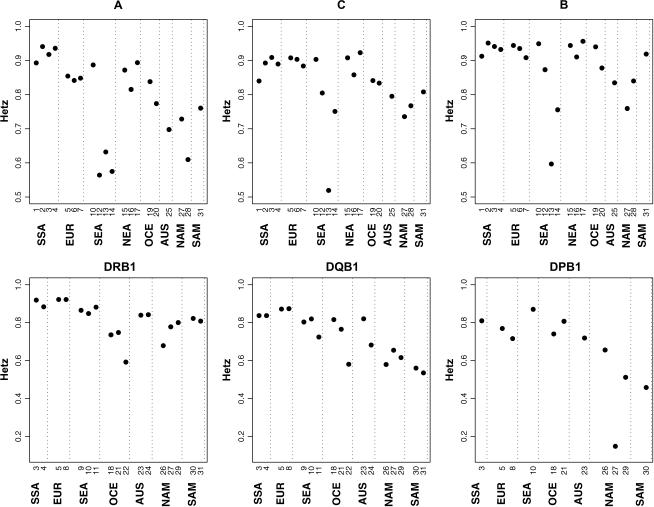
For all class I loci, average heterozygosity within regions is highest in SSA, EUR, and NEA (with little distinction among these regions) and is lowest in SAM and NAM. Populations from SEA span a broad range of heterozygosities (Figure 3). The populations from OCE and AUS occupy intermediate positions. For the class II loci a similar pattern is observed, although the range of heterozygosities for the SEA populations (a different set of populations than for class I) is not as broad (Figure 3).

Figure 3.—

Scatterplots of heterozygosity values for six HLA loci. The population numbers correspond to those in Table 1.

An analysis of variance on ranked heterozygosity values showed significant differences among world regions at HLA-A and -C, DRB1, and DQB1, but not at HLA-B. This is likely due to the overall higher heterozygosity at HLA-B, which causes all populations to occupy a narrow range of values, reducing the differences among them. For the loci where overall differences in heterozygosity among regions were significant, we used the Tukey–Kramer multiple-comparison test (Kramer 1956) to identify geographic regions with significantly different heterozygosities. For HLA-A and -C, all comparisons among regions that yielded significant results involved either NAM or SSA, which represent the two extremes of heterozygosities. Among the populations from SEA, there is a high degree of variability in heterozygosity. The Malay population has high heterozygosity relative to the aboriginal Taiwanese populations (Puyuma, Saisiat, Yami), which have low values and substantial variation among them. These aboriginal Taiwanese populations are a set of relatively isolated groups with little historical or ongoing admixture (Mack et al. 2006). The low heterozygosity is due to one or two high-frequency alleles at each locus that make up over half of the allele frequency spectrum for these populations (A*2402 in all three populations; B*3901 in the Saisiat and B*1525 and B*4002 in the Yami; and C*0801 and C*0304 in the Puyuma, C*0702 in the Saisiat, and C*0304 and C*0403 in the Yami). The A*2402 allele is also at high frequencies in the Yupik, accounting for their low heterozygosity. In addition, the DPB1*0402 in the Mixe is found at a frequency of 0.92, resulting in the lowest heterozygosity seen in the data set.

For DRB1 and DQB1, significant differences in heterozygosities were found when comparing the Americas to other regions and when comparing SSA to other regions. In addition, several other pairs of regions had significantly different heterozygosities. One reason for this difference is the lower variability in heterozygosity within regions for these loci (Figure 3). SSA and EUR showed significantly higher heterozygosity than NAM and SAM populations, as did SEA compared to SAM and EUR compared to OCE. For DRB1 alone, the list of significant regional comparisons also included AUS with SSA, EUR, OCE and NAM; SEA with EUR, OCE, and NAM; and OCE with SSA, EUR, and SAM. For the class I loci the populations from NEA showed comparable levels of genetic diversity to those found in SSA and EUR. The lack of class II data for these NEA populations made it impossible to determine if this trend was present for DRB1 and DQB1. In summary, these results show that the differences between populations from SSA and the Americas (SAM and NAM) are pronounced and significant and that NEA and SSA harbor more genetic diversity than NAM and AUS populations.

Diversity patterns compared to neutral expectations:

The hypothesis of neutrality equilibrium was tested using the Ewens–Watterson test. We found significant deviations from neutrality equilibrium (uncorrected P-value <0.05) at five loci: one population at HLA-A (Zulu), seven populations at HLA-B (Zulu, Shona, Czech, Yuendumu, Korean, Okinawan, and Puyuma), eight populations at HLA-C (Shona, Malay, Yuendumu, Korean, Puyuma, Okinawan, Tuva, and Guarani), three populations at DQB1 (Zulu, Czech, and Slovenian), one population at DRB1 (Shona), and no significant deviations at DPB1 (Table 2). Only one of the deviations (the Zulu at HLA-A) remained significant after correcting for multiple comparisons. This is in part due to the low power of the Ewens–Watterson test. To assess overall locus-level trends we considered the methods described below for combining information across populations.

TABLE 2.

Standardized difference between observed heterozygosity and its expectation under neutrality equilibrium (H_ND)

Population	Region	A	B	C
a. HLA data: class I
Dogon	SSA	0.96	0.48	0.26
Kenyan	SSA	0.85	0.84	0.42
Shona	SSA	0.97	1.10	1.34
Zulu	SSA	1.45	1.12	1.06
Czech	EUR	−0.09	1.28	1.05
Georgian	EUR	−0.55	−0.04	0.76
Irish	EUR	0.63	0.22	1.09
Malay	SEA	0.48	1.18	1.15
Puyuma	SEA	−0.87	1.41	1.20
Saisiat	SEA	0.08	−0.96	−1.70
Yami	SEA	0.41	0.77	0.98
Filipino	OCE	0.49	0.87	0.06
Ivatan	OCE	1.16	0.80	1.12
Yuendumu	AUS	0.35	1.28	1.38
Korean	NEA	1.10	1.30	1.30
Okinawan	NEA	0.99	1.26	1.28
Tuva	NEA	0.17	1.06	1.32
Mixe	NAM	0.55	−0.18	0.61
Yupik	NAM	−1.63	0.35	−0.38
Guarani–Nandewa	SAM	−0.15	−0.35	1.23
Fraction HND > 0		15/20	16/20	18/20
Overall P-value (FPPa)		0.045	0.000	0.000
Overall P-value (t-test)a		0.042	0.000	0.000
Average HND		0.367	0.690	0.777

Population	Region	DRB1	DQB1	DPB1
b. HLA data: class II
Shona	SSA	1.25	0.92	0.13
Zulu	SSA	0.13	1.41
Czech	EUR	0.68	1.32	−0.67
Slovenian	EUR	1.12	1.23	−0.95
Kinh	SEA	−0.19	0.70
Malay	SEA	−0.61	0.64	0.13
Muong	SEA	0.97	−0.76
East Timorese	OCE	−1.76	1.08	0.62
Moluccan	OCE	−0.26	0.59	0.59
PNG Lowlander	OCE	0.65	−0.66
Cape York	AUS	−0.47	0.87	0.26
Kimberley	AUS	0.79	0.69
Canoncito	NAM	−0.02	−0.07	0.49
Mixe	NAM	0.76	1.30	−1.63
Zuni	NAM	0.96	0.30	0.46
Central America	SAM	0.81	1.28	−1.27
Guarani–Nandewa	SAM	−1.05	−0.23
Fraction HND > 0		10/17	13/17	7/11
Overall P-value (FPP)a		0.220	0.004	0.683
Overall P-value (t-test)a		0.299	0.002	0.512
Average HND		0.221	0.625	−0.167

Population	Mean HND	First quartile	Third quartile
c. Frisse data
Hausa	−0.447	−0.863	0.295
Italian	−0.167	−0.749	0.594
Chinese	−0.303	−1.267	1.072

Values for population–locus combinations with a significant uncorrected deviation from neutral-equilibrium expectations are in italics.

^aOverall tests of deviation of a locus from neutrality equilibrium were computed using both Fisher's product of P-values (FPP) method for combining P-values and a t-test for the average H_ND.

One method for summarizing allele frequency results is to quantify the differences between observed sample heterozygosity and neutral-equilibrium expectations using the H_ND-statistic, which standardizes the difference between observed and expected results. For all loci except DPB1, we found that the majority of the populations have H_ND > 0, indicating that sample heterozygosity in general exceeds neutral-equilibrium expectations. The only locus with a mean value of H_ND lower than expected under neutral-equilibrium conditions was DPB1 (H_ND = −0.111). Thus, for the majority of HLA loci in a diverse set of human populations, there was a trend in the direction of higher diversity than expected under neutrality equilibrium. We tested the statistical significance of this trend using both Fisher's method for combining P-values and the t-test for the mean H_ND. On the basis of these tests we found overall significance for HLA-A, -B, and -C and DQB1. The DRB1 and DPB1 loci did not deviate significantly from neutral-equilibrium expectations (Table 2).

The results of the Ewens–Watterson test and the trend toward high heterozygosity must be interpreted in the light of both selective and demographic hypotheses. Population bottlenecks preferentially eliminate low-frequency alleles, thus causing only a small reduction in H_obs but substantially reducing H_eq, since the latter is computed conditional on the number of alleles in the population. As a consequence, bottlenecked populations typically show H_obs > H_eq (i.e., H_ND > 0) (Watterson 1986). On the other hand, population expansion will increase the number of low-frequency alleles, resulting in lower heterozygosity than expected under neutrality equilibrium (H_ND < 0).

For complex demographic scenarios it is difficult to predict the relationship between sample and equilibrium heterozygosities and an ideal approach to account for the effect of demographic history is to survey a set of unlinked and putatively neutral markers in the same individuals. Since no additional markers were available for the sampled populations, we compared the results obtained for the HLA loci to the Frisse data, a survey of three human populations (Hausa, Italian, and Chinese) typed at 10 unlinked noncoding regions by DNA sequencing over ∼1-kb haplotypes (Frisse et al. 2001). This data set was chosen for the following reasons. First, it is composed of a set of independent haplotypes from noncoding regions, which provide information about the demographic history of populations. Second, the data consist of well-defined populations (as opposed to very broad groupings of individuals, such as “Africans” or “Europeans”), thus providing a sampling scheme that resembled the one used for the HLA data. Finally, the data are compatible with the assumptions of an infinite-alleles model, which was also used in the neutrality-equilibrium analyses of HLA polymorphism.

None of the three populations in the Frisse data showed a trend toward H_ND > 0 at these noncoding regions. In fact, the three populations had slightly lower heterozygosity than expected under neutrality equilibrium (mean H_ND was −0.447, −0.167, and −0.303 for the Hausa, Italian, and Chinese, respectively; Table 2c). Although the noncoding regions have lower levels of diversity than the HLA data (average number of haplotypes = 6.75, average heterozygosity = 0.630), this factor is unlikely to account for the differences in H_ND results between these data sets, since a comparison of the sets of noncoding regions with highest and lowest diversity revealed that higher diversity was associated with larger negative values for H_ND. Thus, for three different human populations with distinct demographic histories, excess heterozygosity was not found in a set of putatively neutral markers, in contrast to the HLA class I and DQB1 loci.

Interpopulation variation:

Populations were identified as belonging to one of seven geographic regions (SSA, EUR, SEA, OCE, NEA, NAM, and SAM) for the class I data. For the class II data, there were no populations from NEA, and thus six geographic regions were represented. Populations from AUS were not used in this analysis because they are absent from the CDP data set, which we used for comparison with the HLA results. For class I loci, between 88.7 and 92.8% of the genetic variance was due to variation among individuals within populations, between 3.9 and 4.6% was due to differences among populations within regions, and between 3.0 and 7.4% was due to differences among regions (Table 3). For the class II loci (DRB1 and DQB1) ∼88% of the variation was within populations, between 4 and 5% among populations, and ∼7% among regions (Table 3).

TABLE 3.

Apportionment of genetic variation in HLA loci and microsatellites

	HLAa					Microsatelliteb
	A	B	C	DRB1	DQB1	CDP (I)c	CDP (II)d	95% C.I. (I)	95% C.I. (II)
Among regions (%)	7.41	2.98	3.55	7.47	7.00	5.63	5.62	0.51–14.92	−1.55–18.73
Among populations within region (%)	3.87	4.22	4.55	4.42	5.21	2.67	4.92	0.38–6.08	0.69–12.03
Within populations (%)	88.71	92.80	91.90	88.11	87.79	91.70	89.46	81.67–97.57	77.10–96.64

Values refer to the percentage of the total variance attributable to differences at that hierarchical level.

^aThe HLA class I data consist of the 19 non-Australian populations assigned to the regions given in Table 1. The class II data consist of 13 of the 15 non-Australian populations as described in Methods and Figure 3.

^bThe microsatellite data consist of samples from the 38 CEPH Diversity Panel (CDP) populations that could be assigned to the geographic regions for the HLA data.

^cNineteen populations were sampled from the 38 CDP populations to match the HLA class I distribution of populations. Values are averaged over results for 1000 repeated samples.

^dThirteen populations were sampled from the 38 CDP populations in order to match the HLA class II distribution of populations. Values are averaged over results for 1000 repeated samples.

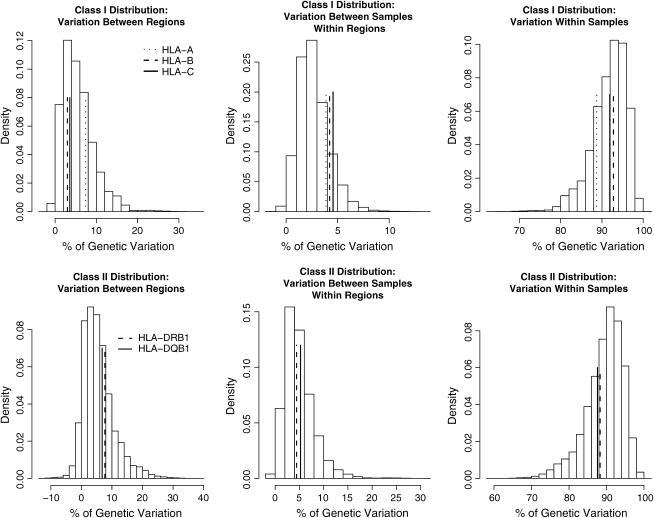
We averaged the values of the variance components over the replicate samples of CDP populations for the two sets of population groupings (those matching the HLA class I distribution of populations among regions first, followed by those matching the class II distribution in parentheses). Our results showed that an average of 91.7% (89.5%) of the variation was within populations, with 2.7% (4.9%) and 5.6% (5.6%) additional variance due to differences among populations within regions and among regions, respectively, for the two sets of CDP population groupings (Table 3). When we compared the variance components obtained for the HLA data with the empirical distribution for the variance components over all 377 microsatellite loci from the CDP, the HLA loci fell within the range of variation for the CDP markers and showed no indication of greater or lesser variation (Figure 4).

Figure 4.—

Distribution of variance components over 377 CDP microsatellite loci. Values are averages over 1000 replicate population resamplings (according to population assignments to regions as described in the Table 3 legend). (Top) Variance components for CDP data using the HLA class I composition of populations among regions, among populations within regions, and within populations; (bottom) variance components for CDP data using the HLA class II composition of populations among regions, among populations within regions, and within populations. The vertical lines indicate the values for the variance components for each of the HLA loci.

The CDP and HLA data have different sample sizes (CDP median 2n = 40, HLA median 2n = 210). To investigate whether our results were robust to a potential sample size effect, we recalculated the variance components for the HLA data using subsamples of 20 individuals from each population for the HLA data. The results (not shown) were essentially the same as those obtained using the full data set, with minor decreases in the within-sample variance (by no more than three percentage points).

A limitation of using surveys based on worldwide levels of differentiation is that they in effect average differentiation over all groups or populations involved. Thus, effects of selection that are geographically restricted could remain undetected. For example, even if there is decreased differentiation within a region due to selection, the effects of other regions could cancel these out. We therefore quantified the amount of intra- and interpopulation differentiation within each region separately (Table 4). The results were concordant with those obtained in the analysis of microsatellites (Rosenberg et al. 2002) and nuclear markers (Tishkoff and Kidd 2004), with the largest levels of differentiation among populations within the Americas and Oceania and the lowest among European populations. Although the quantitative differences between the results of these different studies are difficult to gauge because the identities of the populations differ, they indicate that the demographic differences among regions have shaped variation at HLA, microsatellite, and nuclear SNP data sets.

TABLE 4.

Apportionment of genetic variation among populations within regions

Region	A	B	C	DRB1	DQB1
SAM + NAM	25.47	13.17	11.07	7.06	7.96
EUR	1.25	2.89	2.33	0.66	0.54
SSA	1.34	1.59	2.58	2.91	1.69
NEA + SEA	6.11	7.14	7.63	4.27	9.18
OCE + AUS	8.73	7.21	9.22	18.25	14.61

Values refer to the percentage of the total variance among populations within a region (or set of regions).

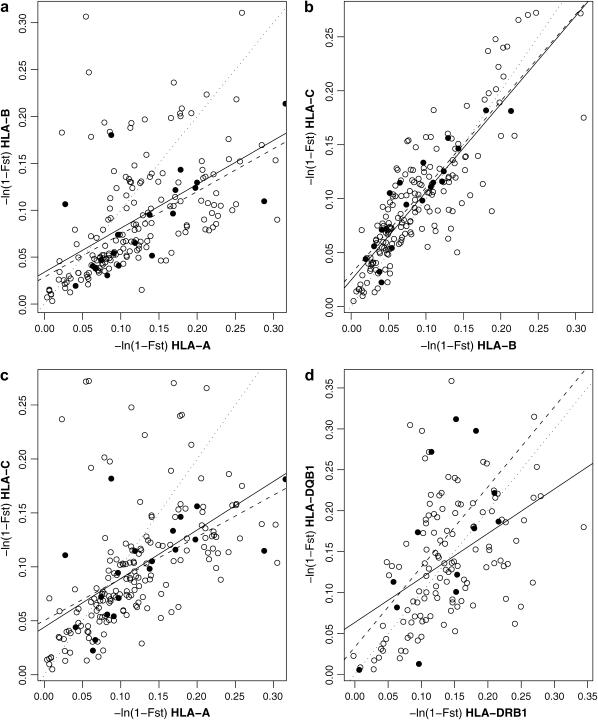
Using an F_ST-based genetic distance [D = −ln(1 − F_ST)], we quantified the genetic differentiation between all pairs of populations (Figure 5). When HLA-A and -B were compared, we found that 140 of the 190 population pairs showed greater differentiation at HLA-A than at HLA-B. This trend is in accord with the overall lower among-population variance seen at HLA-B (Table 3). The greater differentiation seen for HLA-A held for the contrasts between populations from the same region and between populations from different regions, although there were proportionally more population pairs with greater differentiation at HLA-B in the between-region comparisons. This result was driven by comparisons involving populations from the Americas (in particular the Guarani), which showed high levels of divergence at HLA-B compared to populations from other regions. When regressions based on inter- and intraregional differentiation were compared (Figure 5a), we found that the results were extremely similar, indicating that the lower overall differentiation seen at HLA-B occurs at smaller as well as larger geographic distances. Comparisons between HLA-B and -C showed that differentiation at these loci is tightly correlated; a similar result held for comparisons between DQB1 and DRB1, although in this last case the correlation was less tight.

Figure 5.—

Genetic differentiation measured by D = −ln(1 − F_ST) between all pairs of populations for (a) HLA-A vs. HLA-B, (b) HLA-B vs. HLA-C, (c) HLA-A vs. HLA-C, and (d) DRB1 vs. DQB1. Solid circles are comparisons between populations from the same region; open circles are for populations from different regions. The dotted line represents the values for which D is the same for both loci; the solid and dashed lines are best-fit linear regressions for differentiation at the two loci between and within regions, respectively.

Region-specific alleles:

We quantified the proportion of alleles that were region specific (RS), as well as the median frequency of these alleles, for the HLA data using the resampling strategy described in Methods to use the same distribution of populations and sample sizes as in the assessment of interpopulation variation. When computing the number and frequency of RS alleles for the HLA data, we accounted for the effect of sample size on the extent to which RS alleles were found by analyzing subsamples of size n = 20 from the HLA populations. We then computed the proportion of RS alleles in the HLA data over 1000 replicate sets of subsampled populations. Empirical 95% confidence intervals were computed on the basis of the distribution of values over the 1000 sets.

For the combined class I data, the average proportion of nonsingleton alleles that were RS was 32.2%. The average individual values were 30.1, 37.4, 23.5, 23.1, and 3.5% for HLA-A, -B, and -C and DRB1 and DQB1, respectively (Table 5, row 1). As we increased the size of the subsamples, the value for the combined class I data decreased, approaching the value of 25.4% found for the full HLA data set.

TABLE 5.

Region-specific (RS) alleles

	HLA class Ia
A		B		C
Region	Proportion of RS allelesb	Median relative freqc	Proportion of RS allelesb	Median relative freqc	Proportion of RS allelesc	Median relative freqc
ALLd	0.301	0.033	0.374	0.045	0.235	0.033
SSA	0.299	0.033	0.396	0.039	0.110	0.031
EUR	0.046	0.018	0.086	0.023	0.049	0.017
SEA	0.061	0.017	0.062	0.027	0.068	0.029
OCE	0.002	0.001	0.064	0.042	0.005	0.002
NEA	0.088	0.031	0.092	0.027	0.023	0.008
NAM	0.020	0.004	0.137	0.109	0.139	0.046
SAM	0.152	0.056	0.366	0.100	0.175	0.176

HLA class IIa
DRB1		DQB1
Region	Proportion of RS allelesb	Median relative freqc	Proportion of RS allelesb	Median relative freqc
ALLd	0.231	0.043	0.035	0.009
SSA	0.137	0.069	0.016	0.005
EUR	0.138	0.051	0.006	0.003
SEA	0.045	0.013	0.012	0.005
OCE	0.044	0.014	0.001	0.000
NAM	0.069	0.036	0.000	0.000
SAM	0.070	0.032	0.021	0.003

^aResults are averaged over 1000 different samples of size 20 from the IHW populations.

^bThe percentage of alleles that are region specific.

^cThe median relative frequency is computed as the median frequency of the RS alleles among all populations in the region where the RS alleles were found, including zero values for populations where a RS allele was not found.

^dResults for the entire data set.

The frequency contribution of RS alleles was also calculated using the resampling procedure described above. The values, averaged over the 1000 samples of size 20 for the HLA data, were 3.3, 4.5, 3.3, 4.3, and 0.9% for HLA-A, -B, and -C and DRB1 and DQB1, respectively.

Among the world regions surveyed, SSA had the highest percentage of alleles that were RS (Table 5, row 2). Over 29% of the alleles were RS for HLA-A and -B and >11% for HLA-C and DRB1. The SAM populations also had a relatively high proportion of RS alleles, although less so for DRB1. For the class I loci, >15% of the alleles were RS in the SAM population. Values for HLA-DQB1 were particularly low in all regions.

Linkage disequilibrium in the HLA region:

We computed coefficients of linkage disequilibrium and tested the null hypothesis of linkage equilibrium between all pairs of loci within class I and class II (A and B, A and C, B and C, and DRB1 and DQB1). In addition, for a subset of populations for which class I and class II data were available, we computed linkage disequilibrium coefficients between class I and class II loci. Our goal was to compare the magnitude of LD among populations with different demographic histories.

After correcting for the number of comparisons for each pair of class I loci (the number of populations having data for both loci), significant LD was found between all locus pairs in each population, except for the Georgian population in Europe (uncorrected P-values for A:B and A:C of 0.03 and 0.097, respectively) and the Guarani–Nandewa population in SAM (uncorrected P-values for A:B and A:C of 0.007 and 0.017, respectively; Table 6). Among the class II loci, we found significant LD between DRB1 and DQB1 for all populations. When testing the significance of LD between these class II loci and DPB1, we found fewer populations with significant LD (8/14 and 5/14 for the DRB1:DPB1 and DQB1:DPB1 locus pairs, respectively). The drop in LD for locus pairs involving DPB1 has been previously reported for other populations (e.g., Sanchez-Mazas et al. 2000) and is attributed to two recombination hotspots identified between DPB1 and the other class II loci (Cullen et al. 2002).

TABLE 6.

Likelihood-ratio test P-value for significance of LD

	Class I			Class II			Class I/II
Population	A:B	C:B	A:C	DRB1:DQB1	DRB1:DPB1	DQB1:DPB1	A:DRB1	A:DQB1	A:DPB1	C:DRB1	C:DQB1	C:DPB1	B:DRB1	B:DQB1	B:DPB1
Dogon	0.000	0.000	0.000
Kenyan	0.000	0.000	0.000
Shona	0.000	0.000	0.000	0.000	0.000	0.003	0.001	0.000	0.490	0.000	0.000	0.002	0.000	0.000	0.000
Zulu	0.000	0.000	0.000	0.000	0.000	0.013
Czech	0.000	0.000	0.000	0.000	0.129	0.422	0.010	0.697	0.034	0.000	0.000	0.101	0.000	0.000	0.015
Georgian	0.030	0.000	0.097
Irish	0.000	0.000	0.000
Slovenian				0.000	0.102	0.012
Kinh				0.000
Malay	0.000	0.000	0.000	0.000	0.716	0.081	0.002	0.038	0.373	0.004	0.213	0.519	0.178	0.221	0.127
Muong				0.000
Puyuma	0.000	0.000	0.000
Saisiat	0.000	0.000	0.001
Yami	0.000	0.000	0.000
Korean	0.000	0.000	0.000
Okinawan	0.000	0.000	0.000
Tuva	0.000	0.000	0.000
East Timorese				0.000	0.274	0.002
Filipino	0.000	0.000	0.000	0.000	0.000	0.000
Ivatan	0.000	0.000	0.000
Moluccan				0.000	0.000	0.000
PNG Lowlander				0.000
Cape York	0.000	0.000	0.000	0.000	0.000	0.000
Kimberley				0.000	0.067	0.020
Yuendumu	0.000	0.000	0.000
Canoncito				0.000	0.001	0.004
Mixe	0.000	0.000	0.000	0.000	0.937	0.851	0.006	0.002	0.297	0.000	0.000	0.079	0.001	0.000	0.289
Yupik	0.000	0.000	0.000
Zuni				0.000	0.000	0.329
Central America				0.000	0.000	0.051
Guarani–Nandewa	0.007	0.000	0.017	0.000			0.004	0.022		0.000	0.008		0.000	0.006

Uncorrected P-values are listed. Italic values indicate P-values <0.05 after correcting for the number of populations for a locus pair (i.e., in a column).

Tests for LD between class I and class II loci showed several cases of significance (P < 0.05 after correcting for the number of tests for each locus pair), even for loci separated by large physical distances (Table 6). For example, HLA-A and DRB1 (separated by 2.74 Mb) and C and DRB1 (separated by 1.26 Mb) were in significant LD in all five populations with data for these locus pairs. The exceptions to this pattern of significant LD were the comparisons involving DPB1, which showed significant LD with other loci in only a small portion of populations (0/4, 1/4, 1/4, 5/14, with A, C, B, and DQB1, respectively). The only population that had significant LD between DPB1 and a class I locus was the Shona from Africa.

The ubiquity of significant LD for all locus pairs (except those involving DPB1) is a consequence of the fact that we are testing a very extreme null hypothesis, namely that the loci are in linkage equilibrium. With the relatively large sample sizes and high degrees of polymorphism, it is not surprising that we rejected the null hypothesis in most cases that did not involve DPB1. To gain a better understanding of the differences in LD among human populations, measures of the strength of LD can be more informative, as described below.

Demographic history and linkage disequilibrium in the HLA region:

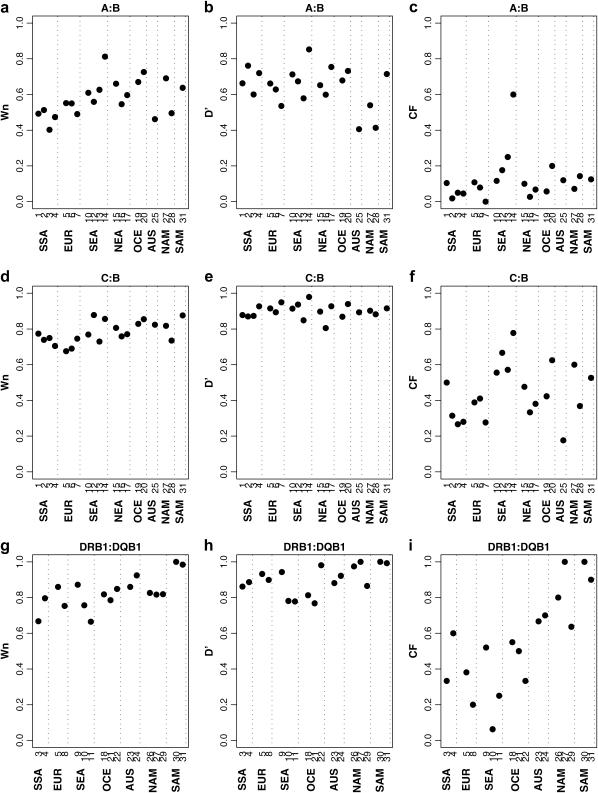
The overall pattern of LD across geographic regions for a given locus pair is complex (Figure 6). Results based on the W_n-statistic, more than those based on D′, showed a pattern that is similar to that seen in SNP-based studies, with lower LD in SSA and increasingly higher LD as populations grow geographically more distant from Africa. The correlation between the average heterozygosity of the two loci and D′ was significant across all locus pairs (Spearman's ρ = 0.37, P-value <0.01). This correlation was not significant for the W_n measure of LD, indicating that this measure of LD may be influenced to a lesser degree by the level of polymorphism.

Figure 6.—

LD by geographic region. D′, W_n, and CF (the fraction of complementary haplotypes) are described in Methods. Population numbers correspond to those in Table 1.

For the A:B and C:B locus pairs, LD was higher in two of the Amerindian populations (Mixe and Guarani) compared to all four populations from SSA, while one population (Yupik) had LD values similar to those of the SSA populations. For the DRB1:DQB1 locus pair the two populations from SAM had the highest LD of all populations, substantially higher than that of Africans. The populations from NAM showed levels of LD similar to those of one of the populations from SSA (Zulu) but higher than those of the Shona.

The fraction of complementary haplotypes (haplotypes with D′_ij = 1) ranged from 0 to 25% for the A:B and A:C locus pairs (see Figure 6c for the A:B locus pair), with the exception of the Yami population from SEA, which had values of 60 and 40% for these locus pairs. The complementary fraction was highest in SEA. The high value for the Yami population is explained by the high-frequency A*2402 allele (frequency of 0.54) being in complete LD with several different B and C alleles. That is, although A*2402 was found with several different B and C alleles, those B and C alleles were not found with other A alleles.

The complementary fraction for C:B haplotypes was quite high in Asia, the Americas, and Oceania. These values were even higher for DRB1:DQB1 haplotypes with >60% in AUS and the Americas. This result corresponds with the low number of DQB1 alleles for these populations and their being associated predominantly with only one DRB1 allele.

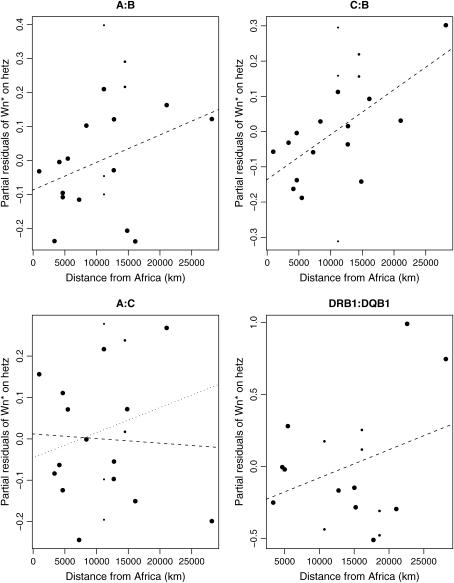
Table 7 presents the partial R²-values for the regression of W_n* = log(W_n/(1 − W_n)) on the distance from East Africa (as computed by Prugnolle et al. 2005a) and the average heterozygosity of the two markers. Observations in these regressions were given a weight equal to the reciprocal of the number of populations from the same country, as in Prugnolle et al. (2005b). The proportion of variance in the W_n*-values explained by the distance from Africa after controlling for the average heterozygosity of the loci is given by R²(dist. afr, W_n* | avg. hetz) in Table 7. Figure 7 shows plots of the partial residuals from the regression of W_n* on average heterozygosity against the distance from East Africa. Dashed lines indicate the fitted regression line. For the A:C plot, the dotted line represents results from fitting the model after removing an influential outlier [the Guarani–Nandewa population, which was identified as an outlier on the basis of having a Cook's distance >1.0 (Cook and Weisberg 1982)]. This population is not an outlier in either of the A:B or C:B plots). For A:B, C:B, and DRB1:DQB1 we observed a trend toward greater LD with increasing distance from Africa. This relationship was significant for the C:B and DR:DQ locus pairs.

TABLE 7.

Squared partial correlation coefficients

Locus pair	R2(avg. hetz, Wn* | dist. afr)a (%)	R2(dist. afr, Wn* | avg. hetz)b (%)
A:B	0.03	13.58
C:B	0.04	47.68**
A:C	9.63	4.26
DR:DQ	5.12	36.02**

Partial R²-values for the regression of W_n* = log(W_n/(1 − W_n)) on the distance from East Africa (see text for details) and the average heterozygosity of the two markers.

^**P-value <0.01.

^aR²(avg. hetz, W_n* | dist. afr) values represent the proportion of variance in the W_n*-values explained by the average heterozygosity of the loci after controlling for the distance from Africa.

^bR²(dist. afr, W_n* | avg. hetz) values represent the proportion of variance in the W_n*-values explained by the distance from Africa after controlling for the average heterozygosity of the loci.

Figure 7.—

LD [W_n* = log(W_n/(1 − W_n)] vs. geographic distance from East Africa (following the routes proposed by Prugnolle et al. 2005a). The size of the data points is proportional to the weights used in the regression model for W_n*. The dotted line in the plot for A:C in the bottom left corresponds to the regression line after removing the outlying Guarani–Nandewa population.

DISCUSSION

To distinguish between the effects of selection and demographic history, we have compared the results obtained for the HLA data to those from other, putatively neutral, markers. An ideal control for demography requires sampling the same populations and individuals for loci with similar levels of polymorphism and mutational mechanism as the HLA loci. In the absence of such a data set, we adjusted the control data sets to match the HLA data as closely as possible, by resampling populations and individuals to obtain data sets with similar compositions and analyzing subsets of markers to determine the influence of levels of polymorphism on the results.

The HLA data sets were generated by surveying multiple polymorphic regions within each locus, rather than by DNA sequencing. Therefore, the potential for ascertainment bias needs to be considered when interpreting the results, since ascertainment bias can lead to incorrect demographic inferences (Clark et al. 2005). There are two possible sources of ascertainment bias (Rogers and Jorde 1996). The first source can arise from defining the polymorphisms to be surveyed (i.e., the polymorphic regions present in the gene, as described in Methods) from an initial analysis in a subset of populations. The second source can arise as a consequence of identifying polymorphisms in a small panel of individuals and thus underrepresenting low-frequency variants. When such biases are present, Wakeley et al. (2001) showed that it is advisable to model the process employed in SNP discovery and account for its effects upon the population genetic analyses. However, our analyses are unlikely to be affected by ascertainment bias due to selection of markers from a subset of populations for two reasons. First, the typing methods for HLA take into account the known allelic diversity in diverse human populations, cataloged in extensive databases of HLA polymorphism (e.g., the Anthony Nolan Trust, http://www.anthonynolan.com/HIG/), and therefore it is unlikely that they overrepresent variation in one or more specific regions. Second, ascertainment bias is least problematic in studies of highly polymorphic markers (Eller 2001), as is the case in the study of HLA variation, and is unlikely to bias measures of F_ST or heterozygosity in this genetic system.

The second source of bias can arise when the a priori definition of the subset of sites (sequence motifs in the case of HLA typing) to be surveyed by the typing method does not adequately represent the underlying genetic diversity. As described in Methods, the identification of alleles is based on the combination of multiple sequence motifs detected in an individual. If low-frequency variants are preferentially missed compared to intermediate-frequency variants, the distribution of surveyed alleles will be skewed toward the higher end of the frequency spectrum (as shown by Clark et al. 2005, for SNPs). We believe that this potential bias is minimized in these HLA data for the following reasons. Our analyses focus on allelic variation rather than the site frequency spectrum studied in SNP-based surveys, and alleles are defined by variation at a large number of sites (described in Methods). The method used to quantify deviations from neutrality equilibrium (the Ewens–Watterson test and the H_ND-statistic) assumes that the data are compatible with an infinite-alleles model (Ewens 1972), according to which each mutation creates a novel allele. This model is appropriate for data sets where alleles are defined by a large number of polymorphisms (sequence motifs) and where a large number of allelic states exist, as is the case for these HLA data sets.

Heterozygosity:

The heterozygosity values for HLA loci vary among world populations in a manner similar to that of non-HLA loci (e.g., Kidd et al. 2000), with high values for sub-Saharan Africa and low values for samples from North and South America. The heterozygosity at HLA loci is lower for populations at greater geographic distances from East Africa (Figure 3). This pattern has been observed in other data sets (e.g., Prugnolle et al. 2005a) and is explained as a result of the loss of variation associated with successive migration events that took place as humans occupied new regions. Our results show that HLA loci bear the signature of the demographic history of human populations. The observation that the demographic history of human populations explains a substantial part of HLA variation was formally quantified by Prugnolle et al. (2005b), who examined the correlation between the distance traveled by human populations since their departure from Africa and the amount of HLA diversity, finding that a substantial portion of HLA diversity (39, 17, and 35% for HLA-A, -B, and -C, respectively) was explained by the variable “distance from Africa.”

Deviation from neutrality equilibrium:

The Ewens–Watterson test, which uses the sample homozygosity as a test statistic, led us to reject the null hypothesis of neutrality equilibrium for a moderate proportion of individual populations (Table 2). When the pattern of deviations was considered for the total set of populations, the overall trend toward more even allele frequencies was significant for all loci except DRB1 and DPB1.

Our finding that most loci show an overall significant deviation from neutrality equilibrium, although many of the individual population samples for which they were typed did not (e.g., a pattern seen for HLA-A and DQB1, Table 2), may be accounted for by the weak statistical power of the Ewens–Watterson test. In a simulation study, Garrigan and Hedrick (2003) showed that the number of generations needed to attain significance for the Ewens–Watterson test in a population experiencing balancing selection can be quite large: ∼50 generations for a population of size 1000 and an overdominant selection coefficient of s = 0.05 equally favoring all heterozygous genotypes (i.e., ∼1000 years of continuous selection). Selection coefficients of ≤5% were in fact estimated by Satta et al. (1994) and Slatkin and Muirhead (2000) for HLA loci.

The demographic history of human populations also offers an explanation for the low proportion of populations with significant deviation from neutrality equilibrium. Population expansion is expected to generate an excess of low-frequency alleles, resulting in a homozygosity value that exceeds neutral-equilibrium expectations (Watterson 1986). In our analysis of haplotype frequencies for 10 noncoding regions in the three human populations of the Frisse data, we found a trend in the direction of homozygosity excess (i.e., H_ND < 0), although nonsignificant. This result is in agreement with those of several studies that indicate a trend toward a negative value for Tajima's D in studies of human populations (Ptak and Przeworski 2002). This trend is expected for populations that have experienced demographic expansions, but is in the opposite direction to that seen for HLA loci. Since the three populations from the Frisse et al. (2001) study represent a range of different demographic histories for human populations, and each shows evidence of demographic expansions, we expect human demographic history to mitigate any signature of balancing selection. The contrast of results among HLA loci is also informative for the roles of demographic history and selection. The fact that DPB1 and DRB1 failed to show the deviation from neutrality equilibrium seen at other HLA loci, even though the typing methodology employed was the same, suggests that demography and typing artifacts are unlikely to explain the observed contrasts. We conclude that the overall excess of intermediate-frequency alleles seen for HLA-A, -B, and -C and DQB1 is attributable to a regime of balancing selection at these loci.

Our results show that approximately equal numbers of populations deviate from neutrality-equilibrium expectations at HLA-B and -C and that the average H_ND for both these loci is similar, higher than that for HLA-A. This hierarchy of evidence for selection differs from that of an early selection estimate based on the ratio of synonymous to nonsynonymous substitutions in the peptide-binding region of these genes Satta et al. (1994), which estimated selection to be highest for HLA-B, intermediate for HLA-A, and substantially lower for HLA-C. However, subsequent analyses (e.g., Hughes and Yeager 1998; Adams et al. 2000) based on larger samples of HLA-C alleles have detected high ratios of nonsynonymous to synonymous substitutions at HLA-C. In the analysis of class II loci, our finding that DPB1 showed no evidence for balancing selection, and the stronger evidence for selection at DQB1 than at DRB1, are in accord with previous studies (e.g., Salamon et al. 1999; Valdes et al. 1999; Tsai and Thomson 2006). The stronger evidence for selection at DQB1 than at DRB1 and at HLA-C than at HLA-A shows that diversity, as measured by the number of alleles, does not have a clear correlation with the evidence for selection, since in both cases the stronger evidence for selection was present in the less diverse locus.

Differentiation among populations at HLA loci:

The finding that most HLA loci show a trend in the direction of greater heterozygosity than neutral-equilibrium expectations is consistent with the action of balancing selection. An expectation for loci under this mode of selection is that F_ST-values will be reduced, relative to the average F_ST of other loci (Bowcock et al. 1991). In the current data we found no indication of significantly reduced differentiation at HLA loci (Figure 4). Below, we discuss possible explanations for this finding.

The demographic history of humans results in low levels of interpopulation differentiation. In this context, directional selection, favoring different alleles in distinct populations, can increase F_ST at the selected loci, making them distinguishable from neutral loci. Loci under balancing selection, on the other hand, experience a reduction in F_ST-values. Such a reduction in differentiation is difficult to detect because the baseline F_ST for putatively neutral markers is itself low.

Second, a model of symmetric overdominant selection, affecting all heterozygous genotypes in all populations in a similar manner, is only one of the selective regimes that can explain the high levels of heterozygosity at HLA loci. The evidence of the involvement of specific alleles in disease susceptibility and resistance (e.g., Carrington et al. 1999), and the fact that these associations sometimes differ among populations (Hill 1998), suggests that selective regimes where specific alleles are favored should also be considered. One such model is that of selection that varies over time, shifting in response to pathogen prevalence. Hedrick (2002) showed that this mode of selection can contribute to the maintenance of the high levels of polymorphism at HLA loci. A regime of selection that varies over time could favor different sets of alleles in different populations and therefore contribute to the maintenance of high amounts of polymorphism without reducing interpopulation variation.

Our analysis showed that demographic history has shaped HLA differentiation among populations in a qualitatively similar way to that seen for neutral markers (Table 3), as is clear by the high degree of differentiation seen among Amerindians and Oceanians, a typical pattern for neutral markers. Thus, selection does not appear to erase the genetic signatures of human demographic history at the intraregional scale.

When we compared differentiation among all pairs of populations at HLA-A with the values for HLA-B and HLA-C, we noted decreased differentiation at HLA-B and HLA-C, both within and between world regions, relative to the values for HLA-A (Figure 5). If selection favored similar sets of alleles within broad geographic regions and different sets of alleles in different regions, we would expect a reduction in within-region differentiation, but not in the among-region differentiation. Our results suggest that the process leading to reduced genetic differentiation at HLA-B and HLA-C is affecting contrasts within, as well as among, regions. If natural selection is the process that explains lower levels of differentiation at HLA-B and HLA-C relative to HLA-A, our results suggest that the broad groupings of populations we have used do not constitute regions of shared selective regimes, a finding that may not be surprising given the very broad geographic scale at which these groups are defined.

Region-specific alleles and geographic variation:

Several features of RS alleles for HLA loci show similarities with results from studies using non-HLA data. Both Zhivotovsky et al. (2003) and Tishkoff and Kidd (2004) found high proportions of RS alleles in African populations compared to populations from other geographic regions. We see a similar result for the HLA data. Rosenberg et al. (2002) found that the frequency contribution of RS alleles is generally low, but Zhivotovsky et al. (2003) point out instances in the Americas where some RS alleles have appreciably high frequencies. The authors suggest that these alleles may have originated with the founders of these American populations. Again, similar results are seen for the HLA data, especially for the class I loci as described below. In contrast to Zhivotovsky et al. (2003), however, we see a relatively high proportion of alleles that are RS for these class I HLA loci in the Americas, but this comparison is complicated by the different numbers of regions, populations per region, and mutational mechanism for the HLA and microsatellite data.

In contrast to the other HLA loci, the DQB1 locus has very few RS alleles. This result may be due in part to the smaller number of alleles found at this locus for the populations studied. The interesting point is that although there are fewer alleles at DQB1 and few that are region specific, this locus has significant evidence of balancing selection, a result seen in this study (Table 2) and others (Salamon et al. 1999; Valdes et al. 1999; Tsai and Thomson 2006).

Although there is a relatively high proportion of RS alleles at the HLA loci, these alleles generally occur at low frequencies. The HLA-B locus is an interesting exception to this pattern, with RS alleles representing a considerable portion of the allelic diversity within specific regions. For example, 36% of the HLA-B alleles in SAM were region specific, and these alleles made up 10% of the allelic frequency in this region. Some of these RS alleles have risen to relatively high frequency in certain populations in SAM and NAM, including B*1504 [frequency (f) = 0.198 in the Guarani population sample], B*4004 (f = 0.104 in the Guarani), and B*3512 (f = 0.225 in the Mixe). High-frequency RS alleles were not found for any of the class II loci or HLA-A. However, some RS alleles at HLA-C occur at a high frequency, notably C*1503 with a frequency of 0.173 in the Guarani and C*0806 with a frequency of 0.101 in the Yupik.

The observed distribution of RS alleles is in agreement with the findings of Parham et al. (1997), who showed that a large number of the HLA-B alleles in indigenous Amerindian populations appear to have originated in the Americas, by gene conversion or point mutation events that modified alleles carried by the individuals that occupied the continent. This concordance is expected since one of the populations originally studied by Parham et al. (1997) was the Guarani, which were also studied here.

The high proportion of class I region-specific alleles in sub-Saharan Africa and the Americas is likely to result from different historical and genetic processes. Samples from sub-Saharan Africa harbor alleles that were present in a population that gave rise to groups that populated the remainder of the globe. In this process, alleles that failed to leave Africa result in RS alleles for this region. The RS alleles present in the Americas, on the other hand, appear to represent variants that arose within this region relatively recently. Parham et al. (1997) proposed that the combined effects of drift (leading to the loss of founding alleles) and selection pressures of a novel environment (favoring novel advantageous alleles) could explain the prevalence of RS alleles in this region.

Demographic history and linkage disequilibrium in the HLA region:

Natural selection is one of the evolutionary processes expected to increase the magnitude of LD, possibly through the selective advantage conferred by combinations of alleles on the same haplotype (Garrigan and Hedrick 2003). Studies of the human MHC have found high levels of LD: Huttley et al. (1999) used microsatellites in European populations and found few regions of the genome with higher LD than in the MHC; Sanchez-Mazas et al. (2000) found significant LD spanning HLA loci separated by as much as 1.3 Mb; Hedrick and Thomson (1986) and Klitz et al. (1992) found that the levels of LD among HLA loci (typed serologically) exceeded that expected for population samples in neutrality-equilibrium conditions.

An understanding of the processes underlying observed levels of LD requires addressing the effects of demographic history, since genetic drift and gene flow can directly influence the level of disequilibrium. We took advantage of broad geographic sampling available for HLA loci and compared the levels of LD among populations from different world regions, for which general features of the demographic history are available. This allowed us to explore the extent to which LD within the human MHC is explained by the demographic history of human populations.

Various studies have documented a decrease in LD for populations that have smaller effective population sizes (Tishkoff and Kidd 2004). This effect is particularly clear in SNP-based studies that include populations from Africa and the Americas, where high LD is observed in the Americas, while African populations display the lowest levels of LD among all world regions. In this study of HLA loci we found that LD measured by the W_n-statistic was generally lower in Africans and Europeans and higher in populations from Oceania and North and South America (Figure 6).

We explored the effect of population history on LD using the approach of Prugnolle et al. (2005a), which involves comparing the distance between East Africa and the current location of populations with population genetic parameters (in our case LD). Our analyses showed a trend toward higher LD with greater distance from East Africa for each locus pair (Table 7), with the exception of A:C where the Guarani–Nandewa population had a surprisingly low degree of LD (removal of this outlying point reveals the same general trend seen for the other locus pairs, but to a lesser extent). The relationship with distance from Africa was significant for the C:B and DRB1:DQB1 locus pairs after controlling for the heterozygosity of the constituent loci.

The effects of demographic history leading to higher LD with greater distance from Africa are mediated by the combined effects of locus heterozygosity being inversely related to distance from Africa (Prugnolle et al. 2005a) and LD being higher for more polymorphic markers. In fact, Mateu et al. (2001) found higher LD in African populations than in non-African populations using polymorphic short tandem repeats in the CFTR gene but the opposite pattern using SNPs within the gene. The C:B locus pair showed the strongest trend of increased LD with increased distance from Africa. The short genetic distance between HLA-C and -B may be small enough, with fewer recombination events breaking down LD, for the relationship with distance from Africa to remain significant in spite of the above-mentioned mediating effects. Although the relationship is also significant for DRB1:DQB1, this result appears to be driven to a large extent by the two populations from the Americas.

Conclusion:

The role of selection in shaping HLA diversity is well established by studies that examine variation at deep evolutionary timescales, which have detected greater rates of nonsynonymous than synonymous substitutions and examples of trans-species polymorphisms (Hughes and Yeager 1998; Garrigan and Hedrick 2003). The role of selection in shaping variation at a more recent timescale, as examined here, has proved more challenging, and in many cases no evidence for selection was obtained at MHC loci studied at the population level (Garrigan and Hedrick 2003). This is a consequence of the fact that the tests employed have low statistical power and that they are sensitive to the demographic history of the population (Nielsen 2001). In this study we found that the combined analysis of several human populations showed an overall deviation from neutral-equilibrium expectations (based on locus-level trends for the Ewens–Watterson homozygosity test) for HLA-A, -B, and -C and DQB1 (Table 2). The combined analysis of many population samples can thus compensate for the lack of statistical power of tests when applied to individual populations. The difficulty of distinguishing the effects of demographic history and natural selection can be addressed by comparing the results among different classes of loci (Goldstein and Chikhi 2002). We used data sets, collected for different groups of populations from those for which we had HLA data, and adjusted the population sampling and sample sizes to make the results comparable. This comparison showed that the deviation from neutral-equilibrium conditions for HLA loci is unlikely to be accounted for by the demographic history of populations. Also, LD levels were high among HLA loci, resulting in significant associations between loci separated by large physical distances. The degree to which this level of LD is indicative of selection will require comparisons to other markers, with similar spacing, typed in the same set of populations. While these two results are concordant with a history of selection acting upon HLA loci, the pattern of interpopulation differentiation at HLA loci was not different from that found at putatively neutral loci. The geographic distribution of region-specific alleles and the worldwide variation in population heterozygosity follow patterns found in several studies based on putatively neutral markers, indicating that both natural selection and demographic history have shaped the observed patterns of variation at HLA loci.