Relaxed Significance Criteria for Linkage Analysis

Abstract

Linkage analysis involves performing significance tests at many loci located throughout the genome. Traditional criteria for declaring a linkage statistically significant have been formulated with the goal of controlling the rate at which any single false positive occurs, called the genomewise error rate (GWER). As complex traits have become the focus of linkage analysis, it is increasingly common to expect that a number of loci are truly linked to the trait. This is especially true in mapping quantitative trait loci (QTL), where sometimes dozens of QTL may exist. Therefore, alternatives to the strict goal of preventing any single false positive have recently been explored, such as the false discovery rate (FDR) criterion. Here, we characterize some of the challenges that arise when defining relaxed significance criteria that allow for at least one false positive linkage to occur. In particular, we show that the FDR suffers from several problems when applied to linkage analysis of a single trait. We therefore conclude that the general applicability of FDR for declaring significant linkages in the analysis of a single trait is dubious. Instead, we propose a significance criterion that is more relaxed than the traditional GWER, but does not appear to suffer from the problems of the FDR. A generalized version of the GWER is proposed, called GWER_k, that allows one to provide a more liberal balance between true positives and false positives at no additional cost in computation or assumptions.

LINKAGE analysis is the process of identifying genetic loci whose segregation patterns are associated with variation in a trait of interest. In a typical linkage analysis, significance tests of linkage are performed at loci positioned throughout the genome. Performing many tests for linkage across the genome presents a substantial multiple-testing problem. Therefore, stringent criteria for declaring a linkage statistically significant have been formulated with the goal of preventing any single false linkage from being declared across a genome scan, called the genomewise error rate (GWER). Typically, a significance cutoff is determined to ensure a GWER <5%. Much work has been done on accurately calculating significance cutoffs to control the GWER, for both quantitative traits (Lander and Botstein 1989; Churchill and Doerge 1994; Doerge and Churchill 1996) and qualitative traits (Morton 1955; Feingold et al. 1993; Dupuis et al. 1995).

Significance criteria for linkage analyses have been successfully formulated for mapping Mendelian traits, where a single major gene contributes to the trait (Morton 1955). However, this has proved to be more challenging for complex traits, where several loci are expected to contribute to the trait (Lander and Kruglyak 1995). As complex traits have become the focus of linkage analysis, it is increasingly common to expect to identify several distinct loci significant for linkage. This is especially true in mapping quantitative trait loci (QTL), where sometimes dozens of QTL are expected to exist, each making a moderate to small contribution to the trait (Lynch and Walsh 1998).

To improve the power to identify several loci contributing to a single trait, one might be willing to allow a small number of false positive linkages to be identified, as long as the relative number of true positive linkages is substantially higher. In this case, controlling the GWER becomes undesirably conservative. Therefore, relaxed criteria for controlling the number of false positives have been explored, particularly the false discovery rate (FDR) criterion (Weller et al. 1998; Mosig et al. 2001; Fernando et al. 2004; Benjamini and Yekutieli 2005). The FDR is defined to be the expected proportion of false positive linkages among the total number of significant linkages (Soric 1989; Benjamini and Hochberg 1995), offering an intuitively pleasing balance between false positives and true positives.

In this article, we characterize some of the complications that arise when relaxing significance criteria for genomewide linkage scans of a single trait. The main complication results from the fact that there are two types of dependence present among linkage statistics obtained from a single chromosome. First, there is dependence in the noise of the linkage statistics (i.e., the random fluctuations of the statistics due to chance). This dependence has been addressed for controlling the GWER by using both theory (Lander and Botstein 1989; Feingold et al. 1993; Dupuis et al. 1995) and numerical resampling methods (Churchill and Doerge 1994; Doerge and Churchill 1996). Dependence among the noise of test statistics has also been addressed for controlling the FDR (Benjamini and Yekutieli 2001; Storey and Tibshirani 2003; Storey et al. 2004), but not explicitly for genomewide linkage scans.

The second type of dependence present in linkage analysis is in the signal. It is easily shown that linkage status among neighboring loci is shared. In other words, the null hypothesis of no linkage to a trait gene is uniformly either true or false for large groups of loci, extending to every locus on a given chromosome according to commonly used models. Since the FDR involves a balance between true and false positives, this dependence in signal turns out to be problematic for interpreting the FDR in the context of linkage analysis, mainly because true positives and false positives come in large dependent clumps. When fixing a significance threshold, we show that one can manipulate the FDR to be any level one wants, without changing the location or effect size of any trait gene. We show that the problems lie in the FDR quantity itself, not in any of the “FDR-controlling” methods available (e.g., Benjamini and Hochberg 1995; Storey 2002) for estimating a proper threshold. In other words, whereas dependence in the noise of the statistics creates problems only for deriving FDR-controlling procedures, large-scale dependence in the signal creates problems in the applicability of the FDR quantity itself.

The true “units of signal” in linkage analysis are the trait genes. For significance measures such as the FDR that take into account the number of “true discoveries,” it is necessary to implement some interpretable measure of the unit of signal that is not easily manipulated. This appears to be rather difficult in linkage analysis, where it is often not possible to distinguish the actual number of trait genes to which a locus is linked. Moreover, it is common practice to call several loci significant, where the understanding is that they all result from a common trait. This does not appear to be taken into account in the current formulation of FDR for linkage analysis, leading to some of the problems we discuss here.

We propose a significance criterion more liberal than the GWER, but that does not suffer from the problems of the FDR. Specifically, we propose a generalized GWER, called the genomewise k-error rate (GWER_k), that guards against more than k false positive linkage results. A major advantage of GWER_k over FDR is that GWER_k can be controlled by considering only the full null case of no linkage among any loci, allowing us to avoid the issues of dependence in signal and defining units of signal; the FDR cannot be meaningfully controlled using the full null case, so one is forced to consider the dependence in signal when employing the FDR. A numerical algorithm based on that for controlling the GWER in the QTL-mapping setting (Churchill and Doerge 1994) is proposed for GWER_k. Some simple numerical comparisons are made to illustrate the performance of these various error measures.

The FDR has also recently been applied to the linkage analysis of thousands of traits simultaneously, in particular, for thousands of “gene expression traits” measured by DNA microarrays (Yvert et al. 2003; Brem et al. 2005; Storey et al. 2005). We briefly point out that the FDR may be appropriately applied across many traits in such a way that it does not suffer from the problems of applying the FDR across several loci for a single trait.

THE STRUCTURE OF A GENOMEWIDE LINKAGE SCAN

We first describe the basic structure of the statistics used for genomewide linkage scans. Although there are important differences among the various methods for linkage analysis performed on human and experimental cross data, they share certain properties that are most relevant to understanding the issues for relaxing the criterion for significance. There is usually an underlying model of the trait in terms of a single locus (or several loci) contributing directly to the trait. For clarity we call these loci “trait genes.” The trait can be more generally modeled in terms of any given locus that is linked to one of these trait genes. Therefore, a model of the trait in terms of a locus being tested for linkage can be parameterized so that, for certain values of the parameter, the tested locus is linked to one of the trait genes. Straightforward examples of these models in various settings are readily available (Lander and Botstein 1989; Feingold et al. 1993; Lynch and Walsh 1998; Ott 1999).

Linkage statistics:

We let the set of parameters for such a model be denoted by 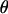, where if 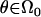, then the null hypothesis of no linkage is true, and if 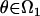, then the alternative hypothesis is true. Different values of 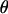are possible at each locus tested. In testing for linkage, a so-called LOD score is usually calculated at each tested locus. Supposing that M loci are tested for linkage, the LOD score at locus i can be written as

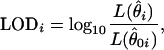for i = 1, 2,…, M. Here, 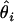is the unconstrained maximum-likelihood estimate of 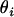, and 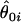is the maximum-likelihood estimate when 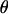is limited to the values of the null hypothesis, Ω₀. The function 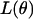is the likelihood based on the set of observed data in the study, making LOD_i the log (base 10) of the generalized likelihood-ratio statistic.

As an example, consider the following model employed in Lander and Botstein (1989). Assume that we observe quantitative trait values y_j for individuals j = 1,…, N in a backcross originating from two inbred lines. If there is a single QTL, we may write y_j = a + bg_j + e_j, where g_j is an indicator variable of the two possible genotypes and e_j is Normal random error due to variation not explained by genetics. Let the genotype of locus i in individual j be denoted by x_ij. When testing locus i for linkage, a model may be constructed for y_j in terms of the x_ij, employing the unknown parameters a and b, as well as the unknown recombination fraction between locus i and the trait gene locus. This model may be fit to the data by maximum likelihood under the constraints of the null hypothesis and then under no constraints. The log₁₀ of the ratio of these two resulting likelihoods as written above forms the LOD score.

The GWER and FDR:

The GWER is the probability that any single false positive occurs. For a given LOD score threshold λ, the GWER is defined as

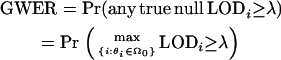A convenient upper bound on this quantity is to assume that all null hypotheses are true, resulting in 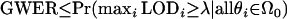. Therefore, most methods for controlling the GWER actually control the quantity .

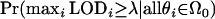Define the function 1(LOD ≥ λ) to be equal to zero when LOD < λ and equal to one when LOD ≥ λ. When employing the threshold λ, the FDR can be written as

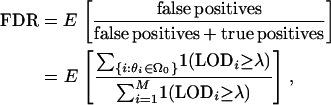where the ratio is set to zero when the denominator is zero (i.e., when no loci are called significant).

An important operating characteristic that affects the interpretation and estimation of the GWER and FDR is the dependence of the LOD scores. The well-known Poisson process model of recombination employed for >50 years implies that any two LOD scores on the same chromosome are dependent—both in noise and in signal. The LOD scores are dependent in noise in the following sense: when there is no trait gene on a chromosome, the LOD_i follow the same null distribution, but they are also probabilistically dependent. This probabilistic dependence has been mathematically characterized, forming the basis of methods to construct genetic maps (Lander and Green 1987), form LOD score cutoffs to control the GWER (Morton 1955; Lander and Botstein 1989; Feingold et al. 1993; Dupuis et al. 1995), and model the crossing-over process (McPeek and Speed 1995). Letting Δ_ij be the genetic distance between markers i and j, it is straightforward to calculate the covariance of LOD_i and LOD_j for a variety of statistics and study designs. The covariance can usually be written as a function of genetic distiance, Cov(LOD_i, LOD_j) = f(Δ_ij), for some function f. When the two loci are located on different chromosomes, the genetic distance is maximized and their covariance is equal to zero. In most scenarios (e.g., in the simple example above), the underlying model implies that f(Δ_ij) decays exponentially in Δ_ij.

Another consequence of the Poisson process model of recombination is that any two loci on the same chromosome are dependent in signal; i.e., they share the same linkage status. Under the commonly used models, the linkage signal of a particular locus can be written as a function of the genetic distance between the locus and the trait gene, as well as the contribution from the trait gene. This implies that if loci i and j are on the same chromosome, then LOD_i follows the null distribution if and only if LOD_j follows the null distribution. Therefore, if loci i and j are called significant for linkage, then locus i is a false positive if and only if locus j is a false positive. Note that for the full null GWER 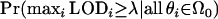, the dependence in signal is not a factor because the calculation is done under the assumption that all loci are not linked. The dependence in signal plays a major role in the operating characteristics of the FDR, and it presents difficulties in the interpretation of the FDR in linkage analysis. Since every tested locus on a QTL-containing chromosome is technically a true positive, this makes the “discovery” of a single QTL highly redundant across these loci, causing the major difficulty in applying the FDR to a linkage scan of a single trait.

INTERPRETING THE FDR IN LINKAGE ANALYSIS

On the basis of this characterization of the structure and dependence among LOD scores, we detail some general problems in interpreting the FDR when applied to a genomewide linkage scan. This is motivated by the following numerical example.

A numerical example:

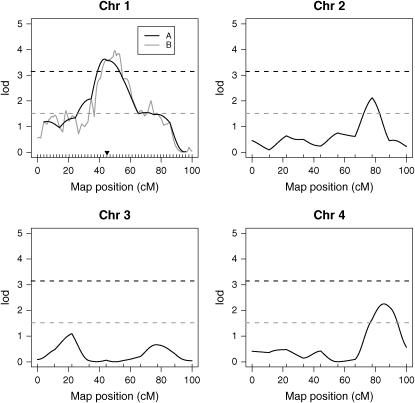
Using R/qtl (Broman et al. 2003), we simulated an intercross experiment with a single quantitative trait, where 250 F₂ offspring were observed. These offspring were modeled as diploid with four pairs of autosomal chromosomes, each of length 100 cM. A single-trait gene was placed at 45 cM on chromosome 1 (indicated by a solid inverted triangle in Figure 1) with additive and dominance effects each of size 0.25. This example was purposely kept simple for illustration purposes. Below, we also perform a number of simulations according to the specifications of the mouse genome.

Figure 1.—

A simulated example showing that marker placement has a strong effect on FDR-based significance. Shown are the LOD score profiles under two scenarios, where the exact same single QTL (denoted by the inverted triangle) is present in each case. In scenario A, there are 10 equally spaced markers on each chromosome. In scenario B, there are 50 equally spaced markers on chromosome 1 and 10 on the remaining chromosomes. The LOD score significance cutoff was calculated so that FDR = 5% in both scenarios. In scenario A, the LOD score cutoff is 3.15 (black dashed line), and in scenario B it is 1.52 (gray dashed line). It can be seen that even though the chromosome 1 LOD score profiles are similar in the two scenarios (A, black; B, gray), the LOD score significance cutoff is substantially lower in scenario B. This occurs because all of the markers adjacent to the QTL are counted as “true discoveries,” even though their signal comes from a single QTL.

We considered two scenarios, where the only difference between the two is in the number of markers placed on chromosome 1. In scenario A, we placed 10 equally spaced markers on each chromosome; in scenario B, we placed 50 equally spaced markers on chromosome 1 and 10 equally spaced markers on chromosomes 2–4. Scenario B is reminiscent of the common practice of “fine mapping,” in which a denser set of markers is typed in a region with previously found suggestive or significant linkage. Therefore, it is not unusual for a study to purposely go from scenario A to scenario B.

A LOD score was calculated at each marker location according to the standard Normal model maximum-likelihood method for calculating LOD scores (Lynch and Walsh 1998) as implemented in R/qtl. Note that any marker on chromosome 1 is technically linked to the trait locus. Therefore, any marker called significant on chromosome 1 is a true discovery, and any marker called significant elsewhere is a false discovery. Because we can exactly identify true discoveries and false discoveries in this example, it is possible to calculate the exact threshold needed to attain a given FDR level. Hence, we then simulated these data 1000 times and calculated the proper threshold in each scenario to attain FDR = 5%. In scenario A, a LOD score cutoff of 3.15 achieves FDR = 5%, and in scenario B a LOD score cutoff of 1.52 achieves FDR = 5%.

Figure 1 shows the LOD score curves and the LOD score significance cutoffs from scenarios A and B. It can be seen that the LOD score curves on chromosome 1 are very similar. This is not surprising given that LOD score curves follow a specific distribution as the marker placement becomes denser (Lander and Botstein 1989). However, the LOD score significance cutoffs are dramatically different (3.15 vs. 1.52). In scenario A, no marker outside of chromosome 1 is called significant, whereas in scenario B, at least one marker on every chromosome is called significant. Thus, while the true signal does not differ, the FDR-based LOD score cutoffs dramatically differ.

FDR applied at the marker level:

The reason for the substantial difference in LOD score cutoffs in the above example is due to the manner in which true positive and false positive counts are employed in the FDR setting. Since every marker called significant on chromosome 1 is a true discovery, there are many more true discoveries available on chromosome 1 in scenario B than in scenario A. Therefore, when increasing the number of markers on chromosome 1 in scenario B, we have simply added many more true positives, even though the true underlying signal structure has not changed at all. Given that the FDR is concerned with the proportion of false positives among all significant linkages, this artificial increase of true positives allows for more false positives to be tolerated elsewhere. In other words, it allows one to substantially decrease the LOD score significance cutoff. Therefore, even though the signal structure is the same in the two scenarios, clearly shown by the LOD score profiles, the FDR-based LOD score cutoff changes radically due to the differing marker placement.

For a LOD score cutoff λ, let C_j(λ) be the number of loci called significant on chromosome j. Also, let 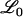be the set of chromosomes with no trait gene and 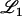be the set with at least one trait gene. The FDR can then be written as

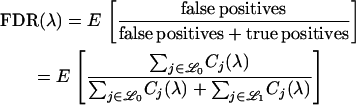(1)

Therefore, when testing for linkage at the markers, it is possible to make the FDR smaller by increasing the numbers C_j(λ) for 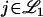. This can be accomplished by simply increasing the relative numbers of markers present on those chromosomes. In other words, if 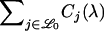remains about fixed, then the FDR can be decreased by increasing 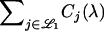. It follows that for a given LOD score cutoff, one can make the FDR arbitrarily small by adding increasing numbers of markers (or even just loci one chooses to test) to any chromosome with a trait locus. This also allows one to take arbitrarily small LOD score cutoffs while controlling the FDR at a particular level. In the above numerical example, the more markers added to chromosome 1, the lower the LOD score cutoff one can take while maintaining FDR = 5%. In practice, it appears to be common to saturate an area of the genome with markers if there is a suspected linkage, leading to this type of phenomenon.

Therefore, FDR-based significance applied to linkage tests at a fixed set of markers is strongly influenced by marker placement. This is an unfortunate property, as it has been shown in several scenarios that for reasonably dense markers, GWER-based significance is not very susceptible to marker placement (Lander and Botstein 1989; Feingold et al. 1993). The main reason for the difference is that the full null GWER is affected only by the dependence in the noise of the statistics, whereas the FDR is also affected by the dependence in the signal of the statistics. One could make the argument that this problem can be avoided if (i) markers are evenly spaced or (ii) each chromosome contains the same number of markers. However, upon further inspection these may still lead to problems in the interpretation of FDR. In either case, the distribution of the C_j(λ) for 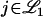is a complicated formula involving the length of the chromosome, the placement of markers, the dependence structure of both signal and noise, the local recombination rate around the trait locus, and the overall signal strength at the trait gene. In light of Equation 1, it is not clear that linkage signals due to distinct trait genes are then represented in an interpretable manner. More work would need to be done to understand the operating characteristics of the FDR in this context.

In the case where every location in the genome is tested for linkage (e.g., interval mapping), the same argument applies to that given above for equally spaced markers. The distribution of the C_j(λ) for 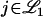as the number of loci tested becomes infinitely dense is again complicated and not clearly representative of the unit of signal that is most interpretable in the linkage setting. Techniques such as composite interval mapping (Jansen 1993; Jansen and Stam 1994; Zeng 1993, 1994), which take into account linkage signal among several loci on each chromosome, may alleviate some of the dispersion of true signal across any chromosome. However, in finite sample sizes there is substantial collinearity between nearby markers, and the signal is still dispersed over a region of any significant chromosome. This can be seen clearly in Figure 2 of Zeng (1994). Thus, interval mapping and its extensions are susceptible to these same problems.

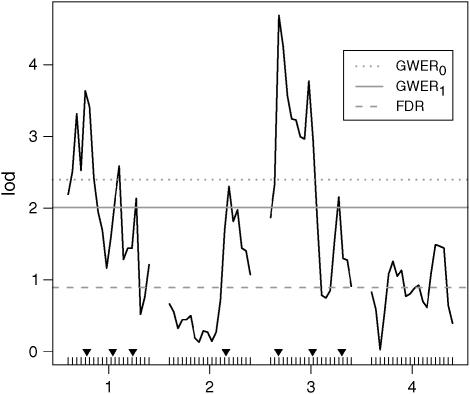
Figure 2.—

A simulated example (details in Multiple QTL on a chromosome) showing that GWER_k may yield LOD score significance cutoffs that differ substantially from GWER₀ and FDR. Shown are the LOD score profiles across four chromosomes for one of the simulated data sets. The QTL are indicated by the inverted solid triangles. The LOD score cutoffs corresponding to controlling GWER₀, GWER₁, and FDR at level 5% are shown. It can be seen that the GWER₁ criterion manages to find all seven QTL, whereas the GWER₀ criterion does not. Furthermore, the FDR yields a number of false positives because of its substantially lower LOD score cutoff.

The most directly interpretable application of the FDR is formulated in terms of counts of distinct linkage signals called significant. A “distinct linkage signal” would be one caused by a single trait gene. It is well known that the existence of more than one QTL can make this characterization difficult (Martinez and Curnow 1992; Haley and Knott 1992) in terms of LOD score peaks. Peak definition is a major underlying problem when using any significance criterion that allows for a false positive to occur (see the generalized gwer as an alternative to the fdr). However, it has been shown that counting the presence of signal on a chromosome basis does lead to reasonably interpretable conclusions (Wright and Kong 1997). Therefore, it appears that applying the FDR at the chromosome level is more straightforward than trying to interpret the FDR in the context of marker-based significance calls.

FDR applied at the chromosome level:

Perhaps, then, the FDR may be more straightforwardly applied to testing each chromosome for the existence of linkage. In this case, the maximum LOD score for each chromosome would be calculated, and an FDR-based significance cutoff would be applied to these. However, this results in a small number of actual hypothesis tests; for example, in humans this will involve testing 22 null hypotheses of no linkage among the autosomal chromosomes. It has been argued that the FDR is difficult to interpret when the number of tests is small (Storey 2002, 2003). Given that the number of chromosomes tested is usually on the order of a dozen or so, the utility of FDR applied at a chromosome level becomes questionable. Moreover, it has been shown that to “control” the FDR in the Benjamini and Hochberg (1995) sense, one must be cautious in interpreting the FDR when there is a substantial probability that nothing is called significant (Zaykin et al. 1998). This has conclusively been shown to be an issue when applying FDR-based significance at the chromosome level (Zaykin et al. 1998). Therefore, it is not yet clear that the FDR is the most desirable significance measure when linkage is tested on a per chromosome basis.

Previous applications of the FDR:

It appears that the FDR has been applied mostly to linkage analysis at the marker level (Weller et al. 1998; Mosig et al. 2001; Jiang et al. 2004). For example, Mosig et al. (2001) performed a genomewide linkage analysis, calculating a LOD score significance cutoff to control the FDR in terms of markers. However, due to the well-known difficulties of specifying the exact make-up of trait loci on a chromosome with significant LOD scores, they then interpreted the significance results at the chromosome level. This approach is problematic for two reasons. First, the issues shown above that occur when the FDR is applied at the marker level would be of concern here. Second, we show below that the FDR at the chromosome level may be much higher than that at the marker level (see Table 1). Therefore, controlling the FDR at, say, 5% among the markers may lead to an FDR on the chromosome level at several times that rate. On the other hand, applying the FDR at the chromosome level with as few as nine chromosomes as described by Bennewitz et al. (2004) may lead to the other potential problems described above.

TABLE 1.

A comparison of power and error rates when determining LOD score cutoffs according to GWER₀, GWER₁, and FDR

		Error rate controlled
Scenario		GWER0	GWER1	FDR (by marker)
A	LOD cutoff	3.374	2.376	2.179
	GWER0	0.050	0.341	0.467
	GWER1	0.002	0.050	0.120
	FDR (by markers)	0.008	0.035	0.050
	FDR (by chromosomes)	0.015	0.085	0.122
	Power	0.662	0.841	0.872
B	LOD cutoff	3.090	2.154	1.683
	GWER0	0.050	0.341	0.661
	GWER1	0.001	0.050	0.264
	FDR (by markers)	0.006	0.026	0.050
	FDR (by chromosomes)	0.010	0.052	0.108
	Power	0.489	0.718	0.831

Each column corresponds to controlling one of the three error rates at 5%. Each row shows the value of each item under the three respective significance criteria. Details of scenarios A and B are given in the text.

Similar concerns about the application of the FDR to population-based association studies exist. If the tested markers are isolated exclusively to a small candidate region and are in strong linkage disequilibrium with one another, then the FDR applied at the marker level, rather than at the trait gene level, may still be susceptible to interpretation issues due to a strong dependence in noise and in signal. For example, Jiang et al. (2004) genotyped 29 SNPs spanning 240 kb around the candidate gene LEP and controlled the FDR at level 5% using the Benjamini and Hochberg (1995) method. The resulting significance cutoff was P-value ≤0.033 when testing all males via a transmission disequilibrium test and P-value ≤0.031 when employing the family-based association test to test all families with an affected male child. The latter analysis led to 17 of 20 tested markers showing significant associations. However, it is not clear whether the significant markers are all being affected by one common signal, making this effectively a single test. In this case, the FDR is likely not the most accurate representation of the error rate.

THE GENERALIZED GWER AS AN ALTERNATIVE TO THE FDR

Definition of GWER_k:

As a potential alternative to the FDR, we propose a generalized version of the GWER. Rather than guarding against any single false positive linkage from occurring, the generalized GWER allows one to guard against exceeding more than k false positive linkages, where k is chosen by the user. For example, if we set k = 1, then the goal is to prevent more than one false positive linkage from occurring. At the cost of possibly incurring this single false positive, the relaxed significance criterion may result in more true positive linkages than what would have been found when employing the traditional GWER. This is a similar motivation to using the FDR, although several of the drawbacks for the FDR do not appear to be present for the generalized GWER.

We call the proposed significance measure the GWER_k, where k is the number of false significant findings that one is willing to incur:

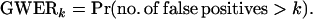Note that GWER₀ is equivalent to the traditional GWER, so we label it as GWER₀ for the remainder of the article. In mathematical terms, controlling the GWER_k at level α means that a significance threshold is determined so that Pr(no. of false positives > k) ≤ α. Several benefits of controlling the GWER_k are the following:

1. A threshold may be chosen so that GWER_k is at a reasonable level for multiple values of k. For example, instead of relaxing the significance criterion so that GWER₀ is rather large, one can instead determine a threshold so that GWER₀ is larger than the usual 0.05, but GWER₁ is still reasonably small.

2. As opposed to the FDR, only the dependence in noise must be taken into account to control the GWER_k, obviating the need to deal with the much trickier dependence in signal.

3. Existing algorithms for controlling GWER₀ (e.g., Churchill and Doerge 1994) can be slightly modified to control GWER_k.

It should be pointed out that GWER_k is different from the “suggestive linkage” criterion of Lander and Kruglyak (1995). Suggestive linkage is defined to be the significance cutoff that yields exactly one expected false positive linkage. Therefore, there may in fact be high probability that more than one false positive occurs. From our experience, the suggestive linkage criterion is more liberal than, say, GWER₁. Benjamini and Yekutieli (2005) point out that suggestive linkage can lead to GWER₀ as high as 60%. We compute GWER₀ for GWER₁-based cutoffs in Tables 1 and 2, where it can be seen that GWER₀ remains at reasonable levels. If GWER_k is considered for several values of k at a particular significance cutoff, then this may very well give more precise information than the suggestive linkage criterion of Lander and Kruglyak (1995).

TABLE 2.

A demonstration that the proposed algorithm controls the GWER_k error rate

		Controlled at 5% level
Scenario		GWER0	GWER1
A	LOD cutoff	3.479	2.584
	GWER0	0.025	0.205
	GWER1	0.000	0.025
	FDR (by chromosomes)	0.006	0.046
	Power	0.624	0.797
B	LOD cutoff	3.481	2.585
	GWER0	0.021	0.133
	GWER1	0.001	0.010
	FDR (by chromosomes)	0.005	0.021
	Power	0.397	0.610

Each column corresponds to the procedure applied to controlling GWER₀ and GWER₁, respectively, at the 5% rate. Each row shows the value of each item under the two procedures. Details of scenarios A and B are given in the main text.

A conservative threshold can be set so that GWER_k is controlled at some level α. For a given LOD score threshold λ, the GWER_k is defined as

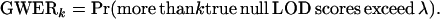A convenient upper bound on this quantity is to assume that all null hypotheses are true, resulting in

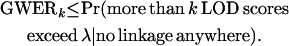(2)

Therefore, it is possible to control the GWER_k by controlling the quantity on the right-hand side of Equation 2, which we call the “full null GWER_k.” The fact that GWER_k can be controlled by controlling the full null GWER_k is an important property. Due to the issues discussed above for the FDR in linkage analysis, it is desirable to avoid having to directly model the dependence in signal in linkage analysis.

An algorithm for controlling GWER_k in QTL mapping:

By extending the procedure of Churchill and Doerge (1994) for controlling GWER₀, we propose an algorithm to control the GWER_k when mapping QTL. (An analogous approach may be adapted for family-based linkage studies.) The rationale of the procedure is based on the fact that if there is any QTL effect in the data set, one can break the association between the trait values and the marker positions by randomly shuffling the trait values, reassigning each trait value to a random individual. In that way, one can obtain a set of full null data. For each random permutation, one can calculate LOD scores at the loci of interest to obtain a set of null statistics. These simulated null statistics can then be used to calculate the proper threshold to control the full null GWER_k. Our algorithm depends on defining “peaks” of LOD scores. We discuss this concept in more detail below. In short, if peaks on LOD score curves are defined unambiguously, then the proposed approach is to call each of the peaks passing a certain threshold a distinct significant linkage finding. However, we do not propose any approach for inferring whether these significant results are due to distinct trait genes.

We propose the following algorithm for controlling the GWER_k at level α:

1. Permute the phenotypic trait values among the individuals and generate a set of null statistics; repeat B times to get B sets of null statistics. To obtain stable estimates, Churchill and Doerge (1994) suggested choosing B ≥ 1000 for α = 0.05 and as many as B = 10,000 for more extreme critical values, such as α = 0.01.

2. For each set of null statistics, obtain the peaks statistics and order them. Take the (k + 1)th highest peak statistic for each of the B null sets and store them together. For example, if we take k = 0, we pick the maximum test statistic for each null set. If we choose k = 1, we take the second highest peak statistic for each of the B permutations.

3. Sort the B (k + 1)th peak statistics in descending order. The 100(1 − α) percentile is the estimated GWER_k threshold value. For example, if we choose B = 1000, k = 1, and α = 0.05, we would take the 50th highest value among all 1000 second-highest peak statistics.

Note that this algorithm can be performed at almost no additional cost in computation compared to the one proposed by Churchill and Doerge (1994).

Interpreting GWER_k control:

In the above algorithm, we distinguished different significant findings by “peak statistics” rather than by simply taking the highest raw statistics. The main purpose of this is to avoid claiming adjacent high statistics as distinct significant findings, especially if they result from a single trait gene. However, defining distinct peaks among the LOD scores is nontrivial. It is well known that LOD score curves are not always smooth. It is also difficult to specify the exact location of the trait gene(s) on a chromosome with true signal. The presence of multiple peaks on a chromosome is generally taken as an indication of multiple QTL—however, such peaks do not necessarily correspond to the correct QTL positions (Martinez and Curnow 1992; Haley and Knott 1992).

One the other hand, it is straightforward to simply define the peaks to be the highest ones on each chromosome. This has been shown to behave reasonably because LOD scores on different chromosomes are independent (Wright and Kong 1997). Therefore, one strategy is to take the maximum LOD score on each chromosome as a peak, thereby controlling the GWER_k in terms of declaring the existence of linkage at the chromosome level. As another strategy, one can divide the chromosomes into bins according to absolute genetic distances, say 20–30 cM, and obtain the maximum LOD scores for these relatively independent intervals. In this case, significant linkages must be interpreted as merely occurring among these predefined intervals, not necessarily due to distinct trait genes. Another alternative is to smooth the LOD score curve and set each local maximum on the smoothed curve as a peak. In general, the necessary component for controlling GWER_k is to be consistent in the definition of distinct linkage peaks, both when formulating significance thresholds and when reporting and analyzing significant loci. If the significance results are interpreted as true signal being present at each significant peak (not necessarily from different trait genes, though), then the GWER_k can be successfully controlled.

NUMERICAL RESULTS

Comparing GWER₀, GWER_k, and FDR:

To illustrate the utility of GWER_k, we performed two simulated examples where GWER_k is shown to provide increased power over GWER₀ without suffering from the problems present for the FDR. These examples are based on the specifications of the mouse genome (Dietrich et al. 1996), where the length and number of chromosomes of the mouse genome were used in each. Using R/qtl (Broman et al. 2003), we simulated 1000 backcross experiments, each with a sample size of 250. We compared the LOD score thresholds, power, and error rates in two scenarios. In scenario A, we placed a single QTL on each of chromosomes 1–5. In scenario B, we placed a single QTL on each of chromosomes 1–10. In both cases, we placed 157 equally spaced markers (10 cM apart from each other) on the 19 chromosomes of the mouse genome. The QTL effects (defined to be half the difference between the homozygote and the heterozygote genotypes) ranged from 0.3 to 0.5 in both cases.

We first compared the different significance measures using LOD score cutoffs that exactly give error rates of 5% for the GWER₀, GWER₁, and FDR. We were able to exactly calculate these cutoffs by using the 1000 sets of simulated data and knowledge of which LOD scores correspond to true null hypotheses. In obtaining the GWER₁ LOD score cutoffs, we defined peaks to be the highest on each respective chromosome. We applied the FDR at the marker level in obtaining its corresponding LOD score cutoffs.

Table 1 shows the results of the simulations in scenarios A and B. Some general trends can be seen. First, the FDR at the chromosome level (i.e., the proportion of chromosomes with a false positive marker among all chromosomes with at least one significant marker) is substantially higher than the marker-based FDR. Second, although the FDR has a lower threshold and suffers from more false positives than the GWER₁ threshold, the power is not drastically different. Third, the power of the GWER₁ cutoff is much greater than that of the GWER₀ cutoff. Fourth, and perhaps most importantly, the GWER₁ coincides nicely with the FDR at the chromosome level. This is not surprising given that there are a relatively small number of chromosomes, implying that a reasonable chromosome-based FDR level would coincide with one or very few false positives occurring. However, as we have argued, the GWER_k is more interpretable when the number of distinct testing units (e.g., chromosomes) is relatively small.

Applying the proposed algorithm:

We used these same simulated data to apply our proposed algorithm to control GWER_k in practice. Through this simulation, we are able to show a specific example where the error rate is in fact controlled. Our algorithm in the previous section was applied for GWER₀ and GWER₁ to all 1000 simulated data sets in each scenario with B = 1000 permutations. We then counted the proportion of times where there were >0 or 1 false positives, respectively. It can be seen in Table 2 that the procedure successfully controlled the error rates at level 0.05 in both scenarios for both GWER₀ and GWER₁.

The difference between scenarios A and B is in the number and locations of the QTL. However, under the full null case they should produce similar LOD score cutoffs. It can be seen in Table 2 that the estimated LOD score cutoffs are equivalent (up to Monte Carlo error) in both scenarios. Because of this, the realized error rates are different, even though all are <0.05. For example, in scenario A the realized GWER₁ is 0.025 and in scenario B it is 0.010. These are less than the user-chosen level of 0.05 because the calculations did not take into account the fact that only a subset of the markers are truly null. Therefore, the more true QTL there are, the more conservative the threshold will tend to be. At this cost, we are able to obviate the issues brought on by there being dependence in the signal.

Multiple QTL on a chromosome:

To further illustrate the behavior of GWER_k relative to GWER₀ and FDR, we simulated a backcross experiment with equally placed markers on four chromosomes of equal length (100 cM each) and 250 backcross individuals being observed. Seven QTL with small effect size were placed on chromosomes 1, 2 and 3. The effect sizes (half the difference between the homozygote and the heterozygote genotypes) are 0.1, 0.15, 0.1, 0.16, 0.2, 0.15, and 0.1, respectively, to their ordering. The positions of the QTL are shown in Figure 2, and the LOD cutoffs that control GWER₀, GWER₁, and FDR at level 0.05 are also plotted in Figure 2. To calculate the appropriate thresholds, we simulated 1000 such data sets and used our knowledge of which loci are true nulls or not.

It can be seen that controlling the FDR at the marker level yields a low LOD score cutoff, also incurring a number of false positive findings. Controlling GWER₀ is too conservative in this case, and three QTL were missed. Controlling GWER₁ using peak LOD scores from predefined 30-cM intervals detected all seven QTL without inducing any false significant findings. Clearly, this example was chosen to show the existence of scenarios where GWER₁ yields a superior LOD score cutoff. In general, the performance would vary, depending on the scenario. However, the main point we illustrate here is that GWER_k offers a flexible error measure that may result in increased true positives over the traditional GWER₀, but is not susceptible to spuriously low cutoffs due to dependence in signal as is sometimes encountered with the FDR.

FDR FOR LINKAGE ANALYSIS OF MANY TRAITS SIMULTANEOUSLY

The FDR has also recently been employed when performing linkage analysis on thousands of traits simultaneously. In particular, QTL for each of thousands of “gene expression traits” measured by DNA 5microarrays have been simultaneously detected using FDR as the significance criterion (Yvert et al. 2003; Brem et al. 2005; Storey et al. 2005). In this setting, the FDR may be appropriately applied so that it does not suffer from the problems we have considered when analyzing a single trait.

In Storey et al. (2005) and Brem et al. (2005) we developed and applied a procedure for mapping multiple loci simultaneously for each expression trait. For each trait, the top linked locus is selected. At this point a P-value may be calculated for each trait–locus pair and the FDR applied to these P-values. Only one locus has been selected for each scan, so applying the FDR across the traits does not suffer from the problems we have mentioned. The dependence here would be dependence in linkage signal across traits. One could argue that dependence in signal across gene expression traits should also be of concern. However, in the genomewide expression setting, the dependence of signal is one of the main properties one hopes to discover. For example, it is common to attempt to identify common functions among genes found to be significant in an expression experiment (Zhong et al. 2004). Therefore, multiple genes under some sort of common transcriptional regulation mechanism (giving them dependence in signal) may actually be considered as distinct discoveries. In a linkage scan of a single trait, the dependence in signal across loci on the same chromosome is obvious and not of interest.

Beyond this, Storey et al. (2005) and Brem et al. (2005) developed a method to select multiple loci for each trait, employing a new FDR technique that tests a more complicated null hypothesis than the usual one of no linkage among any loci. The loci were selected sequentially for each trait, and the previously selected loci were included when assessing the significance for each new locus, thereby removing any dependence in signal. Therefore, the previous justification for employing the FDR for thousands of traits applies here as well: FDR is applied across traits, and the only dependence in signal here is that across traits.

DISCUSSION

We have considered the problem of relaxing the GWER significance criterion that has traditionally been applied in genomewide linkage scans. One criterion that has recently been suggested and applied in the literature is the FDR (Weller et al. 1998; Mosig et al. 2001; Fernando et al. 2004; Benjamini and Yekutieli 2005). In particular, by invoking an earlier result (Benjamini and Yekutieli 2001), Benjamini and Yekutieli (2005) have pointed out that the algorithm of Benjamini and Hochberg (1995) controls the FDR under the dependence induced by a Poisson process model of recombination. However, here we have not been concerned with FDR-controlling procedures. Instead, we have discussed the actual FDR quantity itself.

Fernando et al. (2004) claim to have overcome the dependence issues present in linkage analysis by slightly modifying the definition of FDR. However, under their assumptions the so-called “proportion of false positives” (PFP) definition has previously been shown to be equivalent to the positive FDR (Storey 2003). Moreover, a close inspection of their estimate reveals that it is equivalent, in terms of dependence issues, to one proposed earlier for FDR (e.g., Storey 2002). In other words, even though Fernando et al. (2004) motivate their estimate in terms of the PFP, it is still susceptible to the dependence concerns for direct estimates of the FDR. Most importantly, it can straightforwardly be shown that the issues surrounding the dependence in signal that we have discussed here are also detrimental to the PFP.

We have shown here that it is difficult to interpret the FDR when applied to genomewide linkage scans. Specifically, since neighboring loci share linkage status, the FDR counts multiple true discoveries as being distinct even though they result from the same underlying trait gene. This allows the FDR to be unfairly manipulated by marker placement. In general, the number of true discoveries associated with each trait gene depends on a complicated function of several variables that obfuscate the meaning of a particular FDR level. Some of these issues can be mitigated by applying the FDR in the context of testing each chromosome for linkage. However, in this case one does not expect a large number of significant findings, making the application of FDR less attractive and susceptible to problems already raised (Zaykin et al. 1998).

The FDR allows some false positives in order to increase the number of true positives. With this goal in mind, we have proposed a generalized version of the GWER that is applicable to linkage analyses where it is expected that several trait genes exist. The GWER_k is the probability that more than k false positive linkages are found. Therefore, the user can apply this significance criterion at the appropriate value of k or at several values of k. We have also proposed an algorithm to control GWER_k for QTL mapping. We showed through several numerical examples that our algorithm successfully controls GWER_k in standard situations.

We have discussed some general issues that arise when considering significance criteria more relaxed than the traditional GWER. These issues appear to derive mostly from the fact that the traditional GWER is concerned with the largest null LOD score across the genome, whereas relaxed criteria must consider several LOD score peaks. This problem presents the long-standing challenge of distinguishing distinct linkage signals among high LOD scores present on the same chromosome. We have shown that a straightforward interpretation of the GWER_k occurs when applying this significance criterion to the highest LOD score on each chromosome.