The Adaptive Hypothesis of Clinal Variation Revisited: Single-Locus Clines as a Result of Spatially Restricted Gene Flow

AFTER the establishment of the field of ecological genetics more than 30 years ago (Clarke 1975) rapid progress in molecular marker development and analysis technology has generated a surge of renewed interest in identification of selective footprints of natural selection in a wide range of species (e.g., Schlötterer 2002). Among numerous research strategies developed to infer the evidence of selection in natural populations at the molecular level (reviewed by Nielsen 2005; Vasemägi and Primmer 2005), associations between environmental variables and molecular marker polymorphisms are commonly taken as strong support for the hypothesis that natural selection maintains single-locus clinal variation (e.g., Eanes 1999; Baines et al. 2004). However, it has often been overlooked that single-locus clines can also be the result of various neutral evolutionary processes, such as hybridization of previously isolated populations, founder events, and migrational patterns, such as spatially restricted gene flow (but see also Manly 1985; Storz 2002). In Drosophila melanogaster, for example, extensive research over several decades has suggested the presence of latitudinal clines for a number of genetic polymorphisms, including cosmopolitan inversions (Knibb et al. 1981), allozyme loci (Oakeshott et al. 1982), candidate genes (Schmitd et al. 2000; Duvernell et al. 2003; Frydenberg et al. 2003), and microsatellite loci (Gockel et al. 2001). At the same time, widespread clinal variation has been demonstrated for several quantitative traits, including body size (James et al. 1995), egg size, ovariole number (Azevedo et al. 1996), development time (James and Partridge 1995), and a temperature resistance (Hoffmann et al. 2002). Recently, Sezgin et al. (2004) reported three new significant latitudinal clines in 14 metabolic genes from North America, which together with earlier studies reveal seven clines among 17 genes (41%). Similarly, an earlier study by Gockel et al. (2001) suggested that a considerable proportion of randomly selected microsatellite loci (5 loci out of 19, 26%) exhibited significant linear clines in a north–south transect along the east coast of Australia, providing further support of the presence of extensive single-locus clinal variation in D. melanogaster, both in the northern and the southern hemispheres. However, as argued by Duvernell et al. (2003), if ∼26% of all polymorphisms that show clinal variation are truly affected by selection, then on average every 10th–50th gene (80–400 kb apart) across the Drosophila genome is expected to exhibit an adaptive latitudinal cline along the environmental gradient. Here, I show that results like those of Sezgin et al. (2004) and others can be alternatively explained by an isolation-by-distance (IBD) effect alone, without the need to invoke a widespread multilocus adaptive response, through the use of simple population genetic simulations and assessment of a recently published empirical data set.

The simulation considered a simple neutral population genetic model with 11 subpopulations of 1000 diploid individuals made up of equal numbers of males and females connected by a one-dimensional stepping stone model of migration using six different migration rates (m = 0.001, 0.005, 0.01, 0.02, 0.035, 0.05). This enabled evaluation of how often allele frequencies at 500 neutral loci (mutation rate 5 × 10⁻⁴, two-phase stepwise mutation model with 30% of double-step mutation events, maximum number of possible allelic states 25) exhibited statistically significant clinal variation in the presence of various levels of IBD. The simulations were run first for 2000 generations starting with minimal variability before reducing the migration rate to zero and simulating 0, 50, 150, 250, 350, and 450 generations in isolation. Such a two-step simulation regime is expected to generate a strong IBD pattern during the first migration-drift phase while random genetic drift is expected to reduce the strength of the IBD and increase the level of differentiation during the second isolation phase. Altogether, 72 data sets with various levels of genetic differentiation (pairwise θ values, hereafter F_ST; Weir and Cockerham 1984) and IBD were generated (two replicates for every migration-isolation combination) and 20 individuals per population were sampled for subsequent analyses using the program EASYPOP v.1.8 (Balloux 2001). Note that a two-step migration regime was adopted to generate real-looking data with a wide range of IBD and genetic differentiation levels rather than correspond to real biological populations.

A Mantel test was used (10,000 permutations) to test for a linear association between genetic (F_ST) and spatial distance matrixes measured as the number of steps between subpopulations. The strength of the IBD pattern was quantified as a Pearson correlation coefficient r between F_ST and geographic distance matrixes. Frequencies of the most common allele (MCA) at each locus were used to calculate the proportion of markers showing significant linear regression against spatial distance by comparing the observed value of the slope (b) with the distribution of values from 1000 randomizations as described in Manly (1997) using POPTOOLS v.2.6.9 (Hood 2005). As for the simulated data sets, the strength of the IBD pattern (r) and the proportion of markers showing a significant clinal pattern were re-estimated for the empirical data set of Gockel et al. (2001), which consisted of geographically distinct D. melanogaster samples genotyped at 19 microsatellite loci. A Bonferroni correction for 19 simultaneous tests (P < 0.05; α = 0.00263) was applied for simulated and empirical data sets to make the results from both data sets directly comparable.

In addition, to be able to compare the slopes of the empirical and simulated data sets, spatial distances measured as a number of steps between simulated subpopulations were transformed to the latitudinal scale directly comparable to Gockel et al. (2001). In other words, the spatial distance between the two most distant subpopulations separated from each other by 10 migrational steps was set to 26.19 latitudinal degrees as in Gockel et al. (2001), and thus 1 migrational step in the stepping stone model equals 2.619 degrees of latitudinal distance. Next, the slope (b) and the coefficient of determination (r²) of MCA against latitude were compared for the data of Gockel et al. (2001) and for a single simulated data set that most closely resembled the empirical study in terms of overall F_ST (empirical data F_ST = 0.03; simulated data F_ST = 0.028) and IBD pattern (Mantel test; empirical data r = 0.9, simulated data r = 0.96, both data sets P < 0.001). Note that the proportion of variation explained by latitude (r²) for individual loci was not identical to the values originally reported by Gockel et al. (2001). This discrepancy is most likely caused by the differing numbers of populations/samples used in regression analysis (W. J. Kennington, personal communication). In particular, 11 samples were used for regression analysis in the present study by pooling data from a microgeographic scale (0.005–35 km) while Gockel et al. (2001) treated samples from the individual microgeographic sites as independent observations (W. J. Kennington, personal communication). As one of the assumptions in a regression analysis is that the values of the dependent variable (i.e., allele frequencies of MCA) are independent of one another, pooling microgeographic samples is expected to be a more appropriate strategy to test the regression of MCA against latitude. This is also consistent with the results of Kennington et al. (2003), who did not find significant population substructuring over geographical distances of 0.005–50.4 km in the same north–south transect along the east coast of Australia.

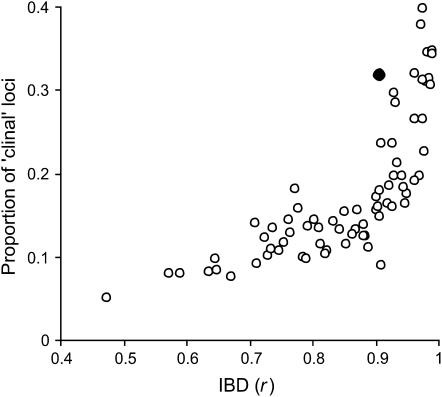
The level of population differentiation (F_ST) varied considerably from 0.015 (m = 0.05) to 0.16 (m = 0.001) depending on the migration rate after 2000 generations and increased further during the isolation phase ranging from 0.037 (m = 0.05; followed by 50 generations in isolation) to 0.244 (m = 0.001; followed by 450 generations in isolation). Importantly, the strength of the IBD relationship was not influenced by the amount of migration per se (e.g., m = 0.005 and 0.05, r = 0.92 and 0.98, respectively) but rather IBD was negatively affected by the number of generations the populations experienced random genetic drift in isolation. Nevertheless, significant IBD pattern was present in all data sets (Mantel test; r = 0.47–0.99, all tests P < 0.01). Similarly, the empirical data set of D. melanogaster from eastern Australia (Gockel et al. 2001) showed a highly significant IBD pattern (Mantel test; r = 0.9, P < 0.001). The proportion of individual loci showing significant clinal variation ranged from 5 to 40% with the proportion of clinal loci increasing with increasing IBD correlation (Figure 1) providing evidence for the positive relationship between the strength of IBD pattern and the prevalence of single-locus clines. Notably, when plotting the strength of IBD pattern r against the proportion of clinal microsatellite loci recalculated from Gockel et al. (2001), the results of the empirical D. melanogaster data are comparable to the simulated data sets under IBD, indicating that a considerable proportion of alleles/loci may exhibit such a clinal pattern even in the absence of selection (Figure 1).

Figure 1.—

Relationship between the strength of IBD pattern quantified as Pearson correlation coefficient (r) and the proportion of loci showing significant clinal variation. Open circles correspond to 72 simulated data sets generated under the neutral evolutionary scenario consisting of 500 loci each; the filled circle represents an empirical D. melanogaster microsatellite data set (19 loci, 11 populations) from Gockel et al. (2001).

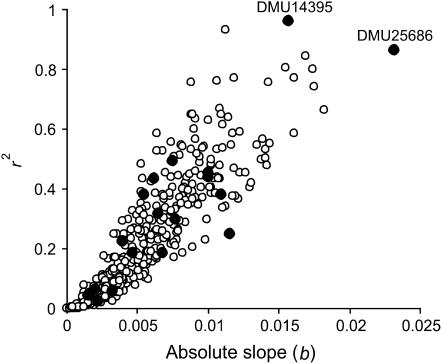
Next, I evaluated whether the empirical D. melanogaster data fit with the neutral evolutionary model affected by migration and random drift only (2000 generations, m = 0.05; followed by 25 generations, m = 0) by plotting the slope (b) and the coefficient of determination (r²) of MCA against latitude (Figure 2). The majority of microsatellite markers (including clinal loci) from Gockel et al. (2001) fall among the simulated loci under the neutral evolutionary scenario with two potential exceptions (DMU14395 and DMU25686). Hence, a statistically significant association between a single-locus cline and an environmental variable (or its derivate, such as latitude) based on regression analysis alone is clearly not enough to imply that a particular locus has experienced divergent natural selection when a genomewide IBD pattern is present. Instead, it might be more useful to explore whether the regression slope b for individual loci is greater than can be explained by genetic drift and IBD alone.

Figure 2.—

Relationship between the slope (b) and the coefficient of determination (r²) of most common allele (MCA) against latitude. Filled circles represent individual loci of the D. melanogaster microsatellite data set from Gockel et al. (2001) and open circles correspond to 500 neutral loci from a simulated data set that most closely resembled the empirical study in terms of overall F_ST and the strength of IBD. The names of the two Drosophila microsatellite loci with the steepest clines are indicated.

It is important to remember that the simulated mutation, drift, and migration processes resulting in various levels of population differentiation and IBD are by no means expected to precisely correspond to the real evolutionary history of D. melanogaster on the east coast of Australia or anywhere else in the world. For example, a strict one-dimensional stepping stone model of migration, the same mutation rate for all microsatellite loci, and the relatively small effective population sizes (N_e = 1000) used in the simulations represent an over-simplistic model of the underlying population structure in Drosophila. Nevertheless, the main feature of the simulations—spatially limited gene flow generating an IBD pattern and single-locus clinal variation—most likely holds for D. melanogaster populations in different continents (see Verelli and Eanes 2001; Kennington et al. 2003 and references therein). Hence, on the basis of simulations and empirical data, I argue that widespread single-locus latitudinal clines in D. melanogaster, which have been traditionally implied to represent an adaptive response to climatic selection, can to a large extent be explained by spatially restricted gene flow. In addition, it is obvious that if clinal variation in D. melanogaster is as common as found by recent studies (e.g., Gockel et al. 2001; Sezgin et al. 2004) then at least a proportion of the reciprocal latitudinal clines in northern and southern hemispheres, which have been traditionally taken as one of the most compelling pieces of evidence of natural selection, could be explained by chance alone. For example, assuming that 26–40% of all polymorphisms show clinal variation because of geographically limited gene flow, then 3–8% of neutral loci are expected to exhibit reciprocal clines in both the northern and the southern hemispheres.

However, it is also evident that selection can have an important role affecting single-locus clinal variation and not all observed single-locus clines can be easily explained by IBD (Simmons et al. 1989; Berry and Kreitman 1993). For example, recent temporal analysis over 20 years in D. melanogaster (Umina et al. 2005) demonstrated that latitudinal clines in the alcohol dehydrogenase (Adh) gene and in a cosmopolitan inversion [In(3R)Payne] along eastern Australia have shifted in a manner consistent with adaptation to increasingly warmer and drier conditions, indicating a likely rapid evolutionary response to climate change. Also, accumulating evidence from QTL mapping (e.g., Gockel et al. 2002) and theoretical work (Kirkpatrick and Barton 2006) suggests that large inverted regions of chromosomes are likely to be involved in adaptive divergence between populations (Hoffmann et al. 2004). Consistent with the hypothesis that inversion polymorphisms tend to capture loci involved in local adaptation, two microsatellites (DMU14395 and DMU25686) that are located within two cosmopolitan inversions, In(3L)Payne and In(3R)Payne, respectively, exhibited the steepest clines against latitude and differed most from the simulated loci under simple neutral evolutionary model. Hence, it is possible that these markers are linked to loci underlying adaptive traits in D. melanogaster.

To conclude, as the number of studies attempting to unravel targets of natural selection using genetic marker–environment associations are steadily increasing, caution to avoid oversimplified interpretation of single-locus clines is recommended, as is rigorous evaluation of genomewide IBD patterns prior to invoking the adaptive explanation of clinal variation. Certainly, clinal patterns can provide useful information about the genes and genomic regions affected by selection, but it is important to determine whether the observed clines are more extreme than those that can be explained by random genetic drift and IBD alone. Further investigations using more biologically realistic simulations are required to evaluate the relationship between single-locus clinal variation and IBD in more detail, while the application of other complementary multilocus neutrality tests (reviewed by Nielsen 2005; Storz 2005) can provide further insights on the relative roles of selection vs. neutral evolutionary forces.