Abstract
In this work, I present the form of the Navier–Stokes equations implied by the Helmholtz decomposition in which the relation of the irrotational and rotational velocity fields is made explicit. The idea of self-equilibration of irrotational viscous stresses is introduced. The decomposition is constructed by first selecting the irrotational flow compatible with the flow boundaries and other prescribed conditions. The rotational component of velocity is then the difference between the solution of the Navier–Stokes equations and the selected irrotational flow. To satisfy the boundary conditions, the irrotational field is required, and it depends on the viscosity. Five unknown fields are determined by the decomposed form of the Navier–Stokes equations for an incompressible fluid: the rotational component of velocity, the pressure, and the harmonic potential. These five fields may be readily identified in analytic solutions available in the literature. It is clear from these exact solutions that potential flow of a viscous fluid is required to satisfy prescribed conditions, like the no-slip condition at the boundary of a solid or continuity conditions across a two-fluid boundary. It can be said that equations governing the Helmholtz decomposition describe the modification of irrotational flow due to vorticity, but the analysis shows the two fields are coupled and cannot be completely determined independently.
Keywords: potential flow, vorticity, Navier–Stokes, self-equilibration, dissipation
Helmholtz Decomposition
The Helmholtz decomposition theorem says that every smooth vector field u, defined everywhere in space and vanishing at infinity together with its first derivatives can be decomposed into a rotational part υ and an irrotational part ∇φ.
where
This decomposition leads to the theory of the vector potential, which is not followed here. The decomposition is unique on unbounded domains without boundaries, and explicit formulas for the scalar and vector potentials are well known. A framework for embedding the study of potential flows of viscous fluids, in which no special flow assumptions are made, is suggested by this decomposition (Eq. 1). If the fields are solenoidal, then
Since φ is harmonic, we have from Eqs. 1 and 4 that
The irrotational part of u is on the null space of the Laplacian, but in special cases, like plane shear flow, ∇2υ = 0, but curlυ ≠ 0.
Unique decompositions are generated by solutions of the Navier–Stokes equation (Eq. 6) in decomposed form (Eq. 7) where the irrotational flows satisfy Eqs. 1 and 3–5 and certain boundary conditions. The boundary conditions for the irrotational flows have a heavy weight in all this. Simple examples of unique decomposition, taken from hydrodynamics, will be presented later.
The decomposition of the velocity into rotational and irrotational parts holds at each and every point and varies from point to point in the flow domain. Various possibilities for the balance of these parts at a fixed point and the distribution of these balances from point to point can be considered as follows:
The flow is purely irrotational or purely rotational. These two possibilities do occur as approximations but are not typical.
Typically, the flow is mixed with rotational and irrotational components at each point.
Navier–Stokes Equations for the Decomposition
To study solutions of the Navier–Stokes equations, it is convenient to express the Navier–Stokes equations for an incompressible fluid,
in terms of the rotational and irrotational fields implied by the Helmholtz decomposition,
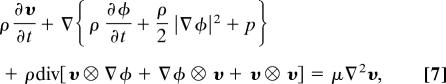 |
or
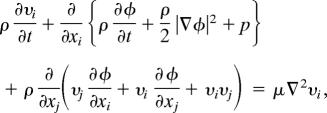 |
satisfying Eq. 4.
To solve this problem in a domain Ω, say, when the velocity u = V is prescribed on ∂Ω, we would need to compute a solenoidal field υ satisfying Eq. 7 and a harmonic function φ satisfying ∇2φ = 0 such that υ + ∇φ = V on ∂Ω. Since this system of five equations in five unknowns is just the decomposed form of the four equations in four unknowns that defines the Navier–Stokes system for u, it should be possible to study this problem using exactly the same mathematical tools that are used to study the Navier–Stokes equations.
In the Navier–Stokes theory for incompressible fluid, the solutions are decomposed into a space of gradients and its complement, which is a space of solenoidal vectors. The gradient space is not, in general, solenoidal because the pressure is not solenoidal. If it were solenoidal, then ∇2p = 0, but ∇2p = −divρu·∇u satisfies Poisson's equation.
It is not true that only the pressure is found on the gradient space. Indeed Eq. 7 gives rise to a Poisson's equation for the Bernoulli function, not just the pressure.
In fact, there may be hidden irrotational terms on the right-hand side of this equation.
The boundary condition for solutions of Eq. 6 is u − a = 0 on ∂Ω, where a is solenoidal field such that a = V on ∂Ω; hence
The decomposition depends on the selection of the harmonic function φ; the traditional boundary condition n·a = n·decomposed form;∇φ on ∂Ω together with a Dirichlet condition at infinity when the region of flow is unbounded and a prescription of the value of the circulation in doubly connected regions, gives rise to a unique φ. Then the rotational flow must satisfy
on ∂Ω. The υ determined in this way is rotational and satisfies Eq. 3. However, υ may contain other harmonic components.
Purely rotational flows υ have no harmonic components. Purely rotational velocities can be identified in the exact solutions exhibited in the examples where the parts of the solution which are harmonic and the parts that are not are identified by inspection. Eq. 18, in which the purely irrotational flow is identified by selecting a parameter α, is a good example. We have a certain freedom in selecting the harmonic functions used for the decomposition. It is possible to formulate problems of potential flow depending on a parameter, say for streaming flow around bodies which would give rise to the rotational flow in Eq. 18 when the body is a sphere. However, in the general case in which explicit solutions are absent and the potential flow is computed numerically, we have at present no way to identify a purely irrotational flow. The examples show the purely rotational flows exist in special cases. It remains to be seen whether this concept makes sense in a general theory.
What is the value added to solutions of the Navier–Stokes equations (Eq. 6) by solving them in the Helmholtz decomposed form† (Eq. 7)? Certainly it is not easier to solve for five rather than four fields; if you cannot solve Eq. 6 then you certainly cannot solve Eq. 7. However, if the decomposed solution could be extracted from solutions of Eq. 6 or computed directly, then the form of the irrotational solution that is determined through coupling with the rotational solution and the changes in its distribution as the Reynolds number changes would be revealed. There is nothing approximate about this; it is the correct description of the role of irrotational solutions in the theory of the Navier–Stokes equations, and it looks different and is different than the topic “potential flow of an inviscid fluid,” which we all learned in school.
The form (Eq. 7) of the Navier–Stokes equations may be well suited to the study of boundary layers of vorticity with irrotational flow of viscous fluid outside. I conjecture that in such layers υ ≠ 0, while υ is relatively small in the irrotational viscous flow outside. Rotational and irrotational flows are coupled in the mixed inertial term on the left of Eq. 7. The irrotational flow does not vanish in the boundary layers, and the rotational flow, although small, probably will not be zero in the irrotational viscous flow outside. This feature is also in Prandtl's theory of boundary layers, but that theory is not rigorous, and the irrotational part is, so to say, inserted by hand and is not coupled to the rotational flow at the boundary. The coupling terms are of considerable interest, and they should play strongly in the region of small vorticity at the edge of the boundary layer. The action of irrotational flow in the exact boundary layer solution of Hiemenz (1911) for steady two-dimensional (2D) flow toward a “stagnation point” at a rigid body (2) and Hamel (1917) flow (2, 3) in diverging and converging channels in the Helmholtz decomposed form at the end of this work.
Effects on boundary layers on rigid solids arising from the viscosity of the fluid in the irrotational flow outside have been considered without the decomposition by Wang and Joseph (4, 5) and Padrino and Joseph (6).
Self-Equilibration of the Irrotational Viscous Stress
The stress in a Newtonian incompressible fluid is given by
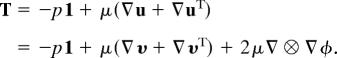 |
Most flows have an irrotational viscous stress. The term μ∇2υ in Eq. 7 arises from the rotational part of the viscous stress.
The irrotational viscous stress τI = 2μ∇ ⊗ ∇φ does not give rise to a force density term in Eq. 7. The divergence of τI vanishes on each and every point in the domain V of flow. Even though an irrotational viscous stress exists, it does not produce a net force to drive motions. Moreover,
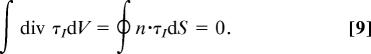 |
The traction vectors n·τI have no net resultant on each and every closed surface in the domain V of flow. We say that the irrotational viscous stresses, which do not drive motions, are self-equilibrated. Irrotational viscous stresses are not equilibrated at boundaries, and they may produce forces there.
Dissipation Function for the Decomposed Motion
The dissipation function evaluated on the decomposed field (Eq. 1) sorts out into rotational, mixed, and irrotational terms given by
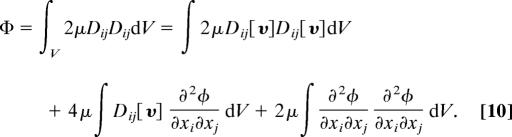 |
Most flows have an irrotational viscous dissipation. In regions V′ where υ is small, we have approximately that
and
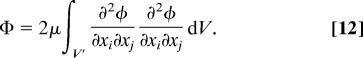 |
Eq. 12 has been widely used to study viscous effects in irrotational flows since Stokes in 1851 (in ref. 7, “historical notes”).
Irrotational Flow and Boundary Conditions
How is the irrotational flow determined? It frequently happens that the rotational motion cannot satisfy the boundary conditions; this well known problem is associated with difficulties in forming boundary conditions for the vorticity. The potential φ is a harmonic function, which can be selected so that the values of the sum of the rotational and irrotational fields can be chosen to balance prescribed conditions at the boundary. The allowed irrotational fields can be selected from harmonic functions that enter into the purely irrotational solution of the same problem on the same domain. A very important property of potential flow arises from the fact that irrotational viscous stresses do not give rise to irrotational viscous forces in the equations of motion (Eq. 7). The interior values of the rotational velocity are coupled to the irrotational motion through Bernoulli terms evaluated on the potential and inertial terms that couple the irrotational and rotational fields. The dependence of the irrotational field on viscosity can be generated by the boundary conditions.
Poiseuille Flow
A simple example that serves as a paradigm for the relation of the irrotational and rotational components of velocity in all the solutions of the Navier–Stokes equations is plane Poiseuille flow
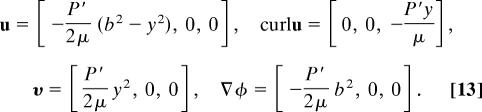 |
The irrotational flow is a constrained field and cannot satisfy the no-slip boundary condition. To satisfy the no-slip condition, we add the irrotational flow ∂φ/∂x = −P′b2/(2μ). The irrotational component is for uniform and unidirectional flow chosen so that u = 0 at the boundary.
Flow Between Rotating Cylinders
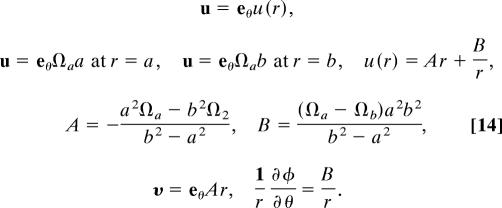 |
The irrotational flow with υ = 0 is an exact solution of the Navier–Stokes equations with no-slip at boundaries.
Stokes Flow Around a Sphere of Radius a in a Uniform Stream U (2, 3)
The Helmholtz decomposition of the solution of the problem of slow streaming motion over a stationary sphere is given in spherical polar coordinates by
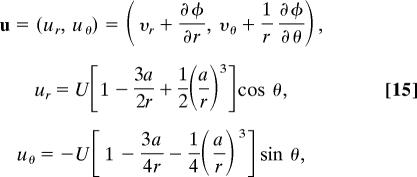 |
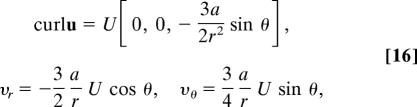 |
The potential for flow over a sphere is
The normal component of velocity vanishes when α = −2, and the tangential component vanishes when α = 4. In the present case, to satisfy the no-slip condition, we take α = 1. Both the rotational and irrotational components of velocity are required to satisfy the no-slip condition.
Streaming Motion Past an Ellipsoid (8)
The problem of the steady translation of an ellipsoid in a viscous liquid was solved by Lamb in 1932 (8) in terms of the gravitational-potential Ω of the solid and another harmonic function χ corresponding to the case in which ∇2 χ = 0, finite at infinity with χ = 1 for the internal space. Citing Lamb (8):
If the fluid be streaming past the ellipsoid, regarded as fixed, with the general velocity U in the direction of x, we assume
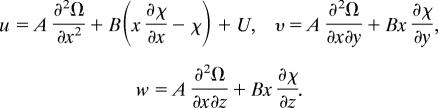 |
These satisfy the equation of continuity, in virtue of the relations ∇2Ω = 0, ∇2χ = 0; and they evidently make u = U, υ = 0, w = 0 at infinity. Again, they make
We note next that ∇2υ = ∇2u. It follows that the rotational velocity is associated with χ and is given by the terms proportional to B. The irrotational velocity is given by ∇φ = ∇(A∂Ω/∂x). The vorticity is given by ω = −ey(2B∂χ/∂z) + ez(2B∂χ/∂y). The vorticity is determined by x times the harmonic function ∂χ/∂x.
Hadamard–Rybyshinsky Solution for Streaming Flow Past a Liquid Sphere
As in the flow around a solid sphere, this problem is posed in spherical coordinates with a stream function and potential function related by Eqs. 15–17. The stream function is given by
The irrotational of Eq. 19 is the part that satisfies ∇2ψp = 0. From this, it follows that
The potential φ corresponding to ψp is given by Eq. 17.
The solution of this problem is determined by continuity conditions at r = a. The inner solution for r < a is designated by ū, ῡ, φ̄, ψ̄, p̄, μ̄, ρ̄.
The normal component of velocity
is continuous at r = a. The normal stress balance is approximated by a static balance in which the jump of pressure is balanced by surface tension so large that the drop is approximately spherical. The shear stress
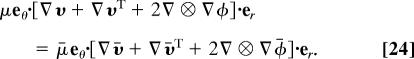 |
The coefficients A, B, C, D are determined by the condition that u = Uex as r → ∞ and the continuity conditions (Eqs. 23 and 24) find that when r ≤ a,
where the r2 term is associated with irrotational flow and when r ≥ a,
where the r2 and a2/r terms are irrotational.
Axisymmetric Steady Flow Around a Spherical Gas Bubble at Finite Reynolds Numbers
This problem is like the Hadamard–Rybyshinski problem, with the internal motion of the gas neglected, but inertia cannot be neglected. The coupling conditions reduce to
and
There is no flow across the interface at r = a, and the shear stress vanishes there.
The equations of motion are the r and θ components of Eq. 1 with time derivative zero. Since Levich in 1947 (in ref. 7, “historical notes”) it has been assumed that at moderately large Reynolds numbers, the flow in the liquid is almost purely irrotational with a small vorticity layer where υ ≠ 0 in the liquid near r = a. The details of the flow in the vorticity layer, the thickness of the layer, and the presence and variation of viscous pressure contribution all are unknown.
It may be assumed that the irrotational flow in the liquid outside the sphere can be expressed as a series of spherical harmonics. The problem then is to determine the participation coefficients of the different harmonics, the pressure distribution, and the rotational velocity υ satisfying the continuity conditions (Eqs. 27 and 28). The determination of the participation coefficients may be less efficient than a purely numerical simulation of Laplace's equation outside a sphere subject to boundary conditions on the sphere, which are coupled to the rotational flow. This important problem has not yet been solved.
Viscous Decay of Free Gravity Waves (8, 9)
Flows that depend on only two space variables such as plane flows or axisymmetric flows admit a stream function. Such flows may be decomposed into a stream function and potential function.
Lamb (8) calculated an exact solution of the problem of the viscous decay of free gravity waves as a free surface problem of this type. He decomposes the solution into a stream function ψ and potential function φ, and the solution is given by
where
This decomposition is a Helmholtz decomposition; it can be said that Lamb solved this problem in the Helmholtz formulation.
Wang and Joseph (9) constructed a purely irrotational solution of this problem, which is in very good agreement with the exact solution. The potential in the Lamb solution is not the same as the potential in the purely irrotational solution because they satisfy different boundary conditions. It is worth noting that viscous potential flow rather than inviscid potential flow is required to satisfy boundary conditions. The common idea that the viscosity should be put to zero to satisfy boundary conditions is deeply flawed. It is also worth noting that the viscous component of the pressure does not arise in the boundary layer for vorticity in the exact solution; the pressure is given by Eq. 29.
Oseen Flow (8, 10)
Steady-streaming flow of velocity U of an incompressible fluid over a solid sphere of radius a, which is symmetric about the x axis and satisfies
where divu = 0 and U = 2kν (for convenience). The inertial terms in this approximation are linearized but not zero. The equations of motion in decomposed form are
Since divυ = 0 and φ is harmonic, ∇2p = 0 and U(∂curlυ/∂x) = ν∇2curlυ. The rotational velocity is determined by a function χ,
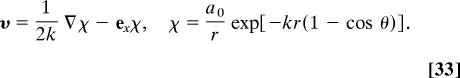 |
The potential φ is governed by the Laplace equation ∇2φ = 0, for which the solution is given by
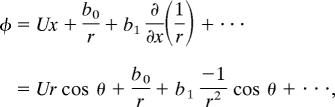 |
where Ux is the uniform velocity term. Using these, the velocity u = (ur, uθ) is expressed as
These should be zero at the sphere surface (r = a) to give
The higher-order terms in the potential vanish.
To summarize, the decomposition of the velocity into rotational and irrotational components is
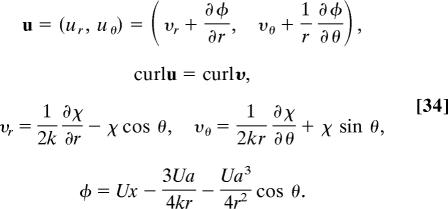 |
Flows Near Internal Stagnation Points in Viscous Incompressible Fluids
The fluid velocity relative to uniform motion or rest vanishes at points of stagnation. These points occur frequently even in turbulent flow. When the flow is purely irrotational, the velocity potential φ can be expanded near the origin as a Taylor series
where the tensor aij is symmetric. At the stagnation point, ∇φ = 0, hence, ai = 0; and since ∇2φ = 0 everywhere, we have aij = 0. The velocity is
at leading order. The velocity components along the principal axes (x, y, z) of the tensor aij are
where a and b are unknown constants relating to the flow field. Irrotational stagnation points in the plane are saddle points; centers are stagnation points around which the fluid rotates. Saddle points and centers are embedded in vortex arrays.
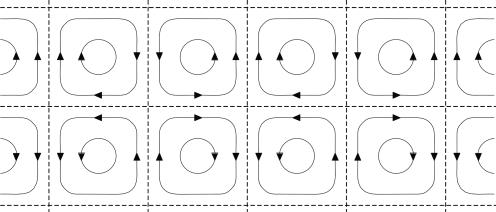
Taylor vortex flow (TVF) is a 2D (x, z) array of counter-rotating vortices (Fig. 1) whose vorticity decays in time due to viscous diffusion (∂tω = ν∇2ω). TVF is an exact solution of the nonlinear time-dependent, incompressible Navier–Stokes equations (Eq. 11). The instantaneous velocity components are
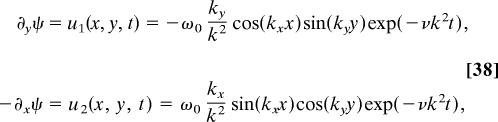 |
where
and
ω(x, y, t) is the vorticity, and ω0 is the initial maximum vorticity, kx and ky are the wave numbers in the x and y directions, and k2 = kx2 + ky2.
Fig. 1.
(After Taylor, ref. 11): Streamlines for system of eddies dying down under the action of viscosity. The streamlines are isovorticity lines; the vorticity vanishes on the border of the cells.
The vorticity vanishes at saddle points (X, Y). After expanding the solution in power series centered on a generic stagnation point, we find that
The vorticity vanishes at (X, Y) = (0, 0) and appears first at second order
The Helmholtz decomposition of the local solution near (X, Y) = (0, 0) is
where
and
This solution is generally valid in eddy systems, which are segregated into quadrants near the stagnation point as in Fig. 1.
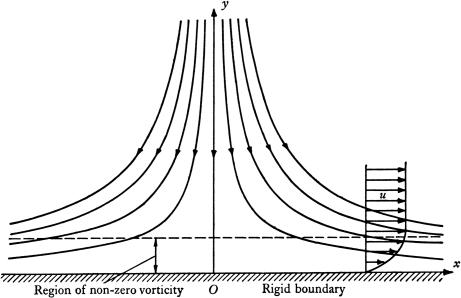
Hiemenz 1911 Boundary Layer Solution for 2D Flow Toward a “Stagnation Point” at a Rigid Boundary (2)
Stagnation points on solid bodies are very important because the pressures at such points can be very high. But stagnation point flow cannot persist all the way to the boundary because of the no-slip condition. Hiemenz looked for a boundary layer solution of the Navier–Stokes equations vanishing at y = 0, which tends to stagnation point flow for large y expressed as
The motion in the outer region is irrotational flow near a stagnation point at a plane boundary. The flow in the irrotational region is described by the stream function, ψ = kxy, where x and y are rectlinear coordinates parallel and normal to the boundary (see Fig. 2), with the corresponding velocity distribution
k is a positive constant, which, in the case of a stagnation point on a body fixed in a stream, must be proportional to the speed of the stream.
Fig. 2.
Steady 2D flow toward a “stagnation point” at a rigid boundary.
The next step is to determine the distribution of vorticity in the thin layer near the boundary from the equation
together with boundary conditions that u = 0 and υ = 0 at y = 0 and that the flow tends to the form of Eq. 48 at the outer edge of the layer. Hiemenz found such a solution in the form
corresponding to u = xf′(y), υ = −f(y), and ω = ∂υ/∂x − ∂u/∂y = −xf″(y), where f(y) is an unknown function and primes denote differentiation with respect to y satisfying −f′f″ + ff‴ + νfiv = 0, and the boundary conditions f = f′ = 0 at y = 0, f → ky as y → ∞. Heimenz (1911) showed that this system could be computed numerically and that it had a boundary layer structure in the limit of small ν (Fig. 2).
Alternatively, we may decompose the solution relative to a stagnation point in the whole space. To satisfy the no-slip condition, the x component of stagnation point flow on y = 0 must be put to zero by an equal and opposite rotational velocity. For the decomposed motion, we have
Instead of Eq. 49, we have the vorticity equation in the Helmholtz decomposed form
The solution of this problem is given by ψ = xF(y), where F(y) = f − ky, F(0) = 0 and F′(0) = −k.
Hamel Flow in Diverging and Converging Channels (2, 3)
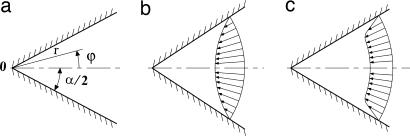
The problem is to determine the steady flow between two plane walls meeting at angle α shown in Fig. 3a. Batchelor's discussion of this problem is framed in terms of the solutions u = (υr, υz, υϕ) = (υ[r, ϕ], 0, 0) of the Navier–Stokes equations (Eq. 6). The continuity equation ∂rυ/∂r = 0 shows that
The function υ̃ (ϕ) is determined by an involved but straightforward nonlinear analysis leading to the cartoons shown in Figs. 3 and 4.
Fig. 3.
Hamel sink flow. (a) Flow channel. (b) Irrotational sink flow. (c) Sink flow with rotational boundary layer.
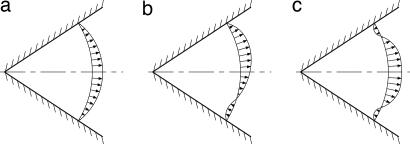
Fig. 4.
Hamel source flow. (a) Irrotational source flow. (b) Asymmetric rotational flow. (c) Symmetric rotational flow.
I next consider the Helmholtz decomposition (Eq. 1) of Hamel flow. Eq. 53 shows that the only irrotational flow allowed in this decomposition is source or sink flow ϕ = C log r, where C is to be determined from the condition that υ̂ (ϕ) + C = 0 at ϕ = ± α. The rotational field υ̂ (ϕ) and constant C can be uniquely determined by an analysis like that given by Batchelor.
The Helmholtz decomposition gives rise to an exact theory of potential flow in the frame of the Navier–Stokes equations in which rotational and irrotational fields are tightly coupled and both fields depend on viscosity. This kind of theory leads to boundary layers of vorticity in asymptotic limits, but the fields are always coupled. The exact theory is different than purely irrotational theories of the effect of viscosity, which can lead to excellent but always approximate results.
Acknowledgments
I thank T. Funada for his help with these calculations, H. Weinberger for discussions of conceptual issues, and G. I. Barenblatt who helped me with this paper and with my work on viscous potential flow over many years. This work was supported by National Science Foundation Chemical and Transport Systems Grant 0302837.
Footnotes
Conflict of interest statement: No conflicts declared.
A cultured lady asked a famous conductor of Baroque music whether J.S. Bach was still composing. The conductor replied, “No madame, he is decomposing.”
References
- 1.Joseph DD. Int J Multiphase Flow. 2006;32:886–887. [Google Scholar]
- 2.Batchelor GK. An Introduction to Fluid Dynamics. Cambridge, UK: Cambridge Univ Press; 1967. [Google Scholar]
- 3.Landau LD, Lifshitz EM. Fluid Mechanics. 2nd Ed. Oxford: Pergamon; 1987. [Google Scholar]
- 4.Wang J, Joseph DD. J Fluid Mech. 2006;557:145–165. [Google Scholar]
- 5.Wang J, Joseph DD. J Fluid Mech. 2006;557:167–190. [Google Scholar]
- 6.Padrino JC, Joseph DD. J Fluid Mech. 2006;557:191–223. [Google Scholar]
- 7.Joseph DD. Int J Multiphase Flow. 2006;32:285–310. [Google Scholar]
- 8.Lamb H. Hydrodynamics. 6th Ed. Cambridge, UK: Cambridge Univ Press; 1932. reprinted (1945) (Dover, New York) [Google Scholar]
- 9.Wang J, Joseph DD. J Fluid Mech. 2006;559:461–472. [Google Scholar]
- 10.Milne-Thomson LM. Theoretical Hydrodynamics. New York: Macmillan; 1968. [Google Scholar]
- 11.Taylor GI. Philos Mag. 1923;XLVI:671–674. [Google Scholar]