Abstract
We use quantitative experimental and theoretical approaches to characterize the vibrational dynamics of the Fe atom in porphyrins designed to model heme protein active sites. Nuclear resonance vibrational spectroscopy (NRVS) yields frequencies, amplitudes, and directions for 57Fe vibrations in a series of ferrous nitrosyl porphyrins, which provide a benchmark for evaluation of quantum chemical vibrational calculations. Detailed normal mode predictions result from DFT calculations on ferrous nitrosyl tetraphenylporphyrin Fe(TPP)(NO), its cation [Fe(TPP)(NO)]+, and ferrous nitrosyl porphine Fe(P)(NO). Differing functionals lead to significant variability in the predicted Fe-NO bond length and frequency for Fe(TPP)(NO). Otherwise, quantitative comparison of calculated and measured Fe dynamics on an absolute scale reveals good overall agreement, suggesting that DFT calculations provide a reliable guide to the character of observed Fe vibrational modes. These include a series of modes involving Fe motion in the plane of the porphyrin, which are rarely identified using infrared and Raman spectroscopies. The NO binding geometry breaks the fourfold symmetry of the Fe environment, and the resulting frequency splittings of the in-plane modes predicted for Fe(TPP)(NO) agree with observations. In contrast to expectations of a simple three-body model, mode energy remains localized on the FeNO fragment for only two modes, an N-O stretch and a mode with mixed Fe-NO stretch and FeNO bend character. Bending of the FeNO unit also contributes to several of the in-plane modes, but no primary FeNO bending mode is identified for Fe(TPP)(NO). Vibrations associated with hindered rotation of the NO and heme doming are predicted at low frequencies, where Fe motion perpendicular to the heme is identified experimentally at 73 cm−1 and 128 cm−1. Identification of the latter two modes is a crucial first step toward quantifying the reactive energetics of Fe porphyrins and heme proteins.
Keywords: nuclear resonance vibrational spectroscopy, iron nitrosyl porphyrin, heme proteins, doming
Introduction
Vibrational spectroscopy provides an incisive probe of the structure, dynamics, and reactivity of biological molecules.2–5 Significant progress has been made in identifying active site vibrations and relating them to the functional dynamics of proteins.6,7 Particularly effective are site-selective techniques such as resonance Raman,2 infrared difference,5 and femtosecond coherence8,9 spectroscopies. These methods only detect vibrations coupled to localized electronic excitations or to a chemical reaction, enormously reducing spectral congestion due to competing signals from the rest of the protein and surrounding solvent. In heme proteins, some active site vibrations have been calibrated as quantitative markers for structural and electronic changes at the protein active site10–12.
However, important challenges remain. Selection rules inherent to infrared and Raman spectroscopies prevent the observation of many important active site vibrations. For example, in-plane vibrations of the heme Fe, which would probe the strength of the Fe-pyrrole bonds, have not been identified in resonance Raman spectra. This reflects the absence of coupling of Eu vibrations with dipole-allowed electronic transitions in the nominal D4h symmetry of the Fe porphyrin. Solvent absorption and other experimental challenges also limit infrared studies of proteins below 1000 cm−1. Reactive modes, which would provide direct information on the energetics of chemical reactions or conformational changes, lie at low frequencies8,9 and are rarely identified with traditional techniques.
One fundamental challenge in applying vibrational spectroscopy to large molecules is assignment of observed vibrational frequencies with normal modes. Isotopic labelling of these large molecules13 remains demanding, in spite of recent progress.14 Until recently, normal mode analysis of molecules containing more than a few atoms relied on the use of empirical force fields. Transformation from the limited experimental information on vibrational frequencies available from infrared and Raman spectroscopies to the large number of adjustable force constants required to specify an empirical potential function is a highly underdetermined problem, except for very small or highly symmetric molecules. Emerging experimental and theoretical approaches are beginning to alter this situation.
On the experimental side, nuclear resonance vibrational spectroscopy (NRVS),1 an emerging synchrotron-based technique, reveals the complete vibrational spectrum of a probe nucleus.15–35 57Fe NRVS is a particularly promising method to identify and characterize Fe-ligand modes at protein active sites.18,27,28,36–43 For heme proteins, these include in-plane Fe vibrations, which have not been reported in resonance Raman investigations, and the Fe-imidazole stretch, which has not been identified in six-coordinate porphyrins. Reactive Fe modes, such as heme doming,8,9,27,44 are of particular interest. The NRVS signal is proportional to the mean square amplitude of the Fe along the direction of the X-ray beam, and all modes involving significant Fe motion will contribute to the measured spectrum.
On the theoretical side, density functional theory (DFT) methods now predict ground state properties for molecules of increasing size,45–58 including detailed descriptions of their vibrational dynamics.24,29,33,59–66 These quantum chemical calculations do not rely on empirical force constants or require prior knowledge of related molecules to constrain the potential. The rich data set of vibrational frequencies, amplitudes, and directions available from NRVS provides a particularly rigorous test of the ability of DFT calculations to predict the vibrational dynamics of transition metals at protein active sites.67–77 For small molecules that are available in large quantities, inelastic neutron scattering (INS) can provide complementary quantitative information about the vibrational dynamics of lighter nuclei.78–82
With rare exceptions,83 living organisms require Fe to exist. Many biological functions of this transition metal involve reactions with diatomic ligands at the active site of heme proteins,84 where the Fe is located at the center of a porphyrin macrocycle. Heme protein reactions involving O2 have been particularly heavily studied.7,85–87 Awareness of, and interest in, the important roles of diatomic molecules in intracellular signalling is increasing. In particular, NO is now implicated in a wide range of intracellular processes, including blood pressure regulation, neurotransmission, and immunoregulation.88–91
The role of heme proteins in these diatomic signalling processes is now well-established.92 Both the source of endogenous NO, nitric oxide synthase (NOS),93–95 and its best characterized target, soluble guanylate cyclase (sGC),96,97 are heme proteins. NO binding weakens the bond to a trans ligated imidazole, and early studies observed rupture of the Fe-imidazole bond following NO binding to the heme in T-state human hemoglobin,98,99 consistent with the expected strain in this bond. More recently, activation of sGC has been attributed to changes in polypeptide conformation that follow rupture of this covalent link between the heme and the protein on NO binding.100–102 Five-coordinate nitrosyl hemes have now been reported in numerous proteins, including human hemoglobin,98,99 sGC,103,104 cytochrome c′,105 partially unfolded106,107 myoglobins at pH 4,108,109 myoglobin mutants with the proximal histidine detached from the polypeptide,110,111 the transcriptional regulator CooA,112 NOS,113–115 cytochrome cbb3 oxidase,116 cystathionine beta-synthase,117 human serum albumin,118 and FixL.119,120 Characterization of the vibrational dynamics of five-coordinate ferrous nitrosyl porphyrins has direct relevance to important physiological processes.
Here, we use NRVS measurements and DFT-based normal mode analysis to characterize the vibrational dynamics of ferrous nitrosyl porphyrins that mimic the active site of five-coordinate heme proteins. The measured spectra are considerably richer for ferrous nitrosyl porphyrins than when the fifth ligand is imidazole,38 indicating that the diatomic ligand fundamentally alters the Fe dynamics. Measurements on a series of ferrous nitrosyl porphyrins with varying group substitutions on the periphery of the heme reveal significant variations in the vibrational dynamics of the central Fe. As a result, meaningful comparison with vibrational predictions requires a calculation on the full molecule, rather than a truncated fragment. DFT calculations on ferrous nitrosyl tetraphenylporphyrin, Fe(TPP)(NO) (Fig. 1), as well as the [Fe(TPP)(NO)]+ cation and ferrous nitrosyl porphine, Fe(P)(NO), yield detailed vibrational predictions. For Fe(TPP)(NO), comparison of calculated and measured Fe dynamics reveals good overall agreement on an absolute scale, suggesting that the calculation provides a reliable guide to the character of the observed vibrational modes.
Figure 1.

Calculated structure of ferrous nitrosyl tetraphenylporphyrin, Fe(TPP)(NO), resulting from geometric optimization with the B3LYP functional and 6-31G* + VTZ basis set to minimize the molecular energy. Selected structural parameters are reported in Table 1.
The predicted spectrum of Fe(TPP)(NO) is dominated by a number of pairs of modes that involve Fe motion in the plane of the porphyrin. The NO binding geometry breaks the fourfold symmetry of the Fe environment, and leads to predicted frequency splittings of the in-plane modes in good accord with those observed experimentally. Two modes localized on the nonlinear FeNO fragment are predicted, the N-O stretch and an Fe-NO stretch with significant FeNO bending character. We are unable to identify a single mode with dominant FeNO bending character in the vibrational spectrum of Fe(TPP)(NO). However, many of the predicted in-plane Fe vibrations have a significant FeNO bending component. Modes associated with hindered rotation of the NO and heme doming are predicted at low frequencies, where Fe motion perpendicular to the heme is identified experimentally at 73 cm−1 and 128 cm−1. Heme doming and ligand reorientation take place during diatomic ligands reactions with porphyrins, and experimental identification of the corresponding vibrational modes is a first step toward quantifying the reactive energetics of Fe porphyrins.
Methods
Porphyrin synthesis
For the NRVS measurements, all compounds were enriched in 57Fe to about 95%. Details of the syntheses are given in the Supporting Information. The identities and purity of the samples were confirmed by a combination of Mössbauer and IR spectroscopy. Because the single crystals of 57Fe(TPP)(NO) were too small to provide adequate signal, a 5×5 array, prepared as described as in the Supporting Information, was used.
Spectroscopic measurements and analysis
NRVS measurements were performed at sector 3-ID-D of the Advanced Photon Source at Argonne National Laboratory. A high-resolution X-ray monochromator121 tuned the energy of the X-ray beam in the vicinity of the 14.4 keV resonance of 57Fe with a resolution of 0.85 meV = 7 cm−1. An APD detector with a 1 cm2 area detected fluorescence emitted by excited 57Fe atoms. Pulses from the APD were recorded by a counter that was enabled after a delay in order to discriminate the fluorescence photons, which arrive with a delay on the order of the 140 ns excited state lifetime, from the large background of electronically scattered 14.4 keV photons, which arrive in coincidence with the X-ray pulse. The background count rate, due to electronic noise and timing errors, is typically 0.03 Hz or less in the presence of a beam with an X-ray flux of 109 Hz.
Polycrystalline powders of Fe(OEP)(Cl) and Fe(TPP)(NO) were loaded into a milled depression on a sapphire block, and covered with a Mylar sheet. The Fe(TPP)(NO) crystal array and other polycrystalline samples were loaded behind a thin X-ray window milled into a polystyrene sample cup. The sample holder was then mounted on the cold finger of a He flow cryostat with X-ray access through either a Mylar window or a beryllium dome.
The resulting spectra as a function of X-ray energy consist of a central resonance, due to the nuclear excited state of 57Fe at E0 = 14.413 keV, and a series of sidebands corresponding to creation or annihilation of one or more vibrational quanta coincident with excitation of the 57Fe nucleus. The vibrational frequency is determined by the energy shift of a one-quantum transition from the recoilless nuclear resonance. A constant background level, estimated on the basis of the observed signal at the high or low (negative) energy extremes, is subtracted from the observed spectrum. Normalization of the spectrum according to Lipkin’s sum rule16,122 then yields an excitation probability with peak areas for each mode representing the mean square amplitude of the Fe. Subtraction of the central resonance yields a vibrational excitation probability
The program PHOENIX123 extracts an Fe-weighted vibrational density of states (VDOS) by removing multiphonon contributions, temperature dependence, and an overall factor proportional to inverse frequency from the vibrational excitation probability . Within the harmonic approximation, the Fourier-log deconvolution procedure employed by PHOENIX is rigorous for a single 57Fe site in an oriented sample or in a randomly oriented sample that is vibrationally isotropic.
Measurements were recorded at low temperatures to minimize multiphonon contributions. The requirement that the ratio equal the Boltzmann factor exp yields the sample temperature. Temperatures determined in this way are more reliable than the readings from a sensor mounted below the sample, which are at least 15 K lower. NRVS measurements on Fe(TPP)(NO) powder were performed at 80 K. Most other polycrystalline porphyrin samples were measured near 30 K. The absorption length is much shorter for the 6.4 keV photons that constitute most of the experimental signal than for the incident 14.4 keV photons, and all measurements were recorded with the X-ray beam at grazing incidence.
To obtain information on the directions of the Fe motion (parallel or perpendicular to the porphyrin plane), NRVS data were also obtained from an oriented array of Fe(TPP)(NO) crystals. For the crystal measurements, the incident wave vector made an angle of 6°to the cell window, with which the porphyrin planes are aligned. Data recorded on an Fe foil at ambient temperature, to confirm the energy calibration of the monochromator, led to a small rescaling of the the energy axis (< 2%) to satisfy the detailed balance condition in the case of the Fe(TPP)(NO) crystal data. The estimated precision of the resulting experimental frequency calibration is 0.3%.
For Raman measurements, Fe(TPP)(NO) was sealed in a 5 mm diameter NMR tube under one atmosphere of NO gas. Raman scattering was excited from the spinning NMR tube using 413 nm output from a krypton laser. Scattered photons were dispersed and detected using a monochromator (LabRamHR, JY Horiba) equipped with a nitrogen-cooled CCD detector and an 2400 groove/mm grating. The frequency calibration was verified using Raman lines of fenchone as a standard.
Computational methods
Density Functional Theory (DFT) is a quantum chemical approach for the calculation of the vibrational modes and the geometry of transition metal complexes.24,29,33,62–66 Here, the method is applied to the following five-coordinate model compounds: ferrous nitrosyl porphine Fe(P)(NO), ferrous nitrosyl tetraphenylporphyrin Fe(TPP)(NO) and ferric nitrosyl tetraphenylporphyrin [Fe(TPP)(NO)]+. All gradient-corrected DFT calculations were performed with Gaussian 98,124 using the 6-31G* basis set for N, O, C and H atoms, and Ahlrich’s VTZ basis set125 for the Fe atom. Calculations on all three molecules employed the Becke-Lee-Yang-Parr composite exchange correlation functional (B3LYP)126,127, which uses the VWN III functional for local and the LYP functional for nonlocal correlation.
In order to provide meaningful vibrational predictions, the molecular geometry is adjusted until the calculated energy reaches a minimum. Diagonalization of the analytically determined Hessian matrix then yields both the frequencies and the relative Cartesian displacements of each atom for each of the 3N –6 vibrational modes of a molecule containing N atoms. The fraction of the kinetic energy of the whole molecule corresponding to the motion of atom j is calculated from these displacements for each mode (Eq. (1)). Unless noted otherwise, reported frequencies and atomic displacements represent output from the Gaussian 98 calculation, without frequency scaling.
The B3LYP calculation on Fe(TPP)(NO) suffered from spin contamination, since the calculated value S (S + 1) = 1.1453 deviates significantly from the ground state observed for ferrous nitrosyl porphyrins.128–130 As a result, the Fe(TPP)(NO) calculation was repeated using the BP86 functional131,132, which yielded S(S + 1) = 0.7502, in agreement with the observed spin. The B3LYP calculation on Fe(P)(NO) yielded S(S + 1) = 0.7516.
Description of normal modes
The mode composition factors which are equal to the fraction of the kinetic energy in mode α due to the motion of atom j, provide a convenient quantitative comparison between measurements and calculations.28 In general, the set of vectors describe the linear transformation from the mass-weighted Cartesian displacements of the individual atoms to the normal coordinates Qαof the system. The kinetic energy distribution given by the mode composition factors provides a straightforward description of normal mode character, because the Cartesian atomic displacements form an orthogonal basis, that is, . This contrasts with the nonorthogonal basis frequently used to describe the potential energy distribution among the degrees of freedom in an empirical potential function, which will depend on the functional form chosen for the potential.
A normal mode calculation describes vibrational eigenvectors using a set of atomic displacements which directly determine the mode composition factors
| (1) |
For comparison with measurements on oriented samples, it is convenient to project out the kinetic energy fraction
| (2) |
due to motion of atom j along a direction .
Spectral areas in the NRVS data are conveniently interpreted in terms of the mode composition factor , with j = Fe.28 In the low temperature limit, a fundamental transition nα → nα+ 1 contributes an area
| (3) |
to the normalized excitation probability Here, meV is the recoil energy of a free 57Fe nucleus upon absorption of a photon of energy Eγ = 14.4 keV, is the thermal occupation factor for a mode of frequency at temperature T, and the recoilless fraction
The partial vibrational density of states (VDOS)
| (4) |
for atom j determined from measurements on a perfectly oriented sample takes the form of a series of bands with areas28,133 equal to the squared projection of along the beam direction Contributions to the finite width of the normalized line shape function include the 7 cm−1 experimental resolution, vibrational lifetime broadening, and dispersion in the molecular crystal. Calculated VDOS are orientationally averaged for comparison with experimental results. Measurements on oriented Fe(TPP)(NO) crystals are averaged over the crystallographically imposed fourfold orientational disorder present in the tetragonal crystals. If the X-ray beam makes an angle θ with a 3-fold or higher axis of rotational symmetry parallel to the unit vector , averaging of Eq. 4 over molecular orientations yields
| (5) |
where
| (6) |
is the partial VDOS along the symmetry axis (perpendicular to the porphyrin plane for Fe(TPP)(NO)) and
| (7) |
is the partial VDOS perpendicular to the axis (parallel to the porphyrin plane).
Measurements on polycrystalline powders, or other randomly oriented samples, are compared to the total VDOS
| (8) |
In terms of the partial VDOS defined in Eqs. 6 and 7, Notice that the normalization of the total vibrational density of states, , differs from the normalization of the partial VDOS along direction .
Results
Fig. 2 presents NRVS data recorded on a series of porphyrins. Each spectrum results from an average over multiple energy scans, followed by subtraction of a constant background and normalization according to Lipkin’s sum rule16,122 to provide the excitation probability NRVS data were recorded near T = 30 K for most polycrystalline compounds and for the oriented Fe(TPP)(NO) crystal array. Measurements were performed at 80 K and 67 K for polycrystalline powders of Fe(TPP)(NO) and Fe(MPIXDME)(NO). In each case, comparison of initial and final scans revealed no differences, confirming the absence of measurable radiation damage.
Figure 2.
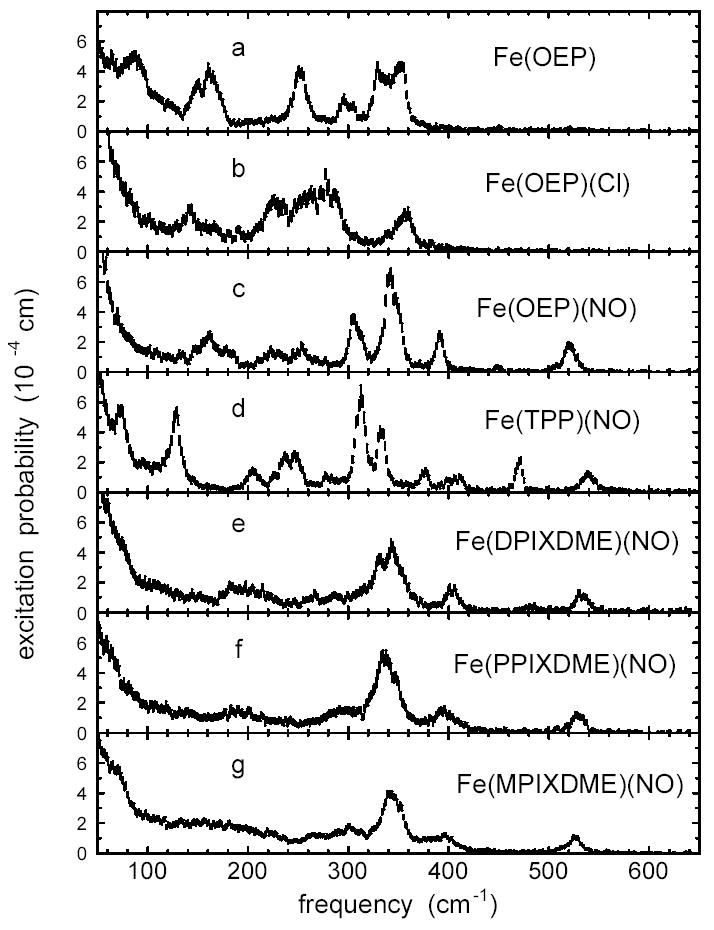
Measured 57Fe excitation probabilities for a series of iron porphyrins. All nitro-syl complexes have an Fe-NO stretch/bend mode in the 520 – 540 cm−1 region. Comparison among the nitrosyl complexes (c-g) reveals that peripheral groups strongly influence the vibrational frequencies and amplitudes of the central Fe. Sample temperatures were 34 K for Fe(OEP), 30 K for Fe(OEP)(NO), 80 K for Fe(TPP)(NO), 35 K for Fe(DPIXDME)(NO), 34 K for Fe(PPIXDME)(NO), and 64 K for Fe(MPIXDME)(NO). The Fe(OEP)(Cl) spectrum is an average over multiple scans with an estimated average temperature of 87 K. Error bars reflect Poisson statistics.
We have previously reported both the measured excitation probability for polycrystalline Fe(TPP)(NO)28 and total Fe VDOS derived from the measured NRVS signal for both the polycrystalline sample and the oriented array of Fe(TPP)(NO) crystals.37 The compounds shown in Fig. 2 share the basic Fe porphyrin core (Fig. 1), but differ in the axial ligand (NO, Cl−, or no axial ligand), Fe oxidation state, and peripheral substituents on the porphyrin. Clearly, these factors lead to significant variations in mode structure, but inspection of Fig. 2 reveals some common features and allows tentative identification of some modes.
In particular, all five ferrous nitrosyl porphyrins (Fig. 2 c-g) have an Fe mode in the 520-540 cm−1 range. In contrast, neither the 4-coordinate reduced complex Fe(OEP), nor the 5-coordinate ferric complex Fe(OEP)(Cl) show features above 400 cm−1. This suggests a significant motion of the FeNO fragment for modes observed at 521 cm−1 in Fe(OEP)(NO), 533 cm−1 in Fe(DPIXDME)(NO), 526 cm−1 in Fe(MPIXDME)(NO), and 528 cm−1 in Fe(PPIXDME)(NO), consistent with our previous identification of the mode at 539 cm−1 in Fe(TPP)(NO)28,37 with Fe-NO stretching. On the other hand, the mode composition factors determined from the spectral areas ( = 0.33 for Fe(OEP)(NO), = 0.27 for Fe(DPIXDME)(NO), = 0.24 for Fe(MPIXDME)(NO), = 0.23 for Fe(PPIXDME)(NO), and = 0.30 for Fe(TPP)(NO)) vary significantly, with the extreme of the range approaching the value = 0.34 expected for a two-body 57Fe-NO oscillator. The value reported here for Fe(TPP)(NO), based on fitting a Voigt function to the 540 cm peak, is slightly lower than the value we previously reported based on a Lorentzian fit to the same data.28
Raman investigations of ferrous nitrosyl porphyrins in solution have assigned Fe-NO frequencies in the range 514 cm−1 to 530 cm−1.134–137 In particular, the Fe-NO stretching frequency is identified at 527 cm−1 for Fe(PPIX)(NO) encapsulated in cholate micelles in aqueous solution137 and ranges from 524 cm−1 to 527 cm−1 for Fe(TPP)(NO) in various solvents.134,136 Fe-NO frequencies were also reported at 527 cm−1 for both Fe(TPP)(NO) and Fe(OEP)(NO) in pyridine,135 although these were originally believed to be six-coordinate complexes with pyridine binding trans to NO. These observations essentially support our Fe-NO assignment, but reported Fe-NO frequencies in solution at room temperature differ by up to 13 cm−1 from the frequencies we measure in the solid state at low temperatures.
In an attempt to clarify this difference, we recorded Raman spectra on Fe(TPP)(NO) powders (Fig. 3). To minimize possible photochemical artifacts, the sample was sealed in a rapidly spinning NMR tube. With sufficiently restricted laser intensity, a band is apparent at 547 cm−1. Increasing the laser power by a factor of 100 resulted in reduction of the relative intensity of this band (Fig. 3), accompanied by a shift of the high frequency ν4 marker band (not shown) from 1369 cm−1 to 1361 cm−1, suggestive of NO photolysis. The difference between this 547 cm−1 Raman frequency and the 540 cm−1 frequency we observe in the NRVS spectra of the low temperature powder is larger than the experimental uncertainty, but may be partly attributed to the the 1.4 cm−1 57Fe/56Fe frequency shift expected28 between the 57Fe-enriched NRVS and natural isotopic abundance Raman samples for a mode with =0.30.
Figure 3.
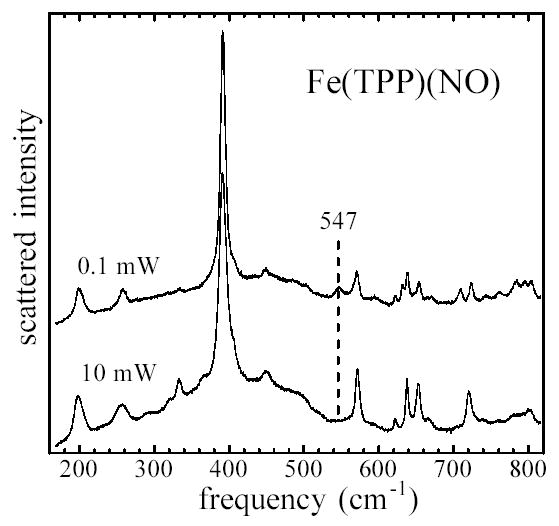
Raman spectra of Fe(TPP)(NO) powders, showing elimination of 547 cm−1 peak with increasing laser flux. Scattering from powder in a spinning NMR tube was excited at 413.1 nm, using laser powers of 0.1 mW and 10 mW.
Additional observations suggest that Raman measurements on this compound must be interpreted with caution. Both low temperature FTIR measurements138 and DFT calculations139 provide evidence for metastable linkage isomers of Fe(TPP)(NO), and recovery of the low power Raman spectra following reduction of the laser power required several minutes. As a result, it is difficult to exclude the possibility of laser-induced photochemistry, even at the lowest laser intensity used here. Moreover, some identically prepared samples showed a peak at the 527 cm−1 frequency reported for Fe(TPP)(NO) in solution at room temperature,134–136 in addition to the 547 cm−1 frequency shown in Fig. 3. We cannot fully resolve the experimental situation at the present time, but plan further Raman measurements to characterize the potentially rich photochemistry of this molecule,138,139 following acquisition of a beam-scanning device that will allow further reductions in the average laser intensity at the sample.
The data in Fig. 2 also raise questions about a previous tentative identification of the 470 cm−1 mode in Fe(TPP)(NO) with FeNO bending,37 since the other four nitrosyl porphyrins in Fig. 2 reveal no mode with comparable amplitude near this frequency.
Another feature common to the ferrous complexes in Fig. 2 is the dominant contributions from modes in the 300–400 cm−1 range. For Fe(TPP)(NO), we previously associated these modes with stretching of the four in-plane Fe-Npyr bonds.28,37 For the ferric complex Fe(OEP)(Cl), IR measurements led to assignment of the stretching of the Fe-Npyr bonds to a mode observed140 at 275 cm−1, coincident with a cluster of modes observed in the NRVS signal (Fig. 2b). These results suggest that the strength of the in-plane Fe-Npyr bonds is quite sensitive to the oxidation state of the Fe.
Note that previous infrared140 and Raman141 investigations identified the Fe-Cl stretching mode of Fe(OEP)(Cl) at 357 cm−1 and 364 cm−1, respectively. This corresponds with a peak at 356 cm−1 in the NRVS signal having = 0.54, comparable to the value = 0.62 expected for a two-body Fe-Cl oscillator.
The upper panel of Fig. 4 compares the experimentally determined vibrational density of states for the oriented array of Fe(TPP)(NO) crystals with that for Fe(TPP)(NO) powder. The crystal data is recorded with the incident X-ray beam 6° above the mean porphyrin plane, and the partial VDOS (Eq. 5) determined from this data is scaled up by a factor three for comparison with the total VDOS determined from powder measurements (Eq. 8). Since the NRVS measurement is only sensitive to Fe motion along the probe direction, the spectral contribution of modes with predominantly in-plane Fe motion are enhanced and the contribution of out-of-plane modes suppressed in the oriented crystal data.
Figure 4.
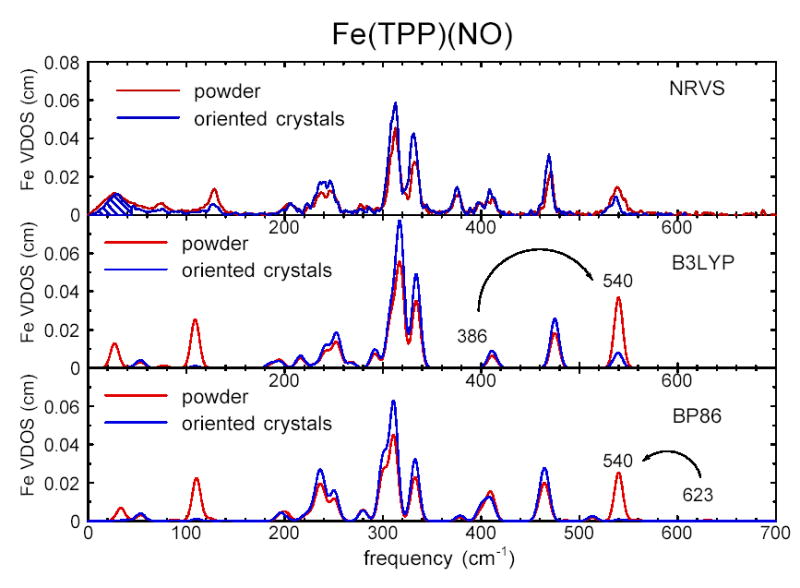
Comparison of the experimental VDOS determined from NRVS measurements on Fe (TPP)(NO) (upper panel) with the VDOS predicted on the basis of DFT calculations using B3LYP (center panel) and BP86 (lower panel) functionals. Black traces represent the partial VDOS 3 for oriented crystals, scaled by a factor 3 for comparison with the total VDOS of unoriented polycrystalline powder (red traces). Since the X-ray beam direction lies 6° from the porphyrin plane, modes involving Fe motion in the plane of the porphyrin are enhanced, and modes with Fe motion primarily normal to the plane are suppressed, in the scaled oriented crystal VDOS relative to the powder VDOS. Cross-hatching in the upper panel indicates the area attributable to acoustic modes. In the lower two panels, the Fe-NO stretch/bend modes, predicted at 386 cm−1 and 623 cm−1, have been artificially shifted to the observed 539 cm−1 frequency to facilitate comparison with the experimental results. Predicted VDOS are convolved with a 10 cm−1 Gaussian.
The comparison of crystal and powder results in Fig. 4 identifies three modes at 74 cm−1, 128 cm−1, and 540 cm−1 with Fe motion perpendicular to the porphyrin plane. In contrast, Fe motion parallel to the porphyrin plane makes the dominant contribution to modes in the 200 cm−1-500 cm−1 range. These observations are consistent with the assignment of the 540 cm−1 mode to the out-of-plane Fe-NO stretch (because its relative amplitude is reduced in the “in-plane” crystal spectrum), as well as the identification of the dominant features in the 300–400 cm−1 range with stretching of the in-plane Fe-Npyr bonds (because their amplitudes are enhanced in the crystal spectrum).
In addition to intramolecular vibrations, translation of the entire molecule contributes to the observed NRVS signal.28 In polycrystalline samples, acoustic modes will contribute to the low frequency experimental VDOS. It is straightforward to identify the fraction of the total VDOS that must be attributed to acoustic modes. For example, numerical integration of the experimental VDOS of oriented Fe(TPP)(NO) crystals from zero to 62 cm−1 yields the area expected for translation of the entire molecule.28 The corresponding area of the oriented crystal VDOS is marked for reference in the upper panel of Fig. 4. Acoustic modes are undoubtedly distributed over a somewhat wider frequency range, but the indicated magnitude of the spectral area is independent of a specific model for these modes. As a result, we expect acoustic modes to dominate the experimental spectrum below 70 cm−1.
Although the removal of multi-phonon contributions by PHOENIX is only approximate for randomly oriented molecules, the following observations suggest that no significant systematic errors are introduced for well-resolved intramolecular vibrations of the polycrystalline samples considered here. First, values determined from the area of features in the density of states agree with those previously determined from direct analysis of the measured excitation probability.28 Second, two- and three-phonon contributions to the measured excitation probability, as determined by PHOENIX (Fig. 5), constitute less than 10% of the total integrated vibrational excitation probability.
Figure 5.
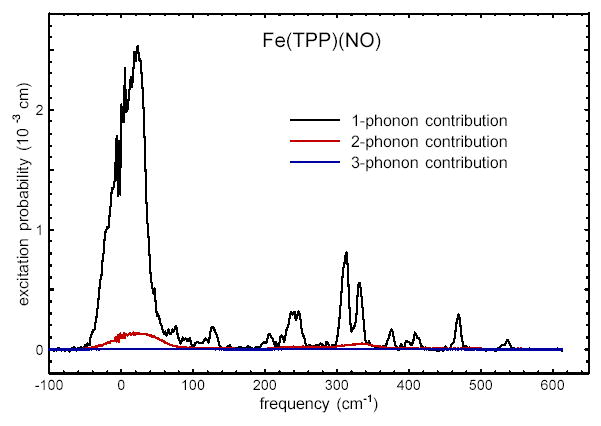
One-, two-, and three-phonon contributions to the vibrational excitation probability for oriented crystals of Fe(TPP)(NO). At the 32 K temperature of the measurements, multiphonon contributions constitute less than 10% of the total integrated vibrational excitation probability.
Fig. 5 indicates that multi-phonon contributions are no longer negligible below 70 cm−1, where acoustic phonons dominate the NRVS signal. However, the calculations presented below are performed on a single molecule, and thus yield no predictions about the latter vibrations. Thus, we expect the density of states formulation to be an effective basis of comparison between measured and calculated vibrational dynamics.
In order to obtain further insight into the vibrational dynamics of these molecules, we compare the experimental results with DFT normal mode calculations for Fe(TPP)(NO). The complete set of information on frequencies, amplitudes, and directions of Fe modes available from NRVS measurements provides a critical test of the normal mode picture provided by the calculations. It is clear from the experimental data in Fig. 2c-g that groups on the periphery of the porphyrin affect the vibrational dynamics of the Fe. The calculation was thus performed on the full Fe(TPP)(NO) molecule rather than a truncated model system, in order to evaluate the capabilities of DFT on such a large molecule and to provide the most meaningful description of the normal modes of the actual molecule. Additional calculations on [Fe(TPP)(NO)]+ and Fe(P)(NO) provide insight into the influence of Fe electronic state, FeNO geometry, and peripheral substituents on the vibrational dynamics of the Fe.
Table 1 lists selected features of the calculated equilibrium geometry of Fe(TPP)(NO), [Fe(TPP)(NO)]+, and Fe(P)(NO), together with values determined from crystal structures. In general, the predicted geometries agree well with reported X-ray structures. In particular, the DFT calculation reproduces the inequivalent Fe-Npyr bond lengths observed in recent structural determinations.142 The Fe-Npyr inequivalence was also reproduced in previous DFT calculations.138,143 An independent calculation on Fe(P)(NO)52 yielded a similar optimized geometry. The Fe(TPP)(NO) calculation using the B3LYP functional overestimates the Fe-NO bond length by almost 10 pm. As a result, the Fe(TPP)(NO) structure was reoptimized using the BP86 functional, which leads to a 170 pm Fe-N bond length and other structural features in good agreement with observations (Table 1). For Fe(P)(NO), the calculated 172 pm Fe-N bond length agrees well with values observed for other ferrous nitrosyl porphyrins.
Table 1.
Selected structural parameters for iron nitrosyl porphyrins
| structural parameter | Fe-Npyra | Fe-NOa | N-Oa | ∠FeNO | |
|---|---|---|---|---|---|
| Fe(TPP)(NO)b | 200c | 172 | 112 | 149° | |
| measured | Fe(OEP)(NO)d | 199–202e | 172 | 117 | 144° |
| Fe(DPIXDME)(NO)f | 199–204e | 172 | 119 | 143° | |
| [Fe(OEP)(NO)]+g | 199 | 164 | 111 | 177° | |
| Fe(TPP)(NO) | 201–203e | 181 | 118 | 139° | |
| calculatedh | Fe(TPP)(NO) (BP86) | 199–203e | 170 | 119 | 143° |
| Fe(P)(NO) | 201–203e | 172 | 120 | 142° | |
| [Fe(TPP)(NO)]+ | 199–200e | 161 | 115 | 180° |
Bond length in pm.
Ref.144
Average bond length. NO disorder among eight equivalent orientations prevents observation of Fe-Npyr bond length inequivalences.
Monoclinic form, ref.142
Range of inequivalent bond lengths.
Ref.145
Solvated form of [Fe(OEP)(NO)]ClO4, ref.146
With the exception of the BP86 calculation on Fe(TPP)(NO), all calculations used the B3LYP exchange functional.
All 231 predicted normal modes of Fe(TPP)(NO) yield real frequencies, ranging from 1 cm−1 to 3296 cm−1 in the B3LYP calculation, and from 8 cm−1 to 3210 cm−1 in the BP86 calculation. Only a fraction of these modes contribute substantially to the predicted NRVS signal. In both Fe(TPP)(NO) calculations, modes above 800 cm−1 contribute , indicating that the experimental frequency range (Fig. 2) is large enough to offer a comprehensive picture of the Fe vibrational dynamics. Fig. 6 shows a cumulative sum of as a function of mode number, ranked in order of , and shows that 24 modes contribute 97% of the total area of the B3LYP-predicted density of states for Fe(TPP)(NO). The predicted frequencies of these modes range from 27 cm−1 to 476 cm−1. (In the BP86 prediction, 27 modes, with frequencies ranging from 33 cm−1 to 623 cm−1, contribute 97% of the total area.) A minority of the predicted modes also dominate the Fe vibrational dynamics of [Fe(TPP)(NO)]+ and Fe(P)(NO).
Figure 6.
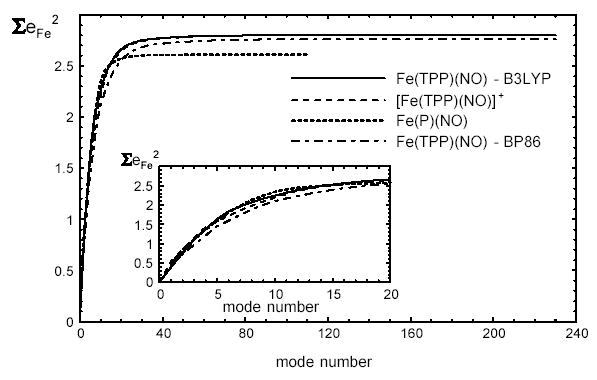
Cumulative contribution of vibrational modes to the Fe VDOS predicted on the basis of B3LYP calculations on Fe(TPP)(NO), [Fe(TPP)(NO)]+, and Fe(P)(NO), and a BP86 calculation on Fe(TPP)(NO). Modes are ranked in decreasing order of The inset shows an expanded view for the first 20 modes. For Fe(TPP)(NO), 23 modes contribute 97% of the area of the total B3LYP-predicted VDOS.
Fig. 7 compares the vibrational densities of states predicted by the B3LYP and BP86 calculations with the experimental density of states for Fe(TPP)(NO) powder. The density of states resulting from a calculation on the isolated molecule is a series of delta functions with areas equal to , and translational motions, with an area corresponding to the intermolecular modes in the experimental spectrum, occur at zero frequency and are not shown. All frequencies are unscaled output from the Gaussian 98 calculation. The most significant difference among the three densities of states is the frequency of the Fe-NO stretch. The 386 cm−1 Fe-NO stretching frequency predicted by the B3LYP calculation is smaller than the measured 540 cm−1 frequency assigned to Fe-NO stretching above, possibly reflecting the excessive length predicted for the Fe-NO bond using this functional. On the other hand, the 623 cm−1 frequency resulting from the BP86 calculation overestimates the observed frequency, and the Fe-N bond length is slightly shorter than the observed value. Both predicted N-O stretching frequencies are larger than the observed144 1670 cm−1 value.
To facilitate comparison with the experimental VDOS, the lower two panels of Fig. 4 display the predicted VDOS after artificially shifting the Fe-NO stretching modes to 540 cm−1 and convolution with a Gaussian lineshape function. Predictions are shown for both powder and oriented crystals, with in-plane modes making an increased, and out-of-plane modes a decreased, contribution to the oriented crystal VDOS. Note that both experimental and computational approaches directly provide vibrational amplitudes that can be compared on the same absolute scale. We avoid the potentially misleading use of arbitrary scale factors. With the exception of the Fe-NO stretch, predicted frequencies differ by less than 15 cm−1 between the B3LYP and BP86 calculations for modes involving significant Fe motion ( > 0.02). Again excepting Fe-NO, both DFT predictions exhibit good agreement with the measured frequencies, amplitudes and directions of modes having a significant Fe contribution.
Figs. 8 and 9 compare the vibrational predictions resulting from all three B3LYP calculations. Fig. 8 displays the in-plane and out-of-plane contributions to the 57Fe VDOS, and defined in Eqs. 7 and 6. The total VDOS, , was shown in Fig. 4 for the Fe(TPP)(NO) calculation. Fig. 9 focusses on the central FeNO fragment and displays the kinetic energy distribution among the three atoms, as given by , and . In contrast with the calculated spectra shown in Figs. 4 and 8, the results in Fig. 9 are displayed as stick spectra, revealing some structure that would not be apparent at the experimental resolution. The Supporting Information tabulates and values for all predicted modes with more than 10% of the mode energy associated with the FeNO fragment.
Figure 8.
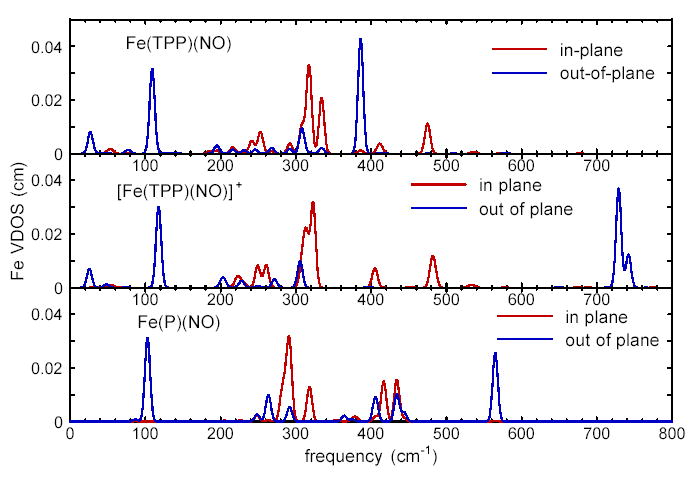
Predicted in-plane and out-of-plane contributions to the total Fe VDOS for Fe(TPP)(NO), [Fe(TPP)(NO)]+, and Fe(P)(NO), predicted on the basis of B3LYP calculations. The partial densities of states perpendicular to the porphyrin plane and parallel to the porphyrin plane contribute to the total VDOS Gaussian line shape functions with 8 cm−1 FWHM are used in Eqs. 7 and 6 to approximate the resolution of the experimental data.
Figure 9.
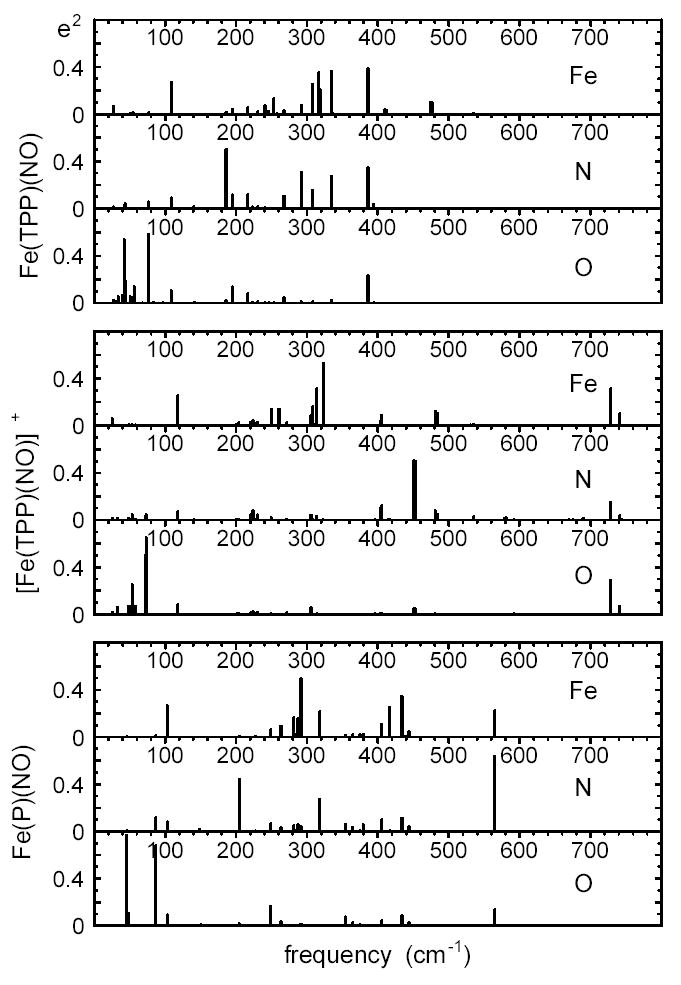
Comparison of vibrational dynamics of Fe and the nitrosyl N and O atoms for Fe(TPP)(NO), [Fe(TPP)(NO)]+, and Fe(P)(NO), predicted on the basis of B3LYP calculations. The heights of the individual bars indicate the fraction of mode energy associated with each of these three atoms. These stick spectra reveal fine structure that is not apparent after convolution with a lineshape function, as in Fig. 7.
Discussion
DFT has been applied to vibrational analysis of molecules of increasing size, but the 361 electrons in Fe(TPP)(NO) approach the current practical limit. Although calculations on a truncated porphyrin can provide qualitative insights into its vibrational properties,67,68,71,73,136,147—151 experimental results (Fig. 2c–g) and calculations (Fig. 8) presented here indicate that peripheral substituents significantly influence the vibrational dynamics of the Fe. These results suggest that calculations on the complete Fe(TPP)(NO) molecule are needed for quantitative comparison with the complete set of Fe vibrational frequencies, amplitudes, and directions provided by NRVS measurements.
The optimized structures of Fe(TPP)(NO) and Fe(P)(NO) resulting from the DFT calculations reproduce other features of the observed Fe coordination (Fig. 1, Table 1). In particular, the predicted FeNO angle is within the range typically observed for ferrous nitrosyl porphyrins.142,144,145,152,153 The calculated structures also reproduce small measured variations among the in-plane Fe-Npyr bond lengths,142,152,153 as reported for previous calculations.52,138,143 With the exception of the B3LYP calculation on Fe(TPP)(NO), the predicted Fe-NO distances also agree well with observations. Geometrical differences between the optimized structures of Fe(TPP)(NO) and [Fe(TPP)(NO)]+ resemble observed changes in iron nitrosyl porphyrin structure with oxidation state (Table 1). The Fe-NO bond length is shorter and the FeNO unit is nearly linear for [Fe(TPP)(NO)]+, consistent with observed structures of ferric nitrosyl porphyrins.146,153
Since the calculations are performed on isolated molecules, they do not include intermolecular interactions and precise prediction of the observed vibrational frequencies is not expected. Nevertheless, the gas-phase calculations reproduce the pattern of vibrational amplitudes (on an absolute scale) and the qualitative directions of Fe motion determined from measurements on oriented crystals (Fig. 4). Except for the Fe-NO frequency, differences between the B3LYP and BP86 predictions appear to be minimal. Successful DFT prediction of this detailed set of experimental information engenders confidence that the calculations capture the character of vibrational modes with a strong Fe component.
In this section, we emphasize a detailed discussion of the normal modes of Fe(TPP)(NO) predicted by the B3LYP calculation, in comparison with NRVS observations. Qualitative descriptions of Fe(TPP)(NO) modes predicted by the B3LYP calculation apply equally to corresponding modes in the BP86 calculation, except where specifically indicated otherwise. Calculations on the related molecules [Fe(TPP)(NO)]+ and Fe(P)(NO) provide further insight into the nature of these vibrations, and the influence of oxidation state and peripheral substituents.
In-plane Fe-Npyr modes
Comparison of NRVS measurements on Fe(TPP)(NO) powder with oriented crystals shows that Fe motion in the porphyrin plane dominates the 200–500 cm−1 region of the experimental spectrum (Fig. 4), and several of the predicted modes of Fe(TPP)(NO) involve motion of Fe within the plane defined by the coordinating pyrrole nitrogen (Npyr) atoms (Figs. 10, 11). For a four-fold symmetric Fe coordination environment, such in-plane Fe modes will occur as degenerate pairs with equal values. The direction of Fe motion in one mode of the pair will be orthogonal to Fe motion in the other. A DFT calculation on the D4h-symmetric four-coordinate Fe(P) revealed two degenerate mode pairs of eu symmetry involving stretching of the Fe-pyrrole (Fe-Npyr) bonds.69 These modes were classified as ν50 and ν53, according to the traditional porphyrin mode numbering scheme developed for Ni(OEP).154
Figure 10.
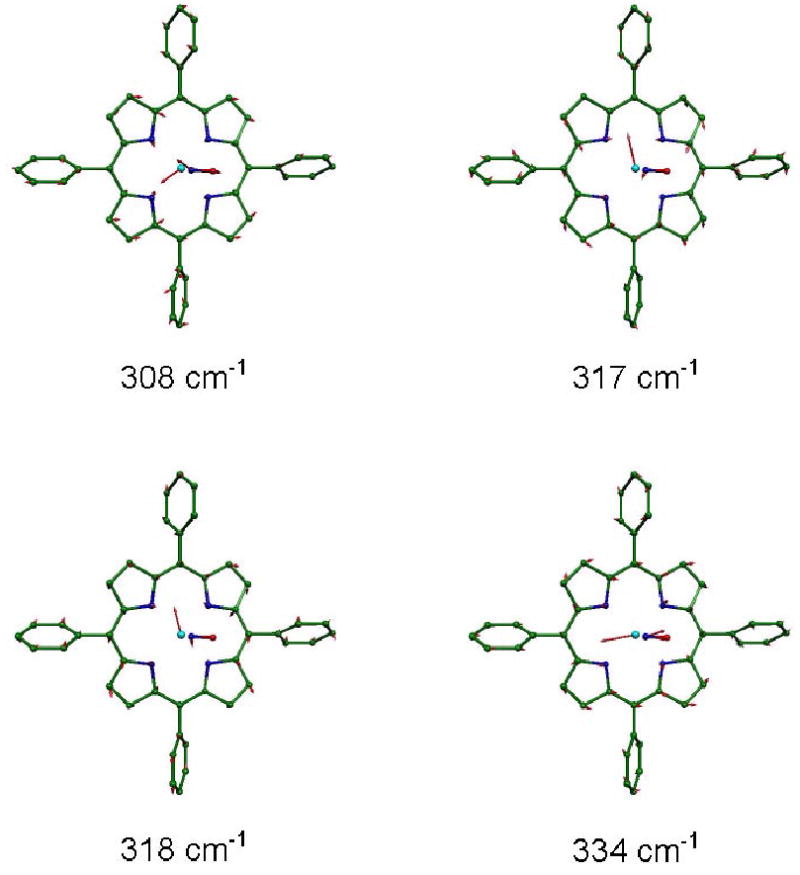
Four in-plane Fe modes, predicted on the basis of B3LYP calculations, contributing to the pair of experimental features at 312 cm−1 and 333 cm−1 in the Fe(TPP)(NO). Arrows represent the mass-weighted displacements of the individual atoms. For ease of visualization, each arrow is 100(mj/mFe)1/2 times longer than the zero point vibrational amplitude of atom j. Color scheme: cyan–iron, green–carbon, blue–nitrogen, red–oxygen. In this and other figures, hydrogens are omitted for clarity.
Figure 11.
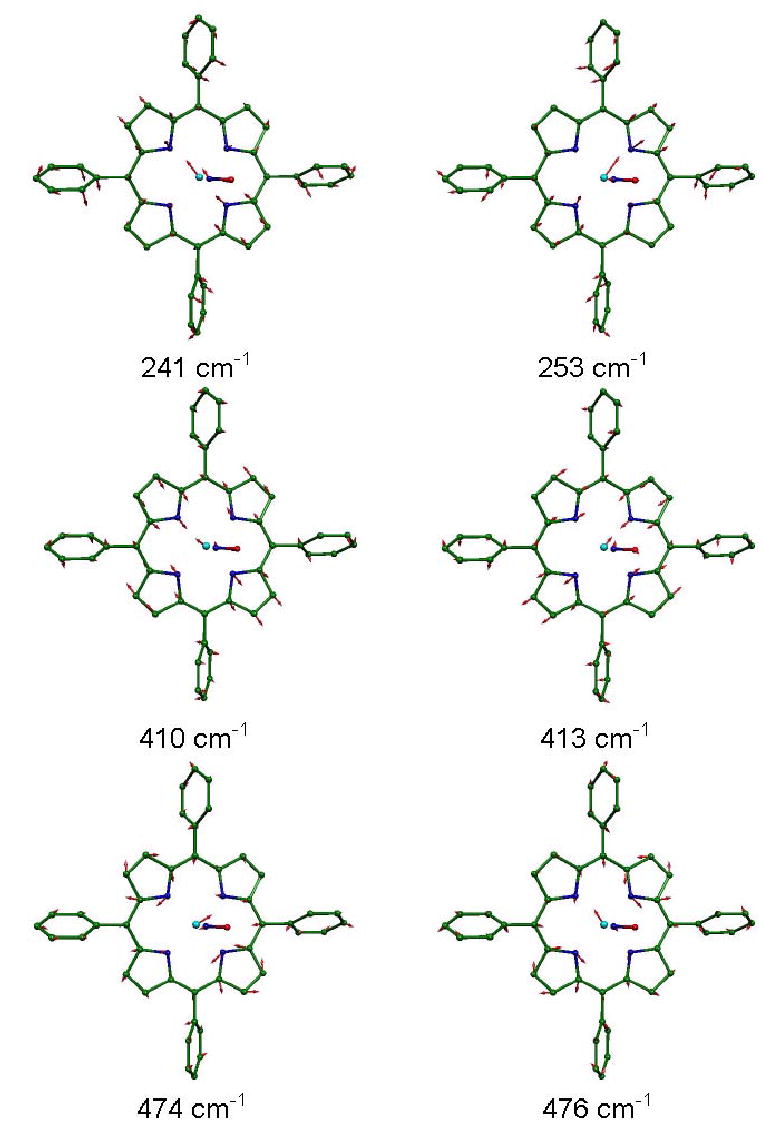
Other modes with significant in-plane Fe motion, resulting from B3LYP calculations on Fe(TPP)(NO). Arrows representing mass-weighted atomic displacements are 100(mj/mFe)1/2 times longer than the zero point vibrational amplitudes. Color scheme as in Fig. 10.
Binding of a fifth ligand that breaks the fourfold symmetry of the Fe environment will lift the degeneracy of the in-plane mode pairs, although the amplitudes are expected to remain nearly equal. The Fe-Npyr stretching modes in the NRVS signal from photolyzed carbonmonoxymyoglobin, for example, conform to this expectation.27 The x-y splitting of the in-plane modes was also observed in a DFT calculation on the simplified model Fe(P)(Im) for the deoxymyoglobin active site.71 We previously attributed the dominant experimental features at 312 cm−1 and 333 cm−1 in Fe(TPP)(NO) to stretching of the Fe-pyrrole (Fe-Npyr) bonds, and suggested that mixing with the FeNO bend contributed to the observed splitting and asymmetric amplitude.28,37
A complex situation occurs in this region of the spectrum predicted from the B3LYP calculation, where two pairs of modes, at 308/318 cm−1 and 317/334 cm−1, contribute (Fig. 10). Note that the 317/334 cm−1 mode pair have nearly equal Fe amplitudes, as do the 308/318 cm−1 pair (Fig. 9). However, the three modes at 308, 317, and 318 cm−1 cannot be resolved at the experimental resolution, and appear as a single feature with a substantially larger area than the resolved mode at 334 cm−1 (Fig. 4, middle panel). This strikingly reproduces the asymmetry between the two features that dominate this region of the experimental VDOS (Fig. 4, top panel).
The B3LYP-predicted 317 cm−1 and 318 cm−1 modes involve Fe motion in the porphyrin plane, but approximately perpendicular to the FeNO plane. The Fe amplitude in the former mode is greater by more than 30%. The predicted Fe motion in the 308 cm−1 and 334 cm−1 modes is approximately parallel to the FeNO plane. Unlike the 317 cm−1 and 318 cm−1 modes, the 308 cm−1 and 334 cm−1 modes have a small component of Fe motion perpendicular to the porphyrin plane. This out-of-plane component is oppositely directed for the two modes, and accounts for less than 25% of the Fe kinetic energy. Examination of the predicted modes (Fig. 10) and the kinetic energy distribution (Fig. 9, also see Supporting Information) reveals significant involvement of the ligand N. Vibrational mixing with FeNO bending and Fe-NO stretching apparently contributes to the predicted frequency splitting and out-of-plane Fe motion for the 308 cm−1 and 334 cm−1 frequencies.
The BP86 calculation also predicts four Fe modes in this frequency region, at 300 cm−1, 304 cm−1, 311 cm−1, and 333 cm−1. As in the B3LYP prediction, the highest and lowest frequency modes of this cluster involve significant motion of the NO ligand, while there is little NO involvement in the 304 cm−1 and 311 cm−1 modes. The detailed mode characters differ somewhat, with the N motion is nearly perpendicular to the FeNO plane for the BP86-predicted 304 cm−1 and 311 cm−1 modes, and the Fe motion also having a significant component perpendicular to this plane. However, the influence of these differences in mode character on the predicted VDOS is limited to a modest increase in the frequency separation among the three lowest frequency modes (Fig. 4, bottom panel).
Other in-plane Fe modes predicted from the B3LYP calculation (Fig. 11) appear as isolated pairs of nearly degenerate modes, as expected. In the one case where the predicted splitting is larger than the experimental resolution, the predicted x-y splitting (241/253 cm−1) agrees well with what is observed (236/248 cm−1).28 For two other pairs, at 410/413 cm−1 and at 474/476 cm−1, the predicted splittings are smaller than the experimental resolution. The reduced Fe amplitudes (compared to the 308–334 cm−1 cluster) reflect a larger energy fraction due to motions of the porphyrin, which are characteristic for each mode. For the predicted 241/253 cm−1 mode pair, two pyrrole rings translate with the Fe so as to minimize stretching of the Fe-Npyr bonds along the direction that the Fe moves. This contrasts with the predicted 410/413 cm−1 mode pair, where the relative phase of Fe and pyrrole translation reverses, maximizing stretching of the Fe-Npyr bonds along the direction that the Fe moves. In the BP86 prediction, two overlapping pairs of modes appear at 400/406 cm−1 and 401/403 cm−1. For both pairs, the relative Fe-pyrrole motion resembles that of B3LYP-predicted 410/413 cm−1 mode pair, but the 401/403 cm−1 pair also involves significant internal distortion of the porphyrin and phenyl, with a consequently reduced Fe amplitude. A mode pair at 236/251 cm−1 in the BP86 prediction strongly resembles the B3LYP mode pair at 241/253 cm−1.
Fe motion accounts for approximately 10% of the total mode energy for the B3LYP-predicted mode pair at 474/476 cm−1, where rotation of two pyrrole groups about the porphyrin normal stretches the Fe-Npyr bonds orthogonal to the direction of the Fe motion. These modes resemble the ν50 mode pair predicted for the four-coordinate complex Fe(P).69 In contrast to the results of a normal mode calculation using an empirical force field,37 the predicted 474 cm−1 and 476 cm−1 modes have no significant contribution from FeNO bending. The BP86 calculation predicts a mode pair with similar character at 461/466 cm−1.
Each of the in-plane Fe mode pairs predicted for Fe(TPP)(NO) corresponds closely, in average frequency, frequency splitting, and amplitude, to an experimentally observed in-plane feature (Fig. 4), and it is likely that Figs. 10 and 11 represent reliable descriptions of the character of the modes responsible for the corresponding experimental features. However, both experimental and computational results indicate that alteration of the specific constellation of peripheral substituents on the porphyrin leads to significant variations in the in-plane Fe vibrations. For example, other ferrous nitrosyl porphyrins lack a feature corresponding in both frequency and amplitude to the band observed at 470 cm−1 for Fe(TPP)(NO) (Fig. 2). Similarly, the nearly degenerate ν50 mode pair predicted at 474/476 cm−1 for Fe(TPP)(NO) using B3LYP no longer appears after removal of the phenyl substituents to form Fe(P)(NO). Rather, a cluster of four predicted modes at 406, 417, 434, and 444 cm−1 (Figs. 8 and 9) has mixed ν50 and FeNO bending character for Fe(P)(NO). Further investigation will be required to establish the detailed character of Fe modes in the 200–500 cm−1 region of ferrous iron nitrosyls other than Fe(TPP)(NO).
Fe-ligand modes
The function of many heme proteins revolves around their interactions with diatomic ligands such as NO, O2, and CO.7,85–87,92 As a result, vibrations of the Fe-diatomic unit have been heavily investigated.11,12,155–158 Analysis of infrared and Raman data has focussed on vibrational frequencies and, until recently,136,151 has typically relied on simplified three-body models.137,156,157,159 A three-body analysis describes FeNO motion in terms of three degrees of freedom, stretching of the Fe-N and N-O bonds and bending of the FeNO angle, and predicts three vibrational modes. Because of the high order of the N-O bond, one of the modes is a nearly pure N-O stretch, while the two remaining modes can be classified in terms of their dominant character as Fe-NO stretching and FeNO bending. Here, we outline a richer picture of the Fe-ligand vibrations, using experimental information on vibrational amplitudes from NRVS data and DFT normal mode characterization of the entire molecule.
We originally attributed the mode observed at 540 cm−1 in NRVS data on solid Fe(TPP)(NO) at 80K to Fe-NO stretching,28 close to the reported 524 cm−1 Fe-NO stretching frequency in the room temperature Raman spectrum of Fe(TPP)(NO) in benzene.136 The value = 0.30 determined from the NRVS data is close to the value = (mN + mO) / (mFe + mN + mO) = 0.34 expected for a two body Fe-NO oscillator, and an 8 cm−1 frequency shift of the corresponding Raman band reported136 upon isotopic substitution with 15NO is also qualitatively consistent with Fe-NO stretching. A previous normal mode analysis of Fe(TPP)(NO) based on an empirical force field reproduced the Fe-NO mode at 540 cm−1 and also predicted the 470 cm−1 mode to involve bending of the FeNO fragment.37
Experimental results presented here suggest a more complex interpretation. No mode with amplitude comparable to the 470 cm−1 mode seen in the Fe(TPP)(NO) NRVS signal is observed in the same frequency region for the other nitrosyl porphyrins examined, raising questions about the proposed FeNO bending assignment.37 On the other hand, the appearance of a mode in the 520–540 cm−1 region in the 57Fe NRVS signal of all ferrous nitrosyl porphyrins measured (Fig. 2), and its absence in Fe(OEP) and Fe(OEP)(Cl), supports involvement of the FeNO fragment. However, the observed Fe mode composition factor varies over a significant range from = 0.23 for Fe(PPIXDME)(NO) to = 0.33 for Fe(OEP)(NO).
DFT normal mode analysis on iron nitrosyl porphyrins also suggests a slightly more complex picture of the FeNO vibrations. Calculations on Fe(P)(NO) and Fe(TPP)(NO) predict two vibrational modes with more than 95% of the mode energy localized on the FeNO unit, as determined from the sum (see Supporting Information). In each case, the higher frequency mode is a nearly pure N-O stretching mode. The lower frequency mode has a mixed character, involving both Fe-NO stretching and FeNO bending (Fig. 12). Below, we identify these modes as N-O stretch and Fe-NO stretch/bend, respectively. Neither the calculation nor the experiment support the presence of a mode near 547 cm−1 involving torsion around the Fe-NO bond in Fe(TPP)(NO), as suggested by a normal mode analysis based on an empirical force field.37 In the [Fe(TPP)(NO)]+ calculation, mixing of the Fe-NO stretch/bend with a porphyrin vibration results in a frequency splitting, but summation of over both modes still yields 0.97.
Figure 12.
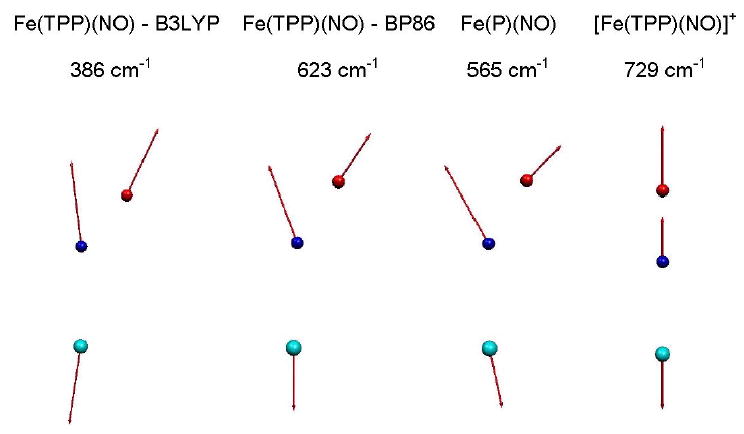
Predicted Fe-NO stretch/bend modes for Fe(TPP)(NO), [Fe(TPP)(NO)]+, and Fe(P)(NO). For the linear FeNO fragment in [Fe(TPP)(NO)]+, the mode resembles a pure Fe-NO stretching modes. In contrast, the relative contribution of Fe-NO stretching and FeNO bending character differs considerably for the similar nonlinear FeNO fragments in Fe(TPP)(NO) and Fe(P)(NO). Note that an independent mode with FeNO bending character is not identified for the B3LYP calculation on Fe(TPP)(NO). Arrows representing mass-weighted atomic displacements are 100(mj/mFe)1/2 times longer than the zero point vibrational amplitudes. Color scheme as in Figs. 10 and 11.
Comparison of the B3LYP and BP86 predictions for Fe(TPP)(NO) reveals that the Fe-NO stretch/bend frequency is highly sensitive to the details of the calculation. The Fe-NO stretch/bend frequency shifts from 386 cm−1 to 623 cm−1 as the predicted bond length decreases from 181 pm to 170 pm. The predicted N-O stretching frequency decreases by 60 cm−1 (see Supporting Information). Other mode frequencies are much less sensitive to the functional used in the calculation (Fig. 4). Moreover, comparison of B3LYP calculations on Fe(TPP)(NO) and [Fe(TPP)(NO)]+ in Fig. 8 suggests that modes other than the Fe-NO bend/stretch are much less sensitive to changes in Fe electronic state. For the Fe(P)(NO) calculation, the predicted 565 cm−1 Fe-NO stretch/bend frequency and 172 pm Fe-N bond length are in good accord with values expected from observations.
The mode character predicted for the FeNO stretch/bend also varies noticeably, as is apparent from the mode representation in Fig. 12 and the kinetic energy distribution in Fig. 9 (see also Supporting Information). For Fe(TPP)(NO), the B3LYP calculation predicts a fairly uniform kinetic energy distribution among the three atoms, similar to a pure Fe-NO stretch with = 0.35, = 0.30, and = 0.35. For Fe(P)(NO), the central N atom of the FeNO fragment carries the dominant kinetic energy fraction, consistent with a stronger component of FeNO bending (Fig. 12). The predicted mode character of the Fe-NO stretch/bend mode predicted on the basis of the BP86 calculation on Fe(TPP)(NO) is intermediate. It is likely that such variations in the relative amount of bending and stretching character contribute to observed variations in the amplitude of the FeNO stretch bend among the series of ferrous nitrosyl porphyrins in Fig. 2.
The B3LYP Fe(TPP)(NO) calculation identifies several other modes with significant contributions from FeNO distortion. In the previous section, we noted significant FeNO bending character for the 308 cm−1 and 334 cm−1 Fe-Npyr modes, in which Fe motion is approximately parallel to the FeNO plane. Other predicted Fe(TPP)(NO) modes with prominent bending character (Fig. 9) include a 186 cm−1 mode with = 0.50 and a 292 cm−1 mode with = 0.31. The BP86 calculation also predicts modes with significant FeNO bending character at 195 cm−1 ( = 0.35), 333 cm−1 ( = 0.40), and 410 cm−1 ( = 0.32). The 410 cm−1 mode has a significant out-of-plane Fe component, visible in the lower panel of Fig. 4. Neither B3LYP nor BP86 calculation suggest the presence of a single primary “bending mode” with the mode energy localized on the FeNO unit, in contrast with what might be expected on the basis of a simplified three-body analysis. Raman isotope-shift measurements on cyanometmyoglobin have also revealed a number of modes with FeCN bending character.160
The predicted contribution of FeNO bending to Fe(P)(NO) vibrations is qualitatively similar, with prominent motion of the ligand N atom in modes at 205 cm−1 and 318 cm−1 (Fig. 9). Similar to Fe(TPP)(NO), only the Fe-NO stretch/bend at 565 cm−1 and the N-O stretch at 1718 cm−1 are localized on the FeNO fragment in Fe(P)(NO). For the [Fe(TPP)(NO)]+ calculation, the FeNO unit is linear, and the predicted N-O stretch and Fe-NO stretch remain localized on the FeNO fragment. Although FeNO bending is associated primarily with a predicted pair of modes at 451 cm−1 and 453 cm−1, only 56% of the mode energy is associated with the FeNO fragment. We also note that the Fe amplitude of the 451 cm−1 and 453 cm−1 modes would be too small to contribute to the [Fe(TPP)(NO)]+ NRVS signal.
Reactive modes
The function of many proteins ultimately involves making or breaking at least one chemical bond, a process that takes place on a subpicosecond time scale. Ideally, vibrational spectroscopy should provide quantitative information on the underlying reactive dynamics. With few exceptions, however, frequency-domain vibrational investigations on biological molecules focus on vibrational “spectators”, modes whose frequencies reflect changes in the molecular conformation and environment.2–5 Indeed, these spectators or marker bands are often important probes and can, in favorable cases, be calibrated to provide quantitative information.10–12 However, the ability to characterize vibrational “participants”, degrees of freedom that contribute to the reaction coordinate, would have great complementary value.
In particular, heme protein reactions with diatomic molecules involve Fe motion relative to the mean porphyrin plane, and control of this out-of-plane Fe motion has been proposed as a means for the protein to influence the reactivity of the active site and to communicate the state of the heme to distant sites.7,161–164 However, comparison of equilibrium structures does not quantify the relative contribution of the various atomic degrees of freedom to the reaction energetics. On the other hand, ultrafast time-domain measurements on myoglobin directly identify reaction-driven low frequency vibrations,8,9 but it remains a challenge to associate these oscillations with specific atomic coordinates.
Low frequency modes involving Fe motion must contribute to the 57Fe NRVS signal, providing a unique opportunity to specifically probe the contribution of Fe to the reaction dynamics. The ability to identify and characterize these reactive modes is a primary motivation for NRVS studies on heme proteins and model compounds. However, the NRVS signal corresponding to the observed reactive modes in myoglobin was significantly smaller than expected for a localized heme doming mode, and we hypothesized that the mode acquires a more global character in the protein, reducing the Fe amplitude.27
In contrast, we identified experimental features at 74 cm−1 and 128 cm−1 (Figs. 2, 4) in Fe(TPP)(NO) as likely candidates for out-of-plane Fe displacement.28 Measurements on oriented crystals of Fe(TPP)(NO) subsequently confirmed the out-of-plane character of these modes37 (Fig. 4). DFT normal mode calculations provide more detailed predictions of the underlying atomic motions, and we inspected the predicted low frequency modes of Fe(TPP)(NO) for vibrations with potential reactive character (Fig. 13).
Figure 13.
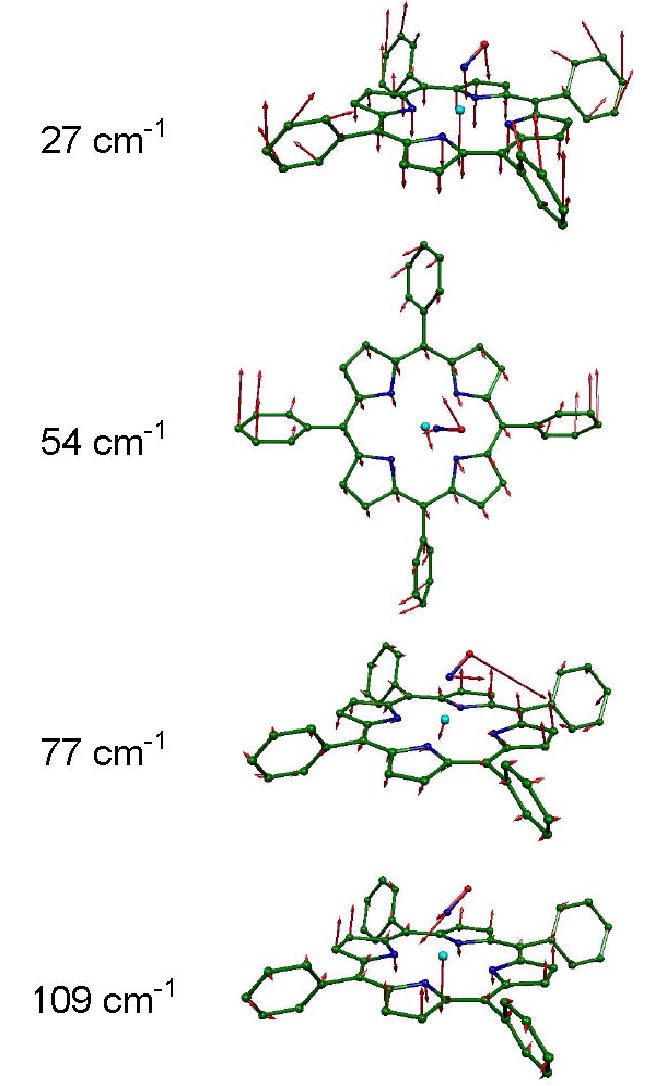
Predicted low frequency Fe modes of Fe(TPP)(NO), resulting from B3LYP calculations. Modes at 27 cm−1, 54 cm−1, 77 cm−1, and 109 cm−1, respectively, primarily involve porphyrin core translation, Fe-NO torsion, FeNO bending, and Fe out-of-plane motion coupled to doming of the porphyrin core. Arrows representing mass-weighted atomic displacements are 100(mj/mFe)1/2 times longer than the zero point vibrational amplitudes. Color scheme as in Figs. 10–12.
The dominant out-of-plane Fe mode in the predicted density of states appears at 109 cm−1 in the B3LYP calculation, and resembles the heme “doming” mode proposed to influence heme protein reactivity.7,163 In this mode, the iron atom moves out of the porphyrin plane and the pyrrole groups swivel to follow, displacing the periphery of the ring in the direction opposite to the Fe motion (Fig. 13). This calculation also predicts an out-of-plane mode at 27 cm−1, with = 0.07, which resembles net translation of the entire porphyrin core, coupled with motion of the four phenyl groups in the opposite direction (Fig. 13). No corresponding mode appears in the Fe(P)(NO) prediction (Fig. 4), in which the phenyl groups are absent. Together with the absence of predicted distortion of the porphyrin core of Fe(TPP)(NO), this suggests that the 27 cm−1 mode will not contribute significantly to the reactive dynamics of the porphyrin.
Several predicted low frequency modes involve reorientation of the bound NO, including two features of the predicted 57Fe NRVS signal at 54 cm−1 and 77 cm−1. For the 77 cm−1 mode, 59% of the kinetic energy is associated with motion of the nitrosyl oxygen (Fig. 9), but correlated motion of the Fe makes a modest contribution to the predicted 57Fe NRVS signal (Figs. 4, 8). Oxygen motion takes place in the FeNO plane for the 77 cm−1 mode, while a cluster of three modes at 51 cm−1, 54 cm−1, and 56 cm−1 involves torsion about the Fe-NO bond, with a significant component of O motion perpendicular to the FeNO plane (Fig. 13). Additional modes involving hindered rotation of the NO ligand occur at at 42 cm−1 and 44 cm−1 (Fig. 9), and are characterized by rotation of the NO ligand about axes perpendicular and parallel to the FeNO plane, respectively. No measurable 57Fe NRVS signal is predicted for the latter two modes.
Such orientational degrees of freedom provide another opportunity for heme proteins to influence ligand binding and dissociation reactions. For example, a diatomic ligand approaching the heme Fe may need to adopt a specific orientation in order to surmount the barrier to binding. In myoglobin, a “docking site” has been proposed to hold photolyzed CO in an orientation perpendicular to its orientation in the bound state and restrict rebinding to the Fe.165
Structures with ligand orientations differing from the stable equilibrium geometry may also lie on reaction pathways. For Fe(TPP)(NO), there is experimental and theoretical evidence138 for an isomer with NO bound end on by the oxygen, which is metastable with respect to the equilibrium N-bound geometry in Fig. 1. Isomers with distinctive vibrational properties have been attributed to side-on binding of O2 to Fe porphyrins in low temperature Ar matrices.166,167 Furthermore, theoretical investigations implicate ligand rotation as a likely reaction coordinate for photodissociation of NO and O2 from ferrous porphyrins.168 For myoglobin, trapping of the ligand in such metastable isomers may account for the reduced quantum yield for photodissociation of NO and O2 compared to CO.169,170
The correspondence between observed and predicted vibrational frequencies is somewhat less apparent below 150 cm−1 (Fig. 4). It is conceivable that intermolecular interactions not included in the present calculations on isolated molecules contribute to differences in frequencies and relative Fe amplitudes. However, we propose that the observed 74 cm−1 and 128 cm−1 modes correspond to the predicted out-of-plane Fe modes at 77 cm−1 and 109 cm−1. This is supported by the diminished amplitudes of both modes in oriented crystals (Fig. 4). The relative amplitudes of the two modes are more nearly equivalent in the experimental spectrum than in the predicted signal, which would indicate some degree of vibrational mixing between the two modes. The potential functional significance of the interaction of these reactive degrees of freedom remains to be investigated.
Acoustic vibrations interfere with the identification of experimental NRVS signals that correspond to the predicted porphyrin core translation and Fe-NO torsion modes at 27 cm−1 and 54 cm−1 in Fe(TPP)(NO). It is possible that the core translation mode may contribute to the excess area in the powder VDOS below 30 cm−1 (Fig. 4). However, the predicted spectra clearly resolve low frequency intramolecular vibrations.
The character of these low frequency modes appears to be relatively insensitive to details of the calculation. Modes appearing at 33 cm−1, 54 cm−1, 88 cm−1, and 110 cm−1 in the BP86 calculation strongly resemble the B3LYP-predicted modes at 27 cm−1, 54 cm−1, 77 cm−1, and 109 cm−1 shown in Fig. 13.
In contrast, the nature of peripheral groups on the porphyrin ring strongly influences the frequency of the doming mode. Previous DFT calculations on unsubstituted Fe(P) and Fe(P)(Im) predicted doming frequencies between 89–99 cm−1 in low spin and between 63–72 cm−1 in high spin states.69,71 Increasing the pyrrole hydrogen mass to 15 reduces the predicted doming frequencies by 17–34 cm−1.69 In the presence of more massive ethyl groups, the predicted doming frequency of Fe(OEP)(Py)(CO) drops to 39 cm−1.44 In contrast to the effect of pyrrole substituents, introduction of the four phenyl groups slightly increases the predicted doming frequency from 103 cm−1 in Fe(P)(NO) to 109 cm−1 in Fe(TPP)(NO).
Effects of peripheral substituents on the low frequencies are also evident in the NRVS data on the series of FeNO porphyrins shown in Fig. 2. For Fe(OEP)(NO), modes at 58 cm−1 (not resolved from the acoustic mode background in Fig. 2) and 161 cm−1 dominate the out-of-plane Fe VDOS determined from oriented single crystal NRVS measurements (to be published elsewhere). The former frequency is close to a broad peak observed in far infrared measurements on Fe(OEP)(Py)(CO).44
Summary and outloook
Quantitative information on the frequencies, amplitudes, and directions of Fe motion from NRVS measurements provides a definitive test of the detailed normal mode predictions provided by modern quantum chemical calculations. Taken together, these methods reveal a consistent picture of the vibrational dynamics of iron nitrosyl porphyrins that is considerably richer than previously available. Peripheral groups significantly influence the vibrational dynamics of the Fe at the center of the porphyrin, necessitating calculation on the full molecule, rather than a truncated fragment. Fe-NO stretch/bend modes are extremely sensitive to details of the calculation, and NRVS measurements reveal substantial variations in Fe-NO mode character among the porphyrins examined here. Bending of the FeNO fragment contributes to several normal modes, but we are unable to identify a single primary FeNO bending mode for Fe(TPP)(NO).
Most important, results presented here identify low frequency modes, including porphyrin doming, expected to control the reactive energetics at the iron. The experimental identification of reactive low frequency Fe out-of-plane modes in Fe(TPP)(NO) establishes a quantitative expectation for the amplitude of a doming mode localized at the heme, and lends credence to the suggestion that vibrational mixing with polypeptide vibrations accounts for the reduced signal for such modes in myoglobin.27 Moreover, the measurements and calculations described here represent a crucial first step toward quantifying the reactive energetics of Fe porphyrins, since these low frequency modes make the principal contribution to the energetics of Fe displacement. In a subsequent publication, we will use NRVS measurements on oriented single crystals to quantify the energetics of Fe displacement perpendicular to the porphyrin plane.
Supporting Information
A. Details of porphyrin synthesis
For NRVS measurements on ferric chloride, 57Fe-enriched Fe(OEP)(Cl) was purchased from Midcentury Chemicals. All other compounds were synthesized for the NRVS measurements.
General Information
All reactions and manipulations were carried out using standard Schlenkware techniques unless otherwise noted. Benzene was distilled over sodium and benzophenone. Nitric oxide was purchased from Specialty Gases and purified by passing through a trap containing 4 Å molecular sieves immersed in an ethanol/dry ice slurry. This removes all higher oxides of nitrogen.1 Fe2O3, (95% enriched in 57Fe) was purchased from Cambridge Isotope Laboratories. H2(OEP) was purchased from Midcentury Chemicals. H2(DPIXDME), H2(MPIXDME) and H2(PPIXDME) were purchased from Porphyrin Products. H2(TPP) was prepared according to the methods of Adler.2 The ferric chlorides, 57Fe(Por)(Cl), were prepared using the metallation procedure described by Landergren and Baltzer.3
Synthesis and isolation of 57FeII(OEP)
57Fe(OEP)(Cl) was converted to [57Fe(OEP)]2O by shaking with aqueous NaOH solution and drying over MgSO4.4,5 150 mg of [57Fe(OEP)]2O was dissolved in benzene prior to several freeze/pump/thaw cycles. The reduction to four-coordinate 57FeII(OEP) was carried out according to Stolzenberg et al.6 by the cannula addition of ~2.5 mL of ethanethiol. The solution was stirred overnight prior to complete removal of all solvent under vacuum. This left the reddish solid 57FeII(OEP) coated to the sides of the Schlenk flask. This complex is extremely susceptible to oxidation and hence, never exposed to air in order to avoid re-oxidation to [57Fe(OEP)]2O. The Schlenk flask was opened in a dry-box under a nitrogen atmosphere. The solid 57FeII(OEP) was loosened from the sides of Schlenk flask by gentle mechanical pressure with a spatula. A small portion of Apiezon M grease on the end of a second spatula was used to transfer the powder sample of 57FeII(OEP) to a glass slide where it was thoroughly mixed with the grease to form a concentrated homogenous mull which was loaded into the sample holder and transported and stored in a biological dry-shipper prior to the NRVS measurements. A small portion of the sample was also examined by Mössbauer spectroscopy at 4.2 K to confirm sample identity and purity. The values of the isomer shift (0.68 mm/sec) and the quadrupole splitting (1.64 mm/sec) agree with values reported previously.7
Synthesis of Polycrystalline 57Fe(Por)(NO)
Polycrystalline powder samples of the five ferrous (nitrosyl)porphyrin complexes, 57Fe(Por)(NO) where Por = OEP, TPP, DPIXDME, MPIXDME and PPIXDME, were prepared in a similar manner to the reductive nitrosylation method described previously.8 120 mg of the ferric chloride 57Fe(Por)(Cl) was dissolved in 5 mL of chloroform in a Schlenk flask. 0.5 mL of methanol and 0.1 mL of pyridine were added and the solution purged with argon. Nitric oxide was bubbled through the solution for approximately 5 minutes. The product was precipitated by addition of a large volume of methanol, isolated by filtration upon sintered glass and washed with several portions of methanol. The resulting polycrystalline samples were mixed with minimal Apiezon M grease and loaded into the sample holder. The identities and purity of the samples were confirmed by a combination of Mössbauer and IR spectroscopy.
57Fe(TPP)(NO) Crystal Array
Single crystals of 57Fe(TPP)(NO) were prepared by a modification of the above procedure. 25 mg of 57Fe(TPP)(Cl) was weighed in a 10 mL beaker which was placed in a crystallization jar, sealed with a 3-hole Twistit rubber stopper and evacuated and refilled with argon. 2.5 mL of chloroform, 0.5 mL of methanol and 2 drops of pyridine were added to the beaker whilst 2 mL of chloroform and 2.5 mL of methanol were added to the jar surrounding the beaker. Argon was bubbled through the jar by means of a 22 gauge needle, initially through the headspace then through the outer solution. The gas flow was changed to nitric oxide which was bubbled through both solutions for approximately 5 minutes. The jar was sealed and crystals were found to form after 2 weeks.
Since the individual crystals were too small to provide adequate signal, 25 crystals were arranged on the inner surface of a polystyrene sample cell in a 5 × 5 array. The unit cell of 57Fe(TPP)(NO) contains a single molecular orientation with crystallographically required eightfold disorder of the bound NO. The crystals possessed a regular tetragonal bipyramidal morphology for which all molecules are arranged in a co-planar fashion coincident with the basal plane of the crystal.8 The crystals within the array were immobilized in a bed of Apiezon M grease and orientated such that the mean porphyrin plane lay parallel to the surface of the sample holder. NRVS data were collected in grazing incidence, with the X-ray beam 6° from the face of the sample cell.
B. FeNO kinetic energy distributions
The following tables give the predicted kinetic energy distributions on the FeNO fragment. The fractional kinetic energies associated with motion of the Fe atom and the nitrosyl N and O atoms are equal to , , and , respectively. Only modes with at least 10% of kinetic energy localized on the FeNO fragment ( > 0.1) are included.
Supplementary Material
Figure 7.
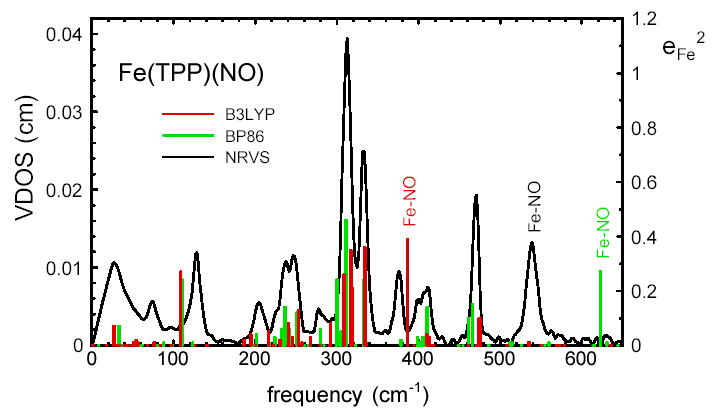
Direct comparison of measured and predicted vibrational densities of states for Fe(TPP)(NO). The measured and calculated Fe-NO frequencies are indicated.
Table 2.
Predicted FeNO kinetic energy distribution for B3LYP calculation on Fe(TPP)(NO).
| (cm−1) | ||||
|---|---|---|---|---|
| 1781 | 0.00 | 0.55 | 0.45 | 1.00 |
| 476 | 0.10 | 0.00 | 0.00 | 0.10 |
| 474 | 0.10 | 0.00 | 0.00 | 0.10 |
| 386 | 0.39 | 0.35 | 0.23 | 0.97 |
| 334 | 0.36 | 0.28 | 0.02 | 0.66 |
| 318 | 0.21 | 0.01 | 0.00 | 0.22 |
| 317 | 0.35 | 0.01 | 0.00 | 0.36 |
| 308 | 0.26 | 0.16 | 0.01 | 0.43 |
| 292 | 0.08 | 0.31 | 0.01 | 0.40 |
| 268 | 0.03 | 0.11 | 0.05 | 0.19 |
| 253 | 0.13 | 0.00 | 0.00 | 0.13 |
| 216 | 0.05 | 0.12 | 0.08 | 0.25 |
| 195 | 0.04 | 0.12 | 0.14 | 0.32 |
| 186 | 0.02 | 0.50 | 0.02 | 0.54 |
| 109 | 0.27 | 0.09 | 0.11 | 0.47 |
| 77 | 0.01 | 0.06 | 0.59 | 0.66 |
| 56 | 0.01 | 0.00 | 0.14 | 0.15 |
| 44 | 0.00 | 0.04 | 0.19 | 0.23 |
| 42 | 0.00 | 0.03 | 0.54 | 0.57 |
| 27 | 0.07 | 0.02 | 0.03 | 0.12 |
Table 3.
Predicted FeNO kinetic energy distribution for BP86 calculation on Fe(TPP)(NO).
| (cm−1) | ||||
|---|---|---|---|---|
| 1721 | 0.00 | 0.57 | 0.43 | 1.00 |
| 623 | 0.27 | 0.49 | 0.19 | 0.95 |
| 466 | 0.15 | 0.03 | 0.01 | 0.19 |
| 461 | 0.10 | 0.01 | 0.00 | 0.11 |
| 410 | 0.14 | 0.32 | 0.15 | 0.62 |
| 333 | 0.24 | 0.40 | 0.01 | 0.65 |
| 300 | 0.24 | 0.08 | 0.01 | 0.33 |
| 280 | 0.06 | 0.09 | 0.09 | 0.24 |
| 251 | 0.12 | 0.00 | 0.01 | 0.13 |
| 236 | 0.14 | 0.03 | 0.03 | 0.20 |
| 232 | 0.06 | 0.01 | 0.04 | 0.11 |
| 195 | 0.03 | 0.35 | 0.02 | 0.40 |
| 110 | 0.24 | 0.08 | 0.09 | 0.40 |
| 88 | 0.01 | 0.09 | 0.55 | 0.65 |
| 60 | 0.00 | 0.02 | 0.09 | 0.11 |
| 44 | 0.00 | 0.01 | 0.35 | 0.36 |
| 40 | 0.00 | 0.02 | 0.14 | 0.16 |
| 37 | 0.00 | 0.03 | 0.41 | 0.44 |
| 33 | 0.07 | 0.02 | 0.03 | 0.11 |
Table 4.
Predicted FeNO kinetic energy distribution for B3LYP calculation on Fe(P)(NO).
| (cm−1) | ||||
|---|---|---|---|---|
| 1718 | 0.00 | 0.56 | 0.44 | 1.00 |
| 565 | 0.22 | 0.64 | 0.14 | 1.00 |
| 444 | 0.05 | 0.04 | 0.03 | 0.12 |
| 434 | 0.35 | 0.11 | 0.09 | 0.55 |
| 417 | 0.26 | 0.01 | 0.00 | 0.27 |
| 406 | 0.11 | 0.10 | 0.04 | 0.25 |
| 354 | 0.01 | 0.06 | 0.08 | 0.15 |
| 318 | 0.22 | 0.28 | 0.00 | 0.50 |
| 292 | 0.50 | 0.04 | 0.01 | 0.55 |
| 287 | 0.16 | 0.06 | 0.00 | 0.22 |
| 282 | 0.17 | 0.05 | 0.00 | 0.22 |
| 264 | 0.09 | 0.03 | 0.04 | 0.16 |
| 248 | 0.06 | 0.07 | 0.17 | 0.30 |
| 205 | 0.01 | 0.44 | 0.02 | 0.47 |
| 103 | 0.27 | 0.08 | 0.09 | 0.44 |
| 87 | 0.01 | 0.12 | 0.68 | 0.81 |
| 49 | 0.00 | 0.00 | 0.11 | 0.11 |
| 46 | 0.00 | 0.01 | 0.77 | 0.78 |
Table 5.
Predicted FeNO kinetic energy distribution for B3LYP calculation on [Fe(TPP)(NO)]+.
| (cm−1) | ||||
|---|---|---|---|---|
| 2001 | 0.00 | 0.61 | 0.38 | 0.99 |
| 742 | 0.11 | 0.04 | 0.07 | 0.22 |
| 729 | 0.31 | 0.15 | 0.29 | 0.75 |
| 484 | 0.11 | 0.05 | 0.00 | 0.16 |
| 481 | 0.12 | 0.08 | 0.01 | 0.21 |
| 453 | 0.00 | 0.50 | 0.05 | 0.55 |
| 451 | 0.00 | 0.51 | 0.05 | 0.56 |
| 406 | 0.09 | 0.12 | 0.01 | 0.22 |
| 403 | 0.04 | 0.10 | 0.01 | 0.15 |
| 323 | 0.53 | 0.00 | 0.00 | 0.53 |
| 314 | 0.31 | 0.03 | 0.01 | 0.35 |
| 308 | 0.16 | 0.00 | 0.00 | 0.16 |
| 305 | 0.08 | 0.04 | 0.06 | 0.18 |
| 261 | 0.14 | 0.00 | 0.00 | 0.14 |
| 249 | 0.14 | 0.02 | 0.01 | 0.17 |
| 230 | 0.03 | 0.05 | 0.02 | 0.10 |
| 224 | 0.05 | 0.08 | 0.02 | 0.15 |
| 117 | 0.26 | 0.07 | 0.08 | 0.41 |
| 73 | 0.00 | 0.05 | 0.65 | 0.70 |
| 72 | 0.00 | 0.03 | 0.50 | 0.53 |
| 53 | 0.01 | 0.05 | 0.26 | 0.32 |
| 48 | 0.01 | 0.02 | 0.07 | 0.10 |
Acknowledgments
We thank G. Y. Georgiev and T. H. Ching for assistance during data collection. We acknowledge financial support from the National Science Foundation (0240955 to J. T. S. and 9988763 to S. M. D.) and the National Institutes of Health (GM-52002 to J. T. S. and GM-38401 to W. R. S.). Use of the Advanced Photon Source was supported by the U. S. Department of Energy, Basic Energy Sciences, Office of Science, under Contract No. W-31-109-Eng-38.
References
- 1.Abbreviations: NRVS, nuclear resonance vibrational spectroscopy (note that the terms nuclear (resonant) inelastic X-ray scattering and phonon-assisted Mössbauer effect have also been used for this technique); DFT, density functional theory; NOS, nitric oxide synthase; sGC, soluble guanylate cyclase; TPP, tetraphenylporphyrin; P, porphine; OEP, octaethylporphyrin; PPIXDME, protoporphyrin IX dimethyl ester; DPIXDME, deuteroporphyrin IX dimethyl ester; MPIXDME, mesoporphyrin IX dimethyl ester; VDOS, vibrational density of states; Npyr, pyrrole nitrogen; Im, imidazole; Py, pyridine.
- 2.Spiro TG, editor. Wiley-Interscience; New York: 1988. Biological Applications of Raman Spectroscopy. [Google Scholar]
- 3.Mäntele W. Trends Biochem Sci. 1993;18:197–202. doi: 10.1016/0968-0004(93)90186-q. [DOI] [PubMed] [Google Scholar]
- 4.Fayer, M. D., Ed.; Ultrafast Infrared and Raman Spectroscopy; Marcel-Dekker: New York, 2001. [Google Scholar]
- 5.Barth A, Zscherp C. Q Rev Biophys. 2002;35:369–430. doi: 10.1017/s0033583502003815. [DOI] [PubMed] [Google Scholar]
- 6.Spiro TG, editor. Biological Applications of Raman Spectroscopy. Wiley-Interscience; New York: 1988. pp. 133–215. Chapter 4. [Google Scholar]
- 7.Suslick KS, editor. Small Substrate Recognition in Heme Proteins. Comprehensive Supramolecular Chemistry Pergamon; Oxford, U. K: 1996. [Google Scholar]
- 8.Zhu L, Sage JT, Champion PM. Science. 1994;226:629–632. doi: 10.1126/science.7939716. [DOI] [PubMed] [Google Scholar]
- 9.Rosca F, Kumar A, Ionascu D, Sjodin T, Demidov A, Champion PM. J Phys Chem. 2001;114:10884–10898. [Google Scholar]
- 10.Parthasarathi N, Hansen C, Yamaguchi S, Spiro TG. J Am Chem Soc. 1987;109:3865–3871. [Google Scholar]
- 11.Phillips GN, Jr, Teodoro ML, Li TS, Smith B, Olson JS. J Phys Chem B. 1999;103:8817–8829. [Google Scholar]
- 12.Park ES, Andrews SS, Hu RB, Boxer SG. J Phys Chem B. 1999;103:9813–9817. [Google Scholar]
- 13.Wells AV, Sage JT, Morikis D, Champion PM, Chiu ML, Sligar SG. J Am Chem Soc. 1991;113:9655–9660. [Google Scholar]
- 14.Rothschild KJ, Gite S. Curr Opin Biotechnol. 1999;10:64–70. doi: 10.1016/s0958-1669(99)80012-3. [DOI] [PubMed] [Google Scholar]
- 15.Seto M, Yoda Y, Kikuta S, Zhang XW, Ando M. Phys Rev Lett. 1995;74:3828–3831. doi: 10.1103/PhysRevLett.74.3828. [DOI] [PubMed] [Google Scholar]
- 16.Sturhahn W, Toellner TS, Alp EE, Zhang X, Ando M, Yoda Y, Kikuta S, Seto M, Kimball CW, Dabrowski B. Phys Rev Lett. 1995;74:3832–3835. doi: 10.1103/PhysRevLett.74.3832. [DOI] [PubMed] [Google Scholar]
- 17.Chumakov AI, Rüffer R, Baron AQR, Grünsteudel H, Grünsteudel HF. Phys Rev B. 1996;54:R9596–R9599. doi: 10.1103/physrevb.54.r9596. [DOI] [PubMed] [Google Scholar]
- 18.Keppler C, Achterhold K, Ostermann A, van Bürck U, Potzel W, Chumakov AI, Baron AQ, Rüffer R, Parak F. Eur Biophys J. 1997;25:221–224. doi: 10.1007/s002490050034. [DOI] [PubMed] [Google Scholar]
- 19.Chumakov AI, Rüffer R, Baron AQR, Grünsteudel H, Grünsteudel HF, Kohn VG. Phys Rev B. 1997;56:10758–10761. [Google Scholar]
- 20.Fultz B, Ahn CC, Alp EE, Sturhahn W, Toellner TS. Phys Rev Lett. 1997;79:937–940. [Google Scholar]
- 21.Fultz B, Stephens TA, Sturhahn W, Toellner TS, Alp EE. Phys Rev Lett. 1998;80:3304–3307. [Google Scholar]
- 22.Kohn VG, Chumakov AI, Rüffer R. Phys Rev B. 1998;58:8437–8444. [Google Scholar]
- 23.Brand RA, Coddens G, Chumakov AI, Calvayrac Y. Phys Rev B. 1999;59:R14145–R14148. [Google Scholar]
- 24.Paulsen H, Winkler H, Trautwein AX, Grünsteudel H, Rusanov V, Toftlund H. Phys Rev B. 1999;59:975–984. [Google Scholar]
- 25.Fultz B, Stephens TA, Alp EE, Hu MY, Sutter JP, Toellner TS, Sturhahn W. Phys Rev B. 2000;61:14517–14522. [Google Scholar]
- 26.Lübbers R, Grünsteudel HF, Chumakov AI, Wortmann G. Science. 2000;287:1250–1253. doi: 10.1126/science.287.5456.1250. [DOI] [PubMed] [Google Scholar]
- 27.Sage JT, Durbin SM, Sturhahn W, Wharton DC, Champion PM, Hession P, Sutter J, Alp EE. Phys Rev Lett. 2001;86:4966–4969. doi: 10.1103/PhysRevLett.86.4966. [DOI] [PubMed] [Google Scholar]
- 28.Sage JT, Paxson C, Wyllie GRA, Sturhahn W, Durbin SM, Champion PM, Alp EE, Scheidt WR. J Phys: Condens Matter. 2001;13:7707–7722. [Google Scholar]
- 29.Paulsen H, Benda R, Herta C, Schünemann V, Chumakov AI, Duelund L, Winkler H, Toftlund H, Trautwein AX. Phys Rev Lett. 2001;86:1351–1354. doi: 10.1103/PhysRevLett.86.1351. [DOI] [PubMed] [Google Scholar]
- 30.Jayasooriya UA, Malone SA, Chumakov AI, Rüffer R, Overweg AR, Nicklin CR. Chem Phys Chem. 2001;3:177–180. doi: 10.1002/1439-7641(20010316)2:3<177::AID-CPHC177>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 31.Struzhkin VV, Mao HK, Hu J, Schwoerer-Böhning M, Shu J, Hemley RJ, Sturhahn W, Hu MY, Alp EE, Eng P, Shen G. Phys Rev Lett. 2001;87:255501. doi: 10.1103/PhysRevLett.87.255501. [DOI] [PubMed] [Google Scholar]
- 32.Mao HK, Xu J, Struzhkin VV, Shu J, Hemley RJ, Sturhahn W, Hu MY, Alp EE, Vocadlo L, Alfe D, Price GD, Gillan MJ, Schwoerer-Böhning M, Häusermann D, Eng P, Shen G, Giefers H, Lübbers R, Wortmann G. Science. 2001;292:914–916. doi: 10.1126/science.1057670. [DOI] [PubMed] [Google Scholar]
- 33.Paulsen H, Rusanov V, Benda R, Herta C, Schünemann V, Janiak C, Dorn T, Chumakov AI, Winkler H, Trautwein AX. J Am Chem Soc. 2002;124:3007–3011. doi: 10.1021/ja016239c. [DOI] [PubMed] [Google Scholar]
- 34.Pasquini L, Barla A, Chumakov AI, Leupold O, Rüffer R, Deriu A, Bonetti E. Phys Rev B. 2002;66:073410. [Google Scholar]
- 35.Hu MY, Sturhahn W, Toellner TS, Mannheim PD, Brown DE, Zhao J, Alp EE. Phys Rev B. 2003;67:094304. [Google Scholar]
- 36.Parak F, Achterhold K. Hyp Int. 1999;123 [Google Scholar]
- 37.Rai BK, Durbin SM, Prohofsky EW, Sage JT, Wyllie GRA, Scheidt WR, Sturhahn W, Alp EE. Biophys J. 2002;82:2951–2963. doi: 10.1016/S0006-3495(02)75636-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rai BK, Durbin SM, Prohofsky EW, Sage JT, Ellison MK, Scheidt WR, Sturhahn W, Alp EE. Phys Rev E. 2002;66:051904. doi: 10.1103/PhysRevE.66.051904. [DOI] [PubMed] [Google Scholar]
- 39.Achterhold K, Keppler C, Ostermann A, van Bürck U, Sturhahn W, Alp EE, Parak FG. Phys Rev E. 2002;65:051916. doi: 10.1103/PhysRevE.65.051916. [DOI] [PubMed] [Google Scholar]
- 40.Bergmann U, Sturhahn W, Linn DEJ, Jenney FEJ, Adams MW, Rupnik K, Hales BJ, Alp EE, Mayse A, Cramer SP. J Am Chem Soc. 2003;125:4016–4017. doi: 10.1021/ja028767+. [DOI] [PubMed] [Google Scholar]
- 41.Rai BK, Durbin SM, Prohofsky EW, Sage JT, Ellison MK, Roth A, Scheidt WR, Sturhahn W, Alp EE. J Am Chem Soc. 2003;125:6927–6936. doi: 10.1021/ja028219w. [DOI] [PubMed] [Google Scholar]
- 42.Achterhold K, Parak FG. J Phys: Condens Matter. 2003;15:S1683–S1692. [Google Scholar]
- 43.Budarz TE, Prohofsky EW, Durbin SM, Sjodin T, Sage JT, Sturhahn W, Alp EE. J Phys Chem. 2003;107:11170–11177. [Google Scholar]
- 44.Klug DD, Zgierski MZ, Tse JS, Liu Z, Kincaid JR, Czarnecki K, Hemley RJ. Proc Natl Acad Sci USA. 2002;99:12526–12530. doi: 10.1073/pnas.152464699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jones DH, Hinman AS, Ziegler T. Inorg Chem. 1993;32:2092–2095. [Google Scholar]
- 46.Ghosh A, Almlof J, Que LJ. J Phys Chem. 1994;98:5576–5579. [Google Scholar]
- 47.Rovira C, Kunc K, Hutter J, Ballone P, Parrinello M. J Phys Chem A. 1997;101:8914–8925. [Google Scholar]
- 48.Ghosh A. Acc Chem Res. 1998;31:189–198. [Google Scholar]
- 49.Rovira C, Carloni P, Parrinello M. J Phys Chem B. 1999;103:7031 –7035. [Google Scholar]
- 50.Kaupp M, Rovira C, Parrinello M. J Phys Chem B. 2000;104:5200–5208. [Google Scholar]
- 51.Rovira C, Parrinello M. Biophys J. 2000;78:93–100. doi: 10.1016/S0006-3495(00)76575-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Patchkovskii S, Ziegler T. Inorg Chem. 2000;39:5354–5364. doi: 10.1021/ic0005691. [DOI] [PubMed] [Google Scholar]
- 53.Patchkovskii S, Ziegler T. J Am Chem Soc. 2000;122:3506–3516. [Google Scholar]
- 54.Rovira C, Schulze B, Eichinger M, Evanseck JD, Parrinello M. Biophys J. 2001;81:435–445. doi: 10.1016/S0006-3495(01)75711-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sigfridsson E, Ryde U. J Inorg Biochem. 2002;91:101–115. doi: 10.1016/s0162-0134(02)00426-9. [DOI] [PubMed] [Google Scholar]
- 56.Ghosh A, Taylor PR. Curr Opin Chem Biol. 2003;7:113–124. doi: 10.1016/s1367-5931(02)00023-6. [DOI] [PubMed] [Google Scholar]
- 57.Siegbahn PE. Q Rev Biophys. 2003;36:91–145. doi: 10.1017/s0033583502003827. [DOI] [PubMed] [Google Scholar]
- 58.Zhang Y, Gossman W, Oldfield E. J Am Chem Soc. 2003;125:16387–16396. doi: 10.1021/ja030340v. [DOI] [PubMed] [Google Scholar]
- 59.Pulay P, Fogarasi G, Pang F, Boggs JE. J Am Chem Soc. 1979;101:2550–2560. [Google Scholar]
- 60.Pulay P, Fogarasi G, Pongor G, Boggs JE, Vargha A. J Am Chem Soc. 1983;105:7037–7047. [Google Scholar]
- 61.Sellers H, Pulay P, Boggs JE. J Am Chem Soc. 1985;107:6487–6494. [Google Scholar]
- 62.Sosa C, Andzelm J, Elkin BC, Wimmer E, Dobbs KD, Dixon DA. J Phys Chem. 1992;96:6630–6636. [Google Scholar]
- 63.Andzelm J, Wimmer E. J Chem Phys. 1992;96:1280–1303. [Google Scholar]
- 64.Delley B, Wrinn M, Lüthi HP. J Chem Phys. 1994;100:5785–5791. [Google Scholar]
- 65.Jonas V, Thiel W. J Chem Phys. 1996;105:3636–3648. [Google Scholar]
- 66.Zhou M, Andrews L, Bauschlicher CW. J Chem Rev. 2001;101:1931–1961. doi: 10.1021/cr990102b. [DOI] [PubMed] [Google Scholar]
- 67.Ghosh A, Bocian DF. J Phys Chem. 1996;100:6363–6367. doi: 10.1021/jp953544+. [DOI] [PubMed] [Google Scholar]
- 68.Kozlowski PM, Jarzecki AA, Pulay P, Li XY, Zgierski MZ. J Phys Chem. 1996;100:13985–13992. [Google Scholar]
- 69.Kozlowski PM, Spiro TG, Bérces A, Zgierski MZ. J Phys Chem B. 1998;102:2603–2608. [Google Scholar]
- 70.Ghosh A, Skancke A. J Phys Chem B. 1998;102:10087–10090. [Google Scholar]
- 71.Kozlowski PM, Spiro TG, Zgierski MZ. J Phys Chem B. 2000;104:10659–10666. [Google Scholar]
- 72.Cao Z, Hall MB. J Am Chem Soc. 2001;123:3734–3742. doi: 10.1021/ja000116v. [DOI] [PubMed] [Google Scholar]
- 73.Franzen S. J Am Chem Soc. 2001;123:12578–12589. doi: 10.1021/ja0108988. [DOI] [PubMed] [Google Scholar]
- 74.Steene E, Wondimagegn T, Ghosh A. J Inorg Biochem. 2002;88:113–118. doi: 10.1016/s0162-0134(01)00396-8. [DOI] [PubMed] [Google Scholar]
- 75.Ohta T, Matsuura K, Yoshizawa K, Morishima I. J Inorg Biochem. 2000;82:141–152. doi: 10.1016/s0162-0134(00)00162-8. [DOI] [PubMed] [Google Scholar]
- 76.Maréchal JD, Maseras F, Lledós A, Mouawad L, Perahia D. Chem Phys Lett. 2002;353:379–382. [Google Scholar]
- 77.Liao MS, Scheiner S. J Chem Phys. 2002;116:3635–3645. [Google Scholar]
- 78.Hudson BS, Braden DA, Parker SF, Prinzbach H. Angew Chem Int Ed Engl. 2000;39:514–516. doi: 10.1002/(sici)1521-3773(20000204)39:3<514::aid-anie514>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 79.Hudson BS. J Phys Chem A. 2001;105:3949–3960. [Google Scholar]
- 80.Schettino V, Pagliai M, Cardini G. J Phys Chem A. 2002;106:1815–1823. [Google Scholar]
- 81.Parker SF, Marsh NA, Camus LM, Whittlesey MK, Jayasooriya VA, Kearley GJ. J Phys Chem A. 2002;106:5797–5802. [Google Scholar]
- 82.Pawlukojc A, Natkaniec I, Nowicka-Scheibe J, Grech E, Sobczyk L. Spectrochim Acta A. 2003;59:537–542. doi: 10.1016/s1386-1425(02)00194-4. [DOI] [PubMed] [Google Scholar]
- 83.Posey JE, Gherardini FC. Science. 2000;288:1651–1653. doi: 10.1126/science.288.5471.1651. [DOI] [PubMed] [Google Scholar]
- 84.Lindley PF. Rep Prog Phys. 1996;59:867. [Google Scholar]
- 85.Antonini E, Brunori M. Hemoglobin and Myoglobin in Their Reactions with Ligands. North-Holland: Amsterdam: 1971. [Google Scholar]
- 86.Springer BA, Sligar SG, Olson JS, Phillips GN., Jr Chem Rev. 1994;94:699–714. [Google Scholar]
- 87.Atwood J, Steed JW, editors. Hemoglobins: O2 Uptake and Transport. Encyclopedia of Supramolecular Chemistry Marcel-Dekker; New York: 2004. [Google Scholar]
- 88.Bredt DS, Snyder SH. Annu Rev Biochem. 1994;63:175–195. doi: 10.1146/annurev.bi.63.070194.001135. [DOI] [PubMed] [Google Scholar]
- 89.Ignarro LJ. Biosci Rep. 1999;19:51–71. doi: 10.1023/a:1020150124721. [DOI] [PubMed] [Google Scholar]
- 90.McMahon TJ, Moon RE, Luschinger BP, Carraway MS, Stone AE, Stolp BW, Gow AJ, Pawloski JR, Watke P, Singel DJA, Piantadosi C, JS JSS. Nat Med. 2002;8:711–717. doi: 10.1038/nm718. [DOI] [PubMed] [Google Scholar]
- 91.Moncada S, Erusalimsky JD. Nat Rev Mol Cell Biol. 2002;3:214–220. doi: 10.1038/nrm762. [DOI] [PubMed] [Google Scholar]
- 92.Rodgers KR. Curr Opin Chem Biol. 1999;3:158–167. doi: 10.1016/S1367-5931(99)80028-3. [DOI] [PubMed] [Google Scholar]
- 93.McMillan K, Bredt DS, Hirsch DJ, Snyder SH, Clark JE, Masters BSS. Proc Natl Acad Sci USA. 1992;89:11141–11145. doi: 10.1073/pnas.89.23.11141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.White KA, Marletta MA. Biochemistry. 1992;31:6627–6631. doi: 10.1021/bi00144a001. [DOI] [PubMed] [Google Scholar]
- 95.Stuehr DJ, Ikeda-Saito M. J Biol Chem. 1992;253:20547–20550. [PubMed] [Google Scholar]
- 96.Ignarro LJ, Degnan NJ, Baricos WH, Kadowitz PJ. Biochim Biophys Acta. 1982;718:49–59. doi: 10.1016/0304-4165(82)90008-3. [DOI] [PubMed] [Google Scholar]
- 97.Craven PA, DeRubertis FR. J Biol Chem. 1978;253:8433–8443. [PubMed] [Google Scholar]
- 98.Perutz MF, Kilmartin JV, Nagai K, Szabo A, Simon SR. Biochemistry. 1976;15:378–387. doi: 10.1021/bi00647a022. [DOI] [PubMed] [Google Scholar]
- 99.Maxwell JC, Caughey WS. Biochemistry. 1976;15:388–396. doi: 10.1021/bi00647a023. [DOI] [PubMed] [Google Scholar]
- 100.Sharma VS, Magde D. Methods. 1999;19:494–505. doi: 10.1006/meth.1999.0892. [DOI] [PubMed] [Google Scholar]
- 101.Zhao Y, Brandish PE, Ballou DP, Marletta MA. Proc Natl Acad Sci USA. 2000;96:14753–14758. doi: 10.1073/pnas.96.26.14753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Ballou DP, Zhao Y, Brandish PE, Marletta MA. Proc Natl Acad Sci USA. 2002;99:12097–12101. doi: 10.1073/pnas.192209799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Yu AE, Hu S, Spiro TG, Burstyn JN. J Am Chem Soc. 1994;116:4117–4118. [Google Scholar]
- 104.Stone JR, Sands RH, Dunham WR, Marletta MA. Biochem Biophys Res Comm. 1995;207:572–577. doi: 10.1006/bbrc.1995.1226. [DOI] [PubMed] [Google Scholar]
- 105.Andrew CR, George SJ, Lawson DM, Eady RR. Biochemistry. 2002;41:2353–2360. doi: 10.1021/bi011419k. [DOI] [PubMed] [Google Scholar]
- 106.Sage JT, Morikis D, Champion PM. Biochemistry. 1991;30:1227–1237. doi: 10.1021/bi00219a010. [DOI] [PubMed] [Google Scholar]
- 107.Sage JT, Morikis D, Li P, Champion PM. Biophys J. 1992;61:1041–1044. doi: 10.1016/S0006-3495(92)81912-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Ascenzi P, Giacometti GM, Antonini E, Rotilio G, Brunori M. J Biol Chem. 1981;256:5383–5386. [PubMed] [Google Scholar]
- 109.Duprat AF, Traylor TG, Wu GZ, Coletta M, Sharma VS, Walda KN, Magde D. Biochemistry. 1995;34:2634–2644. doi: 10.1021/bi00008a030. [DOI] [PubMed] [Google Scholar]
- 110.Decatur SM, Franzen S, DePillis GD, Dyer RB, Woodruff WH, Boxer SG. Biochemistry. 1996;35:4939–4944. doi: 10.1021/bi951661p. [DOI] [PubMed] [Google Scholar]
- 111.Thomas MR, Brown D, Franzen S, Boxer SG. Biochemistry. 2001;40:15047–15056. doi: 10.1021/bi011440l. [DOI] [PubMed] [Google Scholar]
- 112.Reynolds MF, Parks RB, Burstyn JN, Shelver D, Thorsteinsson MV, Kerby RL, Roberts GP, Vogel KM, Spiro TG. Biochemistry. 2000;39:388–396. doi: 10.1021/bi991378g. [DOI] [PubMed] [Google Scholar]
- 113.Huang L, Abu-Soud HM, Hille R, Stuehr DJ. Biochemistry. 1999;38:1912–1920. doi: 10.1021/bi981954t. [DOI] [PubMed] [Google Scholar]
- 114.Couture M, Adak S, Stuehr DJ, Rousseau DL. J Biol Chem. 2001;276:38280–38288. doi: 10.1074/jbc.M105341200. [DOI] [PubMed] [Google Scholar]
- 115.Voegtle HL, Sono M, Adak S, Pond AE, Tomita T, Perera R, Goodin DB, Ikeda-Saito M, Stuehr DJ, Dawson JH. Biochemistry. 2003;42:2475–2484. doi: 10.1021/bi0271502. [DOI] [PubMed] [Google Scholar]
- 116.Pinakoulaki E, Stavrakis S, Urbani A, Varotsis C. J Am Chem Soc. 2002;124:9378–9379. doi: 10.1021/ja0271633. [DOI] [PubMed] [Google Scholar]
- 117.Taoka S, Banerjee R. J Inorg Biochem. 2001;87:245–251. doi: 10.1016/s0162-0134(01)00335-x. [DOI] [PubMed] [Google Scholar]
- 118.Kharitonov VG, Sharma VS, Magde D, Koesling D. Biochemistry. 1997;36:6814–6818. doi: 10.1021/bi970201o. [DOI] [PubMed] [Google Scholar]
- 119.Lukat-Rodgers GS, Rodgers KR. Biochemistry. 1997;36:4178–4187. doi: 10.1021/bi9628230. [DOI] [PubMed] [Google Scholar]
- 120.Rodgers KR, Lukat-Rodgers GS, Tang L. J Biol Inorg Chem. 2000;5:642–654. doi: 10.1007/s007750000150. [DOI] [PubMed] [Google Scholar]
- 121.Toellner TS. Hyp Int. 2000;125:3–28. [Google Scholar]
- 122.Lipkin HJ. Ann Phys (NY) 1962;18:182. [Google Scholar]
- 123.Sturhahn W. Hyp Int. 2000;125:149–172. [Google Scholar]
- 124.Frisch MJ, et al. Gaussian 98, revision A.3. Gaussian, Inc.; Pittsburgh, PA: 1998. [Google Scholar]
- 125.Schafer A, Horn H, Ahlrichs R. J Phys Chem. 1992;97:2571. [Google Scholar]
- 126.Becke AD. J Chem Phys. 1993;98:5684. [Google Scholar]
- 127.Lee C, Yang W, Parr RG. Phys Rev B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 128.Wayland BB, Olson LW. J Am Chem Soc. 1974;96:6037–6041. doi: 10.1021/ja00826a013. [DOI] [PubMed] [Google Scholar]
- 129.Nasri H, Haller KJ, Wang Y, Huynh BH, Scheidt WR. Inorg Chem. 1992;31:3459–3467. [Google Scholar]
- 130.Hayes RG, Ellison MK, Scheidt WR. Inorg Chem. 2000;39:3665–3668. doi: 10.1021/ic000159c. [DOI] [PubMed] [Google Scholar]
- 131.Becke AD. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 132.Perdew JP. Phys Rev B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 133.Sturhahn W, Kohn VG. Hyp Int. 1999;123:367–399. [Google Scholar]
- 134.Choi IK, Liu Y, Feng D, Paeng KJ, Ryan MD. Inorg Chem. 1991;30:1832–1839. [Google Scholar]
- 135.Lipscomb LA, Lee BS, Yu NT. Inorg Chem. 1993;32:281–286. [Google Scholar]
- 136.Vogel KM, Kozlowski PM, Zgierski MZ, Spiro TG. J Am Chem Soc. 1999;121:9915–9921. [Google Scholar]
- 137.Tomita T, Hirota S, Ogura T, Olson JS, Kitagawa T. J Phys Chem B. 1999;103:7044–7054. [Google Scholar]
- 138.Cheng L, Novozhilova I, Kim C, Kovalevsky A, Bagley KA, Coppens P, Richter-Addo GB. J Am Chem Soc. 2000;122:7142–7143. [Google Scholar]
- 139.Wondimagegn T, Ghosh A. J Am Chem Soc. 2001;123:5680–5683. doi: 10.1021/ja004314y. [DOI] [PubMed] [Google Scholar]
- 140.Ogoshi H, Watanabe E, Yoshida Z, Kincaid J, Nakamoto K. J Am Chem Soc. 1973;95:2845–2849. [Google Scholar]
- 141.Kitagawa T, Abe M, Kyogoku Y. J Phys Chem. 1976;80:1181–1186. [Google Scholar]
- 142.Scheidt WR, Duval HF, Neal TJ, Ellison MK. J Am Chem Soc. 2000;122:4651–4659. [Google Scholar]
- 143.Ghosh A, Wondimagegn T. J Am Chem Soc. 2000;122:8101. [Google Scholar]
- 144.Scheidt WR, Frisse ME. J Am Chem Soc. 1975;97:17–21. doi: 10.1021/ja00834a005. [DOI] [PubMed] [Google Scholar]
- 145.Wyllie GRA, Scheidt WR. Inorg Chem. 2003;42:4259–4261. doi: 10.1021/ic034364e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Scheidt WR, Lee YJ, Hatano K. J Am Chem Soc. 1984;106:3191. [Google Scholar]
- 147.Vogel KM, Kozlowski PM, Zgierski MZ, Spiro TG. Inorg Chim Acta. 2000;297:11–17. [Google Scholar]
- 148.Spiro TG, Zgierski MZ, Kozlowski PM. Coord Chem Rev. 2001;219 [Google Scholar]
- 149.Franzen S, Fritsch K, Brewer SH. J Phys Chem B. 2002;106:11641–11646. [Google Scholar]
- 150.Franzen S. J Am Chem Soc. 2002;124:13271–13281. doi: 10.1021/ja017708d. [DOI] [PubMed] [Google Scholar]
- 151.Coyle CM, Vogel KM, Rush TS, III, Kozlowski PM, Williams R, Spiro TG, Dou Y, Ikeda-Saito M, Olson JS, Zgierski MZ. Biochemistry. 2003;42:4896–4903. doi: 10.1021/bi026395b. [DOI] [PubMed] [Google Scholar]
- 152.Ellison MK, Scheidt WR. J Am Chem Soc. 1997;119:7404–7405. [Google Scholar]
- 153.Wyllie GRA, Scheidt WR. Chem Rev. 2002;102:1067–1090. doi: 10.1021/cr000080p. [DOI] [PubMed] [Google Scholar]
- 154.Abe M, Kitagawa T, Kyogoku Y. J Chem Phys. 1978;69:4526–4534. [Google Scholar]
- 155.Potter WT, Tucker MP, Houtchens RA, Caughey WS. Biochemistry. 1987;26:4699–4707. doi: 10.1021/bi00389a016. [DOI] [PubMed] [Google Scholar]
- 156.Kerr E, Yu N-T. Vol. 3. Wiley-Interscience; New York: 1988. Vibrational Modes of Coordinated CO, CN−, O2, and NO; pp. 39–95. Chapter 2. [Google Scholar]
- 157.Li XY, Spiro TG. J Am Chem Soc. 1988;110:6024–6033. doi: 10.1021/ja00226a017. [DOI] [PubMed] [Google Scholar]
- 158.Dong A, Caughey WS. Meth Enz. 1994;232:139–175. doi: 10.1016/0076-6879(94)32047-0. [DOI] [PubMed] [Google Scholar]
- 159.Hu S, Kincaid J. J Am Chem Soc. 1991;113:9760–9766. [Google Scholar]
- 160.Hirota S, Ogura T, Shinzawah-Itoh K, Yoshikawa S, Kitagawa T. J Am Chem Soc. 1996;110:15274–15279. [Google Scholar]
- 161.Perutz MF. Nature. 1970;228:726. doi: 10.1038/228726a0. [DOI] [PubMed] [Google Scholar]
- 162.Dickerson RE, Geis I. Hemoglobin: Structure, Function, Evolution, and Pathology. Benjamin/Cummings; Menlo Park, CA: 1983. [Google Scholar]
- 163.Šrajer V, Reinisch L, Champion PM. J Am Chem Soc. 1988;110:6656–6670. [Google Scholar]
- 164.Perutz MF, Wilkinson AJ, Paoli M, Dodson GG. Annu Rev Biophys Biomol Struct. 1998;27:1–34. doi: 10.1146/annurev.biophys.27.1.1. [DOI] [PubMed] [Google Scholar]
- 165.Lim M, Jackson TA, Anfinrud PA. J Chem Phys. 1995;102:4355–4366. [Google Scholar]
- 166.Watanabe T, Ama T, Nakamoto K. J Phys Chem. 1984;88:440–445. [Google Scholar]
- 167.Proniewicz LM, Paeng IR, Nakamoto K. J Am Chem Soc. 1991;113:3294–3303. [Google Scholar]
- 168.Bersuker IB, Stavrov SS. Coord Chem Rev. 1988;88:1–68. [Google Scholar]
- 169.Ye X, Demidov A, Champion PM. J Am Chem Soc. 2002;124:5914–5924. doi: 10.1021/ja017359n. [DOI] [PubMed] [Google Scholar]
- 170.De Angelis F, Car R, Spiro TG. J Am Chem Soc. 2003;125:15710–15711. doi: 10.1021/ja037373v. [DOI] [PubMed] [Google Scholar]
- 1.Dodd RE, Robinson PL. Experimental Inorganic Chemistry. Elsevier; New York: 1957. p. 253. [Google Scholar]
- 2.Adler AD, Longo FR, Finarelli JD, Goldmacher J, Assour J, Korsakoff L. J Org Chem. 1967;32:476. [Google Scholar]
- 3.Landergren M, Baltzer L. Inorg Chem. 1990;29:556. [Google Scholar]
- 4.Fleischer EB, Srivastava TS. J Am Chem Soc. 1969;91:2403. [Google Scholar]
- 5.Hoffman AB, Collins DM, Day VW, Fleischer EB, Srivastava TS, Hoard JL. J Am Chem Soc. 1972;94:3620. doi: 10.1021/ja00765a060. [DOI] [PubMed] [Google Scholar]
- 6.Stolzenberg AM, Strauss SH, Holm RHJ. Am Chem Soc. 1981;103:4763. [Google Scholar]
- 7.Dolphin D, Sams JR, Tsin TB, Wong KJ. Am Chem Soc. 1976;98:6970. doi: 10.1021/ja00438a037. [DOI] [PubMed] [Google Scholar]
- 8.Scheidt WR, Frisse MEJ. Am Chem Soc. 1975;97:17–21. doi: 10.1021/ja00834a005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


