Modelling the masticatory biomechanics of a pig

Abstract

The relationships between muscle tensions, jaw motions, bite and joint forces, and craniofacial morphology are not fully understood. Three-dimensional (3-D) computer models are able to combine anatomical and functional data to examine these complex relationships. In this paper we describe the construction of a 3-D dynamic model using the anatomical (skeletal and muscle form) and the functional (muscle activation patterns) features of an individual pig. It is hypothesized that the model would produce functional jaw movements similar to those recordable in vivo. Anatomical data were obtained by CT scanning (skeletal elements) and MR imaging (muscles). Functional data (muscle activities) of the same animal were obtained during chewing by bipolar intramuscular electrodes in six masticatory muscles and combined with previously published EMG data. The model was driven by the functional data to predict the jaw motions and forces within the masticatory system. The study showed that it is feasible to reconstruct the complex 3-D gross anatomy of an individual's masticatory system in vivo. Anatomical data derived from the 3-D reconstructions were in agreement with published standards. The model produced jaw motions, alternating in chewing side, typical for the pig. The amplitude of the jaw excursions and the timing of the different phases within the chewing cycle were also in agreement with previously published data. Condylar motions and forces were within expected ranges. The study indicates that key parameters of the pig's chewing cycle can be simulated by combining general biomechanical principles, individual-specific data and a dynamic modelling approach frequently used in mechanical engineering.

Introduction

The masticatory system is a complicated combination of several paired anatomically complex muscles and a mandible supported by two interlinked joints. Relationships among muscle tensions, jaw motions, bite and joint forces, and craniofacial morphology are not fully understood, and critical information is often difficult or impossible to obtain in experiments on living humans. A bioengineering model has been developed in which an artificial skull is used with motors representing the jaw muscles (Takanashi, 1989). This robot has been used to examine the breakdown of an artificial food bolus (Ohtsuki et al. 1995). But even when structural or functional data can be obtained, methods for integrating their analysis often express correlations rather than describing cause and effect. Since the early 1990s, however, it has been possible to combine available experimental data in computer models of biological function (lower back: McGill, 1992; leg: Delp & Zajac, 1992; Hawkins, 1992; shoulder: van der Helm et al. 1992). These models are most beneficial when their anatomical features are expressed in three spatial dimensions and derived, as the functional inputs (such as muscle activation patterns), from living material. Static and dynamic models of the human masticatory system have been used to predict, often unmeasurable, variables like muscle-induced skeletal stresses, strains and deformation (Korioth & Hannam, 1990; Tanaka et al. 1994; van Eijden, 2000), and dynamic changes in muscle tension, jaw position and articular mechanics (Koolstra & van Eijden, 1995; Langenbach & Hannam, 1999).

The practical limitations inherent in human studies include the inability to manipulate the anatomy a priori, to provide adequate control groups and to record sufficient biological data. This has encouraged the use of laboratory animals having musculoskeletal anatomy, patterns of muscle use and jaw motions considered generally analogous to those in humans. Unfortunately, many characteristics are not present in non-human primates, and none of the criteria is satisfied by the rodents and carnivorans commonly used for this purpose (Langenbach & van Eijden, 2001). This is particularly evident with respect to the temporomandibular articulation, where only higher primates and the pig seem to have systems anatomically and functionally close to that in humans (Herring, 1995). Notwithstanding the advantages and disadvantages of various experimental animal models, there remains a universal need to express their functional jaw biomechanics formally, if only to permit the identification of similar and dissimilar operational factors between orders and families. A computer modelling approach used for this purpose in living animals would be especially useful in longitudinal studies concerned with growth.

In this paper we describe the construction of a three-dimensional (3-D) dynamic model using the anatomical (skeletal and muscle form) and the functional (muscle activation patterns) features of an individual pig. We hypothesized that this model, tailored for one specific pig but functioning along similar biomechanical principles used in current human masticatory models (Koolstra & van Eijden, 1995; Langenbach & Hannam, 1999), would produce functional jaw movements similar to those recordable in vivo. The model was therefore verified by the comparison of the predicted and previously published data on masticatory jaw motion in the pig. After verification, such a model would invite comparisons between muscular and articular tensions and forces in pigs and humans, and could be used in future studies to assess the biomechanical consequences of growth, and the effects of surgical or other alterations to the craniomandibular musculoskeleton.

Methods

Musculoskeletal morphology

To visualize and measure the major structural elements of the craniofacial musculoskeleton, we imaged the entire head of an anaesthetized, young female miniature pig (Sus scrofa, 8–10 months) on two separate occasions. CT and MR scans were performed under general anaesthesia (isoflurane). In both instances, the animal was prone, with the jaw closed and the teeth fully intercuspated. Both data-sets were imported into image-analysis software (3DVIEWNIX, University of Pennsylvania, USA) on a Unix workstation (Indigo Extreme, Silicon Graphics Inc., CA, USA). We modified the software to permit specification of voxel face co-ordinates (in mm) relative to common origins in the two data sets.

Skeletal anatomy

To reveal the craniofacial skeleton and teeth, contiguous frontal plane CT slices (0.49 mm per pixel, in a 512 × 512 matrix) were obtained at 1-mm intervals. To determine the mass properties of the jaw and the position of the bite points and joints, voxel-based CT reconstructions of the mandible and skull were created (Fig. 1a). For the calculation of the jaw's mass we used the grey-scale of the voxels to estimate the bone content in each of them (Zhang et al. 2001), resulting in the total bone volume and bone mass, excluding the bone marrow (Fig. 1c). For modelling purposes, clusters of markers were placed on the CT-reconstructions of the entire mandibular surface (including the condyles) and the skull's articular fossae. These ‘point-clouds’ of vertices were most densely distributed in regions of rapidly changing anatomical shape, and less so in flat areas. The vertex co-ordinate triads were imported into software designed for automatic surface reconstruction (Wrap 1.1, Geomagic). This produced topologically consistent meshes exportable to the dynamic solver used for modelling. The massless shells thus represented various parts of the mandible, cranium and dentition. A right-handed co-ordinate system was used to express the 3-D geometry. The origin was midway between the condyles, with positive x-, y- and z-axes directed to the pig's left, cranially and anteriorly (parallel to the occlusal plane), respectively.

Fig. 1.

Three-dimensional reconstruction and modelling of the pig's masticatory system. (a) Caudal (right) and ventral (left, transparent jaw) view of the reconstructed skull and mandible (dark grey), as derived from CT-scans. (b) A horizontal MR-image showing cross-sections ofthe masseter (ms) and medial pterygoid muscles (mp). At the top of the image the snout can be seen with the mandibular teeth. (c) Superimposition of both the skeletal and the muscular reconstructions. A part of the skeletal reconstruction is removed to show the marrow cavity, whichwas excluded from the estimation of the bone mass properties. (d) A latero-frontal view of theconstructed computer model, showing a massless shell representing the mandible and all defined forces depicted by lines.

Muscle anatomy

To estimate the cross-sectional area and the action lines of the masticatory muscles, contiguous frontal plane MR slices (0.94 mm per pixel, in a 256 × 256 matrix) were made at 1.5-mm intervals to reveal the craniomandibular muscles. The jaw muscles were reconstructed by interactively tracing their individual outlines on each MR slice (Fig. 1b). Separate reconstructions were made for the right and left temporalis, masseter, medial pterygoid, lateral pterygoid and digastric muscles. For the measurement of muscle cross-sectional areas, we reformatted the grey-scale whole-muscle volumes into multiple slices perpendicular to the visual long-axis of each muscle. In each case, between five and 10 of these 1.5-mm-thick, reformatted slices were cut through the widest girth of the muscle. The closed outline of each slice was then traced, and its cross-sectional area (in cm²) was measured. The greatest value in each set was used to represent the functional cross-sectional area of the muscle, and it was multiplied by a constant of 40 N cm⁻² (Weijs & Hillen, 1985) to estimate the muscle's maximum possible tension (Table 1). For the muscle mass comprising the masseter and the zygomaticomandibularis, the lower and upper parts (for, respectively, SM and ZM) were sectioned perpendicular to the local regional line of action (Herring & Scapino, 1973) before their cross-sectional measurements were made. According to major differences in fibre orientation, we assigned three parts to the temporalis muscle (zygomatic ZT, superficial ST and deep DT). As the zygomatic part is clearly separated, the cross-sectional area could easily be estimated. The cross-sectional area of the remaining two parts of the temporalis muscle (ST and DT) was measured and divided into two equal parts.

Table 1.

Anatomical data derived from the 3-D reconstruction of the skeletal elements and muscles

	Derived data
Mandible
Mass (in g)	105.6*
3-D position (in mm)
Centre of mass	0.0, −54.5, 92.6
Incisor point	0.0, −52.0, 182.0
First molar right	−18.5, −35.8, 98.8
First molar left	18.5, −35.8, 98.8
Intercondylar width (in mm)	72.0
Moments of inertia (in kg mm−2)
Ixx	265.0
Iyy	315.0
Izz	144.0
Maximum possible muscle tension (in N)
Masseter	304.4
Zygomaticomandibularis	188.8
Temporalis, zygomatic part	64.8
Temporalis, superficial	73.2
Temporalis, deep	73.2
Medial pterygoid	226.8
Lateral pterygoid	100.4
Digastric	56.4

^*Estimated by the method described by Zhang et al. (2001).

For an approximation of the muscle action lines defined by both the muscle and the skull anatomy, the CT (bone) and MR (muscle) reconstructions had to be superimposed (Fig. 1c). A shell-structure of the muscles was created similar to the skeletal tissues created from the CT scans. Since the CT and MR data were obtained from machines with different resolutions, and as it was impracticable to fix the animal's head exactly the same way in each imager, this was achieved manually, by translating and rotating the assembled muscle set tri-axially until an anatomically adjudged ‘best fit’ was obtained. The many clear landmarks and contours provided by the well-defined, deep temporal fossae, zygomatic arches, mandibular ramus, and pterygoid region in the CT model, and the solid, complex, 3-D curvilinear shapes of the combined muscle set which had to fit multiple sites simultaneously, made this comparatively simple.

Our criteria for designating muscle attachment sites were based on previous anatomical descriptions by Herring & Scapino (1973), the reconstructed muscle images themselves and bone surfaces with known muscle attachments. Most attachment areas were unambiguous, allowing placement of markers on bony sites clearly demarcated by surrounding muscle. Only for the deep temporalis, the bulk and curvature of the muscle (Herring & Scapino, 1973) suggested action-lines based on the muscle's central axis, instead of a simple connection of the origin and insertion sites. While the attachment at the coronoid tip was considered bony (i.e. tendinous), the other end was positioned in the mediolateral centre of the visible muscle belly (i.e. at the ‘central aponeurosis’).

Model generation

The 3-D dynamic Model of a pig mastcatory system was constructed using the same approach we have described in detail elsewhere for humans (Langenbach & Hannam, 1999). In brief, the model utilized proprietary dynamic simulation software (ADAMS 9.0.4), and consisted of a mass representing the lower jaw. Actuators linking muscle attachment sites on the mandible to the cranium provided the input drive (see below). The jaw's motions relative to the spatially fixed cranium were restricted by various forces applied to different sites of the jaw. These forces included gravity, as well as those at the joints (reaction forces, tensile ligament forces), bite points (occlusal reaction forces, bolus resistance), and passive muscle tensions.

Table 1 shows the jaw's mass, mass centre and moments of inertia estimated from the CT scans by the method described by Zhang et al. (2001). Guidance for each of the jaw's condyles was furnished by a planar constraint aligned to the reconstructed cranial part of the temporomandibular joint (the latter is strikingly flat, and short anterior–posteriorly). During loaded motion, the condyle could indent this horizontal plane to provide some articular elasticity (i.e. the condylar reaction force increased exponentially to reach 1000 N at 0.25 mm displacement on compression). Full tri-axial rotation and planar translation of the condyle were permitted, and were frictionless. Condylar motion was restricted in the medio-lateral dimension by a medial wall, and forward motion was limited by elastic condylar ligaments.

The locations of three mandibular bite points (buccal cusp tip locations of the bilateral first molar and mid-incisor) were obtained from the reconstructed mandible. Reaction forces at these bite points were assumed to be perpendicular to a flat occlusal plane, and were generated when the jaw reached its theoretical ‘intercuspal position’, where the interocclusal contact force at each bite point increased exponentially to reach 2000 N with 0.25 mm interocclusal compression.

The model also accommodated an optional food bolus. For the masticatory acts in this study, we placed the bolus on the working side first molar (DP4) bite point. This bolus had a compressive resistance which depended on its thickness (equivalent to the distance separating the dental arches at that location). It was 3 mm thick, and soft-edged, i.e. its resisting force increased step-wise over the first 1.5 mm of compression, reaching a maximum of 60 N. Any force less than 60 N (or one of insufficient duration) thus resulted in incomplete bolus compression.

Model muscle physiology

Each muscle actuator included both fibre and tendon components. Fibre/tendon length ratios were defined according to Herring & Scapino (1973), Herring et al. (1984) and Anapol & Herring (1989). Muscle function was simulated as described previously by Langenbach & Hannam (1999). In brief, jaw motion was evoked by active muscle tensions generated by ‘contracting’ muscle fibres. Each muscle's active tension was determined by its maximum possible tension multiplied by a selected level of activation (0–1, where unity represents maximum muscle drive). This value (N) was also scaled according to the muscle's instantaneous length and shortening velocity by means of length–tension and velocity–tension curves appropriate for mammalian muscle (Zajac, 1989). Passive muscle tension induced by stretch and muscle damping were added to the active tension. Passive stretch tensions were mainly present for lengths beyond the optimal muscle lengths (Anapol & Herring, 1989). Because detailed information is lacking on this subject, the optimum length in all muscles was taken as the muscle length at an interincisal distance of 30 mm. For the masseter, this results in a situation similar to what was found by Anapol & Herring (1989). At 50% muscle stretch (Zajac, 1989), and 5% tendon stretch (Close, 1964; McMahon, 1984; Rack & Westbury, 1984; Proske & Morgan, 1987), these muscle parts were modelled to exert a passive force equal to the maximum possible active tension. Passively, the entire system was prevented from oscillating by damping forces in all the muscles. As the muscles have different orientation, 50% of the scaled critical damping coefficient (2mp, where m is the jaw's mass and p the circular frequency; scaling according to the size of the muscles) resulted in satisfactory stability (< 0.4 mm incisor point displacement). Oscillation totally disappeared as soon as active muscle forces were generated.

Simulations

To produce the masticatory cycles, we used activation profiles recorded from the same animal. Electromyographic (EMG) activity was recorded with indwelling wire electrodes (inserted under general anaesthesia with isoflurane) from all muscles except the temporalis. Recordings made unilaterally for some muscles could be extrapolated to the other side by examining another chewing cycle, since the pig chewed alternately left and right. For the temporalis muscle, we used profiles based on averaged measurements described previously for pig mastication by Herring & Scapino (1973). Time-based activation profiles (but not the absolute amplitudes) for the three parts of temporalis were assumed to be identical, which is supported by unpublished data. Each time-dependent profile representing muscle activation during chewing was shaped individually and interactively. In each case, key points in a putative, smoothed activation profile defined a β-spline function. The number of key points varied depending on the complexity of the profile, but included at least the definition of onset, peak activation and end of activity. The total cycle duration (∼350 ms) was defined by the periodical character of the muscle activation profiles.

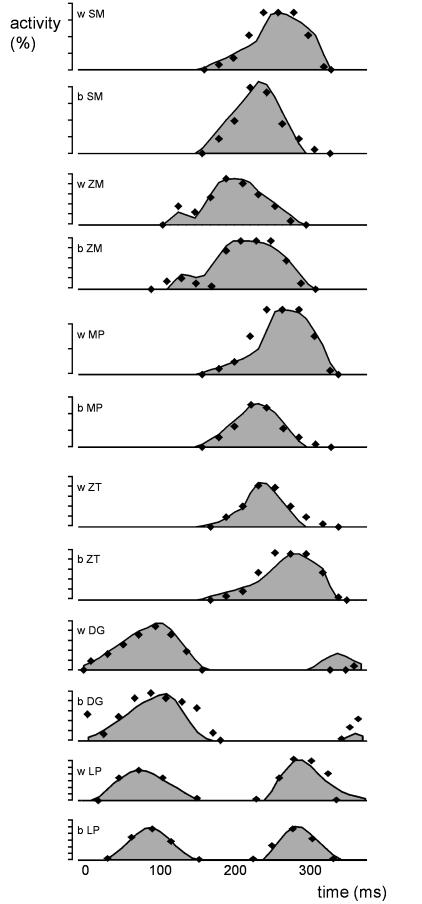
Because masticatory jaw motions are quite variable, the jaw motion predicted by the model was expected to comply with the published ranges found for maximum opening, laterodeviation, and timing of the opening, closing and power stroke phases of the pig chewing cycle (Herring & Scapino, 1973; Herring, 1976). During the power stroke phase the modelled food bolus had to be completely compressed. The interocclusal contact forces following bolus compression were not allowed to exceed 100 N. If a simulated cycle did not move the jaw conforming to these specifications described above, did not generate a complete bolus compression, or did generate occlusal forces higher than 100 N, the simulated cycle was rejected, and one or more of the initial muscle activation profiles was altered by fine-tuning its gain. We considered this step acceptable, since EMG data describing contraction amplitudes are unreliable indicators of absolute muscle drive. If this adjustment failed to satisfy the chewing-cycle design criteria, we then made minor changes to the shapes of the published drive profiles. The final shapes of the profiles we finally used conformed closely to the original EMG activity and were comparable to averaged activity profiles described by Herring & Scapino (1973) for natural mastication (Fig. 2). Note that the differences in EMG-profiles as seen in Fig. 2 are due to the activity patterns recorded in the individual, not due to the small adjustments to satisfy the chewing-cycle design criteria.

Fig. 2.

Comparison of the experimentally obtained (and modelled) EMG-profiles (grey area), and previously published EMG-profiles (dots) for the masticatory muscles of the pig. DG, digastric; LP, lateral pterygoid; MP, medial pterygoid; SM, superficial masseter; ZM, zygomaticomandibularis; ZT, temporalis; b, balancing side; w, working side.

We defined the beginning of each chewing cycle as the onset of digastric muscle activity. Within a pig chewing sequence, the activity patterns of the jaw closers and openers show a considerable time overlap (Herring & Scapino, 1973). Starting a simulation with immediate high muscle tensions is, however, equivalent to introducing an abrupt step function, causing dynamic instability in the first 10⁻⁴ s and creating large, uncharacteristic motions of parts of the model (see also Langenbach & Hannam, 1999). It also increases the calculation time. Therefore, our chewing cycles commenced with digastric and lateral pterygoid activity alone, and each was considered analogous to the initial cycle of a chewing sequence. We found lateral pterygoid drive was needed to counteract the posteriorly directed pull of the digastrics during opening, and at the start of the next cycle the onset of lateral pterygoid activation was similar to that described by Herring & Scapino (1973).

The ADAMS solver predicted the applied forces and the resultant motions of the jaw. We used the following parameters to analyse the model's performance: motion of the midline incisor-point and both condylar centres; reaction forces at the dental arch, food bolus and condyles; and the tensions generated within the muscles and the posterior joint ligament.

Results

Reconstruction

Table 1 summarizes the anatomical data derived from the CT and MR scans. It is noteworthy that most anatomical parameters could be obtained from a living individual. In this way, the gross anatomy of one specific individual could be modelled. Only intrinsic muscle features such as viscoelastic properties, fibre length and optimum muscle length were not attainable, and previously published values had to be used for these. Figure 1(d) shows the points of force application defined within the computer model, according to the obtained anatomical variables. During simulation, these points of force application were important for defining jaw motion.

Incisor point motion

The average muscle-drive patterns produced alternating-side chewing cycles typical for the pig (Fig. 3). The jaw's motion also complied with several other previously published characteristics of pig chewing, although large variation in jaw motion exists (Herring & Scapino, 1973; Herring, 1976). Average jaw excursions in both the vertical and the transverse dimensions were met with clearly submaximal muscle contractions, suggesting that the motion could be more extreme in both dimensions. Also, the timing of the different stages of chewing (opening, closing and the power stroke) were well within the published ranges for pig mastication (Table 2.

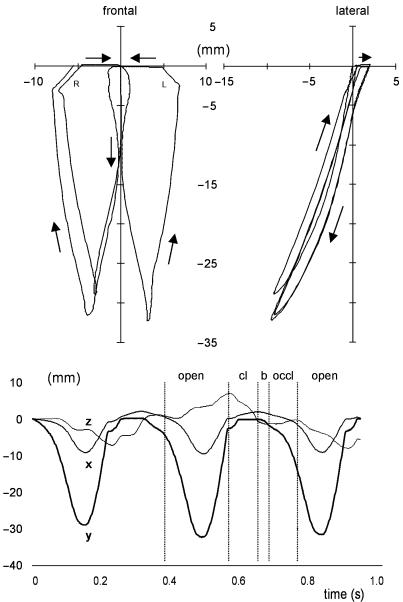
Fig. 3.

Incisor point motion (in mm) during three successive chewing cycles. The top panels represent a lateral (right) and frontal view (left) of the incisor pathway (arrows indicate the motion direction). The bottom figure shows the three motion components (x, anteroposterior; y, dorsoventral; and z, lateromedial) in time. The different phases are indicated for the second chewing cycle by vertical lines; open, jaw opening; cl, jaw closing; b, bolus crush; occl, occlusal (transverse) phase.

Table 2.

Comparison of the predicted incisor point motion with in vivo measurements (Herring & Scapino, 1973; Herring, 1976)

		In vivo measurements
	Predicted	Herring & Scapino (1973)	Herring (1976)
Motion characteristics (in mm)
Maximum opening	29.4–32.2	30–40
Maximum laterotrusion	6.9–8.0	5–13
Timing characteristics (in s)
Opening phase	0.125–0.140*	0.151–0.169	0.100–0.167
Closing phase	0.070–0.090	0.081–0.104	0.067–0.200
Transverse phase	0.120–0.150 †	0.079–0.086	0.033–0.167

^*Combined time of stages 4 and 5 (Herring, 1976). †Combined time of stages 2 and 3 (Herring, 1976).

Figure 3 shows that the three successive cycles modelled have different spatial ranges in the vertical and horizontal directions. This is most obvious in the first cycle, due to the motionless start in the intercuspal position, and the slightly different muscle activation pattern used for this cycle (see Methods). The other two cycles show small inequalities caused by small changes in jaw position and speed.

Close analysis of the second, left-sided chewing cycle revealed the start of jaw opening to be slow and in the midline, but after the first 5–10 mm of gape the rate of motion increased and the jaw deviated laterally. Maximum opening (33 mm) was followed by a fast closure of the jaw combined with a further laterodeviation (7 mm). When the artificial food bolus was reached, the jaw moved back to the midline, closing in a much slower fashion. Vertical jaw motion stopped entirely when the teeth came into contact, resulting in a horizontal slide back to the midline. Viewed laterally, jaw closing was posterior to jaw opening.

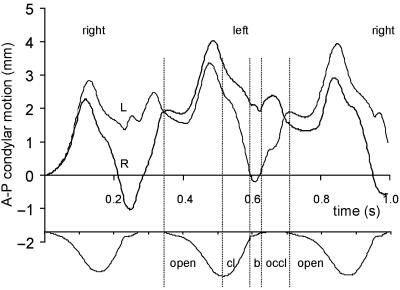
Condylar motion

The motions of the working and balancing side condyles are shown in Fig. 4 During the early stages of jaw opening, both condyles remained in a stable protruded (2 mm) position. Protrusion increased to 4 mm for the balancing side, and to 3 mm for the working side condyle. Condylar retrusion started well before the moment of maximum jaw opening. During jaw closing, the working side joint then retruded to its position at rest (or to a retruded position during the right-sided chews), and finally reached its initial position during bolus compression and the occlusal phase. The balancing side condyle continued to return to its initial position during jaw closing until the next cycle started. Lateral translations of both condyles were small, and restricted by their medial wall constraints.

Fig. 4.

Anteroposterior condylar motion (in mm) during the three successive chewing cycles in time: thick line, right condyle (R); thin line, left condyle (L). For clarity, the vertical incisor point motion is shown at the bottom of the figure. Vertical lines border the same events as indicated in Fig. 3. The chewing side is indicated at top of the figure.

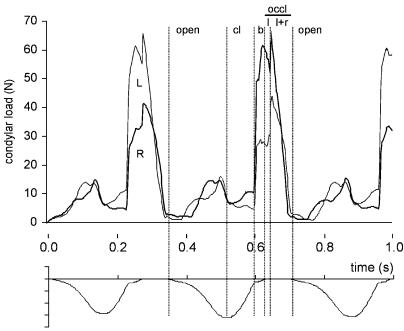
Articular forces

Figure 5 reveals that both joints were in compression during the predicted chewing cycles, although the loads were very low during initial jaw opening (2 N) and closing (5–10 N). Just before maximum jaw opening, the condylar loads increased slightly during the fast opening phase (16 N). They increased sharply, however, at the moment the food bolus was crushed. The increase was twice as large on the balancing side (60 N) than on the working side. This difference diminished as soon as bilateral dental occlusion was attained. During the last phase of occlusion, there was a rapid decrease in condylar loading.

Fig. 5.

Condylar forces (in N) during the three successive chewing cycles in time: thick line, right condyle (R); thin line, left condyle (L). For clarity, the vertical incisor point motion is shown at the bottom of the figure. Vertical lines border the same events as indicated in Fig. 3, and in addition the occlusal phase is divided into working side only occlusal contact (l) and bilateral occlusal contact (l + r).

Although both the medial walls and the posterior ligaments came into function during each of the chewing cycles, their maximum forces never exceeded 3 N. These peak values coincided with the occlusal phase, and late stages of jaw opening, respectively.

Discussion

The study showed that, with the increasing possibilities in information technologies and examination methods, it has become feasible to reconstruct the complex 3-D gross anatomy of an individual's masticatory system. From this reconstruction, we were able to derive many anatomical features, including the position, orientation and size of the jaw muscles, the position and orientation of the temporomandibular joints, the position of the bite points, and the mass properties of the mandible, which are altogether fundamental information necessary to compose a biomechanical model. To our knowledge, this biomechanical model of the masticatory system is the first that has been constructed for a single animal.

While it is clearly desirable to compare the predictions of models with experimental data (for review, see Hannam et al. 1997; Korioth, 1997), these data are often difficult or impossible to record in humans. Their absence is often the reason models were developed in the first place. Thus, most human models might best be considered as provisional hypotheses, using average anatomical information and data obtained in other body regions than the modelled system. Although we assigned arbitrary values to some important features (e.g. fibre and tendon length, optimum fibre length, viscoelastic properties), which were not, and cannot, be obtained non-invasively, we consider our approach offers a substantial improvement in the specificity of input parameters in a living population. We believe this may extend the usefulness of biomechanical modelling in comparative anatomical studies, in experiments involving anatomical intervention, and in studies of growth in experimental animals like the pig, since refined models can be made to include repeat measurements in living animals. Our dynamic model of the pig's chewing apparatus can be viewed as a first step in this process.

As the study wanted to model a living individual, assumptions had to be made about the intramuscular anatomical and physiological details. Some information on fibre/tendon length ratios was published (Herring & Scapino, 1973; Herring et al. 1984; Anapol & Herring, 1989) and included in the model. The optimum length of all muscles was assumed to be achieved at one specified jaw position. Although this resulted in a legitimate estimation for the masseter muscle (Anapol & Herring, 1989), this condition is probably absent in vivo. No information was available for the viscoelastic properties of the masticatory muscles. The assumption was made that the jaw motion had to be stable without decreasing the jaw's responsiveness to muscle activity. This was achieved by including in each muscle tension a damping force related to the size of the muscle and the critical damping coefficient. It is noteworthy that, despite all these assumptions, the model was able to predict a jaw motion, resembling the alternating pig's chewing cycle.

These assumptions were not tested for their influence on the predicted jaw motion. Both the muscle fibre lengths and optimum length relate closely to the susceptibility to muscle stretch. With increasing jaw opening, shorter fibres and shorter optimum lengths will generate earlier and larger passive muscle tension than longer fibres and optimum lengths. A study examining the biomechanics of the human masticatory system (Langenbach & Hannam, 1999) revealed that jaw motion becomes considerably restricted when the optimum muscle lengths were defined at a jaw position with the teeth just 2 mm apart. When the optimum lengths were defined at a jaw position with the teeth 12 mm apart, a position at which the largest bite force can be generated (Manns et al. 1979), the restriction was more in accordance with the situation in vivo. The same results can be expected with shorter fibre length. The assumptions about optimum length and fibre length made in this study enabled a normal functioning of the jaw. Furthermore, despite major anatomical differences in human and pig musculoskeletal architecture, and in muscle activation during chewing, mathematical dynamic models (human: Koolstra & van Eijden, 1995; Langenbach & Hannam, 1999; pig: this study) can successfully produce the different masticatory cycles typical of each species. We suggest the ability of the same basic model to predict plausible jaw motions in both the human and the pig chewing apparatus strengthens the validity of the principles on which it (and ones like it) has been built.

In the present study, the predicted jaw motion was expected to comply with previously published characteristics of pig chewing, i.e. maximum jaw opening, maximum laterodeviation of the jaw, and the timing of various parts of the chewing cycle. All these requirements were met. Although the total length of the chewing cycle was predefined by the cycle duration of the muscle activity patterns (∼350 ms), the predicted durations of jaw opening, closing and power stroke were not, since these were also affected by the passive, viscoelastic properties of the muscles. Moreover, the alternating chewing pattern was the result of clearly submaximal muscle contractions, suggesting that the motion can easily be altered into more variable (in distance and time) jaw excursions. Jaw motion data from published studies show considerable variations in laterodeviation of the jaw and in the way the pelleted food bolus is crushed (Herring, 1976). The modelled food bolus is equal for each chew, a situation not existing in the live animal. Moreover, the bolus is soft-edged for a gradually increasing vertical resistance, but does not exert any horizontal resistance to the molar motion. This results in a smooth process of food-crushing, beneficial in the complex estimation of jaw motion, but quite different from the crushing of pelleted food.

It is notable that despite the use of relatively simple characteristics to produce plausible incisor point motion, several more complex features of the pig's chewing cycle were revealed. First, the incisor point tracked more posteriorly during closing than in opening. This feature has also been described by Herring & Scapino (1973). According to these authors, it is the result of protrusion (1–2 mm) during the power stroke, and indeed protrusion was seen during the power stroke in the model (see Fig. 3). Second, the predicted jaw motion around maximum opening was quite pointed, resembling previous descriptions (Herring, 1976; Herring & Wineski, 1986).

In contrast with that in the human masticatory system, the pig's mandibular condyle is restricted by a strong posterior attachment of the temporomandibular joint disc. Although this ligament was modelled, it did not play an important functional role during the predicted chews, as protrusive condylar motion was small. Moving the jaw in anaesthetized animals reveals that the condyle is readily protruded to a maximum excursion of about 5 mm, and retruded over about 4 mm (Sun et al. 2002), a range larger than the predicted condylar motions during chewing. Large forward motions within the pig joint are presumably undesirable as the articular eminence is short anteroposteriorly, and in this sense the thick posterior attachment may be seen as a protection against excessive forward motion of the condyle.

The condylar forces predicted for the pig chewing cycle were comparable in amplitude with those found in models of the human masticatory cycle (Langenbach & Hannam, 1999), strengthening the idea that the pig can be a useful biological model for human temporomandibular joint research. Liu & Herring (2000) examined bone pressure in the condyle and temporal eminence during stimulated contraction of the masseter and lateral pterygoid muscles. Masseter activation resulted in large internal bony pressures and bone strains. In general, the loads were lower, and opposite in direction during lateral pterygoid contraction. Although it can be expected that the combined action of all jaw closers will have a much larger effect on the joint structures than the actions of the jaw opening muscles, their study shows the load caused by lateral pterygoid can be considerable. The reported resulting strains are consistent with a previous study (Marks et al. 1997) in which bone strains were observed during masseter and temporalis contractions. Combining these strains with the measured stiffness of the pig condyle (Teng & Herring, 1996) provides an estimated condylar loading during chewing of about 135 N, which is about twice the peak load predicted by the model for chewing. It should be noted here that the model's joint was assumed to be a point-contact, while in vivo it is variable in size and location on the condyle, depending on the position of the jaw and the amount of loading (Beek et al. 2001).

In conclusion, our study indicates that key parameters of the pig's chewing cycle can be simulated by combining general biomechanical principles, individual-specific data, and a dynamic modelling approach frequently used in mechanical engineering. The results also suggest the jaw's articular ligaments, while protecting the joint during extreme motions, may be less necessary during normal mastication. Perhaps most importantly, the ease with which models like this can be altered prior to, and in accordance with, experimental findings suggests they may be useful in future studies of articular biomechanics in the pig.