Force- and moment-generating capacities of muscles in the distal forelimb of the horse

Abstract

A detailed musculoskeletal model of the distal equine forelimb was developed to study the influence of musculoskeletal geometry (i.e. muscle paths) and muscle physiology (i.e. force–length properties) on the force- and moment-generating capacities of muscles crossing the carpal and metacarpophalangeal joints. The distal forelimb skeleton was represented as a five degree-of-freedom kinematic linkage comprised of eight bones (humerus, radius and ulna combined, proximal carpus, distal carpus, metacarpus, proximal phalanx, intermediate phalanx and distal phalanx) and seven joints (elbow, radiocarpal, intercarpal, carpometacarpal, metacarpophalangeal (MCP), proximal interphalangeal (pastern) and distal interphalangeal (coffin)). Bone surfaces were reconstructed from computed tomography scans obtained from the left forelimb of a Thoroughbred horse. The model was actuated by nine muscle–tendon units. Each unit was represented as a three-element Hill-type muscle in series with an elastic tendon. Architectural parameters specifying the force-producing properties of each muscle–tendon unit were found by dissecting seven forelimbs from five Thoroughbred horses. Maximum isometric moments were calculated for a wide range of joint angles by fully activating the extensor and flexor muscles crossing the carpus and MCP joint. Peak isometric moments generated by the flexor muscles were an order of magnitude greater than those generated by the extensor muscles at both the carpus and the MCP joint. For each flexor muscle in the model, the shape of the maximum isometric joint moment–angle curve was dominated by the variation in muscle force. By contrast, the moment–angle curves for the muscles that extend the MCP joint were determined mainly by the variation in muscle moment arms. The suspensory and check ligaments contributed more than half of the total support moment developed about the MCP joint in the model. When combined with appropriate in vivo measurements of joint kinematics and ground-reaction forces, the model may be used to determine muscle–tendon and joint–reaction forces generated during gait.

Introduction

The distal forelimbs of horses experience high loads during locomotion, particularly during athletic activities such as galloping and landing from jumps. Coincident with these high loads is the high incidence of injuries to forelimb joints and tendons. However, the relationship between musculoskeletal injuries and loads experienced in the limbs of athletic horses is not known. Furthermore, orthopaedic surgery is commonly performed on the forelimbs of horses, potentially altering the geometry and force–length properties of muscles (e.g. check ligament desmotomy; Alexander et al. 2001), and subsequently influencing their moment-generating capacity. Through a better understanding of the capacity and function of muscles in the distal forelimb, the aetiology of injuries and the mechanical and physiological effects of common orthopaedic surgeries can be assessed. This in turn may lead to improved treatment of injured animals.

Despite the high incidence of injury and interest in diseases of the carpus (Kawcak et al. 2001), to our knowledge only Dimery et al. (1986) have examined the loading of muscles acting about the carpus. By contrast, several studies have estimated or measured loading about the fore digit and metacarpophalangeal (MCP) joint (Bartel et al. 1978; Schryver et al. 1978; Dimery et al. 1986; Biewener, 1998; Willemen et al. 1999; Meershoek & Lanovaz, 2001; Meershoek et al. 2001a; Wilson et al. 2001a). Although peak strains may be underestimated in these models, the pattern of tendon strain across a gait cycle is very similar between model estimates and in vivo measures of strain (Riemersma et al. 1988; van den Bogert et al. 1989; van Weeren et al. 1992; Jansen et al. 1993a, 1998).

Previous studies have neglected to account for active muscle properties in calculations of forelimb muscle and joint loading during activity. Although passive structures such as the superior check, inferior check and suspensory ligaments may play a significant role in musculoskeletal loading of the MCP joint (e.g. Biewener, 1998), the extent of load sharing between the muscles and ligaments in the forelimb of the horse is currently not known. Indeed, when Wilson et al. (2001b) included a contractile model of muscle in their musculoskeletal model of the distal forelimb, they found that the deep and superficial digital flexor muscles played important roles in the attenuation of potentially injurious loads experienced by the forelimb.

Forelimb models previously reported in the literature have also represented muscle–tendon paths in two dimensions, with muscle moment arms modelled using pulleys of constant diameter (van den Bogert et al. 1989; Jansen et al. 1993a, b; Meershoek et al. 2001a). Recent findings suggest that moment arms in the equine forelimb vary as a function of the joint angle (Brown et al. 2003b).

We have developed a detailed musculoskeletal model of the distal equine forelimb to study the force-producing properties of muscles crossing the carpus and MCP joint. In this paper we address four specific questions. (1) What are the moment-generating capacities of the individual extensor and flexor muscles of the distal forelimb? (2) What is the relative influence of geometry (i.e. moment arms) and muscle physiology (i.e. force–length properties) on the maximum isometric joint moment–angle curves generated at the carpal and MCP joints? (3) In what region of the force–length curve does each muscle operate? (4) How do the muscles and ligaments (specifically, the superior check, inferior check and suspensory ligaments) share load during activity?

Materials and methods

Reconstruction of bone surfaces

Computed tomography (CT) scans were taken from one left Thoroughbred forelimb. One-millimetre slices were taken of the digit and the carpal bones. Three-millimeter slices were also taken of the shafts of the metacarpal bones, the radius and ulnar, and the humerus. The CT slices were rendered into three-dimensional polygon surfaces using image-processing software (Mimics, Materialize, USA). A decimation algorithm was used to reduce the number of polygons comprising the bone surfaces, while maintaining the original reconstructed bone volume and surface detail. Polygon surfaces were then converted to a format suitable for importing these data into a musculoskeletal modelling software package (SIMM, Musculographics, USA), which was used to develop models of the joints and muscle paths. The proximal and distal rows of carpal bones were treated as separate segments.

Musculoskeletal model

Bone-fixed reference frames were defined at the proximal end of each bone. The medio-lateral (y) axis of each reference frame was aligned with anatomical landmarks used to identify the approximate axis of rotation of the joint. The z-axis was aligned caudally along the long axis of each bone. The x-axis was formed by taking the vector cross-product of the y- and z-axes. The humeral reference frame was defined as the ground frame in the model.

The distal forelimb skeleton was represented as a five degree-of-freedom (dof) mechanical linkage comprised of eight bones (humerus, radius and ulna combined, proximal carpus, distal carpus, metacarpus, proximal phalanx, intermediate phalanx and distal phalanx) and seven joints (elbow, radiocarpal, intercarpal, carpometacarpal, MCP, proximal interphalangeal and distal interphalangeal joint). Based on anatomical descriptions given in the literature, the radiocarpal and MCP joints appear to function as simple 1-dof hinge joints (Leach & Dyson, 1988; Colahan et al. 1988). Leach & Dyson (1988) also noted that for much of carpal flexion, the centres of rotation of the intercarpal joint were located in the palmar third of the fourth carpal bone, suggesting that this joint also behaves as a hinge. Thus, the radiocarpal, intercarpal and MCP joints were each modelled as a 1-dof hinge. The proximal interphalangeal and distal interphalangeal joints were also represented as 1-dof hinge joints, but the elbow and carpometacarpal joints remained fixed in the model. The elbow angle was fixed at 150°, corresponding to the joint angle reported for quiet stance (Holmstrom et al. 1990). The carpometacarpal joint was locked by aligning the distal carpal and third metacarpal bones in the model (Kainer, 1987), and then rotating these bones until the joint space was approximately 1 mm across the entire joint surface.

To avoid articular surface interpenetration and to maintain a small joint space in the absence of articular cartilage, anterior–posterior and proximal–distal translations (as a function of joint angle) were introduced at each of the five hinge joints in the model: radiocarpal, intercarpal, MCP, proximal interphalangeal and distal interphalangeal joints. Because these translations were prescribed in the model, they were treated as kinematical constraints. Thus, 10 additional constraints were used to ensure that the bones articulated properly on one another during flexion–extension movements of the joints.

Anatomical landmarks at each muscle's origin and insertion were identified from descriptions found in anatomical texts (Pasquini et al. 1978; Kainer, 1987; Denoix, 1994) and by inspecting the surfaces of the reconstructed bones. For muscles inserting over a large area of bone, the centroid of the attachment area was taken as the attachment site. Each muscle's path was calculated from the origin of the muscle to its insertion, with intermediate via points added to prevent the muscle from penetrating the bone surfaces during joint movement.

The lines of action of nine muscles were represented in the model (Fig. 1). The lesser heads of the deep digital flexor, common digital extensor and flexor carpi ulnaris were combined and represented as the humeral heads of these muscles. The actions of the suspensory ligament (and its extension to the proximal phalanx as the palmar sesamoidian ligament) and the inferior and superior check ligaments were included in the model. The suspensory ligament formed a tendinous bone-to-bone connection that wrapped around and supported the MCP joint.

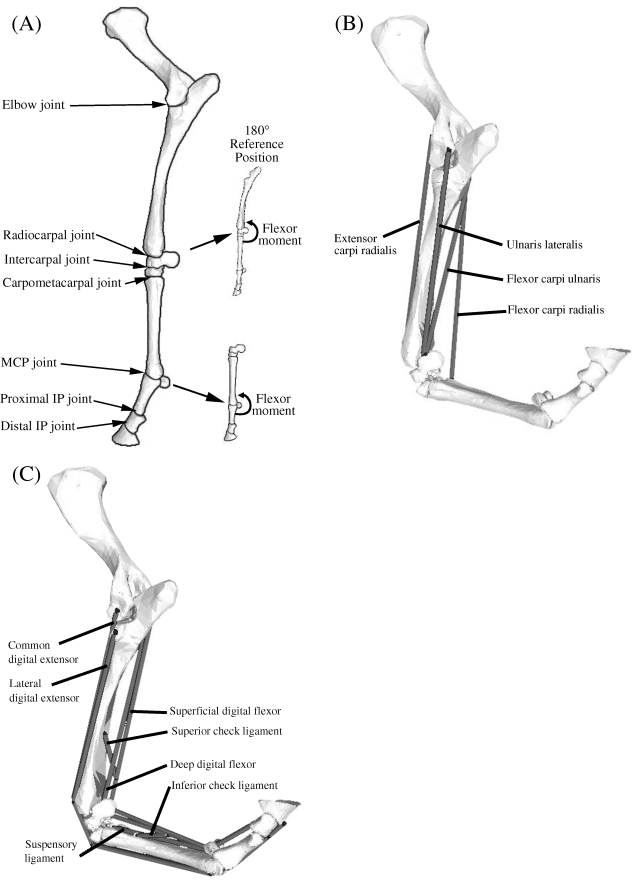
Fig. 1.

(A) Seven joints were included in the model of the equine forelimb: elbow, radiocarpal, intercarpal, carpometacarpal, metacarpophalangeal (MCP), proximal interphalangeal (IP) and distal interphalangeal (IP) joint. The reference position for the carpal and MCP joints was taken to be 180° with the limb extended, and flexor moments were defined on the caudal aspect of each joint as shown. (B) Computer-screen shot showing some of the muscles crossing the carpus in the model of the distal forelimb. Shown are the paths, origins, via points and insertions of the extensor carpi radialis, flexor carpi radialis, flexor carpi ulnaris and ulnaris lateralis. The abductor pollicis longus muscle is not shown as it is located behind the radius and ulnar bones. (C) Computer-screen shot showing the muscles and ligamentous structures crossing the MCP joint in the model. Shown are the paths, origins, via points and insertions of the superficial digital flexor, deep digital flexor, the suspensory ligaments, and the superior and inferior check ligaments. The common and lateral digital extensor muscles are also shown, the former obscured partially by its lateral counterpart. Note that the superior check ligament and the inferior check ligament are tendinous extensions of the deep digital flexor (DDF) and the superficial digital flexor (SDF), respectively.

Each musculotendon actuator was represented as a three-element, Hill-type muscle in series with an elastic tendon (Zajac, 1989; Pandy, 2001). Four parameters specified the force-producing properties of each actuator: peak isometric muscle force and the corresponding (optimum) muscle-fibre length, and pennation angle plus tendon slack length (Table 1). Values of these parameters were found by dissecting seven forelimbs procured from five Thoroughbred horses (Brown et al. 2003a). Optimal fibre length was assumed to be equal to resting fibre length. The physiological cross-sectional area (PCSA) of muscle was calculated as:

$$\text{PCSA}=\text{muscle volume}/\text{muscle-fibre length.}$$ (1)

Table 1.

Muscle properties assumed in the model of the distal forelimb

		(N)	(m)	(m)	αo (degrees)	%slow	kT (GPa)
Superficial digital flexor	SDF	9096.6	0.0075	0.7971	41.6	0.57a	2.03
Deep digital flexor	DDF	9504.3	0.0202	0.8230	21.6	0.39a	1.41
Suspensory ligament	SL	–	–	0.3307	–	–	1.41
Common digital extensor	CDE	1044.4	0.0814	0.7129	13.3	0.50	1.41
Lateral digital extensor	LDE	401.6	0.0422	0.5927	17.5	0.50	1.41
Ulnaris lateralis	UL	5731.1	0.0174	0.3700	34.3	0.50	1.41
Flexor carpi ulnaris	FCU	3982.5	0.0183	0.3625	31.6	0.40a	1.41
Flexor carpi radialis	FCR	535.5	0.0897	0.3647	6.7	0.36a	1.41
Extensor carpi radialis	ECR	2891.7	0.0760	0.4088	16.0	0.21b,c	1.41
Abductor pollicis longus	APL	607.4	0.0186	0.2200	22.6	0.50	1.41

Symbols indicated in the table are: 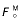, peak isometric force of muscle; 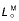, optimal muscle-fibre length at peak isometric force; α_o, muscle pennation angle at peak isometric force; 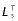, tendon slack length; %_slow, percentage of slow twitch muscle fibres; and k^T, tangent modulus of elasticity for tendon. Percentage of slow-twitch fibres was assumed to be 50% unless otherwise indicated;

^afibre-type data were taken from Hermanson & Cobb (1992)

^bHermanson (1997)

^cAndrews & Spurgeon (1986)

Muscle volume was determined as previously described (Brown et al. 2003a) using a submersion method, whereby the apparent weight of muscle immersed in water decreases by an amount equal to the weight of the volume of water displaced (Archimedes’ Principle). Maximum isometric muscle force was found by multiplying PCSA by maximum muscle stress, with the latter taken as 300 kPa (Wilson et al. 2001b). Optimum muscle-fibre length (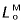) and pennation angle (α) were found by averaging the measurements obtained in vitro from the forelimb specimens.

Tendon was modelled using a linear force–length curve (Meershoek et al. 2001a). Tendon slack length (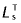) was estimated from the difference in musculotendon length (L^MT) and optimum muscle-fibre length, thus:

(2)

For each actuator, tendon slack length was determined with the carpus fully extended (i.e. joint angle of 180°) and with the MCP joint extended to 13° (i.e. joint angle of 193°). Similar configurations of these joints were used to define the slack lengths of the superior and inferior check ligaments and that of the suspensory ligament (Riemersma et al. 1988, 1996; van den Bogert et al. 1989; Jansen et al. 1993b; Meershoek et al. 2001a).

The elastic moduli of the digital flexor tendons, inferior check ligament and suspensory ligament were calculated from data reported by Cherdchutham et al. (2001), Lochner et al. (1980) and Meershoek et al. (2001a). The slopes of the stress–strain curves for the digital flexor tendons were on average 1.4 GPa (Table 1). The tendons of all muscles, except that of the superficial digital flexor, were assigned this value. As the superficial digital flexor experiences twice as much strain as the deep digital flexor (Dimery et al. 1986), the stiffness of the superficial digital flexor was calculated using strains of the order of 6% (see Table 1). The forces transmitted to the inferior check ligament, superior check ligament and suspensory ligaments in the model were estimated using force–strain data reported by Meershoek et al. (2001a).

Isometric simulations

Maximum isometric joint moments were calculated by fully activating all the extensor and flexor muscles crossing the carpal and MCP joints in the model. At 1° increments throughout the specified range of motion, all the muscles on one side of a joint (either the extensor or the flexor muscles) were fully activated, and muscle length, tendon length and the corresponding musculotendon actuator force were then found. The radiocarpal and intercarpal joints were each flexed 48° beginning from 8° of hyperextension, thereby creating 96° of total carpal flexion. The MCP joint was moved from 130° to 240°. These ranges were selected to correspond with available moment arm data (Brown et al. 2003b) and to include the ranges of joint motion normally seen in walking (Hodson et al. 2000), trotting (van Weeren et al. 1992) and in landing from a jump (Meershoek et al. 2001b).

Results

The three-dimensional paths of the forelimb muscles were accurately represented in the model. At the carpus, there was less than 1 mm difference between the calculated and measured values of the peak moment arms of ulnaris lateralis, flexor carpi ulnaris and flexor carpi radialis (Table 2). The calculated peak moment arms of the superficial and deep digital flexor muscles were also in close agreement with measured values, with mean differences between model and experiment of less than 5 mm (Table 2). At the MCP joint, peak moment arms of the modelled superficial and deep digital flexor muscles were within 2 mm of the values obtained from the in vitro experiments (Table 2). Larger differences were noted for the common and lateral digital extensors at both the carpal and the MCP joints; however, these differences were due mainly to inaccuracies in the experimental data obtained for these muscles (see Table 2). For MCP joint angles in the range 130–180°, experimental and model moment arms differed on average by only 3 mm.

Table 2.

Comparison of peak muscle moment arms calculated in the model and those obtained from the in vitro experiments reported by Brown et al. (2003b)

		Function	Model peak (mm)	Experiment peak (mm)	Mean absolute difference (mm)
Superficial digital flexor	SDF	Flex MCP	32.2	32.9	1.3
Deep digital flexor	DDF	Flex MCP	31.6	33.2	1.7
Common digital extensor	CDE	Ext MCP	24.0	13.7	9.1*
Lateral digital extensor	LDE	Ext MCP	22.2	10.5	8.9*
Superficial digital flexor	SDF	Flex carpus	37.2	41.3	5.1
Deep digital flexor	DDF	Flex carpus	31.3	35.2	3.6
Ulnaris lateralis	UL	Flex carpus	29.4	30.2	0.7
Flexor carpi ulnaris	FCU	Flex carpus	35.3	35.6	0.5
Flexor carpi radialis	FCR	Flex carpus	29.6	30.0	1.0
Common digital extensor	CDE	Ext carpus	33.6	25.6	8.5*
Lateral digital extensor	LDE	Ext carpus	25.7	22.0	8.1*
Extensor carpi radialis	ECR	Ext carpus	27.3	24.3	1.6
Abductor pollicis longus	APL	Ext carpus	8.1	5.7	5.3

Data are for nine muscles crossing the carpal and MCP joints; SDF, DDF, CDE and LDE are biarticular muscles and therefore have moment arms at both joints. Mean absolute difference is the mean of the absolute difference between moment arms determined at 10° intervals across the simulated range of motion for a specific joint. Forelimb muscles were classified by their ability to flex the MCP joint (Flex MCP), extend the MCP joint (Ext MCP), flex the carpal joints (Flex carpus), or extend the carpal joints (Ext carpus).

^*Mean differences between model and experimental moment arms were much larger for CDE and LDE than for the other forelimb muscles because the experimental data for these muscles were unreliable when the carpus and MCP joints were extended beyond 180° (see Brown et al. 2003b).

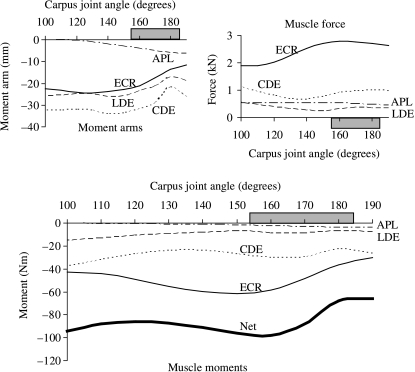
Peak isometric moments generated by the flexor muscles were an order of magnitude greater than those generated by the extensor muscles at both the carpal and the MCP joints. The peak isometric moment generated by all the flexor muscles at the MCP joint was 480 N.m, which occurred at an MCP joint angle of 240° (i.e. 60° of extension). By comparison, the peak isometric moment generated by all the extensor muscles was just 31 N.m at a joint angle of 220° (i.e. 40° of extension) (compare curves labelled ‘net’ in Figs 2 and 3). A similar difference was seen in the peak isometric moments generated by the flexor and extensor muscles of the carpus (compare curves labelled ‘net’ in Figs 4 and 5).

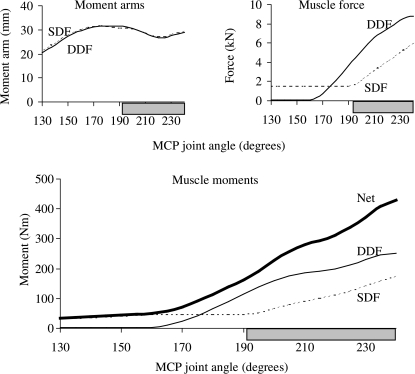
Fig. 2.

Joint moments, moment arms and forces calculated for the muscles that flex the MCP joint in the model. Peak net flexor moment occurred when the MCP joint was moved to 240° and coincided with peak muscle force (upper panel). Muscle force dominated the pattern of the joint moment–angle curves for the flexor muscles. The horizontal shaded bar indicates the joint angles associated with the stance phase of walking and trotting (van Weeren et al. 1993; Hodson et al. 2000).

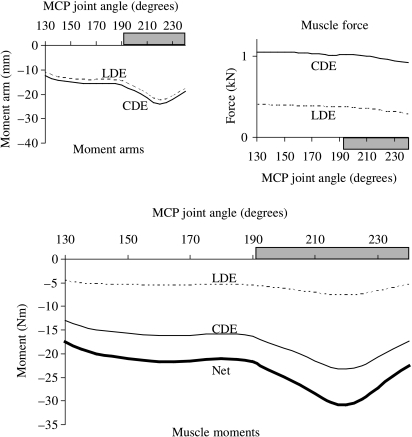
Fig. 3.

Joint moments, moment arms and forces calculated for the muscles that extend the MCP joint in the model. Peak net extensor moment coincided with the peaks in the moment arms of the common and lateral digital extensor muscles (upper panel). Muscle moment arms dominated the variation in joint moment over the simulated range of joint movement and for the joint angles associated with the stance phase of gait (horizontal shaded bar).

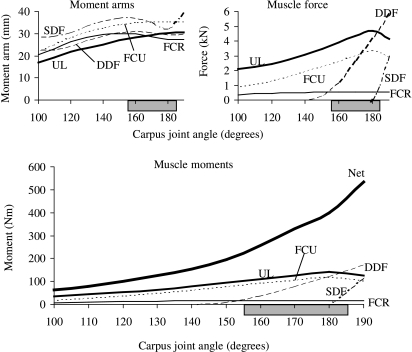
Fig. 4.

Joint moments, moment arms and forces calculated for the muscles that flex the carpal joint in the model. The net flexor moment peaked when the carpal joint was moved to 190° (i.e. 10° of joint extension). This joint angle coincided with the peak muscle force in the superficial and deep digital flexor muscles. The variation in muscle force dominated the joint moment–angle curves over the simulated range of joint movement. The horizontal shaded bar indicates the joint angles associated with the stance phase of walking and trotting (van Weeren et al. 1993; Hodson et al. 2000).

Fig. 5.

Joint moments, moment arms and forces calculated for the muscles that extend the carpus in the model. The peak net extensor carpal moment was due to the moment generated by the common digital extensor and extensor carpi radialis muscles. Muscle force and moment arm influenced the pattern of the joint moment–angle relationship. However, for the joint angles associated with the stance phase of gait (horizontal shaded bar), joint moment was influenced mainly by the variation in muscle moment arm.

The capacity of a muscle to generate a moment is explained by the product of its peak isometric force and its moment arm at the joint in question (i.e. 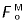× MA). For the forelimb muscles in the model, the flexor muscles generated significantly greater joint moments than the extensor muscles because the product 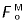× MA was much greater for each flexor than for each extensor muscle (Table 3). Indeed, the product 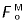× MA for all the flexor muscles of the carpus combined was eight times greater than that for all the extensor muscles (Table 3). The difference was even larger at the MCP joint, where the product 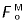× MA for all the flexor muscles was 21 times that for all the extensor muscles (Table 3).

Table 3.

Moment-generating capacities of muscles in the distal forelimb of the horse

		Function	Average MA (mm)	(N)	× MA (N.m)	× MA Combined (N.m)
Superficial digital flexor	SDF	Flex MCP	28.8	9096.6	261.9	Flexors
Deep digital flexor	DDF	Flex MCP	28.3	9504.3	268.7	530.6
Common digital extensor	CDE	Ext MCP	−17.6	1044.4	−18.4	Extensors
Lateral digital extensor	LDE	Ext MCP	−15.8	401.6	−6.4	−24.8
Superficial digital flexor	SDF	Flex carpus	33.7	9096.6	307.1
Deep digital flexor	DDF	Flex carpus	27.8	9504.3	264.0
Ulnaris lateralis	UL	Flex carpus	25.2	5731.1	144.4
Flexor carpi ulnaris	FCU	Flex carpus	31.5	3982.5	125.3	Flexors
Flexor carpi radialis	FCR	Flex carpus	27.1	535.5	14.5	855.3
Common digital extensor	CDE	Ext carpus	−30.2	1044.4	−31.6
Lateral digital extensor	LDE	Ext carpus	−23.0	401.6	−9.3
Extensor carpi radialis	ECR	Ext carpus	−20.4	2891.7	−59.1	Extensors
Abductor pollicis longus	APL	Ext carpus	−2.4	607.4	−1.4	−101.4

Peak isometric force (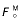) estimated for each muscle was multiplied by that muscle's average moment arm (MA) at the carpal and MCP joints to obtain an estimate of the moment-generating capacity of each muscle in the model (i.e. 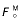× MA). The capacities of the digital flexor muscles at the MCP joint (SDF and DDF) were 21 times greater than those of the extensor muscles (CDE and LDE). Furthermore, the carpal flexor muscles had a far greater capacity to exert joint moments than the corresponding extensor muscles. The biarticular SDF, DDF, CDE and LDE cross both the carpal and the MCP joints and therefore exert moments at both joints simultaneously.

The product 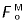× MA was greater for the flexor than the extensor muscles because the peak isometric forces of the flexor muscles were much higher – the moment arms of the flexor and extensor muscles at both the carpal and the MCP joints were roughly equal. For example, the superficial digital flexor in the model had a peak isometric force of 9096 N, whereas the common digital extensor developed only 1044 N in a maximum isometric contraction (Table 1). The moment arms of these muscles at the MCP joint were more or less equal, with peak values differing by approximately 8 mm (Figs 2 and 3 top left, compare SDF and CDE). Thus the moment-generating capacity of the superficial digital flexor at the MCP joint was much greater than that of the common digital extensor because the superficial digital flexor developed significantly greater force in a maximum isometric contraction.

Active muscle force rather than moment arm determined the variation in the joint moment–angle curves for all the flexor muscles in the model. More specifically, for both the carpal and the MCP joints, the shape of each flexor moment–angle curve was determined by the shape of its muscle force–angle curve because changes in muscle force were much larger than changes in moment arm over the range of motion of each joint (Figs 2 and 4, multiply the moment arm–angle curve by the muscle force–angle curve for each muscle and compare with the joint moment–angle curve below). Thus, the moment-generating capacity of each flexor muscle was influenced mainly by the force–length properties of the muscle and not by the muscle's moment arm.

For muscles that extend the MCP joint, the ability to generate a joint moment was determined mainly by the variation in the muscle's moment arm (Fig. 3). For example, the common digital extensor developed a nearly constant force over the full range of motion of the MCP joint, whereas its moment arm changed by a factor of two (Fig. 3, CDE, compare moment arm–angle curve at top left with joint moment–angle curve below). Thus, musculoskeletal geometry (i.e. muscle paths) rather than muscle properties determined the moment-generating capacities of the muscles that extend the MCP joint in the model.

The shapes of the joint moment–angle curves for the extensor muscles of the carpus were determined by the interaction between muscle force and moment arm (Fig. 5). In particular, peak isometric moment generated by the extensor carpi radialis occurred when the carpal joint angle was 150°, coinciding with the joint angle at which peak muscle force and moment arm occurred (Fig. 5, compare moment arm and muscle force curves above with moment–angle curve below).

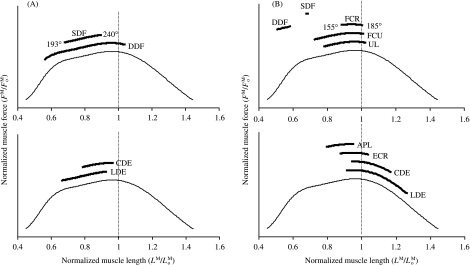
All the flexor muscles in the model operated near the plateau of the force–length curve for the joint angles associated with the stance phase of gait (Fig. 6, upper panels). Thus, these muscles remained at lengths at which maximum force could be developed. By comparison, some of the extensor muscles operated on the descending region of the force–length curve when the carpal joint was moved to 155° and the muscles were maximally activated (Fig. 6B). The common and lateral digital extensor muscles, in particular, could be stretched to lengths approaching 1.2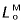, where significant passive muscle force may be generated (compare CDE and LDE in Fig. 6B,A).

Fig. 6.

Operating ranges of the muscles in the forelimb model corresponding to the range of joint angles commonly reported for the stance phase of walking and trotting (van Weeren et al. 1993; Hodson et al. 2000). Muscle force is normalized to peak isometric force (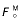) for each muscle in the model (vertical axis). Note that at a muscle length of 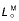, muscle force equals 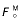. In all panels, the thin line is the standardized force–length curve used to calculate muscle force. (A) Muscles acting about the MCP joint were predicted to operate slightly below their optimal fibre length at the joint angles associated with the stance phase of gait. Thus, if the MCP joint was moved to joint angles beyond 240°, e.g. as in galloping (Butcher & Ashley-Ross, 2002), the superficial and deep digital flexor muscles would probably remain close to their optimal lengths. The joint range of motion for the MCP joint in walking and trotting is reported to be between 193° and 240° (van Weeren et al. 1993; Hodson et al. 2000). (B) At the carpus, the superficial and deep digital flexor muscles in the model operated at less than 0.74 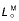for the joint angles associated with the stance phase of gait. The other carpal extensor and flexor muscles were estimated to be near their optimal lengths. The joint range of motion for the carpus in walking and trotting is reported to be between 155° and 185° (van Weeren et al. 1993; Hodson et al. 2000). Note that CDE, LDE, SDF and DDF all cross both the carpus and the MCP joint.

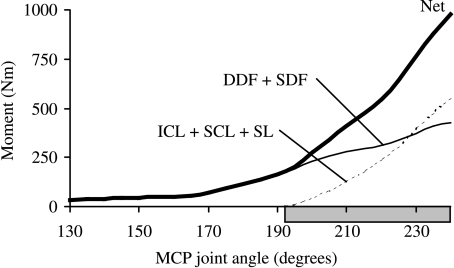
The superior check ligament, inferior check ligament, and suspensory ligament combined supported more than one-half of the total isometric moment developed about the MCP joint at maximum extension (Fig. 7, compare light solid and dashed lines at 240°). When all the flexor muscles were fully activated in the model, the peak net moment exerted about the MCP joint was 480 N.m. When the actions of the suspensory and check ligaments were included, however, the peak net flexor moment increased to 978 N.m when the joint was extended to 60° (i.e. joint angle of 240°) (Fig. 7, compare light solid and dashed lines with ‘net’). The contribution of the suspensory and check ligaments to the total support moment increased as a function of joint angle in the joint range of motion corresponding to the stance phase of gait (Fig. 7, dashed line). Specifically, for small angles of extension of the MCP joint, the ligaments contributed much less than all the flexor muscles combined.

Fig. 7.

Net isometric flexor muscle moments developed about the MCP joint in the model. Also shown are the joint moments contributed by the superior check ligament (SCL), the inferior check ligament (ICL) and the suspensory ligaments (SL). Note that the ligaments did not produce force when the MCP joint was moved to angles less than 190°. At MCP joint angles greater than 230°, however, the check and suspensory ligaments in the model produced a larger flexor moment at the MCP joint than did the superficial and deep digital flexor muscles. Joint angles greater than 190° are those associated with the stance phase of walking and trotting (horizontal shaded bar).

Discussion

The overall goal of this study was to determine the force- and moment-generating capacities of individual flexor and extensor muscles in the distal forelimb of the horse. Because this information cannot easily be obtained from experiment, a detailed computer model of the musculoskeletal system was developed and used to perform simulations of maximum muscle contractions under isometric conditions. The relative influence of muscle architecture and muscle moment arms on the shapes of the joint moment–angle curves was also studied, along with the contributions of the suspensory and check ligaments to the maximum moments developed about the joints.

A modelling approach was taken because of the difficulties associated with measuring muscle force in vivo (i.e. aside from ethical considerations, there are significant issues related to the accuracy and repeatability of such measurements; Zarucco et al. 2000). However, there are also limitations of the modelling approach taken in this study, the foremost related to the maximum isometric simulations performed. During walking, trotting, galloping and landing from jumps, the muscles of the distal forelimb lengthen and shorten during each step, whereas the model results are confined to isometric muscle contractions. Furthermore, all the muscles in the model were fully activated throughout the range of simulated motion, whereas in walking, for example, muscles act phasically and are only partially activated (Jansen et al. 1992). Also, during rotation of the carpal joint, the MCP joint was fixed at 193°, the joint position at initial ground contact in walking (Colborne et al. 1998). Because the MCP joint reaches more extended positions during gait, locking this joint at 193° when simulating maximum isometric contractions about the carpus may mean that the operating lengths and forces predicted for some muscles were underestimated in the model (e.g. superficial and deep digital flexor muscles; Figs 3 and 6).

An additional limitation of this study was that the model predictions could not be validated against maximum isometric joint moment–angle measurements for the horse. However, near-maximal loading conditions presumably exist during landing from jumps. As joint moments for landing have been reported (Meershoek et al. 2001b), maximum isometric moments determined from a simulation with the limb positioned for landing can be compared with the literature data. In the landing configuration, the peak isometric flexor muscle moments calculated for the carpal and MCP joints were 729 and 1020 N.m, respectively, which are within 30% of the peak joint moments reported for landing. Differences between the model estimates and those reported for landing can, in part, be explained by the isometric loading conditions assumed by the simulation. In landing from a jump, the muscles of the forelimb may be stretched and undergo significant eccentric loading. Because the model simulations do not include the effect of muscle's force–velocity property (i.e. the calculations assume isometric contractions), the maximum moments developed about the carpal and MCP joints will be underestimated in landing as well.

Finally, there are limitations associated with the forelimb model itself. First, anterior–posterior and proximal–distal translations were prescribed for five of the hinge joints in the model. The kinematic structure of joints in the equine forelimb is not precisely known, but the close correlation between calculated and measured moment arms (Brown et al. 2003b) suggests that the kinematic structure assumed for the model joints is reasonable. Second, the model was developed from origin and insertion data obtained from anatomical textbooks, architectural data collected from five horses (Brown et al. 2003a) and CT scans taken from one healthy Thoroughbred horse. Although the limb from which CT scans were obtained was also dissected as part of the muscle architecture study, the model represents a composite of data sets. This limitation was exemplified by the finding that the deep digital flexor in the model could produce force only up to an MCP joint angle of 159°. The optimum fibre length of the deep digital flexor in the model was set to 20.2 mm, the average length of the most abundant fibres dissected from this muscle. However, fibres greater than 100 mm in length have been reported in the literature (Hagen et al. 2002) and were also found in the muscle dissection study of Brown et al. 2003a). Fibres of this length would be capable of producing active force as the MCP joint was moved to angles less than 159°.

The finding that the forelimb flexor muscles have much greater moment-generating capacities than the extensor muscles is not surprising in view of gait data found in the literature. During the stance phase of gait, the forelimb experiences peak flexor joint moments at the carpal and MCP joints of approximately 300 N.m in walking (Colborne et al. 1997a, 1998; Clayton et al. 2000), 770 N.m in trotting (Clayton et al. 1998) and 1100 N.m in landing from a jump (Meershoek et al. 2001b). The peak extensor moments at the carpal and MCP joints for the swing phase of walking are reported to be only 14 and 3 N.m, respectively (Clayton et al. 2000). Thus, to accommodate the loads associated with gait, the distal forelimb of the horse must be capable of producing much larger flexor moments about the carpal and MCP joints. Furthermore, the extensor muscles are well suited to the large joint excursions (large 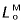) and relatively small loading requirements (small 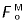) present during the swing phase of gait, whereas the flexor muscles are well adapted to producing large forces (large 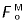) over a more limited range of motion (small 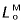) as is needed in stance.

The multi-articular superficial and deep digital flexor muscles provide the majority of support at the carpal and MCP joints during stance. Moreover, when the MCP joint angle reached 240°, the superior check, inferior check and suspensory ligaments contributed as much to support of the MCP joint as the superficial and deep digital flexor muscles. This is a particularly efficient mechanism to support body weight, as these structures provide large passive contributions, minimizing energy expenditure during running (Alexander, 1988). This is also a significant finding in view of the high incidence of injuries to the check and suspensory ligaments.

One particularly interesting finding of this study related to the abductor pollicis longus muscle. The equine distal forelimb primarily flexes and extends during gait, but the abductor pollicis longus has an extremely small extensor moment arm (< 5 mm) and, as evidenced in the model simulations, contributes very little to the net carpal extensor moment (Fig. 5). This muscle wraps around the carpus from its lateral–radial origin to a medial–metacarpal insertion, suggesting that in addition to extending the carpal joint it may also externally rotate the metacarpus on the antebrachium. The need for an external metacarpal rotator muscle in the equine distal forelimb is not clear, but the anatomically analogous human popliteus muscle, which assists in rotational stability of the human knee during flexion and extension (Harner et al. 1998), may provide some clues as to the role of abductor pollicis longus in the horse.

Computer modelling of the musculoskeletal system is an appealing adjunct to in vivo experimentation, especially when direct measurement of tissue force is not easy to obtain. Although the simulations performed in this study are limited by the assumption of maximum isometric muscle contractions, the results lend much insight into the maximum force- and moment-generating capacities of individual muscles crossing the carpal and MCP joints of the horse. When combined with appropriate in vivo measurements of joint kinematics and ground-reaction forces, the model may also be used to determine muscle–tendon and joint–reaction forces generated during gait. Detailed knowledge of muscle and joint–reaction forces could increase current understanding of injuries in athletic horses, and may eventually lead to improved methods for treatment and prevention.