Evaluating alternative gait strategies using evolutionary robotics

Abstract

Evolutionary robotics is a branch of artificial intelligence concerned with the automatic generation of autonomous robots. Usually the form of the robot is predefined and various computational techniques are used to control the machine's behaviour. One aspect is the spontaneous generation of walking in legged robots and this can be used to investigate the mechanical requirements for efficient walking in bipeds. This paper demonstrates a bipedal simulator that spontaneously generates walking and running gaits. The model can be customized to represent a range of hominoid morphologies and used to predict performance parameters such as preferred speed and metabolic energy cost. Because it does not require any motion capture data it is particularly suitable for investigating locomotion in fossil animals. The predictions for modern humans are highly accurate in terms of energy cost for a given speed and thus the values predicted for other bipeds are likely to be good estimates. To illustrate this the cost of transport is calculated for Australopithecus afarensis. The model allows the degree of maximum extension at the knee to be varied causing the model to adopt walking gaits varying from chimpanzee-like to human-like. The energy costs associated with these gait choices can thus be calculated and this information used to evaluate possible locomotor strategies in early hominids.

Introduction

Evolutionary robotics is defined as ‘the biology, intelligence, and technology of self-organizing machines (intelligent robotics and autonomous agents)’ (Nolfi & Floreano, 2000). As a field it is primarily concerned with investigating the learning and development of behaviours that can be loosely described as intelligent such as navigation and obstacle avoidance, but one aspect when dealing with legged robots is the automatic generation of walking and running gaits. Early work in this area looked at static gaits in six-legged robots: either using simulations (Beer & Gallagher, 1992) or by building physical robots (Lewis et al. 1992). In static gait the centre of mass is always above the support polygon formed by the feet on the ground, which means that the robot cannot fall over. More recently, dynamic gaits have been generated such as a trotting and pacing quadruped (Hornby et al. 1999). In dynamic gaits the centre of mass is continuously displaced inside and outside the support polygon, which means that it is very easy for the robot to fall over and consequently makes it much harder to generate a reliable gait. In all these experiments the morphology of the robot is fixed and an optimization procedure based on so-called ‘evolutionary algorithms’ used to program a control system that drives the actuators in the legs. This process is directly analogous to the reconstruction of gait in fossil vertebrates. The morphology is defined by the fossil record and the control system is assumed to be a sophisticated pattern generator that can generate efficient locomotion (Sellers et al. 2003).

There are two components to such a reconstruction. First, a model (either a simulation or a physical model) of the mechanics of the system has to be constructed. Although it is possible to construct biomimetic robots (see, for example, the various robots created by the MIT Leg Laboratory at http://www.ai.mit.edu/projects/leglab/robots/robots.html, or Karsten Berns’ online catalogue of walking machines at http://www.walking-machines.org/), these are extremely expensive and currently can only mimic the linear dimensions of the animal. As yet they cannot duplicate the inertial parameters of the body or the mechanical properties of the soft tissues. However, constructing biomimetic simulations is possible and there are commercial software packages specifically designed for this, including MSC.ADAMS (MSC.Software Corporation, Santa Ana, USA), SIMM (Musculographics Inc., Santa Rosa, USA), and MADYMO (TNO Automotive, Delft, The Netherlands). Similarly, there are a number of general rigid body dynamics simulators designed primarily for robotic use, including several freely downloadable ones such as Dynamechs (http://dynamechs.sourceforge.net) and Open Dynamics Engine (http://opende.sourceforge.net). These provide the necessary flexibility to allow them to be customized for biological use. Using such simulators and also custom-written software a large number of biomimetic simulations have been produced (e.g. Sellers, 1996; Crompton et al. 1998; Ogihara & Yamazaki, 2001; Li et al. 2002).

The second component required is a control system. This can be a simple finite state machine (Brooks, 1989; Sellers et al. 2003) or a more complex neural network (Yamazaki et al. 1996; Ijspeert et al. 1998). The controller generates the activation pattern required for locomotion and is itself controlled by a number of parameters. When using finite state controllers the parameters directly reflect muscle activation levels and are therefore very easy to interpret. With neural network-based controllers the parameters represent the weights associated with the interconnection in the neural net. This approach has the advantage of allowing easy inclusion of feedback mechanisms and sensors but the effects of the components and parameters are much harder to interpret in mechanical terms.

In a biomimetic gait controller the number of parameters has to be sufficient to allow the simulation to produce locomotor movements that match those seen in the subject animal. However, each additional parameter adds an extra dimension to the search space and therefore greatly increases the size of the space and hence the difficulty of the search task. Even with a simple controller the search space is far too large to search exhaustively so some sort of intelligent search process needs to be used. Biological processes are often used as inspiration for developing computation techniques, and evolution is no exception. It has been observed that evolutionary processes have led to highly optimized solutions to complex problems and since the 1950s evolutionary theory has been used by computer scientists as a source of inspiration for optimization and machine learning algorithms. Evolutionary strategies (Rechenberg, 1965) are the most developed of these early techniques. They encode the problem under consideration as a sequence of real numbers and then randomly mutate these numbers. Each time a mutation is created it is compared with the previous solution and, if it performs better according to some metric, it replaces the original solution: otherwise it is discarded. By using a Gaussian mutation (adding a random value selected from a Gaussian probability distribution with a mean of zero) it is possible to generate any sequence although the new sequences are more likely to be similar to the previous sequence than otherwise. This approach takes advantage of the fact that sequences close to the ‘best’ solution are likely to be similar to that solution.

Genetic algorithms were invented by John Holland in the 1960s (Holland, 1975). The genetic algorithm uses a population of solutions. Members of this population (called chromosomes) are allowed to contribute to the next generation by ‘crossover’, whereby two chromosomes exchange subsequences to create two new chromosomes. The selection of parent chromosomes is done randomly but is influenced by their fitness, which is calculated in some way by a fitness function. The genetic algorithm sensu strictu uses a fixed length sequence of bits (zeros or ones) as its chromosome. However, the genetic algorithm has had such a large impact on the field of evolutionary computation that concepts such as populations and crossover have been incorporated into other techniques and the term is now used to cover almost any population-based evolutionary search technique (for a more thorough introduction to genetic algorithms see Davis, 1991). These evolutionary techniques have been widely used for difficult computational search problems and are ideal for finding sets of parameters in gait controller that produce high-quality gait.

The GaitGen bipedal simulator

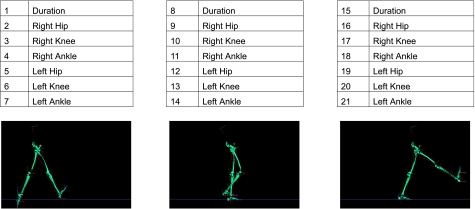
The GaitGen system is a bipedal walking simulator. There is always a compromise between biofidelity and computational cost and to minimize the latter the current implementation is relatively simple. It is essentially two dimensional and uses seven rigid segments: HAT, left and right thighs, legs and feet. These segments are attached to each other by hinge joints representing the hip, knee and ankle joints. Segment movement is effected by six muscle sets acting around these joints. The foot interacts with the substrate via contact points representing the 1st metatarsal head and the heel. These contact points generate a ground-normal reaction force and ground-tangential frictional force to allow forward progression. This represents a simplified morphology without spring elements or biarticulate muscles, although these could easily be added in future versions. The control system is a finite-state engine. It has three states with each state having a duration and activation levels for the six muscle sets. The three states represent half a gait cycle: the second half of the gait cycle is obtained by swapping the left- and right-side activation levels. Thus the controller has 21 parameters and these are translated to a genome as a list of floating point values between −1.0 and 1.0 (for the duration the sign is simply ignored). Figure 1 illustrates the genome encoding used. The system is implemented in C++ using the Dynamechs library to provide the mechanical simulation and a set of custom-written programs to provide the genetic algorithm optimization. This latter part of the system has been written to run as a distributed parallel application running on multiple computers using BSD sockets via the PTypes library (http://www.melikyan.com/ptypes/) to provide interprocess communication. This allows extremely flexible deployment with versions running on Linux, Solaris, Irix, Windows and MacOSX and running at multiple sites connected via the Internet. This allows the fitness of the individual genomes within the population to be tested in parallel on separate computers rather than sequentially on a single computer, which very greatly increases the overall speed. The master genetic algorithm program runs on a single computer and multiple client programs are run on other computers. The master program instructs a client to perform a particular genome, and the client sends back the fitness score when the simulation has finished.

Fig. 1.

Diagram showing the genome encoding used for the gait simulation. Each phase has a duration and activation levels for the muscle sets. Phase 1 corresponds to toe off; phase 2 corresponds to a swing phase with the knee flexed; phase 3 corresponds to a swing phase with the knee extended.

This system has been used previously to generate bipedal gait from a standing position (Sellers et al. 2003) and has successfully produced walking, running, skipping and ankle-walking (where swing-leg ground clearance is achieved by flexing the ankle joint rather than the leg joint) gaits. However, starting from a standstill requires extra states in the finite-state engine, which increases the number of required parameters and hence the difficulty of the search problem. This can be overcome by a gait morphing technique. From previous work we already have good solutions for normal walking in humans. The morphology can be gradually morphed to a new target (such as the morphology of Australopithecus afarensis) and instead of starting out from standstill with each new optimization experiment, the starting conditions (joint angles and angular velocities) are taken from the outcome of the previous successful simulation. In addition, because the morphology is only being changed a small amount between each optimization run the population of previous good solutions is likely to contain moderately good solutions for the new run and can be easily optimized to produce good solutions for the new morphology. This greatly reduces the number of simulation repeats required. This process is illustrated in Fig. 2.

Fig. 2.

Diagram illustrating the process of gait morphing. The linear dimensions, muscle parameters and inertial properties of the model are linearly scaled from human to those derived from AL 288-1. At each stage in the morphing process the optimization is used to produce efficient walking, and the start conditions for the subsequent morph are obtained from the previous morph.

Simulating A. afarensis

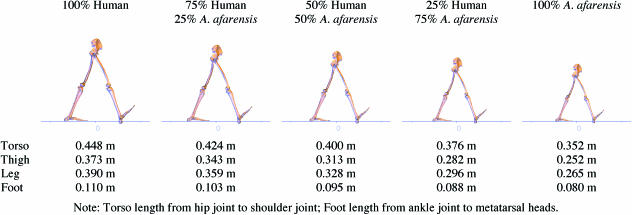
The first step in simulating A. afarensis is to produce a mechanical model representing the morphology of this animal based on reconstruction of the AL 288-1 fossil: the famous ‘Lucy’ skeleton (Johanson et al. 1982). A number of similar models have been produced previously (Crompton et al. 1998; Kramer, 1999; Wang, 1999; Kramer & Eck, 2000) although all differ in the numerical values chosen for various parameters. Segment lengths (the distance between joint centres rather than the lengths of the bones themselves) were taken from Kramer (1999) except for the HAT length (defined as the distance from the hip to the shoulder joint centre), which was estimated from the Lovejoy reconstruction (Weaver et al. 1985). There is considerable disagreement in the total body weight estimations. Aiello & Dean (1990) list values from 12.3 to 38.9 kg; Crompton et al. (1998) use 29.8 and 30.1 kg; Wang (1999) uses 29.8 kg; Kramer (1999) and Kramer & Eck (2000) use 33 kg. In this simulation 33 kg was chosen but it is presumed that any of the values from 29 to 33 kg would give very similar eventual results because the energetic costs are normalized by weight. Both Crompton et al. (1998) and Kramer & Eck (2000) suggest reconstructing the inertial parameters of the segments based on both modern human and modern chimpanzee values because it is currently impossible to estimate these parameters based on the fossil remains and the true values for A. afarensis are likely to lie between these values. Human limb mass proportions were taken from Winter (1990) and chimpanzee mass proportions were taken from Crompton et al. (1998). These were then used, along with the previously calculated segment lengths, to calculate centre of mass locations and moments of inertia according to the formula given in Winter (1990). Moments of inertia in particular are highly variable between individual humans and there is only very limited empirical hominoid data available, which suggested that there was little justification in using the various more complex techniques for calculating moments of inertia (for a review of inertial parameter calculation see Nigg, 1994). Table 1 shows a comparison between the values chosen and those recommended by other authors. The values in this table have been normalized as much as possible with HAT properties calculated from the individual components and moments of inertia recalculated to be about the proximal joint except for the HAT which is about the hip joint. However, the length comparisons should be treated with care because the HAT values given are the torso lengths in Crompton et al. (1998) and Wang (1999), and the foot lengths in these papers are total foot lengths so the value in the table has been estimated using human foot proportions.

Table 1.

Comparison of published inertial parameters for AL 288-1. HAT length is from hip joint to shoulder joint, thigh from hip joint to knee joint, leg from knee joint to ankle joint, foot from ankle joint to 1st metatarsal head. Centre of mass position is the distance along the length of the segment. Moments of inertia are about the proximal joint except for the HAT which is about the hip joint

Segments	Human-based (Crompton et al. 1998)	Chimp-based (Crompton et al. 1998)	Human-based (Wang, 1999)	Human-based (Kramer, 1999)	Chimp-based (Kramer & Eck, 2000)	Human-based	Chimp-based
Length (m)
HAT	0.402	0.402	0.380			0.352	0.352
Thigh	0.260	0.260	0.281	0.252	0.252	0.252	0.252
Leg	0.253	0.253	0.235	0.265	0.265	0.265	0.265
Foot	0.105	0.105	0.115	0.080	0.080	0.080	0.080
Mass (kg)
HAT	20.526	22.900	19.510	22.180	25.620	22.374	25.090
Thigh	3.080	2.190	3.450	3.300	2.240	3.300	2.399
Leg	1.220	0.950	1.450	1.650	0.890	1.535	1.041
Foot	0.360	0.470	0.240	0.460	0.560	0.479	0.515
Centre of mass (m)
HAT	0.193	0.227	0.198	0.000	0.000	0.220	0.220
Thigh	0.104	0.112	0.130	0.126	0.126	0.109	0.109
Leg	0.105	0.128	0.095	0.133	0.133	0.115	0.115
Foot	0.102	0.064	0.050	0.040	0.040	0.040	0.040
Moment of inertia (kg m2)
HAT	1.278	1.706	1.200	2.340	2.710	1.761	1.975
Thigh	0.0546	0.0412	0.0815	0.1100	0.1026	0.0611	0.0444
Leg	0.0202	0.0202	0.0194	0.0480	0.0346	0.0300	0.0204
Foot	0.0042	0.0031	0.0018	0.0037	0.0039	0.0015	0.0016

The model also requires an estimate of the muscle physiological cross-section areas (PCSAs) for the muscle sets and their attachment points. These were obtained by geometric scaling of the human values used previously (Sellers et al. 2003). In the case of nominal attachment points this was a simple linear scaling based on the lengths of the segments; in the case of the PCSAs the scaling was the square of the segment length change. The values used are given in Table 2. The knee joint muscle sets are modelled with a movable midpoint that maintains the moment arm around the joint. The muscles are modelled using Minetti & Alexander's (1997) formulation, which incorporates velocity effects on tension and allows the direct calculation of metabolic energy costs.

Table 2.

The muscle parameters used in the AL 288-1 model. Origin coordinates are local to the proximal limb segment and insertion coordinates are local to the distal limb segment. The knee extensor passes through a midpoint at (0.040 m, 0.274 m) and the knee flexor through a midpoint at (−0.020 m, 0.252 m) local to the thigh

		origin		Insertion
						PCA	Length
Joint	Muscle set	x(m)	y(m)	x(m)	y(m)	(m2)	(m)
Hip	Extensor	−0.055	0.037	0.003	0.190	0.009	0.160
	Flexor	0.052	−0.059	0.018	0.102	0.004	0.160
Knee	Extensor	0.018	0.159	0.027	0.047	0.011	0.142
	Flexor	0.000	0.159	−0.007	0.050	0.005	0.142
Ankle	Extensor	0.020	0.087	0.035	0.000	0.002	0.177
	Flexor	−0.018	0.036	−0.035	0.023	0.012	0.251

To make the simulator produce bipedal locomotion it must find appropriate values of the 21 parameters used in the finite-state control system. The model is given a set of starting conditions (position, orientation, velocity and angular velocity of the HAT segment; angles and angular velocities of the left and right hip, knee and ankle joints) from the middle of a previously successful simulation. Ultimately this derives from a standing-start human model (Sellers et al. 2003) but otherwise it is chosen from previous simulations that are judged to be as similar as possible to the current one. The starting values of the 21 parameters are also taken from the set of solutions produced in a previously successful run. If the conditions are very similar to those of the previous run then these parameters may be able to produce stable locomotion but it is much more likely that initially these parameter values will cause the simulation to fall over in the first step or two. The quality of the parameters is judged by the distance the simulant is able to walk before using up a fixed amount of energy, so a simulant that falls over scores badly. The most efficient stable walker will score the highest. The genetic algorithm optimization scheme described previously is applied iteratively until it is unable to find any better sets of parameters and the cost of travel can then be measured for the simulant. Genetic algorithm optimization is a stochastic process. It relies on applying many small, random changes to the parameter list so that each time it is applied it will produce different outcomes. Because it is searching for the most efficient locomotion only the best value found after a number of repeats is of interest. This also means that a particular optimization run can be ‘unlucky’ and only relatively poor solutions found. To avoid this all optimization runs were repeated at least five times.

In the context of A. afarensis locomotion there is considerable disagreement as to whether this animal walked fully upright or with a chimpanzee-like bent-knee, bent-hip (BKBH) style of bipedalism (Crompton et al. 1998; Stern, 1999). To simulate this the degree of extension available at the knee joint of the model can be altered from 0° in the fully erect state to 40° representing the maximum amount of knee flexion seen in chimpanzee bipedalism (Alexander, 1991). To achieve 0° bipedal walking the human model was morphed to the human-based AL 288-1 model allowing the optimization procedure to find efficient walking at each stage of the morphing process. The model was then morphed to the chimpanzee-based AL 288-1 model, again allowing efficient walking to be achieved at each stage. Both these models were then morphed to versions in which the maximum knee extension was limited to 40°. At all stages multiple optimizations were carried out and the best ones used as starting points for subsequent morphs. Overall an extremely large number of individual simulations were carried out. An optimization run required between 5000 and 50 000 simulations to find a good set of control parameters. Morphing generally used a 5% change between morphs and each morph was repeated at least five times to make sure a good solution was found. This means that at least 10 000 000 simulations were performed. Each simulation took approximately 10 s to run depending on the speed of the computer, equating to over 1000 days of computer time. Fortunately, the ability to use multiple computers running simultaneously means that the actual run time was considerably less than this.

Results

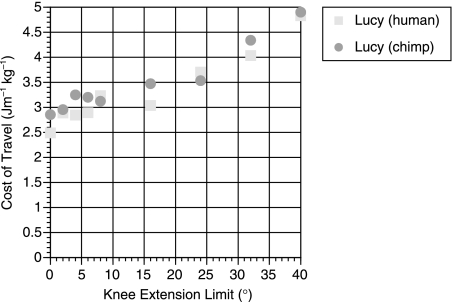
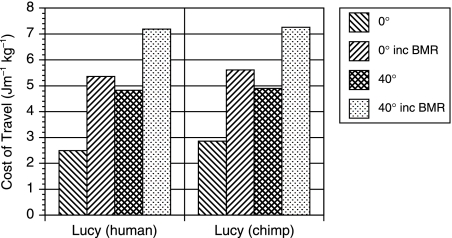
The results for the costs of travel at differing knee extension limits are shown in Fig. 3. This figure shows the results both for the human-like and for the chimpanzee-like inertial parameters. These values represent the energy required by the locomotor muscles alone and do not include the significant cost of maintaining the body itself. To allow a more meaningful comparison with the experimentally derived costs of travel, a value for basal metabolic rate (BMR) of 51.9 W was calculated for AL 288-1 based on the standard empirical relationship between mammalian body mass and BMR (Schmidt-Nielsen, 1983). The average value for a 33-kg human female child is very similar at 55.7 W (Department of Health, 1991). This additional energy cost was then incorporated into the results from the model. Figure 4 shows the effect of knee extension angle on the cost of travel both with and without BMR. Forty degrees of knee extension increases the cost of locomotion by 82% if BMR is ignored and by 32% if it is included. The model also allows the calculation of speed of travel, and these values, along with the numerical values for travel cost, are shown in Table 3.

Fig. 3.

Graphs showing the effect of limiting the amount of knee extension on the cost of travel for the two AL 288-1 simulations.

Fig. 4.

Graph showing the effects on cost of travel of adding a BMR of 51.9 W to the two AL 288-1 models.

Table 3.

The minimum costs of transport and associated walking speed for the different AL 288-1 models

	Knee extension	Lucy (human)	Lucy (chimp)
Cost of transport (J m−1 kg−1)	0°	2.49	2.85
Cost of transport + BMR (J m−1 kg−1)	0°	5.36	5.62
Speed (m s−1)	0°	0.55	0.57
Cost of transport (J m−1 kg−1)	40°	4.83	4.90
Cost of transport + BMR (J m−1 kg−1)	40°	7.19	7.26
Speed (m s−1)	40°	0.67	0.67

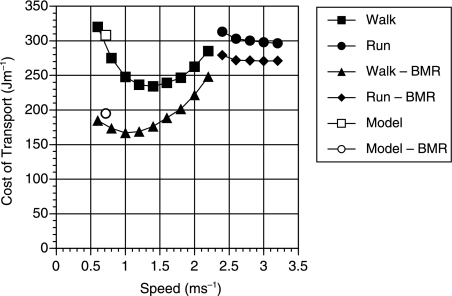
When interpreting these results it is important to compare them with the results obtained from the human simulation. The values obtained using the previous human simulant (Sellers et al. 2003) but without the standing start and allowing for a BMR of 80.1 W for a 68-kg human (Schofield et al. 1985) are shown in Fig. 5. For comparison, the figure also shows experimentally derived values recalculated with and without BMR (Alexander, 1992). As can be seen the simulation values agree very closely with the experimentally derived values and are certainly within the normal variation seen between subjects.

Fig. 5.

Graph showing the speed and cost of transport for the human simulant both with and without a BMR component of 80.1 W. The graph also shows a set of experimentally derived costs of transport for comparison (Alexander, 1992).

Discussion

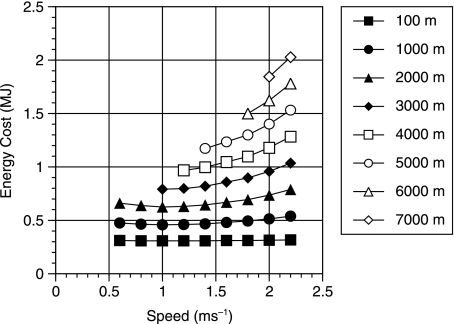
From Fig. 5 it can be seen that there is very close agreement between experimentally derived values and those produced using the human simulant. This is interesting because the model must be underestimating the cost of locomotion as it does not include any of the postural costs associated with maintaining an upright stance in three dimensions such as the necessary activation of the hip abductor muscles to maintain the orientation of the pelvis (Aiello & Dean, 1990). However, it is likely that this underestimation is balanced by the overestimation caused by the lack of human energy-saving mechanisms, such as biarticulate muscles, spring elements and complex joint morphology. It is difficult at present to estimate the size of these under- and overestimates. Postural costs are variously reported as 0.21 W kg⁻¹ (Alexander, 1991), 7% (Aiello & Dean, 1990) and a physical activity ratio (PAR) of 1.2 (Department of Health, 1991), suggesting that these values might be somewhere in the order of 10% of the cost of travel. What is clearer from Fig. 5 is that the preferred walking speed is being significantly underestimated. The choice of optimum walking speed is somewhat more complex than suggested by this figure. Among primates in which a significant part of the day is spent resting it is often more economic to walk at the speed indicated by the minimum of the line where BMR has been removed than at the higher speeds suggested by the line that includes BMR. Figure 6 shows the total cost of a human walking a particular distance in 1 h assuming that any spare time in the hour is spent resting. At low distances the best strategy is to walk at 1 m s⁻¹ and rest for any spare time, not the 1.4 m s⁻¹ predicted by the upper curve. Only when larger distances are required is it necessary to walk faster.

Fig. 6.

Graph showing the energy cost of a human walking various distances in 1 h assuming that the individual walks the distance at a constant speed and then rests for the remainder of the hour.

The results for the human simulant give us a great deal of confidence that the values for the AL 288-1 simulant are reasonably accurate. The similarity of results for the human-like and chimp-like models suggests that the inertial properties have very little effect on the cost of travel (which is fortunate because these values are extremely uncertain). This finding agrees with studies on human biomechanics (Yoko et al. 1998). However, the effect of restricting the maximum extension at the knee joint is unsurprising. As shown in Fig. 3 there is a more or less linear increase in travel costs with knee angle, reflecting the postural cost of maintaining the flexed knee. The 82% increase in purely locomotor costs is extremely large and certainly supports the findings found in previous simulation experiments (Crompton et al. 1998; R. H. Crompton, pers. comm.), and the 32% increase when the fixed cost of BMR is taken into consideration agrees with experimental values of 38% for a 45° extension limit in humans (Stern, 1999). Identifying the role of BMR goes a large way to reconciling the differences found between simulation and experimental studies. Purely on the grounds of locomotor efficiency it seems unlikely that any hominid would opt to use a BHBK gait unless the time spent bipedally was very small. This suggests that more work needs to be done on why chimpanzees maintain a BHBN gait and whether these selective pressures would still apply to A. afarensis.

The model would benefit from greater biofidelity. For example, it could be fully three-dimensional; it could incorporate sensory feedback to modulate the performance and improve balance; the muscle groups could be subdivided into smaller functional units including two-joint as well as single-joint muscles; the finite-state control system could employ a greater number of states in the control system to provide more precise control; and spring elements could be incorporated into the muscle model. This would both increase the reliability of current predictions and allow the investigation of other factors associated with bipedalism: energy-saving mechanisms; influences of pelvic dimensions; importance of rotational movement of the upper body. However, this increase in model complexity poses two problems. First, the simulation itself would then take longer to compute, which would increase the duration of the fitness evaluation. Secondly, a more complex model would require a larger genome to specify the parameters and this would very greatly increase the size of the search space. The simulation problem is not completely intractable, especially given the parallel nature of the genetic algorithm approach. It would run efficiently on the next generation of 1000 processor clusters with very little overhead. This would reduce the current experimental time of weeks to hours so that considerable increase in model complexity would be possible. The search space problem is more difficult to solve because the size of the space grows far too rapidly to be overcome by simply increasing the computational power available. However, an incremental evolutionary approach may be the answer because we can evolve a set of good parameters from the current model and use these as the starting point for a series of more complex models. In this way we should be able to restrict the search to a region of the search space that is likely to be profitable.

Conclusions

The results from the human simulation suggest that at the speeds shown in Table 3 the energetic costs would be likely to be very close to those given. However, it is too early to say whether these points represent the minimum values on the energy cost graph. The current optimization process, although ostensibly only selecting for energy efficiency, will also select for stability. This may cause it to prefer slower speeds even when travelling faster would be more efficient, as indicated in Fig. 5. In future it will be necessary to alter the optimization process so that it can find the energy costs at different speeds and this will allow us to add more points to the cost of travel graph so that we can identify the minima and calculate the preferred speed in any context.