No change in neuron numbers in the dentate nucleus of patients with schizophrenia estimated with a new stereological method – the smooth fractionator

Abstract

The dentate nucleus is phylogenetically the most recent nucleus in the cerebellum. Owing to its connections to the thalamus and the prefrontal cortex it may be involved in the symptomathology in schizophrenia and other psychiatric illnesses. In this stereological study we implemented the smooth fractionator, which combines the unbiased principles of the optical fractionator with a new and more efficient sampling strategy to the dentate nucleus. The smooth fractionator represents the most efficient sampling strategy described so far in stereology, in terms of reducing the sampling variance and thus increasing the efficiency. It is the first application of the smooth fractionator to human brain tissue and presents estimations of total number of neurons in the dentate nuclei of eight patients with schizophrenia compared to eight control persons. The total number of neurons in the dentate nucleus was estimated to 3.36 × 10⁶ in subjects with schizophrenia, which was not statistically significant different from 3.65 × 10⁶ in control subjects (P = 0.63). The advantages and disadvantages of the smooth fractionator method are discussed and its precision in practical application is estimated.

Introduction

The cerebellum is one-third larger in humans than in non-human primates; a similar phylogenetic increase in size is also seen in the prefrontal cortex, and the two have strong anatomical connections. This suggests that the cerebellum in humans might be involved in both cognitive and motor functions (Passingham, 1975; Leiner et al. 1989, 1991; Schmahmann, 1991; Schmahmann & Pandya, 1995). The cerebellum is well suited to function as a parallel processor because of its cellular arrayed architecture. It may be involved in cognitive functions such as working memory, implicit and explicit learning, memory and language (Leiner et al. 1993; Schmahmann & Sherman, 1998). Patients with lesions involving the posterior lobe and the vermis have clinically prominent behavioural changes, suggesting that cognitive and emotional changes might be due to cerebellar damage in some patients (Schmahmann & Sherman, 1998).

Classic descriptions of cerebellar disorders include abnormalities of voluntary body movements, dysmetria (incoordination of the limbs), ataxia and dysarthria; abnormalities that are all also implicated in the pathology of schizophrenia. Kraepelin et al. (1919) described a subgroup of schizophrenic patients with disorders of equilibrium, adiadochokinesia and tremor, while Bleuler (1911) noted disturbed co-ordination of limb movements and gait peculiarities. Both sets of observations, made prior to the introduction of neuroleptic treatment, implicated primary cerebellar motor dysfunction in schizophrenia.

During the last decades positron emission tomography (PET) studies have shown that patients with schizophrenia have a reduced blood flow in cerebellar and prefrontal regions during both a practised and a novel recall task, indicating that the prefrontal–cerebellar connection may be impaired (Andreasen et al. 1996). Bernstein et al. (2002) found an increased number of nitric oxide synthase immunoreactive Purkinje cells and dentate nucleus neurons in patients with schizophrenia. Since cerebellar activation during working memory tasks may be mediated by neurons in the ventral dentate nuclei (DN), which project to the prefrontal cortex via the thalamus (Kim et al. 1994; Middleton & Strick, 1994), we decided to study in detail this particular neuron complex.

Pathological findings in cerebella from patients with schizophrenia are conflicting. The most common results are decreased volumes of the vermis and the inferior posterior lobe, without reduction of total cerebellar volume (Weinberger et al. 1980; Lohr & Jeste, 1986; Hopkins & Lewis, 2000). A post-mortem study did not show any differences in neuron number or volumes in the cerebellar cortical regions in patients with schizophrenia compared with a control group (Andersen & Pakkenberg, 2003).

We have used a new stereological sampling method: the smooth fractionator (SF), which has not previously been applied to cerebellar tissue. The SF method was applied to the dentate nucleus to test whether the cerebellar symptoms found in patients with schizophrenia are based on changes of the total number of neurons or the volume of DN. The smooth fractionator is a modification of the ordinary fractionator principle and combines a newly designed systematic, uniformly random sampling (SURS) scheme and disector counting, with a higher precision than other stereological techniques.

Materials and methods

Materials

Cerebella from eight men with schizophrenia and eight age-matched control men with no neurological disorders were obtained at post-mortem in accordance with Danish laws governing autopsied human tissue and accepted by the local ethical committee (no. 11-010/01). As the granule cells in the cerebellar cortex may undergo a pH- and season-dependent caryolysis rather rapidly after death all sections were examined, and only cerebella free of caryolysis were included. The clinical and post-mortem data of schizophrenic and control subjects are shown in Tables 1 and 2.

Table 1.

Clinical data and post-mortem data of the schizophrenic patients

	Age (years)	Body height (cm)	Body weight (kg)	Age at 1st admission (years)	Years in psychiatric hospital	Sub-diagnosis	Years of neuroleptic treatment	Cause of death	Brain weight (g)	Terminal period (days)	Post-mortem interval (h)	Fixat ion period (years)
	30	178	70	26	1	simplex	3	Suicide	1420	0.1	66	13
	41	184	70	22	19	hebephrenic	20	Cr. pancreatic	1485	28	48	22
	45	175	58	20	23	paranoid	23	C. coli	1330	1.0	39	20
	52	186	56	16	22	simplex	25	AMI	1427	2.0	35	19
	65	185	73	25	36	simplex	30	C. pulm.	1268	21	40	27
	70	175	70	20	37	paranoid	26	AMI	1450	0.1	10	15
	78	166	72	22	56	simplex	13	AMI	1325	0.1	9	22
	79	178	73	41	34	paranoid	24	C. hep.	1142	30	27	21
Mean	57.5	178.4	67.8	24.0	28.5		20.5		1355.9	10.3	34.3	19.9

C. coli, colon cancer; Cr. pancreatic, chronic pancreatitis; AMI, acute myocardial infarction; C. pulm., lung cancer; C. hep, liver cancer.

Table 2.

Data of control group

	Age (years)	Body Height(cm)	Body weight(kg)	Cause of death	Brain weight(g)	Terminal period (days)	Post-mortem interval(h)	Fixation period (years)
	28	180	76	Stab wound	1400	0.1	12	9
	38	180	96	AMI	1390	1	24	10
	43	175	82	AMI	1560	0.1	24	10
	48	186	110	AMI	1290	0.1	24	10
	60	175	73	AMI	1500	0.1	24	10
	65	173	85	AMI	1420	0.1	24	10
	81	176	75	Gastric ulcer	1390	2	12	13
	84	166	56	Pleuritis	1205	2	15	10
Mean	55.9	176.4	81.6		1394	0.7	19.9	10.3

AMI, acute myocardial infarction.

Anatomy

The white matter of the cerebellar hemispheres contains four pairs of central nuclei, of which the largest and phylogenetically most recent is the DN. DN is the most lateral of the nuclei placed close to the vermis. It consists of a thin layer of nerve cells and appears, on sections, as a convoluted band of grey matter having the shape of a folded bag with the opening or hilus directed medially and dorsally. It is found as a definite nucleus only in mammals, and becomes greatly enlarged in humans and the anthropoid apes (Passingham, 1975). The early deep cerebellar neurons are generated during the first trimester of fetal life, during which the newly formed nerve cells migrate from the ventricular zone to the intermediate zone of the cerebellum in two broad bands, a medial and a lateral. The medial migratory band will contribute to all four deep cerebellar nuclei, while the lateral band will almost exclusively form the DN (Rüdweberg, 1961; Rakic & Sidman, 1970).

DN neurons can be classified into two groups on the basis of their size; the large, projecting neurons in the rostral part of DN, and the smaller, local circuit neurons (Braak & Braak, 1983). Axons of the large, projecting neurons acquire a myelin sheath while still in the nucleus and pass out as fibres of the superior cerebellar peduncle. The small stellate neurons are observed in between and their axons apparently aborize within the nucleus. Furthermore, afferent fibres from a dense fibre plexus, the amiculum, are seen around the nucleus. No differentition was made between the two neuron types in the present study. The DN serves, via axons of Purkinje cells, as the major relay station for the output of cerebellar cortex. The large projecting neurons have been proposed to be the source of the dentothalamic projection.

Tissue processing

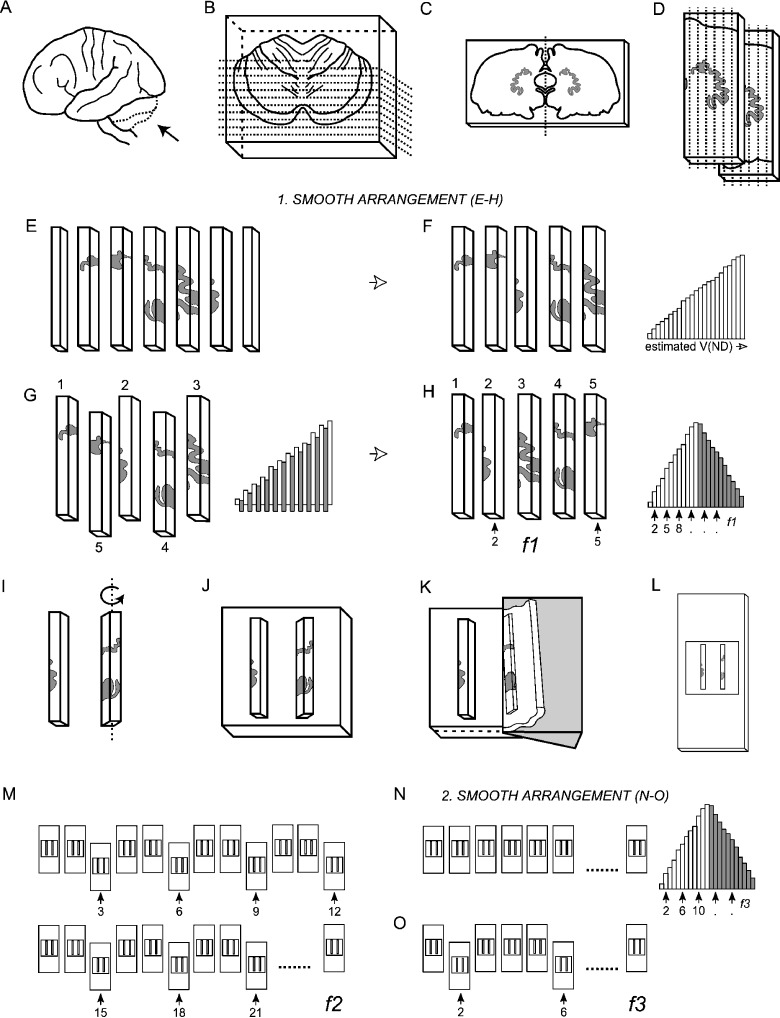
The cerebellum was embedded in 7% agar and sliced coronally into 4-mm-thick sections with a random starting position within the first slab thickness. The DN was identified on 4–6 slices and cut out. The 4-mm-thick sections were re-embedded in agar and cut into 2-mm-thick slices using a guide spacer (Fig. 1). The DN was now identified on 10–12 slices. The left or right DN was chosen systematically randomly, which in this study turned out to be in favour of the right DN. The DN was dissected out from every slice in which it was observed, and cut into 2-mm-thick bars, also with a uniformly random start, providing a total of about 60 bars. The bars were sorted in an ascending manner according to the amount of DN they contained in the so-called smooth design (Gundersen, 2002); see below. From this sequence every second bar was pushed out and rearranged into a smooth arrangement (Fig. 2). Depending on sample size every 3rd−5th bar was sampled systematically from the smooth arrangement with a random start between bar 1 and bars 3–5, respectively, providing 12–20 bars per specimen.

Fig. 1.

A guide spacer, an instrument for cutting tissue in mm-thick-sections.

Fig. 2.

The smooth fractionator sampling design. (A) The cerebellum was dissected from the brainstem at the level of the 3rd cranial nerve (B) embedded in agar and sliced coronally into 4-mm-thick, and later 2-mm-thick slices with a random starting position within the slab thickness. (C) The dentate nucleus was identified on 10–12 of the 2-mm-thick slices. (D,E) The left or right dentate nucleus was chosen systematically randomly, dissected and cut into bars. (F) The bars were sorted in an ascending manner according to the amount of DN they contained. (G) From the sorted sequence every second bar was pushed out and rearranged into a smooth arrangement. (H) Depending on sample size a predetermined fraction (f1) was now sampled systematically randomly from the smooth arrangement using a random number table, providing 12–20 bars for further processing. (I) The bars were rotated around their longitudinal axis (see text), (J) embedded in agar, (K) sectioned exhaustively on a vibratome into 100-µm-thick sections, and (L) mounted on microscope slides. (M) From the complete series of sections a predetermined fraction (f2), in this case every 3rd section, was sampled. (N) These sections were again arranged into a smooth fractionator design (O) before a final fraction (f3) was subsampled for cell counting.

Based on the principle of vertical sections (Baddeley et al. 1986), the resulting 12–20 bars were rotated around their longitudinal axis (Gundersen et al. 1988) and embedded in agar with 2–3 bars in each block. The vertical design used in the present study provides randomly rotated sections, which is not required for number estimation but is a requirement for estimation of individual cell volumes (Gundersen et al. 1988) for possible future studies. The blocks were sectioned exhaustively on a vibratome (Bio-Rad Micro-Cut H1200) into 100-µm-thick sections and mounted on silane-coated microscope slides. From the complete series of 150–350 sections, every 3rd section was sampled systematically, uniformly randomly. These sections were rearranged into a smooth design, and every 3rd−5th section was subsampled for final cell counting (Fig. 2). The sampled sections were stained with a modified Giemsa stain.

After drying, dehydration, staining and mounting, the vibratome sections, originally cut at 100 µm, had shrunken to an average thickness of 45.5 µm. The disector of height 20 µm was placed in the central part of the section. To obtain a mean value of the section-thickness, the z-axis was measured centrally in every disector with a cell count. In our thick vibratome sections a loss of cells, anisotropic deformation and a non-uniform shrinkage was observed except in the central 70% of the section height. Therefore corrections were applied using upper and lower guard zones as described in Andersen & Gundersen (1999). A recent study finds differential tissue shrinkage and compression in the z-axis in thick vibratome sections, leading to depletion of cells in the central part of a section (Gardella et al. 2003). This could be due, among other possibilities, to staining difficulties in the thick sections or differential shrinkage in perfusion-fixed animals compared with long-term formalin-fixed human tissue; however, we did not encounter these problems (Andersen & Gundersen, 1999).

Estimation of total cell number

The total number of cells in the DN was estimated using the optical fractionator method (West et al. 1991) following the smooth arrangement of the individual fractionator items. The smooth fractionator is an SURS strategy and involves a particularly small sampling error even for relatively small samples from three-dimensional objects (Bendtsen et al. 2002; Gundersen, 2002). If the natural sequence of the pieces in an ordinary fractionator sampling design provides a population distribution that is far from smooth, the gain in efficiency by using the smooth fractionator may be considerable (Gundersen, 2002).

According to the optical fractionator design the total neuron number, N, is estimated by multiplying the total number of particles counted with the reciprocal sampling fractions:

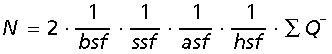where bsf is the bar sampling fraction, ssf the section sampling fractions, asf the area sampling fraction, hsf the height, or section thickness sampling fraction, and ∑Q⁻ the total number of counted particles. The bilateral cell number is estimated by multiplying the unilateral estimate by two. This is an unbiased estimator because the right or left dentate nuclei were sampled uniformly random.

The asf is the area of the counting frame of the disector relative to the area associated with each xy-step movement of the disector. The height sampling fraction is estimated as:

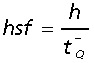where h is the disector height, 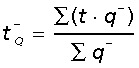is the Q⁻ weighted mean section thickness where t is the local section thickness centrally in the counting frame with a disector count of q⁻ (particles) (Dorph-Petersen et al. 2001).

Sampling with the optical disector

Cell counting is performed using the optical disector (Gundersen, 1986). The optical disector is a probe that samples isolated particles with a uniform probability in a three-dimensional space irrespective of their size, shape or orientation in the tissue. The principle of the optical disector is applied to the thick vibratome sections in which the plane of focus is moved up or down. An unbiased rectangular counting frame is superimposed on the magnified image of the tissue on a computer screen and movements in the z-direction are measured with a digital microcator (Heidenhain, VRZ 401) with a precision of 0.5 µm. The area of the counting frame was 7791 µm². All cell counts were obtained using a BH-2 Olympus microscope with a 60× oil-immersion objective with a high numerical aperture (NA = 1.40) and a motorized stage. We used the CAST-GRID software (Olympus, Denmark). The cells were identified as neurons if they had a clearly defined neuronal cytoplasm and a centrally located nucleolus. The nucleolus was used as the counting item and an average of 190 (range 98–296) neuronal nucleoli were counted per brain (Table 3).

Table 3.

The sampling scheme and total number of neurons and volume in the dentate nucleus

	Sampling fraction			No. of sections	Stepsize (x,y) (µm)	∑ Q−	Total neuron number (106)	Total volume (mm3)
	f1	f2	f3
Schizophrenia group
	5	3	5	12	700 × 350	172	3.08	933
	4	3	4	16	700 × 700	185	3.22	896
	3	3	4	19	800 × 800	126	2.33	616
	3	3	5	21	600 × 600	237	3.05	689
	3	3	5	20	700 × 700	209	3.78	808
	3	3	5	17	700 × 700	225	3.08	955
	4	3	3	18	800 × 800	148	2.26	585
	4	3	5	26	700 × 700	244	6.12	1182
Mean (CV)	3.6	3	4.5	18.6		193	3.36 (0.36)	833 (0.24)
Control group
	3	3	4	17	800 × 800	230	4.60	806
	5	3	5	11	700 × 700	125	3.52	1139
	4	3	4	27	400 × 800	173	1.98	716
	5	3	5	10	800 × 800	98	3.63	1243
	5	3	5	8	400 × 800	170	3.29	917
	3	3	4	15	800 × 800	237	3.82	742
	5	3	6	10	600 × 300	167	2.66	490
	3	3	4	18	700 × 700	296	5.73	1101
Mean (CV)	4.1	3	4.8	14.5		187	3.65 (0.31)	894 (0.28)

Estimation of the total volume of the dentate nuclei

Applying the fractionator estimator for volume, the total bilateral volume of DN was estimated from:

$$V_{\text{DN}}=2·\sum P·a\left(p\right)·t·k_1·k_2·k_3$$

where a(p) is the area per point, i.e. the x- and y-step lengths, ∑P is the number of all frame corner-points hitting DN divided by four because all four corners were counted per frame, t is the average section thickness, i.e. the cut final section thickness (see O in Fig. 2), k₁ is the inverse bar sampling fraction, k₂ is the inverse first section sampling fraction and k₃ is the inverse second section sampling fraction. Notice that these volumes were not used for the estimation of total neuron number, the fractionator estimates of total neuron number are independent of the containing volume and its shrinkage and deformation.

Statistical analyses and estimation of precision

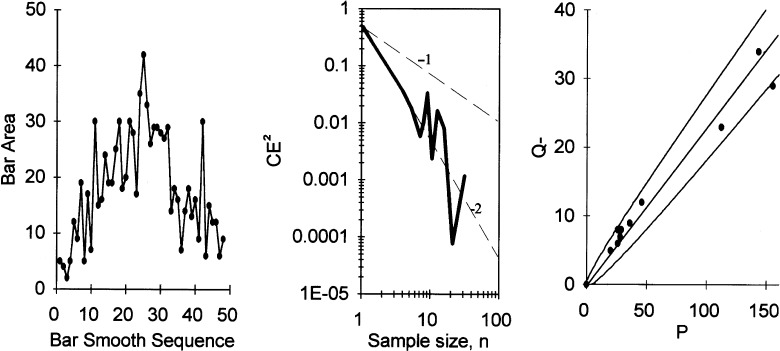
Differences between means were analysed using an unpaired two-tailed Student's t-test. Variability is shown in parentheses as the coefficient of variation (CV = SD/mean) (Table 3). The precision of the estimate of the total neuron number in the DN in each subject was estimated as the coefficient of error (CE = SEM/mean), caused by sampling error related to the systematic, uniform random sampling and the counting noise, which is ∼1/√∑ Q⁻ = 1/√190 = 0.07 in this case. Usually, the sampling variance can be predicted using just one SURS sample, in this case one DN (Gundersen et al. 1999; Bendtsen et al. 2002), but the sampling variance of the smooth fractionator design is particularly difficult to predict (Gundersen, 2002). The principle of the smooth fractionator, illustrated in Fig. 2, allows a very precise sampling based on the visual impression of the containing space size in the sampling items (blocks or bars) of very varying size. However, in this application, contrast between DN and the surrounding white matter was in many cases too poor to allow a precise judgement of DN fractions of the bars. As a result of this uncertainty, the smooth arrangement was much less effective than intended (Fig. 3). We therefore estimated the sampling variance due to bar size variation by estimating the area (and thereby the volume) of the containing volume in all 48 bars from one case, which, like all the other cases, was first arranged smoothly using visual cues. By resampling all possible combinations of sample sizes and random starts, the sample variability (CE) due to size variation was estimated as a function of sample size. It turned out that CE² only decreases by a power of roughly −2 of the sample size, much less than for an ideal smooth fractionator (Gundersen, 2002). For a sample size of n, the relationship in Fig. 3 predicts 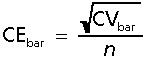, where CV_bar= 0.71 is the variability ofthe bar volumes.

Fig. 3.

Left: bars from human dentate nucleus (DN) sorted according to the smooth fractionator using the apparent size of the containing space. After arranging the bars, the sectional areas of DN were point counted under a microscope. Middle: the variability of the sample total area when a varying sample size is taken SURS from the arrangement shown to the left. The dashed line indicates slopes of −1 and −2, respectively, in the log–log plot. Right: The number of neurons counted, Q⁻, as a function of the area of DN in sections. The slope is the numerical density; regression through the origin is illustrated. The variability around the regression line is no more than the counting noise on individual estimates Q⁻, indicated by the two tolerance curves (± SD).

The other source of variability in a smooth fractionator, the inhomogeneity of the containing space, was essentially nil in all cases (Fig. 3, right panel).

Accordingly we could estimate the imprecision of the estimate of total number to be of order 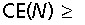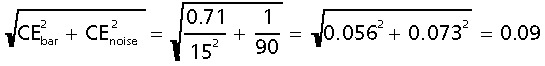for an initial sample of 15 bars, wherein ∼190 cells were finally counted. Without the smooth arrangement, the number of bars necessary for the same precision would have been all bars! The inequality in the above equation indicates that a variance contribution may come from the sampling of sections in a smooth arrangement (Fig. 2), but the large number of sections in that arrangement makes the contribution insignificant.

As always we aimed at a precision of the estimator, CE, which compares with the actual biological variability, CV_biol, in the sample of humans studied. The two measures are related through the basic equation (the additivity of variances):

where CV_obs is the observed variation of the estimates. In this case, CV_obs ∼ 0.34 (see Table 3). Sufficient precision simply means that CE² should be somewhat less than 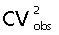, i.e. ${\text{CE}}^2/{\text{CV}}_{\text{obs}}^{\text{2}}<\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. In this case ${\text{CE}}^2/{\text{CV}}_{\text{obs}}^{\text{2}}-{0.09}^2/{0.34}^2-0.07$, which indicates an ample precision.

Results

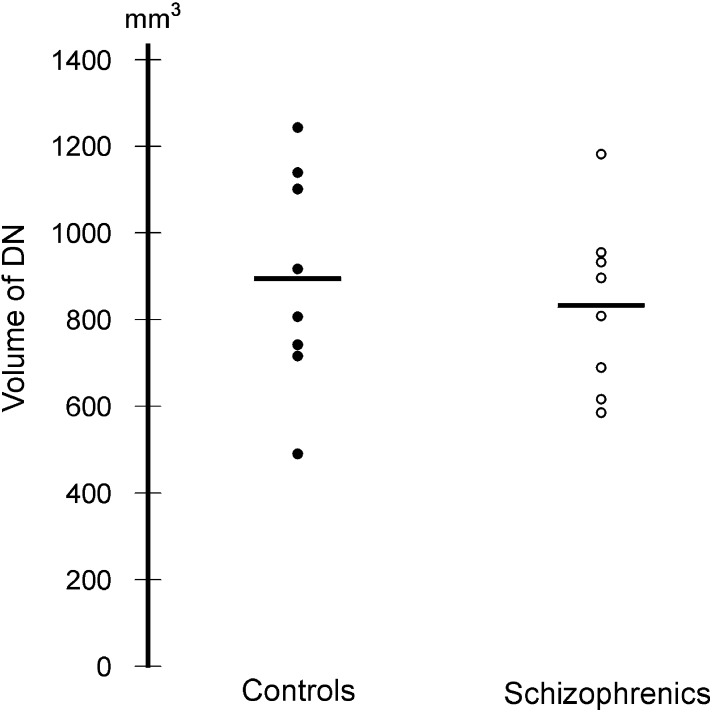
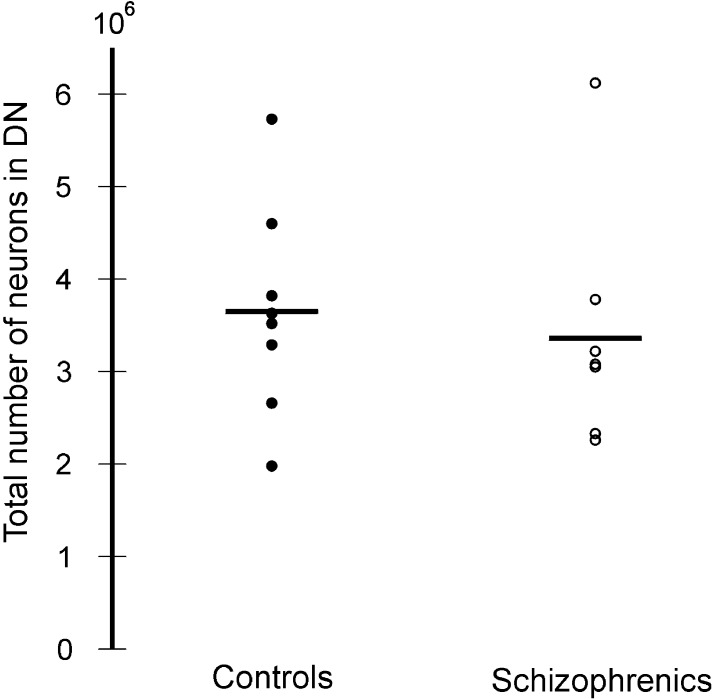
In the two groups there was no significant difference in the mean total neuron number or the mean total volume of the DN (Fig. 4). The mean total neuron number of the DN was 3.36 × 10⁶ (0.36) in the schizophrenia group and 3.65 × 10⁶ (0.31) in the control group (P = 0.63). The mean total volume of the DN was 833 mm³ (0.24) and 894 mm³ (0.28) for the schizophrenia and control group, respectively (P = 0.47) (Fig. 5). The observed mean differences between group means did not imply a biological significance and therefore study over a larger scale was not considered.

Fig. 4.

The total volume of the dentate nucleus in control subjects and patients with schizophrenia.

Fig. 5.

The total number of neurons in the dentate nucleus in control subjects and patients with schizophrenia.

Discussion

The total number of neurons in DN was not statistically different in brain tissues from schizophrenia patients compared with control subjects, and no differences were found in DN volume in the two groups. Several studies have indicated cerebellar involvement in schizophrenia, both in motor and in cognitive function (Andreasen et al. 1996; Katsetos et al. 1997). Earlier studies conducted in cerebellar cortex from schizophrenic patients have revealed no consistent neuron or volume loss (Weinberger et al. 1980; Reyes & Gordon, 1981; Nasrallah et al. 1991; Andersen & Pakkenberg, 2003).

The total neuron number of DN has previously been estimated stereologically in a study of control subjects using optical disectors in combination with the Cavalieri method (Andersen et al. 1992). For this study a new stereological sampling design, the smooth fractionator (SF), was used. The strength of the SF is its efficiency in the sampling strategy, which, however, turned out not to be as optimal as expected. In particular, the inability to identify the DN on the physical slabs in the first sampling step reduced the efficiency substantially. This is illustrated as an uneven distribution of the associated variable from the original smooth arrangement. It should be further noted that for optical fractionator designs based on vibratome sections, loss of cell nuclei and anisotropic deformation of the thick sections must be considered (Andersen & Gundersen, 1999; Dorph-Petersen et al. 2001). The shrinkage is non-uniform except in the central 70% of the section height and there is a pronounced cell loss close to both section surfaces (Andersen & Gundersen, 1999). We corrected for these potential biases by using upper and lower guard zones.

Volume estimates of the DN were not used in the estimation of total neuron number, but were included to reveal a possible change in the volume of DN despite a normal neuron number – which was not the case. To obtain this extra information it is necessary to keep track of the total number of corners of the disectors sampled hitting DN, which amounts to very little extra work.

In conclusion, our practical experience with the SF revealed that it is a stereological method with great potential, but that several requirements must be fulfilled to obtain the full effect of this method. Because most brain cell nuclei have a distribution of neurons that are organized in a rather smooth sequence (starting with a low number in the ends of the nucleus and with the highest number of neurons in the centre of the nucleus) we doubt that the SF will be the optimal sampling strategy in most brain studies where neuronal number is estimated.

Developing a neuroanatomical model that can explain the multiple and diverse symptoms of schizophrenia is a fundamental problem in schizophrenia research. One possible model could be that the diverse symptoms of schizophrenia reflect abnormalities in connectivity in the circuitry that links prefrontal and thalamic regions, and cerebro-cerebellar connectivity may be disrupted (Andreasen et al. 1998). Because a decreased total number of neurons in the mediodorsal thalamus (MD) and nucleus accumbens in patients with schizophrenia compared with control subjects has been found by some (Pakkenberg, 1990), and DN has afferents to the MD, it seemed possible that a cerebellar change in total neuron numbers in patients with schizophrenia could be located within the DN. The unchanged number of DN neurons in patients with schizophrenia, and the unchanged number of Purkinje and granular cells found in a previous study (Andersen & Pakkenberg, 2003), indicates that the structural fundament for normal function, the number of nerve cells, is intact in the cerebella of patients with schizophrenia. That is to say, the most conclusive evidence of irreversible brain damage, loss of neurons, is not part of the structural deficit in cerebella of patients with schizophrenia.