Functional specialisation of pelvic limb anatomy in horses (Equus caballus)

Abstract

We provide quantitative anatomical data on the muscle–tendon units of the equine pelvic limb. Specifically, we recorded muscle mass, fascicle length, pennation angle, tendon mass and tendon rest length. Physiological cross sectional area was then determined and maximum isometric force estimated. There was proximal-to-distal reduction in muscle volume and fascicle length. Proximal limb tendons were few and, where present, were relatively short. By contrast, distal limb tendons were numerous and long in comparison to mean muscle fascicle length, increasing potential for elastic energy storage. When compared with published data on thoracic limb muscles, proximal pelvic limb muscles were larger in volume and had shorter fascicles. Distal limb muscle architecture was similar in thoracic and pelvic limbs with the exception of flexor digitorum lateralis (lateral head of the deep digital flexor), the architecture of which was similar to that of the pelvic and thoracic limb superficial digital flexors, suggesting a functional similarity.

Introduction

The two primary requirements of locomotor muscle are to support the centre of mass (COM) and to move the limbs. During steady-state locomotion, metabolic energy is primarily required to support the trunk against gravity (e.g. Taylor, 1985; Kram & Taylor, 1990). This role is most effectively fulfilled by short-fibred, pennate muscles with long tendons, such as those found in the distal limbs of horses (Hermanson & Cobb, 1992; Hermanson, 1997; Brown et al. 2003a) and many other cursorial animals (Alexander, 1977; Maloiy et al. 1979; Alexander et al. 1981; Pollock & Shadwick, 1994a). Much of the musculotendinous length change required for generating the work (i.e. muscle fascicle length change times muscle force) in steady-speed locomotion occurs not in the muscle fibres themselves but by elastic recoil of the associated tendon and muscle aponeurosis (Roberts et al. 1997; Biewener & Roberts, 2000). The force–length properties are thus predominantly passive (and hence fixed, Monti et al. 2003) and the muscle–tendon unit (MTU) acts as the spring in a spring–mass system (Cavagna et al. 1977; Blickhan, 1989; Farley et al. 1993; Lindstedt et al. 2002). Tendon springs are particularly useful in cursorial locomotion as they facilitate the exchange of kinetic, potential and elastic strain energy and reduce the amount of mechanical work that muscles must perform in order to move an animal's limbs and COM (Alexander, 1977; Ker et al. 1988; Pollock & Shadwick, 1994b; Alexander, 2002). Yet locomotion in athletic horses is rarely steady-state; gait is perturbed when accelerating from standing, running uphill or jumping over obstacles, for example. During such activities, net muscle work must increase to increase either the kinetic or potential energy of the COM (Biewener & Roberts, 2000). Muscles that are useful for doing work on the system have long, parallel fibres and limited in-series elastic tissue and are, in most cursors, primarily found in the proximal limb. Certainly, the moment-generating capacity of muscles (i.e. muscle force times moment arm) and force–length and force–velocity properties of the MTUs are also crucial (Brown et al. 2003a,b); here we focus on how the muscle and tendon architecture of the equine pelvic limb is specialised in regards to locomotion.

Functional specialisation of muscle architecture has been observed in a wide range of animals, where proximal limb muscles are specialised for doing work and distal limb muscles are specialised for economically generating large forces (e.g. Roberts, 2001; Biewener et al. 2004; Hutchinson, 2004; Payne et al. 2005). Horses and other quadrupeds have the additional capacity for functional specialisation between limbs. Ground reaction forces (GRF) under the hoof reveal that approximately 60 percent of the total vertical impulse (required for supporting the COM) is directed through the thoracic limbs (57 : 43, thoracic : pelvic, Witte et al. 2004). However, horizontal (acceleratory) impulses are greatest in the pelvic limb (e.g. Merkens et al. 1993). We might expect this functional difference to be reflected in muscle–tendon architecture. A purely qualitative investigation of thoracic and pelvic limb external anatomy shows similarity in the arrangement, shape and size of the distal region, but that the proximal pelvic limb (rump) is larger and more rounded than the equivalent shoulder region (see Fig. 1A–C). The action of individual pelvic limb muscles locomotion has been estimated from anatomical position (Table 1 and 2). However, specific data on the volume and architecture of equine pelvic limb muscles are not available, impairing assessments of muscle functional capacity. Muscle power is directly proportional to muscle volume; hence if we have additional information on muscle fascicle length, we can speculate about the velocity of contraction and range of motion over which the muscle can develop force. Muscle volume and muscle fascicle length data can then be combined to provide an estimate of physiological cross-sectional area (PCSA) and hence capacity for maximum isometric force generation, F_max. The energy stored in a tendon is related to its dimensions and to the stress imposed on it. We can thus estimate tendon elongation (at F_max of the attached muscle belly) and hence energy-storing capacity from information on tendon rest length and tendon mass.

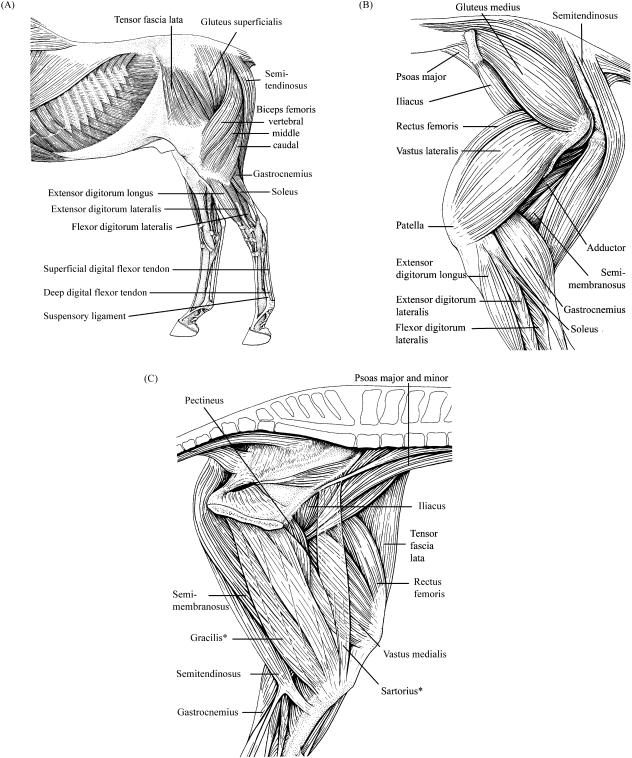
Fig. 1.

(A)Lateral superficial, (B)lateral deep and (C) medial deep view of the anatomy of equine pelvic limb. *Sartorius and gracilis are transparent so that deeper muscles can be visualised (Figures adapted from König & Liebich, 2004).

Table 1.

Origin, insertion and action of the major muscles of the proximal pelvic limb

Muscle	Abbreviation	Origin	Insertion	Action
Psoas minor	PMN	Ventral bodies of last 3 thoracic and first 3–4 lumbar vertebrae, crura of diaphragm	Psoas minor tubercle of femur	Flexion of hip
Psoas major	PMJ	Vertebral aspect of last 2 ribs, bodies and transverse processes of all lumbar vertebrae	With iliacus onto lesser trochanter of femur	Flexion of hip
Iliacus	IL	Pelvic surface of ilium, sacrum and tendon of psoas minor	Lesser trochanter of femur	Flexion of hip
Gluteus superficialis	GSP	Gluteal fascia	Third trochanter of femur and ischiadic tuber	Flexion and abduction of hip
Gluteus medius	GMD	Gluteal fascia, sacrum and sacro-iliac ligament	Greater trochanter of femur	Extension and abduction of hip
Gluteus profundus	GPF	Ischiatic spine	Greater trochanter of femur	Extension and abduction of hip
Tensor fascia lata	TFL	Tuber coxae	Via fascia lata onto patella and tibia	Flexion of hip, extension of stifle
Biceps femoris
Vertebral head	BFV	Spinous and transverse processes of last three sacral vertebrae, caudal fascia, broad pelvic ligament, ischiadic tuber	Blend with femoral and crural fascia and insert onto patella ligament, patella, tibial crest and lastly onto calcaneal tuber via calcaneal tendon	Extension and abduction of hip during stance, flexion of stifle and extension of hock during swing
Middle head	BFM	Ischiatic tuber and ischium	As above	As above
Caudal head	BFC	As above	As above	As above
Semitendinosus
Vertebral head	STV	Last spinous and transverse processes of sacrum, caudal fascial, first 3–4 caudal vertebrae and broad pelvic ligament	Medial tibial crest with aponeuroses of gracilis and sartorius and calcaneal tuber via calcaneal tendon which unites with that of biceps femoris to become accessory tendon	Extension of hip during stance, flexion of stifle and extension of hock during swing
Pelvic head	STP	Ischiadic tuber	As above	As above
Semimembranosus
Vertebral head	SMV	First caudal vertebra and broad pelvic ligament	Medial condyle of femur, medial collateral ligament and medial aspect of tibia	Extension of hip during stance, adduction of hip and flexion of stifle during swing
Pelvic head	SMP	Ischiadic tuber	As above	As above
Sartorius	SRT	Iliac fascia and aponeurosis of PMJ	Via crural fascia onto medial aspect of tibia and onto medial straight patella ligament	Flexion and adduction of hip, flexion of stifle during swing
Gracilis	GRC	Pelvic symphysis, tendon of insertion of rectus abdomius and accessory ligament	Via crural fascia onto tibial crest and onto medial straight patella ligament	Adduction of hip, flexion of stifle during swing
Pectineus	PCT	Pubis, terminal tendon of rectus abdomius and accessory ligament	Medial shaft of femur (linea aspera)	Adduction of hip
Adductor
Magnus	ADM	Pelvic symphysis	Medial shaft of femur (linea aspera)	Adduction and extension of hip
Brevis	ADB	As above	As above	As above
Quadriceps femoris
Rectus femoris	RF	Body of ilium	Middle patella ligament to tibial tuberosity and tibial crest	Flexion of hip, extension of stifle
Vastus medialis	VM	Craniomedial femoral shaft	As above	Extension of stifle
Vastus intermedius	VI	Cranial femoral shaft	As above	As above
Vastus lateralis	VL	Craniolateral femoral shaft	As above	As above

Primary action at each joint is listed first, followed by secondary/auxillary actions (Nickel et al. 1986). Piriformis is part of GMD in the horse and so is not listed as a separate muscle. The hamstring muscles flex the stifle joint during swing but constrain extension during the first half of stance due to the antagonistic action of rectus femoris and the cranial position of the vertical ground reaction force vector (Clayton et al. 2001).

Table 2.

Origin, insertion and action of the major muscles of the distal pelvic limb

Muscle	Abbreviation	Origin	Insertion	Action
Popliteus	PP	Popliteal fossa of lateral femoral condyle	Proximal 1/3 of caudomedial tibial shaft	Flexion and pronation of stifle
Gastrocnemius
medialis	GM	Distal femoral shaft	Via common calcaneal tendon onto tuber calcanei	Extension of hock and flexion of stifle
lateralis	GL	As above	As above	As above
Soleus	SL	Head of fibula	Blends with GL aponeurosis	Extension of hock but rudimentary
Flexor digitalis superficialis	SDF	Supracondylar fossa	Tubercalcaneum (calcanean cap) and plantar aspect of middle phalanx	Flexion of digit, extension of hock and auxiliary flexion of stifle as part of passive stay apparatus
Flexor digitorum profundus	DDF
Flexor digitorum medialis	FDM	Caudal aspect and lateral condyle of tibia and fibula	Via deep flexor tendon onto palmar aspect of phalanx III	Flexion of digits and auxillary extensor of hock
Tibialis caudalis	TCD	Lateral condyle of tibia and fibula	As above	As above
Flexor digitorum lateralis	FDL	Caudal aspect of lateral condyle of tibia	As above	As above
Interosseus medius (suspensory ligament)	IM	Palmar aspect of proximal end of metacarpal bone	Proximal sesamoid bones	Fix fetlock joint as part of stay apparatus
Tibialis cranialis	TCN	Shaft, lateral condyle and crest of tibia, proximal fibula	Medial and intermediate cuneiforms and metatarsal III	Flexion of hock
Peroneus tertius	PT	Extensor fossa of femur	Lateral cuneiform and metatarsal III	Passive stay apparatus linking stifle and hock motion
Extensor digitorum longus	EDLO	Extensor fossa of femur	Extensor process of distal phalanx	Extension of digits and flexion of hock
Extensor digitorum lateralis	EDLA	Fibula and lateral collateral ligament of stifle	Blends with terminal tendon of EDLO	Extension of digits and flexion of hock

Primary action at each joint is listed first, followed by secondary/auxillary actions (Nickel et al. 1986).

In this study, we supplement our existing work on equine thoracic limb anatomy (Payne et al. 2005) by providing equivalent and detailed information on the volume and architectural properties of the major MTUs of the pelvic limb. These data are integrated with available experimental data to infer how the pelvic limb MTUs of horses may function during locomotion. We then compare these data with existing data on equine thoracic limb muscles in order to explore anatomical and functional specialisation in equine thoracic and pelvic limbs.

Materials and methods

Seven pelvic limbs from five Thoroughbreds, one Thoroughbred–Cross and one Arab horse (Equus caballus) with no history of musculoskeletal pathology were obtained from a local abattoir (Holts, Stanstead Abbots, UK) and used in this study (Table 3). All horses were killed for reasons unrelated to the study. Each limb was obtained within 24 h of death and stored at 4 °C for a maximum of 48 h prior to dissection. The limbs were skinned and the individual muscles were identified, dissected free from fascia and then removed. Muscle belly length (mm) was obtained using a ruler laid to one side of the muscle belly and by measuring the distance from the most proximal fibres to the most distal fibres. Any substantial external tendon (origin/insertion) was removed from the muscle belly and its mass (to the nearest 0.1 g) and resting length (to the nearest mm) recorded using electronic scales (EKS®, UK) and a flexible tape measure, respectively. Tendon cross-sectional area was then estimated by dividing tendon volume [i.e. mass divided by density (1.12 g cm⁻³, Ker et al. 1988)] by tendon length. In order to reveal the muscle fascicles, a cut was made along the length of the muscle belly, at 90° to the internal tendon. If the muscle did not have an internal tendon (e.g. sartorius), fascicles were revealed by making incisions from origin to insertion through the muscle belly until the plane of the muscle fascicles had been obtained (i.e. when the entire fascicle bundle could be seen). At least 10 measurements of fascicle length (20 for muscles over 2000 g) were taken from randomly distributed areas and depths within the muscle belly. Resting pennation angle (e.g. Alexander, 1977; Gans & De Vree, 1987) was obtained by measuring the angle between the internal tendon or aponeurosis and the fascicles using a protractor. Finally, the internal tendon was removed and muscle mass was determined using electronic scales. Muscles heavier than 2000 g were weighed in several pieces.

Table 3.

Subject details

Subject	Age (years)	Mass (kg)	Height (cm)	Breed
1	20	430	142	Arab
2	30	500	157	TB
3	10	560	147	TB
4	30	480	147	TB
5	28	600	147	TB
6	24	500	143	TBX
7	28	500	152	TB

Height was measured from ground to withers. TB = Thoroughbred, TBX = Thoroughbred–Cross.

Muscle volume was determined by dividing muscle mass by muscle density (1.06 g cm⁻³, Mendez & Keys, 1960; Brown et al. 2003a). F_max was estimated by multiplying PCSA (volume/fascicle length) by the maximum isometric stress of vertebrate skeletal muscle (0.3 MPa, see Wells, 1965; Woledge et al. 1985; Zajac, 1989; Medler, 2002). Maximum contraction velocity (V_max) was estimated to be 5 L₀ s⁻¹ (L₀ = muscle fibre resting length). This figure was based on the assumption that equine pelvic limb muscles are predominantly composed of type IIA fibres (see Snow, 1983; van den Hoven et al. 1985). If V_max of type IIA fibres in equine soleus is 1.33 L₀ s⁻¹ at 15 °C (Rome et al. 1990), then each 10 °C rise in temperature results in an approximate doubling of contraction velocity (Gasser & Hill, 1924). Hence 5 L₀ s⁻¹ is a reasonable starting estimate of the typical V_max of equine pelvic limb muscles; we then estimated the absolute value of V_max for each muscle as the muscle fascicle length (in metres) multiplied by 5 L₀ s⁻¹. Finally, muscle power was estimated as one tenth of the product of F_max and V_max (Hill, 1938; Woledge et al. 1985).

Results

Muscle volume and architecture

Muscle data are provided in Table 4. It was not possible to separate the two heads of semimembranosus (SMV and SMP) or the two adductor muscles (ADM and ADB), and so each pair of muscles was considered as one. Gluteus medius (GMD, mean mass 8577 g) and biceps femoris (mean mass of all three heads: 7928 g) were by far the heaviest muscles of the entire pelvic limb. Gastrocnemius medialis and gastrocnemius lateralis were the heaviest muscles of the distal limb (mean mass of both heads: 1625 g). Fascicle length was more variable both within (individual muscles) and between (the same muscle in different subjects) muscles of the proximal limb (see Table 4). Absolute range in fascicle length (i.e. all measurements for that muscle from all subjects) was greatest in semimembranosus (range: 80–760 mm) and the adductors (range: 80–390 mm) and smallest in flexor digitorum superficialis (SDF: 1–6 mm) and the flexor digitorum lateralis (FDL) head of the deep digital flexor (DDF; range: 3–55 mm). Relative range in fascicle lengths was however, greatest in FDL.

Table 4.

Muscle data

	Muscle mass (g)	Volume (cm3)	Belly length (mm)	Fascicle length (mm)	PCSA (cm2)	Pennation angle (°)	Force (N)	Power (W)
Psoas major	1182 (821–1652)	1116	312	198 (95–280)	56	29 (20–35)	1694	177
Psoas minorb	432 (282–740)	408	331	67 (50–205)	61	37 (35–38)	1833	65
Iliacus	1395 (1288–1507)	1316	340	244 (170–305)	54	26 (15–40)	1617	209
Glutaeus superficialis	646 (439–768)	609	433	102 (55–190)	60	36 (28–50)	1793	97
Glutaeus medialis	8577 (6390–12200)	8091	440	203 (135–300)	398	28 (15–45)	11942	1287
Glutaeus profundus	1351 (1121–1755)	1275	286	118 (42–220)	108	30 (15–40)	3249	203
Tensor fascia lata	1448 (1071–2349)	1366	278	97 (60–150)	140	34 (20–43)	4210	217
Biceps femoris (intermediate head)	870 (552–1210)	820	313	235 (190–260)	35	27 (20–40)	1048	130
Biceps femoris (vertebral head)	6112 (4876–8030)	5766	586	258 (130–330)	223	37 (28–50)	6705	917
Biceps femoris (caudal head)	946 (700–1260)	892	337	245 (170–300)	36	39 (30–45)	1092	142
Semitendinosus (vertebral head)	2684 (2000–4031)	2532	543	274 (105–289)	92	28 (20–35)	2770	403
Semitendinosus (pelvic head)	1727 (959–2721)	1630	367	312 (180–355)	52	35 (25–45)	1567	259
Semimembranosus (vertebral & pelvic heads)	3834 (2982–5171)	3617	616	342 (80–760)	106	35 (20–45)	3171	575
Gracilis	1760 (1064–2538)	1661	320	123 (80–175)	135	31 (22–35)	4037	264
Sartorius	484 (333–738)	456	431	376 (250–460)	12	21 (20–25)	364	73
Adductor (magnus & brevis)	3924 (2942–5464)	3702	451	176 (80–390)	211	35 (25–40)	6322	589
Pectineus	447 (284–647)	422	261	78 (49–320)	54	29 (13–50)	1614	67
Rectus femoris	2291 (1747–3000)	2161	360	98 (40–152)	220	40 (25–53)	6610	344
Vastus medialis	1878 (1496–2406)	1772	326	119 (90–145)	148	33 (25–41)	4448	282
Vastus intermedius	501 (280–725)	473	284	105 (60–220)	45	41 (30–55)	1355	75
Vastus lateralis	1734 (1073–2227)	1636	323	155 (92–220)	105	36 (30–40)	3163	260
Popliteus	280 (171–423)	264	235	38 (21–170)	70	42 (35–50)	2107	42
Gastrocnemius medialis	817 (512–1132)	771	254	48 (25–99)	161	36 (20–45)	4836	123
Gastrocnemius lateralis	808 (592–1389)	762	262	56 (36–70)	137	34 (30–45)	4098	121
Soleusa	6 (4–9)	6	155	121 (110–151)	0	22 (22–22)	15	1
Flexor digitorum superficialis	111 (70–139)	105	214	3 (1–6)	417	52 (40–60)	12514	17
Flexor digitorum medialis	161 (143–188)	152	270	70 (4–100)	22	27 (12.0–40)	652	24
Flexor digitorum lateralis	660 (391–922)	622	297	10 (3–55)	644	44 (30–60)	19324	99
Tibialis caudalis	224 (148–308)	211	242	57 (40–117)	37	31 (20–60)	1106	34
Extensor digitorum lateralis	192 (152–275)	181	284	70 (35–110)	26	28 (20–45)	776	29
Extensor digitorum longus	462 341–557)	435	271	81 (60–110)	54	29 (25–45)	1620	69
Tibialis cranialis	309 (216–398)	291	326	40 (17–218)	73	41 (25–60)	2199	46
Total hindlimb muscle mass	49478

Fascicle length range is the range of all fascicle length measurements taken from that muscle in all subjects.

^aSoleus is very small and difficult to distinguish from GL; it was only found in 2 out of 6 horses.

^bIliacus was damaged in subject 4 so n = 6 for that muscle.

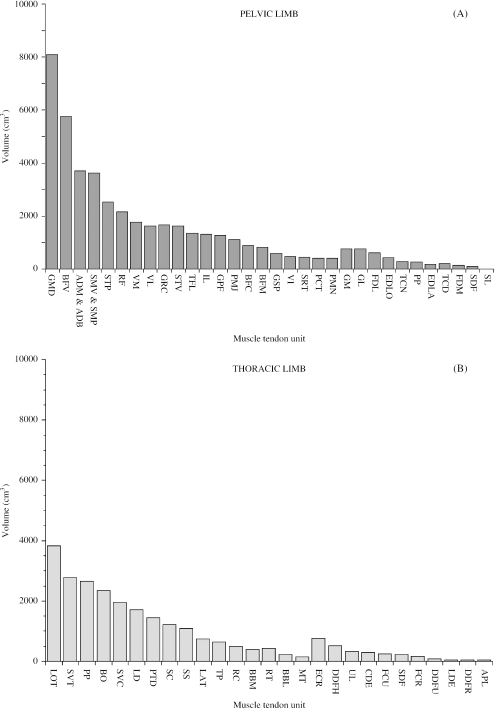
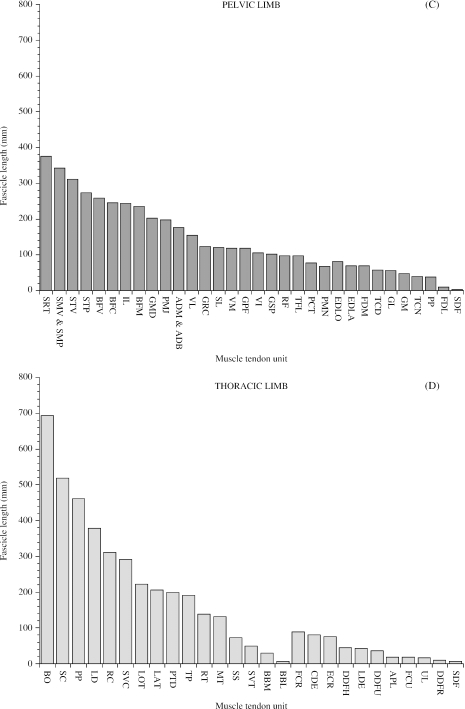
In order to visualise proximal-to-distal patterns of muscle volume and architecture, muscle volume and fascicle length data for each muscle were plotted (Fig. 2A,C). Thoracic limb volumes and fascicle lengths were also plotted in this figure (Fig. 2B,D) but the data will not be discussed until later in the paper (see “functional specialisation of the thoracic and pelvic limbs”). There was a distinct proximal-to-distal reduction in both muscle volume and muscle fascicle length in pelvic limb muscles. However, the largest muscles did not always have the longest fascicles, just as the smallest muscles did not necessarily have the shortest fascicles. In the proximal limb, GMD, vertebral head of biceps femoris, the adductors (ADM and ADB), semimembranosus (SMV and SMP) and semitendinosus (STV and STP) all had large volumes (range of mean volumes for this group of muscles: 3617–8090 cm³) and long fascicles (range of mean fascicle lengths: 176–342 mm). Psoas minor, gluteus superficialis, gluteus profundus, tensor fascia lata (TFL), gracilis, pectineus, rectus femoris, vastus medialis and vastus intermedius had smaller volumes (range of mean values: 408–2160 cm³) and shorter fascicles (range of mean values: 67–123 mm). Psoas major, iliacus, caudal head of biceps femoris, middle head of biceps femoris, vastus lateralis and sartorius had small volumes (range of mean values: 456–1640 cm³) but longer fascicles (range of mean values: 155–376 mm). Of the distal limb muscles, gastrocnemius medialis and gastrocnemius lateralis had relatively large volumes (mean values 771 cm³ and 762 cm³, respectively) and shorter fascicles (mean values 48 mm and 56 mm, respectively). The other distal limb muscles had smaller volumes (range of mean values: 6–435 cm³) and short/medium-length fascicles (range of mean values: 38–121 mm). The FDL head of the DDF however, had a relatively large mean volume (622 cm³) and very short fascicles (mean value 10 mm) and SDF had a small mean volume (105 cm³) and very short fascicles (mean value 3 mm; see Fig. 3).

Fig. 2.

Muscle volume (A & B) and mean muscle fascicle length (C & D) for pelvic and thoracic limb muscles. Muscles are plotted starting with the proximal muscle with the largest mean volume/fascicle length and ending with the distal muscle with the smallest mean volume/fascicle length. Abbreviations for pelvic limb muscles are given in Tables 1 and 2. Thoracic limb muscle abbreviations are as follows: LOT (long head of triceps brachii), SVT (serratus ventralis thoracis), PP (pectoralis profundus), BO (brachiocephalicus and omotransversarius); SVC (serratus ventralis cervicis), LD (latissimus dorsi), PTD (pectoralis transvs. and pectoralis descendens), SC (subclavius), SS (supraspinatus), LAT (lateral head of triceps brachii), TP (trapezius), RC (rhomboideus cervicis), BBM (medial head of biceps brachii), RT (rhomboideus thoracis), BBL (lateral head of biceps brachii), MT (medial head of triceps brachii), ECR (extensor carpi radialis), DDFH (humeral head of flexor digitorum profundus), UL (ulnaris lateralis), CDE (extensor digitorum communis), FCU (flexor carpi ulnaris), SDF (flexor digitorum superficialis), FCR (flexor carpi radialis), DDFU (ulna head of flexor digitorum profundus), LDE (long digital extensor), DDFR (radial head of flexor digitorum profundus), APL (abductor pollicis longus).

Fig. 3.

Internal architecture of flexor digitorum superficialis [(A), SDF] and tibialis cranialis [(B), TCN]. The muscles have been sectioned through the muscle belly to reveal the arrangement of the fascicle bundles. Note the striped appearance of the internal aponeurotic tendon of SDF and contrast that with the single internal tendon of TCN.

As expected, most distal limb muscles were more highly pennate than proximal limb muscles. However, there were some exceptions to this pattern. Specifically, resting pennation angle was low in sartorius (21°) and soleus (22°) and high in SDF (52°), FDL (44°), popliteus (42°), tibialis cranialis (41°), vastus intermedius (41°), rectus femoris (40°) and in the caudal head of biceps femoris (39°).

In the proximal limb, PCSA was greatest in GMD and the vertebral head of biceps femoris (mean values 398 cm² and 223 cm², respectively). In both muscles, large PCSAs were due to large muscle volumes as fascicle lengths were also relatively long (> 200 mm). The adductor muscles and rectus femoris also had large PCSAs (in excess of 200 cm²) which could be related to their larger volumes and shorter fascicle lengths (< 179 mm). Distal limb muscles SDF and FDL had the largest PCSAs of any of the pelvic limb muscles (mean values 417 cm² and 644 cm², respectively).

In order that comparisons could be made between subjects of different sizes, muscle mass and fascicle length data were scaled assuming geometric similarity (Table 5) – that is, muscle mass was scaled as a fraction of body mass (kg) and fascicle length as a fraction of [body mass (kg)]^1/3. When scaled, muscle masses were similar among the seven subjects. The exceptions were GMD (scaled mean muscle masses for this muscle ranged from 12.8 to 20.3 g kg⁻¹ body mass) and the pelvic head of semitendinosus (scaled mean values ranging from 4.0 to 8.06 g kg⁻¹ body mass). There was a greater amount of intersubject variation in scaled mean fascicle lengths than in scaled muscle masses. This variation was particularly marked in the vertebral head of semitendinosus [range of scaled mean fascicle lengths: 20.4–45.1 mm/(kg body mass)^1/3] and in semimembranosus [range of scaled mean fascicle lengths: 24.8–62.7 mm/(kg body mass)^1/3].

Table 5.

Muscle mass as a fraction of body mass and fascicle length as a fraction of (body mass)^1/3

	Muscle mass (g)/body mass (kg)							Fascicle length (mm)/[body mass (kg)]1/3
Subject	1	2	3	4	5	6	7	1	2	3	4	5	6	7
Psoas major	–	1.71	1.47	2.47	2.63	2.00	3.30	–	18.3	21.9	28.1	24.4	24.2	30.9
Psoas minorb	–	0.56	0.82	0.70	1.23	0.67	0.88	–	7.8	8.7	8.3	7.4	8.4	9.4
Iliacus	0.00	2.58	2.69	–	2.40	2.62	2.87	–	32.8	25.5	–	31.1	31.3	30.2
Glutaeus superficialis	1.48	0.88	1.37	1.40	1.10	1.51	1.09	10.2	10.9	11.9	14.2	16.9	12.4	9.6
Glutaeus medialis	–	12.78	16.73	14.8	20.3	15.60	17.20	–	22.6	20.9	32.4	29.2	26.2	20.3
Glutaeus profundus	–	2.53	2.00	2.67	2.92	2.41	2.97	–	13.6	14.4	15.3	13.4	18.6	12.6
Tensor fascia lata	6.40	7.60	8.77	6.77	9.11	7.32	6.89	7.0	12.2	11.1	15.4	11.6	12.9	9.6
Biceps femoris (intermediate head)	2.33	2.82	2.67	2.36	3.92	3.20	2.16	23.1	31.5	28.4	30.0	30.8	25.5	29.0
Biceps femoris (vertebral head)	1.20	1.68	1.82	1.29	2.02	1.83	1.87	26.6	27.9	30.5	40.2	35.0	31.9	27.2
Biceps femoris (caudal head)	10.60	10.80	13.93	10.63	13.38	11.80	11.35	25.9	31.2	27.7	33.6	32.4	34.8	23.3
Semitendinosus (vertebral head)	2.05	1.40	2.14	1.50	2.10	1.97	1.63	20.4	34.0	31.9	27.3	45.1	36.0	29.7
Semitendinosus (pelvic head)	5.10	8.06	4.22	6.67	4.24	4.00	4.60	35.8	28.5	29.2	45.0	53.7	46.2	29.6
Semitendinosus (vertebral & pelvic heads)	4.67	2.15	4.08	2.00	4.54	2.80	3.00	30.6	24.8	41.3	38.3	62.7	42.6	45.1
Gracilis	6.48	7.98	8.21	7.08	8.62	6.54	6.85	12.0	11.7	14.7	21.0	13.7	14.1	17.2
Sartorius	2.87	4.03	4.11	2.22	4.23	3.19	2.98	36.9	48.3	37.7	50.6	47.4	52.7	44.2
Adductor (magnus & brevis)	0.72	0.85	1.01	1.04	1.23	0.82	0.84	12.7	17.9	17.7	25.7	20.5	23.4	26.1
Pectineus	3.28	4.17	4.23	3.37	4.01	3.33	2.99	6.0	8.1	8.5	10.4	12.9	10.2	8.4
Rectus femoris	3.80	4.81	5.36	4.16	4.47	4.23	4.18	10.3	10.8	12.0	19.0	12.1	10.3	9.2
Vastus medialis	0.65	1.00	0.91	0.90	1.08	0.92	0.57	13.9	12.9	14.0	16.7	13.4	14.9	17.5
Vastus intermedius	0.61	1.25	1.29	0.86	1.21	0.86	0.62	5.8	10.2	14.9	15.3	11.3	11.6	15.2
Vastus lateralis	2.33	3.17	3.98	3.47	3.67	3.00	3.77	7.8	16.0	18.3	28.1	17.5	12.2	24.2
Popliteus	0.41	0.72	0.76	0.46	0.60	0.34	0.47	0.0	3.4	5.1	4.7	5.3	4.6	4.9
Gastrocnemius medialis	1.11	1.80	1.62	1.26	1.89	1.79	1.53	5.9	6.2	7.1	9.6	4.5	4.0	4.4
Gastrocnemius lateralis	1.29	1.48	2.48	1.80	1.35	1.29	1.24	3.9	6.9	6.8	6.7	5.9	7.5	7.8
Soleus	0.02	0.02	0.01	–	–	–	0.01	19.6	14.9	16.7	–	–	–	13.9
Flexor digitorum superficialis	0.21	0.25	0.25	0.26	0.12	0.18	0.27	0.3	0.5	0.3	0.5	0.2	0.2	0.2
Flexor digitorum medialis	0.32	0.38	0.30	0.30	0.26	0.34	0.31	10.7	9.2	10.9	11.5	8.1	6.5	6.1
Flexor digitorum lateralis	0.85	1.33	1.65	1.41	1.26	1.51	0.90	0.7	1.9	0.7	2.4	0.7	0.7	0.9
Tibialis caudalis	0.44	0.44	0.55	0.45	0.45	0.41	0.30	5.2	7.1	6.8	7.0	8.0	8.6	5.1
Extensor digitorum lateralis	0.33	0.47	0.49	0.36	0.28	0.31	0.38	5.9	6.2	9.7	10.9	8.6	9.8	7.3
Extensor digitorum longus	0.75	0.94	0.99	0.89	0.93	1.08	0.68	8.5	8.3	10.9	11.9	9.0	10.5	9.8
Tibialis cranialis	0.47	0.74	0.71	0.57	0.61	0.56	0.51	2.4	3.1	9.2	7.0	4.0	4.3	2.4

Estimates of muscle force and power

In order to distinguish which muscles had the greatest capacity for maximal force or power, these values were estimated (as described in the Materials and methods section) and are presented in Table 4. Proximal limb muscles tended to be more powerful than distal limb muscles and in many cases were capable of generating higher forces. Of the proximal limb muscles, GMD was estimated to have the highest capacity for force (11 900 N) and power (1130 W). However, biceps femoris (BFV, BFI and BFC: 8840 N and 1190 W), semitendinosus (STV and STP: 4340 N and 662 W), adductors (ADM and ADB: 6320 N and 589 W) and semimembranosus (SMV and SMP: 3170 N and 575 W) were also estimated to have the capacity for high force and power compared to other pelvic limb muscles. Of the distal limb muscles, DDF (FDM, FDL and TCD: 21 100 N and 157 W) and SDF (12 500 N and 17 W) were estimated to have the capacity for high force but relatively low power. Gastrocnemius (GM and GL) was similar in this regard but was estimated to have a greater capacity for power (8930 N and 244 W).

Tendon properties

Tendon data for the pelvic limb muscles are given in Table 6. The majority of proximal limb MTUs did not have sufficient tendon to take measurements from. The exceptions were psoas major, gluteus superficialis, biceps femoris, semimembranosus, gracilis, sartorius and TFL. Proximal limb tendons were light (mean tendon mass ranged from 5.3 to 34.2 g) when compared to distal limb tendons (mean values ranged from 44.8 to 208.7 g). The exception was the tendon of biceps femoris, which was the heaviest (mean value 106 g) of the proximal limb tendons and had the largest CSA of all pelvic limb tendons (mean value 9.54 cm²). Of the distal limb MTUs, tendon CSA was largest in DDF (mean value 3.64 cm²), followed by gastrocnemius (tendo calcaneus, mean value 3.32 cm²), tibialis cranialis (mean value 2.61 cm²) and flexor digitorum superficialis (mean value 2.25 cm²). All other mean tendon CSAs were less than 2.00 cm². Using these estimates of tendon CSA, we estimated the maximum stresses that could occur in these tendons under the maximal isometric force (F_max) generated by their attached muscle bellies. The tendon of FDL was estimated to experience the highest stress (98 MPa) of the pelvic limb MTUs. Stress in tendo calcaneus was estimated at 27 MPa. Stress in the long digital extensor tendon was low at 14 MPa. The properties of internal tendons/aponeuroses (e.g. in gastrocnemius or SDF) were not considered here.

Table 6.

Mass, volume, rest length, cross-sectional area stress, strain and length change of selected pelvic limb tendons

Muscle tendon unit	Mass (g)	Volume (cm3)	Rest length (mm)	CSA (cm2)	Stress (MPa)	Strain (%)	Length change (mm)
Psoas major	7.4	6.6	90	0.73	22.9	1.53	1.37
Glutaeus superficialis	14.0	12.5	90	1.39	13.0	0.87	0.78
Tensor fascia lata	34.2	30.5	227	1.35	31.2	2.08	4.72
Biceps femoris	106.8	95.4	100	9.54	9.2	0.61	0.61
Semimembranosus	11.9	10.6	105	1.01	31.5	2.10	2.21
Gracilis	15.4	13.8	114	1.21	33.5	2.23	2.55
Sartorius	5.3	4.7	104	0.46	7.9	0.53	0.55
Gastrocnemius	90.7	81.0	244	3.32	27.0	1.80	4.39
Flexor digitorum superficialis	188.9	168.7	748	2.25	55.5	3.70	27.68
Flexor digitorum medialis	56.7	50.6	409	1.24	5.3	0.35	1.45
Flexor digitorum lateralis	127.0	113.4	574	1.98	97.8	6.52	37.42
Tibialis caudalis	6.1	5.4	131	0.42	26.7	1.78	2.33
Extensor digitorum lateralis	21.0	18.8	308	0.61	12.8	0.85	2.63
Extensor digitorum longus	59.6	53.2	472	1.13	14.4	0.96	4.53
Tibialis cranialis	26.9	24.0	92	2.61	8.4	0.56	0.52
Peroneus tertius	64.3	57.4	362	1.59	–	–	–
Suspensory ligament	44.8	40.0	328	1.22	–	–	–

The density of tendon was assumed to be 1220 kg m⁻³ (Ker, 1981) and volume was estimated from mass using this value. Tendon rest length was measured from the muscle–tendon junction to the point of insertion and then tendon cross-sectional area (CSA) was estimated by dividing tendon volume by tendon length. Tendon strain was estimated by dividing tendon stress (muscle F_max/tendon CSA) by the Young's Modulus of tendon (1500 MPa; Bennet et al. 1986; Ker et al. 1988). Tendon length change was estimated from the product of tendon rest length and tendon strain, and normalised by mean muscle fascicle length (Table 4) to provide an estimate of MTU stiffness.

Discussion

Proximal-to-distal specialisation of muscle architecture

We quantified the proximal-to-distal specialisation of muscle architecture in the equine pelvic limb. Our results confirm our expectations that the proximal limb was characterised by muscles with large volumes and long fascicles and the distal limb was characterised by muscles with small volumes and short, pennate fascicles (see Table 4 and Fig. 2A,C). Hence in general, proximal pelvic limb musculature is specialised for doing work, while distal pelvic limb musculature is specialised for generating force economically. This matches findings from other recent biomechanical analyses of several different tetrapods, including turkeys (Roberts, 2001), wallabies (Biewener et al. 2004) and various bipeds (Hutchinson, 2004).

Muscle volume and architecture

Muscle architecture is certainly more complex than can be described using gross dissection alone (see Swanstrom et al. 2005). For example, functional compartmentalisation of GMD has been described in detail by Lopez-Rivero and colleagues (e.g. Lopez-Rivero et al. 1992; Rivero et al. 1993; Serrano et al. 1996). During fibre-typing experiments, they observed superficial sections with predominantly type IIB fibres and deep sections with predominantly type I fibres. Although a wide range of fascicle lengths were observed in this and other hip extensor muscles during our dissections (e.g. gluteus medialis 135–300 mm; vertebral and pelvic heads of semitendinosus 105–355 mm; vertebral and pelvic heads of semimembranosus 80–760 mm), we did not observe a clear superficial to deep gradation of fibre length.

Pennation angle (θ) is another aspect of muscle architecture that can vary widely between muscles. However, research has shown that pennation angle has little influence on muscle function, particularly when the angles are of 20° or less (Burkholder et al. 1994). This is because, in pennate muscle, the force transmitted to the tendon is the product of PCSA and cos(θ). In muscles with pennation angles of 20° or less, cos(θ) is close to 1.0 and thus pennation angle has very little effect on force transmission (Alexander, 1968). All of the muscles studied here had pennation angles above 20° (in fact, many were in excess of 35°; see Table 4), but we did not include pennation angle in our estimations of F_max. This is because pennation angle will undergo substantial changes through a contraction and 2D muscle models cannot represent the changes in architecture that occur in 3D, in a real muscle. For in-depth discussion of these and other aspects of muscle function, see, for example, Otten (1988) and Zajac (1989).

In spite of the general (proximal-to-distal) pattern of muscle volume and architecture described above, a wide range of different volume/fascicle length combinations were observed. The mono-articular hip extensor GMD and the biarticular vertebral head of biceps femoris (BFV) were by far the largest muscles of the pelvic limb. These muscles, along with, but to a lesser extent, semimembranosus, semitendinosus and the adductors, formed a group of muscles characterised by large volumes and long fascicles. This pattern is typical of muscles specialised for doing work and achieving high power output; however, GMD and BFV were also capable of generating high forces as their enormous bulk resulted in large PCSAs (in spite of their long fascicles, Table 4). The pelvic limb is said to be the primary propulsor of the horse (e.g. Merkens et al. 1993) and thus one might expect the hip extensors to be relatively powerful.

Muscles crossing the cranial aspect of the hip (i.e. the limb protractors: psoas major, psoas minor, iliacus and rectus femoris) were not as large as the more caudal hip extensors. The architecture of this group of muscles was such that relative to the hip extensors, they were not capable of generating either large forces or powerful contractions (Table 4). The mechanisms underlying hindlimb protraction have not yet been determined; however, Electromyographical records suggest that protraction is initiated at the end of stance via active shortening of the hip flexor muscles (Tokuriki & Aoki, 1995) but maintained through swing via passive recoil of elastic structures such as the aponeurosis of TFL (Tokuriki & Aoki, 1995) and the reciprocal apparatus (SDF and peroneus tertius; Wentink, 1978). This system of combining the initial activity of relatively small muscles (with small PCSAs) to release the limb with subsequent passive elastic recoil of tendons is likely sufficient for limb protraction (see also Wilson et al. 2003). This is because the protracting limb need only overcome forces associated with air resistance and its own weight and inertia (and not against the GRF and inertia of the trunk as is the case in retraction).

Muscle volume and mean muscle fascicle length data were more similar among the distal limb muscles. Gastrocnemius lateralis and medialis were the largest of these muscles, with relatively short pennate fascicles (Table 4) and a long, thick common tendon (Table 6). Although gastrocnemius is certainly capable of performing a small amount of muscular work, the extensive tendinous structures (serial and parallel to muscle fibres) point to a capacity for economical force generation via tendinous stretch and recoil. The other distal limb muscles had smaller volumes but similar fascicle and tendon lengths (with varying tendon cross sectional areas) to gastrocnemius. These structural similarities point to similar functional roles, elastic energy storage and recoil and reduction in mass of the distal limb. The most extreme example of this form of muscle design was observed in the long digital flexors SDF and the FDL head of DDF, which had long, thick tendons and very short, highly pennate fascicles. In comparison to the other distal limb muscles, SDF and FDL had large amounts of aponeurotic tendinous tissue running through the belly so that they had a striped appearance (see Fig. 3). This pattern of muscle–tendon architecture (i.e. the replacement of muscle with tendinous tissue) has been described in the thoracic limb SDF (Wilson et al. 2001; Brown et al. 2003a) and has been linked with a reduced need for muscular work in that muscle. The suspensory ligament (modified interosseous muscle) represents the end point of such a specialisation where muscle fibres are almost completely absent in the adult horse.

In studies of animal locomotion it is often useful to make comparisons within a species. However, as we only used cadavers euthanased for reasons unrelated to our studies, it can be difficult to obtain cadaveric material that has been matched for breed, age or size. Our data set is from a population of mainly Thoroughbred horses (two of the seven subjects were not Thoroughbreds) of varying age (age range 10–30 years) and body mass (body mass range 430–600 kg). Thus we scaled our muscle mass and fascicle length data assuming geometric similarity (see the Material and methods section) and compared the results (Table 5). There was little variation in scaled muscle masses or fascicle lengths between the seven subjects. The hamstring and gluteal muscles were the exception as their muscle masses and fascicle lengths varied widely between the subjects. As discussed earlier, the caudal proximal limb muscles are the primary propulsive muscles of the horse. Thus it may be that differences in activity level were responsible for the observed variation in mass (i.e. due to training induced hypertrophy, Narici et al. 1989). Unfortunately we do not have information on premortem activity levels for the subjects and so cannot speculate further on this matter. Mean scaled fascicle length ranges were particularly high in semitendinosus and semimembranosus. In these muscles fascicles either ran from origin to insertion or were staggered along the muscle belly, which might be the reason for the differences seen. In any case, the observed complexity and variation in muscle volume and architecture supports the need to include detailed muscle architecture in models of the equine pelvic limb (see also Otten, 1988).

Tendon properties

Tendons (i.e. collagenous tissue in series with the muscle fibres) were measured where feasible. The energy stored in a tendon is a direct function of the product of its volume and the stress imposed on it. Here, we assume that the tendon stress is related to the force generating capacity of the muscle and the tendon cross sectional area since the effects of activation and velocity conditions for individual muscles are beyond the scope of this paper. The majority of proximal limb muscles inserted directly onto bone but some originated from/inserted onto broad sheets of aponeurosis (gluteus superficialis, GMD and TFL) and thus would have some element of in-series compliance that we were unable to assess accurately. The exception was biceps femoris, the tendon of which was relatively heavy but short and was estimated to experience low stress (9.2 MPa, Table 6). Proximal limb tendons (with the exception of those muscles with sheet-like aponeuroses) are thus likely to be less useful for storing and returning elastic strain energy than distal limb tendons.

Tendon CSAs were particularly large in the distal limb muscles: tibialis cranialis, SDF, FDL and gastrocnemius (range of mean values: 1.98–3.64 cm³). Using these estimates of tendon CSA, we estimated the maximum stresses that could occur in the tendons under the maximal isometric force generated by their attached muscle bellies (these stresses would of course be larger if the muscles were being actively stretched; Table 6). Estimates of maximum in vivo stress were highest in FDL (98 MPa). This value was similar to that reported in Ker et al. (1988) (105 MPa) but higher than that reported in Biewener (1998) (40–50 MPa). Stress in gastrocnemius was estimated at 27 MPa, which is similar to values reported in Ker et al. (1988) (47 MPa) and Biewener (1998) (30 MPa). Stress in the digital extensor tendon was low (14 MPa) compared to the value reported in Ker et al. (1988) (36 MPa). If, as has been suggested, tendons fail at stresses of approximately 120 MPa (Zajac, 1989), then the tendon of FDL would be operating close to this when generating force isometrically and above this threshold when actively lengthening (Cavanagh et al. 1981). Similar estimates of maximum in vivo stress have, however, been published for the plantaris tendon in other ungulates (elk, 92–96 MPa; bearded gnu, 173 MPa; white tailed deer, 52–101 MPa; dog, 89–107 MPa; Pollock and Shadwick, 1994a,b). With such high stresses, it remains unclear why pelvic limb digital flexor tendons are rarely damaged during equine locomotion. Firstly, it is possible that the failure stress of tendon has been underestimated owing to difficulties in clamping tendons and with achieving homogeneous stress within the tendon during mechanical testing. Secondly, muscles are presumably never fully isometric and fully activated during locomotion.

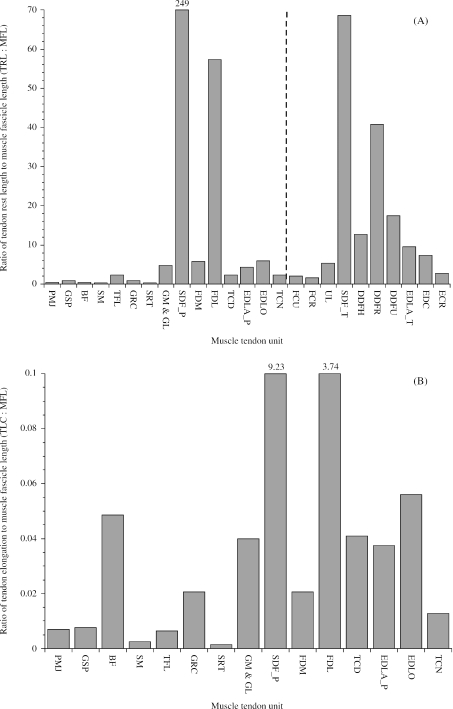
In their investigation of equine thoracic limb muscles, Brown et al. (2003a) used the ratio of tendon rest length to muscle fascicle length as an indication of the relative compliance or stiffness of an MTU. They applied the term stiff to denote an MTU designed to function whilst undergoing active length change (TRL : MFL ratios close to 1) and compliant to denote an MTU designed to function with a high component of passive length change (TRL : MFL ratio exceeding 10; see Zajac, 1989; Pollock & Shadwick, 1994a). These definitions are different from the mechanical terms ‘stiff’ and ‘compliant’. To enable interlimb comparison of MTU properties, pelvic limb TRL : MFL ratios were plotted along with equivalent thoracic limb TRL : MFL ratios (Fig. 4A; Brown et al. 2003a). In general, pelvic limb MTUs were stiffer than thoracic limb MTUs. This would suggest that there is a greater scope for elastic energy storage in thoracic limb tendons than in pelvic limb tendons. All MTU TRL : MFL ratios fell between 1 (stiffer) and 10 (more compliant) except for the tendons of SDF and DDF in both the pelvic and thoracic limbs, which were very compliant. The tendon of SDF was, however, over three times more compliant in the pelvic limb (TRL : MFL = 249) than in the thoracic limb (TRL : MFL = 69) and the FDL tendon of DDF in the pelvic limb was more compliant (TRL : MFL = 57) than any of the tendons of DDF (humeral, radial and ulna heads) in the thoracic limb (TRL : MFLs of 12, 41 & 17, respectively). The relative compliance of SDF and FDL in the pelvic limb was due to the MTUs having both relatively shorter muscle fascicles and relatively longer (in the case of SDF : SDF_T, 459 mm; SDF_P, 748 mm) tendons. The fascicles of highly pennate muscles such as SDF and FDL are too short to allow the muscles to apply a significant amount of stretch to their tendon. Specifically, if the muscle fascicles shortened by 25% then SDF could shorten by less than 1 mm and FDL could shorten by 2.5 mm, which would have very little effect on the length of or the force in an MTU (see Table 6 for tendon rest lengths). However, by nature of their large PCSAs, the muscles might resist the high forces required to withstand the vertical impulse.

Fig. 4.

(A) Ratio of tendon rest length to muscle fascicle length in pelvic and thoracic limb muscles. A vertical broken line separates pelvic limb MTUs from thoracic limb MTUs. Pelvic limb abbreviations follow those given in Tables 1 and 2. Pelvic and thoracic limb muscles with the same name are distinguished by the suffixes _P and _T, respectively. Thoracic limb abbreviations are as follows: FCU (flexor carpi ulnaris); FCR (flexor carpi radialis); UL (ulnaris lateralis); SDF_T (flexor digitorum superficialis); DDFH (humeral head of flexor digitorum profundus); DDFR (radial head of flexor digitorum profundus); DDFU (ulna head of flexor digitorum profundus); EDLA_T (extensor digitorum lateralis); EDC (extensor digitorum communis), ECR (extensor carpi radialis). Thoracic limb muscle tendon unit data are from Brown et al. (2003a). In order that muscle tendons with smaller TRL : MFL ratios can be seen, the y-axis is restricted to 70 and the value for SDF_P is given at the top of the column. (B)Ratio of estimated tendon stretch when the muscle exerts its maximum isometric force to mean muscle fascicle length in pelvic limb muscles. Mean muscle fascicle lengths were taken directly from Table 4. For those muscles with several bellies but a single tendon of insertion (i.e. biceps femoris and gastrocnemius), mean fascicle length was weighted according to muscle belly mass following the methods of Alexander et al. (1981).

The above approach assumes uniform properties of tendon and muscle, however, this is rarely the case. For example; if a muscle has fibres of a given length, its compliance will depend on the distribution of connective tissue within the muscle belly (aponeurosis). Similarly, not all tendons are created alike; a tendon with a large CSA could not be expected to have the same engineering stiffness (Nm⁻¹) as a tendon with a smaller CSA. In this study, we were not able to quantify the parallel elastic element but can include (external to muscle belly) tendon properties (series elasticity) in our estimations of MTU functional properties. The ratio of tendon elongation at maximum isometric muscle stress (TLC) to muscle fascicle length thus gives us a more realistic picture of the relative compliance of the MTUs. We were not able to include thoracic limb MTUs in this analysis because Brown et al. (2003a) did not provide masses or CSAs for their tendons. In Fig. 4(B), the ratio TLC : MFL is plotted for the pelvic limb MTUs described in Table 6. The TLC : MFL ratios were very similar among the distal limb muscles and biceps femoris (between 0.2 and 0.6). The exceptions were SDF and the FDL head of DDF, which had relatively high TLC : MFL ratios (9.23 and 3.74, respectively). Presumably, if internal tendon (aponeurosis) elasticity could also be taken into account then estimations of MTU compliance would be even greater in these two muscles (see Fig. 3).

Although there was a general qualitative agreement in the two different methods of estimating MTU stiffness (Fig. 4A,B), there were quantitative differences for some muscles. For example, the estimated compliance of biceps femoris was closer to that of the distal limb muscles when tendon properties and muscle F_max were taken into account (Fig. 4A,B). Similarly, there was an approximate four-fold difference in the estimated compliance of SDF and FDL when using TRL : MFL (Fig. 4A) but only a two-fold difference when using TLC : MFL (Fig. 4B).

Functional specialisation of the thoracic and pelvic limbs

In both pelvic and thoracic limbs, proximal muscles had larger volumes and longer fascicles than distal limb muscles (Fig. 2A,B, Brown et al. 2003a; Watson, 2004; Payne et al. 2005). However, proximal pelvic limb muscles had larger volumes than proximal thoracic limb muscles (particularly GMD, the hamstrings and the adductors), whereas proximal thoracic limb muscles had longer fascicles than proximal pelvic limb muscles (particularly brachiocephalicus, omotransversarius, subclavius, latissimus dorsi and pectoralis profundus). The exceptions were the thoracic limb muscles, long head of triceps and serratus ventralis thoracis, which had particularly large volumes, and the pelvic limb muscle sartorius, which had a relatively small volume and long fascicles. Distal limb thoracic and pelvic limb muscles had similar volumes and fascicle lengths; this was particularly true of SDF (SDF_T & SDF_P). These differences in proximal limb muscle architecture support the common conception that there are differences in function between the thoracic and pelvic limbs. Pelvic limb muscles have likely sacrificed the ability to exert force over a wide range of motion for the ability to produce large amounts of force. Further, pelvic limb muscles often have more than one belly (e.g. biceps femoris, semitendinosus, semimembranosus) so that proximal bellies have more proximal origins and insertions and distal bellies have more distal origins and insertions. This way, the entire muscle is able to exert force over a wide range of joint positions without the requirement for particularly long muscle fascicles. Finally, thoracic limb muscles inserting onto the scapula might require relatively longer fascicles in order to compensate for translation of the scapula on the rib cage during locomotion.

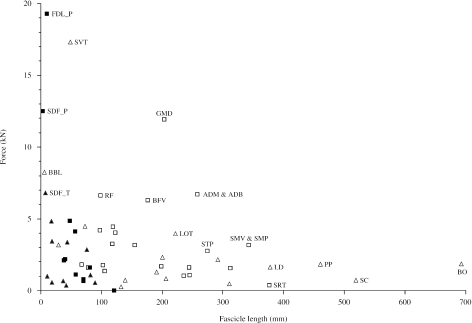
In order to investigate thoraco-pelvic and proximo-distal trends in muscle force, power and velocity of contraction, we plotted estimated maximum isometric muscle force (F_max) against mean muscle fascicle length (Fig. 5). Muscles fell into four approximate groups: (1) muscles in the upper left quadrant of the plot had large PCSAs and short fascicles (serratus ventralis thoracis, lateral head of biceps brachii, thoracic limb superficial digital flexor and pelvic limb superficial digital flexor) and are specialised for developing force (economically); (2) muscles in the lower right quadrant had small PCSAs and long fascicles (brachiocephalicus and omotransvs, subclavius, pectoralis profundus, sartorius, latissimus dorsi and semimembranosus) and are specialised for velocity of contraction and range of motion; (3) muscles in the middle of the plot had large PCSAs and long fascicles (GMD and to a lesser extent adductor magnus and adductor brevis, vertebral head of biceps femoris and long head of triceps brachii) and are specialised for powerful contraction (as area times length gives volume, and power is directly related to volume); and (4) the remaining muscles (includes all distal limb muscles except the three mentioned above) which fell within the lower left quadrant and were cable of neither high force nor significant length change. When the data are viewed in this way, it is apparent that the force-generating antigravity muscles of the proximal thoracic limb (SVT and BBL) have no functional equivalent in the proximal pelvic limb. Instead, the proximal pelvic limb muscles capable of generating large forces (i.e. the propulsive hip extensors) have longer fascicles and less substantial elastic elements and hence are potentially very powerful. TFL and biceps femoris are the only proximal pelvic limb muscles with substantial elastic elements (Table 6), yet our estimates of compliance reveal that the aponeurosis of TFL and the tendon of biceps femoris were relatively stiff (Fig. 4 Further, electromyographical records from TFL suggest that the muscle is most important in stabilising the stifle during the stance phase (Tokuriki & Aoki, 1995). Although proximal thoracic limb muscles do not have similar capacities for power as the proximal pelvic limb muscles (long head of triceps was the only proximal thoracic limb muscle to approach the upper right quadrant), they do, however, have many muscles specialised for a considerably high velocity of contraction and a wide range of motion (e.g. brachiocephalicus and omotransversarius, latissimus dorsi, subclavius and pectoralis profundus). These findings again support the idea that there is functional specialisation between the thoracic and pelvic limbs of horses.

Fig. 5.

A comparison of maximum force and mean fascicle length for pelvic and thoracic limb muscles. Data are of proximal (solid squares) and distal (open squares) pelvic limb and proximal (solid triangles) and distal (open triangles) thoracic limb muscles. Thoracic limb extrinsic muscle data are from Payne et al. (2005); supraspinatus, biceps brachii and triceps brachii are from Watson (2004) and all other intrinsic muscle data are from Brown et al. (2003a). Thoracic limb muscle abbreviations: SVT (serratus ventralis thoracis); BBL (lateral head of biceps brachii); SDF_T (thoracic limb flexor digitorum superficialis); SC (subclavius); LD (latissimus dorsi); BO (brachiocephalicus and omotransversarius); LOT (long head of triceps brachii); PP (pectoralis profundus). Force (F_max) was estimated from muscle PCSA and maximum isometric stress of skeletal muscle (0.3 MPa, Woledge et al. 1985; Zajac, 1989; Medler, 2002). Only those muscles with high force and/or long fascicle lengths are labelled.

The pelvic limb DDF (DDF_P) was estimated to have the capacity to generate four times the force of its forelimb equivalent (DDF_T). The internal architecture of the FDL head of DDF_P was similar to that of the thoracic and pelvic limb SDFs (SDF_T and SDF_P) – that is, the muscle belly was characterised by extremely short fascicles interwoven between numerous strands of internal tendon (aponeurosis). This is not true of any of the heads of DDF in the thoracic limb (Brown et al. 2003a). The most common site of tendon injury in horses is the thoracic limb SDF tendon. This is thought to be because the MTU experiences the greatest loads (of the thoracic limb digital flexor tendons) during the stance phase of locomotion (Wilson et al. 2000). The architecture of SDF is thus useful for generating large forces whilst allowing the tendon to undergo extension, storing elastic energy that can be released later in the stride. SDF may also function in attenuating the high-frequency (and potentially damaging) vibrations known to occur during the stance phase of locomotion (Wilson et al. 2001). Due to similarities in architecture, it is likely that the FDL head of DDF functions in a similar way to SDF (in both thoracic and pelvic limbs), i.e. in vibration damping (Wilson et al. 2000, 2001) or in some other role that we are yet to uncover.

Conclusions

We have produced the first quantitative dataset on the volume and architecture of the MTUs of the equine pelvic limb, showing how muscles seem to be specialised proximally for powerful contraction and distally for economical force generation. Although there is some structural diversity among these muscles, this general pattern is likely to hold regardless of our assumptions about muscle maximal isometric stress or maximal contraction velocity. Furthermore, we have shown that similar proximal-to-distal specialisation exists in the tendons: proximal limb tendons, where present, are short, whereas distal limb tendons are long in comparison to their mean fascicle length and hence are presumably more useful as elastic energy stores.