Abstract
The purpose of the study was to demonstrate and evaluate the use of digital-image photography to measure the central thickness and equatorial diameter of whole fresh human crystalline lenses free of all zonular attachments. Forty-one human donor postmortem intact clear crystalline lenses, with a mean age of 28.5 ± 16.4 years, were obtained by the contributing eye banks. The lenses were removed by the eye bank and shipped in Optisol-GS, a physiologic preservative storage medium, at 7 °C. The lenses were stored at the same temperature and in the same preservative throughout this study. This medium has been demonstrated to maintain the morphometric characteristics of epithelial cells. After freeing the lenses of all residual zonular attachments, digital photographs were obtained within an average of 20.9 ± 13.4 h after death. The digital images were used to determine the central thickness and equatorial diameter of the crystalline lenses. By carefully calibrating the digital images and maintaining the lenses in physiological storage medium, reliable dimensional measurements were obtained. The dimensions for central thickness for each lens were compared to published, age-matched lenses, measured in vivo, and were found to duplicate these in vivo measurements reliably.
Keywords: central thickness, cubic function, equatorial diameter, genetic control, power function
Introduction
The human crystalline lens is completely of ectodermal origin (Mann, 1969). It grows throughout life (Last, 1968; Mann, 1969). The pattern of growth determines its surface shape and, thereby, its optical characteristics. The fetal lens is spherical (Mann, 1969). During childhood, the center of the lens thins (Zadnik et al. 1995; Mutti et al. 1998; Zadnik et al. 2003), while its equatorial diameter increases so that by adulthood the crystalline lens is an asymmetric oblate spheroid, similar to other mammals (Kuszak et al. 2004), with its equatorial diameter approximately twice its central thickness (Last, 1968; Mann, 1969). The purpose of the study is to demonstrate and evaluate the use of digital-image photography to measure the central thickness and equatorial diameter of whole fresh human crystalline lenses free of all zonular attachments.
Materials and methods
Forty-one intact clear human crystalline lenses from eight female and 17 male donors, with a mean age of 28.5 ± 16.4 years and an age range from 3 to 58 years, were studied. Nine lenses were from separate donors and 32, 16 pairs, were from 16 donors. None had a history of significant ocular disease. The donors died of trauma, cardiac arrest, stroke or cancer. The tissues were obtained under protocol from federally approved eye banks located within the United States. The lenses were obtained and managed in accordance with the provisions of the Declaration of Helsinki for research involving human tissue. The intact lenses were dissected and placed in sterile OptisolTM-GS (Bausch & Lomb Corneal Storage Media, Lynchburg, USA) within 9.4 ± 5.3 h of the donor's death and maintained at 7 °C. We did not have a method for assessing the effect of the time delay between death and placement of the lenses in Optisol-GS. Optisol-GS preserves epithelial (Means et al. 1996) and epithelial stem cells (Tsubota et al. 1995) with minimal damage for up to 5 days, and is associated with less than a 5% change in the dimensions of intact crystalline lenses for up to 5 days after death (Schachar, 2004a). Cooling slows energy-dependent fluid hydrodynamics. However, because the lenses were exposed to a similar environment, the hydrational effects of cooling would be expected to be fairly uniform between lenses and therefore should have negligible effect on the direction of the measurements.
Profile photographs of the crystalline lenses were taken with a digital camera (Canon EOS D30 with a Macro 100-mm lens; Canon, Lake Success, NY, USA), which was rigidly fixed to an optical bench. These measurements were obtained within an average of 20.9 ± 13.4 h of the donor's death and within 1 h of receipt of the lens at our laboratory. The intact crystalline lens was placed with its posterior surface on a flat polymethylmethacrylate (PMMA) block. The crystalline lens was carefully centered under the shaft of a micrometer (Model # 262, L.S. Starrett Co., Athol, MA, USA), which was rigidly fixed to the optical bench. The micrometer shaft has a diameter of 5.97 mm with a tolerance of +0.0 to −0.0025 mm. It served as the fixed reference of known diameter in each photograph (Fig. 1). It was positioned directly above the center of the crystalline lens being measured (Fig. 1). The profile photographs were taken with the digital camera at one to one magnification at room temperature, 20 °C within 3 min of being removed from the Optisol-GS. The images were downloaded onto a computer. For each image, a pixel count measurement of the diameter of the micrometer shaft was made, followed by a pixel count of the central thickness and equatorial diameter of the sphere or the crystalline lens. This measurement was independently repeated in the same order five times. The mean and standard deviation of the five measurements were used for the analysis. The lenses were not moved between measurements in order to keep measuring time at a minimum and to avoid damage of the lenses, which might alter their dimensions.
Fig. 1.
A profile photograph used to measure central thickness of the human crystalline lens.
The photographic measurement system was calibrated by taking profile photographs of each of 10 precision steel spheres (Bal-tec, Los Angeles, CA, USA) at 20 °C, which had been carefully centered under the same micrometer shaft. These steel spheres, with increasing diameters from 1 to 10 mm in 1-mm steps, have a certified tolerance of ±0.0006 mm that is traceable to the National Institute of Standards and Technology (NIST). Ten independent placements of the 6-mm sphere were photographically recorded to determine the variation associated with centering this sphere under the micrometer shaft.
All images were downloaded onto a computer. For each image, a pixel count measurement of the diameter of the micrometer shaft was made, followed by a pixel count of the central diameter of the sphere. The diameter of each sphere, measured in pixels, was converted to millimeters, based upon this unique relationship. The same observer independently repeated this measurement five times. The mean and standard deviation of these five measurements were determined. The process was repeated for each image of the 10 spheres. The mean and standard deviation of the diameters of the spheres, as measured photographically, were established. Statistical analysis was performed using commercial software (SPSS Version 11.5; SPSS Inc, Chicago, IL, USA).
Results
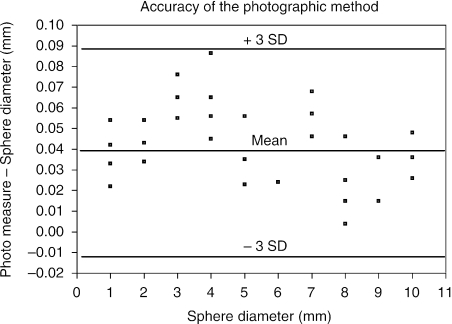
Calibration of digital lens measurements was achieved by the use of photographic images of certified, precision steel spheres (Bland & Altman, 1986; Kirkwood & Sterne, 2003; Fig. 2). The mean difference between the 10 re-centered measurements of the 6-mm sphere was 0.05 ± 0.02 mm. The mean difference for all 10 calibration spheres was 0.04 ± 0.02 mm. Therefore the mean difference, 0.04 mm, was used as the calibration factor and was subtracted from all photographic measurements of the crystalline lens central thickness and equatorial diameter. The 99% accuracy of the digital photographic measurement was better than 0.1 mm (3 standard deviations).
Fig. 2.
(A) Bland–Altman-style plot of the 50 photographic measurements of the 10 precision spheres, which includes reference lines for the mean and ± 3 standard deviations (3 SD).
The five repetitive measurements of the central thickness and equatorial diameter of each lens resulted in a mean standard deviation of 0.01 ± 0.004 mm. The high precision of these measurements demonstrates the reproducibility of data acquired and indicates stability of the lens dimensions during the 3-min period while the digital images were obtained. There was no significant difference, using the two tailed student t-test, in either the equatorial diameter or the central thickness between lenses from fellow eyes of the same donor; P = 0.75 and 0.89, respectively.
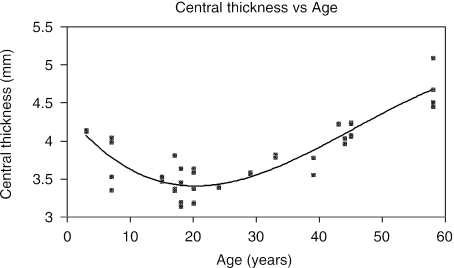
Based upon the 41 eyes measured, ranging in age from 3 to 58 years, the central thickness of the crystalline lens decreases over the initial 20 years of life and then increases (Fig. 3). This change in central thickness with age was best described by the following cubic equation:
| (1) |
The correlation coefficient for this cubic fit gives R2 = 0.82.
Fig. 3.
Plot of central thickness of the human crystalline lens vs age. The central thickness of the human crystalline lens decreases in childhood, reaching a minimum at approximately 20 years and then increases with additional age.
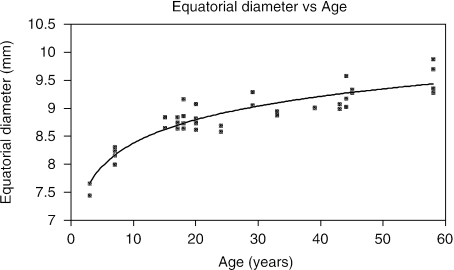
Based upon the 41 eyes measured, ranging in age from 3 to 58 years, the equatorial diameter of the crystalline lens grew rapidly for approximately the initial 20 years of life and then grew at a slower rate (Figs 4 and 5). The age-related growth of the equatorial diameter was best fitted to the following equation:
| (2) |
Fig. 4.
Plot of the equatorial diameter of the human crystalline lens vs age. The equatorial diameter grows rapidly for approximately 20 years and then increases at a slower rate with age.
Fig. 5.
Profile photographs of human crystalline lenses of different ages demonstrating, in the horizontal plane, the progressive increase in equatorial diameter with age. The central thickness is measured perpendicular to this equatorial diameter. The thickness, measured vertically, can be seen to decrease after age 3 and increase again after the second decade of life.
(R2= 0.86), which can be transformed to the following power function:
| (3) |
The implications of these mathematical models will be discussed in the following section.
Discussion
Our studies carefully calibrated the digital photographic method used to measure the crystalline lens diameters. The mean difference of both calibration methods was greater than zero, suggesting a systematic bias. An appropriate calibration factor was applied to the photographically obtained crystalline measurements to address this issue and provide the actual millimeter measurement. The etiology of this bias may result from the observer's eye dominance and parallax while centering the sphere in relation to the micrometer shaft or when measuring the object on the computer screen.
During the measurements, the crystalline lenses were supported on their posterior surface and therefore were subjected to potential alteration in their shape from the unequal force distribution on their posterior surface due to gravity. Any effect of gravity might be expected to cause a decrease in central thickness accompanied by an increase in equatorial diameter. Another site for a gravitational effect is the unsupported equatorial region, potentially causing it to flex downward in the older, more elliptical lenses, with the central anterior surface steepening and an apparent decrease in equatorial diameter with age. In order to evaluate this, in an independent study, we measured the anterior surface curvature of crystalline lenses from donors of ages 17 to 58 years while floating on gel (Weale, 1982) or while on a firm PMMA block (Schachar, 2004a). We found a small steepening in the anterior lens surface when the support for the posterior surface of the crystalline lens was changed from floating on a gel to a solid PMMA block. These findings make it highly unlikely that gravity contributed to our observation of an increase in equatorial diameter with age.
Optisol-GS maintained the dimensions of the crystalline lenses during the time of this study. The human crystalline lenses in this study were obtained within 15 h of death and preserved in Optisol-GS and examined within 35 h of the donor's death. Optisol-GS contains: base media that is a mixture of TC-99 and minimal essential media (MEM), 1% dextran, 2.5% chondroitin sulfate, HEPES Buffer, gentamicin, streptomycin sulfate, sodium carbonate, nonessential amino acids, and vitamins. Optisol-GS, although containing dextran and chondrotion sulfate, is isotonic and does not cause shrinkage of either corneal endothelial (Lindstrom et al. 1992; Means et al. 1995) or epithelial cells (Means et al. 1996). The corneal deturgescence noted during Optisol storage is principally due to endothelial activity and not passive osmosis (Walkenbach et al. 1992). A 10-day study of intact human crystalline lenses kept in Optisol-GS demonstrated that the lenses maintained their dimensions for 2 days and then began to swell linearly (Schachar, 2004a). Therefore it is unlikely that Optisol-GS significantly altered the dimensions of the crystalline lenses during the time of this study.
The present study confirms the age-related equatorial growth of the human crystalline lens. It demonstrates that equatorial growth is rapid during childhood and then slowly increases after the 20th year. Previous studies have demonstrated an average 0.020 mm year−1 increase in equatorial diameter of extracted intact crystalline lenses for all ages (Rafferty, 1985), which is consistent with the average equatorial growth that would be predicted from equation (3). The cubic equation description of the age-related change in central lens thickness growth is consistent with the findings of a large in vivo phakometric study of children (Zadnik et al. 1995). There were only four crystalline lenses in this study that were within the age group examined by Zadnik et al. (1995) and therefore a quantitative comparison is not appropriate. However, there were 30 crystalline lenses within the age group of the subjects included in the in vivo Scheimpflug study of central crystalline lens thickness performed by Koretz et al. (1989). A regression analysis of their in vivo measurements by Scheimpflug photography of the central thickness of 100 unaccommodated crystalline lenses between the ages of 18 and 70 years provided the following equation (Koretz et al. 1989):
| (4) |
Substitution of the mean age, 35.1 years, of the 30 crystalline lenses of this study between the ages of 18 and 58 years into equation (4) gives a central thickness of 3.867 ± 0.161 mm. The measured mean central thickness in this study of 3.866 ± 0.483 mm, for the 30 crystalline lenses between ages 18 and 58 years, indicates that the difference between our in vitro and their in vivo measurements of central lens thickness is negligible.
Visualization of the equator of the living human crystalline lens has not been possible photographically owing to the presence of the iris. Therefore, no in vivo photographic studies of the age-associated changes in the equatorial diameter of the human crystalline lens are available. However, an in vivo magnetic resonance imaging (MRI) study has been performed, which concluded that the equatorial diameter does not increase with age (Strenk et al. 1999). This observation is contrary to that found in our study. Because the lens is totally of ectodermal origin and because all ectodermal tissues continue to grow throughout life, lenticular growth resulting from cellular mitosis and cortical deposition at the equator might be anticipated to be associated with increase in the equatorial diameter with age. Although human nuclear lens fibers undergo compaction, histological examination has demonstrated that nuclear compaction occurs in the anterior posterior meridian and not in the equatorial meridian (Al-Ghoul et al. 2001; Freel et al. 2003). The contradictory results obtained by the MRI study may reflect the lower resolution of the MRI and a lack of fixed references, eye tracking and control of accommodation to insure reliability of their measurements (Levy, 2000; Schachar, 2004b).
In view of the absence of reliable in vivo measurements of lenticular equatorial diameter, the measurements of equatorial diameter were compared to in vitro studies. Bluestein et al. (1996) found that lenticular equatorial diameter increased approximately 3.0 mm from birth to 16 years. Substitution of the ages 1 month and 16 years into our equation (3) reveals that lenticular equatorial diameter increases by 2.7 mm over this time period. Sakabe et al. (1998) and Lim et al. (1998) found that lenticular equatorial diameter increased by 0.01 mm year−1 from 16 to 100 years. Substitution of the ages 16 and 100 years into equation (3) reveals the same 0.01 mm year−1 age-related increase. Furthermore, equation (3) significantly correlates (P < 0.02, R2 = 0.84) with the compilation by Weale (1982) of the age-related equatorial lenticular diameter measurements made in vitro by multiple independent investigators from 1883 to 1982.
How the crystalline lens thins centrally during childhood is not fully understood (Brown & Bron, 1996). Crystalline lens growth occurs as a result of an increase in the number of lens fibers, which grow from the equatorial region (Last, 1968; Kuszak et al. 2004). There is very little difference in width, thickness or hexagonal cross section of lens fibers between mammals (Kuszak et al. 2004). Variation in lens shape is attributed to differences in lens fiber length, suture patterns, the presence of a minority of lens fibers with a pentagonal cross section, and anterior posterior compaction of the lens nucleus (Al-Ghoul et al. 2001; Freel et al. 2003). Childhood central crystalline lens thinning is probably attributable to one or more of these factors.
The age-related changes in lenticular equatorial diameter and central thickness were demonstrated to mathematically fit power and cubic functions. At approximately 20 years old, lenticular central thickness begins to increase and the rate of equatorial growth declines. The simultaneous occurrence of these two events implies that lenticular growth is controlled by at least two separate genes that are precisely coordinated. Because the central thickness and surface curvatures of the crystalline lens are not significantly different in myopes and emmetropes (Goss et al. 1997), the genes controlling biometry of the crystalline lens are probably different than those controlling axial length and corneal curvature, and the proteins that these different genes produce probably function independently.
Conclusions
This study demonstrates the reliability of using well-calibrated digital photography to obtain accurate biometry of Optisol-GS maintained human crystalline lenses. The in vitro measurements of the central lenticular thickness give results nearly identical to those independently reported from in vivo measurement techniques. This study also demonstrates changes in the equatorial diameter and central thickness of the human crystalline lens with age. These age-associated changes in both central thickness and equatorial diameter of the human crystalline lens can be expressed mathematically. The mathematical growth of the central thickness fits a cubic function and the equatorial diameter fits a power function. The timing of these age-related growth patterns suggests that there are at least two separate coordinated genes controlling lenticular growth.
Acknowledgments
The author wishes to thank Ellen Heck and staff of UT Southwestern Transplant Services in Dallas, Texas; the Georgia Eye Bank, Inc. in Atlanta, Georgia; the Lions Eye Bank of Oregon in Portland, Oregon; and The Eye-Bank for Sight Restoration, in New York, New York for supplying the crystalline lenses.
References
- Al-Ghoul KJ, Nordgren RK, Kuszak AJ, Freel CD, Costello MJ, Kuszak JR. Structural evidence of human nuclear fiber compaction as a function of ageing and cataractogenesis. Exp Eye. Res. 2001;72(3):199–214. doi: 10.1006/exer.2000.0937. Medline . [DOI] [PubMed] [Google Scholar]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986:1. Medline . [PubMed] [Google Scholar]
- Bluestein EC, Wilson ME, Wang XH, Rust PF, Apple DJ. Dimensions of the pediatric crystalline lens: implications for intraocular lenses in children. J. Pediatr. Ophthalmol. Strabismus. 1996;33:18–20. doi: 10.3928/0191-3913-19960101-06. Medline . [DOI] [PubMed] [Google Scholar]
- Brown NP, Bron AJ. Lens Disorders: a Clinical Manual of Cataract Diagnosis. Oxford, UK: Butterworth-Heineman; 1996. [Google Scholar]
- Freel CD, Al-Ghoul KJ, Kuszak JR, Costello MJ. Analysis of nuclear fiber cell compaction in transparent and cataractous diabetic human lenses by scanning electron microscopy. BMC Ophthalmol. 2003;3(1):1. doi: 10.1186/1471-2415-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goss DA, van Veen HG, Rainey BB, Feng B. Ocular components measured by keratometry, phakometry, and ultrasonography in emmetropic and myopic optometry students. Optom Vis Sci. 1997;74:489–95. doi: 10.1097/00006324-199707000-00015. Medline . [DOI] [PubMed] [Google Scholar]
- Kirkwood BR, Sterne JAC. Essential Medical Statistics. Malden, MA, USA: Blackwell Science, Inc; 2003. [Google Scholar]
- Koretz JF, Kaufman PL, Neider MW, Goeckner PA. Accommodation and presbyopia in the human eye — Aging of the anterior segment. Vision Res. 1989;29:1685–1692. doi: 10.1016/0042-6989(89)90150-8. Medline . [DOI] [PubMed] [Google Scholar]
- Kuszak JR, Zoltoski RK, Sivertson C. Fibre cell organization in crystalline lenses. Exp Eye Res. 2004;78:673–687. doi: 10.1016/j.exer.2003.09.016. Medline . [DOI] [PubMed] [Google Scholar]
- Last RJ. Eugene Wolff's Anatomy of the Eye and Orbit. 6. Philadelphia, PA, USA: W.B. Saunders Company; 1968. [Google Scholar]
- Levy NS. Comparing MRIs with movement artifact (eLetter) Invest. Ophthalmol. Vis. Sci. 2000. http://www.iovs.org/cgi/eletters/40/6/1162 .
- Lim SJ, Kang SJ, Kim HB, Kurata Y, Sakabe I, Apple DJ. Analysis of zonular-free zone and lens size in relation to axial length of eye with age. J. Cataract Refract. Surg. 1998;24:390–396. doi: 10.1016/s0886-3350(98)80329-5. Medline . [DOI] [PubMed] [Google Scholar]
- Lindstrom RL, Kaufman HE, Skelnik DL, Laing RA, Lass JH, Musch DC, et al. Optisol corneal storage medium. Am. J. Ophthalmol. 1992;114:345–356. doi: 10.1016/s0002-9394(14)71803-3. Medline . [DOI] [PubMed] [Google Scholar]
- Mann I. The Development of the Human Eye. New York, USA: Grune & Stratton, Inc; 1969. [Google Scholar]
- Means TL, Geroski DH, Hadley A, Lynn MJ, Edelhauser HF. Viability of human corneal endothelium following Optisol-GS storage. Arch. Ophthalmol. 1995;113:805–809. doi: 10.1001/archopht.1995.01100060131047. Medline . [DOI] [PubMed] [Google Scholar]
- Means TL, Geroski DH, L'Hernault N, Grossniklaus HE, Kim T, Edelhauser HF. The corneal epithelium after Optisol-GS storage. Cornea. 1996;15:599–605. Medline . [PubMed] [Google Scholar]
- Mutti DO, Zadnik K, Fusaro RE, Friedman NE, Sholtz RI, Adams AJ. Optical and structural development of the crystalline lens in childhood. Invest. Ophthalmol. Vis. Sci. 1998;39:120–133. Medline . [PubMed] [Google Scholar]
- Rafferty NS. Lens morphology. In: Maisel H, editor. The Ocular Lens. New York, USA: Marcel Dekker; 1985. pp. 2–6. [Google Scholar]
- Sakabe I, Oshika T, Lim SJ, Apple DJ. Anterior shift of zonular insertion into the anterior surface of human crystalline lens with age. Ophthalmology. 1998;105:295–299. doi: 10.1016/s0161-6420(98)93172-4. Medline . [DOI] [PubMed] [Google Scholar]
- Schachar RA. Central Surface Curvatures of postmortem extracted intact human crystalline lenses: Implications for understanding the mechanism of accommodation. Ophthalmology. 2004a;111:1699–1704. doi: 10.1016/j.ophtha.2004.03.033. Medline . [DOI] [PubMed] [Google Scholar]
- Schachar RA. The change in intralenticular pressure during human accommodation (eLetter) Invest. Ophthalmol. Vis. Res. 2004b. http://www.iovs.org/cgi/eletters/45/2/539#151 .
- Strenk SA, Semmlow JL, Strenk LM, Munoz P, Gronlund-Jacob J, DeMarco JK. Age-related changes in human ciliary muscle and lens: A magnetic resonance imaging study. Invest. Ophthalmol. Vis. Sci. 1999;40:1162–1169. Medline . [PubMed] [Google Scholar]
- Tsubota K, Toda I, Saito H, Shinozaki N, Shimazaki J. Reconstruction of the corneal epithelium by limbal allograft transplantation for severe ocular surface disorders. Ophthalmology. 1995;102:1486–1496. doi: 10.1016/s0161-6420(95)30841-x. Medline . [DOI] [PubMed] [Google Scholar]
- Walkenbach RJ, Boney F, Ye GS. Corneal Function after storage in Dexsol and Optisol. Invest Ophthalmol Vis Sci. 1992;33:2454–2458. Medline . [PubMed] [Google Scholar]
- Weale RA. A Biography of the Eye: Development, Growth, Age. London, UK: H.K. Lewis; 1982. [Google Scholar]
- Zadnik K, Manny RE, JA Yu, et al. Ocular component data in schoolchildren as function of age and gender. Optom. Vis. Sci. 2003;80:226–236. doi: 10.1097/00006324-200303000-00012. Medline . [DOI] [PubMed] [Google Scholar]
- Zadnik K, Mutti DO, Fusaro RE, Adams AJ. Longitudinal evidence of crystalline lens thinning. Invest. Ophthalmol. Vis. Sci. 1995;36:1581–1587. Medline . [PubMed] [Google Scholar]