Regulation of human D₁, D_2(long), D_2(short), D₃ and D₄ dopamine receptors by amiloride and amiloride analogues

Abstract

1. The modulatory effects of the allosteric effectors methylisobutylamiloride (MIA), benzamil and amiloride have been examined at human D₁, D₂, D₃ and D₄ dopamine receptors. The subtype selectivity and the mechanism of action of this allosteric regulation was examined.

2. In radioligand dissociation experiments each modulator accelerated dissociation from all four receptor subtypes indicating allosteric regulation. MIA displayed selectivity for the D₃ subtype for acceleration of radioligand dissociation.

3. In equilibrium binding (pseudo-competition) experiments the three compounds inhibited radioligand binding at the four receptor subtypes. Inhibition curves for D₁, D_2(short), D_2(long) and D₃ receptors were described by Hill coefficients exceeding unity and data were fitted best by a model that assumes binding of modulator to both the primary and allosteric binding sites of the receptor (the allosteric/competitive model).

4. At the D₄ subtype, Hill coefficients of unity described the binding data for amiloride and benzamil, consistent with competitive inhibition. The Hill coefficient for MIA at the D₄ subtype was less than unity and data could be fitted well by the allosteric/competitive model, but it was not possible to define unambiguously the modulatory mechanism. For this effect a better definition of the mechanism could be obtained by simultaneous analysis of data obtained in the presence of a range of concentrations of a purely competitive ligand.

5. MIA reduced the potency with which dopamine stimulated [³⁵S]-GTPγS binding at the D₂ receptor. The effects of MIA could be described by the allosteric/competitive model with effects of MIA to inhibit the binding of dopamine but not its ability to induce a response.

Introduction

Five subtypes of dopamine receptors have been cloned, termed D₁, D₂, D₃, D₄ and D₅ dopamine receptors. Activation of D₁ and D₅ dopamine receptors leads to the stimulation of adenylyl cyclase, whereas activation of D₂, D₃ and D₄ subtypes is coupled to inhibition of the enzyme (Sibley & Monsma, 1992; Neve & Neve, 1997). The former subtypes can be classified as ‘D₁-like' and the latter as ‘D₂-like,' based on the original pharmacological classification of this receptor family. D₂-like dopamine receptors, in common with other receptors coupled to inhibitory G-proteins, have been shown to modulate either directly or indirectly a number of other signalling pathways (Sibley & Monsma, 1992; Neve & Neve, 1997), including potassium and calcium channels and inositol phospholipid metabolism (Simmonds & Strange, 1985; Vallar & Meldolesi, 1989). All of the receptors belong to the superfamily of G-protein-coupled receptors, which are predicted to possess seven membrane-spanning α-helices (Probst et al., 1992). For receptors that bind low molecular weight ligands, such as dopamine and acetylcholine, the binding site for agonists and antagonists is believed to be located within a pocket formed by the clustering of the putative membrane spanning regions (Strader et al., 1995).

A number of G-protein-coupled receptors are affected by agents that bind to an allosteric binding site, separate from the primary ligand binding site (Birdsall et al., 1995). The best characterized examples are gallamine and alcuronium, which allosterically modulate muscarinic acetylcholine receptors (Stockton et al., 1983; Proska & Tucek, 1994; Tucek & Proska, 1995). Allosteric modulators may provide therapeutic advantages compared with conventional competitive ligands (Birdsall et al., 1995). The primary site may be similar for a family of receptors that bind the same endogenous ligand since within a receptor family the putative membrane spanning regions, which are thought to form this site, are highly conserved. The allosteric site is spatially distinct from the primary site and so may be located at less conserved regions of the receptor, providing the potential for the development of ligands with greater subtype selectivity (Birdsall et al., 1986). For the five subtypes of muscarinic acetylcholine receptors, no strongly selective competitive ligands have been developed to date. However, the allosteric ligand gallamine displays a broad range of potencies for the five receptor subtypes; the highest potency interaction (at the M₂ subtype) being approximately 150 fold more potent than the lowest (at the M₅ receptor) (Ellis et al., 1991).

Allosteric modulation is also more flexible than receptor regulation by ligands that bind to the primary site. The nature of the allosteric effect can be defined by the cooperativity between allosteric and primary sites (Birdsall et al., 1995). Negative cooperativity implies that the allosteric effector inhibits binding of ligands at the primary site, whereas for positive cooperativity binding is enhanced (a mode of regulation that is not possible with ligands that bind to the primary site). A third possibility is that the binding of an allosteric modulator does not affect the affinity of a ligand at the primary site (Lazareno & Birdsall, 1995). This latter possibility, in principle, may allow the development of completely selective drugs. For example, a modulator may exhibit negative cooperativity with respect to endogenous ligand binding at one receptor but ‘neutral' cooperativity at another. At saturating concentrations, such a drug would inhibit endogenous ligand binding at the former subtype but would not affect binding at the latter receptor (Lazareno & Birdsall, 1995). For such a modulator, this selectivity would be independent of differences of modulator affinity at the receptors. Brucine derivatives have been shown to exhibit this subtype-dependent cooperativity at muscarinic acetylcholine receptors (Birdsall et al., 1997).

An allosteric site associated with the rat D₂ dopamine receptor and the α₂ adrenergic receptor is recognized by amiloride and analogues of this diuretic drug (Howard et al., 1987; Neve, 1991; Hoare & Strange, 1996; Leppik et al., 1998). Allosteric modulation of [³H]-spiperone binding to the former receptor has been demonstrated by the ability of the compounds to accelerate dissociation of the radioligand (Neve, 1991; Hoare & Strange, 1996). Modulation of equilibrium [³H]-spiperone binding by MIA was consistent with a model in which the modulator binds to both an allosteric site and the primary site. Negative heterotropic cooperativity was inferred between allosteric binding of MIA and binding of [³H]-spiperone, whereas positive homotropic cooperativity was inferred for binding of MIA at the allosteric and primary sites (Hoare & Strange, 1996). We have termed this mechanism the allosteric/competitive model. The same model has been applied to the modulation of radioligand binding at cardiac muscarinic acetylcholine receptors by certain ligands (Waelbrock, 1994).

Allosteric regulators may provide great potential for the development of selective drugs but it is important to define the nature of this selectivity among related receptor subtypes and the nature of the modulatory mechanism. In the current study, subtype selectivity of the allosteric effects of amiloride and amiloride analogues at D₁, D₂, D₃ and D₄ dopamine receptors was probed in radioligand dissociation experiments. The modulation of radiolabelled antagonist binding was examined in equilibrium binding assays and the modulation of agonist action was explored using [³⁵S]-GTPγS binding assays.

Methods

Materials

[³H]-spiperone (65-140 Ci/mmol) was obtained from Amersham International and [³H]-SCH-23390 (71 Ci/mmol) was purchased from DuPont NEN. Amiloride and non-radioactive spiperone were obtained from Sigma. Benzamil, MIA, and non-radioactive R(+)-SCH-23390 were from Research Biochemicals.

Cell lines

Ltk⁻ mouse fibroblasts expressing the recombinant human D₁ dopamine receptor were obtained from Dr O. Civelli, Health Sciences University of Oregon (Zhou et al., 1990). Two other Ltk⁻ cell lines, expressing either the short or long isoform of a cloned human D₂ dopamine receptor (Grandy et al., 1989), were obtained from the same source. A CHO cell line that expresses the long form of this receptor (Hayes et al., 1992) was obtained from The Garvan Institute, Sydney, Australia. CHO cell lines expressing a recombinant human D₃ (Sokoloff et al., 1990) or D_4.4 (Asghari et al., 1995) dopamine receptor were respectively obtained from Dr P. Sokoloff, INSERM, Paris and Dr H. van Tol, Clark Institute of Psychiatry, Toronto. The Ltk⁻ cell lines were cultured in DMEM supplemented with 10% FBS. DMEM / Ham's Nutrient Mix F12 (1 : 1) supplemented with 10% FBS was used for the culture of CHOhD_2long cells. CHOhD₃ cells were cultured in DMEM supplemented with 10% dialysed FBS, 2% MEM amino acids, 100 nM methotrexate and 0.5 μM (−)-sulpiride. CHOhD_4.4 cells were grown in alpha-MEM (without nucleosides) supplemented with 5% FBS and 0.4 mg/ml geneticin. Frozen cell pellets were kindly supplied by Dr C. Mannix, SmithKline Beecham Pharmaceuticals, Great Burgh, Surrey, U.K.

Preparation of cell homogenates

Frozen cell samples were thawed at room temperature. Tris buffer (mM): Tris 50 EDTA 5, NaCl 120, KCl 5, MgCl₂ 1.5, pH 7.4 was added to the thawed cell pellet (20 ml per 10⁹ cells) and the cell suspension homogenised using a Janke and Kunkel Ultra Turrax polytron homogenizer (6×5 s bursts, 5 s between bursts at 3/4 maximum speed). Polypropylene tubes containing the cell suspensions were placed in a beaker of ice during this procedure, in order to prevent heating of the preparation. Cell lysates were centrifuged at 30,000×g for 15 min at 4°C (Sorvall RC5C centrifuge, SS34 rotor). The homogenate pellet was resuspended in 30 ml fresh Tris buffer then homogenized and centrifuged as described above. The homogenate pellet from the second centrifugation step was resuspended in 50 mM Tris, pH 7.4. Aliquots of cell homogenates (0.5 ml or 1 ml) were stored at −80°C. Homogenate protein concentration was measured using the method of Bradford, using bovine serum albumin as a standard.

Radioligand dissociation experiments

Measurement of [³H]-spiperone dissociation from D₂-like dopamine receptors

Homogenates (20–90 μg protein per tube), and [³H]-spiperone at a final concentration of 0.75 nM, were incubated in 1 ml volume polystyrene tubes (Skatron) in a volume of 0.4 ml assay buffer (mM): HEPES 20, EDTA (free acid) 1, EGTA (free acid) 1, adjusted to pH 7.4 with KOH for 3 h at 25°C. Preliminary [³H]-spiperone association experiments showed that specific binding was within 3% of the asymptotic equilibrium value at 3 h for all the D₂-like dopamine receptors. Radioligand dissociation from CHOhD₂long membranes was measured using 130–140 μg homogenate protein per tube. Following the equilibration reaction, dissociation was initiated by the addition of 1 μM non-radioactive spiperone (final concentration, contained in a volume of 0.1 ml), either alone, or in the presence of allosteric modulators or the appropriate vehicle. MIA and benzamil were dissolved in DMSO and the final DMSO concentration did not exceed 0.75%. Amiloride was soluble in distilled water, acidified with 0.01% acetic acid. The temperature was maintained at 25°C during the dissociation phase and after different times of dissociation bound [³H]-spiperone was separated from free radioligand by rapid filtration through a GF-B glass micro fibre filter (Whatman), using a Brandel cell harvester. Assay tubes and filters were washed five times with 1 ml ice cold PBS buffer (mM): NaCl 140, KCl 3, KH₂PO₄ 1.5, Na₂HPO₄ 5, pH 7.4. Measurement of the bound radioactivity at each time point was carried out in triplicate. Filters were pre-soaked with 0.3% (v/v) polyethyleneimine (PEI) in distilled water. Total binding was measured by filtration immediately following the addition of 0.1 ml buffer or the appropriate vehicle in the absence of non-radioactive spiperone, and non-specific binding was determined by addition of dissociation buffer prior to equilibration. The presence of MIA, benzamil or amiloride did not affect non-specific binding. Filters were then soaked for at least 1 h in 4 ml Ultima Gold MV scintillation fluid (Packard), before determination of radioactivity by scintillation counting on a Packard 2500TR TRI-CARB liquid scintillation analyser.

Measurement of [³H]-SCH-23390 dissociation from the D₁ dopamine receptor

The procedure used was similar to that for measurement of [³H]-spiperone dissociation from D₂-like dopamine receptors. Equilibration of 10–20 μg homogenate of LtkhD₁ cells with 0.5 nM [³H]-SCH-23390 was carried out for 2 h at 25°C. In preliminary radioligand association experiments, specific [³H]-SCH-23390 binding to the D₁ subtype was within 3% of the asymptotic equilibrium value at 2 h. The samples were then placed in a water bath at 15°C and incubated for a further 30 min. At this lower temperature dissociation in the presence of high modulator concentrations was slow enough to be measured accurately using the rapid filtration technique. The dissociation reaction was initiated by addition of 1 μM non-radioactive SCH-23390 (final concentration) in the presence or absence of allosteric modulators or the appropriate vehicle. Total binding of radioligand was measured by filtration immediately following the addition of 0.1 ml buffer or the appropriate vehicle in the absence of non-radioactive SCH-23390 and non-specific binding was determined by the addition of dissociation buffer before equilibration.

Inhibition of radioligand binding to recombinant dopamine receptors

In these experiments the binding of a fixed concentration of radioligand was determined in the presence of a range of concentrations of MIA, benzamil or amiloride. These assays are referred to as ‘Pseudo-competition' experiments. The experiments were set up using a BIOMEK 1000 Automated Workstation (Beckman Instruments). Duplicate determinations of the binding of [³H]-spiperone (0.2 nM final concentration) to D₂-like dopamine receptors, or [³H]-SCH-23390 (0.5 nM) to the D₁ subtype, were performed in the presence of 10 concentrations of modulator. Cell homogenates (10–40 μg per tube) were incubated with radioligand and modulator in a total volume of 0.5 ml assay buffer at 25°C for 3 h (D₂-like dopamine receptor experiments) or 2 h (D₁ subtype). Triplicate measurements of total binding and non-specific binding were performed, replacing the modulator with, respectively, distilled water or the appropriate non-radioactive drug (spiperone or SCH-23390) at a final concentration of 10 μM. Filtration for assay termination and measurement of bound radioactivity were carried out as described for radioligand dissociation experiments. Total binding was less than 20% of the free radioligand concentration, except for a number of assays for the D₃ subtype. In these experiments, the bound / free ratio was between 16 and 39%. Similar estimates of IC₅₀ and n_H were obtained for low and high bound / free values. Non-specific binding was not affected by any of the modulators.

In additional MIA/[³H]-spiperone pseudo-competition experiments for the D₄ dopamine receptor, a range of radioligand concentrations was used (0.25–1.6 nM). In a further series of assays for this receptor, inhibition of [³H]-spiperone binding (final radioligand concentration of 0.6 nM) by MIA was measured in the presence of a range of concentrations of benzamil (3.2, 10 and 32 μM). In both series of experiments using these higher radioligand concentrations, non-specific binding was slightly reduced (below that measured using 10 μM non-radioactive spiperone) at the highest MIA concentrations (by 4–8% of the value obtained in the presence of 10 μ non-radioactive spiperone). For analysis of these data (see below), non-specific binding was fixed at that measured in the presence of non-radioactive spiperone.

Dopamine stimulation of [³⁵S]-GTPγ binding

CHO-D2_(long) membranes (20–50 μg) were incubated in triplicate with a range of concentrations of dopamine for 30 min at 30°C in 0.9 ml buffer (HEPES 20 mM, MgCl₂ 10 mM, NaCl 100 mM, pH 7.4, supplemented with DTT 100 μM and GDP 1 μM). MIA or vehicle (0.25% DMSO) was included in this incubation. [³⁵S]-GTPγS (0.1 ml) was added to a final concentration of 100 pM. After 20 min, bound radioligand was collected by filtration through GF/C filters. For each set of assays in which MIA was included, [³⁵S]-GTPγS binding was measured in the absence of MIA in order to determine basal binding (no dopamine) and maximal binding (100 μM dopamine).

Data analysis

Time course data from radioligand dissociation experiments were fitted by non-linear regression (using 1/y² weighting) to single-exponential and double-exponential decay functions using the KINETIC programme of LIGAND (Elsevier-Biosoft). Statistical analysis of the improvement of fit for the biexponential fit, compared with the monoexponential expression, was computed by comparing the sum of squares using a partial F-test. A P value of <0.05 was used to determine that a statistically significant improvement had been made by the biexponential fit. Data were occasionally fitted to a triple-exponential function but in all cases the analysis did not provide a significant improvement (P>0.05) compared with the biexponential fit.

In other dissociation experiments the effect of modulators was measured at a single time point (20 min). The allosteric effect was quantified as the specific binding of radioligand after 20 min dissociation in the presence of modulator, divided by the value obtained for the vehicle control. The dependence of this value (Y) on the modulator concentration (X) was fitted to the following four parameter-logistic equation:

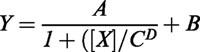where A is the range of Y values, B is the minimal plateau, C is the value of X at the midpoint of the curve (EC₅₀) and D is the Hill coefficient. This analysis was performed using GraFit (Erithacus Software Ltd.). This analysis was also performed for other concentration-dependence curves (indicated in the text).

Data from radioligand pseudo-competition experiments were analysed using the EBDA programme of LIGAND. The programme fits the amount of radioligand bound as a function of the inhibitor concentration using the four-parameter logistic equation above. Pseudo-competition data were also fitted to the more complex equations of the Appendix, using SigmaPlot 3.0 (Jandel Scientific). Simulated data generated using the equations of the Appendix were obtained using Excel 5.0 (Microsoft). These data were fitted to the four parameter-logistic equation above, using SigmaPlot 3.0.

In order to compare fits to the three models presented in the Appendix, a partial F-test was performed, comparing the residual sum of squares for the different fits according to the ‘Extra sum of squares' principle, as used in Hoare & Strange (1996). The F-value was calculated using the following equation:

where SS₁ and SS₂ are the residual sum of squares for the fit to the simpler equation (fewer parameters) and more complex equation (more parameters) respectively, and where df₁ and df₂ refer to the corresponding degrees of freedom for the residuals. The symmetry of these fitted curves was calculated using the method described by Koshland et al. (1966). The value R_A was calculated using the following equation:

where (S_0.9), (S_0.1) and (S_0.5) are the modulator concentrations that result in fractional radioligand occupancy of 0.9, 0.1 and 0.5 respectively. An R_A value of unity indicates a symmetrical curve. Statistical significance was determined using Student's t-test.

Results

Radioligand dissociation in the absence of modulators

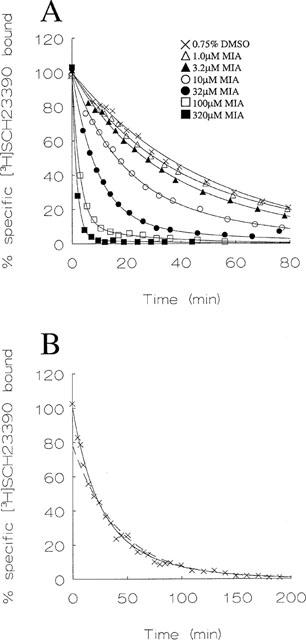
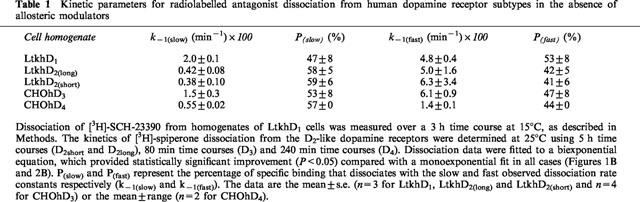
Dissociation of [³H]-SCH-23390 from the LtkhD₁ cell homogenate and [³H]-spiperone from homogenates of cells expressing D_2(long), D_2(short), D₃ and D₄ dopamine receptors was described by a biexponential rate function provided the time course was long enough (data for D₁ and D_2(long) subtypes shown in Figure 1 and 2). The dissociation of [³H]-spiperone and [³H]-SCH-23390 therefore occurred with two observed rate constants (Table 1). The biexponential fit yields estimates of the proportions of radioligand bound that dissociate at the two rates (Table 1).

Figure 1.

Dissociation of [³H]-SCH-23390 from the human D₁ dopamine receptor in the presence of MIA. The time course of radioligand dissociation from LtkhD₁ cell homogenates was determined as described in Methods in the presence of 0.75% DMSO or varying concentrations of MIA. (A) Eighty minute time course. Radioligand dissociation is described by biexponential fits in the presence of MIA, which provided a significant improvement (P<0.05) compared with a monoexponential fit. The vehicle control data for this time course are described by a monoexponential curve, the biexponential fit providing no improvement (P>0.05). The data are from a single experiment that was repeated twice. (B) Three hour time course of [³H]SCH-23390 dissociation. The dissociation kinetics in the presence of 0.75% DMSO are described by a biexponential function (solid line), which represented a significant improvement (P<0.05) compared with the single rate fit (dashed line). The data are from an experiment that was repeated twice with similar results. The 100% value represents the estimate of initial specific binding provided by the curve-fitting analysis, which was in good agreement with the measured value (A. 7874 d.p.m.; B. 11167 d.p.m.).

Figure 2.

Dissociation of [³H]-spiperone from the long isoform of the human D₂ dopamine receptor in the presence of MIA. Radioligand dissociation from LtkhD_2(long) homogenates was measured as described in Methods in the presence of 0.75% DMSO or varying concentrations of MIA. (A) Measurement of [³H]-spiperone dissociation for 80 min. Data in the presence of the vehicle and 1 μM MIA are described by a monoexponential function whereas biexponential curves improved the goodness of fit (P<0.05) in the presence of higher concentrations of MIA. The data are from a single experiment that was repeated three times with similar results. (B) Five hour time course of [³H]-spiperone dissociation. The extended time course reveals the biexponential nature of dissociation in the presence of 0.75% DMSO (×) and 1 μM MIA (Δ). Curves are all biexponential fits which represented an improvement (P<0.05) over monoexponential functions. The monoexponential fit for data in the presence of the vehicle is represented by the dashed line. Data are from representative experiments that were repeated twice. The 100% value represents the estimate of initial specific binding provided by the curve-fitting analysis, which was in good agreement with the measured value (A. 4956 d.p.m.; B. 5536 d.p.m.).

Table 1.

Kinetic parameters for radiolabelled antagonist dissociation from human dopamine receptor subtypes in the absence of allosteric modulators

Allosteric regulation of dopamine receptor subtypes by MIA

The allosteric effects of MIA on human dopamine receptor subtypes were measured to determine whether the modulator acts with varying potency at the different receptors. MIA accelerated dissociation of [³H]-SCH-23390 from the D₁ subtype and [³H]-spiperone from the D_2(long), D_2(short), D₃ and D₄ dopamine receptors in a concentration-dependent fashion (data for the D₁ and D_2(long) subtypes are shown in Figures 1 and 2). Radioligand dissociation data were described by biexponential fits at all MIA concentrations for each receptor subtype providing the time course was long enough (Figures 1 and 2).

The allosteric effect of MIA was quantified by calculating the t_1/2 for radioligand dissociation and fitting the data to a four parameter logistic equation (Figure 3A). MIA displayed selectivity for the D₃ subtype for this effect; the EC₅₀ was 35, 24, 10 and >25 fold greater for D₁, D_2long, D_2short and D₄ dopamine receptors respectively. This allosteric modulation was investigated further by analysing the concentration-dependence of the biphasic dissociation parameters i.e. the fast and slow observed rate constants for dissociation and the proportion dissociating at the fast rate (P_(fast)). At the D₁ dopamine receptor, MIA increased the fast [³H]-SCH-23390 observed dissociation rate constant but did not affect the slow observed dissociation rate constant, except at 320 μM (Figure 3). MIA also increased the proportion of specific [³H]-SCH-23390 binding that dissociated at the rapid rate (P_(fast)) in a concentration-dependent fashion (Figure 3). Modulation of [³H]-spiperone dissociation from the D₂-like dopamine receptors by MIA involved increases of both the fast and slow observed rate constants for dissociation, and an increase of P_(fast) (Figure 3). For each parameter (fast and slow observed rate constants of radioligand dissociation and P_(fast)) the effects of MIA were seen at lower concentrations for the D₃ receptor.

Figure 3.

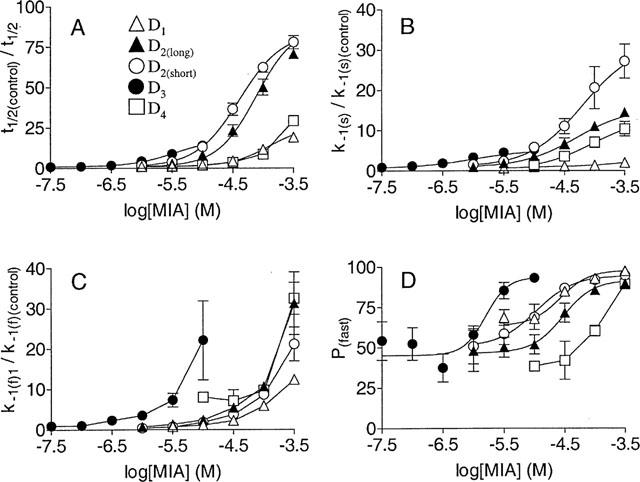
Effect of MIA on kinetic parameters for radioligand dissociation from recombinant human dopamine receptors. The procedures outlined in Methods were used to measure the time course of dissociation of [³H]-spiperone from D_2(long), D_2(short), D₃ and D₄ dopamine receptors and of [³H]-SCH-23390 from the D₁ subtype. The data points are the mean±s.e. (n=3 or 4). (A) Reduction of t_1/2 for radioligand dissociation by MIA. Time course data from short time course experiments (100 min or less) were fitted to mono- and biexponential dissociation functions, the best fit determined and t_1/2 calculated. The dependence of the fold reduction of t_1/2 on MIA concentration was fitted to a four parameter logistic equation. The curves are defined by the mean parameters from three or four independent experiments. The derived data for EC₅₀ (μM) and fold decrease in t_1/2 (mean±s.e.mean) are respectively as follows: D₁ 140±50, 26±5; D_2long 94±42, 88±14; D_2short 41±4, 84±4; D₃ 4±1.3, 18±1; D₄>100, not determined. B-D Effect of MIA on kinetic parameters from biexponential dissociation fits. The parameters were obtained from biexponential fits that represented an improvement over the single-rate fit (P<0.05). For low concentrations of MIA, a time course of several hours was required to reveal biexponential radioligand dissociation (except at the D₃ subtype). Biexponential fits are described by two observed rate constants for dissociation (k_−1(slow) and k_−1(fast)) and the proportions of initial specific binding that dissociate at these rates (P_(slow) and P_(fast)). (Control values for radioligand dissociation in the absence of MIA are presented in Table 1). (B) Effect of MIA on the slow observed rate constant for radioligand dissociation (k_−1(slow)). k_−1(slow) in the presence of MIA was divided by k_−1(slow) for the vehicle control (Table 1). The dependence of this acceleration value on the MIA concentration was fitted to a four parameter-logistic equation for the D_2(long), D_2(short), D₃ and D₄ subtypes. The curves are fits to the pooled data. (C) Effect of MIA on the fast observed rate constant for radioligand dissociation (k_−1(fast)). k_−1(fast) in the presence of MIA was divided by k_−1(fast) for the vehicle control. (D) Modulation of P_(fast) by MIA. P_(fast) represents the proportion of specific radioligand binding that dissociates at the more rapid rate. The dependence of this value on MIA concentration was fitted to a four parameter-logistic equation for the D₁, D_2(long), D_2(short) and D₃ subtypes. The curves are fits to the pooled data.

Allosteric effects of amiloride and benzamil

The allosteric effects of two other compounds related to MIA were examined (the parent compound, amiloride, and the terminal guanidino-substituted derivative, benzamil). In these experiments dissociation was quantified as the amount of radioligand left bound to the receptor as measured at a single time point (20 min). For comparison, analogous data for the effects of MIA were derived by calculating the amount of radioligand bound to receptors at 20 min using parameters from curve fitting of time course data.

From the potency values (EC₅₀) for the modulators the structure-activity relationship for the compounds at the individual receptors was determined and the potencies of a particular modulator at the different receptors were compared. It should be noted that these potency values represent the potencies at the radioligand-bound receptor. The rank order of potency was MIA>benzamil>amiloride at all the receptor subtypes (Table 2). The rank order of potency of MIA for the different receptor subtypes was D₃>D_2(long)=D_2(short)>D₁>D₄ (Table 2). The rank order of potency for benzamil and amiloride, however, was D₃>D_2(long)=D_2(short)>D₄>D₁(Table 2).

Table 2.

Structure-activity relationship data for MIA, benzamil and amiloride for acceleration of radiolabelled antagonist dissociation from human dopamine receptor subtypes

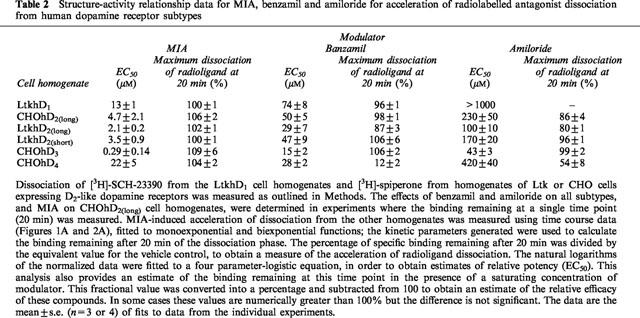
A measure of the maximal effect of these compounds for acceleration of dissociation was also calculated (see legend to Table 2). With the exception of the D₃ and D₄ dopamine receptors, MIA elicited the largest effect, benzamil the next highest and amiloride the smallest (Table 2). At the D₃ dopamine receptor, the modulators were equally effective at saturating concentrations (Table 2). Modulation of the D₄ subtype was unusual in that benzamil was less effective than amiloride. At this receptor both drugs produced a relatively weak maximal allosteric effect compared with the other receptors (Table 2).

Regulation of [³H]-spiperone dissociation from homogenates of CHOhD_2(long) cells was also measured, to enable a comparison of dopamine receptor modulation in the two cell types used (Ltk⁻ and CHO cells). With one exception (the maximal effect of benzamil) parameters for allosteric modulation were not significantly different when compared for the two cell types (P>0.05). The receptor therefore appears to be regulated in a similar manner for both cell types, which has also been observed for the binding of several antagonists to the rat D_2long) dopamine receptor expressed in Ltk- cells and CHO cells (Castro & Strange, 1993).

Effects of modulators on equilbrium radioligand binding

The modulatory action of MIA, benzamil and amiloride was also examined in pseudo-competition experiments in order to evaluate cooperativity and to examine the regulation of equilibrium binding. In this series of assays, the fractional occupancy of receptor by radioligand was measured in the presence of a single concentration of the radioligand and a range of concentrations of modulator enabling the effects of the modulators at radioligand-bound and free receptors to be studied. This is in contrast to the kinetic experiments which probe the effects of the modulators on the radioligand-bound receptors only.

MIA, benzamil and amiloride inhibited radiolabelled antagonist binding to all the dopamine receptor subtypes (Figures 4, 5 and 6). Binding in the presence of saturating inhibitor concentrations was the same as that in the presence of a high concentration (10 μM) of the appropriate non-radioactive ligand. Data were fitted by non-linear regression to a four parameter-logistic equation to generate estimates of IC₅₀ and the Hill coefficient (n_H). Inhibition for all three modulators at the D₁, D_2(long), D_2(short) and D₃ dopamine receptors was defined by curves with n_H values greater than unity (Figures 4, 5 and 6). Where enough replicates were available to perform Student's t-tests, the n_H values were found to be significantly different from unity (P<0.05) (Table 3). In contrast, the inhibition of [³H]-spiperone binding to the D₄ dopamine receptor by benzamil and amiloride was consistent with a one site model having Hill coefficients close to one (Table 3). The effect of MIA (Figure 4), however, was defined by a n_H value significantly less than unity (P<0.05).

Figure 4.

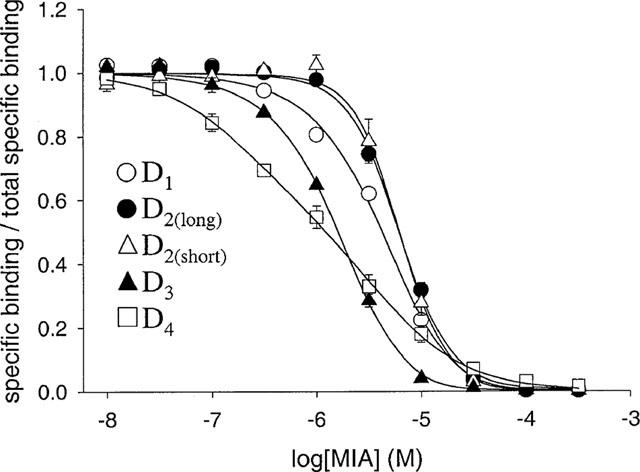
Inhibition of radioligand binding to human dopamine receptor subtypes by MIA. Pseudo-competition experiments were performed as described in Methods, using [³H]-SCH-23390 to label D₁ dopamine receptors and [³H]-spiperone to label D₂-like dopamine receptors. The data were initially analysed using a four parameter-logistic equation to obtain estimates of IC₅₀ and n_H; the values obtained are presented in Table 3. The 100% value represents the estimate of specific binding in the absence of modulator provided by this analysis (D₁−80 pM; D_2(long)−22–31 pM; D_2(short)−14–24 pM; D₃−20–43 pM; D₄−18–20 pM; corresponding values for the non-specific binding were D₁−3.5–4.7 pM, D_2long−1.3–1.8 pM, D_2short−1.5–2.0 pM, D₃−1.2–1.4 pM, D₄−1.8–3.4 pM). The total radioligand concentration was 500 pM for [³H]-SCH23390 and 200 pM for [³H]-spiperone. The data were also analysed using three binding models – competitive inhibition (Equation 3 of the Appendix), simple allosteric modulation (Equation 4, left-hand side of Scheme 1) and a model that assumes modulator can bind at primary and allosteric sites (Scheme 1, Equation 2). The data points are the mean±s.e. from three experiments. (For many data points the error bar is enclosed within the symbol.) The curves for the D_2-like receptors are the best fits of pooled data to Equation 2, which provided the better fit compared with the other two models in all cases (see Table 3). The data for the D₄ subtype were also fitted equally well by a model that assumes MIA competitively inhibits radioligand binding at two independent classes of binding site (Equation 5). The curve for the two-site fit overlies that for Equation 2.

Figure 5.

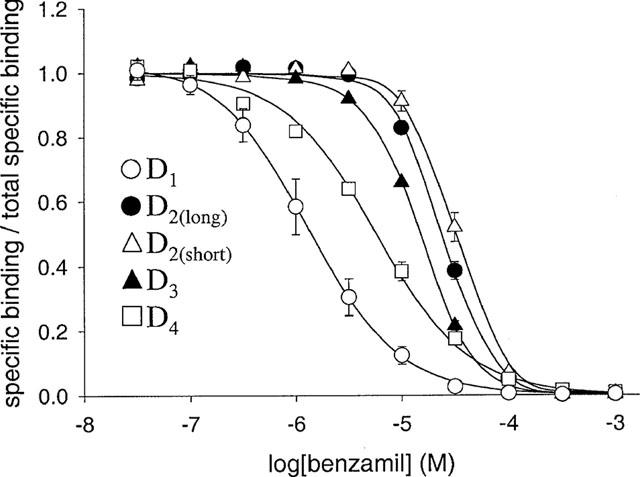
Inhibition of radioligand binding to human dopamine receptor subtypes by benzamil. Pseudo-competition experiments were performed as described in Methods, using [³H]-SCH-23390 to label D₁ dopamine receptors and [³H]-spiperone to label D₂-like dopamine receptors. Data were analysed as described in the legend to Figure 4. The 100% value represents the estimate of specific binding in the absence of modulator provided by analysis of data using a four parameter-logistic equation (D₁−90 pM; D_2(long)−19–32 pM; D_2(short)−14–26 pM; D₃−22–45 pM; D₄−16–19 pM; corresponding values for the non-specific binding were: D₁−3.0–3.4 pM, D_2long−1.7–2.1 pM, D_2short−1.7–1.8 pM, D₃−1.3–1.4 pM, D₄−2.1–3.0 pM). The total radioligand concentration was 500 pM for [³H]-SCH-23390 and 200 pM for [³H]-spiperone. Data points are the mean±s.e. (n=3) for D₂-like dopamine receptors and the mean±range (n=2) for the D₁ subtype. The curves are the best-fits of pooled data to Equation 2 (Scheme 1, D_2(long), D_2(short) and D₃) or Equation 3 (competitive inhibition, D₄).

Figure 6.

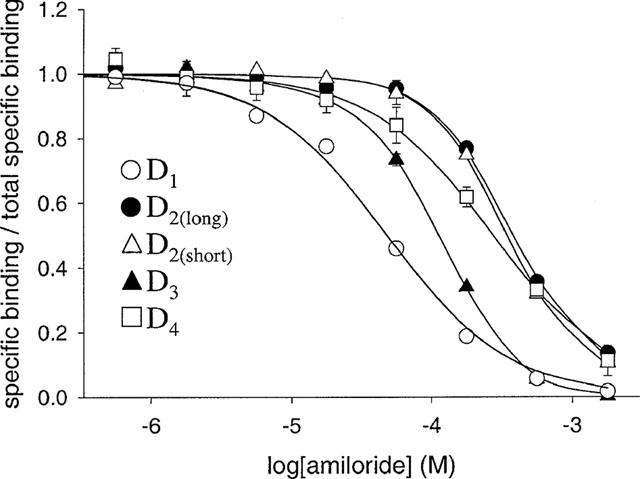
Inhibition of radioligand binding to human dopamine receptor subtypes by amiloride. Pseudo-competition experiments were performed as described in Methods, using [³H]-SCH-23390 to label D₁ dopamine receptors and [³H]-spiperone to label D₂-like dopamine receptors. Data were analysed as described in the legend to Figure 4. The 100% value represents the estimate of specific binding in the absence of modulator provided by analysis of data using a four parameter-logistic equation (D₁−80 pM; D_2(long)−23 pM; D_2(short)−26–29 pM; D₃−42–48 pM; D₄−15 pM; corresponding values for the non-specific binding were: D₁−3.1–3.6 pM, D_2long−2.4–2.6 pM, D_2short−1.9–3.1 pM, D₃−1.8–3.4 pM, D₄−2.1–2.9 pM). The total radioligand concentration was 500 pM for [³H]-SCH-23390 and 200 pM for [³H]-spiperone. Data points for the D₁ subtype are the mean±s.e. (n=3) whereas data for D₂-like dopamine receptors are the mean±range (n=2). The curves are the best-fits of pooled data to Equation 2 (Scheme 1, D_2(long), D_2(short) and D₃) or Equation 3 (competitive inhibition, D₄). At the D₁ subtype the three binding models tested could not be statistically distinguished using these data (Table 3). The curves for these models are shown and overlie each other.

Table 3.

Data from modulator/[3H]-spiperone and modulator/[3H]-SCH-23390 pseudo-competition experiments, using homogenates of cells expressing recombinant dopamine receptors

A crude examination of subtype selectivity was made using IC₅₀ values from analysis of pseudo-competition data. Neither MIA nor amiloride were greatly selective for any one dopamine receptor subtype (Figures 4 and 6, Table 3). Benzamil was slightly selective for the D₁ subtype (Figure 5 and Table 3). However, the data from these experiments do not take into account the varying radioligand affinities at the different dopamine receptor subtypes (Neve & Neve, 1997). In addition, the IC₅₀ value does not directly represent the affinity of modulator binding for curves that are described by Hill coefficients that differ from unity. Models that can account for Hill coefficients that differ from unity are required in order to directly compare modulator affinities.

Three different binding models were used to fit pseudo-competition data – competitive inhibition (Equation 3 of the Appendix), simple allosteric modulation (Equation 4) and a model that assumes modulator binds at allosteric and primary sites (the allosteric/competitive model (Waelbroeck, 1994; Hoare & Strange, 1996) Scheme 1, Equation 2). For the D_2long, D_2short and D₃ dopamine receptors the allosteric/competitive model provided a statistically better fit to the data for MIA, benzamil and amiloride than competitive inhibition or simple allosteric regulation (Table 3). The model provided a better fit to these data because it could account for the steepness of the competition curves (Figures 4, 5 and 6). At the D₁ receptor the effects of MIA and benzamil were better described by the allosteric/competitive model but for amiloride it was not possible to distinguish the most suitable mechanism since the data were fitted equally well by all three models (Table 3). At the D₄ subtype the effect of MIA was best described by the allosteric/competitive model or a model that assumes inhibition of radioligand binding at two independent sites (Figure 4, Table 1). However, it proved impossible to obtain satisfactory estimates of the parameters of the allosteric/competitive model using these data. This was partly due to the large number of parameters in the equations used and partly because the inhibition curves were symmetrical (Table 3) and required only two parameters to be defined.

In order to obtain a qualitative interpretation of the modulatory mechanism in pseudo-competition experiments, experimental data were compared with simulated data using Scheme 1 (results not shown). For modulation that results in Hill coefficients exceeding unity the most likely mechanism was that binding of modulator to the allosteric site favoured binding of modulator over radioligand at the primary site (i.e. β>α). This mechanism describes the modulatory effect of MIA, benzamil and amiloride at D_2(short), D_2(long) and D₃ subtypes and the effect of MIA and benzamil at the D₁ receptor. For the effect of MIA at the D₄ receptor (producing a Hill coefficient of less than unity) an unambiguous conclusion could not be reached using the simulations.

Simple pseudo-competition experiments do not permit an accurate estimation of the parameters of Scheme 1. We attempted to develop methods that could result in more accurate estimation of the model parameters and which could permit the discrimination of different binding models. The effect of MIA on [³H]-spiperone binding to the D₄ dopamine receptor was used for this purpose.

Detailed analysis of the effects of MIA on [³H]-spiperone binding to D₄ dopamine receptors

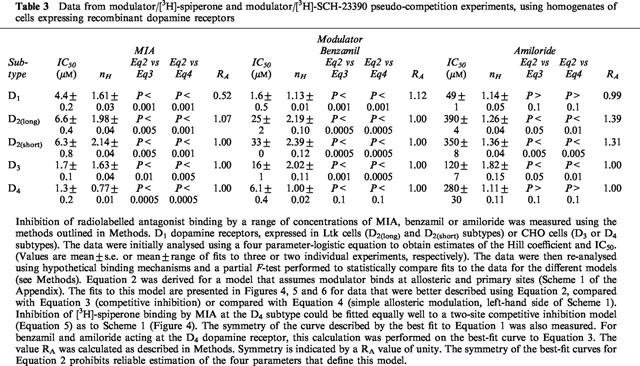
In the first series of experiments, MIA/[³H]-spiperone pseudo-competition experiments were performed using a range of radioligand concentrations. Data from all experiments (six) were analysed simultaneously (Figure 7). The fitted parameter values for Scheme 1 (Equation 6) were still associated with large approximate standard errors, but the data were better described (P<0.05) by this model than a two-site fit (Equation 7, Figure 7). For the allosteric/competitive model the data were fitted equally well by two different sets of parameter estimates. In a second series of experiments, the pseudo-competition assays were performed in the presence of a range of concentrations of benzamil (using a single concentration of radioligand). This compound was assumed to bind only to the primary site on the receptor at the concentrations used as it exhibited a Hill coefficient of 1 in pseudo competition experiments (Table 3) and elicited only a small amount of dissociation of [³H]-spiperone (Table 2). Equations were derived that describe models of the interactions of the three ligands with the receptor, based on Scheme 1 (Equation 8) and a two-site model (Equation 9). This procedure allowed discrimination between the allosteric/competitive mechanism and the two-site model; Equation 8 (for the former model) provided a significantly better fit (P<0.05) than Equation 9 (for the latter model). For these experiments including the unlabelled competitive ligand (Figure 8), the approximate standard error of the fitted parameter estimates in a single experiment was lower than in for example Figure 7. Independent analyses of data from two separate experiments yielded similar parameter values for Scheme 1. However, in both experiments two different sets of parameter values of the allosteric/competitive model fitted the data equally well, termed here Fit 1 and Fit 2 (mean±range, n=2–Fit 1–K_A=9.7±6.6×10⁷ M⁻¹, K_C=2.8±0.9×10⁶ M⁻¹, α=0.91±0.03, β=0.20±0.06; Fit 2–K_A=1.9±1.8×10⁷ M⁻¹, K_C=1.7±4.2×10⁴ M⁻¹, α=0.77± 0.04, β=2.54±0.25).

Figure 7.

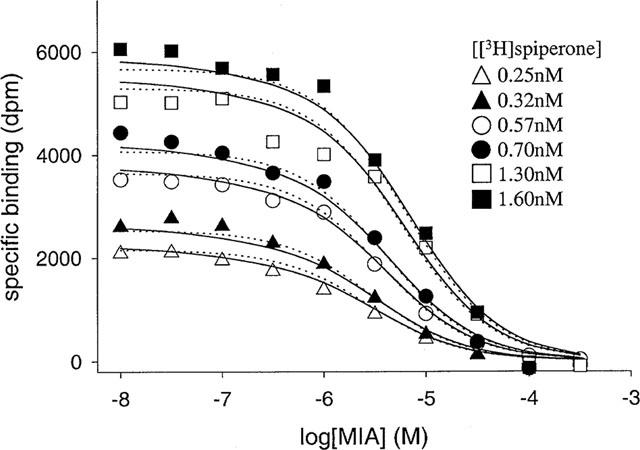
MIA/[³H]-spiperone pseudo-competition data for the D₄ dopamine receptor obtained with a range of free concentrations of radioligand. The assays were performed and data analysed as described in Methods. Data were analysed using the allosteric/competitive model for MIA binding (Scheme 1, Equation 6, solid line) and a model that assumes competitive inhibition at two independent binding sites (Equation 7, dashed line). The value of K_L used in this analysis was 1.38×10⁹ M⁻¹ (mean value from two [³H]-spiperone saturation experiments). All six inhibition curves were analysed simultaneously, using MIA concentration and radioligand concentration as independent variables. The curves shown are the best fits to Scheme 1 which provided a better description of the data (P<0.05) than the two-site model.

Figure 8.

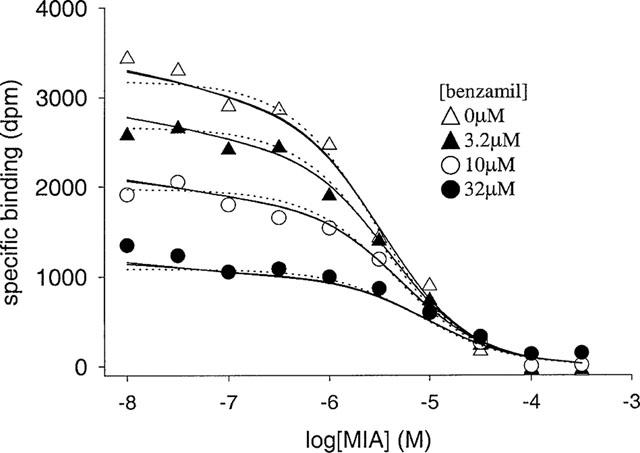
MIA/[³H]-spiperone pseudo-competition data for the D₄ dopamine receptor measured in the presence of a range of concentrations of benzamil. Assays were performed and data analysed as described in Methods. Data were analysed using the allosteric/competitive model for MIA binding (Scheme 1, Equation 8, solid line) and a model that assumes competitive inhibition at two independent binding sites (Equation 9, dashed line). The values of K_L and [L] used in this analysis were 1.38×10⁹ M⁻¹ and 5.55×10⁻¹⁰ M. All four inhibition curves were analysed simultaneously, using MIA concentration and benzamil concentration as independent variables. The curves shown are the best fits to Scheme 1 which provided a better fit (P<0.05) than Equation 9. The experiment was repeated once with similar results.

Effects of MIA on dopamine stimulation of [³⁵S]-GTPγS binding

The effect of MIA on dopamine stimulated [³⁵S]-GTPγS binding was determined in membranes from CHO cells expressing D2_(long) receptors in order to compare the modulation of agonist and antagonist actions at this receptor. The EC₅₀ for dopamine stimulation of [³⁵S]-GTPγS binding in CHO-D2_(long) membranes (in the presence of 0.25% DMSO) was 630±170 nM (Figure 9A). MIA produced a concentration dependent, rightward shift of the dopamine dose response curve, indicating that the modulator inhibited dopamine mediated receptor activation (Figure 9A). The rightward shift was parallel and the Hill coefficients of the dose response curves were not significantly different (single factor analysis of variance P>0.05).

Figure 9.

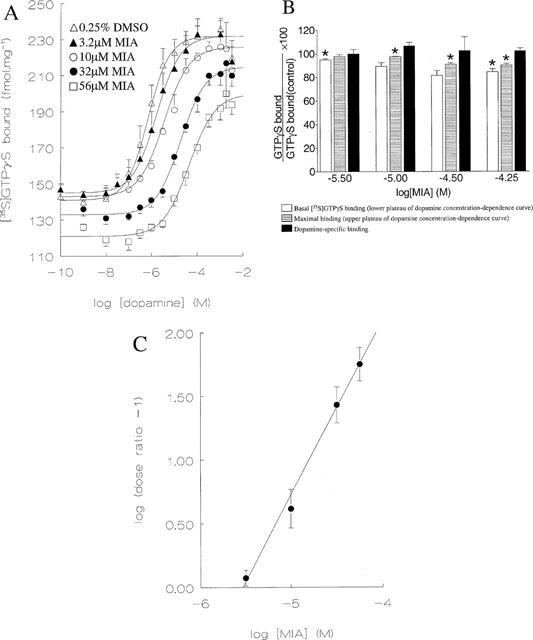
Effect of MIA on dopamine-stimulated binding of [³⁵S]-GTPγS at CHO-D2L membranes. Data are means±s.e.mean from three independent experiments. (A) Concentration-dependence data for dopamine in the presence of MIA. Data were fitted to a four parameter-logistic equation to determine Hill slope, EC₅₀ and the basal and maximal stimulated levels of binding. (B) Effect of MIA on concentration-dependence parameters for [³⁵S]-GTPγS binding from A. Unfilled bars – effect on basal binding. For each concentration of MIA the fitted lower plateau was divided by the control binding value for the absence of dopamine and MIA. Striped bars – effect on maximal binding. The upper plateau was divided by the control binding value measured in the presence of 100 μM dopamine and absence of MIA. Solid bars – effect on dopamine-specific binding. The incremental increase of binding in the presence of MIA was divided by the value for the absence of MIA. While MIA affected basal and maximal binding of [³⁵S]-GTPγS (statistical significance (P<0.05, paired Student's t-test) indicated by asterisk) the modulator did not affect the dopamine-specific binding (P>0.05). The controls were included in each assay for MIA to enable an accurate comparison of basal and maximal binding in the presence and absence of MIA. (C) Schild plot for dopamine-stimulated [³⁵S]-GTPγS binding in the presence of MIA. The slope value obtained from linear regression was 1.37±0.12.

MIA slightly decreased binding of [³⁵S]-GTPγS in the absence of dopamine and reduced the total binding of the radioligand elicited by a maximally stimulating concentration of agonist (Figure 9B). MIA did not, however, affect the magnitude of the agonist-sensitive binding. (Figure 9B). Haloperidol, a competitive antagonist did not affect any of these parameters (data not shown). A similar reduction of [³⁵S]-GTPγS binding was seen for MIA in untransfected CHO-K1 cells. Taken together, these data indicate that MIA produced a receptor-independent and dopamine-independent reduction of [³⁵S]-GTPγS binding and it was assumed, therefore, that MIA did not alter the magnitude of the response to dopamine.

To examine the mechanisms of MIA action in the dopamine-stimulation experiments, Schild analysis was used to analyse the rightward shift produced by the modulator. This analysis gave a Schild slope of 1.37±0.12 (Figure 9C), which was significantly different from unity (P<0.05). Haloperidol, a competitive antagonist, yielded a slope of 0.97±0.07 in a similar experiment. The data for MIA were subsequently analysed using equations derived for the allosteric/competitive model (see Appendix Equation 10), simple competitive inhibition (the logistic Schild equation) or simple allosteric modulation (Equation 37 of Lazareno & Birdsall, 1995) (Figure 10). In all experiments the allosteric/competitive model provided a significantly better fit than simple allosteric modulation (P values of 0.0011, 0.00015, 0.022 for three experiments). Comparison of the allosteric/competitive model with competitive inhibition gave P values of 0.0064, 0.0017, 0.070. For the allosteric/competitive model the use of two independent variables in the analysis (the concentrations of dopamine and MIA) provided reproducible estimates of model parameters (Equation 10): α=0.093±0.070, β=2.1±1.0, K_A=113000±44000, K_C=144000±20000, n=0.81±0.01 (mean±s.e.mean, n=3).

Figure 10.

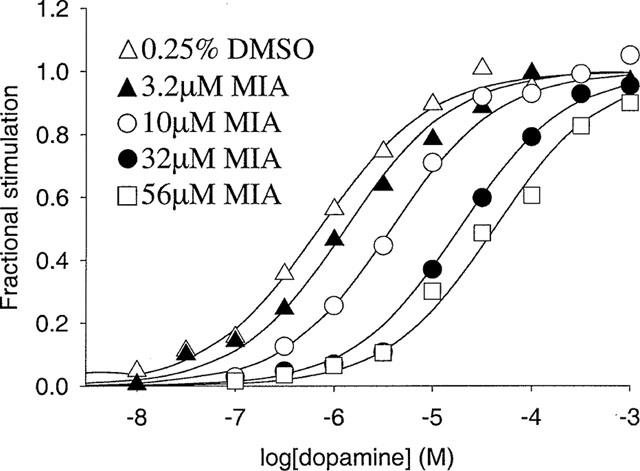
Modulation by MIA of dopamine-stimulated [³⁵S]-GTPγS binding at CHO-D2L membranes, analysed using the allosteric/competitive model. Fractional stimulation of binding by dopamine was calculated by subtracting basal binding followed by division of the dopamine-specific binding. MIA did not affect dopamine-specific binding of [³⁵S]-GTPγS (Figure 9). The curves show the fit to the allosteric/competitive model (Equation 10) which represented a significantly better fit than competitive inhibition (P<0.005; the logistic Schild equation) or simple allosteric modulation (P<0.0005; Equation 37 of Lazareno & Birdsall, 1995). The graph is from a representative experiment that was repeated twice with similar results.

Discussion

Compounds of the amiloride series modulate the activities of a diverse group of cation-binding proteins, such as the L-type calcium channel and Na⁺/H⁺ antiport proteins (Kleyman & Cragoe, 1990). The compounds have also been shown to affect ligand binding at two G-protein-coupled receptors – α₂ adrenergic and D₂ dopamine receptors (Howard et al., 1987; Neve, 1991; Hoare & Strange, 1996; Leppik et al., 1998). In this study, modulation of a number of human dopamine receptor subtypes has been examined in order to probe the modulatory mechanisms and measure subtype selectivity.

Radioligand dissociation experiments were carried out to measure allosteric effects at the radioligand-bound receptor. In the absence of modulators, biphasic dissociation kinetics were observed for [³H]-spiperone at D₂-like dopamine receptors and [³H]-SCH-23390 at the D₁ subtype (Figure 1 and 2). This observation is consistent with the presence of two classes of binding site, present in approximately equal proportions, from which ligands dissociate with fast and slow observed dissociation rate constants. For the rat D_2(long) receptor it has been demonstrated that these states probably represent two distinct but interconvertible states of the receptor (Hoare & Strange, 1996). The molecular nature of the states is unclear at present but there are reports that G-protein coupled receptors may exist in different oligomeric forms (Chidiac, 1998) that could be related to these observations.

At human D_2(long), D_2(short), D₃ and D₄ dopamine receptors, MIA increased the slow and fast observed [³H]-spiperone dissociation rate constants in a concentration-dependent fashion (Figure 3). The modulator also increased the proportion of binding that dissociated with the fast observed dissociation rate constant (P_(fast)). Modulation of [³H]-SCH-23390 dissociation at the D₁ subtype was slightly different; the fast dissociation rate constant and P_(fast) were increased, but the slow observed dissociation rate constant was increased to a small extent and only at the highest MIA concentration tested (Figure 3). MIA displayed selectivity for the D₃ subtype for these effects in that its effects occurred at lower concentrations at this receptor compared to the other D₂-like receptors tested. (Figure 3). MIA also displayed selectivity for the D₃ subtype when its effects were evaluated using the amount of radioligand bound after 20 min and using the t_1/2 for radioligand dissociation (Figure 3). These methods provide complementary qualitative assessments of the effects of the modulator but owing to the complexity of the dissociation data the derived data do not correspond to ligand affinity constants.

The rank order of potency for the three modulators tested was MIA>benzamil>amiloride at all the receptor subtypes (Table 2). This suggests that a similar regulatory site (or similar sites) is present on all the subtypes examined. Although the analysis used for the determination of the structure-activity relationship provided only an approximate measure of efficacy of the modulators, it suggested that the maximal effect of benzamil and amiloride was small at the D₄ dopamine receptor compared with the other subtypes (Table 2).

Allosteric regulation of both the radioligand-bound and free receptor states was examined in pseudo-competition experiments. The aim of these experiments was to examine the mechanism of regulation of equilibrium binding and the cooperativity involved. Inhibition curves for MIA, benzamil or amiloride versus [³H]-spiperone or [³H]-SCH-23390 were analysed using a four parameter-logistic equation. With the exception of benzamil and amiloride at the D₄ dopamine receptor, Hill coefficients significantly different from unity were obtained (Table 3). These results were not consistent with competitive inhibition or the simple allosteric model (left-hand side of Scheme 1 (Appendix)) developed for muscarinic acetylcholine receptors (Stockton et al., 1983). For the D₂-like dopamine receptors, the data were fitted well by a model that assumes binding of modulator to the primary and allosteric sites on the receptor (the allosteric/competitive model; Scheme 1). This model can also account for the modulatory effects of MIA at the rat D_2(long) dopamine receptor (Hoare & Strange, 1996). The model is also appropriate for the allosteric effects of methoctramine and pentamethylene-bis(4-diphenylacetoxymethylpiperidine) at cardiac muscarinic acetylcholine receptors (Waelbroeck, 1994) and has also been applied to modulation of acetylcholinesterase (Mooser & Sigman, 1974). A theoretical interpretation of the model has also been carried out (Tomlinson & Hnatowich, 1988). It was not possible to obtain independent estimates of the model parameters in the present study by non-linear regression because of the complexity of the model and the symmetrical nature of the curves (Table 3) which meant that they could be defined using two parameters. This prevented an examination of subtype selectivity at the allosteric site for the free receptor, because K_A could not be estimated reliably.

A qualitative interpretation of cooperative interactions of the model of Scheme 1 has been obtained by a comparison of experimental data (Table 3) with simulated pseudo-competition data. Within this model, cooperativity between allosteric binding of modulator (M) and binding of radioligand (L) is defined by α and homotropic cooperativity between allosteric and competitive binding of M is defined by β. For MIA, benzamil and amiloride at the D₁, D_2(long), D_2(short) and D₃ subtypes, Hill coefficients of greater than unity were obtained (Table 3). From the results of the simulations (not shown) it seems that the mechanism of action of the three modulators at these receptors may be such that the binding of modulator at the allosteric site favours the binding of modulator over radioligand at the competitive site i.e. β>α. This mechanism is the same as that inferred for the rat D_2(long) dopamine receptor (Hoare & Strange, 1996). For modulation that was described by Hill coefficients exceeding 1.6, these simulations predict that β exceeds unity, indicating that the binding of modulator at the allosteric and primary sites is positively cooperative. This positive homotropic cooperativity may be appropriate for the effect of MIA at all the dopamine receptor subtypes examined except D₄ (Table 3). Inhibition of [³H]-spiperone binding by benzamil and amiloride at the D₄ dopamine receptors was described by curves with n_H values not differing significantly from unity (Table 3). Although other mechanisms cannot be ruled out based on this finding, it is likely that the modulators act primarily as competitive inhibitors in these experiments because they produced a small allosteric effect at very low potency in radioligand dissociation assays (Table 2). The Hill coefficient for inhibition by MIA was significantly less than unity for the D₄ subtype, in contrast to the other dopamine receptor subtypes where the value was significantly greater than unity (Table 3). The data were fitted equally well by the allosteric/competitive model and by a model that assumes competitive inhibition at two independent sites (Figure 4).

Different mechanistic schemes that fit binding data equally well can be discriminated by increasing the number of independent variables (Wells, 1992; Sinkins & Wells, 1993). This approach was used here to discriminate the two models that could describe the shallow Hill slope at the D₄ subtype and to attempt to obtain parameter estimates that fitted Scheme 1 with less variability. It was clear that analysis of single pseudo-competition curves did not provide reliable estimates of the model parameters. For the rat D₂ dopamine receptor (Hoare & Strange, 1996) [³H]-spiperone saturation analyses were conducted in the presence of different concentrations of MIA in order to provide better estimates of parameters but this was difficult for the D₃ and D₄ receptors owing to the lower affinities for the radioligand. Therefore in the present study MIA/[³H]-spiperone pseudo-competition experiments were performed using a range of radioligand concentrations, and using this procedure, it was demonstrated, for the D₄ dopamine receptor, that Scheme 1 provided a statistically better fit to the data than a model which assumes competitive inhibition at two independent sites (Figure 7). A similar result was obtained by conducting pseudo-competition experiments (MIA versus [³H]-spiperone) in the presence of benzamil, a ligand that binds primarily to the primary site (Figure 8). These more complex analyses revealed that the same basic mechanism, the allosteric/competitive model, can account for the effects of MIA at all dopamine receptor subtypes tested, including the D₄ receptor. The model, with two interacting sites for the modulator, can account for Hill coefficients of greater or less than unity. The experiment conducted in the presence of the unlabelled primary site ligand provided reproducible and less ambiguous estimates of the parameters for the allosteric/competitive model for the D₄ receptor (Figure 8). Therefore, conducting modulator/radioligand pseudo-competition experiments in the presence of a second unlabelled ligand that binds only to the primary site may be a suitable procedure for obtaining more accurate parameter estimates for the allosteric/competitive model. A ligand that only binds to the allosteric site, particularly an antagonist at this site, would probably be equally useful, but no such compounds have been identified to date.

In the equilibrium binding experiments the bound radioligand was generally less than 20% of the added free radioligand but in a few experiments with the D₃ receptor bound radioligand represented a higher fraction of the added radioligand. Depletion of radioligand, even up to 20%, could have affected the data seen. In separate experiments (Strange, 1997) we have shown that using the bound radioligand in such assays is a good guide to the radioligand depletion i.e. there is little additional depletion via binding that would not be trapped on the filter, for example via low affinity binding to tissue. Thus the free radioligand in such assays may be estimated by subtraction of the bound radioligand from the added radioligand. In order to probe this further we carried out pseudo-competition assays for the D_2(short) receptor (5 pM) with MIA versus [³H]-spiperone (250 pM) in 10 ml volumes with 7 h incubation times, where depletion is minimal (<3%) and obtained data (not shown) very similar to those shown in Figure 4 (Hill coefficient 1.9±0.3, mean±s.e.mean, n=3). This shows that the Hill coefficients greater than one that are seen in these assays are not artefacts of ligand depletion.

The effect of allosteric modulators on agonist action at the D_2(long) dopamine receptor was assessed in experiments using the dopamine stimulation of [³⁵S]-GTPγS binding. MIA produced a rightward shift in the dopamine dose-response curve and also elicited a small reduction in basal and maximal [³⁵S]-GTPγS binding. Since a similar effect on the basal [³⁵S]-GTPγS binding was seen in parent untransfected CHO cells it was assumed that MIA affected the ability of dopamine to bind to the receptor but not its ability to produce a response. Analogous effects of an allosteric modulator on agonist affinity but not efficacy have been described for muscarinic acetylcholine receptors (Lazareno & Birdsall, 1995). Schild analysis of the effects of MIA on the dopamine dose-response curves gave a Schild slope significantly greater than unity whereas in an analogous experiment with the competitive antagonist haloperidol the Schild slope was close to one. The data for MIA were fitted well by the allosteric/competitive model with β>α in agreement with data from experiments on antagonists described above. Indeed, the parameter estimates of the model for regulation of agonist interactions at the human D₂ receptor in this study are similar to those measured for regulation of antagonist binding at the rat D₂ receptor (Hoare & Strange, 1996). These considerations suggest that MIA affects agonist and antagonist interactions similarly at the D₂ dopamine receptor.

In conclusion, amiloride and amiloride analogues modulate the D₁, D₂, D₃ and D₄ dopamine receptors allosterically and competitively but the pattern and potency of the effects is different for the different receptor subtypes. The further characterization of this allosteric site may provide a new route to the design of sub-type selective drugs acting at these receptors.

Abbreviations

CHO

Chinese hamster ovary

d.p.m.

disintegrations per minute

FBS

foetal bovine serum

MIA

5-[N-methyl-N-isobutyl]amiloride

rss

residual sum of squares

Appendix

A general model for the interaction of an allosteric modulator (M) with the primary and allosteric binding sites of a receptor for a ligand (L) is shown below.

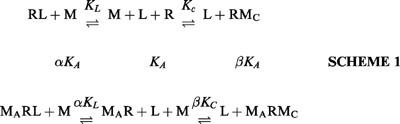M_A and M_C denote modulator (M) bound to the allosteric and primary sites of the receptor (R) respectively. K_L is the equilibrium association constant for the binding of ligand (L) to the primary site, K_A is the equilibrium association constant for binding of M to the allosteric site, K_C is the equilibrium association constant for binding of M to the primary site, and α and β are the cooperativity factors for M (acting at the allosteric site) affecting the binding of L or M respectively at the primary site.

For this model the concentration of radioligand bound in the presence of M can be expressed as a fraction of the total receptor concentration ([R_tot]).

The concentration of RL in the absence of modulator ([RL₀]) is defined by the following occupancy function:

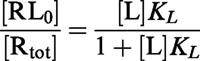By division of Equation 1 by this occupancy function, the concentration of bound radiolabelled ligand L in the presence of M can be expressed as the fraction of that in the absence of M:

The equation that describes competitive inhibition of radioligand binding, using this notation, is:

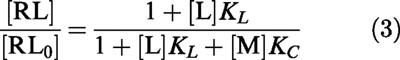Simple allosteric modulation (left-hand side of Scheme 1) is described by:

In some cases data were fitted to a model that assumes competitive inhibition of radioligand binding to two independent classes of binding site. This model assumes that radioligand binds with equal affinity to both sites and is described by the following equation:

where K_C1 and K_C2 are the affinity constants of M for site 1 and site 2, respectively, and where F₁ represents the fraction of total specific binding that is inhibited by M binding to site 1.

Data from pseudo-competition experiments using MIA, benzamil and amiloride can be fitted well by Scheme 1 (Figures 4, 5 and 6, Table 3). However, it was not possible to obtain independent estimates of the model parameters because of the symmetrical nature of the curves (Table 3).

Analysis of data using two independent variables

MIA/[³H]-spiperone pseudo-competition experiments were performed for the D₄ dopamine receptor in which varying radioligand concentrations were used or varying concentrations of benzamil were added. Data were analysed using equations derived from Scheme 1 or a model that assumes competitive inhibition at two classes of binding site.

In the presence of varying radioligand concentrations, Scheme 1 can be described by the following equation:

where [RL_tot] is the measured specific binding. A two-site model for this experiment can be described by the following:

For pseudo-competition data obtained in the presence of benzamil, equations were derived that assumed that this modulator binds only to the primary site. For Scheme 1, the binding interactions can be described by the following:

where [B] is the concentration of benzamil, K_benz represents the affinity of benzamil at the primary site and γ defines the cooperativity between allosteric binding of MIA and the binding of benzamil to the primary site. For a two-site model, the following equation was used to analyse the data:

In the experiments on the effects of MIA to inhibit dopamine stimulation of [³⁵S]-GTPγS binding the equation that describes modulation of an agonist-stimulated response, according to the allosteric/competitive model, is:

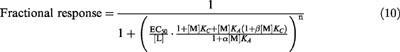In this equation [L] is the concentration of agonist and n is the logistic exponent and it is assumed that the effects of MIA to inhibit dopamine responses are via inhibition of dopamine binding and not inhibition of the activity of the receptor i.e. LR and LRM_A have the same functional activity although the affinity of L (dopamine) may be reduced in the latter species. It should be noted that Equation 10 assumes an explicit mechanistic effect of MIA on the binding of dopamine, although for ease of description the effects of dopamine are described using an empirical expression with a logistic exponent.