Skip to main content
PMC home page
British Journal of Pharmacology logoLink to British Journal of Pharmacology
. 2001 Dec;134(8):1796–1804. doi: 10.1038/sj.bjp.0704406

Blood-brain barrier transport and brain distribution of morphine-6-glucuronide in relation to the antinociceptive effect in rats – pharmacokinetic/pharmacodynamic modelling

M René Bouw 1, Rujia Xie 1, Karin Tunblad 1, Margareta Hammarlund-Udenaes 1,*
PMCID: PMC1572896  PMID: 11739257

Abstract

  1. The objective of this study was to investigate the contribution of the blood-brain barrier (BBB) transport to the delay in antinociceptive effect of morphine-6-glucuronide (M6G), and to study the equilibration of M6G in vivo across the BBB with microdialysis measuring unbound concentrations.

  2. On two consecutive days, rats received an exponential infusion of M6G for 4 h aiming at a target concentration of 3000 ng ml−1 (6.5 μM) in blood. Concentrations of unbound M6G were determined in brain extracellular fluid (ECF) and venous blood using microdialysis and in arterial blood by regular sampling. MD probes were calibrated in vivo using retrodialysis by drug prior to drug administration.

  3. The half-life of M6G was 23±5 min in arterial blood, 26±10 min in venous blood and 58±17 min in brain ECF (P<0.05; brain vs blood). The BBB equilibration, expressed as the unbound steady-state concentration ratio, was 0.22±0.09, indicating active efflux in the BBB transport of M6G. A two-compartment model best described the brain distribution of M6G. The unbound volume of distribution was 0.20±0.02 ml g brain−1. The concentration-antinociceptive effect relationships exhibited a clear hysteresis, resulting in an effect delay half-life of 103 min in relation to blood concentrations and a remaining effect delay half-life of 53 min in relation to brain ECF concentrations.

  4. Half the effect delay of M6G can be explained by transport across the BBB, suggesting that the remaining effect delay of 53 min is a result of drug distribution within the brain tissue or rate-limiting mechanisms at the receptor level.

Keywords: Antinociceptive effect, blood-brain barrier, effect delay, microdialysis, morphine-6-glucuronide, pharmacokinetic-pharmacodynamic modelling

Introduction

Several studies have confirmed that the in vivo analgesic potency of morphine-6-glucuronide (M6G) is highly dependent on the site of administration. Although the potency of M6G is almost equal to that of morphine following systemic administration, it is reported to be 10 – 650 times greater after i.t. or i.c.v. administration (Shimomura et al., 1971; Abbott & Palmour, 1988; Paul et al., 1989a; Frances et al., 1992). As the affinity of both substances for the μ-receptor has been reported to be similar (Christensen & Jorgensen, 1987; Pasternak et al., 1987), a possible explanation for this observation could involve differences in the permeability of the blood-brain barrier (BBB) to morphine and M6G. Several investigators have reported a 4 to 57 fold lower BBB permeability to M6G than to morphine according to the intravenous injection methods (Murphey & Olsen, 1994; Bickel et al., 1996; Wu et al., 1997). Stain-Texier et al. (1999) showed that, using microdialysis, the ratio in areas under the curve (AUC) between brain extracellular fluid (ECF) and blood for morphine was 0.51 and for M6G 0.56 after subcutaneous administration.

As for morphine, the pharmacokinetic-pharmacodynamic (PK-PD) relationship of M6G exhibits a temporal delay (hysteresis) between the time course of drug concentration in blood and the time course of the observed antinociceptive response (Hasselström et al., 1996; van crugten et al., 1997; Gårdmark & Hammarlund-Udenaes, 1998). The effect delay of M6G was quantified with a half-life of 85 min (Gårdmark & Hammarlund-Udenaes, 1998), which is considerably longer than the effect delay half-life of 10 – 38 min observed for morphine using the electrical stimulation vocalization method to determine the antinociceptive effect (Paalzow, 1992; Ekblom et al., 1993; Gårdmark et al., 1993; Bouw et al., 2000). It has been suggested that this longer duration of effect of M6G might be explained by its lower rate of transport across the BBB (Frances et al., 1992; Gårdmark & Hammarlund-Udenaes, 1998). Both the rate and extent of drug transport across the BBB can be quantified by measuring brain and blood concentrations in parallel using microdialysis.

Thus, there are two factors which could affect the degree and onset of M6G antinociceptive effects: (i) a smaller intensity in effect for M6G than morphine after systemic administration than after i.t. or i.c.v. administration due to a lower extent of transport into the brain, and (ii) a profound delay in M6G effects due to a slow transport across the BBB.

This study was designed to investigate the rate and extent of BBB equilibration of M6G and to quantify the contribution of BBB transport to the antinociceptive effect delay of M6G, by measuring the unbound concentrations of M6G in blood and brain ECF simultaneously with microdialysis. The antinociceptive effect was measured following an exponential infusion of M6G for 4 h on two consecutive days. A PK-PD model was developed to describe the BBB transport characteristics and to quantify the contribution of the BBB transport to the overall delay in the onset of the antinociceptive effect.

Methods

Chemicals

Morphine-6-glucuronide (M6G) was supplied by Lipomed (Lipomed AG, Arlesheim, Switzerland). Enfluran® was obtained from the Uppsala Hospital Pharmacy (Uppsala, Sweden). Low molecular weight heparin was provided by Sigma (Sigma Chemical Co, St Louis, MO, U.S.A.). The perfusion solution (Ringer) for microdialysis contained (in mM): NaCl 145, KCl 0.6, MgCl2 1.0, CaCl2 1.2 and ascorbic acid 0.2 in phosphate buffer 2, pH 7.4. All chemicals were of analytical grade and solvents were of HPLC grade. Microdialysis probes, CMA/12 (3 mm, 400 μm inner diameter (i.d.), 500 μm outer diameter (o.d.)) and CMA/20 (10 mm, 500 μm i.d., 670 μm o.d.), were supplied by CMA/Microdialysis (CMA, Solna, Sweden). The probe membranes have a 20,000 Dalton molecular weight cut off.

Animals

Male Sprague Dawley rats, weighing 280 – 330 g, were used in this study (Møllegaard, Denmark). The rats were adapted to the new environment in groups of four for at least 7 days before surgery was performed. The rats were kept in a regulated room with a 12 h light/dark cycle (lights on 0700 – 1900 h), at a temperature of 22±1°C and a humidity of 55%. Standard diet and water were provided ad libitum. The protocol was approved by the Animal Ethics Committee of Uppsala University (C328/95).

Surgical preparation

Surgery of the rats was performed under inhalational anaesthesia with 2% Enfluran and 1.51 min−1 nitrous oxide balanced with 1.51 min−1 oxygen during the procedure (Day 0). Two indwelling polyethylene catheters (PE-50 fused with 2 cm PE-10) were inserted into the left femoral artery and vein for the collection of blood samples and the administration of M6G, respectively. The arterial catheter was heparinized and then closed until blood sampling. For blood microdialysis, a CMA/20 probe (CMA, Solna, Sweden) with a 10 mm membrane length was inserted into the right jugular vein and anchored to the pectoral muscle. During insertion, the probe was perfused with a 0.1% low molecular weight heparin solution to minimize the incidence of clotting.

A CMA/12 guide cannula with a dummy probe was stereotaxically placed in the striatum of the right brain hemisphere (anterior: 0.8 mm and lateral: 2.7 mm with bregma as a reference and 3.8 mm ventral to the brain surface). The guide cannula was fixed to the skull by a screw and dental cement, over which the skin was sutured. Two pieces of steel suture were placed intracutaneously, 1 and 3 cm distal from the root of the tail. During surgery, the body temperature of the rat was maintained at 38°C by means of a heating pad. A 20 cm long PE-50 tubing was looped subcutaneously distal to the posterior surface of the neck, allowing the perfusion solution to reach the body temperature of the rat before it entered the brain probe. Protruding ends of all catheters and probe tubing were tunnelled subcutaneous to the posterior surface of the neck, and were protected by a plastic cap sutured to the skin. Finally, the dummy probe was replaced by a brain probe (CMA/12, 3 mm membrane length) and the rats were allowed to recover for 24 h. After surgery and during the experiment, the rats were placed in a CMA/120 system for freely moving animals with free access to food and water.

Microdialysis calibration

Brain and blood MD probes were perfused with blank Ringer solution for 60 min to stabilize the system and to obtain blank samples. Retrodialysis (RD) using M6G was then applied to calibrate the MD probes in vivo (Bouw & Hammarlund-Udenaes, 1998) by perfusing the MD probes for 75 min with a Ringer solution containing 0.22 μM (100 ng ml−1) M6G. The in vivo recovery of M6G was calculated by measuring the loss of M6G from the perfusion solution before drug administration according to:

graphic file with name 134-0704406e1.jpg

where Cin is the M6G concentration entering the probe, and Cout is the M6G concentration in the outgoing dialysate. The unbound M6G concentrations in brain ECF and blood were calculated from the dialysate concentrations after adjustment for the in vivo recovery.

After the RD period the probes were perfused with blank perfusion solution throughout the experiment. There was a wash-out period of 75 min between the in vivo calibration and the start of the experiment. During this period, M6G concentrations were measured to ensure that no M6G was presented in the dialysate. M6G was undetectable at the end of wash-out period. Microdialysate fractions were collected automatically by a CMA/140 Microfraction collector. The MD probes were perfused at a flow rate of 1 μl min−1 using a CMA/100 Microinjection pump (CMA, Solna, Sweden). At the end of the blank, retrodialysis and wash-out periods, the antinociceptive effect and blood gas status were measured. The same procedure was repeated before the start of the experiment on day 2.

Experimental design

Seven rats were investigated over two consecutive days. On day 1, the rats received an exponential infusion of M6G dissolved in saline over 4 h so as to immediately reach the target total plasma concentration of 6.5 μM (3000 ng ml−1) using the STANPUMP computer controlled infusion (CCI) software (Shafer et al., 1988). The pharmacokinetic parameters used by the software to calculate the infusion scheme were obtained from Gårdmark & Hammarlund-Udenaes (1998).

On day 2, the experiment was repeated in order to detect any time dependency in the BBB equilibration of M6G compared to day 1. Two rats were decapitated immediately after cessation of the infusion to obtain total brain concentrations of M6G. The brain tissue was collected and frozen at −20°C pending analysis. On both days, microdialysates from brain and blood probes were collected over a period of 6 h into pre-weighed vials. Samples were taken at 15 min intervals during the infusion, at 10 min intervals over the following hour and at 15 min intervals over the remaining hour. Arterial blood samples (100 – 150 μl) were collected at 0, 30, 60, 120, 180, 240, 245, 255, 270, 300, 330 and 360 min.

Effect measurement

Nociception was measured using the electrical stimulation vocalization method, in which an electrical stimulus was applied to two electrodes implanted in the tail of the rat using a GRASS S88 (Carroll & Lim, 1960; Paalzow & Paalzow, 1973). The vocalization response was recorded as the endpoint, i.e. the pain threshold. The baseline value of the pain threshold was estimated three times at 15 min intervals before the start of the experiment. Antinociception was recorded at 5, 15, 30, 45, 60, 75 and 90 min after the start of the infusion and thereafter every 30 min up to 6 h, with two additional measurements at 245 and 255 min.

Monitoring of blood gas status

The blood gas status (pO2, pCO2, O2 saturation and pH) of the rats was obtained by injection of 50 μl arterial blood into an AVL Compact II blood gas analyser (AVL Medical Nordic, Stockholm, Sweden). A sample for measurement of the baseline values for the respiratory parameters was collected at the start of the blank period and at the end of the retrodialysis and washout periods. During the experiment the blood gas status was monitored at 30 and 60 min after the start of the infusion and thereafter every 60 min up to 6 h, with an additional measurement at 270 min.

Drug analysis

The chromatographic system consisted of a pump (ESA 580, Chelmsford, MA, U.S.A.), a Nucleosil column (C18, 25 cm×4.6 mm i.d., Chrompack, Middelburg, The Netherlands), an electrochemical detector (ESA Coulochem II, Chelmsford, MA, U.S.A.) in combination with a 5020 guard cell and a 5011 high sensitivity dual analytical cell. For the quantification of M6G in the microdialysates, samples of 13 μl were injected by a Triathlon auto injector (Spark Holland, The Netherlands). The potentials of the guard cell and dual analytical cell were set to 600, 0 and 450 mV, respectively. The mobile phase consisted of 670 ml 0.01 M phosphate buffer, pH 2.1, containing 0.2 mM dodecyl sulphate, 330 ml methanol and 25 ml tetrahydrofyran, and was delivered at a flow rate of 1.0 ml min−1. Peak height was recorded with an integrator (Shimadzu CR-5A, Shimadzu Europe, Sweden). The standard curve was linear up to 1.1 μM (500 ng ml−1) and the limit of quantification of M6G in microdialysate was 5.6 nM (2.6 ng ml−1) with a within-day coefficient of variation (CV) of 7.9%.

The M6G concentrations in plasma were determined as described by Joel et al. (1988) with some modifications. The plasma samples of M6G were extracted with Sep-Pak C18 cartridges (Waters), which were first activated with 5 ml methanol, 3 ml 0.01 M phosphate buffer (pH 2.1) and 5 ml distilled water filtered through the cartridge under vacuum in order. Plasma (diluted with blank plasma to 100 μl) was mixed with 3 ml of 0.5 M ammonium sulphate buffer (pH 9.3) in a 10 ml polystyrene tube for 5 s, and transferred to the reservoir. The plasma samples were filtered through the cartridges, which were subsequently washed with 20 ml 5 mM ammonium sulphate buffer (pH 9.3), 0.5 ml distilled water, and 0.1 ml methanol under vacuum. Lastly, 3 ml methanol was added and the eluates were collected and evaporated under a stream of nitrogen at 45°C. The organic layer was evaporated to dryness under a gentle stream of nitrogen (45°C). The residue was reconstituted in 150 μl of mobile phase and analysed with a slightly modified chromatographic system as described above. The potential of the analytical cell 1 was increased from 0 to 350 mV. The mobile phase consisted of 680 ml 0.01 M phosphate buffer, pH 2.1, containing 0.2 mM dodecyl sulphate, 320 ml methanol and 25 ml tetrahydrofuran. Samples (55 μl) were injected using a CMA/200 autoinjector (CMA, Solna, Sweden). The standard curves were linear within the concentration range of 22 nM (10 ng ml−1) to 22 μM (10 μg ml−1). The limit of quantification for a 100 μl plasma sample was 22 nM with a within-day coefficient of variation (CV) of 9.3%.

The total concentrations of M6G in brain tissue were determined by homogenizing the probe-bearing hemisphere of the brain with a 5 fold larger volume of 0.1 M perchloric acid. The homogenate was centrifuged (1800 × g) for 20 min at 4°C and a volume of 400 μl of the supernatant was extracted in the same way as the plasma samples described above. Quantification of M6G concentrations was achieved using the same chromatographic system as for plasma samples. The standard curves were linear up to 3.7 nmol g-brain−1 (1.7 μg g brain−1) and the limit of quantification was 75 pmol g brain−1 (34 ng g brain−1) with a within-day coefficient of variation (CV) of 9.5%.

Pharmacokinetic analysis

The terminal half-life (t1/2) of M6G in arterial blood, venous blood and brain ECF was estimated using log-linear regression of the terminal phase of the concentration-time curve. The extent of equilibration of M6G across the BBB was expressed as the unbound steady-state concentration ratio between brain ECF and venous blood (Cu,ss,br/Cu,ss,bl).

Pharmacokinetic-pharmacodynamic modelling

Two PK-PD models, in which either the arterial (Model 1) or brain ECF (Model 2) concentrations of M6G were related to the antinociceptive effect, are presented in Figure 1. The combined data from all rats were fitted simultaneously. The model building process was performed in two steps and different models were tested.

Figure 1.

Figure 1

Open in a new tab

The pharmacokinetic-pharmacodynamic models discussed. (A) Model 1 in which the arterial blood concentration is used as the driving force for the nociceptive response of M6G. (B) Model 2 in which the brain ECF concentration is the driving force. BBB=blood-brain barrier.

The arterial concentrations of unbound M6G were obtained after correction for a protein binding of 17% (Bickel et al., 1996). A mammilary three-compartment model, expressed in terms of clearance and volume, best described the unbound arterial concentration time profiles. The individual estimates of the parameters defined by the post-hoc Bayesian analysis, obtained from this step were used as a forcing function during the characterization of the concentration-effect relationship for M6G (Model 1, Figure 1).

The individual parameter estimates from the arterial concentration time profiles from Model 1 were also used as a forcing function to fit the brain ECF concentrations of M6G (Figure 1, Model 2), in order to predict the BBB transport parameters and to quantify the contribution of transport processes to the effect delay. A two-compartment model was necessary to characterize the brain ECF concentrations of M6G well. The effect of mass transfer of drug from the brain on the mass change of drug in the arterial compartment was ignored. The distribution of M6G in the brain ECF is given by the following differential equation:

graphic file with name 134-0704406e2.jpg

where Cu,art is the arterial plasma concentration of unbound M6G, Cu,br1 and Cu,br2 are the unbound M6G concentrations in the respective brain compartments, CLin and CLout are the influx and efflux clearances into and out of the brain, respectively, Qbr is the intercompartmental clearance connecting brain compartments 1 and 2, respectively and Vu,br1 is the volume of distribution in brain compartment 1. The apparent volume of distribution (Vu,app) in the brain ECF, required for the characterization of the kinetic model in terms of volume and clearance, was calculated by (Welty et al., 1993):

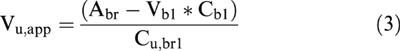graphic file with name 134-0704406e3.jpg

where Abr is the total amount of M6G per g-brain, Vbl and Cbl are the volume of blood in 1 g of brain and the concentration of M6G in arterial blood, respectively, and Cu,br1 is the concentration of unbound M6G in brain ECF at steady-state. The volume of distribution of unbound M6G in brain compartment 2 (Vu,br2) is equal to (Vu,app – Vu,br1). The blood-to-plasma ratio of M6G at a haematocrit of 44% is 0.54 (Skopp et al., 1998), and Vbl was taken to be 15 μl g brain−1 in the calculation of Vu,app (Bickel et al., 1996). It is assumed that haematocrit was the same for days 1 and 2. In the regression analysis, Vu,app was fixed at the value that was estimated from Equation 3.

Correlation of the antinociceptive effect of M6G with arterial blood concentrations and brain ECF concentrations was tested using both the link model (Sheiner et al., 1979) and the indirect response model (Dayneka et al., 1993). However, since the link model appeared to perform better, results from this model are presented below. The time course of the effect site concentration is described by the rate constant keo out of the effect compartment (Sheiner et al., 1979). Several pharmacodynamic models (i.e., linear, Emax and sigmoid Emax) were tested. The sigmoid Emax model best described the relationship between the concentration of unbound M6G in both tissues and the antinociceptive effect as depicted in Models 1 and 2 (Figure 1), according to:

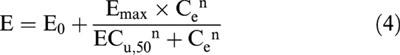graphic file with name 134-0704406e4.jpg

where E is the antinociceptive effect at the effect site with concentration Ce, E0 is the baseline effect when no M6G is present, ECu,50 is the plasma steady-state concentration of unbound M6G that corresponds to 50% of the maximal effect (Emax) and n is a constant, expressing the sigmoidicity of the curve.

Both unbound concentration and effect data were analysed using nonlinear mixed effect modelling with the program NONMEM (version VI) incorporating the first order (FO) method and the first order conditional estimation (FOCE) method (Beal & Sheiner, 1992). Mean population parameters were assessed, as well as interindividual and residual variability. Individual parameter values were obtained using post-hoc Bayesian analysis. An exponential variance model was used to describe the interanimal variability for all parameters and the residual errors were characterized using a proportional error model. Graphical analysis of the residuals and predictions, implemented in Xpose 2.0 (Jonsson & Karlsson, 1999) and comparison of the objective function (−2*log likelihood) provided by NONMEM, were used to discriminate between the different models. The difference between the objective function values for two hierarchical models is approximately chi-square distributed, where the degree of freedom is based on the difference between the number of parameters, and this can therefore be used for model selection purposes. However, for studies like this, which have rich data, the change in objective function value should exceed the critical value of 3.84, as set for model discrimination in sparse data analysis.

Statistics

Any significant differences in t1/2 and steady-state concentration ratio between days 1 and 2 were evaluated by paired t-test. Comparisons between different tissue t1/2, keo, n and EC50 values from Models 1 and 2 were made by ANOVA, followed by a post-hoc paired t-test. A probability value less than 0.05 was considered to be significant. All pharmacokinetic data are reported as mean±standard deviation (s.d.). The precision of the population parameter estimates from the NONMEM output is expressed as the relative standard error (R.S.E.).

Results

In vivo recovery of M6G in the blood probes was comparable between day 1 and day 2 (49.5±15.4% and 43.1±7.0%, respectively), and in the brain probes (8.5±3.9% and 9.2±3.4%, respectively).

As expected by the exponential infusion regimen, steady-state concentrations in blood were achieved rapidly, i.e. the total plasma concentration of 2888±397 (ng ml−1) at the first sample (30 min), was very close to the expected 3000 ng ml−1. While the attainment of the M6G steady-state concentration in brain ECF was slower (Figure 2). The steady-state concentration ratios of unbound M6G in brain ECF to that in blood were 0.27 and 0.20 for days 1 and 2 (P=0.099), respectively, with an average ratio of 0.22 (Table 1). The terminal half-life in brain ECF was significantly longer than that in blood within the experimental period, with an average value of 58 min in brain, and 23 or 26 min in arterial blood and venous microdialysis samples, respectively (Table 1).

Figure 2.

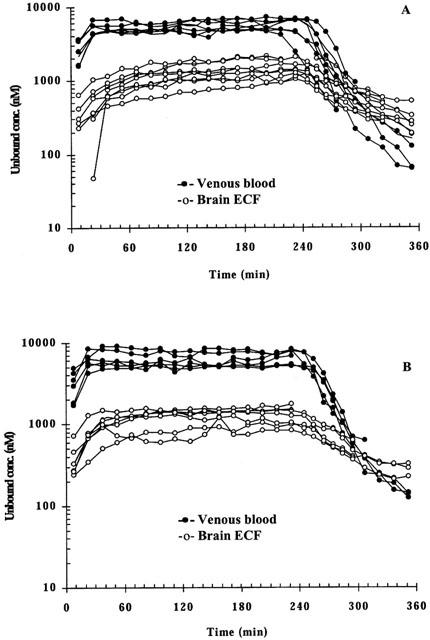
Figure 2

Open in a new tab

Individual unbound M6G concentration-time profiles following an exponential intravenous infusion of M6G over 4 h on day 1 (A) and day 2 (B).

Table 1.

Pharmacokinetic parameter estimates obtained after an exponential infusion of M6G for 4 h in rat (mean ±s.d.)

graphic file with name 134-0704406t1.jpg

Open in a new tab

A three-compartment model provided the best fit for the arterial concentrations of unbound M6G; population values of CLu and Vu,ss were 11.1 (5.2%) ml min−1 and 167 ml, respectively in rats weighing on average 305±16 g. Systemic pharmacokinetic parameters were not day-dependent.

For the BBB distribution model analysis, a two-compartment model was required to describe the disposition of unbound M6G in brain ECF and the population estimates of CLin and CLout were 0.35 (28%) and 2.17 (40%) μl min−1 g brain−1. The intercompartmental clearance Qbr of 1.11 μl min−1 g brain−1 was lower than the efflux clearance, and indicated that redistribution within the brain was the rate limiting step for the elimination of M6G out of the brain. The volume of distribution of unbound M6G in brain ECF was 0.20±0.02 ml g brain−1, with estimated unbound volumes of distribution of 0.07 and 0.13 ml g brain−1 for brain compartments 1 and 2, respectively. The population estimated ratio of unbound CLin/CLout was 0.16, which was slightly below the unbound steady-state concentration ratio (Cu,ss,br/Cu,ss,bl) of 0.22.

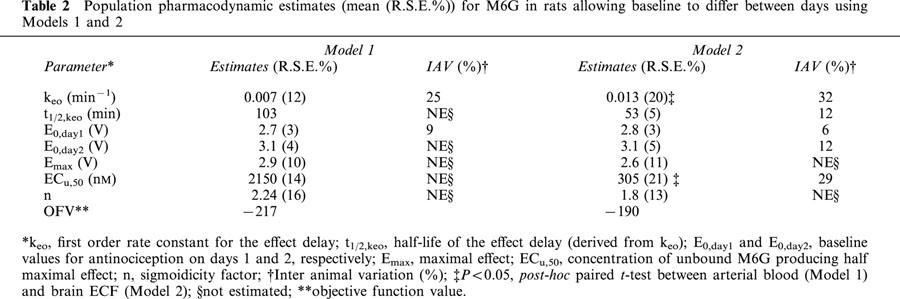
The baseline nociceptive response remained stable during the blank period, the in vivo calibration period and the wash-out period for both days. The peak antinociceptive effect increased from a baseline value of 2.7 to 5.3 V for day 1. On day 2, the averaged baseline nociception was 3.1 V and the peak effect was the same as day 1 (Figure 3). The observed hysteresis in the brain ECF concentration-antinociceptive effect relationship was smaller than that of the blood concentration-antinociceptive effect (Figure 3). In the PD model analysis, a link compartment and different baseline values (E0) for days 1 and 2 were necessary to characterize the concentration-effect relationship well. For both Models 1 and 2, the sigmoid Emax model best described the antinociceptive effect of M6G (Figure 4), yielding an effect delay half-life of 103 min (12%) or 53 min (20%) related to arterial or brain ECF concentrations of M6G, respectively (Table 2). Similar values for E0 and Emax were obtained with respect to either blood or brain ECF concentrations of M6G. As expected, the brain concentration-effect relationship of M6G resulted in a significantly lower ECu,50 value compared to the blood concentration-effect relationship, in line with the 0.22 brain to blood ratio (Table 2, P<0.05).

Figure 3.

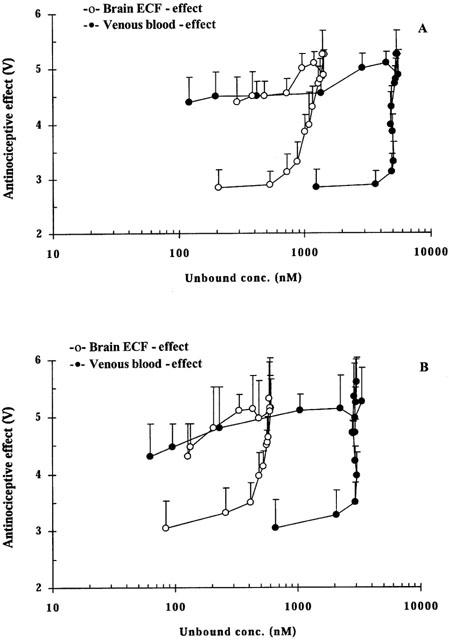
Figure 3

Open in a new tab

Averaged concentration-antinociceptive effect relationship of M6G in and brain ECF upon administration of an exponential intravenous infusion of M6G over 4 h on day 1 (A) and day 2 (B).

Figure 4.

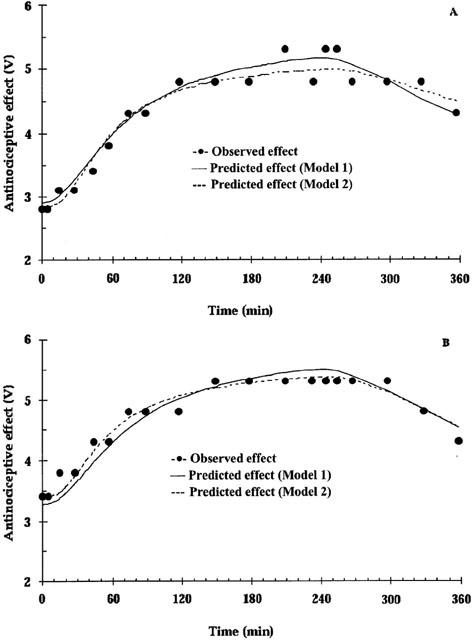
Figure 4

Open in a new tab

The antinociceptive effect over time related to M6G concentrations following an exponential intravenous infusion of M6G over 4 h on day 1 (A) and day 2 (B) of a representative rat. During the modelling process, E0 is allowed to vary between experimental days.

Table 2.

Population pharmacodynamic estimates (mean (R.S.E.%)) for M6G in rats allowing baseline to differ between days using Models 1 and 2

graphic file with name 134-0704406t2.jpg

Open in a new tab

Only moderate changes from baseline values for pH, O2 saturation and pCO2 were observed. However, pO2 was decreased at 180 min only compared to baseline, from 12.4 to 8.5 kPa on day 1 (P<0.05), and from 11.5 to 7.9 kPa on day 2 (P<0.05).

Discussion

The rate and extent of drug transport across the BBB will have a large impact on the degree, onset and duration of any central effect. The rate is highly dependent on the physicochemical properties of the drug itself, while the extent of drug transport is also influenced by the involvement of active transport mechanisms located at the BBB.

In the present study, the unbound concentration ratio of M6G in brain ECF to blood of 0.22 is an indicator of the presence of active efflux mechanisms at the BBB. This ratio is similar to that of morphine, being 0.28 – 0.22 after a 10 min i.v. infusion (Bouw et al., 2000), indicating that morphine and M6G unexpectedly have similar extent of BBB transport, although they differ in lipophilicity with log P values of 0.9 for morphine and −0.76 for M6G (Avdeef, 1996). Stain-Texier et al. (1999) also found similar AUC ratios of unbound morphine and M6G of 0.51 and 0.56, respectively. Therefore, the difference in in vivo potency between morphine and M6G after i.t./i.c.v. vs systemic administration cannot be caused by a difference in the extent of BBB transport.

Regarding the rate of BBB transport, the population value of the influx clearance of 0.35 μl min−1 g brain−1 for M6G was higher than the permeability surface area product (PS) of 0.11 – 0.14 μl min−1 g brain−1 (Bickel et al., 1996; Wu et al., 1997). The PS values were determined by the intravenous injection technique, which is based on the assumption that the PS value is not affected by the efflux during the 60 min measurement period. If bidirectional transport does exist, the PS value will be underestimated. The efflux clearance of M6G was larger than the influx clearance. The size of the efflux clearance of 2.17 μl min−1 g brain−1 from our MD experiment indicates that efflux clearance cannot be neglected in the determination of the BBB permeability of M6G. For morphine the corresponding CLin and CLout were 14 and 40 μl min−1 g brain−1 (Bouw et al., 2000) and for morphine-3-glucuronide (M3G) 0.11 and 1.15 μl min−1 g brain−1 (Xie et al., 2000), respectively. These values indicate that M6G is more slowly transported into the brain compared to morphine. Thus, the higher potency of M6G after i.t./i.c.v. administration might be partly explained by a slower BBB penetration of M6G than of morphine, as i.p. or s.c. administration will not give as much time for BBB penetration of M6G as for morphine. In this context it is also important to consider the blood pharmacokinetics of the drug when comparing the in vivo potency between M6G and morphine. If the same dose is administered (mg kg−1), the concentrations of M6G in blood will exceed those of morphine due to a lower clearance and volume of distribution (Aasmundstad et al., 1995). This will result in higher brain ECF concentrations for M6G compared to morphine and therefore a higher analgesic activity can be expected for M6G than morphine on a dose comparison basis.

The unbound volume of distribution in brain of M6G (0.20 ml g brain−1) was comparable to that of M3G (0.23 ml g brain−1) (Xie et al., 2000). Both these values are close to the volume fraction of 0.21 for ions (cation tetramethylammonium and anion α-napthalenesulphonate) (Nicholson & Phillips, 1981), suggesting that binding or accumulation in brain tissue is minimal and M6G is mainly distributed throughout the extracellular space. The volume of distribution of morphine in brain was 1.55 ml g brain−1 (Xie et al., 1999). Only small amounts of hydrophilic substances generally penetrate into the cells compared to what is present extracellularly, resulting in lower total brain concentrations and therefore a smaller total ratio than unbound ratio. This has been described for M6G by Stain-Texier et al. (1999), where the AUC ratio of whole brain tissue to plasma was 0.05, while the AUC ratio of brain ECF to plasma was 0.56. As a two-compartment model was necessary to elucidate the brain disposition of M6G in brain tissue, it is possible that intracellular penetration to some extent may occur, or that the diffusion of M6G in brain ECF is slow.

M6G displayed a significantly longer half-life in brain ECF than in blood, 58 vs 22 min, respectively. Model 2 showed that the rate constant from brain compartment 2 to 1 was the smallest in magnitude compared to kout, indicating that redistribution within the brain is the rate-limiting step for M6G elimination from the brain. The brain half-life found in this study was shorter than the half-life of 82 min reported by Aasmunstad et al. (1995) also with microdialysis. An even longer half-life of 106 min was found in mice brain based on total M6G concentrations after i.c.v. injection (Frances et al., 1992). Thus, once in brain ECF, M6G does not easily disappear. This might also be a factor of importance for the higher potency of M6G than morphine after i.t./i.c.v. administration.

The effect delay half-life of 103 min with respect to unbound arterial concentrations obtained in this study was similar to an earlier value of 84 min reported by our group, after administration of M6G as either i.v. bolus, i.v. infusion or stepwise infusion (Gårdmark & Hammarlund-Udenaes, 1998). However, these reported values are in conflict with the only other reported effect delay for M6G of 10 min (Hasselström et al., 1996). The difference may be the result of methodological differences, since M6G was given as an i.p. dose of 0.1 or 0.2 mg kg−1 and antinociception was determined using the hot plate test (Hasselström et al., 1996). Other studies have also revealed the very long duration of M6G after s.c. administration of M6G, although not having characterized the effect delay half-life (Frances et al., 1992; Stain-Texier et al., 1999; van crugten et al., 1997).

The observed effect delay half-life is the sum of the delays due to the BBB transport, the distribution within the brain to the site of action and the pharmacodynamic response at the receptor level. The sequential PK-PD model developed here allowed us to differentiate between and quantify some of these. The keo value for Model 1 includes the distribution of M6G from arterial blood to brain ECF with a resulting t1/2,ke0 of 103 min. Model 2 explains the delay between the measured brain ECF concentration of M6G and the antinociceptive effect with a t1/2,ke0 of 53 min. The difference between Models 1 and 2 indicates that the transport across the BBB contributes with 50% to the total effect delay of M6G. The remaining effect delay of 53 min might be explained by distribution within the brain tissue, or by a pharmacodynamic delay at the receptor level, or that it takes time to develop an integrated response at different levels in the CNS. To test the hypothesis of distribution resulting in a delay, we also modelled the effect directly connected to the peripheral brain compartment. This resulted in a remaining half-life for the effect delay of 16 min, with a very large relative standard error. Thus, it cannot be concluded that the delay is either caused by distribution or pharmacodynamic events, rather by a contribution of both. The corresponding half-life for the effect delay from brain ECF for morphine was 5 min, and from blood 32 min (Bouw et al., 2000). In both studies, we have measured the unbound concentrations in striatum, indicating that the difference in effect delay half-life can also be the result of antinociceptive effects mediated through different subtypes of the μ-receptor localized at different levels in the CNS (Pasternak & Wood, 1986; Paul et al., 1989b).

In summary, M6G was transported at a slower rate but to the same extent across the BBB compared to morphine. The unbound brain to blood steady-state concentration ratio of 0.22 is a proof of the involvement of active efflux mechanisms at the BBB acting on M6G. It was shown that BBB transport could explain half the delay in effect of M6G of 103 min. The remaining delay is likely caused by a combination of drug distribution within the brain tissue and pharmacodynamic events.

Acknowledgments

The authors wish to thank Mrs Britt Jansson for her skilful assistance with the chemical analysis. This study was supported by the Swedish Medical Research Council (Project no. 11558) and by the Goljes Memory Fund.

Abbreviations

AUC

area under the concentration-time curve

BBB

blood-brain barrier

Brain ECF

brain extracellular fluid

CNS

central nervous system

M6G

morphine-6-glucuronide

PK

pharmacokinetics

PD

pharmacodynamics

References

  1. AASMUNDSTAD T.A., MORLAND J., PAULSEN R.E. Distribution of morphine 6-glucuronide and morphine across the blood-brain barrier in awake, freely moving rats investigated by in vivo microdialysis sampling. J. Pharmacol. Exp. Ther. 1995;275:435–441. [PubMed] [Google Scholar]
  2. ABBOTT F.V., PALMOUR R.M. Morphine-6-glucuronide: analgesic effects and receptor binding profile in rats. Life Sci. 1988;43:1685–1695. doi: 10.1016/0024-3205(88)90479-1. [DOI] [PubMed] [Google Scholar]
  3. AVDEEF A. Octanol-, chloroform-, and propylene glycol dipelargonat-water partitioning of morphine-6-glucuronide and other related opiates. J. Med. Chem. 1996;39:4377–4381. doi: 10.1021/jm960073m. [DOI] [PubMed] [Google Scholar]
  4. BEAL S.L., SHEINER L.S. University of California, San Francisco, CA; 1992. NONMEM user's guide–part VII. NONMEM Project Group. [Google Scholar]
  5. BICKEL U., SCHUMACHER O.P., KANG Y.S., VOIGT K. Poor permeability of morphine 3-glucuronide and morphine 6-glucuronide through the blood-brain barrier in the rat. J. Pharmacol. Exp. Ther. 1996;278:107–113. [PubMed] [Google Scholar]
  6. BOUW M.R., GÅRDMARK M., HAMMARLUND-UDENAES M. Pharmacokinetic-pharmacodynamic modelling of morphine transport across the blood-brain barrier as a cause of the antinociceptive effect delay in rats–a microdialysis study. Pharm. Res. 2000;17:1220–1227. doi: 10.1023/a:1026414713509. [DOI] [PubMed] [Google Scholar]
  7. BOUW M.R., HAMMARLUND-UDENAES M. Methodological aspects of the use of a calibrator in in vivo microdialysis - further development of the retrodialysis method. Pharm. Res. 1998;15:1673–1679. doi: 10.1023/a:1011992125204. [DOI] [PubMed] [Google Scholar]
  8. CARROLL M.N., LIM R.K.S. Observation on the neuropharmacology of morphine and morphinelike analgesia. Arch. Int. Pharmacodyn. Ther. 1960;125:383–403. [PubMed] [Google Scholar]
  9. CHRISTENSEN C.B., JORGENSEN L.N. Morphine-6-glucuronide has high affinity for the opioid receptor. Pharmacol. Toxicol. 1987;60:75–76. doi: 10.1111/j.1600-0773.1987.tb01724.x. [DOI] [PubMed] [Google Scholar]
  10. DAYNEKA N.L., GARG V., JUSKO W.J. Comparison of four basic models of indirect pharmacodynamic responses. J. Pharmacokinet. Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. EKBLOM M., HAMMARLUND-UDENAES M., PAALZOW L.K. Modeling of tolerance development and rebound effect during different intravenous administrations of morphine to rats. J. Pharmacol. Exp. Ther. 1993;266:244–252. [PubMed] [Google Scholar]
  12. FRANCES B., GOUT R., MONSARRAT B., CROS J., ZAJAC J.M. Further evidence that morphine-6 beta-glucuronide is a more potent opioid agonist than morphine. J. Pharmacol. Exp. Ther. 1992;262:25–31. [PubMed] [Google Scholar]
  13. GÅRDMARK M., EKBLOM M., BOUW R., HAMMARLUND-UDENAES M. Quantification of effect delay and acute tolerance development to morphine in the rat. J. Pharmacol. Exp. Ther. 1993;267:1061–1067. [PubMed] [Google Scholar]
  14. GÅRDMARK M., HAMMARLUND-UDENAES M. Delayed antinociceptive effect following morphine-6-glucuronide administration in the rat-pharmacokinetic/pharmacodynamic modelling. Pain. 1998;74:287–296. doi: 10.1016/s0304-3959(97)00180-2. [DOI] [PubMed] [Google Scholar]
  15. HASSELSTRÖM J., SVENSSON J.O., SAWE J., WIESENFELD-HALLIN Z., YUE Q.Y., XU X.J. Disposition and analgesic effects of systemic morphine, morphine-6-glucuronide and normorphine in rat. Pharmacol. Toxicol. 1996;79:40–46. doi: 10.1111/j.1600-0773.1996.tb00239.x. [DOI] [PubMed] [Google Scholar]
  16. JOEL S.P., OSBORNE R.J., SLEVIN M.L. An improved method for the simultaneous determination of morphine and its principal glucuronide metabolites. J. Chromatog. 1988;430:394–399. doi: 10.1016/s0378-4347(00)83176-x. [DOI] [PubMed] [Google Scholar]
  17. JONSSON E.N., KARLSSON M.O. Xpose - an S-PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput. Methods Programs Biomed. 1999;58:51–64. doi: 10.1016/s0169-2607(98)00067-4. [DOI] [PubMed] [Google Scholar]
  18. MURPHEY L.J., OLSEN G.D. Diffusion of morphine-6-beta-D-glucuronide into the neonatal guinea pig brain during drug-induced respiratory depression. J. Pharmacol. Exp. Ther. 1994;271:118–124. [PubMed] [Google Scholar]
  19. NICHOLSON C., PHILLIPS J.M. Ion diffusion modified by tortuosity and volume fraction in the extracellular microenvironment of the rat cerebellum. J. Physiol. 1981;321:225–257. doi: 10.1113/jphysiol.1981.sp013981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. PAALZOW G., PAALZOW L. The effects of caffeine and theophylline on nociceptive stimulation in the rat. Acta Pharmacol. Toxicol. 1973;32:22–32. doi: 10.1111/j.1600-0773.1973.tb01448.x. [DOI] [PubMed] [Google Scholar]
  21. PAALZOW L.K.Measurement and modeling analgesic drug effect The in vivo study of drug action - Principles and applications of kinetic-dynamic modelling 1992Elsevier Science Publishers B.V.: Amsterdam; 133–153.ed. van Boxtel, C.J., Holford, N.H.G. & Danhof, M [Google Scholar]
  22. PASTERNAK G.W., BODNAR R.J., CLARK J.A., INTURRISI C.E. Morphine-6-glucuronide, a potent mu agonist. Life Sci. 1987;41:2845–2849. doi: 10.1016/0024-3205(87)90431-0. [DOI] [PubMed] [Google Scholar]
  23. PASTERNAK G.W., WOOD P.J. Multiple mu opiate receptors. Life Sci. 1986;38:1889–1898. doi: 10.1016/0024-3205(86)90217-1. [DOI] [PubMed] [Google Scholar]
  24. PAUL D., STANDIFER K.M., INTURRISI C.E., PASTERNAK G.W. Pharmacological characterization of morphine-6 beta-glucuronide, a very potent morphine metabolite. J. Pharmacol. Exp. Ther. 1989a;251:477–483. [PubMed] [Google Scholar]
  25. PAUL D., BODNAR R.J., GISTRAK M.A., PASTERNAK G.W. Different mu receptor subtypes mediate spinal and supraspinal analgesia in mice. Eur. J. Pharmacol. 1989b;168:307–314. doi: 10.1016/0014-2999(89)90792-9. [DOI] [PubMed] [Google Scholar]
  26. SHAFER S.L., SIEGEL L.C., COOKE J.E., SCOTT J.C. Testing computer-controlled infusion pumps by simulation. Anesthesiology. 1988;68:261–266. doi: 10.1097/00000542-198802000-00013. [DOI] [PubMed] [Google Scholar]
  27. SHEINER L.B., STANSKI D.R., VOZEH S., MILLER R.D., HAM J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: Application to d-tubocurarine. Clin. Pharmacol. Ther. 1979;25:358–371. doi: 10.1002/cpt1979253358. [DOI] [PubMed] [Google Scholar]
  28. SHIMOMURA K., KAMATA O., UEKI S., IDA S., OGURI K., YOSHIMURA H., TSUKAMOTO H. Analgesic effect of morphine glucuronides. Tohoku J. Exp. Med. 1971;105:45–52. doi: 10.1620/tjem.105.45. [DOI] [PubMed] [Google Scholar]
  29. SKOPP G., POTSCH L., GANSSMANN B., ADERJAN R., MATTERN R. A preliminary study on the distribution of morphine and its glucuronides in the subcompartments of blood. J. Anal. Toxicol. 1998;22:261–264. doi: 10.1093/jat/22.4.261. [DOI] [PubMed] [Google Scholar]
  30. STAIN-TEXIER F., BOSCHI G., SANDOUK P., SCHERRMANN J.M. Elevated concentrations of morphine-6-beta-D-glucuronide in brain extracellular fluid despite low blood-brain barrier permeability. Br. J. Pharmacol. 1999;128:917–924. doi: 10.1038/sj.bjp.0702873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. VAN CRUGTEN J.T., SOMOGYI A.A., NATION R.L., REYNOLDS G. Concentration-effect relationships of morphine and morphine-6 beta- glucuronide in the rat. Clin. Exp. Pharmacol. Physiol. 1997;24:359–364. doi: 10.1111/j.1440-1681.1997.tb01202.x. [DOI] [PubMed] [Google Scholar]
  32. WELTY D.F., SCHIELKE G.P., VARTANIAN M.G., TAYLOR C.P. Gabapentin anticonvulsant action in rats: disequilibrium with peak drug concentrations in plasma and brain microdialysate. Epilepsy Res. 1993;16:175–181. doi: 10.1016/0920-1211(93)90078-l. [DOI] [PubMed] [Google Scholar]
  33. WU D., KANG Y.S., BICKEL U., PARDRIDGE W.M. Blood-brain barrier permeability to morphine-6-glucuronide is markedly reduced compared with morphine. Drug Metab. Dispos. 1997;25:768–771. [PubMed] [Google Scholar]
  34. XIE R., BOUW M.R., HAMMARLUND-UDENAES M. Modelling of the blood-brain barrier transport of morphine-3-glucuronide studied using microdialysis in the rat: involvement of probenecid-sensitive transport. Br. J. Pharmacol. 2000;131:1784–1792. doi: 10.1038/sj.bjp.0703759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. XIE R., HAMMARLUND-UDENAES M., DE BOER A.G., DE LANGE E.C.M. The role of P-glycoprotein in blood-brain barrier transport of morphine: transcortical microdialysis studies in mdr1a (−/−) and mdr1a (+/+) mice. Br. J. Pharmacol. 1999;128:563–568. doi: 10.1038/sj.bjp.0702804. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from British Journal of Pharmacology are provided here courtesy of The British Pharmacological Society

RESOURCES