An improved model for the binding of lidocaine and structurally related local anaesthetics to fast-inactivated voltage-operated sodium channels, showing evidence of cooperativity

Abstract

1. The interaction of lidocaine-like local anaesthetics with voltage-operated sodium channels is traditionally assumed to be characterized by tighter binding of the drugs to depolarized channels. As inactivated and drug-bound channels are both unavailable on depolarization, an indirect approach is required to yield estimates for the dissociation constants from channels in inactivated states. The established model, originally described by Bean et al., describes the difference in affinity between resting and inactivated states in terms of the concentration dependence of the voltage shift in the availability curve. We have tested the hypothesis that this model, which assumes a simple Langmuir relationship, could be improved by introducing a Hill-type exponent, which would take into account potential sources of cooperativity.

2. Steady-state block by lidocaine was studied in heterologously (HEK 293) expressed human skeletal muscle sodium channels and compared with experimental data previously obtained for 2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol. Cells were clamped to membrane potentials from −150 to −5 mV, and a subsequent test pulse was used to assess the number of channels available to open.

3. All compounds shifted the voltage dependence of channel availability in the direction of negative prepulse potentials. Prediction of the concentration dependence of the voltage shift in the availability curve was improved by the modified model, as shown by a marked reduction in the residual sum of squares.

4. For all compounds, the Hill-type exponent was significantly greater than one. These results could be interpreted in the light of the contemporary hypothesis that lidocaine functions as an allosteric gating effector to enhance sodium channel inactivation by strengthening the latch mechanism of inactivation, which is considered to be a particle-binding process allosterically coupled to activation. Alternatively, they could be interpreted by postulating additional binding sites for lidocaine on fast-inactivated sodium channels.

Introduction

Lidocaine-like local anaesthetics and antiarrhythmic drugs produce a voltage-dependent inhibition of voltage-gated sodium channels through preferential binding to depolarized channel conformations. Membrane depolarization before a test depolarization that elicits a sodium current increases the fraction of current that is blocked by lidocaine. Allosteric coupling, in turn, causes high-affinity drug binding to depolarized channels to stabilize these conformations relative to the conformations with low drug affinity, resulting in a shift of the steady-state availability curve in the direction of negative membrane potentials. Drug binding to inactivated channels is hardly accessible to a direct experimental approach, because inactivated channel states and all drug-bound channel states are unavailable on depolarization. A model-dependent method has therefore been used to determine the affinity of lidocaine-like local anaesthetics to inactivated channel states; the method is based on the concentration dependence of the shift in the availability curve (Bean et al., 1983). The underlying assumption is that the higher amount of channel blockade achieved with consecutive membrane depolarization is determined by the distribution of channels between resting and fast-inactivated states along the voltage axis, and by the different binding affinities of the blocking drug for the two-channel states. The model has been used to yield estimates for a change in inactivated state affinity induced by a mutant (Fan et al., 1996; Haeseler et al., 2001b), to describe the affinity of fast- vs slow-inactivated channels for lidocaine (Balser et al., 1996b), and to characterize the pharmacological properties of various sodium channel blockers (Haeseler et al., 2001a; Haeseler et al., 2002). However, as was already revealed by Bean's own data, the difference between the experimental data and the prediction made by the model is generally relatively large, as the model tends to overestimate the effect of low drug concentrations and to underestimate the effect of high drug concentrations. It was our hypothesis that the model fit to the experimental data could be improved when the assumption that the binding of local anaesthetics to depolarized channel states, as revealed by the voltage shift in the steady-state availability curve, ΔV_0.5, follows a simple Langmuir relationship, was replaced by the assumption that it follows a Hill equation in which a Hill-type exponent n is introduced as follows:

We have studied the effects of lidocaine and three phenol derivatives that closely resemble lidocaine's aromatic tail (2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol) on heterologously expressed α-subunits of human skeletal muscle (hSkM1) sodium channels. The α-subunit is the primary pore-forming subunit of voltage-operated sodium channels and functions as an ion channel when expressed alone (Catterall, 1992). The α-subunits of hSkM1 sodium channels have normal gating characteristics (with respect to experiments in native tissue) when expressed in the background of a mammalian cell line (Chahine et al., 1994). Except for the lidocaine data, the results have been published previously (Haeseler et al., 2001a; 2002). However, we have reanalysed them here, in order to investigate binding to the inactivated state of the channel.

Methods

Transfection and cell culture

The methods have been previously described in more detail (Haeseler et al., 2002). Stably transfected human embryonic kidney cell, expression system (HEK 293) cell lines expressing the α-subunit of hSkM1 sodium channels were a gift from Professor Lehmann-Horn, Ulm, Germany. The clones have been used in several investigations (Mitrovic et al., 1994; Haeseler et al., 2002). Successful channel expression was verified electrophysiologically.

Solutions

Lidocaine and 4-chlorophenol (Sigma Chemicals, Deisenhofen, Germany) were injected directly into the bath solution before the experiments; 2,6-dimethylphenol (FLUKA, Deisenhofen, Germany) and 3,5-dimethyl-4-chlorophenol (Sigma Chemicals, Deisenhofen, Germany) were prepared as 1 M stock solutions in ethanol, light protected, and stored in glass vessels at −20°C. The stock solution was dissolved directly in the bath solution immediately before experiments. Drug-containing vials were vigorously vortexed for 60 min. Solutions were applied via a glass–polytetrafluoroethylene perfusion system and a stainless-steel superfusion pipette. The bath solution contained (mM) NaCl 140, MgCl₂ 1.0, KCl 4.0, CaCl₂ 2.0, HEPES 5.0, dextrose 5.0. Patch electrodes contained (mM) CsCl₂ 130, MgCl₂ 2.0, EGTA 5.0, HEPES 10. All solutions were adjusted to 290 mosm l⁻¹ by the addition of mannitol and to pH 7.4 by the addition of Cs(OH)₂. The effects of the diluent ethanol corresponding to higher drug concentrations were tested in a previous study up to a maximum ethanol concentration of 17.4 mM, corresponding to a drug concentration of 1000 μM. At this concentration, the block caused by ethanol is less than 20% (Haeseler et al., 2001c).

Electrophysiology

Standard whole-cell voltage-clamp experiments (Hamill et al., 1981) were performed at 20°C. Each experiment consisted of test recordings with the drug present at only one concentration, and of drug-free control recordings before and after the test. Each cell was exposed to one test concentration only. At least three experiments were performed at each concentration.

For data acquisition and further analysis, we used the EPC9 digitally controlled amplifier in combination with Pulse and Pulse Fit software (HEKA Electronics, Lambrecht, Germany). The EPC9 provides automatic subtraction of capacitance and leakage currents by means of a prepulse protocol. The data were filtered at 10 kHz and digitized at 20 μs per point. The input resistance of the patch pipettes was 2.0–3.5 MΩ and the capacitances of the cells were 9–15 pF; the residual series resistance (after 50% compensation) was 1.2–2.5 MΩ. Experiments in which there was a rise in series resistance were rejected. To minimize time-dependent shifts in the voltage dependence of steady-state inactivation (Wang et al., 1996), all test experiments were performed within 5 min of patch rupture. Under these experimental conditions, time-dependent hyperpolarizing shifts in control conditions were less than −2 mV (Haeseler et al., 2000).

In order to determine the affinity of resting channels, concentration–response plots for the first pulse block were obtained at hyperpolarized membrane potentials (–150 mV). The residual sodium current (I/I_max) in the presence of drug (with respect to the current amplitude in the control solution) was plotted against the applied concentration of the drug [C]. The averaged data were fitted using the Hill equation, equation (1), yielding the concentration for half-maximum channel blockade in the resting state (ECR₅₀) and the Hill coefficient n_H.

As the Hill coefficients at −150 mV were equal to or very close to one for all compounds, the (ECR₅₀) at −150 mV holding potential represented the dissociation constant for the resting state K_dR.

The voltage dependence of the block and the affinity for depolarized channel states was further assessed by applying a double-pulse protocol. After brief depolarizations, sodium channels enter a fast-inactivated state, from which they cannot readily reopen. Currents elicited by test pulses (I_test), starting from varying prepulse potentials (from −150 to −5 mV), normalized to the current elicited at the most hyperpolarized prepotential (–150 mV), represent the relative fraction of channels that have not been inactivated during the 50–100 ms inactivating prepulse. Boltzmann fits to the resulting current–voltage plots yield the membrane potential at half-maximum channel availability (V_0.5) and the slope factor k, reflecting the ‘voltage sensitivity' of inactivation gating (see equation.

In control conditions, the parameters of the Boltzmann fits reflect the voltage dependence of the distribution between resting and fast-inactivated channels. In the presence of drug, the steady-state availability curve reflects drug association primarily with rested and fast-inactivated channels. No relevant degree of slow inactivation is expected with prepulses shorter than 100 ms (Vilin et al., 1999), and the open state is only transiently occupied and does not influence steady-state block after long prepulses. The principal assumptions underlying the model of Bean et al. (1983) have been discussed previously (Bean et al., 1983; Balser et al., 1996b), but are presented here again in order to explain our modification of the model. According to the modulated receptor model, the local anaesthetic receptor of the channel has at least three major states, which differ in their binding affinities (Hille, 1992).

K_dR and K_dI are the affinities of the local anaesthetic (L) for the resting (R) and fast-inactivated (I) states, respectively. [L] denotes the concentration of the local anaesthetic. In all other cases, square brackets indicate relative occupancy.

The expression for occupancy of R as a function of voltage follows the Boltzmann equation (equation, after simplification (I/I_max is the fraction of [R] available to open relative to the total number of channels [I_F]+[R]).

where V is the membrane potential, V_0.5 is the membrane potential when [I_F]=[R] in control conditions, and k is the Boltzmann slope.

The total occupancy must be unity; hence,

By substituting equations (3.1) and (3.2) into equation (5), we obtain

R is maximal when I_F=0

Occupancy of R is half-maximal when

Substituting equation (8) into equation (6) and solving for I_F gives the following simplified expression when [R] is half-maximal:

Substituting equations (8) and (9) for the occupancy of [I_F] and [R] when [R]=R_max/2 into equation (4) gives

where in this case, V is actually the potential of half-maximal channel availability, V_0.5 (test), in the presence of the local anaesthetic, and V_0.5 is the potential of half-maximal channel availability in the control experiment, V_0.5 (control). Logarithmic transformation and solving for V gives

In more general terms, the voltage shift ΔV_0.5 in the presence of a drug would depend upon the drug concentration [C] according to:

We have tested the hypothesis that the fit of the model to the experimental data can be improved when the assumption made in equation (3.2), namely that drug binding to inactivated states follows a simple Langmuir relationship, is changed to a Hill equation in which an exponent n is introduced; in order to take into account potential cooperativity, the parameter K_dI is labelled ECI₅₀, K_dR is labelled ECR₅₀ in this term

Statistical analysis

The slope factor k derived from summarized control experiments and the respective values of K_dR were inserted as constant factors into the equation. Nonlinear least-squares regression was used to fit both equation (11) and its modification to the original data. The results derived from the analyses have been expressed as means±s.e.m. The mean residual sum of squares [,∑Δ²/(n-1) or ∑Δ²/(n-2)], where Δ² is the residual square deviation and n is the number of observations, reflecting n−1 degrees of freedom in the case of the established model or n−2 degrees of freedom in the modified model, was used to compare the quality of the fit of both equations. Significance of the difference of the Hill-type exponent n from one was calculated on the basis of the parameter estimation of n and its asymptotic standard error using normal approximation. In view of the fact that an improvement in the original fit to Bean's data (Bean et al., 1983) as well as to our data for 2,6-dimethyl-phenol, 3,5-dimethyl-4-chloral-phenol, and 4-chloral-phenol (Figure 3, left-hand side) could only have been achieved by increasing the steepness of the slope, it was predictable that the respective value of n could only be greater than one. Thus, we considered the calculation of one-sided P-values and one-sided statistical testing to be justified. The null hypothesis that the Hill-type exponent n was not significantly greater than one was rejected at P<0.05. The small differences between the K_dI values for 3,5-dimethyl-4-chlorophenol and 4-chlorophenol that we found in this study and the respective values published previously (Haeseler et al., 2001a) are due to the difference in analysis.

Figure 3.

Concentration–response plots previously obtained for 2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol. Each symbol represents the mean value derived from at least three different experiments; error bars are standard deviations. The solid lines show the fits of equation (11) (left) or its modification (right) with the indicated parameters. The slope factor k of 7.4 and the respective values of K_dR or ECR₅₀, respectively, were entered into the model as constant factors. The Hill coefficients for binding to resting channels were equal to or very close to one for all compounds. The modification improved the fit for (from top to bottom) 2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol, yielding values for the Hill-type exponent n for binding to fast-inactivated channels that were significantly greater than one in each case.

Results

In 20 cells, we investigated the effect of lidocaine on the one hand with respect to block of resting channels, and on the other with respect to inactivated state binding using the original model of Bean et al. (1983) or our modification of it. In addition, we analysed our previously published data from 42 cells obtained with 2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol.

The summarized control data show that half of the channels were unavailable at −60.0±4.0 mV because of fast inactivation. The slope factor k was 7.4±1.0 and this was inserted as a constant factor into the models.

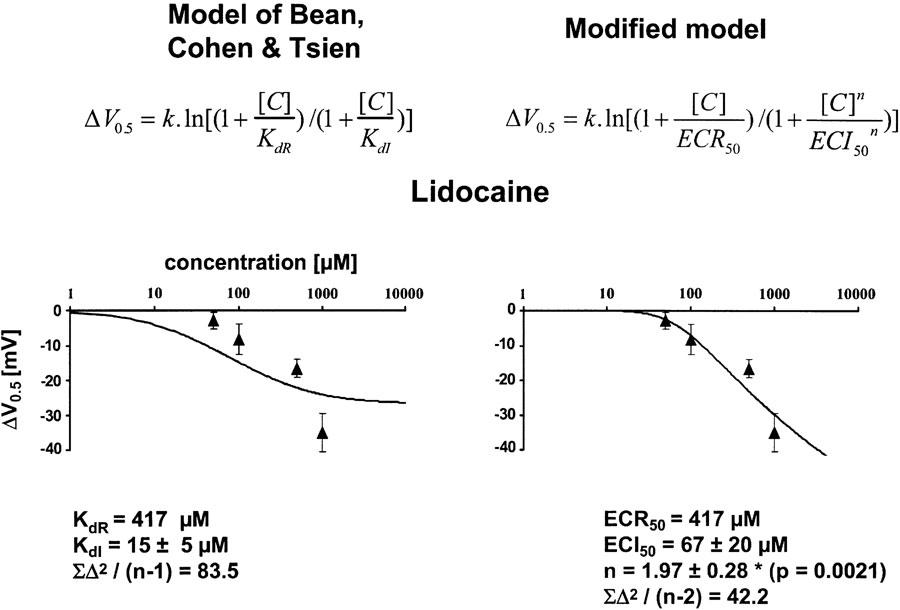
Block of resting channels by lidocaine required a half-maximum blocking concentration ECR₅₀ of 417 μM, derived from a fit of the Hill equation (equation) to the concentration–response plots for block at hyperpolarized holding potentials (−150 mV). The Hill coefficient n_H for the binding of lidocaine to channels in the resting state was 1.05.

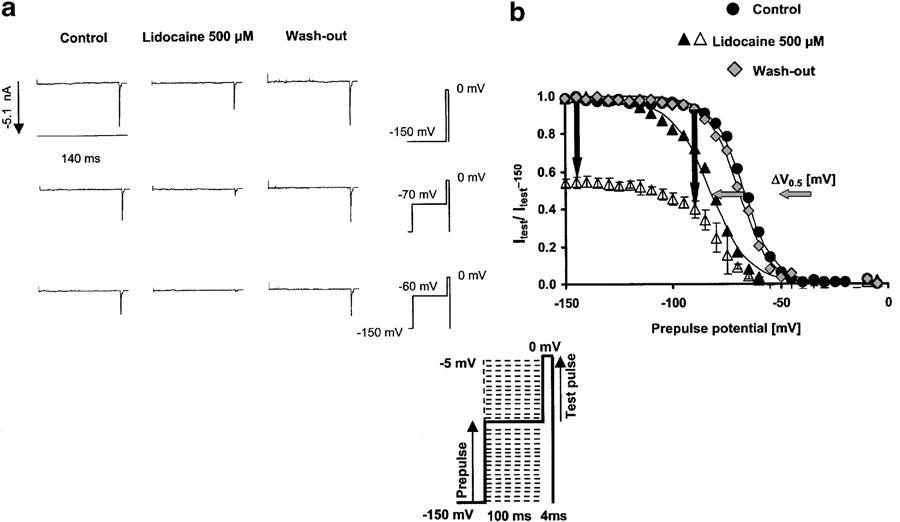
The dissociation constant from the fast-inactivated state K_dI, estimated from the concentration dependence of the shift in the availability curve using the original model of Bean et al. (1983) was 15±5 μM. These results perfectly mirror the results previously obtained by others for the effects of lidocaine on hSkM1 channels expressed in HEK293 cells (Fan et al., 1996). Figure 1 shows representative current traces obtained at different prepulse potentials with and without drug, and the steady-state availability curves obtained from four different cells in the absence (control and wash out) or presence of 500 μM lidocaine. Drug effects on the voltage dependence of channel availability were reversible during wash out, taking into account the fact that a small hyperpolarizing shift can occur as a function of the recording time until completion of the wash-out experiments.

Figure 1.

Effects of lidocaine on fast-inactivated channels, assessed by shifts in the steady-state availability curve. (a) (Left): Representative current traces in the control condition and with 500 μM lidocaine during short (4 ms) test pulses to 0 mV, following a 100 ms prepulse to either −150 mV (first row of traces), −70 mV (second row of traces), or a membrane potential close to the potential for half-maximum channel inactivation in the controls (−60 mV). There is no current activation during the prepulse from −150 mV to the indicated prepulse potential. All current traces elicited by the test pulses have been scaled to maximum value at −150 mV prepulse potential, indicated at the left of the first row. The traces show the increase in peak current suppression achieved by lidocaine at more depolarized prepulse potentials. (b) (Right): Steady-state availability curves assessed by a two-pulse protocol in the absence (control; circles, wash out; rhombs) and presence of 500 μM lidocaine (triangles). Each symbol represents the mean fractional current derived from at least three different experiments, elicited by a 4 ms test pulse to 0 mV, following a 100 ms inactivating prepulse from −150 mV to the indicated prepulse potential. Currents were normalized to maximum value (in each series at −150 mV prepotential); solid lines represent the best Boltzmann fit (equation (2)) to the data with the indicated parameters for control and test, respectively. Error bars are standard deviations. Currents were normalized either to maximum values in the presence of drug (filled symbols) or to maximum values in the controls (empty symbols). Vertical arrows show the increase in the peak current suppression induced by 500 μM lidocaine at more depolarized holding potentials vs hyperpolarized holding potentials. This reduction in channel availability at depolarized prepotentials resulted in a voltage shift in the midpoints of the availability curve (ΔV_0.5), indicated by the horizontal arrows.

The concentration dependence of the voltage shift in the presence of lidocaine is shown in Figure 2. Each symbol represents the mean value obtained from at least three different cells for each concentration tested, and the solid line represents a fit of either the original model (left diagram) or the modified model. The modified model clearly improved the fit to the data, shown by a two-fold reduction in the residual sum of squares [∑Δ²/(n-1) or [∑Δ²/(n-2). The model fit to the data yielded a Hill-type coefficient for fast-inactivated state binding of 1.97±0.28, which was significantly different from one.

Figure 2.

Concentration dependence of the drug-induced negative shifts in the midpoints (ΔV_0.5) of the steady-state availability plots relative to the starting values for lidocaine. Each symbol represents the mean value derived from at least three different experiments; error bars are standard deviations. The solid line shows the fit of equation (11) (left) or its modification (right) with the indicated parameters. The slope factor k of 7.4 and the respective values of K_dR or ECR₅₀, respectively, were entered into the model as constant factors. The Hill coefficient n_H for the binding of lidocaine to channels in the resting state was approximately 1. The modification clearly improved the fit, as shown by a reduction in the mean residual sum of squares [∑Δ²/(n−1) or ∑Δ²/(n−2), where n is the number of observations], yielding a value of 1.97±0.28 for the Hill-type exponent n for lidocaine binding to fast-inactivated channels, which is significantly larger than 1.

For the phenol derivatives, 2,6-dimethylphenol, 3,5-dimethyl-4-chlorophenol, and 4-chlorophenol, similar results were obtained (see Figure 3). For all compounds, the Hill coefficients for binding to resting channels were equal to or very close to one. The modified model clearly improved the quality of the fit to the data, and the model fit yielded Hill-type coefficients for inactivated state binding significantly greater than one, ranging from 1.57 to 2.09. The respective fit parameters entered as constants (K_dR or ECR₅₀, respectively, and the slope factor k) and the variables K_dI or ECI50, respectively, and n, as well as the residual sum of squares and the respective P-values are shown in the figures.

Discussion

The idea to conduct this study originated from our observation that, when we used the equation

(Bean et al., 1983), in order to yield estimates for a change in inactivated state affinity for phenol derivatives in a mutant sodium channel (Haeseler et al., 2001b), the fits showed the same imperfection that was already visible in the original paper. It was therefore clear that the assumption of a simple Langmuir relationship for lidocaine binding to fast-inactivated channels states was an oversimplification leading to an overestimation of the effects of low drug concentrations and to an underestimation of the effect of higher concentrations on the shift in voltage-dependent availability. A reasonable solution seemed to be to modify the model of Bean et al. (1983) by introducing a Hill-type exponent n into the term of the original equation that addresses the inactivated state affinity. In this context, it is worth noting that in our investigation, the Hill coefficient n_H derived for resting state binding of lidocaine at hyperpolarized holding potentials (−150 mV) was 1.05. In this respect, the assumption of a Langmuir relationship is justified and can be maintained.

Thus, one major finding of our study is that the introduction of a Hill-type exponent n into the established model, in order to yield estimates of the affinity of inactivated channel states, clearly improves the model's ability to predict experimental data for lidocaine as well as for a number of lidocaine-like sodium channel blockers. In the case of our whole-cell experiments, this improvement is reflected in the marked reduction in the residual sum of least-squares deviation between the actual value of the voltage shift found experimentally and the model prediction.

Our other major finding is that the respective Hill-type slopes that ranged from 1.6 to 2.1 were all significantly greater than one. In this respect, it should be stressed that our approach, like the Hill equation itself, is an empirical concept that does not necessarily describe any known physical mechanism. When dealing with voltage-operated ion channels, the fraction of inactivated channels is usually plotted against the membrane potential (V (mV)). This plot is then fitted with the appropriate form of the Boltzmann equation that has exactly the same form as the logistic equation. Consequently, a plot of I_norm against voltage (not log voltage) has the same form as the Hill equation plotted against log_{concentration} (Colquhoun 1998). Instead of half-maximum effect concentrations (EC₅₀), the Boltzmann equation now yields the membrane potential of half-maximum channel availability (V_0.5). On this basis, our data, like the data of Bean et al. (1983), show that lidocaine-like local anaesthetics enhance the effect of membrane depolarization on channel inactivation, thereby shifting the potential of half-maximum channel availability into the direction of hyperpolarized membrane potentials. This is comparable to the effect of an allosteric coactivator of ligand-gated ion channels that enhances the effect of the natural agonist, thereby shifting the agonist effect curve in the direction of smaller agonist concentrations. The most important aspect of the results produced by our modified model is the steepness of the slope of model fits to plots of these shifts of ΔV_0.5 against drug concentration that mirror the fact that the increase in the fraction of nonconducting channels with increasing concentration is greater than predicted by the established model assuming one-to-one binding of lidocaine-like local anaesthetics to inactivated channels. It is worth noting that in our experiments, the steady-state availability curve reflects drug association primarily with rested and fast-inactivated channels because no relevant degree of slow inactivation is expected with prepulses shorter than 100 ms (Vilin et al., 1999), and the open state is only transiently occupied and does not influence steady-state block after long prepulses. Fast inactivation, in turn, in a contemporary model of sodium channel gating, is considered as a particle-binding process allosterically coupled to activation (Kuo & Bean, 1994). The fact that our modified model yielded Hill-type exponents significantly greater than one provides evidence of cooperativity, which we define simply as deviation from a value of one of the Hill-type exponents (Laurence & Carpenter, 1998). The question of how to interpret this cooperativity mechanistically is, of course, beyond the means of our modified model, but other investigators, using a variety of experimental techniques, have published the hypothesis that lidocaine acts as an allosteric effector that, on binding to the channel, enhances channel inactivation by strengthening the postulated latch mechanism of inactivation that holds the gate shut (Balser et al., 1996a). Recently, Vedantham & Cannon (1999) found that lidocaine does not compete with the fast-inactivation gate, and does not measurably affect the rate of recovery of the fast-inactivation gate, but potentiates the degree to which depolarization favours closure of the fast-inactivation gate. Thus, as increased steady-state voltage sensitivity of the latch mechanism can be considered to be analogous to increased affinity of a second agonist binding site, the cooperativity revealed by our model would reflect cooperativity of binding.

However, our results could, alternatively, be interpreted as suggesting the existence of one or more additional binding sites for lidocaine on inactivated sodium channels. If this hypothesis were true, it would imply that channel inactivation unmasks extra binding sites, sites that are not otherwise available in other channel states. This case could be explained in a Monod–Wyman–Changeux context as considered by Colquhoun (1998). There would be no need to postulate different affinities. Cooperativity would arise not from binding but from concerted confirmation transition.

Last, but not least, while our model was capable of reproducing the experimental data in whole-cell experiments, it still yielded markedly smaller affinity constants for the inactivated, as opposed to the resting channel state, for example, in the case of lidocaine, an ECI₅₀ of 67 μM vs an ECR₅₀ of 417 μM. Thus, our data support the traditional paradigm for the binding of lidocaine to voltage-operated sodium channels by confirming the formation of drug-associated nonconducting states with high affinity for the inactivated channel.

In conclusion, binding of lidocaine and lidocaine-like sodium channel blockers to fast-inactivated sodium channels, as determined by the voltage shift in the steady-state availability curve cannot be properly described under the assumption that it follows a simple Langmuir relationship. Our modified model, which introduces a single additional factor into the original equation of Bean et al. (1983), a Hill-type exponent n, offers a parsimonious solution to this problem.

Abbreviations

HEK293

human embryonic kidney cell, expression system

hSkM1

voltage-gated human skeletal muscle sodium channel

ECR₅₀

concentration for half-maximum blocking effect in the resting state

ECI₅₀

concentration for half-maximum effect in the inactivated state

I_norm: I/I_max

sodium current normalized to maximum inward current

K_dR

dissociation constant for the resting state

K_dI

dissociation constant for the inactivated channel state

k

Boltzmann parameter, slope factor of the availability curve

n

Hill-type coefficient

V_0.5 (mV)

Boltzmann parameter, voltage of half-maximum channel availability

ΔV_0.5 (mV)

shift in the voltage dependence of channel availability