Simultaneous central nervous system distribution and pharmacokinetic–pharmacodynamic modelling of the electroencephalogram effect of norfloxacin administered at a convulsant dose in rats

Abstract

1. The objective of this study was to investigate the contribution of norfloxacin blood–brain barrier (BBB) transport to its delayed electroencephalogram (EEG) effect in rats.

2. Norfloxacin was injected as a bolus dose of 150 mg kg⁻¹. Blood samples were collected for total norfloxacin plasma concentration measurements. The corresponding unbound levels were determined in brain extracellular fluid (ECF) using microdialysis. Quantitative EEG recording was conducted during 9 h post-dose.

3. Brain ECF norfloxacin concentrations were much lower than plasma levels (AUC ratio=9.7±2.8%) but peaked very early, and concentration versus time profiles were parallel in both biological fluids. The best pharmacokinetic (PK) modelling was obtained by considering that ECF concentrations were part of the central compartment, with a proportionality factor. The peak of EEG effect was delayed and the effect versus plasma concentration curves exhibited a dramatic hysteresis. A PK–pharmacodynamic (PD) effect compartment model with a spline function to describe the relationship between effect and concentration at the effect site successfully described the data.

4. Comparisons of PK–PD parameters estimated from plasma and ECF concentrations show that most of the delayed norfloxacin EEG effect is not due to BBB transport, but also that PD parameters derived from plasma data must be carefully interpreted when drug distribution at the effect site is restricted, as may often be the case for centrally acting drugs.

Introduction

Pharmacokinetic–pharmacodynamic (PK–PD) modelling has recently been used to characterise the electroencephalographic (EEG) effect of imipenem (Dupuis et al., 2001) and norfloxacin (Chenel et al., 2003) in rats. A dramatic time delay was observed between the EEG effect versus time and plasma concentration versus time curves. Experimental data were fitted using PK–PD models, including an effect compartment, and the robustness of these models was assessed in various experimental settings. However, these models may lack physiological significance. Owing to their physicochemical characteristics, the distribution of these two antibiotics in the brain is presumably low, which could possibly explain or at least contribute to the delayed effect. In contrast, according to Hammarlund-Udenaes et al. (1997), when the drug influx rate to the brain is slower than the efflux, drug concentrations within the brain are expected to be lower than in the plasma, but with an early peak. Furthermore, in a recent study using intracerebral microdialysis in rats, we have observed that the ECF brain concentrations of norfloxacin are actually much lower than the corresponding plasma levels, but also that they peak early after drug administration as a bolus dose (Marchand et al., 2003). Therefore, the delayed EEG effect of norfloxacin should not be explained by its central nervous system (CNS) distribution characteristics. The above studies (Chenel et al., 2003; Marchand et al., 2003) were conducted in different rats with different experimental settings (e.g. different doses). Thus, the objective of the current study was to appropriately characterise the contribution of the CNS distribution process to the overall delayed effect. This study was based on simultaneous CNS distribution using microdialysis and PK–PD modelling of the EEG effect in the same rat treated with a convulsant dose of norfloxacin.

Methods

Chemicals

Norfloxacin was obtained from Sigma (Saint-Quentin Fallavier, France). A Norfloxacin salt was prepared as previously described (Delon et al., 1997). Ciprofloxacin hydrochloride was provided by Bayer Pharma (Puteaux, France). The perfusion solution (Ringer) for microdialysis contained 145 mM NaCl, 0.6 mM KCl, 1.0 mM MgCl₂, 1.2 mM CaCl₂, 0.2 mM ascorbic acid, in a 2 mM potassium phosphate buffer, pH 7.4 (Moghaddam & Bunney, 1989). All chemicals used were of analytical grade and analytical solvents were of high-performance liquid chromatography (HPLC) grade.

Animals

Male Sprague–Dawley rats (n=12) from Depres Breeding Laboratories (St Doulchard, France), weighing 299±15 g, were used. The animals were placed in wire cages in a 12 h light–dark cycle for a minimum of 8 days before the beginning of the experiment, in order to adjust to the new environment and to overcome stress possibly incurred during transit. During this period, rats had free access to food (Extralabo M20, U.A.R. Laboratories, France) and water. Ethical approval was obtained from the Animal Ethics Committee of the Faculty of Pharmacy (BHE/2001/12/AE).

Surgical Procedure

Implantation of cortical electrodes and guide cannula

At 5 days before the experiment, each rat was anaesthetised by isofluran (Forene®; Abbot) inhalation. The rat was placed in a hermetic enclosure, which was supplied with air–isofluran mixture (3.7%) at a flow of 500 ml min⁻¹ (Anaesthesia Unity: Univentor 400; Phymep; France and air pump: Pomps LDT, Charles Austen). When the animal was sleeping, a mask was placed on its muzzle and the isofluran percent was decreased to 1.7% for the rest of the surgery. The anaesthetised rat was placed on a stereotaxic instrument (David Kopf Instruments, Tujunga, U.S.A.) and then connected to a CMA 150 temperature controller (Homeothermic Blanket Control Unit, Phymep, Paris, France). A midline incision was made in order to expose the skull and four electrodes were screwed into little holes drilled into the skull at the following positions, in relation to the bregma: 2 mm anterior, 2 mm lateral (F1 and F2); 5 mm posterior, 2 mm lateral (O2); and 6 mm anterior, 2 mm lateral (reference electrode). The stainless steel electrodes were connected to a miniature plug (Electro Din 5 pins, ref. MDF5B; OHM électronique; Poitiers, France). A microdialysis CMA/12 guide cannula was then implanted into the left dorsal hippocampus with coordinates: lateral –4.8 mm, anterior –5.6 mm, ventral –4.7 mm relative to the bregma (Paxinos & Watson, 1986). The miniature plug and guide cannula were fixed to the skull with two types of dental cement. The first type, a cement with aqueous solvent (Aquacem, Promodentaire, Gonesse, France), was used directly in contact with the skull. The second type, a cement with organic solvent (Heliotone, Promodentaire, Gonesse, France), was used to finalise the mounting. The animal was placed in thermostated chamber (27°C) and was allowed to recover for 4 days before catheter implantation.

Implantation of blood femoral catheters

On the day before the experiment, rats were anaesthetised by isofluran inhalation as previously described. Polyethylene catheters corresponding to the connection of two catheters with different diameters: the first, which had a small diameter (inside diameter, 0.26 mm; outside diameter, 0.61 mm; Phymep, Paris, France), were inserted and connected to a larger catheter (inside diameter, 0.58 mm; outside diameter, 0.96 mm; Harvard Apparatus, Les Ulis, France). Two catheters filled with 0.9% NaCl were implanted: one in the left femoral vein for drug administration and the other in the left femoral artery for blood sample collection. Animals were housed individually in plastic cages. They had free access to food and water.

Drug administration

Norfloxacin was injected as an intravenous bolus at a dose of 150 mg kg⁻¹ of body weight. The norfloxacin solution was prepared by dissolving an adequate quantity of norfloxacin salt in 0.9% NaCl, so that the final volume of administration was set to 1 ml. Drug injections were conducted between 10:30 and 11:00 h.

Experimental design

On the day of the experiment, a CMA/12 microdialysis probe (CMA microdialysis, Stockholm, Sweden) was inserted into the left dorsal hippocampus via the guide cannula. The microdialysis probe was infused at a flow rate of 1 μl min⁻¹ for 1 h, with a Ringer solution containing the calibrator (ciprofloxacin, 400 nM) to stabilise the system. After the stabilisation period, the intravenous bolus administration of norfloxacin was performed via the left femoral vein. Arterial blood samples (200–250 μl) were collected in heparinised vials at 5, 10, 20, 30, 60, 180, 300, 420 and 540 min. Blood was replaced by an equal volume of 0.9% NaCl solution. After collection, blood samples were centrifuged at 11,000 × g (centrifuge A14, Jouan, St Herblain, France) for 10 min at 4°C, and plasma was harvested and frozen at −20°C until analysis. Microdialysates were collected in pre-weighed vials, using a Univentor 820 microsampler (B29 Bulebel Industrial Estate, Zejtun, Malta). The time to flush the dead volume was estimated to be 15 min. Microdialysate sample collection was therefore started 15 min post-injection, and subsequently at 10 min intervals during the first hour and then at 30 min intervals over the remaining 8 h. Microdialysates sample were assayed the day of experiment.

In vivo calibration of the microdialysis probes

The in vivo recovery of the probe was estimated using the method of retrodialysis by loss. Ciprofloxacin at a concentration of 400 nM was selected as a calibrator (Marchand et al., 2003). The relative recovery by loss (RL) in vivo was calculated using the following relation:

where C_in is the concentration of the calibrator into the perfusate solution and Cout the concentration of the calibrator in the microdialysate sample.

Unbound concentrations of norfloxacin in hippocampus were obtained by correcting the measured dialysate concentrations by the mean recovery by loss of ciprofloxacin estimated during the 9 h experiment.

EEG measurement

On the day of the experiment, each rat was maintained in a plastic bowl, and the miniature plug was connected to a moving connector to record the EEG signal. Bipolar EEG leads (F1–F2 and F2–O2) were continuously recorded using both the Bio-Logic® software and a paper polygraph (System 50,000 EEG recorder, Van Gogh, Medelec, France). The signal was band-pass filtered from 0.3 to 70 Hz. The EEG signal from the frontal cortical lead (F1–F2) was simultaneously sampled at 128 Hz and analysed online by fast Fourier transform (FFT) to determine the EEG total power in the frequency band from 0.5 to 30 Hz (Data Wave Technologies®). The FFTs were calculated every 2 s, giving a first EEG power trend that could be visualised before being stored on the hard disk. Subsequently, after artifact removal from this power trend, a data reduction was calculated by averaging this first FFT trend every 5 min, resulting in a second trend. Consequently, each data point of the second trend was the mean of 150 consecutive points of the first trend. The corresponding data points of the second trend were used as effect measures for PK–PD modelling. The EEG recordings started 90 min before norfloxacin intravenous bolus and continued until the signals had returned to their baseline values. Total EEG recording duration was about 9 h.

Sample analysis

Microdialysis samples

In all, 10 μl of the microdialysis samples were directly injected onto a Kromasil C18 column (5-μm-diameter particles, 250 × 3 mm inner diameter, Varian, Paris, France). The chromatographic system consisted of a Shimadzu LC-10AT pump and a Waters 717 plus Autosampler connected to a fluorescence detector (Waters 470). Data were recorded and processed using a Waters 746 integrator. The mobile phase consisted of 0.1 M aqueous citric acid solution containing 8% (v v⁻¹) acetonitrile and 10 mM tetra butyl ammonium perchlorate, and the flow rate was 1 ml min⁻¹. The excitation and emission wavelengths were 280 and 445 nm, respectively. The norfloxacin and ciprofloxacin retention times were 4.8 and 5.8 min, respectively.

The between-day variability of ciprofloxacin was characterised at 400 nM, with the coefficient of variation and accuracy equal to 7 and 98% (n=10), respectively. The between-day variability of norfloxacin was characterised at 50, 200 and 800 nM, with a coefficient of variation equal to 2, 8 and 13% (n=10), respectively, and accuracy equal to 98, 111 and 104% (n=10), respectively.

The limit of quantification of norfloxacin in microdialysate was 25 nM, with a coefficient of variation and an accuracy (n=10) equal to 2.5 and 101.3%, respectively, for an injected volume of 10 μl. The six initial samples (10 μl) collected at 10 min intervals over the first hour following the bolus administration of norfloxacin were diluted using Ringer solution in order to obtain a 30 μl volume. In all, 10 μl of the 30 μl were injected onto the column.

Plasma samples

The chromatographic system used to analyse norfloxacin in plasma samples consisted of a Shimadzu LC-6A pump, a Waters 710A Autosampler connected to a fluorescence detector (Waters 470). Data were recorded and processed using a Waters 746 integrator. The flow rate was 0.8 ml min⁻¹ and the mobile phase consisted of 0.1 M aqueous citric acid solution containing 8% (v v⁻¹) acetonitrile and 10 mmol l⁻¹ tetra butyl ammonium perchlorate. The excitation and emission wavelengths were 280 and 445 nm, respectively. The retention time of norfloxacin was equal to 3.8 min.

Proteins from plasma samples (50 μl) were precipitated by the addition of 200 μl of perchloric acid (0.1 N). The mixture was then centrifuged (11,000 × g during 5 min) and 20 μl of the supernatant was injected onto a Kromasil C18 column (5-μm-diameter particles, 150 × 3 mm inner diameter, Varian, Paris, France). Initial samples (5, 10, 20, 30 and 60 min) were diluted with rat plasma (1/4, v v⁻¹). The within-day variability of the method was characterised at two concentrations: 1.56 and 100 μM, with coefficients of variation (n=6) equal to 4.5 and 8.8%, respectively, and accuracies (n=6) equal to 103.1 and 100.4%, respectively. The between-day variability of the method was characterised at two different concentrations: 6.25 and 50 μM, with coefficients of variation equal to 8.0 and 4.2% (n=12), respectively, and accuracies equal to 103.9 and 97.3% (n=12), respectively.

PK and PK–PD analysis

Noncompartmental PK analysis

Plasma norfloxacin PK parameters, including total area under the plasma concentration versus time curve (AUC_plasma), total body clearance (CL_plasma), steady-state volume of distribution (V_ss,plasma) and elimination half-life (t_1/2plasma) were determined in each individual rat by a noncompartmental approach according to standard procedures (Gibaldi & Perrier, 1982), using the software WinNonLin (version 4.0. 1. Pharsight Corporation, Mountain View, CA, U.S.A.), as previously done (Chenel et al., 2003; Marchand et al., 2003).

Brain ECF concentrations of norfloxacin in the hippocampus were obtained by correcting the measured microdialysate concentrations by the mean RL of ciprofloxacin estimated during the 9 h experiment (Marchand et al., 2003). The corresponding PK parameters in brain ECF were also determined in each individual rat by a noncompartmental approach. The apparent elimination half-life in brain (t_1/2,brain) was estimated by ordinary least-squares (OLS) fit of data points (time, log brain drug concentration), in the terminal phase of the decline. The AUC_brain was calculated according to the method used for plasma data analysis. Since norfloxacin is mostly (>80%) unbound in plasma (Delon et al., 1997), the ratio R was calculated in each individual rat using total plasma concentrations, as AUC_brain/AUC_plasma.

Compartmental PK analysis

A two-compartment open model was used to characterise individual plasma concentration (C_p)–time profiles of norfloxacin after intravenous bolus administration:

where C_p(t) is the concentration of norfloxacin in plasma at time t, A and B are the intercept values expressed in μM, α and β are the exponential coefficients expressed per minute. Model parameters were estimated by nonlinear regression using the OLS method. The chosen algorithm was the Gauss–Newton algorithm with the Hartley modification. Goodness of fit was assessed by visual inspection, low variation coefficients associated for each estimated parameter and random repartition of weighted residues (Chenel et al., 2003).

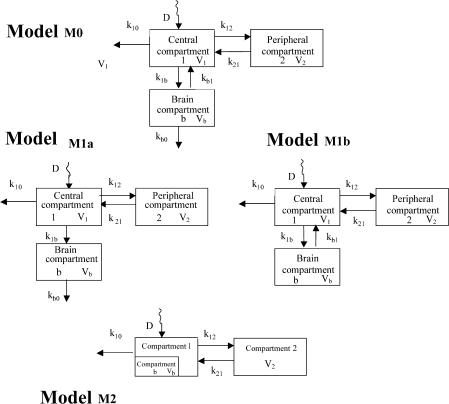
Several modified versions of previously proposed models (Hammarlund-Udenaes et al., 1997; Tunblad et al., 2003) were tested for simultaneous modelling of plasma and brain ECF data. All were derived from a traditional two-compartment open model to which a brain compartment connected to the central compartment was added (Figure 1, model M0). In this full model, drug could disappear from the brain compartment both by redistribution within the central compartment and elimination, corresponding to CSF bulk flow and possible brain metabolism. Differential equations corresponding to this initial model (Figure 1, model M0) are as follows:

Figure 1.

Model for plasma, peripheral and brain compartments, where k₁₂ and k₂₁ are the transfer microconstants between the central and the peripheral compartments, k₁₀ is the elimination microconstant from the body, k_1b and k_b1 are the transfer microconstants between the central and the brain compartments, k_b0 is the elimination microconstant from the brain, k′_b0 is the sum of elimination and redistribution microconstants from the brain and D is the injected dose of norfloxacin. V₁, V₂ and V_b are the volumes of the compartments: central (V₁), peripheral (V₂) and cerebral (V_b), respectively.

However, in order to reduce the number of parameters, this model was simplified as only elimination (Figure 1, model M1a) and redistribution (Figure 1, model M1b) from the brain.

Model M1a: Owing to the limited size of the brain, minute amounts of the drug reach the CNS and therefore plasma concentrations govern brain ECF concentrations, but not the reverse (Hammarlund-Udenaes et al., 1997). Accordingly, k_1b and k_b1 are negligible compared to k₁₀ and Equation (3a) can be simplified to Equation (3b).

By the same reasoning, drug redistribution from the brain can be included within elimination, and the two microconstants k_b0 and k_b1, appearing in Equation (5a) corresponding to the full model M0, can be reduced to a single one k_b0′. Equation (5a) was then rearranged by substituting transfer microconstants (k_1b and k_b0′) by the corresponding clearance terms, leading to Equation (5b).

In Equation (5b), CL_in,b corresponds to distribution clearance into the brain, with CL_in,b=k_1b^*V₁, and CL_out,b to the sum of the redistribution and elimination clearances out of the brain, with CL_out,b=k_b0′^*V_b, where V₁ and V_b are the apparent volumes of distribution of drug in the body and the brain. At equilibrium, the rate of change of concentrations in the brain is zero and therefore CL_in,b^*C₁=CL_out,b^*C_b, which for a single dose can be expressed as CL_in,b/CL_out,b=AUC_brain/AUC_plasma=R (Wang & Welty, 1996; Sawchuk & Yang, 1999; Sawchuk & Elmquist, 2000). The ratio R could be estimated from the ratio of AUCs estimated by the noncompartmental approach in the brain and plasma, respectively, in each individual rat, and was therefore entered as a constant in Equation (5b). The brain distribution volume V_b, which represents the proportionality factor between the norfloxacin brain ECF concentration determined by microdialysis and the corresponding amount present in the brain, was also entered as a constant in Equation (5b). A mean value of this parameter was estimated from another experiment conducted in our laboratory, in which the total amount of norfloxacin in brain (Qb) and the corresponding plasma concentration were determined in 55 rats treated by various doses of norfloxacin. The ratio between the two (Qb/Cp) was on average equal to 0.15±0.06 ml kg⁻¹ (data not shown). Considering that the ratio C_ECF/Cp is equal to 0.097 on average (Table 1 in the Results section), one can then get an estimate of Vb (Vb=Qb/C_ECF=Qb/Cp^*Cp/C_ECF) equal on average to 1.0 ml kg⁻¹ of rat body weight or 1.6 ml g⁻¹ of brain.

Table 1.

PK parameter estimates obtained after an intravenous bolus administration of 150 mg kg of body weight⁻¹ norfloxacin in rats by noncompartmental (NC) and compartmental (C) approaches^a

Parameters (n=10)	CLbplasma (ml min−1 kg−1)	Vbss,plasma (ml kg−1)	tc1/2,plasma (min)	tc1/2,brain (min)	Rds (%)
NC	13.0±2.2	4004±469	221±34	255±97	9.7±2.9
C	13.9±2.7	3622±492	202±45	−	8.9±2.8

^aPK parameter values are means±standard deviations.

^bNonstatistically significant differences between mean values according to the approach used – compartmental (C) or noncompartmental (NC) – based on the paired Student's t test.

^cNonstatistically significant differences between mean values of t_1/2,brain and t_1/2,plasma based on the paired Student's t-test.

^dNonstatistically significant difference between the mean value of R calculated by AUC ratio and the mean value of R_mod estimated by the simultaneous modeling.

The final equation used for the modelling, where CL_out,b is the only parameter remaining for estimation, was therefore as follows:

Model M1b: This model was slightly different from the previous, the only difference being that excretion from the brain was considered as negligible compared to redistribution, meaning that k_b0<<k_b1 (Figure 1, model M1b).

Model M2: In this model, the distribution equilibrium of norfloxacin within the brain was supposed to be attained instantaneously. Then at any time, the brain-to-plasma concentration ratio is equal to R, and therefore plasma and brain ECF data were analysed simultaneously, considering that brain ECF was part of the central compartment, with a tissue penetration factor (R_mod) relating brain ECF and plasma concentration (Figure 1, model M2).

Parameters were estimated by nonlinear regression using a weighting coefficient of 1/C_pred.², where C_pred. is the predicted concentration calculated using the equation of the chosen model. The chosen algorithm was the Nelder–Mead algorithm. Goodness of fit was individually assessed by visual inspection of the fitting and residues analysis and from the coefficients of variation associated with parameter estimates. The software used was WinNonLin (version 4.0.1., Pharsight Corporation, Mountain View, CA, U.S.A.).

PK–PD modelling

PK–PD modelling was conducted using PK model M2 (Figure 1). Previously estimated PK parameters were fixed, and the PD model was regressed to the EEG data for each individual rat by using the nonlinear least-squares program WinNonLin. An effect compartment model (Sheiner et al., 1979) with uniform weights was applied for analysis of the PK–PD relationship using Equation (6) for minimisation of the hysteresis observed in the plasma concentration–EEG effect relationship:

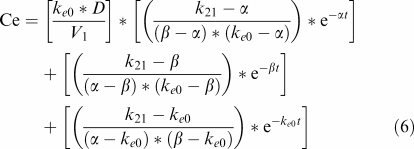In Equation (6), Ce is the drug concentration in the effect compartment at time t, and k_e0 is the rate constant for elimination of the drug from the effect compartment. Other parameters are PK parameters previously defined.

The profile of the EEG effect was described using a spline function derived from the Hill equation (Della Paschoa et al., 1998), as previously (Chenel et al., 2003):

In Equation (7), P is the total power (EEG effect) expressed in square millivolts and corresponding to Ce, P₀ is the baseline effect value estimated by averaging the first 90 min of the EEG recording expressed in square millivolts, Bⁿ is the combined parameter E_max/EC₅₀ⁿ expressed in square millivolts per micromolar concentration, and n is a sigmoidicity factor determining the steepness of the curve. The modelling analysis was carried out using concentration–time and effect–time data for individual rats. A semi-parametric method was used in order to select the PD model (Equation (7)), and then a parametric method was used. PK–PD modelling was also performed from brain ECF concentrations with the same procedure as for plasma concentrations. Goodness-of-fit was individually assessed by visual inspection of the fitting and residues analysis and from the coefficients of variation associated with parameter estimates.

Statistics

All PK and PK–PD parameter estimates are reported as means±standard deviations (s.d.). Paired Student's t-test was used to compare values of derived parameters (AUC_plasma, CL_plasma, V_ss,plasma and R) calculated by noncompartmental and compartmental methods (P<0.05). Paired Student's t-test was used to compare t_1/2,plasma and t_1/2,brain (P<0.05).

Results

All rats of this study have presented norfloxacin-induced seizures, and among the 12 rats initially enrolled two died from seizures. Consequently, the presented results correspond to a total of 10 animals.

In plasma, the decay of norfloxacin concentrations with time was bi-exponential, and no statistical difference was observed between the mean values of PK parameters estimated by compartmental and noncompartmental approaches (Table 1).

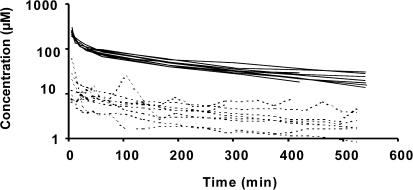
In vivo probe recovery was equal to 9.4±2.8% on average (extremes: 5.1–13.8). The highest brain ECF concentrations of norfloxacin were always observed within the initial 30 min following the beginning of the collection, and on six occasions in the first dialysate (0–10 min) (Figure 2). Brain ECF and plasma concentration versus time profiles were comparable and the AUC ratio between brain ECF and total plasma concentration was equal to 0.097±0.029 on average. Mean half-lives in plasma and brain were, respectively, equal to 221±34 and 255±97 min, and not significantly different (Table 1).

Figure 2.

Individual unbound norfloxacin concentrations in brain ECF (dashed lines) and total norfloxacin concentrations in arterial blood (solid lines) upon administration of 150 mg kg of body weight⁻¹.

Model M0 resulted in identifiability problems, and high coefficients of variation (between 70 and 100%) were associated with Cl_out,b estimates using model M1a. No better modelling was obtained with model M1b. The best results were obtained with PK model M2. No significant difference was observed between the AUC ratios, calculated with the noncompartmental method (R) and estimated by the simultaneous modelling (R_mod) (Table 1).

Perfusion of the microdialysis probes during the blank period with the Ringer solution containing calibrator (ciprofloxacin, 400 nM) had no effect on the baseline EEG signal. Isolated spikes with only limited effects on the total power of the EEG signal appeared at about 20 min after the intravenous bolus injection of norfloxacin on average. The frequency and amplitude of the spikes then increased dramatically, leading to a relatively sudden increase of the total power, with a maximum effect observed between 70 and 190 min post-dosing depending on the animal. This EEG effect was accompanied by behavioural troubles, including tremors and seizures. Except for the two animals who died from seizures, the total power of the EEG signal eventually returned progressively to baseline.

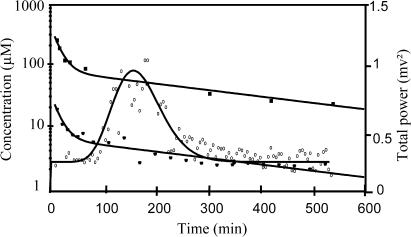
The selected effect compartment model provided a good fit to the data (plasma concentrations and EEG total power), as illustrated for a representative animal on Figure 3, and leading to PK–PD parameter estimates presented in Table 2. No statistical difference was observed between k_e0 and n values estimated from plasma and brain ECF data. However, the mean value of the B parameter estimated from brain ECF concentrations was on average 13.8-fold higher than the mean value estimated from plasma concentrations, in agreement with the previously estimated R values.

Figure 3.

Total concentrations of norfloxacin in plasma, unbound concentrations of norfloxacin in brain and EEG effect versus time for a representative rat. The broken line represents the best PK fit to the measured concentrations of norfloxacin in plasma, with the following values for PK parameters: A=272 μM (96.7 mg l⁻¹), B=109 μM (38.7 mg l⁻¹), α=0.119 min⁻¹ and β=0.00351 min⁻¹. The solid line represents the best fit to the measured total power of the EEG signal effect, according to the effect compartment model, with the following values for PD parameters: P₀=0.25 mV², B=0.0158 mV² μM⁻¹, n=17.7, k_e0=0.008 min⁻¹.

Table 2.

PK–PD parameter estimates^a obtained after an intravenous bolus administration of 150 mg kg⁻¹ norfloxacin in rats using the link model approach and the spline function model, with PK parameters obtained from plasma or brain ECF concentrations

Parameters (n=10)	Ke0b (min−1)	P0 (mV2)	Bc (mV2 μM−1)	nb
PK–PD from plasma concentrations	0.014±0.004	0.12±0.03	0.0122±0.0031	9±9
PK–PD from brain ECF concentrations	0.014±0.009	0.12±0.03	0.168±0.095	12±13

^aPK–PD parameter values are means±standard deviations.

^bNonstatistically significant differences between mean values according to the PK data used, plasma or brain ECF concentrations based on the paired Student's t-test.

^cStatistically significant differences between mean values according to the PK data used, plasma or brain ECF concentrations based on the paired Student's t-test.

Discussion

In the present study, intracerebral microdialysis for drug determination and CNS distribution modelling was combined with quantitative EEG recording for PK–PD modelling of the effect. The results are in good agreement with those previously obtained during separate experiments on norfloxacin brain distribution (Marchand et al., 2003) and PK–PD modelling of its EEG effect in rats (Chenel et al., 2003), indicating that the presence of intracerebral microdialysis probes did not interfere with the norfloxacin EEG effect.

In the present study, the number of microdialysate samples was increased to six during the initial hour post-dosing, by reducing the collection period to 10 min, in order to better characterise norfloxacin influx into the brain than during our previous study with dialysates collected every 30 min only (Marchand et al., 2003). In agreement with these previous observations (Marchand et al., 2003), the highest brain ECF concentrations were observed in the earliest microdialysate fractions. Yet, this does not mean that norfloxacin influx rate into the brain is elevated. In fact, according to a simulation study (Hammarlund-Udenaes et al., 1997), and consistent with the low R value (0.097±0.029), this rather suggests that drug efflux from the brain is much more rapid than its influx. The previously proposed CNS distribution model with a mono-exponential decay of plasma concentrations with time (Hammarlund-Udenaes et al., 1997) was extended to the norfloxacin situation with a bi-exponential decay, keeping essentially the same assumptions. In particular, it was considered that minute amounts of drug get into the CNS and therefore that plasma concentration govern brain ECF concentrations, but not the reverse (Figure 1, model M1a), meaning that drug redistribution from brain to plasma can be ignored to characterise plasma data. Yet, the increased number of parameters lead to identifiability problems, and was therefore further reduced, first by entering the individual R values obtained from the noncompartmental PK analysis as constants, and second by fixing a mean value of V_b estimated from complementary data obtained in another experiment. Then, CL_out,b was the only parameter remaining to be estimated. This parameter represents drug efflux from the brain, mainly excretion to CSF bulk flow, since brain metabolism is most likely negligible (Marchand et al., 2003), and also its redistribution to plasma, which still exists although not considered separately in the model (Figure 1, model M1). Unfortunately, CL_out,b could not be estimated accurately from the modelling, since high CVs were associated with this parameter estimate.

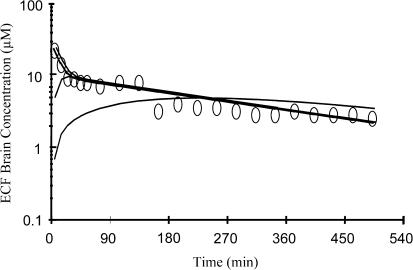
In order to clarify this point, simulations were conducted with various values of CL_out,b, from 2.5 μl min⁻¹, a value close to CSF bulk flow in rats (Bergman et al., 1998), which corresponds to the minimum value from a physiological standpoint to higher values corresponding to higher relative contributions of the brain to plasma redistribution. Since the CL_in,b/CL_out,b ratio was kept constant, these simulations assessed the effect of CL_out,b on the apparent rate, but not the extent of norfloxacin distribution within the brain. A CL_out,b value equal to 2.5 μl min⁻¹ leads to major discrepancies between the observed and simulated brain ECF concentrations during early post-dosing, since it predicts an entrance phase within the brain, which in most rats was not observed experimentally (Figure 4). Higher CL_out,b values lead to simulated profiles which were in better agreement with the experimental data, in particular during the early post-dose period. Yet, as illustrated in Figure 4, further increase of CL_out,b had virtually no effect on these initial profiles, meaning that in this situation many different values of CL_out,b may account for the observed data, which explains the high CVs associated with CL_out,b estimates. Therefore, these simulations suggest that CL_out,b is likely to be several fold higher than CSF bulk flow in rats, providing indirect evidence for the presence of norfloxacin efflux transport systems at the blood–brain barrier, although it has previously been demonstrated that norfloxacin is not a P-glycoprotein substrate (De Lange et al., 2000), and that its CNS distribution in rats is linear in a wide range of doses administered (Marchand et al., 2003).

Figure 4.

Simulation of brain concentrations (solid lines) using the model M1a (Figure 1) with different values of CL_out,b from 8.3 × 10⁻⁶ (1) (CSF bulk flow value=2.5 μl min⁻¹) to 8.3.10⁻³ (2) l min⁻¹ kg⁻¹ of body weight and using the previously estimated parameter values of a representative rat: V₁=1.192 l kg⁻¹, V₂=2.264 l kg⁻¹, V_b=0.00195 l kg⁻¹, R=0.094, k₁₂=0.074 min⁻¹, k₂₁=0.0364 min⁻¹, k₁₀=0.0093 min⁻¹, for a dose equal to 150 mg kg⁻¹. The observed ECF brain concentrations are represented by round (0) for the same representative rat.

Norfloxacin peaks very early within the brain, from which k_b0′ in Equations (5a)–(5c) is much greater than k_1b, making CL_out,b estimation difficult. No benefit was obtained by using model M1b instead of M1a. Similar features govern metabolite pharmacokinetics, whereby, as frequently encountered, metabolite formation rate limits elimination. For practical purposes, it was possible to consider that brain ECF concentrations were part of the central compartment, except for the existence of a proportionality factor between both concentrations (Figure 1, model M2). The best modelling was obtained with this approach, as illustrated in Figure 3.

PK-PD modelling results are consistent with previously published data (Chenel et al., 2003). A PK-PD model with an effect compartment provided good data fit, whereas an indirect effect model did not. Yet, simultaneous use of intracerebral microdialysis has demonstrated that the delayed effect is not due to a delayed drug distribution within the CNS, although it was best described by an effect compartment model. Contribution of the CNS distribution process to the overall delayed central effect of morphine and morphine-6-glucuronide (M6G) in rats has been assessed by comparing k_e0 values derived from PK-PD analysis conducted from plasma and ECF concentration values (Bouw et al., 2000, 2001). In all, 80% and about half of the delay was caused by transport across the BBB for morphine and M6G, respectively. The possible involvement of rate-limiting mechanisms at the receptor level or distributional phenomena was proposed for the remaining effect delay. It should also be reminded that the effect compartment model has initially been derived under the assumption that at equilibrium C_e, the concentration in the effect compartment, was equal to C_u, the unbound concentration in the central compartment (Sheiner et al., 1979; Hammarlund-Udenaes et al., 1997). This is probably true for most tissues, but there is enough evidence now to suggest that this may not be the case for the CNS (Bouw et al., 2000, 2001), which was further confirmed by the present experiment. In such conditions, one should be aware that the EC₅₀ (concentration that corresponds to 50% of the maximal effect) value of the Hill equation (or the B value in Equation (7) for the spline function) estimated from plasma data is in fact an apparent value not only determined by the PD characteristics of the drug but also by its CNS distribution characteristics, namely the R value. This proportionality factor may therefore complicate correlation between in vitro and in vivo estimates of EC50. Another important consequence is that any particular situation, such as age, inflammation, drug–drug interaction…, which may alter CNS distribution characteristics (changing R), would have an effect on the EC₅₀ value estimated from PK-PD modelling using plasma data, which would be falsely interpreted as a PD alteration when it is in fact a PK change.

In conclusion, this study provides an example of an important time delay between CNS effect and plasma concentration, best described by an effect compartment model although not due to slow drug distribution to the biophase. It also emphasises the potential pitfalls in interpreting PK-PD parameters obtained from plasma data for drugs with restricted CNS distribution.

Abbreviations

AUC

area under the concentration–time curve

BBB

brain–blood barrier

CL

total body clearance

CNS

central nervous system

ECF

extracellular fluid

EEG

electroencephalogram

FFT

fast Fourier transform

HPLC

high-performance liquid chromatography

OLS

ordinary least square

PD

pharmacodynamic

PK

pharmacokinetic

PK–PD

pharmacokinetic–pharmacodynamic

Qb

total amount of norfloxacin in brain

RL

recovery by loss

t_1/2

the elimination half-life

V_ss

the steady-state volume of distribution