Abstract
The precision with which individual termination codons in mRNA are recognized by protein release factors (RFs) has been measured and compared with the decoding of sense codons by tRNA. An Escherichia coli system for protein synthesis in vitro with purified components was used to study the accuracy of termination by RF1 and RF2 in the presence or absence of RF3. The efficiency of factor-dependent termination at all sense codons differing from any of the three stop codons by a single mutation was measured and compared with the efficiency of termination at the three stop codons. RF1 and RF2 discriminate against sense codons related to stop codons by between 3 and more than 6 orders of magnitude. This high level of accuracy is obtained without energy-driven error correction (proofreading), in contrast to codon-dependent aminoacyl-tRNA recognition by ribosomes. Two codons, UAU and UGG, stand out as hotspots for RF-dependent premature termination.
Keywords: protein synthesis, translational processivity, premature termination
Sixty-one of the 64 base triplets in the genetic code are sense codons, which are translated in bacteria to the 20 standard amino acids in proteins by about 50 aminoacyl-tRNAs. The remaining three codons usually signal termination of translation and the release of completed proteins from ribosomes by release factors RF1 and RF2. Efficient translation requires both rapid binding to their respective codons of cognate aminoacyl-tRNAs, in ternary complex with elongation factor EF-Tu and GTP, and fast termination of protein synthesis at stop signals by RFs. In addition to fast signal processing, codon translation must attain a high level of accuracy so that nonacceptable amino acid replacements in nascent proteins do not impair cell growth and viability. Similarly, misrecognition by RFs of sense codons as stop signals leads to truncated proteins, an energetically costly event, the frequency of which also must be contained.
Pauling was among the first to reflect on the errors that must occur during protein synthesis because of the limited maximum differences in interaction standard free energies between different pairs of amino acids, and he concluded that amino acid substitutions theoretically should occur at frequencies in the percent range (1). Though later shown to be overly pessimistic (2), these predictions led to theoretical studies showing that enzymatic selection can, under certain conditions, be more accurate than the instrinsic selectivity of a single step.
The accuracy (A) of simple enzyme selection schemes, defined as the probability of correct product formation divided by the probability of an error at equal concentrations of cognate and noncognate substrates, is limited by the standard free energy difference between the transition state leading to product formation and ground state for cognate (ΔGc) and noncognate (ΔGnc) substrates by the inequality
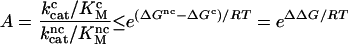 |
(3). The precision of codon translation depends on differences in H-bond energies between cognate and noncognate tRNA-codon interactions, though other interactions like steric repulsion also may be important. H-bonds alone probably cannot explain the average error frequency of about one mistake per 2,000 codons (1). Indeed, biochemical experiments show that the precision of codon translation is achieved by kinetic proofreading (4–6), where a moderate ΔΔG value is used twice or more in successive selection steps (7–9). To satisfy the rules of thermodynamics, such reactions must be accompanied by extra dissipation of free energy, provided during translation by the hydrolysis of GTP on EF-Tu (4–6).
Each sense or stop codon is related to the members of a set of nonsynonymous codons by a single nucleotide change and must be distinguished on this basis by the decoding tRNAs and RFs that continuously probe the ribosomal A-site. These two classes of molecule recognize codons by different types of interaction. Missense errors ultimately depend on the selectivity of RNA–RNA interactions, which must be enhanced by proofreading mechanisms, whereas termination errors depend on the selectivity of protein–RNA interactions. It was therefore of interest to investigate how RFs achieve rapid and accurate translation termination, a problem of recognition of central importance to the cell but about which little is known. The ribosome provides a unique opportunity to compare the specificity with which nucleotide triplets in a similar environment, namely, the ribosomal A-site, can be recognized by tailor-made RNA molecules (tRNAs) or by proteins (RF1 and RF2). The ribosome therefore also provides a general model system, where the ultimate limits of precision in protein–RNA and RNA–RNA interactions can be probed and compared in a controlled way.
Termination of protein synthesis in prokaryotes depends on RF1 and RF2. RF1 normally terminates at UAA and UAG and RF2 at UAA and UGA (10). The dissociation of both factors from the ribosome after hydrolysis of the ester bond in peptidyl-tRNA connecting peptide chain with tRNA is accelerated by a third RF, the G-protein RF3 (11–13), and this seems so far to be its only function (14). The three stop codons together have about 20 sense codons as nearest neighbors (Tables 1 and 2), and hot spots for false stops are likely to be found within this set of sense triplets. Estimates of the overall in vivo frequencies of termination errors by RF1 and RF2 have been made by observing the decrease in translational processivity when one or other of the RFs is overproduced in vivo. Thus, RF1 produces approximately one false stop per 100,000 codons (15), but no biochemical data on termination rates at individual sense codons have been reported so far. We also wanted to explore the possibility that the G-protein RF3 enhances termination specificity by proofreading the erroneous pretermination complexes that arise when RF1 or RF2 bind to ribosomes with near-cognate codons in the A-site. This might occur, for example, by the presence of two recognition steps for RF1 and RF2 selection: one in the presence of RF3 and one after GTP hydrolysis and dissociation of RF3.
Table 1.
The accuracy of RF1: The fold decrease in kcat/KM for RF1 at codons differing from RF1 stop codons (UAA and UAG) by 1 nt in the presence or absence of RF3
| Codon | Fold decrease in kcat/KM (×10−3)
|
|||||
|---|---|---|---|---|---|---|
| −RF3 | (σ) | +RF3 | (σ) | |||
| AAA | * | * | ||||
| AAG | * | * | ||||
| GAA | * | 400 | 100 | |||
| GAG | * | 600 | 300 | |||
| CAA | 400 | 100 | 90 | 20 | ||
| CAG | 500 | 100 | 90 | 10 | ||
| UGA | 136 | 7 | 37 | 2 | ||
| UGG | 47 | 5 | 11 | 1 | ||
| UCA | 15 | 2 | 4.1 | 0.1 | ||
| UCG | 19 | 1 | 5.1 | 0.4 | ||
| UUA | 26 | 2 | 7.6 | 0.4 | ||
| UUG | 13 | 2 | 3.6 | 0.4 | ||
| UAC | 20 | 1 | 5.6 | 0.6 | ||
| UAU | 1.1 | 0.3 | 0.4 | 0.1 | ||
A high value for the fold decrease in kcat/KM means that the accuracy is high. For example, from this table, the codon UCG is read by RF1 19,000 times less efficiently (in the absence of RF3) than RF1 reads the stop codon UAA. The results are the mean of three experiments with SD of the mean (σ). Unresolvable values are represented by *, where release is too slow in relation to peptidyl-tRNA dissociation to be measurable. The fold change in kcat/KM for these points is greater than 106. Bases in bold are those that differ from the sequence of a normal stop codon.
Table 2.
The accuracy of RF2: The fold decrease in kcat/KM for RF1 at codons differing from RF2 stop codons (UAA and UGA) by 1 nt ± RF3
| Codon | Fold decrease in kcat/KM (×10−3)
|
|||||
|---|---|---|---|---|---|---|
| −RF3 | (σ) | +RF3 | (σ) | |||
| AAA | * | * | ||||
| AGA | 370 | 40 | 170 | 20 | ||
| GAA | 900 | 300 | 400 | 100 | ||
| GGA | 150 | 20 | 85 | 5 | ||
| CAA | 37 | 2 | 16 | 5 | ||
| CGA | 14 | 2 | 6.5 | 0.6 | ||
| UUA | 18 | 2 | 14 | 1 | ||
| UCA | 6.6 | 0.2 | 4.2 | 0.4 | ||
| UAG | 1.75 | 0.05 | 1.07 | 0.07 | ||
| UGG | 2.4 | 0.1 | 1.5 | 0.2 | ||
| UAC | 18 | 9 | 11 | 2 | ||
| UGC | 16 | 3 | 7 | 1 | ||
| UAU | 40 | 8 | 18 | 3 | ||
| UGU | 22 | 3 | 9 | 1 | ||
The results are the mean of three experiments with SD of the mean (σ). Unresolvable values are represented by *; see legend to Table 1. Bases in bold are those that differ from the sequence of a normal stop codon.
Materials and Methods
RFs.
RF1 and RF2 were required in large amounts to perform the accuracy assays. RF1 was prepared from an overproducing strain as described by Dinçbas et al. (16). RF2 overproduced from the wild-type gene is toxic to the cell and shows reduced activity in biochemical assays (17, 18), especially with short peptidyl-tRNAs (our observations). RF2ala, which contains a threonine to alanine change at amino acid position 246, as in RF2 from Salmonella typhimurium (19), can be overproduced and yields a protein with enzymatic parameters close to those of RF2 prepared from normal cells: direct comparison with chromosomally produced RF2 shows that kcat is 2-fold lower. This RF2 variant has been used for the accuracy measurements. RF2ala and the chromosomal RF2 were prepared as described by Pavlov et al. (18).
Release Complexes.
Ribosomal release complexes were made as described by Freistroffer et al. (14), except that the Escherichia coli total tRNA fraction used was purified to produce a tRNA mixture (tBulk) that contained only the tRNA species needed for the production of release complexes. Briefly, total tRNA was aminoacylated and the amino group of the amino acid was derivatized with the heterobifunctional reagent SPDP [N-succinimidyl 3-(2-pyridyldithio)propionate, Amersham Pharmacia Biotech]. The derivatized tRNA was bound to a solid phase that separates it from noncharged tRNA, eluted, and treated with peptidyl-tRNA hydrolase (prepared as described by Karimi et al., ref. 20) to remove the derivatized amino acid. On a preparative scale, this procedure yielded, in total, 1 μmol of purified tRNAIle, tRNAThr, and tRNAPhe (details to be published elsewhere).
Measurement of kcat and KM.
The parameters for peptide release were measured as described by using an E. coli system (14) with RF1 and RF2ala (ref. 19, see above). About 5 pmol of ribosomal complex containing [14C]peptidyl-tRNA was reacted with RF1 or RF2, added at different concentrations up to 100–170 μM. After incubation times between 5 s and 6 min depending on the kinetics of the reaction, 5% trichloroacetic acid was added and the sample spun down at 14,000 rpm in an Eppendorf centrifuge. The supernatant (900 μl), which contained the released 14C-labeled peptide, was withdrawn and counted in 5 ml of Aquasafe 300 Plus scintillation fluid (Zinser Analytic, Frankfurt, Germany). The total number of releasable peptides (a value needed for the calculation) was obtained by incubating release complexes with 100 μM puromycin during 30 s and treating the samples in the same way as described above. Details of the treatment of the data are given in the legend to Fig. 1.
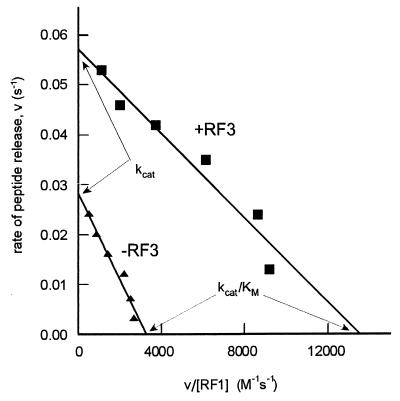
Figure 1.
Measurement of kinetic parameters for translation termination by RF1 at the near-cognate codon UAC in the presence or absence of RF3: an example of an RF accuracy experiment. The rate v for peptide release was measured as described in the text at different concentrations of RF. The rate v was estimated from the relation v = −ln(1 − R/RO)/T, where R/RO is the fraction of released oligopeptide during the incubation time T, and depends on the concentration [RF] of RF1 or RF2 as in a normal Michaelis–Menten equation: v = [RF]⋅kcat/(KM + [RF]). The y-intercept(s) gives the kcat, the x-intercept(s) gives the kcat/KM, and the slope is equal to −KM.
The fold change values for kcat/KM, kcat, and KM shown in Tables 1–4 were calculated by using the following measured values for the cognate (correct) kcat, KM, kcat/KM: RF1 kcat = 0.5 s−1, KM = 8.3⋅10−9 M, kcat/KM = 6.0⋅107 M−1⋅s−1; RF2ala kcat = 1.5 s−1, KM = 6.6⋅10−8 M, kcat/KM = 2.3⋅107 M−1⋅s−1. The mRNAs used for the cognate and noncognate termination experiments had the sequence CGGGCCCUUGUUAACAAUUAAGGAGGUAUACUAUGUUUACGAUU(STOP)CUGCAG(A)21.
Table 4.
The fold change in kcat and KM for RF2 at codons differing from the RF2 stop codons (UAG and UAA) by 1 nt: The contribution to accuracy from kcat and KM
| Codon | Fold change in the kcat and KM parameters
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −RF3
|
+RF3
|
|||||||||||
| kcat | (σ) | KM | (σ) | kcat | (σ) | KM | (σ) | |||||
| AAA | * | * | * | * | ||||||||
| AGA | 1,300 | 100 | 290 | 20 | 480 | 30 | 370 | 30 | ||||
| GAA | 3,200 | 500 | 260 | 70 | 2,000 | 300 | 200 | 30 | ||||
| GGA | 540 | 20 | 290 | 30 | 300 | 20 | 280 | 20 | ||||
| CAA | 90 | 10 | 440 | 40 | 50 | 10 | 350 | 90 | ||||
| CGA | 61 | 5 | 240 | 50 | 34 | 2 | 190 | 20 | ||||
| UUA | 200 | 100 | 120 | 40 | 140 | 50 | 130 | 50 | ||||
| UCA | 3.1 | 0.2 | 2,100 | 70 | 2.13 | 0.03 | 2,000 | 200 | ||||
| UAG | 7.2 | 0.7 | 250 | 30 | 4.4 | 0.2 | 240 | 20 | ||||
| UGG | 8 | 1 | 310 | 30 | 5.8 | 0.2 | 260 | 50 | ||||
| UAC | 30 | 10 | 500 | 100 | 33 | 5 | 350 | 40 | ||||
| UGC | 34 | 3 | 500 | 100 | 20 | 1 | 300 | 50 | ||||
| UAU | 80 | 10 | 500 | 100 | 46 | 9 | 400 | 90 | ||||
| UGU | 51 | 2 | 430 | 40 | 32 | 1 | 290 | 30 | ||||
The results are the mean of three experiments with SD of the mean (σ). Unresolvable values are represented by *; see legend to Table 1. Bases in bold are those that differ from the sequence of a normal stop codon.
Results
RFs Terminate with High Precision.
To measure termination errors by RFs 21 mRNAs were prepared, each encoding the tetrapeptide Met-Phe-Thr-Ile, followed by one of the three stop codons or by one of the 18 sense codons that can be reached by a single mutation from one of the stop codons. Ribosomes were initiated with initiation factors and in the presence of EFs were allowed to translate the first four codons to yield the tetrapeptide, the last amino acid being 14C-labeled. The ribosomes paused with the fifth codon in the A-site, because of the absence of RF or cognate aminoacyl-tRNA to recognize this codon, and tetrapeptidyl-tRNAIle in the P-site. To obtain a set of well-defined substrates to study the kinetics of proper and false termination events these ribosomal complexes subsequently were separated from all other components by gel filtration (see Materials and Methods, ref. 14). The maximal rate of termination (kcat), the concentration of RF at half the maximal termination rate (KM), and the parameter for the efficiency of the termination reaction (kcat/KM) (3) were measured for RF1 and RF2 by acting on two subsets of ribosomal complexes either in the presence or absence of RF3. A typical experiment is shown in Fig. 1. The decrease in termination efficiency by mutation of a stop codon to a related sense codon is shown as fold reduction (A) in kcat/KM for RF1 in Table 1 and RF2 in Table 2. This reduction in kcat/KM is our measure of the accuracy (A) with which the RFs discriminate against false termination events at the chosen sense codons. At 37°C and in the absence of kinetic proofreading the value for ΔΔG is the upper limit for 0.619⋅ln(A) (from RT⋅ln(A)≤ΔΔG, see above). This compares standard free energies for the efficiency of termination at sense codons with those at stop codons. It is therefore a fundamental parameter for the characterization of RNA-sequence recognition.
The data reveal that the termination efficiencies of both RF1 and RF2 are most sensitive to first position changes in the stop codons. We first will focus on data obtained in the absence of RF3, where there is no GTP to drive a putative proofreading mechanism. When U is changed to A or G in the first position of the stop codon the efficiency of termination by RF1 is reduced below the detection limit, corresponding to an accuracy better than 106 (ΔΔG>8.6 kcal/mol) (Table 1), an experimental limit set by the rate of spontaneous peptidyl-tRNA dissociation from the ribosome (21). The same U to A or G changes in the first position reduce the efficiency of termination by RF2 somewhat less with accuracy values ranging from larger than 106 (for AAA) down to 1.5⋅105 (for GGA) (Table 2). RF1 discriminates against CAA and CAG codons corresponding to a U to C switch in first position with the remarkably high accuracy values of about 5⋅105 (ΔΔG>8.1 kcal/mol) whereas the corresponding pyrimidine to pyrimidine changes led to between 14,000- and 40,000-fold reductions for RF2.
For comparison, the efficiency of aminoacylation of T7-transcribed tRNAmMet by methionyl-tRNA synthetase is reduced 104-fold when the native CAU anticodon is changed to UAU and 1.2⋅105-fold when it is replaced by GAU (22). These data suggest that RF1 is much more sensitive and RF2 is moderately more sensitive to base changes in the first codon position than is methionyl-tRNA synthetase to base changes in the first position of the anticodon of tRNAmMet. Although a straightforward thermodynamic interpretation of these aminoacylation experiments cannot be made, because proofreading of the tRNAs may contribute to the selectivity of the methionyl-tRNA synthetase but not the RFs, the comparison highlights the remarkable codon recognition accuracy of RF1 and RF2.
Two hot spots for termination errors, one for each RF, can be identified immediately from Tables 1 and 2. Thus, in the case of RF1, termination accuracy at the UAU codon (Tyr) is as low as 1.1⋅103 (ΔΔG>4.3 kcal/mol) in the absence of RF3. For RF2 the most error-prone sense codon is UGG (Trp), where the accuracy without RF3 is 2.4⋅103 (ΔΔG>4.8 kcal/mol).
These effects of base changes in the stop codons can be compared with the magnitude of “context effects,” where bases adjacent to the stop codons are mutated. The effects of changing bases immediately downstream of stop codons on the termination efficiencies of RF1 and RF2 have been measured biochemically, and the largest context effect to be found is only a factor of 5 (18). This finding confirms that stop codons should be defined by their classical base triplets (23) and that nucleotide context can be responsible only for a fine-tuning of the termination reaction.
The accuracy of enzymatic selections normally depends on both binding parameters and catalytic rate constants (3). Termination of translation by RFs is a comparatively simple reaction. The binding contribution to accuracy therefore may be summarized as a fold increase in KM value and the contribution from catalytic rates by a fold decrease in kcat value when the RF target is changed from a stop to a sense codon. How the accuracy (Tables 1 and 2) is partitioned between binding and catalytic rate is shown in Table 3 for RF1 and Table 4 for RF2. For both RFs the KM values contribute by about 3 orders of magnitude to the accuracy with relatively small variations between codons. The kcat value reductions, in contrast, vary from about 2-fold to more than 1,000-fold. In other words, the kcat values determine the differences in termination efficiency at the different sense codons, whereas the KM values contribute a basic, and in most cases dominant, factor to the overall discrimination against near-cognate codons.
Table 3.
The fold change in kcat and KM for RF1 at codons differing from the RF1 stop codons (UAG and UAA) by 1 nt: The contribution to accuracy from kcat and KM
| Codon | Fold change in the kcat and KM parameters
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −RF3
|
+RF3
|
|||||||||||
| kcat | (σ) | KM | (σ) | kcat | (σ) | KM | (σ) | |||||
| AAA | * | * | * | * | ||||||||
| AAG | * | * | * | * | ||||||||
| GAA | * | * | 790 | 40 | 500 | 200 | ||||||
| GAG | * | * | 700 | 300 | 900 | 500 | ||||||
| CAA | 180 | 10 | 2,000 | 400 | 53 | 1 | 1,600 | 300 | ||||
| CAG | 160 | 10 | 3,000 | 1,000 | 52 | 2 | 1,700 | 200 | ||||
| UGA | 57 | 5 | 2,400 | 300 | 20 | 1 | 1,900 | 100 | ||||
| UGG | 38 | 2 | 1,250 | 70 | 15.2 | 0.8 | 760 | 30 | ||||
| UCA | 14.7 | 0.2 | 1,000 | 100 | 7.0 | 0.2 | 600 | 30 | ||||
| UCG | 19.3 | 0.8 | 990 | 60 | 8.6 | 0.3 | 600 | 50 | ||||
| UUA | 23 | 1 | 1,200 | 200 | 9.67 | 0.06 | 780 | 40 | ||||
| UUG | 12 | 1 | 1,060 | 50 | 5.3 | 0.7 | 690 | 10 | ||||
| UAC | 17.2 | 0.3 | 1,180 | 60 | 8.2 | 0.6 | 700 | 100 | ||||
| UAU | 2.5 | 0.1 | 400 | 100 | 2.1 | 0.2 | 170 | 70 | ||||
The results are the mean of three experiments with SD of the mean (σ). Unresolvable values are represented by *; see legend to Table 1. Bases in bold are those that differ from the sequence of a normal stop codon.
It is striking how U-to-purine changes in the first position cause huge drops in the kcat values, whereas the binding of RFs is reduced to about the same degree as for other less error-resistant sense codons. The fact that the transition state for hydrolysis of peptidyl-tRNA is so effectively blocked suggests that steric effects may play an important role in these cases.
RF2 recognizes UAA and UGA with about equal efficiency (14), so it might have been expected that the efficiency with which the factor reads the sense codons AAA and AGA or GAA and GGA would be similar. In contrast, we find that RF2 becomes much more error-prone when G rather than A is present in the second position, although both dinucleotides AA and AG are part of the normal stop codons of the factor (Table 4). A partial explanation may come from the recent observation (24) that RF2 has a 2-fold higher affinity for UGA than UAA after cleavage of the ester bond in peptidyl-tRNA.
Another unexpected result in Table 4 concerns reading of UUA and UCA by RF2. The overall termination efficiencies are very similar in these two cases (Table 2), but how the accuracy parameter is partitioned between binding and catalysis is radically different. The efficiency for UUA is reduced about equally by a KM increase and a kcat decrease, but for UCA almost the whole reduction in termination efficiency comes from a vast increase in KM. It is conceivable that the amine group of the C in UCA interferes strongly with the binding of RF2 to the ribosome, either by charge or by size. This interference might provide part of the explanation for this remarkable switch in rejection strategy by RF2 when dealing with two very similar sense codons.
RF3 Is Slightly Deleterious for the Accuracy of Termination.
A possible function of the G-protein RF3 is to provide the necessary thermodynamic driving force (7–9) for multiple step selection of RF1 or RF2 by linking GTP hydrolysis to termination of protein synthesis. The experiment in Fig. 1 and the data in Tables 1 and 2 show clearly that this is not the case, because the addition of RF3 always reduces the accuracy, in some instances as much as 5-fold. Thus bacterial RFs do not use kinetic proofreading to attain acceptable levels of termination accuracy. Because, in contrast, precise tRNA selection requires proofreading (4–6) these experiments suggest that very sequence-specific recognition of RNA may in general be more easily carried out by proteins than by RNA molecules.
These results might appear difficult to reconcile with previous findings that RF3 does not affect the kinetics of proper termination events with a stop codon in the A-site, and that the only role of RF3 seems to be to stimulate release of RF1 or RF2 after hydrolysis of peptidyl-tRNA (14). A likely explanation for this asymmetry with respect to the action of RF3 between termination at stop and sense codons is that a noncognate enzymatic reaction is in general more sensitive to small perturbations in substrate binding than a cognate one. One clear conclusion that can be drawn from the results in Tables 1–4 is that RF3 must be able to bind to ribosomes before cleavage of peptidyl-tRNA, which is consistent with the previous conclusion that RF3 together with ribosome release factor (RRF) and EF-G stimulates drop-off of peptidyl-tRNA from the ribosome (16, 21).
The hot spots mentioned above for termination errors at Tyr (UAU) and Trp (UGG) codons are even more pronounced in the presence of RF3, with the accuracy in the case of UAU as low as 400 (Table 1). At first sight, it might appear that the data obtained in the presence of RF3 would be those most relevant to the situation in vivo, because the factor normally is present in bacteria (11–13). However, this conclusion should be treated with caution, because our biochemical experiments all were carried out with a tetrapeptidyl-tRNA in the A-site, and the ability of RF3 to interfere with termination events at sense codons may well depend on the length of the peptide chain in peptidyl-tRNA.
Discussion
RFs achieve a remarkable level of accuracy and do so without proofreading. Thus, the accuracy parameters in Tables 1–4 are directly interpretable in terms of ΔΔG values for cognate and near-cognate termination events. It seems unlikely that H-bonds can explain the values of more than 8 kcal/mol that separate the termination reaction at CAA/G from that at UAA/G (Tables 1 and 3). It therefore will be an experimental challenge to determine the molecular basis for the impressive degree of discrimination shown by RF1 against certain near-cognate codons. No comparable systematic measurements of error in aminoacyl-tRNA/EF-Tu/GTP ternary complex selection have been made. From the scarce data that exist (refs. 4 and 25; R. Karimi and D.V.F., unpublished results), one tentatively may conclude that tRNAs have the same ability to discriminate between their own and neighboring codons as RFs. However, the fact that tRNAs achieve this with the help of proofreading suggests that the ΔΔG values available for tRNA–mRNA interactions are inherently smaller than those that have evolved for protein–RNA interactions.
It is conceivable that when large ΔΔG values evolve there is a price to be paid. The efficiency of binding (kcat/KM) of RFs to ribosomes programmed with stop codons is comparable to that found for the binding of aminoacyl-tRNAs in complex with EF-Tu and GTP to ribosomes programmed with their corresponding sense codons (14, 26). However, the downstream processing of ternary complexes is much faster than the hydrolytic reaction of peptidyl-tRNA induced by RFs. After binding of a ternary complex containing Phe-tRNAPhe to the A-site the peptidyl-transfer reaction is completed after 30 ms on the average (26). In contrast, RF1 requires as long as 2.0 s to hydrolyze peptidyl-tRNA and RF2 as long as 0.7 s. Both of these minimal termination times are, therefore, very much longer than the time needed for a tRNA to accept a nascent oligopeptide after its first contact with the ribosome. To our knowledge, there exists no strict physical argument implying that a high ΔΔG value for an enzymatic selection must be associated with a slow catalytic rate constant. However, from these data it is tempting to suggest that such a constraint may indeed exist and that the very high ΔΔG values developed by both RFs are fundamentally linked to their poor catalytic performance.
The error spectra for RF1 and RF2 presented here can be used to predict processivity errors in vivo because of RF-dependent errors. The processivity errors for the set of all E. coli proteins (27) were calculated by using the kcat/Km values for the RFs in Tables 1 and 2, previously reported RF1 and RF2 concentrations (15), and tRNA isoacceptor levels reported by Dong et al. (28). Assuming that all ternary complexes have the same kcat/Km value (2.2⋅107 M−1⋅s−1) for their cognate interactions with the ribosome (29), the expected frequency of false stops in E. coli proteins is approximately proportional to sequence length, reaching about 20% for proteins of 1,500 aa. In the case of individual proteins, the predicted processivity errors depend strongly on the highly variable content of UAU and UGG codons. These calculated values may be compared with the frequency of RF1-dependent false stops in β-galactosidase observed by Jørgensen et al. (15), who reported that the processivity of β-galactosidase synthesis is reduced from 60% to 30% when RF1 is overproduced by a factor of about 35. From our in vitro results a similar drop in processivity is obtained for this protein by a simulated 12-fold overproduction of RF1, a difference that is not unexpected in view of the numerous assumptions required to compare these two sets of data. In either case, it is clear that the specificity of recognition by RFs is such that only a small proportion of processivity failures can be attributed to the action of chromosomally expressed factors.
The finding that two sense codons alone among the set that we have studied are likely to be responsible for about 50% of RF-dependent false stops in E. coli may have evolutionary implications. It is clear that the choice of codons for both Trp and Tyr, and the meaning of the stop codons that signal stop in the “near-universal” genetic code are subject to variation (30). Thus, UGA encodes Trp in some Mycoplasma and nonplant mitochondria and UAA codes for Tyr in planaria. Indeed it has been suggested that all four codons of the UAN family coded for stop in an archetypal code, before the capture of UAU and UAC as Tyr codons (30), a scenario that goes far to explain the behavior of UAU as a hot spot for errors of recognition by RF1.
Acknowledgments
We thank Dr. Richard Giegé, Strasbourg, France, for comments and suggestions. This work was supported by the Swedish Natural Science Research Council, the Swedish Research Council for Engineering Sciences, and the Centre National de la Recherche Scientifique, France (UPR9073).
Abbreviations
- RF
release factor
- EF
elongation factor
Footnotes
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.030541097.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.030541097
References
- 1.Pauling L. Festschrift Arthur Stoll. Basel: Birkhauser; 1957. pp. 597–602. [Google Scholar]
- 2.Fersht A R. Proc R Soc London Ser B. 1981;212:351–379. doi: 10.1098/rspb.1981.0044. [DOI] [PubMed] [Google Scholar]
- 3.Fersht A. Enzyme Structure and Mechanism. San Francisco: Freeman; 1977. [Google Scholar]
- 4.Thompson R C, Stone P J. Proc Natl Acad Sci USA. 1977;74:198–201. doi: 10.1073/pnas.74.1.198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Thompson R C, Dix D B, Eccleston J F. J Biol Chem. 1980;255:11088–11090. [PubMed] [Google Scholar]
- 6.Ruusala T, Ehrenberg M, Kurland C G. EMBO J. 1982;1:741–745. doi: 10.1002/j.1460-2075.1982.tb01240.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ninio J. Biochimie. 1975;57:587–595. doi: 10.1016/s0300-9084(75)80139-8. [DOI] [PubMed] [Google Scholar]
- 8.Hopfield J J. Proc Natl Acad Sci USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ehrenberg M, Blomberg C. Biophys J. 1980;31:333–358. doi: 10.1016/S0006-3495(80)85063-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Scolnick E M, Tompkins R, Caskey C T, Nirenberg M. Proc Natl Acad Sci USA. 1968;61:768–774. doi: 10.1073/pnas.61.2.768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mikuni O, Ito K, Moffat J, Matsumura K, McCaughan K, Nobukuni T, Tate W, Nakamura Y. Proc Natl Acad Sci USA. 1994;91:5798–5802. doi: 10.1073/pnas.91.13.5798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Milman G, Goldstein J, Scolnick E, Caskey T. Proc Natl Acad Sci USA. 1969;63:183–190. doi: 10.1073/pnas.63.1.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grentzmann G, Brechemier-Baey D, Heurgué V, Mora L, Buckingham R H. Proc Natl Acad Sci USA. 1994;91:5848–5852. doi: 10.1073/pnas.91.13.5848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Freistroffer D V, Pavlov M Y, MacDougall J, Buckingham R H, Ehrenberg M. EMBO J. 1997;16:4126–4133. doi: 10.1093/emboj/16.13.4126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jørgensen F, Adamski F M, Tate W P, Kurland C G. J Mol Biol. 1993;230:41–50. doi: 10.1006/jmbi.1993.1124. [DOI] [PubMed] [Google Scholar]
- 16.Dinçbas V, Heurgué-Hamard V, Buckingham R H, Karimi R, Ehrenberg M. J Mol Biol. 1999;291:745–759. doi: 10.1006/jmbi.1999.3028. [DOI] [PubMed] [Google Scholar]
- 17.Mikuni O, Kawakami K, Nakamura Y. Biochimie. 1991;73:1509–1516. doi: 10.1016/0300-9084(91)90185-4. [DOI] [PubMed] [Google Scholar]
- 18.Pavlov M Y, Freistroffer D V, Dincbas V, MacDougall J, Buckingham R H, Ehrenberg M. J Mol Biol. 1998;284:579–590. doi: 10.1006/jmbi.1998.2220. [DOI] [PubMed] [Google Scholar]
- 19.Uno M, Ito K, Nakamura Y. Biochimie. 1996;78:935–944. doi: 10.1016/s0300-9084(97)86715-6. [DOI] [PubMed] [Google Scholar]
- 20.Karimi R, Pavlov M, Buckingham R H, Ehrenberg M. Mol Cell. 1999;3:601–609. doi: 10.1016/s1097-2765(00)80353-6. [DOI] [PubMed] [Google Scholar]
- 21.Heurgué-Hamard V, Karimi R, Mora L, MacDougall J, Leboeuf C, Grentzmann G, Ehrenberg M, Buckingham R H. EMBO J. 1998;17:808–816. doi: 10.1093/emboj/17.3.808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schulman L H, Pelka H. Science. 1988;242:765–768. doi: 10.1126/science.3055296. [DOI] [PubMed] [Google Scholar]
- 23.Nirenberg M, Leder P. Science. 1964;145:1399–1407. doi: 10.1126/science.145.3639.1399. [DOI] [PubMed] [Google Scholar]
- 24.Pavlov M Y, Freistroffer D V, Heurgué-Hamard V, Buckingham R H, Ehrenberg M. J Mol Biol. 1997;273:389–401. doi: 10.1006/jmbi.1997.1324. [DOI] [PubMed] [Google Scholar]
- 25.Dix D B, Thompson R C. Proc Natl Acad Sci USA. 1989;86:6888–6892. doi: 10.1073/pnas.86.18.6888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bilgin N, Claesens F, Pahverk H, Ehrenberg M. J Mol Biol. 1992;224:1011–1027. doi: 10.1016/0022-2836(92)90466-w. [DOI] [PubMed] [Google Scholar]
- 27.Berg O G, Silva P J. Nucleic Acids Res. 1997;25:1397–1404. doi: 10.1093/nar/25.7.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dong H, Nilsson L, Kurland C G. J Mol Biol. 1996;260:649–663. doi: 10.1006/jmbi.1996.0428. [DOI] [PubMed] [Google Scholar]
- 29.Diaz I, Ehrenberg M, Kurland C G. Mol Gen Genet. 1986;202:207–211. doi: 10.1007/BF00331638. [DOI] [PubMed] [Google Scholar]
- 30.Osawa S, Jukes T S, Watanabe K, Muto A. Microbiol Rev. 1992;56:229–264. doi: 10.1128/mr.56.1.229-264.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]