Roles of discontinuities in bio-inspired adhesive pads

Abstract

Morphological intricacies of the biological attachment pads generate considerable interest owing to their remarkable ability to control adhesion to various surfaces. Motivated by the adhesive microstructures of insects, we examine the behaviour of adhesion and crack propagation in patterned adhesive films. These films are made of silicone elastomers that were patterned with lateral, longitudinal or crosswise incisions from which a thin silanized glass plate was removed in a displacement-controlled peel experiment. The behaviours of crack propagation on these patterned adhesive films are controlled by simple incision patterns, their depths and spacing. With the crosswise incisions, significant enhancement (×10–20) of fracture energy has been achieved. These findings point towards an important mechanism by which of biological organisms might enhance adhesion, and provide a simple design principle for manipulating the interfacial fracture in a variety of artificial attachment devices.

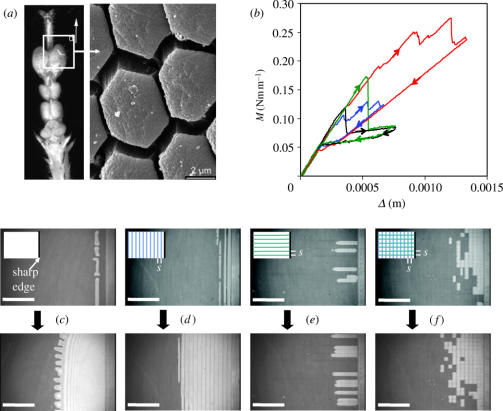
Biological attachment pads, which present a variety of microscopically textured surfaces, are abundant in nature (Ruibal & Ernst 1965; Autumn et al. 2000, 2002; Scherge & Gorb 2000, 2001; Federle et al. 2001). Their structural morphologies endow exceptional ability to biological species in creating strong attachment to, and easy detachment from, various surfaces. The design principles of the adhesive pads of motile biological species are in contrast to those of man-made adhesives, in which the roles of viscoelasticity and chemical interactions predominate. While chemical interactions and viscoelasticity effectively enhance adhesion strength, they either lead to irreversible bonds and/or increase the interfacial relaxation time to such an extent that they are not optimum for biological adhesion and locomotion. Apart from the fact that the viscoelastic adhesives are prone to fouling by particulate contamination, its greatest drawback might be that the adhesion strength is rate dependent, thus requiring a nonlinear control of locomotion in order to achieve desired speeds. Nature has devised ways (Scherge & Gorb 2001; Autumn et al. 2002) to optimize adhesion using the simplest denominators of material properties of adhesives—elasticity and van der Waals forces coupled with structural morphology—in that the attachment and detachment processes could be controlled linearly by manipulating the mode (e.g. peel angle, shear versus normal traction) of remote loading.1 A particular kind of attachment pad is found in the bush cricket (Scherge & Gorb 2000, 2001), which is segmented and exhibits hexagonal symmetry (see figure 3). Despite considerable interest generated in this and other types of structural morphologies found in the insect world, we know little about the mechanisms of crack initiation and propagation with such textured surfaces.

Figure 3.

(a) Scanning electron micrograph of the Tarsus of the leg of a bush cricket (reproduced with kind permission from S. Gorb (Scherge & Gorb 2000)). We are trying to mimic the adhesion originating from the discontinuities resulting from such segmentation. (b) The peeling moment, M, as a function of the plate displacement, Δ, for differently incised films made of PDMS of shear modulus 0.9 MPa and thickness 305 μm, using cover plate of rigidity D=0.05 Nm. All incisions were made to a maximum depth δ of ∼100 μm with the lateral and longitudinal spacing (s) of ∼250 μm each. Black curve: no incision, edge crack; blue curve: multiple lateral incisions; green curve: multiple longitudinal incisions; red curve: multiple crosswise incisions. (c)–(f) Sequences of the crack opening modes: (c) edge crack, (d) lateral incisions, (e) longitudinal incisions and (f) crosswise incisions. The scale bars in (c)–(f) are 2 mm. In all cases, the crack propagates from right to left.

Recently, motivated by the exquisite structural morphologies of insect adhesive pads, we studied the behaviour of the initiation and propagation of cracks in thin elastomeric films (shear modulus μ, thickness h) endowed with sharp discontinuities (Ghatak et al. 2004). A brief summary of the previous observations and the main results are given in the following paragraph. When a flexible glass plate is removed from a bonded thin PDMS (polydimethylsiloxane) film having an edge crack, the moment (M) on the cantilever increases with displacement (Δ) almost linearly up to the point of crack initiation. Concomitantly, bubbles are formed (Ghatak & Chaudhury 2003; Ghatak et al. 2004) just behind the film edge (figure 1), which grow and coalesce to form two viable cracks. When one of these cracks is annihilated at the free edge of the film, the applied moment drops, as the other crack continues to propagate on the smooth part of the film accompanied with a wavy undulation (Ghatak et al. 2000) of the contact line.

Figure 1.

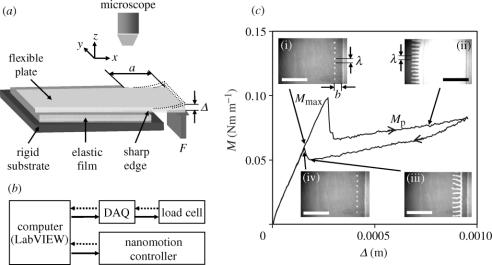
(a) (b) Schematic of the displacement controlled peel experiment ((a) is reproduced from Ghatak et al. 2004) in which the free edge of a flexible plate adhering to the elastomeric (PDMS) film is delaminated at a constant rate of 5 μm s⁻¹. The elastomeric film bonded to the lower rigid substrate may have either a sharp edge or be decorated with incision (see figure 3). (c) illustrates the moment–displacement (M–Δ) data of a thin silanized glass plate of flexural rigidity 0.05 Nm peeling from a PDMS film (thickness 150 μm, shear modulus 0.9 MPa) having an edge crack. During the delamination cycle, bubbles first nucleate (i) at a distance b inside the sharp edge, followed by their growth and coalescence as reported in Ghatak et al. (2004). At the onset of crack propagation, M reaches its maximum value (M_max). Once the crack opens up, it propagates (ii) on the smooth adhesive film with a lower M (M_p). The slight upward slope of M is owing to the fact that the energy release rate in this phase is not entirely given by the bent plate, but contributed by the shear deformation of the PDMS film as well. The above sequence can be reversed by decreasing the plate displacement Δ (iiiiv). The degree of the reversibility of the crack opening and closing are illustrated in the M–Δ plots. The scale bars in (c) are 3 mm.

Before describing the motivation and the details of the current studies, it would be instructive to consider figure 1, which summarizes the results of a peel experiment very much like those reported previously (Ghatak & Chaudhury 2003; Ghatak et al. 2004), but with some important further insights. In particular, when a silanized glass plate of flexural rigidity (D) is removed from the PDMS film, the moment (M) rises sharply and then falls as the crack continues to propagate. Here, we also report the healing of the crack resulting from the decrease of the external moment. We note that the morphological features of the instability and its evolution from cavitation bubbles to fingering patterns are also reversible. The crack opening and healing, however, exhibit a small hysteresis of the peeling moment giving rise to the corresponding fracture energies (∼M²/2D) of 55 and 36 mJ m⁻², respectively. The fact that these fracture energies are close to its thermodynamic work of adhesion (∼44 mJ m⁻²; Vorvolakos & Chaudhury 2003) indicates that the interfacial fracture toughness is essentially reversible with only a small dissipation. The significant hysteresis in the overshoot of the peeling moment during the initiation and final disappearance of the crack, on the other hand, is mechanical and not entirely interfacial. An important objective of the current study is to augment and sustain this dissipation in order to achieve an overall enhancement of fracture toughness.

Ghatak et al. (2004) already pointed out that multiple incisions in the adhesive film cause interfacial delamination to occur in an intermittent manner involving sequential events of initiation, propagation and arrest of crack. It was conjectured that the spacing between the incisions should be smaller than the characteristic length (k⁻¹) of stress decay (Dillard 1989) for the enhancement of fracture toughness. In this paper, we redress the problem by studying more carefully the mechanisms of the initiation and propagation of crack on PDMS films by systematically varying the spacing of the incisions in the lateral and longitudinal directions. Once the relevant length-scales are identified, we use them to create crosswise incision patterns and study how the fracture toughness can be further enhanced by varying the thickness of the PDMS film.

Before describing the details of these experiments, it would be instructive to consider the profiles of the stress (σ) that develop in thin films along the length of the cantilever by solving the beam equation:

$$\sigma =D{\xi }_{xxxx}.$$ (1) (1)

Here, ξ is the displacement of the plate–film interface from its undisturbed state as a function of x, measured parallel to the interface from the edge of the film, and D is the flexural rigidity of the plate. The plate–film interface is represented by x<0, and that of the free plate as x>0. ξ_xxxx indicates the fourth derivative, d⁴ξ/dx⁴. The above equation needs to be solved in conjunction with the following sets of equations (see Dillard 1989; Ghatak et al. 2004, and the references therein):

$${\xi }_{xxxxxx}-\frac{12\mu }{D{h}^3}\xi =0\text{for}x<0,$$ (2) (2)

$${\xi }_{xxxx}=0\text{for}0<x<a,$$ (3) (3)

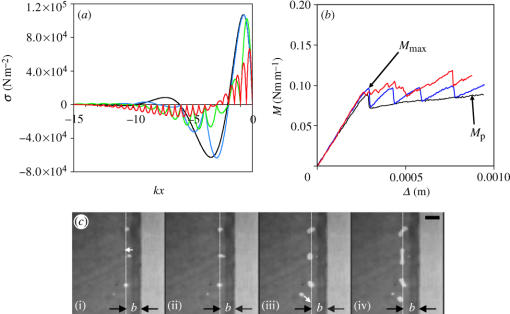
subject to the following boundary conditions: the displacement, slope, bending moment, vertical shear force and pressure at the edge and incisions are continuous; the pressure vanishes at the edge, incisions and at infinity; the pressure gradient vanishes at infinity, and the integral of the stress in the plate ${\int }_{-\infty }^0\sigma \text{d}x$ yields the force F applied at its end (x=a). We begin by defining a dimensionless system parameter (sk), which is the ratio of the separation distance between lateral incisions (s) to the stress decay length k⁻¹=(Dh³/12μ)^1/6. The condition sk=∞ implies the limiting case of a single edge discontinuity for which the normal traction exhibits alternating regions of tension and compression (figure 2). The traction attains a maximum positive value at a distance b from the edge, where bubbles cavitate. With large incision spacing (sk=2), cavitating bubbles still appear at the same distance behind the incision (figure 1b). The regular spacing of the bubbles is, however, determined by another periodic stress profile that develops in the film at x=−b owing to its geometric confinement in the y direction.2 This stress profile is $\sigma \approx {\sigma }_{\text{m}}+(Ev/h)\text{sin}(2\pi y/\lambda )$, where σ_m is the maximum tensile stress at x=−b, v/h is the ratio of the amplitude of deformation to the thickness of the film, and λ is the wavelength of perturbation that characterizes the instability in terms of cavitation spacing and fingering width. As a result of the superposition of the above two, the resultant stress profile at the film–substrate interface is two-dimensional, with pressure cusps lining up parallel to the edge at x=−b. Interfacial migrations of bubbles (figure 2c) nucleated occasionally from random defect sites to specific locations at x=−b, providing evidence for the existence of these minimum pressure cusps.

Figure 2.

(a) Variation of the normal stress at the interface between the rigid plate and the laterally incised elastomeric film as a function of dimensionless distance from the edge (kx), showing alternating regions of tension and compression. The bubbles nucleate where the tensile stress is maximum, which is slightly inside the edge of the film. These calculations are done for sk=∞ (black), sk=2.0 (blue), sk=1.0 (green) and sk=0.5 (red). (b) The moment–displacement (M–Δ) data for the PDMS films (h=150 μm, μ=0.9 MPa) of different incision widths (black: sk=∞, blue: sk=10, and red: sk=0.5). The saw-tooth characteristics in the blue curve can be decomposed into individual behaviours of edge cracks having different initial arm lengths. When sk=0.5, we see stick–slip behaviour that involves saw-tooth-like peaks with much smaller amplitude. The crack propagation moment is maintained nearly at the same level as that of the crack initiation moment (M_max). (c) The bubbles, cavitated either right or left of the line denoted as x=−b, move towards the line where the pressure has a local minimum. The scale bar in (c) is 300 μm.

When the incision spacing becomes comparable to, or less than, the stress decay length (sk=1.0 and 0.5), the stress profile (along x) is altered dramatically, in which the distance b is restricted by the spacing of the incisions. Evidently, (figure 2a) the maximum tensile stress produced for sk=0.5 is lower than for sk=∞ with the same amount of applied external moment. Thus, in order to raise the tensile stress to the level required for crack propagation, a moderately larger external moment would be required for sk=0.5 than for sk=∞. Figure 2b summarizes the crack initiation and propagation results for sk=(0.5, 10 and ∞). While the crack propagates in a saw-tooth manner for sk=10 (figure 2b), we see stick–slip behaviour for sk=0.5 that involves saw-tooth-like peaks with much smaller amplitudes. In the latter case, the bubbles cavitate between the incisions but, as they coalesce, they grow laterally rather rapidly as the peeling continues. Nevertheless, because of the close proximity of the next incised segment, bubble nucleation proceeds in successive segments without allowing the external moment to drop to a lower value. Consequently, the average crack propagation moment on the film with lateral incisions is larger than that of the smooth film.

The enhancement of the fracture toughness of those with either the edge crack (during the initiation stage) or those with the multiple incisions via bubble nucleation are closely related to the Cook–Gordon mechanism (Gordon 1976) of the toughening of composite laminates. According to this picture, when a crack penetrates a laminate, defects are nucleated at the interface ahead of the crack, which then deflects the crack parallel to the interface, thus preventing its catastrophic penetration through the laminate. Our experiment is a two-dimensional version of the Cook–Gordon mechanism, in which both the propagation and deflection of the crack occur at the interface itself. Formation of this defect is controlled by local cohesive stress rather than the intrinsic fracture toughness of the interface (Hill et al. 2003). It is important to recognize that no real crack actually penetrates the interface along the delamination direction for sk=0.5. Instead, a virtual crack propagates as a result of the growth of the coalesced bubbles at each segment parallel to the incisions. This is in striking contrast to the case with sk=10, in which a real crack propagates intermittently from one incision to next, so that it is cohesive stress controlled at the incision but interfacial toughness controlled while in transit. Combination of these effects gives rise to the saw-tooth profile to the external moment.

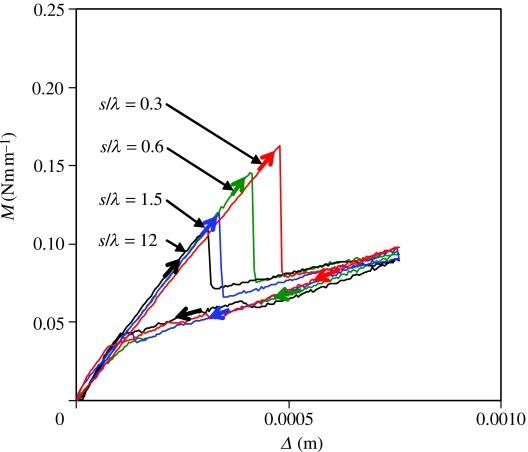
From the above observations, it can be inferred that the overall crack initiation moment could be enhanced if the lateral growth of the coalesced bubbles could be inhibited, which is exactly what happens with longitudinal incisions in the film (figure 3). Here, although the overall crack initiation behaviour is similar to that of an edge crack, the initiation moment is enhanced as the applied force must support the cohesive stresses of all the cracks at the incised segments. Note that the crack opening and closing behaviours as well as the corresponding M–Δ data on the longitudinally incised film are same as those on the smooth film without any incisions (figure 3b). Here again, the Cook–Gordon mechanism is in action in enhancing the crack initiation moment. However, after the crack is fully initiated at the interface, there is no mechanism to deflect the crack; thus the fracture toughness of the propagating crack is same as that of the smooth interface. At this juncture, one may ponder what the cut-off length-scale of the longitudinal incision is above which no enhancement of crack initiation moment occurs. This length-scale should be the wavelength of elastic instability of (λ∼4h). The ratio of the incision spacing to the instability wavelength (s/λ) defines the degree of lateral confinement in the film. For s/λ>1, the film is highly confined, i.e. all the parts of the film communicate with each other via a shear stress field, for which no significant enhancement of the crack initiation moment is expected. However, for s/λ<1, the segments behave independently, causing the crack initiation moment to increase beyond what is found with the edge crack. This expectation has been verified with experiments with PDMS films of different thicknesses. A typical result is shown in figure 4.

Figure 4.

Effect of the longitudinal incision spacing on the crack initiation moment of a PDMS film of 200 μm thickness. Here, λ(∼4h or 800 μm) is the wavelength of instability (see figure 1). The ratio s/λ defines the degree of stress confinement of the film in the lateral direction. Note that the incision spacing has very little effect on crack initiation moment when s/λ>1. Significant increase in moment occurs for s/λ<1.

The behaviours of the crack propagation on the laterally and longitudinally patterned films immediately suggest that the maximum effect of discontinuity can be gained by creating incisions in a crosswise manner, with the longitudinal and lateral length-scales less than k⁻¹ and λ, respectively. Indeed, as shown in figure 3b, significant enhancement of the crack initiation moment occurs with crosswise incision, resulting in an appreciable augmentation (×10) of fracture energy (M²/2D). The movement of the crack on such a film, however, does not occur smoothly; it exhibits a stick–slip-type instability. As shown in figure 3f, the bubbles first cavitate between incisions, and subsequently are arrested, increasing the external moment (‘stick’ event). As the moment continues to increase, a threshold point is reached when the contacting segments surrounded by the incisions open up, thus releasing much of energy stored in the system (‘slip’ event) up to this point. As the crack slows down, the above process repeats again. The factors that govern these instabilities appear to be the depth and spacing of incisions that control the frictional sliding3 of PDMS in the incised zone, which determine the extent to which the segments respond to normal stress.

The three types of experiments described in figure 3 illustrate two important modes of the enhancement of fracture toughness in these systems. The incisions in the film parallel to the edge serve to deflect the crack laterally, thus preventing its catastrophic penetration at the interface perpendicular to the edge. The incisions perpendicular to the edge, on the other hand, only delay the crack initiation to higher stress without affecting the intrinsic toughness of the interface. The best result is clearly observed with crosswise incisions, in which the high initiation stress is sustained while the virtual crack propagates through the interface.

Coupled to the above scenario is the mechanism of energy dissipation in the film that is the key to the enhancement of fracture energy. An effectively equal amount of surface area is created with both the smooth films and those with crosswise incisions, each requiring only about 44 mJ m⁻² of interfacial energy. However, a four‐ to fivefold increase in the crack propagation moment translates into an amplification of the fracture energy by a factor of 16 to 25. Where did all the extra energy go? The answer to this question may be found in the macroscopic version of the Lake–Thomas effect (Lake & Thomas 1967). For a crack propagating on a smooth film, the strain energy at the crack tip zone reaches a critical level that is sustained as long as the crack propagates along a continuous interface. As soon as a discontinuity is encountered, the segments ahead of and at the rear of the crack behave independently. The stressed segment behind the crack relaxes at zero load, thus dissipating the stored elastic energy, whereas the segment ahead of the crack has to be stressed and re-initiated for the process to repeat itself. The cohesive stress in this case is distributed nearly equally in all of the segments bridging the crack, so that the effective stress is the areal density of the segments times the force supported by each of them. The failures of a few segments in the extended cohesive zone do not matter much, just as the failure of a few strands of fibre in a rope does not affect its overall strength (Kendall 2001). This is the consequence of equal load sharing that underlies the enhanced fracture toughness of ropes, polymer craze, pressure sensitive adhesives (Kendall 2001), fibrillar adhesives (Glassmaker et al. 2004), as well as the cross-linked rubbery networks (Lake & Thomas 1967).

Dissipation of elastic energy by a macroscopic relaxation process is evident in an elegant experiment reported by Hill et al. (2003), in which a wedge crack was initiated in a double cantilever beam geometry of mica. Farther ahead of the crack, a defect was produced by inserting a thin fibre in between the two mica films. As the external crack approached the internal crack, its growth was retarded by the defect, producing an increase in the fracture resistance. At this point the surfaces of the mica in between the two cracks are held together by the cohesive forces. With continued loading, as the two cracks coalesce, the adhered segments of the mica films pop out of contact at zero load, thereby dissipating some of its elastic energy. Our experimental results are similar to that of Hill et al. (2003); the main difference is that a pre-formed crack existed in the former, but they naturally arose, owing to instabilities in our experiment.

In view of the above experiments, it is important to know what fraction of the energy dissipation in our experiment is owing to the relaxation of the beam and what is owing to the stretching and relaxation of the elastomeric segments. An approximate analysis of the problem can be done by comparing the spring constant (k₁) of the PDMS segments (μs²/δ) with that (k₂) of the cantilever (D/s²). Using the typical values of μ, s, D and δ as 1 MPa, 200 μm, 0.05 Nm and 100 μm, we find that the ratio k₂/k₁ is ∼10³. Since the spring constant of the cantilever is much larger than that of the PDMS segment, the ratio of the energy dissipations resulting from the relaxations of the beam and the PDMS segment on the order of k₁/k₂, which is negligible. Thus the source of primary dissipation appears to be in the elastomer, which is on the order of $\sim {\sigma }_{\text{c}}^2\delta /6\mu$, σ_c being the critical stress at which the elastomeric segment dissociates from the glass surface and δ the depth of incision.

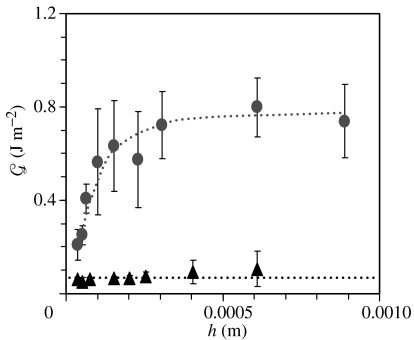
Experiments carried out with PDMS of various incision depths corroborate with the above expectation quite nicely. As shown in figure 5, the fracture energy increases almost linearly with the film thickness (h) as long as h<δ (100 μm). These values extrapolated to zero δ (in this case h) yield a fracture energy ($\mathcal{G}$∼0.05 J m⁻²) corresponding to that of the smooth interface. However, as the thickness of the film becomes larger than δ, $\mathcal{G}$ becomes independent of film thickness. The plateau value of the fracture energy is nearly 16 times higher than that observed with the smooth films. From the slope (${\sigma }_{\text{c}}^2/6\mu$∼5×10³ N m⁻²) of the linear part of the $\mathcal{G}$–δ plots in figure 5, the critical cohesive stress is estimated to be only about 160 kPa, which is about 2.5 times higher than that (60 kPa) of a cavitation-initiated twin cracks (Ghatak et al. 2004) for sk=∞. This difference may be attributed to larger numbers of cracks that are produced in crosswise incisions compared with that in an edge crack. Distribution of loads in multiple cracks on a discontinuous film is just one of the mechanisms for enhancing fracture toughness of interfaces. Pioneering studies of Kendall (1975) suggest that sharp gradients of either the film thickness or the elastic properties could also lead to an enhancement of fracture toughness of composite interfaces. There is also theoretical and experimental evidence that a surface comprising long fibrils (Geim et al. 2003; Persson 2003; Sitti & Fearing 2003; Glassmaker et al. 2004; Peressadko & Gorb 2004) could enhance fracture toughness by the mechanism of load sharing. Some of the mechanical subtleties of these fibrillar adhesives are different from the case studied here as the diameter to length ratios of these fibrils is vanishingly small.

Figure 5.

Average fracture energy ($\mathcal{G}$) of crosswise incised films (μ=0.9 MPa) as a function of film thickness (h; circles). All of incisions were made to a maximum depth δ of ∼100 μm and spacing (s) of ∼250 μm. When h<100 μm (δ=h), the film has low fracture energy but the energy increases with the film thickness. When h>100 μm, $\mathcal{G}$ slowly reaches a plateau. This suggests that the fracture energy is strongly dependent on the incision depth. Error bars represent the standard deviation about the average fracture energy, which represents the magnitude of the stick–slip instability. The triangles represent the fracture energies of the smooth films that do not depend on h.

To summarize, these studies demonstrate that the crack initiation and propagation on adhesive films patterned with discontinuities behave quite differently from smooth films. While an array of lateral or longitudinal incisions are effective in pinning the crack, the best result is obtained with crosswise incisions, which pin the crack in two orthogonal directions. From the results of these model studies, we surmise that the segmented adhesive pads of biological organisms could likewise arrest crack growth. The hexagonal symmetry of the segmented morphology in a bush cricket could give rise to greater isotropy than can be achieved with our square-like patterns. Whether these or other insects take advantage of stick–slip instability is unknown to us. The design of adhesive pads with such instability could be useful in terms of gaining high initiation force, which is conducive to strong attachment, but minimizing the net energy expenditure during the detachment process. Smooth peeling, nonetheless, can be engineered using spatial isotropy, decreasing the depth of discontinuity and finally eliminating the sliding contact of the discrete segments. Our ongoing studies show that the stick–slip instability can indeed be reduced or eliminated altogether by lithographically designed patterns in which both the incision depth and the sliding of the incised polymer segments can be controlled (see Electronic Appendix).