Abstract
The stochastic partial differential equations (SPDEs) stated by Steyn-Ross and co-workers constitute a model of mesoscopic electrical activity of the human cortex. A simplification in which spatial variation and stochastic input are neglected yields ordinary differential equations (ODEs), which are amenable to analysis by techniques of dynamical systems theory. Bifurcation diagrams are developed for the ODEs with increased subcortical excitation, showing that the model predicts oscillatory electrical activity in a large range of parameters. The full SPDEs with increased subcortical excitation produce travelling waves of electrical activity. These model results are compared with electrocortical data recorded at two subdural electrodes from a human subject undergoing a seizure. The model and observational results agree in two important respects during seizure: (i) the average frequency of maximum power, and (ii) the speed of spatial propagation of voltage peaks. This suggests that seizing activity on the human cortex may be understood as an example of pathological pattern formation. Included is a discussion of the applications and limitations of these results.
Keywords: mesoscopic cortical dynamics, dynamical systems theory, electrocorticogram, epilepsy, seizures, pattern formation
1. Introduction
Over 50 million people worldwide suffer from epilepsy, a debilitating condition of chronic unprovoked seizures. There exist many different classifications of seizures (e.g. simple partial seizures, complex partial seizures, generalized seizures), yet all seizures share the general characteristic of inducing a hyperexcitation of the cortex (the outer few millimetres of the brain). The microscopic behaviour of individual cortical neurons during this hyperexcitation is well documented and is the basis for some drug treatments. However, comprehensive microscopic recordings are infeasible, especially in human patients. Therefore, physicians record the macroscopic electrical behaviour of the seizing human cortex and collect the scalp electroencephalogram (EEG) and electrocorticogram (ECoG). At this macroscopic level, which involves interactions between millions of individual neurons, cortical seizures are less well understood (Quyen et al. 2003).
In this paper, we describe a model of the mesoscopic electrical behaviour of the seizing human cortex. We employ a recently developed continuum model of cortical electrical activity, which consists of a system of stochastic partial differential equations (SPDEs; Steyn-Ross et al. 2003). These SPDEs (and the related ordinary differential equations; ODEs) have been successfully applied to study the electrical properties of the anaesthetized human cortex (i.e. the anaesthetodynamic model of cortical function). In a series of papers, Steyn-Ross and colleagues showed that the model equations predict changes in the scalp EEG of anaesthetized patients consistent with experimental results (Steyn-Ross et al. 1999, 2001a,b, 2003).
Here, we consider whether these SPDEs can model the mesoscopic electrical behaviour recorded from the human cortex during a seizure. Our methods differ from previous discussions. We do not assume that some variables equilibrate much faster than others (the slow-membrane or adiabatic approximation; Steyn-Ross et al. 1999), nor do we apply techniques of stochastic calculus (such as the Ornstein–Uhlenbeck equation) to the linearized SPDEs (Steyn-Ross et al. 2003). Instead, we approach the SPDEs from a dynamical systems perspective and employ ideas and tools from bifurcation theory. We show that in some parameter regimes, the SPDEs predict pathological oscillatory behaviour—characterized by a bifurcation to a large-amplitude, coherent travelling wave against a background of spatio-temporal fluctuations—in some important ways consistent with ECoG recordings from the seizing cortex.
The organization of this paper is as follows. In §2, we discuss clinical ECoG data recorded at two subdural electrodes from a human subject during his typical complex partial seizures. In §3, we review the model equations, the dimensionless SPDEs we use here, and the variable of principal interest: the excitatory mean soma potential he. In §4, we consider a simplified version of the SPDEs that possesses neither spatial variance nor stochastic input; we call this system the dimensionless ODEs. In §§4.1 and 4.2, we compute bifurcation diagrams for the dimensionless ODEs at two different parameter values. We show that in both cases oscillatory activity (as expected during a seizure) occurs. For typical parameter values, the oscillatory activity is unstable and short-lived. For other parameter values (which may be consistent with the seizing cortex), the oscillatory activity is stable and long-lived. In §5, we analyse the complete dimensionless SPDEs. We show that results from this system agree qualitatively with results from the simpler dimensionless ODEs, and that travelling wave solutions exist. In §6, we compare the model solutions with the experimental recordings, and in §7, we discuss these results.
2. Observational data: ECoG seizure recordings
The cellular mechanisms of a seizure have been extensively studied and some general microscopic characteristics have been deduced (Dichter & Ayala 1987). Preceding a seizure, thousands of individual neurons in the seizure focus (the brain region where a seizure begins, also known as the epileptogenic zone) undergo depolarization shifts followed by an afterhyperpolarization. As long as this behaviour is confined to the seizure focus, there may be no clinical manifestation (although this synchronous activity can be detected as an interictal spike or a sharp wave in the EEG or ECoG). Gradually, as the seizure develops, the magnitude of the afterhyperpolarization decreases and individual neurons generate nearly continuous action potentials. The inhibition surrounding the seizure focus weakens, the seizure spreads to other cortical neurons, and a clinical seizure occurs. Here, we will not consider this microscopic behaviour of individual neurons, nor will we consider ictogenesis (the initiation of the seizure, which may occur in deeper brain regions). Instead, we investigate the mesoscopic characteristics of seizure activity on the cortical surface as made manifest in subdural ECoG recordings.
Large amounts of ECoG data are often recorded from the seizing cortex (i.e. ictal data) as part of clinical care of patients with intractable epilepsy. These patients whose seizures do not respond well to drug treatments may undergo surgery to remove a region of cortex that is believed to contain the seizure focus. Such resective surgery offers a chance to eliminate or ameliorate the seizures. In the process of planning such surgery, clinicians must accurately locate the seizure focus, and identify any surrounding areas of functional cortex that should be preserved to minimize post-operative deficits. If necessary, to define the seizure focus more precisely with respect to structural and functional anatomy, clinicians may implant subdural electrodes on the brain surface for extended time periods (typically one week) to obtain recordings during seizures and locate the seizure onset. The electrodes are placed over the region of cortex suspected to contain the seizure focus based on: (i) semiologic features of the patient's seizures (i.e. the observable features of the seizure, such as eye deviation or limb jerking), (ii) scalp EEG recordings made during typical seizures, (iii) abnormalities observed in the ECoG recorded intraoperatively at the time of electrode implantation (i.e. interictal recordings), or (iv) abnormalities seen on brain images. After the electrodes are implanted and the patient experiences his or her typical seizures, physicians locate the seizure focus through visual analysis of the ECoG recordings and formulate the surgical plan.
In this paper, we consider data collected from a 49-year-old male who had electrode implantation as part of his care at the University of California, San Francisco (UCSF) Epilepsy Center. He had medically refractory complex partial seizures that began with staring and manual automatisms and frequently generalized into convulsions. Prior scalp EEG recordings had suggested that his seizures originated in the right temporal lobe, but MRI showed left mesial temporal sclerosis, raising the possibility that his seizures arose from the left temporal lobe instead. To better lateralize seizure onset, subdural and depth electrodes were implanted, with subdural electrode strips placed over the left and right lateral frontal regions and the left and right subtemporal regions. In addition, bilateral hippocampal depth electrodes were placed, although we will not discuss these hippocampal recordings here. Each subdural electrode strip contained six 4 mm diameter platinum–iridium discs arrayed in a single row, embedded in a 1.5 mm thick silastic sheet with 2.3 mm diameter exposed surfaces and 10 mm spacing between the discs. After electrode implantation, the patient was brought to the video–telemetry unit, where his antiseizure medications were slowly withdrawn. ECoG data were recorded continuously at 400 Hz from all electrodes for 5.5 days. During this time, observations of eight typical seizures were captured. These recordings were of good quality and were determined, based on clinical review by board-certified clinical neurophysiologists, to show seizure onset from right medial temporal regions, with a pattern characteristic of seizures arising from this region. The patient went on to have a right anterior temporal lobectomy based on these clinical data.
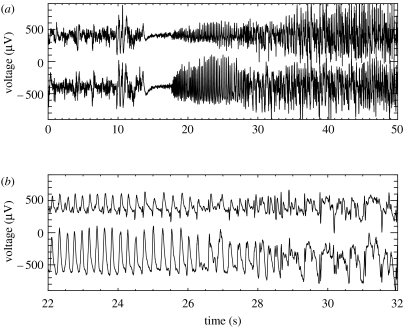
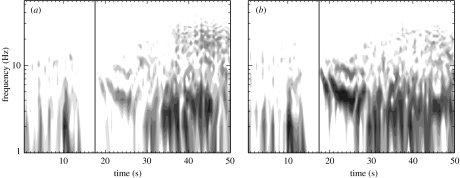
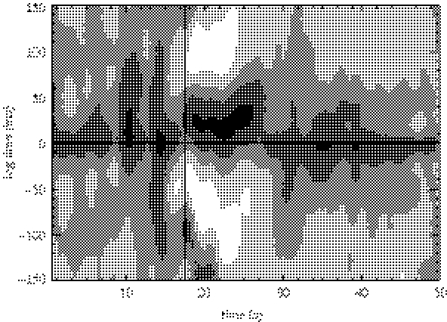
ECoG epochs containing six of the patient's seizures were extracted from the clinical record and reviewed for research purposes in accordance with UCSF and University of California, Berkeley human subjects guidelines. (Two of the seizure data files were corrupted and no longer available for extraction.) In figure 1, we show ECoG data leading up to and during a seizure recorded at two neighbouring subdural electrodes above the right lateral frontal region. We refer to the time-series recorded at these two electrodes as X (lower curve) and Y (upper curve). The ECoG data shown in this figure possess three notable features. First, we observe that large-amplitude voltage oscillations occur during the seizure (t>17.5 s). We determine the frequency of these oscillations by computing the windowed power spectrum (WPS) of X and Y. To compute the WPS, we partition the 50 s of data plotted in figure 1 into 100 overlapping windows of 1.0 s duration and 0.5 s overlap. For example, the first window includes data for 0.0 s≤t≤1.0 s, the second 0.5 s≤t≤1.5 s, the third 1.0 s≤t≤2.0 s and so on. We then multiply the data in each window by the Hanning function and compute the power spectrum. We plot the WPS results for X and Y in figure 2a,b, respectively. The horizontal axis in each figure corresponds to the centre times of the windows, and the solid vertical line to the time of seizure onset. We note, in the seconds preceding the seizure, the suppression of power at both electrodes for all frequencies. After seizure onset, the regions of largest power occur at frequencies between 1 and 10 Hz. The second notable feature in the observed data is the abrupt transition from normal ECoG activity (for t<14 s) to seizing activity (for t>17.5 s). This can be observed both in the original time-series data (figure 1a) and in the WPS (figure 2). Lastly, we find that the oscillations recorded at the two electrodes are slightly out of phase. One may deduce this conclusion directly from figure 1b; we note that peaks in the oscillations in X (lower trace) appear to precede those in Y (upper trace) until t≈29 s. At this point, the relationship between the two time-series becomes more complicated. To determine how the phase relationship between these two electrodes changes over time, we compute the windowed cross-correlation (WCC). In a manner similar to the WPS calculation, we partition the data into overlapping windows and compute the cross-correlation between X and Y in each window. We show the results in figure 3. Following seizure onset (denoted by the vertical line in the figure), two regions of strong correlation occur: the first from 17.5 s<t<27 s, and the second from 28 s<t<50 s. In the first region, X leads Y (i.e. the lag time is positive) while in the second region, X lags Y (i.e. the lag time is negative but near zero). In §6, we quantify the WPS and WCC results for six seizures recorded from the subject. We compare these results with the solutions to the SPDEs, discussed in §3.
Figure 1.
ECoG data recorded at two neighbouring subdural electrodes (separated by 10 mm) located on the surface of the right lateral frontal lobe. We label the time-series X (lower trace in each figure) and Y (upper trace in each figure). To ease visual comparison we subtract 400 μV from X and add 400 μV to Y. (a) Here, we show 50 s of ECoG activity recorded at two electrodes. There are three regions of ECoG activity: normal ECoG activity (0 s<t<14 s), followed by voltage suppression (14 s<t<17.5 s), and seizure (t>17.5 s). (b) Here, we show the data from (a) for 22 s<t<32 s. We note that initially oscillations in X and Y have the same shape, and that oscillations in X are of larger magnitude and appear to precede those in Y. For t>27 s the relationship between X and Y becomes more complicated.
Figure 2.
The windowed power spectra (WPS) for the two ECoG time-series shown in figure 1. Here, subfigures (a) and (b) correspond to the time-series X and Y in figure 1, respectively. The WPS are plotted in logarithmic greyscale with black and white denoting regions of high power (greater than 30 μV2) and low power (less than 0.03 μV2), respectively. The vertical line in the figure at t=17.5 s denotes the approximate onset of seizure.
Figure 3.
The windowed cross-correlation between the two ECoG time-series shown in figure 1. The WCC are plotted in linear greyscale with regions of strong correlation (greater than 0.8) and anticorrelation (less than −0.8) denoted by black and white, respectively. The vertical line in the figure at t=17.5 s denotes the approximate onset of seizure. The horizontal line in the figure denotes the zero lag.
3. Model: dimensionless SPDEs
An ideal model of the human cortex would describe the electrical behaviour of each individual neuron and its surrounding extracellular environment. This discrete model—applied over the entire three-dimensional cortex—would contain over 1010 dynamical variables and would be intractable. Fortunately, the physiology of the cortex (e.g. dense local connections) and numerous experimental results suggest that neurons act in populations or assemblies (Singer 1993; Singer & Gray 1995). Moreover, most methods for observing the human cortex (e.g. the ECoG time-series of interest in this work) record the summed electrical activity from populations of order 105 cortical neurons (Nunez 1995). For these reasons, researchers have developed continuum models of cortical electrical activity.
Such continuum models are not new; some of the earliest were developed by Freeman (1964) and Wilson & Cowan (1972, 1973). Here, we utilize the system of SPDEs stated by Steyn-Ross et al. (2003). These SPDEs were introduced in Steyn-Ross et al. (1999), where the authors included stochastic input to the system of PDEs first stated by Liley et al. (1999). To develop this model, Liley et al. (2002) considered a spatially averaged approximation to the human cortex. Microscopic elements (like individual neurons) were averaged over columnar volumes (perpendicular to the cortical surface) whose diameter was chosen to lie below the spatial resolution of EEG or ECoG recordings. The resulting mesoscopic model (with the addition of stochastic input) consists of 14 coupled, nonlinear SPDEs (Steyn-Ross et al. 2003).
By solving the SPDEs in Steyn-Ross et al. (2003) numerically, one computes solutions for all 14 variables as functions of space and time. One of these variables, he, is the spatially averaged excitatory soma membrane potential. Researchers have demonstrated that the deviation of he from rest is proportional to the sign-reversed value of the extracellular local field potential (LFP). Because the ECoG represents the spatially averaged LFP, we assume that he is linearly related to the ECoG (Liley et al. 2002). In this way, the model variable he is related to the observational ECoG data. In what follows, we compare he calculated in numerical solutions to the SPDEs with ECoG data recorded during seizure. We show that increasing the subcortical excitatory input to the model cortex produces behaviour in he that mimics ECoG data recorded from the seizing cortex.
In appendix A, we discuss a procedure to non-dimensionalize the SPDEs and associated functions. The main advantage of recasting the equations in dimensionless form is a reduction in the number of parameters. There are 20 parameters in the dimensionless SPDEs whereas in the original SPDEs there are 29. We define each dimensionless variable and parameter in terms of its dimensional counterparts from Steyn-Ross et al. (2003) in tables 1 and 2, respectively. In what follows, we study a simplified ODE version of the dimensionless model in §4, and compute numerical solutions to the complete dimensionless SPDE model in §5. Readers less interested in the mathematical details may like to skip to §6 where we compare the model solutions and observational results.
Table 1.
Dynamical variable definitions for the dimensionless SPDEs neural macrocolumn model. (The dimensionless variables (left column) are defined in terms of the dimensional symbols (middle column) found in table 1 of Steyn-Ross et al. (2003). The variables are described in the right column. Subscripts e and i refer to excitatory and inhibitory.)
| symbol | definition | description |
|---|---|---|
| he,i/hrest | population mean soma dimensional electric potential | |
| Iee,ieγe/(Geexp(1)Smax) | total e→e, i→e input to excitatory synapses | |
| Iei,iiγi/(Giexp(1)Smax) | total e→i, i→i input to inhibitory synapses | |
| ϕe,i/Smax | long range (corticocortical) input to e, i populations | |
| t/τ | dimensionless time | |
| dimensionless space |
Table 2.
Parameter values for the dimensionless SPDEs neural macrocolumn model. (The dimensionless symbols (first column) are defined in terms of the dimensional variables (second column) found in table 1 of Steyn-Ross et al. (2003). The variables are described in the third column and typical values are shown in the fourth column.)
| symbol | definition | description | typical value |
|---|---|---|---|
| e, i | (as subscript) excitatory, inhibitory cell populations | ||
| Γe,i | influence of input on the mean soma membrane values | 1.42×10−3, 0.0774 | |
| dimensionless cell reversal potential | −0.643, 1.29 | ||
| Te,i | τγe,i | dimensionless neurotransmitter rate constant | 12.0, 2.6 |
| λe,i | dimensionless characteristic corticocortical inverse-length scale | 11.2, 18.2 | |
| Pee,ie | pee,ie/Smax | subcortical input to e population | 11.0, 16.0 |
| Pei,ii | pei,ii/Smax | subcortical input to i population | 16.0, 11.0 |
| — | total number of synaptic connections from distant e populations | 4000, 2000 | |
| — | total number of local e and i synaptic connections | 3034, 536 | |
| ge,i/hrest | dimensionless sigmoid slope at inflection point | −19.6, −9.8 | |
| θe,i/hrest | dimensionless inflection point for sigmoid function | 0.857, 0.857 |
4. Simulations: dimensionless ODEs
Our goal is to determine whether the dimensionless SPDEs in equation (A 1a–h) can be used to model the mesoscopic electrical activity observed on the seizing cortical surface, as discussed in §2. However, the size of the system (14 first-order differential equations and 20 parameters), the stochastic input in equation (A 1c–f) and the spatial dependence in equation (A 1g,h) make this a challenging model. Therefore, to gain what insight we can from a simpler model, we ignore for the moment the spatial dependence and stochastic input in equation (A 1a–h). The resulting equations form a system of ODEs, which we call the dimensionless ODEs. Although there are many tools available for the study of ODEs, we use Auto (continuation and bifurcation software for ODEs) to determine fixed points, their stability type, limit cycles and bifurcations in the phase portraits (Doedel et al. 2000).
During a seizure, the cortex typically enters a state of hyperexcitation, manifest in ECoG data through large-amplitude oscillations (Niedermeyer & DaSilva 1999). This activity corresponds to spatially coherent oscillations in the variable he. In this direction, we investigate whether oscillations in he occur in the dimensionless ODEs owing to changes in the excitatory parameters. We note that different types of seizures produce different oscillatory patterns in EEG and ECoG recordings (Spencer et al. 1992; Ebersole & Pacia 1996). Here, we seek to model the seizing cortex in a qualitative way suggestive of the typical ECoG data shown in figure 1. Specifically, we require that: (i) the model produces stable oscillations in he, (ii) the frequency of the oscillations agree (roughly) with clinical observations, and (iii) the transition to oscillatory behaviour occurs abruptly.
The general statement that increased excitation (or decreased inhibition) incites cortical seizure activity masks the numerous associated physiological changes that occur in the seizing neuronal assemblies (Dichter & Ayala 1987; Morimoto et al. 2004). At the cellular level, these physiological changes are observed in experiment and can be compared to results computed from detailed computational models of a single neuron (Traub et al. 2001). It is not clear how the cellular mechanisms or single neuron models relate to mesoscopic seizure recordings or continuum models. Seizures induced in animal models allow mesoscopic ECoG recordings and some control over parameters related to continuum models. For example, Freeman (1992) discusses electrocortical data recorded from a seizing animal's olfactory bulb. He compares these recordings with his KIII model of the olfactory system and finds that a parameter connecting excitatory subsets of the model must increase to induce seizures. Analogies between such animal models and human seizure activity can be made but, as for the cellular models, these relationships are not clear.
In our analysis, we vary only two parameters, Pee and Γe, both related to the excitation of the model. We choose these parameters for two reasons. First, as mentioned previously, the general claim that increased excitation incites seizures is well known. Thus, we select two parameters related to the excitation of the model. Second, an increase in the level of the membrane potential of a neuronal population is thought to be an important control factor in inducing seizures (Dichter & Ayala 1987; da Silva et al. 2003). We show that increases in Γe raise the excitatory mean soma potential he of the stable fixed points. A similar result holds for Pee but is not shown. We fixed the remaining 18 dimensionless parameters at the typical values shown in table 2. In terms of dimensional variables, the dimensionless parameter Pee is: (i) directly proportional to pee (the subcortical excitatory spike input to the excitatory neurons of the cortex), and (ii) inversely proportional to Smax (the maximum firing rate induced by the soma voltage). Thus, an increase in Pee represents either an increase in the subcortical excitation of the cortex or a decrease in the maximum firing rate. To model an increase in excitatory input (from a subcortical region, such as the thalamus) to the cortex, the parameter Pee is increased. The dimensionless parameter Γe is: (i) directly proportional to Smax and Ge (the peak excitatory postsynaptic potential; EPSP), and (ii) inversely proportional to γe (the EPSP neurotransmitter rate constant) and (the magnitude of the difference between the excitatory reversal and resting potentials). Thus, an increase in Γe represents either an increase in peak EPSP amplitude or maximum firing rate, or a decrease in the difference between the excitatory reversal and resting potentials or the EPSP neurotransmitter rate constant. The latter corresponds to an increase in the EPSP duration. We note that the typical values of Pee and Γe are 11.0 and 1.42×10−3, respectively (see table 2).
It is perhaps easier to interpret the parameters Pee and Γe directly from equation (A 1a–h). The parameter Pee appears only in equation (A 1c). This parameter controls the strength of the (non-stochastic) excitatory subcortical input to excitatory neurons in the cortex. The parameter Γe appears in equation (A 1a,b), and controls the influence of excitatory input on the mean soma membrane potentials. For example, when Γe is large, the effect of the excitatory inputs ( and ) on the potentials ( and ) is increased. We will show that solutions of the model equations agree qualitatively with ECoG data recorded from the seizing cortex when Pee is dramatically increased, and Γe is slightly decreased.
In what follows, we compute bifurcation diagrams and numerical solutions of the dimensionless ODEs at two values of Pee. We first consider the results for Pee=11.0 (the typical value) and show that oscillations in he occur but are unstable and short lived. We then show that for Pee=548.066 (nearly 50 times the typical subcortical excitation), he undergoes large-amplitude, stable oscillations, and that similar oscillations occur over a wide range of parameter values. The results in each case are compared with the clinical data discussed in §2.
4.1 Example: dimensionless ODEs at Pee=11.0
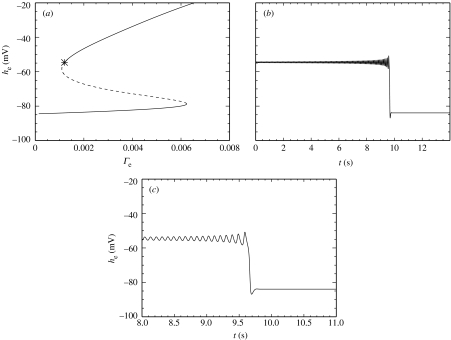
In the first example, we fix Pee at its typical (dimensionless) value of 11.0 and vary the parameter Γe. In figure 4a, we plot he for the fixed points of the dimensionless ODEs versus the parameter Γe. Note that in this figure, we plot the dimensional variable he (with units mV), which is related to by the scale factor . The solid lines and dashed line in figure 4a correspond to the stable and unstable fixed points of the dimensionless ODEs, respectively. We note that an increase in Γe produces an increase in both curves of the stable fixed point value of he (i.e. increased steady-state values of the spatially averaged excitatory soma membrane potential).
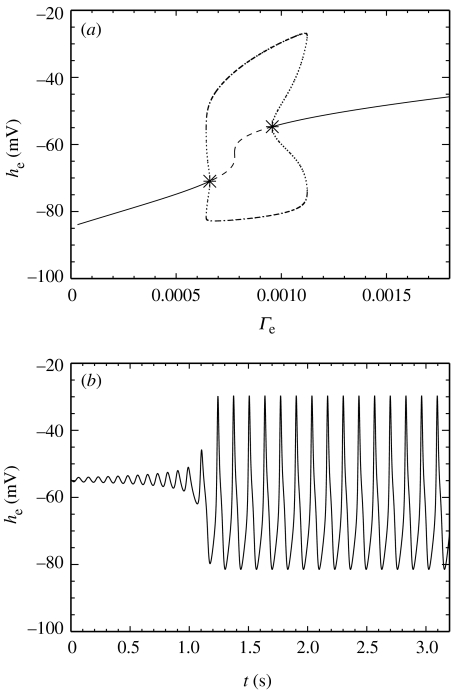
Figure 4.
(a) Bifurcation diagram for the dimensionless ODEs at Pee=11.0. As the dimensionless parameter Γe is varied, the stable (solid lines) and unstable (dashed line) fixed points in he of the dimensionless ODEs are shown. The asterisk denotes the Hopf bifurcation. There are two saddle–node bifurcations also visible in the figure. (b) Numerical solution to the dimensionless ODEs at Γe=1.21×10−3 and Pee=11.0, near the Hopf bifurcation shown in (a). Dimensional he is plotted as a function of dimensional time t. The oscillations in he increase in amplitude until the oscillations cease and he→−84 mV. (c) The transition from transient oscillatory motion in he to the fixed point at finer resolution.
The S-shape and stability of the fixed points is similar to that discussed in Steyn-Ross et al. (1999, 2003). In those works, the authors varied the (dimensional) inhibitory neurotransmitter rate constant γi. Here, the parameter Γe is inversely proportional to the (dimensional) excitatory neurotransmitter rate constant γe. We have found, but do not show, similar bifurcation diagrams for the dimensional ODEs with γi→γi/λ or γe→γeλ and parameter λ varied between 0.1 and 1.5.
In addition to the saddle–node bifurcations of fixed points, the dimensionless ODEs at Pee=11.0 also undergo a Hopf bifurcation at Γe=1.20×10−3. (We note that this represents a 15% decrease in the typical value of Γe=1.42×10−3.) We mark this Hopf bifurcation in figure 4a with an asterisk. We are particularly interested in Hopf bifurcations because, at a Hopf bifurcation, the dynamics of he can change from stationary behaviour to oscillatory behaviour. To illustrate the oscillatory behaviour of he near the Hopf bifurcation, we compute a numerical solution to the dimensionless ODEs near the Hopf bifurcation at Γe=1.21×10−3 and Pee=11.0. We choose the initial conditions so that the dynamics begin just outside the basin of attraction of the stable fixed point and compute the trajectory using a fourth-order Runge–Kutta method with a time-step of 0.4 ms. We plot in figure 4b (dimensional) he as a function of dimensional time t. For 0 s<t<9.5 s, he oscillates at approximately 8 Hz. The amplitude of the oscillations steadily increases until t=9.5 s, at which point he abruptly moves to the stable fixed point near −84 mV. We show this transition with finer resolution in figure 4c.
We have shown that for Pee=11.0 the dynamics of he undergo a Hopf bifurcation at Γe=1.20×10−3. Near the Hopf bifurcation there exist transient oscillations in he that increase in amplitude until the dynamics undergo a transition to a stable fixed point near −84 mV. We have not shown but note that adding noise to the system decreases the time of the transient oscillations. These unstable oscillations in he do not mimic the electrical activity of the seizing cortex where the oscillations maintain a large amplitude and are necessarily stable to incessant perturbations from other cortical, as well as deeper, brain regions.
4.2 Example: dimensionless ODEs at Pee=548.066
Here, we consider an example more closely related to the seizing cortex. To increase the excitation of the model cortex, we fix Pee=548.066 (nearly 50 times the typical value). This can be interpreted as increased excitatory input from deeper brain regions to the cortex, say. As in §4.1, we vary the parameter Γe and plot in figure 5a the bifurcation diagram in he for the dimensionless ODEs. The solid lines and dashed line in figure 5a correspond to stable and unstable fixed points of the dimensionless ODEs, respectively, and the asterisks to Hopf bifurcations. We note that an increase in Γe produces an increase in both curves of stable fixed points of he.
Figure 5.
(a) Bifurcation diagram for the dimensionless ODEs at Pee=548.066. The parameter Γe is varied and the stable (solid lines) and unstable (dashed line) fixed points in he are shown. The asterisks denote the two Hopf bifurcations. The dash–dot lines denote the maximum and minimum values of he achieved during a stable limit cycle. The dotted lines denote the maximum and minimum values of he achieved during an unstable limit cycle. The branch of limit cycles is born and dies in two subcritical Hopf bifurcations; two saddle–node bifurcations of limit cycles lead to large-amplitude stable oscillations with sudden onset. (b) Numerical solution to the dimensionless ODEs at Γe=0.96×10−3 and Pee=548.066, near the rightmost Hopf bifurcation in (a). Dimensional he is plotted as a function of dimensional time t. The oscillations in he occur at a frequency near 7.5 Hz and are stable to perturbations.
There are additional curves in figure 5a absent from figure 4a. These curves indicate the extremal values and stability type of the limit cycles born in the Hopf bifurcations. The dash–dot lines in figure 5a represent the maxima and minima of he achieved during a stable limit cycle. The dotted lines represent the maxima and minima of he achieved during an unstable limit cycle. Thus, for 0.67×10−3<Γe<0.96×10−3, the dynamics of he feature a stable limit cycle of large amplitude. We note that a 32% decrease in the typical value of Γe=1.42×10−3 is required to enter this range. The stable, oscillatory behaviour of he satisfies one of our criteria for modelling the seizing cortex.
To illustrate the stable oscillations in he for 0.67×10−3<Γe<0.96×10−3, we compute a numerical solution to the dimensionless ODEs at Γe=0.96×10−3 and Pee=548.066 using the fourth-order Runge–Kutta method with a time-step of 0.4 ms. In figure 5b, we plot he (with dimensions mV) as a function of dimensional time t. After an initial transient, he is entrained by a large-amplitude limit cycle with a dominant frequency near 7.5 Hz. We note that these oscillations are not sinusoidal. The frequency of the he oscillations is qualitatively consistent with the clinical observations from a seizing patient shown in figure 1.
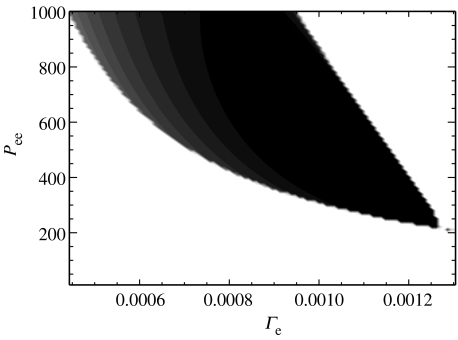
The true environment of the human cortex is continually changing, for example, in response to sensory stimuli. Therefore, any model of the seizing cortex must behave properly over a broad range of parameter values. Here, we require that oscillatory activity in he occur over extended regions of the parameters Pee and Γe. To confirm this, we compute numerical solutions to the dimensionless ODEs for 11.0<Pee<1000.0 and 0.5×10−3<Γe<1.4×10−3 using the fourth-order Runge–Kutta method with a time-step of 0.4 ms. We then determine the difference between the maximum and minimum achieved by the solution he after transient behaviour has decayed. If he approaches a fixed point, then the maximum and minimum are nearly equal and their difference approaches zero. However, if he is entrained by a limit cycle (e.g. figure 5b), then the difference between the maximum and minimum achieved by he is non-zero. In figure 6, we plot the difference between the maximum and minimum achieved by he as a function of the parameters Pee and Γe. The difference is plotted in greyscale with white representing a 0 mV difference and black representing a 50 mV difference. We find that oscillations in he (represented by the dark regions in figure 6) extend over a broad range of parameter values beginning near Pee=250.0 and Γe=1.3×10−3. These regions of oscillatory activity in he illustrate the parameter values at which the dimensionless ODEs ‘seize’. We have found that the Hopf bifurcation (and thus the oscillatory activity) is born in a codimension two bifurcation of the Takens–Bogdanov type at Pee=53.2 and Γe=2.98×10−3 (Kramer 2005). We note that increasing Pee, and thus raising the subcortical excitatory input to the model cortex, enlarges the region of Γe over which oscillations in he occur.
Figure 6.
The difference between the maximum and minimum achieved by (the dimensional) he in solutions of the dimensionless ODEs for parameters Pee and Γe. The difference is plotted in linear greyscale with white representing a 0 mV difference and black representing a 50 mV difference. The dark region corresponds to stable oscillations of he and broadens as Pee is increased. The parameter values used to create figure 5b (Γe=0.96×10−3 and Pee=548.066) are near the centre of this figure.
5. Simulation: dimensionless SPDEs
We have considered in some detail the dimensionless ODEs. There is no direct conclusion that the analysis of this simplified system allows one to draw for the full dimensionless SPDEs. The stochastic inputs or the spatially distributed dynamics may destroy the interesting features we observed in the dimensionless ODEs. We have shown in §4.2 that the dimensionless ODEs undergo a Hopf bifurcation near Pee=548.066 and Γe=0.96×10−3, and that oscillations in he persist over a broad region of parameter values. Here, we shall examine whether the full dimensionless SPDEs exhibit similar oscillatory behaviour. We will consider three examples. For each example, we compute numerical solutions to the dimensionless SPDEs using the Euler–Maruyama algorithm with fixed steps in space and time, 14 mm and 0.1 ms, respectively (Higham 2001). We consider only one spatial dimension ; the system can now be visualized as describing a line of closely spaced electrodes, such as the strip of subdural electrodes described in §2. In each example, we enforce periodic boundary conditions in space, fix Γe and α (representing the noisy input from subcortical sources to the cortex) to be uniform in and , and vary the spatial and temporal dependence of Pee. In the first example, we set Pee to be uniform in space and time. In the second, we set Pee to be Gaussian in space and constant in time, while in the third, we set Pee to be Gaussian in space and non-uniform in time. In §6, we compare the results of these simulations and the clinical seizure data.
We start by computing numerical solutions to the dimensionless SPDEs at Γe=1.04×10−3 and Pee=548.066, near the parameter values used in §4.2. In this example, both Pee and Γe are uniform in space and time. We note that, at these parameter values, the noise-free dimensionless ODEs are near the Hopf bifurcation. In figure 5a, the simplified system would be just to the right of the rightmost asterisk. In figure 7a, we show the solution to the dimensionless SPDEs with α=0.001. In this figure, we plot (dimensional) space on the horizontal axis, (dimensional) time on the vertical axis, and the value of he in linear greyscale; white corresponds to he=−65 mV, and black to he=−45 mV. From this figure it is clear that the value of he is approximately constant (near −53 mV, the fixed point of the dimensionless ODEs) in both space and time.
Figure 7.
Numerical solution to the dimensionless SPDEs with parameters: Γe=1.04×10−3, Pee=548.066, and periodic boundary conditions in space. Space (in mm) and time (in ms) are plotted along the horizontal and vertical axes, respectively. (a) Here, α=0.001. The value of he is plotted in linear greyscale over space-time with he=−65 mV in white and he=−45 mV in black. There are no large-amplitude oscillations in he. (b) Here, α=0.002. The value of he is plotted in linear greyscale with he=−100 mV in white and he=0.0 mV in black. Oscillations in he appear to start near 200 mm<x<300 mm, and spread rapidly over the whole domain near t=2000 ms. The waves travel to the right with an approximate speed of 2.2 m s−1 and temporal frequency of 10 Hz.
In figure 7b, we show the solution to the dimensionless SPDEs with α=0.002. Here, we have increased the strength of the spatially uniform stochastic input, and plotted he in linear greyscale with white corresponding to he=−100 mV, and black to he=0.0 mV. Otherwise, the parameters, initial conditions and plotting scheme are identical to those used to compute and display the previous numerical solution. There are two interesting features to note in figure 7b. First, travelling waves are engendered in he. In the figure, these are represented by repeated white and black ridges inclined with respect to the horizontal. These waves travel rapidly to the right with an approximate speed of 2.2 m s−1 and oscillate in time with an approximate frequency of 10 Hz. We compare this wave speed and frequency with that derived for the clinical data in §6. Second, these waves appear quite abruptly (near t=2000 ms) and show a high degree of spatial organization, similar to the clinical seizure data discussed in §2. Careful examination reveals that the oscillations appear to be triggered near 200 mm<x<300 mm, and subsequently spread across the whole domain.
Waves in continuum models of the human cortex are not new. Steyn-Ross et al. (2003) investigate the dimensional SPDEs and show that spatial modes develop when the corticortical e→i diffusivity dominates the corticortical e→e diffusivity. Jirsa & Kelso (2000) show that spatio-temporal patterns (reminiscent of the seizing cortex) occur in a continuum model of cortical electrical activity with a single inhomogeneous connection. By adjusting the extent of this inhomogeneous connection, the stability of the spatio-temporal patterns changes. In addition, Pinto & Ermentrout (2001) show how travelling waves may develop in a model derived from the physiology of a neocortical slice.
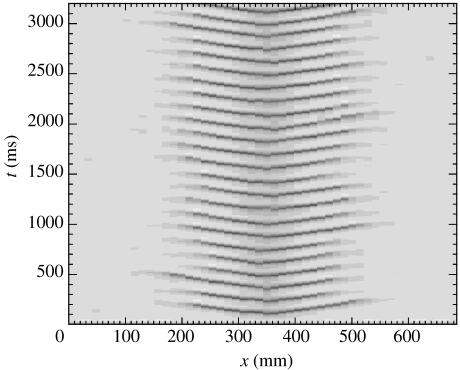
In the second example, we consider numerical solutions to the dimensionless SPDEs for Pee non-uniform in space and constant in time. Here, we set Pee to be a Gaussian function in x with maximum at x=350 mm, full width at half maximum of 46 mm, and minimum Pee=11.0. The localized region of hyperexcitation near x=350 mm may be thought of as the seizure focus in our simple model. We solve the dimensionless SPDEs with Γe=0.87×10−3, α=0.001 (both uniform in space and time) and show the solution in figure 8. We find that localized oscillations (the dark ridges in figure 8) emerge from the region of hyperexcitation near x=350 mm, travel outward with approximate speed 1.2 m s−1 and approximate frequency 7.5 Hz, and then dissolve in the regions of lower excitation, where Pee→11.0. This localized oscillatory activity is more representative of a localized seizure than the global oscillations illustrated in figure 7b.
Figure 8.
Numerical solution to the dimensionless SPDEs with parameters: Γe=0.87×10−3, α=0.001, Pee a Gaussian function in space with maximum 548.066 at x=350 mm and full width at half maximum 46 mm, and periodic boundary conditions in space. Space (in mm) and time (in ms) are plotted along the horizontal and vertical axes, respectively. The value of he is plotted in linear greyscale with he=−100 mV in white and he=0.0 mV in black. Waves in he travel outward from the region of hyperexcitation near x = 350 mm with approximate speed 1.2 m s−1 and approximate frequency 7.5 Hz.
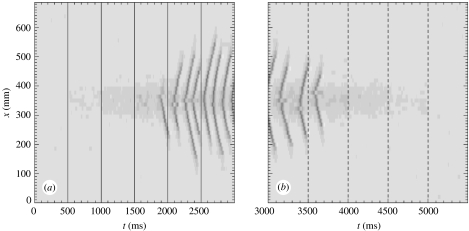
In the final example, we compute numerical solutions to the dimensionless SPDEs for Pee non-uniform in space and time. As in the previous example, we fix Γe=0.87×10−3 and α=0.001 (both uniform in space and time). However, unlike the previous example, we vary Pee in time. At t={0, 5000} ms, we fix Pee=11.0 uniform in space. For 500 ms<t<5000 ms, we set Pee to be a Gaussian function in x with maximum at x=350 mm, full width at half maximum of 46 mm, and minimum Pee→11.0. At t={500, 1000, 1500, 2000, 2500} ms, we increase in steps of 100 so that , respectively. These increases are marked by the solid vertical lines in figure 9a. We then decrease in steps of 100 so that for t={3000, 3500, 4000, 4500} ms, , respectively. These decreases are marked by the dashed lines in figure 9b. We show in figure 9 that localized oscillations in he (the dark ridges) begin at t=1900 ms, where . The frequency of these oscillations increases when we increase to 510 at t=2500 ms. Then, as we decrease between 3000 ms<t<5000 ms, the oscillations in he decrease in frequency and eventually disappear.
Figure 9.
Numerical solution to the dimensionless SPDEs with parameters Γe=0.87×10−3, α=0.001, and periodic boundary conditions in space. At t={0, 5000}, Pee=11.0 uniform in space. For 500 ms<t<5000 ms Pee is a Gaussian function in space with maximum at x=350 mm and full width at half maximum 46 mm. In subfigure (a), the maximum at t={500, 1000, 1500, 2000, 2500} ms, respectively. These increases in are denoted by the solid vertical lines. In subfigure (b), the maximum at t={3000, 3500, 4000, 4500} ms, respectively. These decreases in are denoted by the dashed vertical lines. Space (in mm) and time (in ms) are plotted along the vertical and horizontal axes, respectively. The value of he is plotted in linear greyscale with he=−100 mV in white and he=0.0 mV in black. Waves in he are localized in space and time to the region of hyperexcitation near x=350 mm for 1800 ms<t<3800 ms.
This simple example provides a crude model for the evolution of the seizing cortex. At normal levels of subcortical excitation (Pee=11.0) there exist only disorganized spatio-temporal fluctuations in he and no pathological oscillatory activity. Only when exceeds a threshold level do localized oscillations in he appear. As the subcortical excitation is increased further, the frequency of the oscillations increases. Then, as is decreased, the oscillations slow and eventually disappear.
6. Results
In §2, we showed ECoG data recorded at two neighbouring electrodes during seizure, and in §§3–5, we computed numerical solutions to a continuum model of cortical electrical activity. Here, we compare the observed ECoG data with the model solutions for he. Specifically, we compute two quantities: (i) the average frequency at which the power spectrum achieves its maximum during seizure, and (ii) the average speed at which the voltage peaks propagate between two subdural electrodes during seizure. We denote these quantities f0 (the peak frequency) and v (the propagation speed), respectively. We show that f0 and v, computed from the model solutions and the ECoG seizure data, are roughly in agreement.
In our determination of f0, we consider data collected at the same two subdural electrodes (e.g. X and Y) for each of six seizures from the same patient. Part of one such seizure is shown in figure 1. To compute f0, we first low pass filter the ECoG data X and Y below 55 Hz, and then compute the WPS. For example, in figure 2a we show the WPS for the time-series X recorded during a typical seizure. In this case, the maximum power occurs between 1 and 10 Hz following seizure onset (at t≈17.5 s). To determine f0, we calculate the average frequency of maximum power in the WPS for the duration of the seizure (here, for 17.5 s<t<50 s). We list f0 and its standard deviation over the duration of the seizure for both electrodes (i.e. X and Y) and each seizure in table 3. For reference, we label the seizures S1 to S6, where S1 corresponds to the data discussed in §2. We also compute the average of f0 over the six seizures for X and Y and find 4.1±0.8 and 5±1 Hz, respectively.
Table 3.
The peak frequency f0 for the ECoG time-series data recorded at electrodes X (first row) and Y (second row) for each of six seizures and the average over the six seizures. (For each seizure, we write the mean and the standard deviation of the mean. To compute the uncertainty in the average, we assume the uncertainties in f0 for each seizure are independent and random and propagate the uncertainties in the standard way.)
| seizure label | S1 | S2 | S3 | S4 | S5 | S6 | average |
|---|---|---|---|---|---|---|---|
| f0 of X (Hz) | 3.9±0.2 | 3.6±0.2 | 3.1±0.3 | 4.3±0.3 | 4.3±0.3 | 5.4±0.6 | 4.1±0.8 |
| f0 of Y (Hz) | 5.1±0.5 | 3.8±0.3 | 3.9±0.3 | 4.6±0.4 | 5.3±0.4 | 6.2±0.5 | 5±1 |
Propagating waves of electrical activity have been observed in numerous mammalian systems and during seizures in rats and in cats (Chervin et al. 1988; Connors & Amitai 1993; Pinto & Ermentrout 2001). Here, we assume that, during each seizure, voltage peaks propagate between the two neighbouring subdural electrodes (with time-series X and Y). That this assumption is valid can be inferred from the data shown in figure 1b. We note for 17.5 s<t<27 s the similarity of the wave forms in X and Y and that peaks in X precede peaks in Y. To determine the average propagation speed v of these voltage peaks, we first low pass filter the time-series below 55 Hz. We then compute the WCC between X and Y, as shown in figure 3 for S1. At each time in the WCC, a maximum correlation occurs for some lag time. For example, at t=20 s, the maximum correlation occurs at a lag of approximately 25 ms. We compute this lag at which the maximum correlation occurs for the duration of the seizure. We find that, in general, the lag values are consistent over two temporal intervals. The first interval (I1) includes the time of seizure onset and the 10 s that follow. The second interval (I2) includes all later times (i.e. all times 10 s after the seizure onset until seizure termination). For example, in S1 the two time-intervals over which the lag of maximum correlation is consistent are: I1=17.5 s<t<27 s and I2=28 s<t<50 s. Such intervals can be chosen for each seizure except S6. For this seizure, the lag values of maximum correlation are near zero for all times following seizure onset. Therefore, we do not include S6 in our analysis of v. We determine v in each interval by dividing the known electrode separation (10 mm) by the average lag in each interval. We list v and its standard deviation in each interval and for each seizure in table 4. We note that for S3 the average lag is 0 ms in I2 and therefore v is infinite. We compute the average and standard deviations of v in I1 (over S1 to S5) and I2 (over S1, S2, S4 and S5) to find 0.5±0.1 and −3±1 m s−1, respectively. We note that travelling waves of electrical activity on animal cortices have been reported with speeds of 0.06–0.09 m s−1 (Chervin et al. 1988).
Table 4.
The speed v at which excitation propagates during two time-intervals I1 (immediately following seizure onset) and I2 (the later portion of the seizure) for each of six seizures. (The averages are computed in interval I1 using seizures S1 to S5, and in interval I2 using seizures S1, S2, S4 and S5. For each seizure, we write the mean and the standard deviation of the mean. To compute the uncertainty in the average, we assume the uncertainties in v for each seizure are independent and random and propagate the uncertainties in the standard way.)
| seizure label | S1 | S2 | S3 | S4 | S5 | S6 | average |
|---|---|---|---|---|---|---|---|
| v in I1 (m s−1) | 0.42±0.02 | 0.49±0.03 | 0.75±0.06 | 0.45±0.02 | 0.63±0.7 | — | 0.5±0.1 |
| v in I2 (m s−1) | −2.6±0.2 | −5±1 | ∞ | −4.3±0.8 | 0.51±0.03 | — | −3±1 |
To compare these observational results with the model results, we compute f0 and v from the numerical solutions to the model cortex for the variable he. We tabulate the results in table 5 for the dimensionless ODEs simulation shown in figure 5a, and the dimensionless SPDEs simulations shown in figures 7b and 8. We note that the results of the simulations agree with the observed data for f0 (within a factor of 2) and v in I1 (within a factor of 5).
Table 5.
The peak frequency f0 and wave speed v determined for the model solutions of he.
7. Discussion
Our aim was to consider the potential of the SPDEs to provide a model of the mesoscopic electrical activity on the seizing cortex. In our analysis of the dimensionless ODEs, we have shown that there do exist limit cycles in he associated with Hopf bifurcations in the dynamics. We have also shown that the simpler dimensionless ODEs suggest behaviour in the complicated dimensionless SPDEs that is consistent with the clinical seizure data. Specifically, we have shown that at typical parameter values Γe=1.42×10−3 and Pee=11.0, a reduction in Γe (to Γe=1.20×10−3) produced oscillatory behaviour in he. However, this oscillatory behaviour was transient and did not produce the large-amplitude, stable oscillations characteristic of the seizing cortex. Moreover, this oscillatory behaviour occurred at a single value of Γe. Thus, the parameter values of the model cortex would have to be carefully tuned to reach this point.
To increase the excitability of the model cortex and make it ‘seize’, we increased Pee. We show in figures 5a and 6 that for Pee>250.0 there exist stable, large-amplitude limit cycles in he over a wide range of Γe. We suggest in §5 that these oscillations are associated with travelling wave dynamics in the dimensionless SPDEs. Thus to produce behaviour in he consistent with that observed in the seizing cortex, we must: (i) increase Pee, and (ii) decrease Γe in the dimensionless SPDEs. In dimensional terms, we must increase the subcortical excitation pee or decrease the maximum firing rate Smax, and we must increase the EPSP neurotransmitter rate constant γe or the difference between the reversal and resting potentials or decrease the peak excitatory postsynaptic potential Ge or Smax.
That we must decrease Γe to induce a seizure seems counterintuitive. We expect that an increase in the strength of excitatory inputs would promote seizing activity. However, the decrease in Γe, from 1.42×10−3 to 0.87×10−3 used to create figure 9, represents only a 39% change. The change in Pee required to induce a seizure is much larger. We show in figure 9 that this parameter must increase by at least 2700%. We may interpret the changes in these two parameters required for seizure induction following the models in da Silva et al. (2003). Alterations of the epileptic brain, owing to genetic or environmental (e.g. injury) effects, for example, predispose it to seizures. In modelling the epileptic cortex, we may interpret this predisposition as a permanent (model I) or a gradual (model II or model III) change of a model parameter. The results shown in figure 9 illustrate the latter case; with Γe fixed, a gradual increase in Pee induces seizing activity in he. Because the change in Pee is gradual and affects the dynamics of he we could try to anticipate these types of seizures. We may also interpret these results following the model I framework. For example, consider a permanent increase in Pee from 11.0 to 310.0. When modelling the cortical activity of any individual (either healthy or epileptic), we may assume that the model parameters undergo routine fluctuations in their normal values. In healthy individuals (with the typical parameter value Pee=11.0), a small negative fluctuation in the model parameter Γe may induce a harmless, transient oscillation (like that shown in figure 4) but not a seizure. This same fluctuation in Γe will cause the predisposed epileptic cortex to seize. In this case, the increased value of Pee allows the dynamics to cross the separatrix (or boundary) between the normal and seizing states (Robinson et al. 2002). Thus, only a small change in Γe is necessary to produce pathological oscillations in he. Because a random fluctuation in Γe induces the seizure, these types of seizures cannot be anticipated. From the results presented here, we suggest a large change in Pee and a small change in Γe may provide a model of the seizing cortex.
In tables 3–5 we compute two results, the average peak frequency f0 and the average propagation speed v, derived from clinical ECoG recordings and solutions to the SPDEs. We find that the values derived from the observational and model data approximately agree (f0 within a factor of 2 and v in I1 within a factor of 5), but note the following important issues. First, the subdural electrode strips used in the clinical recordings consist of six electrodes each separated by 10 mm. Thus, the spatial sampling of the cortex is poor and we cannot observe detailed wave behaviour in the voltage. It may be true that electrodes X and Y lie on either side of a sulcus (a groove or furrow in the cortex); the precise locations are not known. It may also be true that a wave in electrical potential is propagating obliquely with respect to the shortest path between electrodes X and Y. Future recordings that utilize high-density electrode grids with small interelectrode spacing would provide better results to compare with the theory. Second, the lead/lag relationships determined from the WCC are ambiguous. For example, we showed in figure 3 that for 17.5 s<t<27 s, the oscillations at electrode X lead the oscillations at electrode Y by approximately 25 ms. During this interval, these time-series are nearly sinusoidal with a well-defined frequency near 4 Hz; see the data in figure 1b or the WPS in figure 2. The cross-correlation of two sinusoids is itself a sinusoid, and therefore ambiguous; although we suggest X leads Y by approximately 25 ms, it is also true that Y leads X by approximately 225 ms (the period of the 4 Hz cycle minus 25 ms). We chose the case X leads Y for two reasons: (i) the amplitude of oscillations in X is bigger than in Y, and (ii) a correlation at 25 ms between two closely spaced electrodes is more reasonable than a correlation of 225 ms. It does not seem possible to resolve this ambiguity of the cross-correlation. Third, we have assumed that the same voltage wavefront passes through both electrodes. If the wave source lies between the two electrodes, then this assumption is incorrect. Smaller electrode spacing may help locate the wave source more accurately. Fourth, given such a complicated model (14 nonlinear first-order stochastic differential equations and 20 parameters), we could potentially produce any desired behaviour in he by properly tuning the parameters. Here, we chose to adjust two parameters, both related to the excitation of the model cortex. In this way, we used the physiology of the seizing cortex to constrain the adjustable parameters in the model. Finally, we do not mean to suggest that the SPDEs provide an accurate model of all human cortical seizure activity. Here, we have only compared the model results with data collected from a single subject, and shown that the model and observational data agree in an approximate way.
Although confounding factors exist both in the model and observations, these results still illustrate an important use of the SPDEs and other continuum models: establishing links between the known ECoG data and unknown cortical physiology. Traditionally, neurophysiologists visually analyse ECoG data recorded from a seizing patient. No attempt is made to link the changes observed in these time-series with corresponding changes in cortical physiology. Continuum models of cortical electrical activity allow one to consider such links in a quantitative way. This is especially important for human cortical data, where invasive procedures are inappropriate. For example, Robinson et al. (2002) consider an ODE model of the corticothalamic network. Unlike the SPDEs model presented here, these models explicitly include the interactions of cortical neurons with the thalamus. The authors show that the model can produce the 3 Hz spike wave characteristic of absence seizures and how the model parameters relate to the period of the seizures. A corticothalamic model is used to study other types of epilepsy in da Silva et al. (2003). In this work, we relate the emergence of pathological oscillations in the measured cortical voltage to changes in two parameters: a small decrease in Γe and a large increase in Pee. In this way, we suggest a link between the ECoG data and the physiology of the cortex.
Measures of dynamical quantities may also be computed from observed and simulated time-series and compared. For example, the correlation dimension, largest Lyapunov exponent (LLE), and synchronization have been shown in observations to decrease preceding a seizure (Quyen et al. 2003; Iasemidis 2003). Such quantities are calculable from the model equations. Dafilis et al. (2001) vary two dimensional parameters (pee and pei) and compute the LLE and Kaplan–Yorke dimension for the dimensional ODEs model from Liley et al. (1999). A similar analysis may be performed in which one varies the parameters Pee and Γe of the dimensionless ODEs model presented here. Although the dimension and LLE determined from noisy ECoG data are of limited accuracy, a comparison of the theoretical and observational results may provide verification or suggest improvements to the model (Freeman 1992).
Understanding both the ECoG patterns of cortical ictal activity and the related changes in cortical physiology may help shape new strategies for seizure detection and focus location. This, in turn, may allow clinicians to deliver abortive seizure therapy that is targeted both in time and in space. For example, experimental methods such as focal cooling, brief pulse cortical electrical stimulation and local drug delivery all depend on reliable algorithms for the detection and prediction of seizures (Eder et al. 1997; Lesser et al. 1999; Yang et al. 2002). The combination of parameters one can change in a well-motivated, physiologically relevant model to simulate these dynamics may suggest strategies for therapeutic intervention.
Acknowledgments
M.A.K. would like to acknowledge the support of a Graduate Fellowship from the U.S. National Science Foundation, and a Berkeley Fellowship from the University of California. The authors are grateful to Nicholas M. Barbaro, MD, for electrode placement and surgical management.
Appendix A.
Here, we non-dimensionalize the SPDEs from Steyn-Ross et al. (2003). To do so we replace each dynamical variable, as well as space x and time t, with its dimensionless counterpart. For example, we replace he (the population mean soma voltage in Steyn-Ross et al. 2003) with , where and is dimensionless. The main advantage of recasting the equations in dimensionless form is a reduction in the number of parameters. There are 20 parameters in the dimensionless SPDEs; in the original SPDEs there are 29. We find for the dimensionless SPDEs:
| (A1a) |
| (A1b) |
| (A 1c) |
| (A1d) |
| (A1e) |
| (A1f) |
| (A1g) |
| (A1h) |
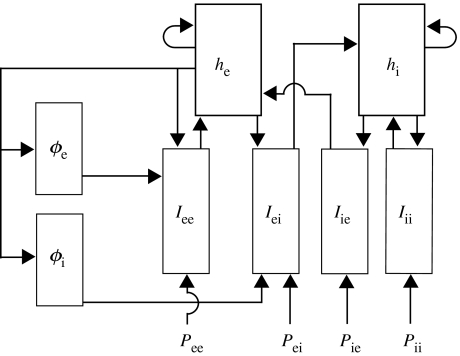
The eight dynamical variables in this system (, , , , , , and ) are functions of dimensionless space and time, and , respectively. We illustrate the connections between these dynamical variables in figure 10. The dimensionless variables and parameters are defined in tables 1 and 2, respectively. Each variable and parameter is expressed in terms of its dimensional counterparts from Steyn-Ross et al. (2003). In these tables, we have made the notational simplifications in agreement with the values used in Steyn-Ross et al. (2003): , and . The dynamical variable is the key observable and related to the scalp EEG or ECoG signal (Liley et al. 2002).
Figure 10.
A schematic of the eight dynamical variables (boxed) and the four subcortical inputs (Pee, Pei, Pie, Pii). The variables are defined in table 1; they appear in the dynamical equations (A 1a–h). We indicate the interactions between the variables using arrows. A schematic of the cortical macrocolumn may be found in fig. 2 of Liley et al. (1999).
We also define the dimensionless sigmoid transfer functions:
| (A2a) |
| (A2b) |
and the dimensionless stochastic input terms:
| (A3a) |
| (A3b) |
| (A3c) |
| (A3d) |
The terms in equations (A 3a–d) represent the noise that arises from subcortical inputs to the cortex. Here, the ξk are Gaussian distributed white noise sources with zero mean and δ-function correlations. In numerical simulations, the ξk are approximated as
| (A4) |
where and , (m, n integers), specify space and time coordinates on a lattice with (dimensionless) grid spacings, and , respectively. Here, we set αee=αei=αie=αii=α as in the stochastic simulations of the spatio-adiabatic one-dimensional cortex in Steyn-Ross et al. (2003).
References
- Chervin R.D, Pierce P.A, Connors B.W. Periodicity and directionality in the propagation of epileptiform discharges across neocortex. J. Neurophysiol. 1988;60:1695–1713. doi: 10.1152/jn.1988.60.5.1695. [DOI] [PubMed] [Google Scholar]
- Connors B.W, Amitai Y. Generation of eliptiform discharge by local circuits of neurocortex. In: Schwartkroin P.A, editor. Epilepsy: models, mechanisms, and concepts. Cambridge University Press; Cambridge: 1993. [Google Scholar]
- Dafilis M.P, Liley D.T.J, Cadusch P.J. Robust chaos in a model of the electroencephalogram: implications for brain dynamics. Chaos. 2001;11:474–478. doi: 10.1063/1.1394193. [DOI] [PubMed] [Google Scholar]
- da Silva F.L, Blanes W, Kalitzin S.N, Parra J, Suffczynski P, Velis D.N. Epilepsies as dynamical diseases of brain systems: basic models of the transition between normal and epileptic activity. Epilepsia. 2003;44:72–83. doi: 10.1111/j.0013-9580.2003.12005.x. [DOI] [PubMed] [Google Scholar]
- Dichter M.A, Ayala G.F. Cellular mechanisms of epilepsy: a status report. Science. 1987;237:157–164. doi: 10.1126/science.3037700. [DOI] [PubMed] [Google Scholar]
- Doedel, E., Paffenroth, R., Champneys, A., Fairgrieve, T., Kuznetsov, Y. A., Sandstede, B. & Wang, X. 2000 Auto 2000: continuation and bifurcation software for ordinary differential equations (with homcont. See http://sourceforge.net/projects/auto2000/
- Ebersole J.S, Pacia S.V. Localization of temporal lobe foci by ictal eeg patterns. Epilepsia. 1996;37:386–399. doi: 10.1111/j.1528-1157.1996.tb00577.x. [DOI] [PubMed] [Google Scholar]
- Eder H.G, Stein A, Fisher R.S. Interictal and ictal activity in the rat cobalt/pilocarpine model of epilepsy decreased by local perfusion of diazepam. Epilepsy Res. 1997;29:17–24. doi: 10.1016/s0920-1211(97)00061-2. [DOI] [PubMed] [Google Scholar]
- Freeman W.J. A linear distributed feedback model for prepyriform cortex. Exp. Neurol. 1964;10:525–547. doi: 10.1016/0014-4886(64)90049-4. [DOI] [PubMed] [Google Scholar]
- Freeman W.J. Tutorial in neurobiology: from single neurons to brain chaos. Int. J. Bifurcat. Chaos. 1992;2:451–482. [Google Scholar]
- Higham D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001;43:525–546. [Google Scholar]
- Iasemidis L.D. Epileptic seizure prediction and control. IEEE Trans. Biomed. Eng. 2003;50:549–558. doi: 10.1109/tbme.2003.810705. [DOI] [PubMed] [Google Scholar]
- Jirsa V.K, Kelso J.A.S. Spatiotemporal pattern formation in neural systems with heterogeneous connection topologies. Phys. Rev. E. 2000;62:8462–8465. doi: 10.1103/physreve.62.8462. [DOI] [PubMed] [Google Scholar]
- Kramer, M. A. 2005 Nonlinear dynamics and neural systems: synchronization and modeling. PhD dissertation, University of California, Berkeley.
- Lesser R.P, Kim S.H, Beyderman L, Miglioretti D.L, Webber W.R.S, Bare M, Cysyk B, Krauss G, Gordon B. Brief bursts of pulse stimulation terminate afterdischarges caused by cortical stimulation. Neurology. 1999;53:2073–2081. doi: 10.1212/wnl.53.9.2073. [DOI] [PubMed] [Google Scholar]
- Liley D.T.J, Cadusch P.J, Wright J.J. A continuum theory of electro-cortical activity. Neurocomputing. 1999;26–27:795–800. [Google Scholar]
- Liley D.T.J, Cadusch P.J, Dafilis M.P. A spatially continuous mean field theory of electrocortical activity. Network Comput. Neural Syst. 2002;13:67–113. [PubMed] [Google Scholar]
- Morimoto K, Fahnestock M, Racine R.J. Kindling and status epilepticus models of epilepsy: rewiring the brain. Prog. Neurobiol. 2004;73:1–60. doi: 10.1016/j.pneurobio.2004.03.009. [DOI] [PubMed] [Google Scholar]
- Niedermeyer E, DaSilva F.L, editors. Electroencephalography: basic principles, clinical applications, and related fields. Lippincott Williams and Wilkins; New York: 1999. [Google Scholar]
- Nunez P.L, editor. Neocortical dynamics and human EEG rhythms. Oxford University Press; New York: 1995. [Google Scholar]
- Pinto D.J, Ermentrout G.B. Spatially structured activity in synaptically coupled neuronal networks. I. Traveling fronts and pulses. SIAM J. Appl. Math. 2001;62:206–225. [Google Scholar]
- Quyen M.L.V, Navarro V, Martinerie J, Baulac M, Varela F.J. Toward a neurodynamical understanding of ictogenesis. Epilepsia. 2003;44:30–43. doi: 10.1111/j.0013-9580.2003.12007.x. [DOI] [PubMed] [Google Scholar]
- Robinson P.A, Rennie C.J, Rowe D.L. Dynamics of large-scale brain activity in normal arousal states and epileptic seizures. Phys. Rev. E. 2002;65:041924. doi: 10.1103/PhysRevE.65.041924. [DOI] [PubMed] [Google Scholar]
- Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]
- Singer W, Gray C.M. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- Spencer S.S, Guimaraes P, Katz A, Kim J, Spencer D. Morphological patterns of seizures recorded intracranially. Epilepsia. 1992;33:537–545. doi: 10.1111/j.1528-1157.1992.tb01706.x. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross M.L, Steyn-Ross D.A, Sleigh J.W, Liley D.T.J. Theoretical electroencephalogram stationary spectrum for a white-noise-driven cortex: evidence for a general anesthetic-induced phase transition. Phys. Rev. E. 1999;60:7299–7311. doi: 10.1103/physreve.60.7299. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross M.L, Steyn-Ross D.A, Sleigh J.W, Wilcocks L.C. Toward a theory of the general-anesthetic-induced phase transition of the cerebral cortex. I. A thermodynamics analogy. Phys. Rev. E. 2001;64:011917. doi: 10.1103/PhysRevE.64.011917. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross D.A, Steyn-Ross M.L, Wilcocks L.C, Sleigh J.W. Toward a theory of the general-anesthetic-induced phase transition of the cerebral cortex. II. Numerical simulations, spectral entropy, and correlation times. Phys. Rev. E. 2001;64:011918. doi: 10.1103/PhysRevE.64.011918. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross M.L, Steyn-Ross D.A, Sleigh J.W, Whiting D.R. Theoretical predictions for spatial covariance of the electroencephalographic signal during the anesthetic-induced phase transition: increased correlation length and emergence of spatial self-organization. Phys. Rev. E. 2003;68:021902. doi: 10.1103/PhysRevE.68.021902. [DOI] [PubMed] [Google Scholar]
- Traub R.D, Whittington M.A, Buhl E.H, LeBeau A.B.F.E.N, Boyd S, Cross H, Baldeweg T. A possible role for gap junctions in generation of very fast eeg oscillations preceding the onset of, and perhaps initiating, seizures. Epilepsia. 2001;42:153–170. doi: 10.1046/j.1528-1157.2001.26900.x. [DOI] [PubMed] [Google Scholar]
- Wilson H.R, Cowan J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson H.R, Cowan J.D. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. doi: 10.1007/BF00288786. [DOI] [PubMed] [Google Scholar]
- Yang X.F, Duffy D.W, Morley R.E, Rothman S.M. Neocortical seizure termination by focal cooling: temperature dependence and automated seizure detection. Epilepsia. 2002;43:240–245. doi: 10.1046/j.1528-1157.2002.33301.x. [DOI] [PubMed] [Google Scholar]