Effects of coiling on the micromechanics of the mammalian cochlea

Abstract

The cochlea transduces sound-induced vibrations in the inner ear into electrical signals in the auditory nerve via complex fluid–structure interactions. The mammalian cochlea is a spiral-shaped organ, which is often uncoiled for cochlear modelling. In those few studies where coiling has been considered, the cochlear partition was often reduced to the basilar membrane only. Here, we extend our recently developed hybrid analytical/numerical micromechanics model to include curvature effects, which were previously ignored. We also use a realistic cross-section geometry, including the tectorial membrane and cellular structures of the organ of Corti, to model the apical and basal regions of a guinea-pig cochlea. We formulate the governing equations of the fluid and solid domains in a curvilinear coordinate system. The WKB perturbation method is used to treat the propagation of travelling waves along the coiled cochlear duct, and the O(1) system of the governing equations is solved in the transverse plane using finite-element analysis. We find that the curvature of the cochlear geometry has an important functional significance; at the apex, it greatly increases the shear gain of the cochlear partition, which is a measure of the bending efficiency of the outer hair cell stereocilia.

1. Introduction

Spiral or helical shapes are seen in many biological systems, such as the double helix structure of DNA, the spiraling of plants, the helical bends of arteries and the snail-like shape of the mammalian cochlea. Is there a functional significance to having a particular shape? In this paper, we study cochlear coiling. The mammalian cochlea, located in the inner ear, has a snail-like shape, which is commonly believed to pack the hearing organ into a very limited space of the skull. Whether its shape also has a functional role as well has attracted the attention of auditory researchers for many years. However, owing to technical difficulties, both measuring and modelling the motion of the cochlear partition (CP) and its surrounding fluid present extremely difficult challenges. As a result, the assessment of the functional significance of the spiral nature of the cochlea is poorly understood and inconclusive.

In those few cochlear models where coiling has been considered, the CP was often reduced to the basilar membrane (BM) only (Viergever 1978; Loh 1983; Steele & Zais 1985; Kagawa et al. 1987; Kohllöffel 1990; Manoussaki & Chadwick 2000; Givelberg & Bunn 2003). Most of these models reported a negligible effect of curvature on cochlear macromechanics. An exception is the paper of Manoussaki & Chadwick (2000) who concluded that coiling helps to lower the fluid impedance in the cochlea. Huxley (1969) also speculated that coiling of the cochlear geometry could mechanically isolate adjacent sections along the CP and provide a sharp resonance effect. West (1985) studied the relationship of the spiral turns and the length of the BM to the range of audible frequencies in ground dwelling mammals. In his hybrid three-dimensional model, Steele (1999) included cochlear curvature by modelling the structures of the organ of Corti (OC) as orthotropic shells, but did not report effects of coiling on cochlear function.

In cochlear micromechanics, one studies the vibration of the different parts of the CP relative to each other, as well as the detailed motions of the cellular structures within the OC, while in macromechanics, one studies the vibration of the CP, which is often reduced to the BM only, relative to its surrounding bony structures. What, then, is the role of coiling in cochlear micromechanics? To answer this question, we extend our recently developed hybrid analytical/finite-element approach (Cai & Chadwick 2003; Cai et al. 2004) to a curvilinear coordinate system to investigate the significance of curvature in the hearing organ. The new computational model includes the detailed cellular structures within the OC, the interactions between the cochlear partition and fluid, as well as the coiling of the cochlear duct. The fluid is assumed to be viscous and incompressible whose dynamics follows the linearized Navier–Stokes equation. The BM is modelled as a clamped annular spiral plate whose deflection is calculated by the Green's function method. The local annular geometry introduces a radial bending asymmetry which is not present for a straightened geometry. The OC and the tectorial membrane (TM) are modelled as Voigt solids whose governing equations are also formulated in the curvilinear coordinate system, using linear elastic theory. We use the WKB method to treat the propagation of the travelling wave along the coiled cochlear duct, and use the finite-element method (FEM) to solve the O(1) system of the governing equations in the transverse plane. We use an iterative algorithm to solve an eigenvalue problem for the wavenumber of the travelling wave, the solid displacements, and the pressure and velocity fields of the fluid. As no local forcing is applied in the cross-section in solving the eigenvalue problem, we can calculate only the relative displacements of the cochlear structures (Cai et al. 2004). Simulations are taken in the apical and basal regions of a guinea-pig cochlea. The effects of cochlear curvature on the structure of the travelling wave and the function of the cochlea are analysed. Simulation results are compared with those of our straightened cochlear model (Cai & Chadwick 2003; Cai et al. 2004).

2. Model formulation

To model the curvature effects in the cochlea, we adopt a curvilinear coordinate system (θ¹, θ², θ³)=(R, S, Z), in which R represents the radial distance from the modiolar (the Z-) axis, S is the arc length along the coiled cochlear duct and Z, the modiolar axis. The positive direction of Z points out of the R–S plane in figure 1a. This coordinate system is simplified from the helicoidal coordinates used in Manoussaki & Chadwick (2000), by setting the pitch of the helix equal to zero.

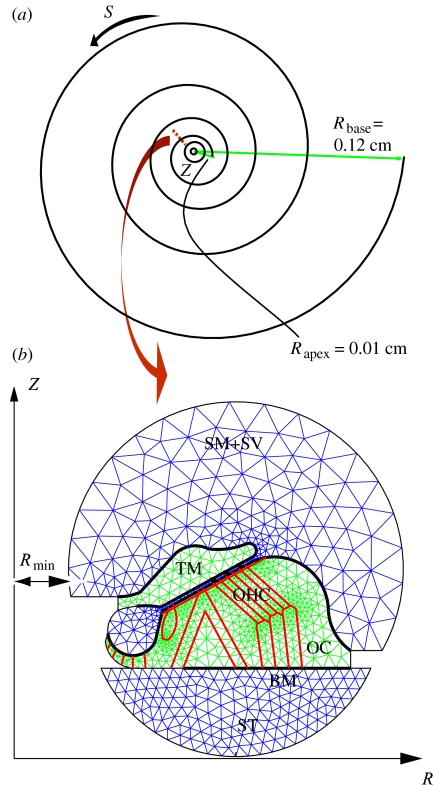
Figure 1.

Curvilinear coordinate system and cochlear geometry. (a) Model representation of a guinea-pig cochlea with four turns of coiling. Z is the modiolar axis, with the positive direction pointing out of R–S plane; S is along the coiled duct; R is the radial distance from the Z-axis. R_base and R_apex represent the minimum R at the base and the apex of the cochlea, respectively. (b) Magnified view of a cross-section at the apical region. Tectorial membrane (TM) and organ of OC are represented by two-dimensional elastic domains. The OC rests on the BM. The stereocilia of the OHC elastically couple the TM and OC. The scala tympani (ST) is the fluid chamber on the lower side, whereas the upper fluid region is the combined scala media (SM) and scala vestibuli (SV).

We also assume the geometry of the cochlear partition and fluid changes slowly with S, slower than the rate of change along R and Z (Manoussaki & Chadwick 2000), which allows us to use the WKB approximation to treat the propagation of the travelling waves along the coiled cochlear duct. We then use FEM in the transverse R–Z plane, which is divided into fluid and elastic domains (figure 1) and is meshed by Matlab PDE Toolbox (Mathworks, Natick, MA). The lower fluid chamber in figure 1b represents the scala tympani (ST), and the upper fluid domain is the combined scala media and scala vestibuli (SM+SV), with Reissner's membrane removed in the present model. The OC and TM solid domains are coupled by the cochlear fluid and the outer hair cell (OHC) stereocilia. The OC rests on the BM, which is modelled as a vibratory clamped annular plate. The cellular structures in the OC include the inner and outer pillar cells, the Deiter's cells, and the inner and outer hair cells. The cross-section of the cochlea is bounded by rigid walls, represented by circular arcs and straight segments in figure 1.

2.1 Non-dimensional coordinate system

We introduce the following non-dimensional coordinates

$$r=R/H_0,z=Z/H_0,s=S/S_0,$$ (2.1)

where H₀ is some characteristic dimension of the cochlear cross-section, and S₀ is the total arc length of the CP from the apex to the base of the cochlea.

Let θ be the polar angle around the modiolar axis, then

$$\text{d}S=\sqrt{R^2+{(\text{d}R/\text{d}\theta )}^2}\text{d}\theta .$$

We can show (dR/dθ)² is small compared with R² (slowly varying geometry) as follows. Suppose R is related to θ by

$$R(\theta )=R_{\text{apex}}\text{exp}\left\{\frac{a}{2\pi N}\right\}\theta ,$$

where N is the number of turns of the cochlear spiral, then

$${\left(\frac{\text{d}R}{\text{d}\theta }\right)}^2/R^2={(a/2\pi N)}^2.$$

As R_apex=0.01 cm, R_base=0.12 cm, and θ varies from 0 to 8π from the apex to the base of a guinea pig cochlea (N=4, figure 1), we obtain (a/2πN)²≈0.01. The corresponding arc length can then be approximated as

$$S=\underset{0}{\overset{\theta }{\int }}R({\theta }^{\prime })\text{d}{\theta }^{\prime }=\theta {\overline{R}}_{\theta },$$

where ${\overline{R}}_{\theta }$ is the average value of R within the interval of [0,θ]. The total arc length of the CP is then

$$S_0=\underset{0}{\overset{2\pi N}{\int }}R(\theta )\text{d}\theta =\underset{0}{\overset{8\pi }{\int }}R(\theta )\text{d}\theta =8\pi {\overline{R}}_0,$$

where ${\overline{R}}_0$ is the average value of R within the interval of [0,8π], i.e. ${\overline{R}}_0=(1/8\pi )\underset{0}{\overset{8\pi }{\int }}R(\theta )\text{d}\theta$. As R increases from the apex to the base of the cochlea, ${\overline{R}}_{\theta }\le {\overline{R}}_0$. Therefore, the non-dimensional arc length is s=ϵθ, where

$$ϵ=\frac{1}{8\pi }\frac{{\overline{R}}_{\theta }}{{\overline{R}}_0}\le \frac{1}{8\pi }\ll 1,$$ (2.2)

for a guinea-pig cochlea with four turns of coiling. Note that ϵ will serve as the small perturbation parameter in the WKB analysis.

The non-dimensional coordinates (r, s, z) are related to the Cartesian coordinate system (x¹, x², x³)=(X, Y, Z) by

$$\{X,Y,Z\}=H_0\{r\text{cos}({ϵ}^{-1}s),r\text{sin}({ϵ}^{-1}s),z\},$$ (2.3)

and the contravariant base vectors $({\mathit{g}}^m=(\partial {\theta }^m/\partial x^n){\mathit{i}}_n)$ of the curvilinear coordinate system are

$$\{{\mathit{g}}^1,{\mathit{g}}^2,{\mathit{g}}^3\}=H_0^{-1}\left\{{\mathit{e}}_r,\frac{ϵ}{r}{\mathit{e}}_s+O({ϵ}^2),{\mathit{e}}_z\right\},$$ (2.4)

from which we can obtain the gradient operator $(\mathrm{\nabla }={\mathit{g}}^m(\partial /\partial {\theta }^m))$

$$\mathrm{\nabla }=H_0^{-1}\left({\mathit{e}}_r\frac{\partial }{\partial r}+\frac{ϵ}{r}{\mathit{e}}_s\frac{\partial }{\partial s}+{\mathit{e}}_z\frac{\partial }{\partial z}\right)+O({ϵ}^2),$$ (2.5)

and the Laplacian operator ${\mathrm{\nabla }}^2\varphi =\mathrm{\nabla }·(\mathrm{\nabla }\varphi )$ (Green & Zerna 1968)

$${\mathrm{\nabla }}^2=H_0^{-2}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{{ϵ}^2}{r^2}\frac{{\partial }^2}{\partial s^2}+\frac{{\partial }^2}{\partial z^2}\right)+O({ϵ}^3),$$ (2.6)

which are useful for deriving governing equations of the cochlear fluid and structures in the following sections. Thus, to O(ϵ²), the curvilinear coordinate system reduces to essentially a cylindrical coordinate system.

2.2 Fluid domains

We assume that the fluid velocity $\tilde{\mathit{V}}$ and pressure $\tilde{P}$ satisfy the linearized Navier–Stokes and mass conservation equations

$$\rho \frac{\partial \tilde{\mathit{V}}}{\partial t}=-\mathrm{\nabla }\tilde{P}+\mu {\mathrm{\nabla }}^2\tilde{\mathit{V}},$$ (2.7)

and

$$\mathrm{\nabla }·\tilde{\mathit{V}}=0,$$

where ρ and μ are the density and viscosity, respectively, of the cochlear fluid. For such a fluid, the pressure is harmonic (apply the divergence operator to equation (2.7))

$${\mathrm{\nabla }}^2\tilde{P}=0.$$ (2.8)

To apply the WKB expansion of (2.8), we assume a wave propagates along s from the base to the apex of the cochlea, and express the pressure in the form

$$\tilde{P}=(P_0+ϵP_1+\cdots )\text{exp}\left\{\text{i}\left(\omega t-{ϵ}^{-1}\underset{0}{\overset{s}{\int }}k(s^{\prime })\text{d}{s}^{\prime }\right)\right\},$$

where k(s) is the dimensionless complex-valued wavenumber normalized by H₀, and ω is the radian frequency. Similar expansions are used for all other dependent variables.

Equations (2.6) and (2.7) lead to

$$r^2\left(\frac{{\partial }^2{P}_0}{\partial r^2}+\frac{{\partial }^2{P}_0}{\partial z^2}\right)+r\frac{\partial P_0}{\partial r}-k^2{P}_0=0,$$ (2.9)

which is the dominant equation of the WKB expansion of (2.8). Note that equation (2.9) does not contain a ∂/∂s term, and therefore can be solved in the r–z plane. Computations are performed in the r–z plane; however, we still retain the coupling in the fluid along the coiled arc length s through the wavenumber k. Although we introduce an additional unknown, the wavenumber k, through the WKB expansion, it is still computationally simpler to find k as the square root of the eigenvalue than to numerically compute all of the sections coupled together (Cai et al. 2004).

We use the no-slip condition in the normal direction as the boundary conditions for the pressure (Cai & Chadwick 2003),

$$\mathit{n}·\mathrm{\nabla }\tilde{P}=-\rho \frac{{\partial }^2{\tilde{U}}_n}{\partial t^2},$$ (2.10)

where t represents time, ρ is the density of the solid domains and $\mathit{n}=n_r{\mathit{e}}_r+n_s{\mathit{e}}_s+n_z{\mathit{e}}_z$ is the outward unit normal of the boundary segments of fluid domains. ${\tilde{U}}_n$ is the normal component of the displacement vector of solid domains.

From (2.5) and (2.10), we obtain

$$n_r\frac{\partial P_0}{\partial r}+n_z\frac{\partial P_0}{\partial z}=\rho {\omega }^2{H}_0{U}_{n0},$$ (2.11)

where U_n0 is the dominant term in the expansion of ${\tilde{U}}_n$.

2.3 OC and TM solid domains

We solve an almost incompressible plane strain problem (without axial coupling) for the OC and TM solid domains. The equation of motion is

$$-\mathrm{\nabla }·\tilde{\sigma }+\rho \frac{{\partial }^2\mathit{U}}{\partial t^2}=0,$$ (2.10)–(2.12)

where the stress tensor $(\tilde{\sigma })$ is related to displacement vector $(\mathit{U}=\tilde{u}{\mathit{e}}_r+\tilde{w}{\mathit{e}}_z)$ by

$$\left(\begin{array}{l}{\tilde{\sigma }}_{rr}\hfill \\ {\tilde{\sigma }}_{zz}\hfill \\ {\tilde{\sigma }}_{rz}\hfill \end{array}\right)=C\overline{V}\left(\begin{array}{l}\frac{\partial \tilde{u}}{\partial r}\hfill \\ \frac{\partial \tilde{w}}{\partial z}\hfill \\ \frac{1}{2}\left(\frac{\partial \tilde{u}}{\partial z}+\frac{\partial \tilde{w}}{\partial r}\right)\hfill \end{array}\right),$$ (2.13)

where

$$C=\frac{H_{0}E}{(1+\nu )(1-2\nu )},$$

and

$$\overline{V}=\left(\begin{array}{lll}1-\nu \hfill & \nu \hfill & 0\hfill \\ \nu \hfill & 1-\nu \hfill & 0\hfill \\ 0\hfill & 0\hfill & (1-2\nu )\hfill \end{array}\right),$$

where E and ν are the Young's modulus and Poisson's ratio, respectively.

Again, we express $\tilde{u}$ and $\tilde{w}$ in the form

$$\tilde{\varphi }=({\varphi }_0+ϵ{\varphi }_1+\cdots )\text{exp}\left\{\text{i}\left(\omega t-{ϵ}^{-1}\underset{0}{\overset{s}{\int }}k(s^{\prime })\text{d}{s}^{\prime }\right)\right\}.$$ (2.14)

Combining (2.5) and (2.10)–(2.12), we obtain

$$\begin{array}{c}(1-\nu )\left(\frac{{\partial }^2{u}_0}{\partial r^2}+\frac{1}{r}\frac{\partial u_0}{\partial r}\right)+\frac{1}{2}(1-2\nu )\frac{{\partial }^2{u}_0}{\partial z^2}+\frac{1}{2}\frac{{\partial }^2{w}_0}{\partial r\partial z}\\ +\frac{\nu }{r}\frac{\partial w_0}{\partial z}=-\rho {\omega }^2{H}_0^2\frac{(1+\nu )(1-2\nu )}{E}{u}_0,\\ \frac{1}{2}\frac{{\partial }^2{u}_0}{\partial r\partial z}+\frac{1}{2r}(1-2\nu )\frac{\partial u_0}{\partial z}+\frac{(1-2\nu )}{2}\left(\frac{{\partial }^2{w}_0}{\partial r^2}+\frac{1}{r}\frac{\partial w_0}{\partial r}\right)\\ +(1-\nu )\frac{{\partial }^2{w}_0}{\partial z^2}=-\rho {\omega }^2{H}_0^2\frac{(1+\nu )(1-2\nu )}{E}{w}_0.\end{array}\}$$ (2.15)

We compute the unknown displacement components (u₀ and w₀) in (2.15) by an iterative algorithm that couples (2.9) and (2.15). Equations (2.9) and (2.15) are solved separately, and loads are transferred at the common boundaries of the fluid and solid between iterations (see §2.5).

Boundary conditions for the two-dimensional solid domains are fully discussed in Cai & Chadwick (2003). Note that the stereocilia of the OHCs couple elastically the TM and RL, which is the top boundary of the OC.

2.4 Vibratory annular spiral plate

We calculate the deflection of the BM via a plate Green's function G (Cai & Chadwick 2003). To obtain the Green's function of an annular plate in the coordinate system (r, s, z), we follow Timoshenko & Woinowsky-Krieger (1959), who described the bending displacement (Y) of plates by

$${\mathrm{\nabla }}^2{\mathrm{\nabla }}^{2}Y=\frac{q}{D},$$ (2.16)

where q is the intensity (force/area) of load on the plate, D is the radial rigidity of the plate and

$${\mathrm{\nabla }}^2=\frac{{\partial }^2}{\partial R^2}+\frac{1}{R}\frac{\partial }{\partial R}+\frac{1}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}$$

is the Laplacian operator in the R−θ plane, which has the form of

$${\mathrm{\nabla }}^2=H_0^{-2}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{{ϵ}^2}{r^2}\frac{{\partial }^2}{\partial s^2}\right)$$

in the r–s plane. Thus, for a vibratory BM, the Green's function G satisfies

$${\mathrm{\nabla }}^2{\mathrm{\nabla }}^{2}G-\frac{{\rho }_{\text{b}}{H}_{\text{b}}}{D}\frac{{\partial }^{2}G}{\partial t^2}=-\frac{\delta (r-r^{\prime })}{D},$$ (2.17)

where ρ_bH_b is the mass per unit area of the BM, δ is the Dirac delta function and r′ represents the radial location where load is applied. Hence, we have

$$\begin{array}{c}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{k^2}{r^2}\right)\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{k^2}{r^2}\right)G_0\\ -\frac{{\rho }_{\text{b}}{H}_{\text{b}}{\omega }^2{H}_0^4}{D}{G}_0=-\frac{H_0^4\delta (r-r^{\prime })}{D},\end{array}$$ (2.18)

where G₀ is the dominant term of G. Equation (2.18) can be transformed to

$$\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{k^2}{r^2}-{\kappa }^2\right)\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{k^2}{r^2}+{\kappa }^2\right)G_0(r,r^{\prime })=-\frac{H_0^4\delta (r-r^{\prime })}{D},$$ (2.19)

where ${\kappa }^4=\rho H_{\text{b}}{\omega }^2{H}_0^4/D$. The solution of (2.19) is of the form

$$G_0(r,r^{\prime })=\{\begin{array}{c}{G}_{\text{L}}(r)=C_1{J}_k(\kappa r)+C_2{Y}_k(\kappa r)\\ +C_3{I}_k(\kappa r)+C_4{K}_k(\kappa r)\text{if}r\le r^{\prime },\\ G_{\text{R}}(r)=D_1{J}_k(\kappa r)+D_2{Y}_k(\kappa r)\\ +D_3{I}_k(\kappa r)+D_4{K}_k(\kappa r)\text{if}r>r^{\prime },\end{array}$$ (2.20)

where J and Y are, respectively, Bessel functions of the first and second kind, and I and K are the modified Bessel function of the first and second kind, respectively. In the present study, we neglect the axial coupling in the plate Green's function to solve a plane strain problem. The arbitrary constants C_i and D_i (i=1, 2, 3, 4) are to be determined by the following boundary conditions for a clamped annular plate

$$G_{\text{L}}(b_1)=0,G_{\text{R}}(b_2)=0,\frac{\partial G_{\text{L}}}{\partial r}(b_1)=0,\frac{\partial G_{\text{R}}}{\partial r}(b_2)=0,$$

and continuity conditions

$$\begin{array}{c}{G}_{\text{L}}(r^{\prime })=G_{\text{R}}(r^{\prime }),\frac{\partial G_{\text{L}}}{\partial r}(r^{\prime })=\frac{\partial G_{\text{R}}}{\partial r}(r^{\prime }),\\ \frac{{\partial }^2{G}_{\text{L}}}{\partial r^2}(r^{\prime })=\frac{{\partial }^2{G}_{\text{R}}}{\partial r^2}(r^{\prime }),\frac{{\partial }^3{G}_{\text{R}}}{\partial r^3}(r^{\prime })-\frac{{\partial }^3{G}_{\text{L}}}{\partial r^3}(r^{\prime })=-\frac{H_0^3}{D},\end{array}$$

where b₁ and b₂ are the radial coordinates of the BM endpoints. Note that the continuity conditions at the loading point (at r=r′) are obtained by integrating both sides of equation (2.19) across the loading point. These boundary and continuity conditions form a 8×8 linear algebraic system, which is numerically solved for the C_i and D_i in Matlab (Mathworks, Natick, MA). The deflection of the BM then can be calculated by

$$Y_{\text{b}0}(r)=H_0\underset{b_1}{\overset{b_2}{\int }}{G}_0(r,r^{\prime })\mathrm{\Delta }{\sigma }_{n0}(r^{\prime })\text{d}{r}^{\prime },$$ (2.21)

where Δσ_n0 is the difference between the pressure at the lower surface of the BM and the negative of the normal stress at the lower surface of the OC (Cai & Chadwick 2003).

2.5 Numerical algorithm

We solve the above fluid–solid interaction eigenvalue problem by an iterative algorithm. First, we guess values of the wavenumber k and of the displacements of BM, TM and OC, and solve the elliptic problem in the fluid domains for the pressure field P₀, by using the Matlab elliptic solver $(-\mathrm{\nabla }·(c\mathrm{\nabla }{P}_0)+a{P}_0=f)$ to solve equation (2.9). Then, we solve the two-dimensional plane strain problems sequentially for the OC and TM using the Matlab elliptic system solver of the form

$$-\mathrm{\nabla }·(\tilde{c}\otimes \mathrm{\nabla }{\mathit{U}}_0)+\overline{a}{\mathit{U}}_0=\mathit{f},$$

where ${\mathit{U}}_0={(U_{0r},U_{0z})}^{\text{T}}$ is the displacement vector, ${\mathit{f}}_0={(f_r,f_z)}^{\text{T}}$ is the volume-force vector, $\overline{a}$ is a rank-two tensor and $\tilde{c}$ is a rank-four tensor, which is written as four 2×2 matrices, c₁₁, c₁₂, c₂₁, c₂₂, with the form

$$c_{ij}=\left(\begin{array}{ll}{c}_{ij11}\hfill & c_{ij12}\hfill \\ c_{ij21}\hfill & c_{ij22}\hfill \end{array}\right),i,j=1,2.$$

By the notation $\mathrm{\nabla }·(\tilde{c}\otimes \mathrm{\nabla }{\mathit{U}}_0)$, we mean the 2×1 vector with (i, 1)-component

$$\sum _{j=1}^2\left(\frac{\partial }{\partial r}{c}_{ij11}\frac{\partial }{\partial r}+\frac{\partial }{\partial r}{c}_{ij12}\frac{\partial }{\partial z}+\frac{\partial }{\partial z}{c}_{ij21}\frac{\partial }{\partial r}+\frac{\partial }{\partial z}{c}_{ij22}\frac{\partial }{\partial z}\right)U_{0j}.$$

After obtaining the displacements of OC, we compute the stress within the OC, which are used to calculate the updated deflection of the BM in (2.21). The impedance of the deformable surfaces is then defined as $Z_n=-P_0/U_{n0}$, which provides the eigenvalue solver

$$(-\mathrm{\nabla }·(c\mathrm{\nabla }{P}_0)+a{P}_0=\lambda d{P}_0)$$

mixed homogeneous boundary condition. The eigenvalue solver gives the updated wavenumber, which is used in the elliptic solver for the next iteration, and so on (Cai & Chadwick 2003). At each iteration, we calculate the real and imaginary parts of the wavenumber k, as well as the amplitude of the shear gain, and compare these values with those of the previous iteration. A convergent solution is thought to be found when the relative changes of all these values are smaller than 1%.

Matching between the coefficients of the governing equations and the PDE coefficients of the Matlab solvers is needed; for example, for solving P₀ in (2.9), we let f=0, a=−k²/r, c=−r in the elliptic solver, and for solving the eigenvalue k² and eigenvalue pressure, we let c=−r, d=1/r and a=0 in the eigenvalue solver. The boundary condition for solving P₀ is the generalized Neumann type,

$$\mathit{n}·(c\mathrm{\nabla }{P}_0)+q{P}_0=g,$$

and we use q=0 and $g=-r\rho {\omega }^2{H}_0{U}_{n0}$ (U_n0=0 for rigid walls) for the elliptic solver, and g=0 and $q=r\rho {\omega }^2{Z}_n$ for the eigenvalue solver, respectively. For solving U₀ in (2.15), the PDE-coefficients matching for the Matlab elliptic system solver and for its boundary conditions is a similar process (see Cai & Chadwick 2003).

The inputs to the computation are geometry and mesh of the cross-section (figure 1), the material properties, and the frequency ω. The outputs are wavenumber k, the relative displacements of the TM, OC and BM, together with the corresponding modal fluid pressure fields in the scalae. To study the curvature effects alone, we keep in the present model the same inputs (cross-section geometry and mesh, Young's modulus and Poisson's ratio of the cochlear structures) as in Cai et al. (2004).

3. Results and discussion

We first compute the detailed deformations within the TM and OC and obtain the orbits of simulated microspheres, by tracing the points on the surface of TM and Hensen cells during a vibrational cycle. Then we compare our simulation results to those of our previous developed straight model (Cai et al. 2004). Unless otherwise indicated, computations are done at the apex, where the curvature is the greatest, with 1 kHz of stimulation frequency and the minimum apical radius R_min=0.01 cm.

Curvature effects can be clearly seen from the changes of the trajectory of a simulated microsphere on the TM surface (figure 2): (a) the inclination of the long axis of the orbits changes from transversal in the straight model to radial in the coiled model; (b) the rotation direction of the simulated microsphere changes from counter-clockwise in the straight model to clockwise in the coiled model. The simulation results of the coiled model agree with the observation at the same frequency (1 kHz) of Gummer et al. (1996), who measured the trajectories of microspheres on the top of the TM at the apex of the guinea-pig cochlea. Without coiling (Cai et al. 2004), however, the orbit of the simulated microsphere on the TM is similar to the observation of Hemmert et al. (2000) at a lower frequency (0.5 kHz). In addition, the detailed movements within the OC is rather vertical in the curved model (figure 2), following more efficiently the motion of the BM.

Figure 2.

Detailed movements of the CP in (a) straight and (b) coiled models at the apex. Orbits are shown for three simulated microspheres on the tectorial membrane, Hensen cells and basilar membrane, respectively, during a vibrational cycle. The snapshot of CP motions is represented by arrows, whose direction and size represent, respectively, the direction and relative amplitude of the CP displacements. The position of the solid triangles on the trajectories indicates the initial time at which the snapshots are taken. The rotation of the simulated microsphere on the TM is counter-clockwise in the straight model and clockwise in the coiled model. Stimulation frequency is 1 kHz. R_min=0.01 cm in the coiled model.

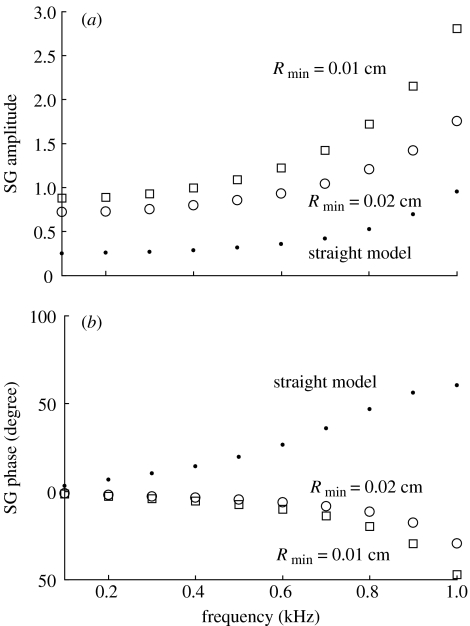
From the relative motion of the CP, we can compute the shear gain (SG) of the cochlea, which is defined as the ratio of shearing displacement of the TM and the top of the OC to the BM deflection (Rhode & Geisler 1967; Allen 1980). The shear gain thus defined is a complex number whose amplitude and phase represent, respectively, the bending efficiency of the OHC stereocilia and the phase (timing) difference between the deflections of the OHC stereocilia and the BM. We calculate the shearing motion at the second row of OHCs. The BM deflection is computed at its centre, near the footplate of the Deiter's cell of the first row. Figure 3 shows the comparison of our computed shear gain in straight and coiled models. At 1 kHz, the coiled model (R_min=0.01 cm) gives a shear gain of ca 2.7, against ca 0.96 in the straight model, a more than 180% of increase in amplitude. The phase of the shear gain changes sign in straight and coiled models. Note that, without losing generality, we define the zero phase for the BM as the instant when BM is in its equilibrium position (zero deflection) and tends to displace towards scala vestibuli, and for the OHC stereocilia as the instant when the stereocilia is in its equilibrium position (zero rotation) and tends to rotate towards the highest row (clockwise). In the coiled model, the motions of the BM, TM and OC correlate in such a manner that when the BM deflects towards the scala vestibuli, the shearing movement between the TM and the OC bends the OHC stereocilia in the excitatory direction.

Figure 3.

The (a) amplitude and (b) phase of the SG at the apex of the cochlea. SG is defined as the ratio of shearing displacement of the tectorial membrane and the top of the organ of Corti to the basilar membrane deflection. SG is a complex number whose phase represents the timing difference between the OHC-stereocilia deflection and the basilar membrane displacement. Curvature improves greatly the shear gain, which is a measure of the bending efficiency of the outer hair cell stereocilia.

As pointed out by West (1985), although von Békésy (1960, 1970) described a similarity of the BM vibrational patterns in straight and curved models, he did not suggest that cochlear coiling was unimportant to hearing. Rather, he suggested that while the curvature did not affect the pattern of the travelling wave on the BM, it did affect the deflection of the hair cells in the OC and the motion of the TM. Our present passive model (without OHC electromechanical motility) confirms the suggestions of von Békésy.

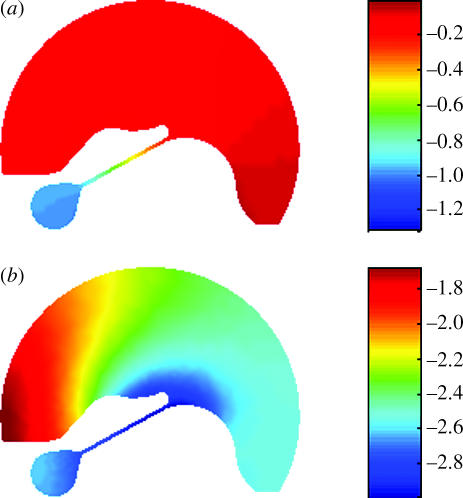
The spiral shape of the cochlear geometry may affect the travelling wave in the cochlea by changing the loading condition in the fluid–structure interaction process. In a straight tube, there may not be as much interaction of the fluid with the solid structures as in a curved one. Figure 4 shows the difference of the fluid pressure fields in the combined scalae media and vestibuli (SM+SV) between the straight and coiled models. Pressure fields are normalized by their maximum absolute value and scaled by BM deflection. In the coiled model, the pressure distributed on the upper surface of the TM exhibits a larger radial variation. This is consistent with predictions from our macromechanics model of the effects of curvature (Manoussaki et al. submitted).

Figure 4.

Comparison of the apical spatial distribution of cochlear fluid pressure in SM+SV in the (a) straight and (b) coiled models. Pressure fields are normalized by their maximum absolute value and then scaled by the BM deflection. The snapshots of the pressure distributions are taken at the initial time (t=0) when the basilar membrane moves towards the SV.

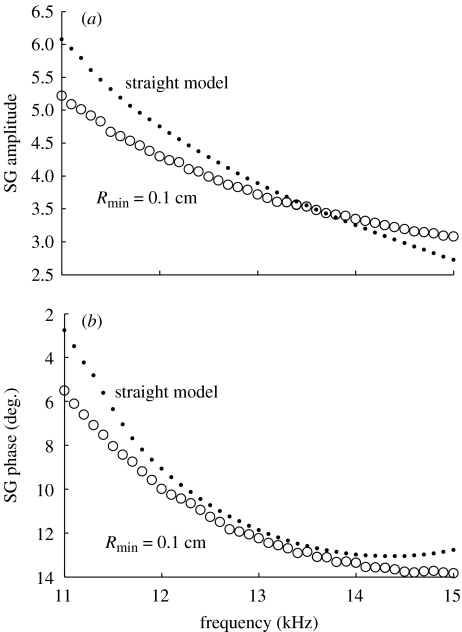
What are the curvature effects on cochlear micromechanics at the basal region of the hearing organ? Figure 5 shows the comparison of our computed shear gain in straight and coiled models at the basal portion of the cochlea. These results indicate that the coiling effects are not as significant as in the apical region of the cochlea. In the frequency range of 11–13.5 kHz, we even see a decrease in the shear gain amplitude in the curved model. The phases of the shear gain are negative in both straight and coiled models, and the effects of curvature on the shear gain phase are small compared with those at the apical portion. Our simulation results suggest that cochlear curvature helps detection of low-frequency sounds at the apex of the cochlea, but does not help for the detection of the sounds of high frequencies at the base. The radius of curvature is the main parameter responsible for the difference between the effects of coiling in the basal and apical regions of the cochlea.

Figure 5.

The (a) amplitude and (b) phase of the SG at the base of the cochlea. Simulation results show that the cochlear curvature does not play as important role in the basal region as it does in the apical portion of the cochlea.

One limitation of our present model is that we can calculate only the relative motions of the cochlear structures (eigenvalue solution), and therefore cannot compute the effects of coiling on the absolute amplitude of the CP vibration. In our simplified macromechanics model, we show how this limitation can be removed by carrying out the analysis to O(ϵ) (Manoussaki et al. submitted).

In summary, the bending mechanism of the hair bundles is very important to the understanding of the stimulation of the inner and outer hair cells, which opens the mechanotransduction channel in the hearing process (Dallos et al. 1996; Robles & Ruggero 2001; Zwislocki 2002). Our results show that the curvature of the cochlear geometry affects cochlear micromechanics; it greatly improves the apical shear gain (both amplitude and phase) of the cochlear partition, which is a useful index to quantify the bending efficiency of the hair bundles.