Absolute Binding Free Energy Calculations Using Molecular Dynamics Simulations with Restraining Potentials

Abstract

The absolute (standard) binding free energy of eight FK506-related ligands to FKBP12 is calculated using free energy perturbation molecular dynamics (FEP/MD) simulations with explicit solvent. A number of features are implemented to improve the accuracy and enhance the convergence of the calculations. First, the absolute binding free energy is decomposed into sequential steps during which the ligand-surrounding interactions as well as various biasing potentials restraining the translation, orientation, and conformation of the ligand are turned “on” and “off.” Second, sampling of the ligand conformation is enforced by a restraining potential based on the root mean-square deviation relative to the bound state conformation. The effect of all the restraining potentials is rigorously unbiased, and it is shown explicitly that the final results are independent of all artificial restraints. Third, the repulsive and dispersive free energy contribution arising from the Lennard-Jones interactions of the ligand with its surrounding (protein and solvent) is calculated using the Weeks-Chandler-Andersen separation. This separation also improves convergence of the FEP/MD calculations. Fourth, to decrease the computational cost, only a small number of atoms in the vicinity of the binding site are simulated explicitly, while all the influence of the remaining atoms is incorporated implicitly using the generalized solvent boundary potential (GSBP) method. With GSBP, the size of the simulated FKBP12/ligand systems is significantly reduced, from ∼25,000 to 2500. The computations are very efficient and the statistical error is small (∼1 kcal/mol). The calculated binding free energies are generally in good agreement with available experimental data and previous calculations (within ∼2 kcal/mol). The present results indicate that a strategy based on FEP/MD simulations of a reduced GSBP atomic model sampled with conformational, translational, and orientational restraining potentials can be computationally inexpensive and accurate.

INTRODUCTION

Molecular recognition phenomena involving the association of ligands to macromolecules with high affinity and specificity play a key role in biology (1–3). Although the fundamental microscopic interactions giving rise to bimolecular association are relatively well understood, designing computational schemes to accurately calculate absolute binding free energies remains very challenging. Computational approaches currently used for screening large databases of compounds to identify potential lead drug molecules must rely on very simplified approximations to achieve the needed computational efficiency (4). Nonetheless, the calculated free energies ought to be very accurate to have any predictive value. Furthermore, the importance of solvation in scoring ligands in molecular docking has been stressed previously (5).

In principle, free energy perturbation molecular dynamics (FEP/MD) simulations based on atomic models are the most powerful and promising approaches to estimate binding free energies of ligands to macromolecules (6–11). Indeed, test calculations have shown that FEP/MD simulations can be more reliable than simpler scoring schemes to compute relative binding affinities in important biological systems (12,13), and that it can naturally handle the influence of solvent and dynamic flexibility (14). There is a hope that calculations based on FEP/MD simulations for protein-ligand interactions could become a useful tool in drug discovery and optimization (15–22). Nonetheless, despite outstanding developments in simulation methodologies (23), carrying out FEP/MD calculations of large macromolecular assemblies surrounded by explicit solvent molecules often remains computationally prohibitive. For this reason, it is necessary to seek ways to decrease the computational cost of FEP/MD calculations while keeping them accurate.

To simulate accurately the behavior of molecules, one must be able to account for the thermal fluctuations and the environment-mediated interactions arising in diverse and complex systems (e.g., a protein binding site or bulk solution). In FEP/MD simulations, the computational cost is generally dominated by the treatment of solvent molecules. Computational approaches at different level of complexity and sophistication have been used to describe the influence of solvent on biomolecular systems (24). Those range from MD simulations based on all-atom models in which the solvent is treated explicitly (10,25), to Poisson-Boltzmann (PB) continuum electrostatic models in which the influence of the solvent is incorporated implicitly (24,26). There are also semianalytical approximations to continuum electrostatics, such as generalized Born (27–31), as well as empirical treatments based on solvent-exposed surface area (32–40). However, even though such approximations are computationally convenient, they are often of unknown validity when they are applied to a new situation.

An intermediate approach, which combines some aspects of both explicit and implicit solvent treatments (41–43), consists in simulating a small number of explicit solvent molecules in the vicinity of a region of interest, while representing the influence of the surrounding solvent with an effective solvent-boundary potential (41–50). Such an approximation is an attractive strategy to decrease the computational cost of MD/FEP computations because binding specificity is often dominated by local interactions in the vicinity of the ligand while the remote regions of the receptor contribute only in an average manner. The method used in this study is called the generalized solvent boundary potential (GSBP) (43). GSBP includes both the solvent-shielded static field from the distant atoms of the macromolecule and the reaction field from the dielectric response of the solvent acting on the atoms of the simulation region. GSBP is a generalization of spherical solvent boundary potential, which was designed to simulate a solute in bulk water (41). In the GSBP method, all atoms in the inner region belonging to ligand, macromolecule, or solvent can undergo explicit dynamics, whereas the influence of the macromolecular and solvent atoms outside the inner region are included implicitly.

It is also possible to reduce the computational cost of FEP/MD simulations and even improve their accuracy by using a number of additional features. For example, the Weeks Chandler Andersen (WCA) separation of the Lennard-Jones potential can be used to efficiently calculate the free energy contribution arising from the repulsive and dispersive interactions (51,52). Furthermore, biasing potentials restraining the translation, orientation, and conformation of the ligand can help enhance the convergence of the calculations (17,21,22,53,54). Such a procedure can provide correct results as long as the effect of all the restraining potentials is rigorously taken into account and unbiased. Combining these elements yields the present computational strategy, which consists in FEP/MD simulations of a reduced GSBP atomic model with enhanced sampling using conformational, translational, and orientational restraining potentials.

In this study, the absolute (standard) binding free energies of eight FK506-related ligands to FKBP12 (FK506 Binding Protein) are calculated using FEP/MD simulations with GSBP to explore the practical feasibility of such a computational strategy. FKBP12 is a rotamase catalyzing the cis-trans isomerization of peptidyl-prolyl bonds (55). FK506 is a key drug used for immunosuppression in organ transplant. It binds strongly to FKBP12 (56) and the FKBP12/FK506 complex, in turn, binds and inhibits calcineurin, thus blocking the signal transduction pathway for the activation of T-cells (57,58). In addition to its obvious importance as a pharmacological target, FKBP12 was chosen in this study for three main reasons. First, crystal structures of FKBP12 in complex with several ligands are available (59–61). Second, the binding constants of those FK506-related ligands with FKBP12 have been experimentally determined (60). Third, this system serves as a rich platform to test and validate different computational strategies to estimate binding free energies (62–65). This study is part of an ongoing collaborative effort involving two other groups (Pande (63) and J. A. McCammon, personal communication, 2005) with the goal of comparing the results of calculations based on different treatments and approximations but using the same force field (AMBER). Pande and co-workers (63) and Shirts (64) carried out extensive all-atom free energy perturbation (FEP) molecular dynamics (MD) simulations. With the same system, J. M. Swanson and J. A. McCammon (personal communication, 2005) used molecular mechanics/Poisson-Boltzmann-and-surface-area (MM-PBSA), a popular approach that relies on a mixed scheme combining configurations sampled from molecular dynamics (MD) simulations with explicit solvent, with free energy estimators based on an implicit continuum solvent model (66).

In the next two section, the theoretical formulation and the computational details are given. Then, all the results of the computations are presented and discussed in the following section. The article ends with a brief conclusion summarizing the main points.

METHODS

Theoretical formulation

The theoretical formulation for the equilibrium binding constant used here was previously elaborated in Deng and Roux (52). Briefly, the equilibrium binding constant K_b for the process corresponding to the association of a ligand L to a protein P, L + P LP, can be expressed as

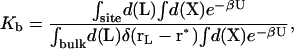(1)

where L represents the coordinates of the ligand (only a single ligand needs to be considered at low concentration), X represents the coordinate of the solvent and the protein, β ≡ 1/k_BT, U is the total potential energy of the system, r_L is the position of the center-of-mass of the ligand, and r* is some arbitrary position (far away) in the bulk solution. The subscripts site and bulk indicate that the integrals include only configurations in which the ligand is in the binding site or in the bulk solution, respectively. Eq. 1 can be related to the double decoupling method (17,21), though the derivation in Deng and Roux (52) proceeds from population configurational ensemble averages rather than the traditional treatment that consists in equating the chemical potentials of the three species, L, R, and LR. In particular, it should be noted that, K_b has dimension of volume because of the δ-function δ(r_L–r*) in the denominator. This δ-function arises from the translational invariance of the ligand in the bulk volume (see (52)).

For computational convenience, the reversible work for the entire association/dissociation process is decomposed into eight sequential steps during which the interaction of the ligand with its surrounding (protein and solvent) as well as various restraining potentials are turned “on” and “off” (see Appendix A). Various potentials restraining the conformation, position, and orientation of the ligand are used throughout the step-by-step process. Those are designed to reduce the conformational sampling workload of the free energy simulations by biasing the ligand to be near its bound configuration (conformation, position, and orientation) as it becomes completely decoupled from its surrounding. This approach has the advantage of focusing the sampling on the most relevant conformations, though it is essential that the biasing effect of the restraining potentials be rigorously handled and that the final result from the computation be independent of the restraints. The usage of biasing restraints in computations of binding free energies goes back to early work by Hermans and Subramaniam (67), with a number of recent variants (21,22,52–54).

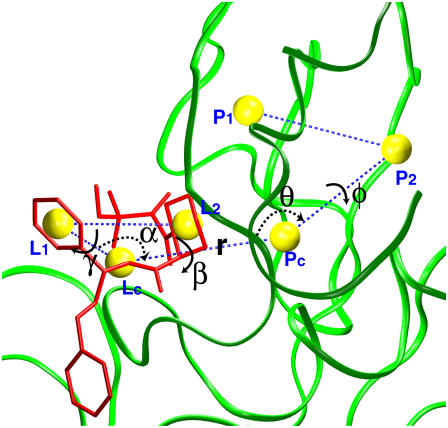
The translational and orientational restraining potentials are constructed from three point-positions defined in the protein (P_c, P₁, and P₂) and three point-positions defined in the ligand (L_c, L₁, and L₂) (Fig. 3). Specifically, P_c is the center-of-mass of the protein residues forming the binding site, and L_c is the center-of-mass of the ligand. P₁ and P₂ are the center-of-mass of two groups of atoms in the protein, while L₁ and L₂ are the center-of-mass of two groups of atoms in the ligand. The choice of the six reference point-positions is more or less arbitrary, as long as they are not co-linear and allow us to define the orientation of the ligand relative to the protein. The translational restraint is defined as u_t = 1/2[k_t(r_L − r₀)² + k_a(θ_L − θ₀)² + k_a(φ_L − φ₀)²], where r_L is the distance P_c − L_c, θ_L is the angle P₁ − P_c − L_c, and φ_L is the dihedral angle P₂ − P₁ − P_c − L_c; k_t and k_a are the force constants, and r₀, θ₀, and φ₀ are the average values of the fully interacting ligand in the binding site taken as a reference. Similarly, the orientational restraining potential is defined as u_r = 1/2[k_a(α_L − α₀)² + k_a(β_L − β₀)² + k_a(γ_L − γ₀)²], where the angle α_L (P_c − L_c − L₁), the dihedral angle β_L (P₁ − P_c − L_c − L₁), and the dihedral angle γ_L (P_c − L_c − L₁ − L₂) are three angles defining the rigid body rotation; k_a is the force constant, and α₀, β₀, and γ₀ are the reference values taken from the fully interacting ligand in the binding site. Generally, the reference values and the force constants are taken from an average based on an unbiased simulation of the fully interacting ligand in the binding site. The magnitude of the force constants is estimated from the fluctuations of its associated coordinates as k_x ≈ k_BT/〈Δx²〉. This has been shown to yield the optimal biasing in free energy perturbations (53). The conformational restraining potential u_c is also constructed as a quadratic function, u_c = k_c(ζ[L;L_ref])², where k_c is a force constant, and ζ is the root mean-square deviation (RMSD) of the ligand coordinates L relative to the average structure of the fully interacting ligand in the binding site L_ref, taken as a reference structure.

FIGURE 3.

Translational and rotational restraints on ligand 8. Three random point-positions in the protein (P_c, P₁, P₂) and three random point-positions in the ligand (L_c, L₁, and L₂) were chosen to set up the translational and rotational restraints. They are the center-of-mass of the protein (green) in the sphere, residue Val-101, residue Tyr-26, the ligand (red), atoms labeled in red in Fig. 1, and atoms labeled in blue in Fig. 1, respectively. These positions are shown in yellow spheres with dashed blue lines connecting them. The translational restraint is defined by r (P_cL_c), θ (P₂P_cL_c), and φ (P₁P₂P_cL_c). The rotational restraint is defined by α (P_cL_cL₁), β (P₂P_cL_cL₁), and γ (P_cL_cL₁L₂).

With these definitions, the sequential steps corresponding to the dissociation process with the fully interacting ligand in the protein binding site as initial state are (see also Table A1 in Appendix A):

1. A potential u_c is applied to the fully interacting ligand (U₁) in the binding site to maintain its conformation near the average bound state.

2. A potential u_t is applied to the center-of-mass of the fully interacting ligand (U₁) restrained by u_c to maintain its relative position in the binding site.

3. A potential u_r is applied to the fully interacting ligand (U₁), restrained by u_c and u_t, to maintain its relative orientation in the binding site.

4. The interactions of the ligand, restrained by u_c, u_t, and u_r, with the binding site are turned off (decoupling: U₁ ⇌ U₀).

5. The potential u_r applied to the decoupled ligand (U₀), restrained by u_c and u_t, is released.

6. The restraining potential u_t applied to the decoupled ligand (U₀), restrained by u_c, is released.

7. The interaction of the ligand, restrained by u_c, with the surrounding bulk solution is turned on (coupling: U₀ ⇌ U₁).

8. The potential u_c applied to the fully interacting ligand in the bulk solution (U₁) is finally released.

As shown in Appendix A, the standard binding free energy ΔG°_bind is given by

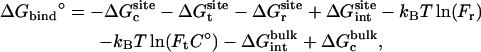(2)

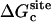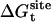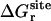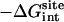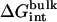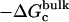where , , , , k_BT ln F_r, k_BT ln(F_tC°), , and correspond to the reversible work done in Steps 1–8, respectively. Since the ligand is decoupled from its environment in Steps 5 and 6, the factor F_r can be evaluated as a numerical integral over three rotation angles, and the factor F_t can be evaluated as a numerical integral over the translation of the ligand center-of-mass in three-dimensional space. The constant C° insures conversion to the standard state concentration (= 1 M or 1/1661 Å⁻³). All the remaining ΔG contributions must be calculated using FEP/MD simulations. It is useful to combine the corresponding contributions in Eq. 2 and express the standard binding free energy as

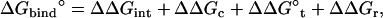(3)

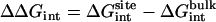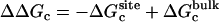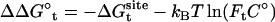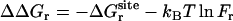where corresponds to the free energy contribution arising from the interactions of the ligand with its surrounding (bulk and/or protein), while , , and correspond to the conformational, translational, and orientational restriction of the ligand upon binding, respectively. Equation 3 makes the interpretation of each contribution intuitively clear (see below). Lastly, if the ligand has symmetry and can bind in a number of equivalent ways, it is necessary to include the effect of the symmetry factor n as − k_BT ln(n).

PRACTICALITIES

Translational and orientational contributions

It is customary to describe bimolecular binding as a process in which a ligand free in solution loses translational and orientational degrees of freedom, as it associates with the protein. The unfavorable contribution to the standard binding free energy caused by the loss of freedom is compensated for, as the ligand gains favorable interactions with proteins. In this regard, it is informative to consider 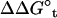, the free energy contribution associated with the translation of the ligand, obtained by combining 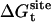and the factor F_t,

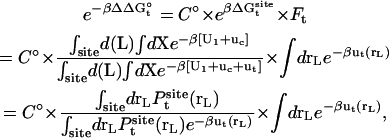(4)

where 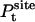is the probability distribution of ligand position in the binding site. If the translational restraining potential u_t(r_L) is strong and centered on r_m—the most probable position of the ligand center-of-mass in the binding site (the maximum of 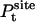)—the probability distribution with the restraint is sharply peaked at r_m,

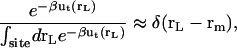(5)

and the translational contribution is

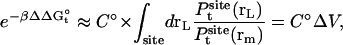(6)

where ΔV is an effective accessible volume for the center-of-mass of the ligand in the binding site. This volume, which is evaluated naturally in units of ų with MD simulations, can be converted to the standard state volume by the constant C°. One may note that the effective volume ΔV is typically on the order of ∼1 ų. Therefore, for all practical purposes, it is always much smaller than the standard state volume of 1661 ų, e.g., a ΔV equal to 1 ų (a typical value) yields the well-known standard state offset factor −k_BT ln(C°) of 4.4 kcal/mol. For this reason, the reduction in translational freedom of the ligand makes an unfavorable contribution to binding free energy.

Similarly, it is informative to consider the total free energy contribution associated with the rotation of the ligand ΔΔG_r obtained by combining 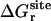and F_r,

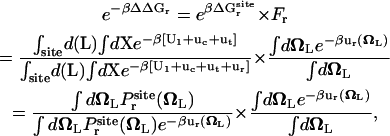(7)

where 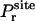is the distribution of the orientation angles (this 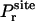depends on u_t). In the limit of strong rotational restraint potential u_r(Ω), the bias potential acts essentially as a δ-function,

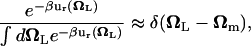(8)

which is sharply peaked at Ω_m, the maximum of 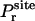, i.e., the most probable orientation of the ligand in the binding site. For a nonlinear ligand, it follows that

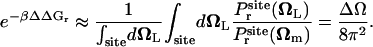(9)

It may be noted that the factor ΔΩ/8π² is necessarily smaller than (or equal to) 1. For this reason, the reduction in rotational freedom of the ligand always makes an unfavorable contribution to binding free energy.

The above analysis shows that reduction in both translational and orientational freedom yield unfavorable contributions to the binding free energy. To clarify the significance of this result further, it is useful to relate ΔV and ΔΩ to the properties of the bound ligand. Assuming that the thermal fluctuations of the (fully interacting) ligand in the binding site are Gaussian, ΔV has the closed-form expressions

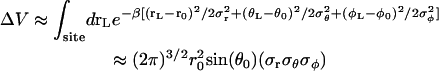(10)

and ΔΩ,

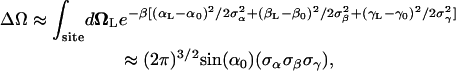(11)

where 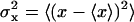represent the thermal fluctuations of each variable. Such Gaussian approximation may be advantageous if one is attempting to estimate the translational and orientational contributions to the standard binding free energy using only the information extracted from an unbiased simulation of the fully interacting ligand, i.e., without actually performing FEP/MD simulations. One may note also some similarity with the MM-PBSA scheme (68), in which the translational and orientational contributions are estimated using a quasi-harmonic approximation (69,70).

Solvation free energy of the ligands

Step 7 provides the solvation free energy of a ligand that is restrained by u_c to remain near its bound conformation. This does not correspond to the true solvation free energy of a flexible ligand (e.g., the process ligand in vacuum ⇌ ligand in solvent). The latter may be expressed as

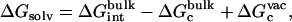(12)

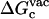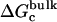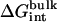where is the free energy corresponding to applying the conformational restraint on the ligand decoupled from its surrounding (≡ vacuum). The values and are the same as defined above. Therefore, one additional quantity (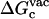) must be computed if one is interested in evaluating the solvation free energy of the ligand. For the sake of comparison with the results of Pande, Shirts and co-workers (63,64), we also computed the solvation free energy of the ligands, though in practice, this quantity is not required to compute the standard binding free energy.

Atomic models and computational details

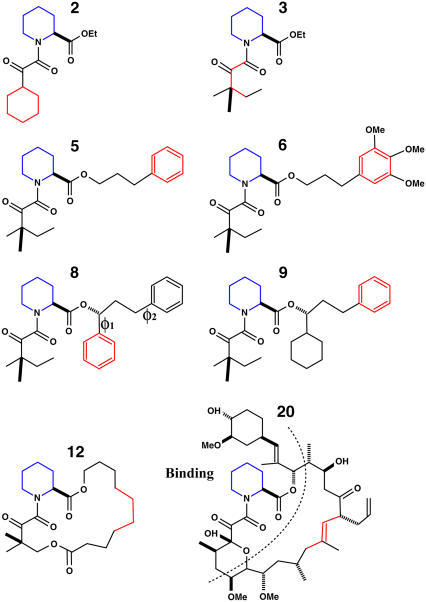
The eight FK506-related ligands (ligands 2, 3, 5, 6, 8, 9, 12, and 20) are shown in Fig. 1. These ligands are numbered according to previous experimental (60) and computational work (63). Ligand 20 is the molecule FK506 (56). Three types of starting structures were considered for the computations. The first set comprises the crystal structures with ligands 8, 9, and 20 (PDB code 1FKG, 1FKH, and 1FKJ, respectively). The second set corresponds to models for ligands 3 and 5 obtained by construction from the crystal structure of FKBP12 in complex with ligand 9. Replacing the cyclohexyl group of ligand 9 with a hydrogen gives ligand 5, while replacing the phenylmethyl group of ligand 5 with a hydrogen gives ligand 3. Ligands 3 and 5 are highly similar to ligand 9, and the direct modeling is justifiable. The third set was provided by M. R. Shirts and V. S. Pande (personal communication, 2005); it corresponds to atomic coordinates of docking models of ligands 2, 3, 5, 6, and 12 and crystal structures for ligands 8, 9, and 20, followed by 200 ps of MD simulations with explicit solvent. In all the tables, the three sets are referred to as x-ray, mod, and MD, respectively. The CHARMM biomolecular simulation program was used for all the simulations. To compare with previous calculations by Pande, Shirts and co-workers (63,64) and J. M. Swanson and J. A. McCammon (personal communication, 2005), the same atomic force field was used in this study. The force field for the protein is AMBER99, and that for the ligands is from the 2002 version of general AMBER force field (71) as provided by M. R. Shirts (personal communication, 2005)). The charges of the ligands are from AM1/BCC (72). The conversion of the AMBER force field to CHARMM format is given in Appendix B.

FIGURE 1.

Structural formulae of the eight ligands used in the calculation. Ligands 2, 5, 6, 8, and 9 have one or two physically symmetric units (phenyl or cyclohexyl group). Flat-bottom dihedral restraints were applied on these symmetric units to prevent exchange between physically equivalent conformers. Ligand 20 is also referred to as FK506 in the literature (60). The atoms labeled in red and blue are the atom used to define the point-positions L₁ and L₂, respectively in Fig. 3.

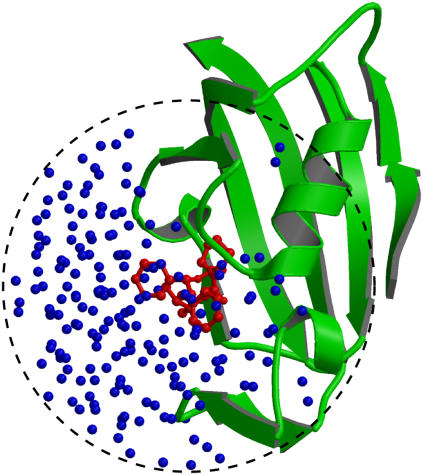
The GSBP method (73,74), implemented in the biomolecular simulation program CHARMM (75), was used to solvate a spherical region centered on the FKBP12 binding site. In GSBP, the system is divided into an outer and an inner region. In the inner region, the ligand, the solvent molecules, and part of the macromolecule are simulated explicitly with MD. In the outer region, the remaining protein atoms are included explicitly while the solvent is represented as a continuum dielectric medium. The influence of the surrounding outer region on the atoms of the inner region is represented in terms of a solvent-shielded static field and a solvent-induced reaction field. The reaction field due to changes in charge distribution in the dynamic inner region is expressed in terms of a basis set expansion of the inner simulation region charge density. The basis set coefficients correspond to generalized electrostatic multipoles. The solvent-shielded static field from outer macromolecular atoms and the reaction field matrix, representing the couplings between the generalized multipoles, are both invariant with respect to the configuration of the explicit atoms in the inner simulation region. They are calculated only once for macromolecules of arbitrary geometry using the finite-difference PB equation, leading to an accurate and computationally efficient hybrid MD/continuum method for simulating a small region of a large biological macromolecular system. A spherical inner region of 15 Å radius was used for all the ligands. The size of the GSBP simulated systems is typically ∼2500 atoms. The systems were hydrated with a fixed number of water molecules, though this could be generated dynamically using grand canonical Monte Carlo (76). Dielectric constants of 80 and 4 were assumed for the solvent and the protein in the outer region, respectively. The static field arising from the protein charges in the outer region and the generalized reaction field matrix including five electric multipoles were calculated using the PBEQ module (77,78) of CHARMM (75) and stored for efficient simulations. A spherical restraining potential was applied to keep the water molecules from escaping the inner region using the MMFP GEO command. The spherical GSBP simulation system is illustrated in Fig. 2 in the case of ligand 8. During the simulation, protein atoms near the edge of the boundary are fixed while a nonpolar potential keeps the water molecules inside the sphere. Each system of ligand/FKBP12 solvated with GSBP was equilibrated for 2 ns at 300 K using Langevin dynamics. A friction coefficient of 5 ps⁻¹ was assigned to all nonhydrogen atoms. A time-step of 2 fs was used. The average structure of the ligand was calculated from the equilibration trajectory (typically from 0.4 ns to 2 ns), which was then used as a reference structure L_ref in the conformational restraining potential u_c. The fluctuations of the six internal variables (r_L, θ_L, φ_L, α_L, β_L, and γ_L) used in the translational and rotational restraining potentials were monitored to estimate the force constants for the biasing restraining potentials.

FIGURE 2.

A sphere containing FKBP12, ligand 8, and water molecules in the GSBP method. The crystal structure (pdb code: 1FKG) of the complex of FKBP12 (green, cartoon) and ligand 8 (red, ball-and-stick) is solvated in water molecules (blue, small spheres). In the GSBP method, only atoms in a sphere (15 Å radius) centered on the ligand are represented explicitly. All atoms outside the sphere were removed and were represented implicitly using the continuum method. The dielectric constants of the solvent and the protein in the outer region are 80 and 4, respectively.

Protocol for binding free energy (steps 1–8)

Conformational restraints (steps 1 and 8)

For better accuracy, the free energies associated with the conformational restriction of the ligand near the reference conformation, 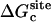and 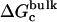(Steps 1 and 8), was not obtained directly by FEP/MD simulations, but was calculated by integration of the Boltzmann factor of the RMSD potential of mean force (PMF) obtained from umbrella sampling simulations. For the ligand in the bulk, 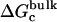is given by

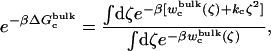(13)

where 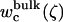is the ligand PMF as a function of the RMSD relative to L_ref in bulk solution. Similar expressions hold for 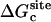and 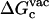. The umbrella sampling method (79) was used to evaluate the PMF as a function of RMSD. To insure a uniform sampling of the RMSD, the simulations were generated using a quadratic biasing potential of the form k_c(ζ[L;L_ref] − ζ_i)² centered on successive values of ζ_i. Specifically, 21 biasing windows were used with the RMSD offset value increasing from 0.0 to 4.0 Å in steps of 0.2 Å for the ligand in the binding site, and 21 windows were used with the RMSD offset value increasing from 0.0 to 5.0 Å in steps of 0.25 Å for the ligand in the bulk solution. The initial configurations for the 21 umbrella sampling windows were generated using a short initial run with a strong force constant k_c (500 kcal/mol/Ų). Then, each window was equilibrated using a force constant of 10 kcal/mol/Ų, and after sufficient equilibration; a 1-ns simulation was used for sampling. No translational or orientational restraining potential is present during those simulations. The weighted histogram analysis method (80–82) was used to unbias the results and compute the PMF as a function of RMSD. An optimal force constant for the conformational restraining potential u_c = k_cζ² was determined from the RMSD-PMF of the ligands in solution and in the binding site. Specifically, a value of 10 kcal/mol/Ų was chosen for k_c so that the normalized Boltzmann probability of the conformationally restrained ligand in the bulk or bound to the protein both have their most probable values around the same small RMSD (∼0.5–1.0 Å).

Some ligands have symmetric structural elements (e.g., the two phenyl groups of ligand 8 as shown in Fig. 1), which can undergo isomerization and exchange between physically equivalent conformations. Sampling all these (physically indistinguishable) conformations may become prohibitively slow when the ligand is in the binding site, but less so in the solvent. With finite-length trajectories, isomerizations could take place frequently during the FEP/MD simulation of the ligand in solvent, but not in those of the bound complex. A proper accounting of the relative conformational entropy cost upon ligand binding will be compromised by such nonequivalence in sampling one state of the system, but not the other. This problem can be avoided by limiting the conformational space to a single one of the physically equivalent rotamers of the ligand in all the FEP/MD simulations. In the present calculations, a steep flat-bottom dihedral restraining potential was applied to all the symmetric units of the ligand to prevent exchange between identical rotameric states during the simulations. It should be noted that such flat-bottom restraining potential does not affect the physical properties of the ligand and the final binding free energy as long as it is present during all the computations, with the ligand in the solvent and in the binding site. The restriction was applied to the ligand during all the free energy calculations involving the conformational restraining potential u_c (the ligand in the binding site, in solution, and in vacuum for the solvation free energy calculations). The force constant for the flat-bottom restraint is 500 kcal/mol/rad².

Translational and rotational restraints (Steps 2 and 3)

The free energies corresponding to the translational and rotational restraints with the ligand in the binding site, 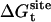and 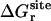, were calculated using FEP/MD simulations. The translational (u_t) and rotational (u_r) restraints were gradually turned on via the linear coupling parameters κ_t and κ_r (with values of 0.0, 0.025, 0.05, 0.075, 0.1, 0.2, 0.4, 0.6, 0.8, and 1.0). The six point-positions in the protein (P_c, P₁, and P₂) and the ligand (L_c, L₁, and L₂) used to define the relative position and orientation of the ligand with respect to the protein are illustrated in Fig. 3 in the case of ligand 8.

Interaction energy (Steps 4 and 7)

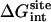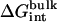The contribution corresponding to the interaction energy of the ligand with its surrounding, and , were calculated with FEP/MD simulations. For this purpose, the Lennard-Jones (LJ) potential was separated into repulsive and dispersive free energy using the Weeks Chandler Andersen (WCA) method (51,83). A nonlinear coupling parameter s was introduced to control the repulsive part, and a linear coupling parameter ξ was introduced to control the dispersive part. Furthermore, a linear coupling parameter λ was introduced to control the electrostatic interactions. Such separation of the potential with these coupling parameters permits an accurate evaluation of the free energy and a clear step-by-step decomposition of the nonbond interactions into repulsive, dispersive, and electrostatic contributions (52). Though the free energy decomposition of the nonbonded interactions formally depends on the order in which each of these contributions are activated, introducing the repulsive core in the first step is an unavoidable physical necessity. A molecular entity with dispersive attraction and charges, but no core repulsion, makes no physical sense (the energy does not have a lower bound). The dispersion and electrostatics could be interchangeably introduced as in second or third steps, with little impact on the free energy decomposition, because those do not greatly affect the structure of the solvent. Therefore, the resulting free energy decomposition can lead to useful observations because the step-by-step FEP/MD procedure goes through physically meaningful intermediates. In the context of a particle insertion process, the repulsive interaction is first introduced gradually (s = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1), while the dispersive and electrostatic interactions are turned off (ξ = 0 and λ = 0). Then, in the presence of the repulsive interaction (s = 1), the dispersive interaction is turned on gradually (ξ = 0.0, 0.25, 0.5, 0.75, and 1.0) while the electrostatic interaction is turned off (λ = 0). Finally, the electrostatic interaction are gradually turned on (λ = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0) in the presence of both the repulsive and dispersive interactions. For each set of coupling parameters, 120-ps Langevin dynamics was generated and averages were calculated using the last 100 ps (additional simulations of 1 ns were generated to check the convergence). The results were unbiased using the weighted histogram-analysis method facility of CHARMM. The free energy components (repulsive, dispersive, and electrostatic free energies) were calculated for the ligand in the binding site or in the bulk solution. For the GSBP simulations, the atoms of the protein in the outer region are not kept explicitly for the sake of computational efficiency. All the FEP window simulations were generated concurrently starting from the structure of the equilibrated system. The contribution from the long-range van der Waals dispersive interaction with the (missing) atoms of the outer region (solvent and protein) was evaluated from a snapshot of a large all-atom model of the solvated protein with its ligand, and was included in the free energy. The large system was built with 8000 water molecules (length ∼ 60 Å) and the full protein for the ligand in the binding site. For the ligand in the bulk solution, 1000 water molecules (length of ∼30 Å) were used. The difference between the bulk and the binding site nearly cancel out, with the magnitude of each component being on the order of −1.0 kcal/mol. For example, the long-range corrections of ligand 8 in the binding site and in the bulk are −0.9 and −1.5 kcal/mol, respectively. Though the magnitude of the long-range correction depends on the cutoff used for the nonbonded interactions, its net impact on the total binding free energy is similar to the values of Pande, Shirts and co-workers (63,64) for similar cutoff (see Table 5.2 in (64)).

All the results are given in Table 1.

TABLE 1.

Nonbond free energy components for the binding of ligands to FKBP12

Lig	Struct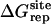
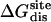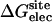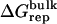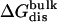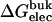2	MD	30.8	−47.3	−17.5	30.5	−28.8	−13.6
3	mod	34.9	−47.7	−18.1	29.5	−26.2	−13.5
3	MD	35.7	−45.5	−23.8	25.4	−21.3	−19.8
5	mod	35.9	−51.3	−21.2	30.6	−27.3	−15.2
5	MD	36.4	−53.1	−21.0	34.5	−32.1	−16.3
6	MD	40.4	−57.4	−25.9	38.9	−38.2	−19.6
8	X ray	41.2	−62.3	−22.1	42.3	−41.2	−18.4
8	MD	45.4	−63.1	−22.2	44.4	−42.0	−18.8
9	X ray	44.5	−61.6	−21.4	45.3	−43.2	−15.9
9	MD	51.0	−66.0	−21.0	45.1	−42.3	−15.9
12	MD	41.6	−58.1	−28.8	34.2	−31.4	−24.6
20	X ray	58.8	−84.4	−31.1	59.4	−61.9	−32.5
20	MD	56.5	−84.0	−30.9	57.0	−60.2	−32.2

Three sets of structures were used. X-ray means x-ray crystal structure; mod means the structure is modified from the crystal structure of ligand 9 by replacing some groups with hydrogen. MD means the structure is modeled from crystal structures and equilibrated for ∼200 ps by Shirts (64). The nonbond free energy components include repulsive (ΔG_rep), dispersive (ΔG_dis), and electrostatic (ΔG_elec) free energy. The long-range van der Waals correction is included in ΔG_dis. The superscripts site and bulk indicate the ligand is in the binding site or in the bulk solution, respectively.

Translational and orientational factors (Steps 5 and 6)

The translational factor F_t was calculated numerically from the expression

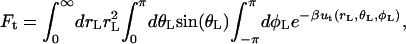(14)

where u_t = 1/2[k_t(r_L − r₀)² + k_a(θ_L − θ₀)² + k_a(φ_L − φ₀)²] is a quadratic translational restraining potential. The value k_t is the force constant for the distance restraint, and k_a is the force constant for the angle and dihedral restraints; r₀, θ₀, and φ₀ are the reference values of the distance, angle, and dihedral determined from an average of the equilibration trajectory and subsequently used to define the position of the ligand.

Similarly, the orientational factor F_r was calculated numerically from the expression

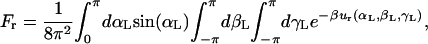(15)

where u_r = 1/2[k_a(α_L − α₀)² + k_a(β_L − β₀)² + k_a(γ_L − γ₀)²] is a quadratic orientational restraining potential. The value k_a is the force constant for the angle and dihedral restraints; α₀, β₀, and γ₀ are the reference values of the angle and dihedrals determined from an average of the equilibration trajectory and subsequently used to define the orientation of the ligand.

RESULTS AND DISCUSSION

The calculated standard binding free energy with the various components are given in Table 2 for the eight FK506-related ligands shown in Fig. 1. In the following, the various steps of the FEP/MD methodology for computing the standard binding free energy are illustrated in the case of ligand 8. Then, general observations are made about the results for the eight ligands.

TABLE 2.

Free energy components for the binding of ligands to FKBP12

Lig	Struct		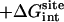	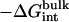+ ΔΔGc	+ ΔΔGt	+ ΔΔGr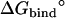
2	MD	−34.0	11.8	2.2	3.2	4.4	−12.3
3	mod	−30.9	10.2	3.1	3.7	5.2	−8.7
3	MD	−33.6	15.7	2.0	3.3	3.5	−9.0
5	mod	−36.7	12.0	5.5	3.5	5.4	−10.2
5	MD	−37.8	13.9	3.5	3.5	5.2	−11.6
6	MD	−42.9	19.0	5.5	3.3	5.4	−9.7
8	X ray	−43.3	17.2	6.9	3.4	5.4	−10.3
8	MD	−39.9	16.3	5.6	3.3	4.2	−10.3
9	X ray	−38.6	13.8	4.5	3.5	5.0	−11.7
9	MD	−35.9	13.0	3.4	3.4	4.6	−11.6
12	MD	−45.2	21.8	1.0	3.4	5.3	−13.7
20	X ray	−56.7	34.9	2.7	3.3	5.6	−10.1
20	MD	−58.4	35.5	3.3	3.4	5.4	−10.8

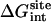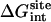Note each free energy component was corrected with the sign already. The ligands are labeled as in Table 1. The value and are the total nonbond free energies, which are equal to the sum of nonbond free energy components in Table 1. The values ΔΔG_c, ΔΔG_t°, and ΔΔG_r are the net free energies corresponding to the conformational restraints, the translational restraint, and the rotational restraint, respectively (Eq. 3). The value ΔG_bind° is the standard binding free energy.

Illustrating the FEP/MD method with ligand 8

The reduced FKBP12/ligand GSBP system is shown in Fig. 2. Only the atoms in the inner region (defined as a sphere of 15 Å radius) are simulated explicitly. The inner region includes the ligand (red, ball-and-stick), the water molecules (blue, small spheres), and a part of the protein (green, cartoon). The influence of the remaining atoms in the outer region (protein and solvent) is included implicitly. The static and reaction field arising from the protein and solvent in the outer region is evaluated using a continuum electrostatic approximation. The static field represents the electrostatic influence from the protein charges in the outer region, shielded by the complex geometry of the protein-solvent interface. The reaction field represents the polarization of the dielectric solvent in the outer region in response to the explicit charges in the inner region.

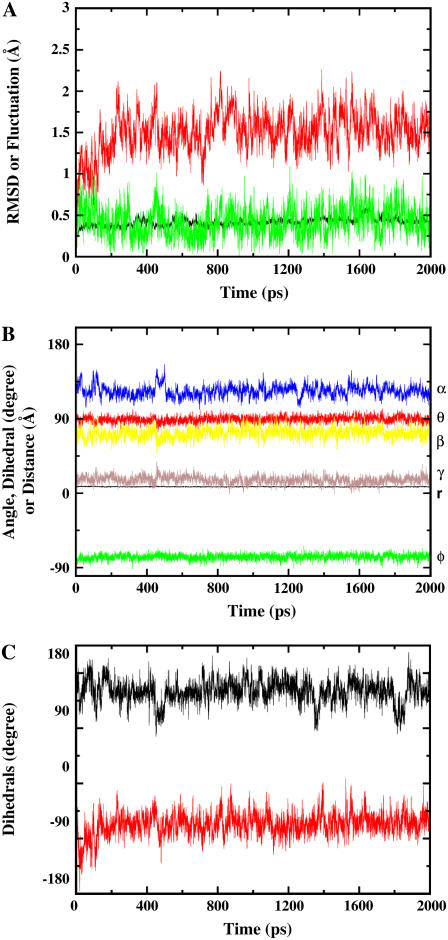
First, the FKBP12/ligand GSBP system was equilibrated (for 2 ns) with Langevin dynamics without any biasing restraint. The final snapshot of the equilibration (rather than some average) was used as the input structure for FEP/MD simulations. Fig. 4 A shows the RMSD fluctuations of the nonhydrogen atoms of the protein (black), ligand (red), and the fluctuation of the center-of-mass of the ligand (green). The simulated system appears to be very stable. Fig. 4 B shows the fluctuation of the six relative coordinates (r_L, θ_L, φ_L, α_L, β_L, and γ_L), which are used subsequently to implement translational and rotational restraining potential. Those internal coordinates are defined from six point-positions constructed from the Cartesian coordinates of the protein-ligand complex (see Fig. 3). The RMS fluctuation in the distance r_L (black) is ∼0.5 Å, while those of the angles are ∼10°. As shown previously, an optimal value of the force constant for a restraining potential is to choose k_x ≈ k_BT/〈Δx²〉 (53). Thus, for the FEP/MD simulations, the force constants for the distance restraint and the angle/dihedral restraint were chosen as 1 kcal/mol/Ų and 200 kcal/mol/rad², respectively.

FIGURE 4.

Equilibration of the GSBP system containing ligand 8 in complex with FKBP12. (A) RMSDs of the heavy atoms in the protein (black) and in the ligand (red), and the fluctuation of the center-of-mass of the ligand (green). (B) The fluctuation of the six parameters used to define the translational and rotational restraints. The curves are labeled with r (black), θ (red), φ (green), α (blue), β (yellow), and γ (brown), respectively. (C) The fluctuation of the two dihedrals next to the two symmetric phenyl groups shown in Fig. 1. The fluctuation of φ₁ is shown in black and the fluctuation of φ₂ is shown in red.

Nonbond interaction free energy

The nonbond free energy calculation bears the major part of the computational cost to calculate the standard binding free energy. The conformational, translational, and orientational restraining potentials are applied on the ligand during the FEP/MD simulations (Steps 4 and 7). (The translational and orientational potentials have no influence on the FEP/MD simulations of the ligand in the isotropic bulk.) As a result, the uncoupled ligand retains its bound conformation (on average), and remains in place even after its interactions with the protein and the solvent are turned off. This is clearly advantageous because a floppy and uncoupled ligand wandering freely in the simulation system dramatically increases the size of the configurational space that needs to be explored during the FEP/MD simulations, which can give rise to significant sampling problems. A faster convergence can be achieved using restraining potentials (see also the discussion in Boresch et al. (21) and Woo and Roux (22)). However, one should keep in mind that the specific values for the nonbonded contribution depend on the applied translational, orientational and conformational restraints; variations on the order of 1.0 kcal/mol between different runs with slightly different reference values for the restraints are common.

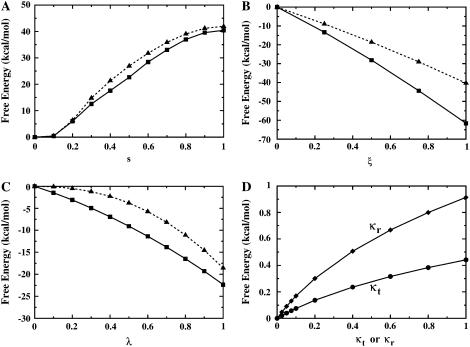
To further improve the convergence, the LJ interaction is separated into dispersive and repulsive free energy using the WCA decomposition (51). This separation of the LJ potential into pure repulsive and dispersive parts is somewhat arbitrary (others would be possible), though it has the advantage of clearly identifying positive- and negative-definite contributions to the free energy, respectively. The nonbond free energy components (dispersive, repulsive, and electrostatic free energies) are calculated with FEP/MD simulations by gradually varying the coupling parameters ξ, s, and λ, respectively (see Methods). Fig. 6, A–C, shows the nonbond free energy components as a function of the corresponding coupling parameters for ligand 8 in the binding site (solid square) and in the bulk solution (dashed triangle), respectively. The repulsive free energy (Fig. 6 A) both in the binding site (solid) and in the bulk solution (dashed) is ∼40 kcal/mol. Thus, the repulsive part of the LJ potential makes only a small net contribution to the binding free energy. In contrast, the dispersive free energy (Fig. 6 B) in the binding site (solid) is much larger than that in the bulk solution (dashed). The difference is ∼−20 kcal/mol, strongly favoring ligand binding. The electrostatic free energy (Fig. 6 C) in the binding site (solid) is ∼4 kcal/mol more negative than that in the bulk solution (dashed), and thus contributes favorably to binding. Therefore, the dispersive van der Waals attraction strongly favors binding. In other words, an isosteric nonpolar analog to ligand 8 would still bind to FKBP, even without any electrostatic contributions from ligand partial-charges. This is a general observation for all the ligands considered here (see below).

FIGURE 6.

The free energy components are gradually turned on as the parameters increase from 0 to 1 for ligand 8 in complex with FKBP12. The nonbond free energy components (A–C) for the ligand in the binding site (solid line, square) and the ligand in the bulk solution (dashed line, triangle) are shown as solid and dashed lines, respectively. (A) Repulsive free energy. (B) Dispersive free energy. (C) Electrostatic free energy. (D) The free energies corresponding to the translational (shown with circle symbols and κ_t) and rotational (shown with ♦ and κ_r) restraints applied to the ligand in the binding site.

RMSD potential of mean force

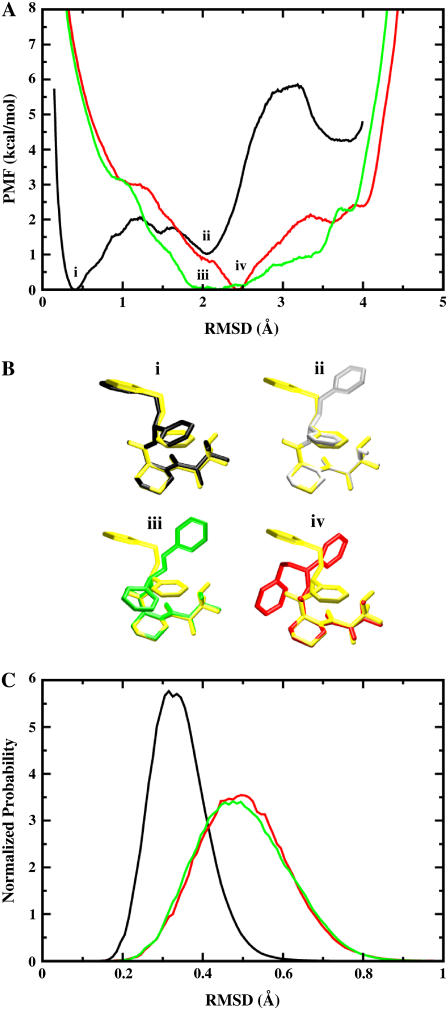
A key feature of the present strategy is the RMSD restraining potential u_c, designed to keep the ligand near the bound conformation. Such restraining potential is an effective device to control the global conformation of a molecule (84,85). Though usefulness of such RMSD restraint becomes more limited in the case of very large structures, drug-like ligands are generally small molecules and their conformation can be accurately controlled without problem. To clarify the significance of the contribution from the RMSD restraining potential, we examine the PMF of the ligand as a function of the RMSD relative to its conformation when bound to the protein. Fig. 5 A shows the PMF as a function of the RMSD values calculated for ligand 8 in the binding site, in the bulk solution, and in vacuum using umbrella sampling simulations. The PMF for the binding site (black) has an absolute minimum at ∼0.4 Å, with a secondary minimum at ∼2 Å. The PMF shows that in the binding site, ligand 8 is stable around its average bound structure calculated from the equilibration trajectory. It also indicates that ligand 8 can adopt a different conformation, which is slightly less favorable by ∼1.3 kcal/mol, while it remains bound to FKBP12. The main (i) and secondary (ii) ligand configurations, illustrated in Fig. 5 B, differ mostly by the rotation of one aromatic ring that interacts weakly with the protein. The PMF in the bulk solution (green) shows a broad minimum at ∼2 Å. The most stable conformation of ligand 8 in the solvent (iii), illustrated in Fig. 5 B, differs mostly by the rotation of two of the aromatic rings. The PMF shows that any conformations differing from the bound state by 1.5 to 3.5 Å RMSD should be accessible through thermal fluctuations. Obviously, there is a free energy penalty to bring the conformation of the ligand, moving freely in the bulk solution, to the conformation it must adopt in the binding site. The free energy required to restrict the conformation of the ligand is determined numerically using Eq. 13. The value of 6.9 kcal/mol given in Table 2 can be easily understood from a direct comparison of the two PMFs in Fig. 5 A. The PMF of the ligand in the solvent (green) goes up to 7 kcal/mol at an RMSD corresponding to the minimum of the PMF in the binding site (black, ∼0.4 Å). In other words, ∼7 kcal/mol of conformational free energy is required to transform the ligand from its most probable conformation in the bulk (iii), to its most probable conformation in the binding site (i). The PMF in vacuum (red) has many similarities with the PMF in the bulk solution, though the minimum at 2.5 Å is not as broad.

FIGURE 5.

PMF calculations on the conformational restraints for ligand 8 in complex with FKBP12. (A) PMF curves for ligand 8 in the binding site (black), in the bulk solution (green), and in vacuum (red). The callouts i and ii label the minima of the PMF for the ligand in the binding site. The callouts iii and iv label the minima of the PMFs for the ligand in the bulk solution and in vacuum, respectively. (B) The average structures of the ligand around the minima are shown together with the average structure of the ligand in the equilibration (shown in yellow). The average structures of the ligand around the minima i, ii, iii, and iv are colored in black, gray, green, and red, respectively. The structures are aligned along the piperidine ring in ligand 8. (C) The normalized Boltzmann factors exp[−β(w_c(ξ) + k_cξ²)] with a force constant k_c = 10 kcal/mol/Ų for the ligand in the binding site (black), in the bulk solution (green), and in vacuum (red).

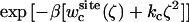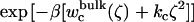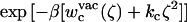The optimal force constant k_c to restrict the ligand around its average bound conformation was determined from the calculated PMF. Fig. 5 C shows the normalized (biased) Boltzmann distribution , , and as a function of the RMSD ζ for the ligand in the binding site (black), in the bulk solution (green), and in vacuum (red), respectively. With a force constant of 10 kcal/mol/Ų, the conformational distribution functions of the ligand in all the systems (binding site, bulk solution, and vacuum) have a high overlap at ∼0.5 Å RMSD. Such force constant insures that the ligand is kept near the reference conformation L_ref during the calculations for Steps 2, 3, 4 and 7.

Using restraints of different strength

The present computational strategy attempts to enhance the configurational sampling of the molecular systems using biasing restraints. Optimal values for the calculations use a force constant k_c for the conformational restriction of 10 kcal/mol/Ų, a distance force constant k_t of 1 kcal/mol/Ų, and an angle/dihedral force constant k_a of 200 kcal/mol/rad². Fig. 6 D shows the progression of the free energies corresponding to the translational (circles) and rotational (diamonds) restraints applied to the ligand in the binding site. The resulting values are typically on the order of 1–2 kcal/mol, and the FEP/MD simulations converge without problems. However, a legitimate concern might be that the final results for the binding free energy remain tainted by the choice of force constants for the restraints.

To address this issue, the absolute binding free energy was recalculated for ligand 8 using different force constants k_c, k_t, and k_a. The results are given in Table 4. It is observed that the final binding free energy is nearly independent of the biasing restraints, even when the force constants are varied by a large amount. All the calculations in Table 3 used the same set of force constants, with k_c = 10 kcal/mol/Ų, k_t = 1 kcal/mol/Ų, and k_a = 200 kcal/mol/rad². When the force constants k_t and k_a are varied, only the following free energy components change: the net free energy contribution associated with the translational and rotational freedom (ΔΔG_t and ΔΔG_r), and the nonbond interaction free energy contribution of the ligand in the binding site (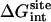). In the case of the conformational restraint, it may be noted that the accuracy appears to be somewhat compromised if the force constant is <∼1.0 kcal/mol/Ų. The main reason is that the uncoupled ligand in the binding site begins to adopt conformations different from the average bound conformation, which makes the calculation slower to converge. It is therefore advantageous to use restraints that are sufficiently strong to avoid this problem.

TABLE 4.

Binding free energy of the FKBP12/ligand 8 complex (started from the x-ray structure) at different force constants for the RMSD potentials, the translational restraint, and the rotational restraint

kc	kt	ka		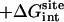	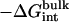+ ΔΔGc	+ ΔΔGt	+ ΔΔGr	ΔG°bind
1	1	200	−38.6	16.0	2.5	3.4	5.1	−11.6
10	1	200	−43.3	17.2	6.9	3.4	5.4	−10.3
10	0.2	40	−42.1	17.2	6.9	2.4	4.4	−11.1
10	10	1000	−44.4	17.2	6.9	4.5	5.5	−10.2
10	100	4000	−44.8	17.2	6.9	5.0	5.8	−9.8
30	1	200	−44.5	17.2	7.6	3.5	5.4	−10.8
100	1	200	−47.5	19.3	8.5	3.5	5.6	−10.6

The value k_c (in kcal/mol/Ų) is the force constant for the RMSD potentials. The value k_t (in kcal/mol/Ų) is the distance force constant for the translational restraint. The value k_a (in kcal/mol/rad²) is the angle/dihedral force constant for the translational and rotational restraints.

TABLE 3.

Binding free energy and solvation energy compared with other results

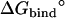
					ΔGsolv
Lig	Struct	This work	Experiments	Shirts (64)	This work	Shirts (64)
2	MD	−12.3 ± 1.4	−7.8 ± 0.1	−5.42	−11.4 ± 1.1	−13.56
3	mod	−8.7 ± 0.7	−8.4 ± 0.1	NA	−9.7 ± 0.5	NA
3	MD	−9.0 ± 1.1	−8.4 ± 0.1	−8.22	−13.8 ± 0.7	−16.98
5	mod	−10.2 ± 1.1	−9.5 ± 0.1	NA	−12.9 ± 0.1	NA
5	MD	−11.6 ± 2.1	−9.5 ± 0.1	−6.92	−12.7 ± 0.5	−15.02
6	MD	−9.7 ± 2.8	−10.8 ± 0.3	−8.29	−18.2 ± 1.7	−17.36
8	X ray	−10.3 ± 0.4	−10.9 ± 0.1	NA	−17.3 ± 0.9	NA
8	MD	−10.3 ± 1.2	−10.9 ± 0.1	−10.42	−15.4 ± 1.9	−15.21
9	X ray	−11.7 ± 1.0	−11.1 ± 0.2	NA	−12.6 ± 0.8	NA
9	MD	−11.6 ± 0.1	−11.1 ± 0.2	−9.11	−11.8 ± 0.8	−13.95
12	MD	−13.7 ± 2.8	−10.3 ± 0.2	−7.51	−22.1 ± 2.9	−23.49
20	X ray	−10.1 ± 1.2	−12.7 ± 0.2	NA	−35.1 ± 0.7	NA
20	MD	−10.8 ± 3.0	−12.7 ± 0.2	−13.34	−36.4 ± 1.4	−35.15

The calculated binding free energies are compared with the experimental results (60) and the previous calculations by Shirts (64). The force constants used are: k_c = 10 kcal/mol/Ų, k_t = 1 kcal/mol/Ų, and k_a = 200 kcal/mol/rad². The error bars in the calculations are the standard deviations of three or more independent runs. The solvation free energies by M. R. Shirts and co-workers are from personal communication (2005) . NA means data are not available.

Standard binding free energies

In Table 3, the results of the calculations for the eight ligands are compared with the experimental values (60), and the results from extensive FEP/MD calculations by Pande, Shirts and co-workers (64). The results are in good agreement with the experimental results, especially in the case of ligands for which it is possible to have a good starting structure of the complex either from x-ray crystallography (ligands 8, 9, and 20) or by simple direct modeling (ligands 3 and 5). The differences are within 1 kcal/mol for most ligands, which is roughly the order of magnitude of the statistical errors of calculations. The calculated binding free energies for a given ligand obtained from different starting structures, e.g., ligand-8 x-ray and MD (64), are very similar, though the errors appear to be smaller for crystal structures in general. The solvation free energy of the ligands offers one additional (simpler) quantity to directly assess the accuracy of the present computations by comparing with the previous results of V. S. Pande and co-workers (personal communication, 2005). As shown in Table 3, the solvation free energies calculated according to Eq. 12 are very consistent with those results, except for ligands 3 and 5. Overall, we conclude that the present strategy, based on FEP/MD simulations of a reduced GSBP atomic model sampled with conformational, translational, and orientational restraining potentials, is accurate and efficient.

Nonbond contribution

Table 1 shows the nonbond free energy components (dispersive, repulsive, and electrostatic free energy) for all ligands in the binding site and in the bulk solution. The nonbond free energy of the ligand in the binding site 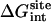is typically ∼20 kcal/mol more negative than that of the ligand in the bulk solution 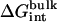. Generally, 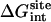and 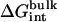increase with the size of the ligand (in the order 2, 3, 5, 6, 8, 9, 12, and 20). As expected for nonpolar ligands, there is only a minor contribution from the electrostatic free energy. The net contribution from the repulsive free energy appears to be generally small for most ligands. The reason for this may be that the binding pocket is at the surface of FKBP12 and that the bound ligand remains solvent-exposed. The trend was somewhat different for the binding of aromatic ligands to a mutant of T4 lysozyme engineered to have a buried nonpolar cavity. In that case, the calculated contribution from the repulsive interaction was more important (52). For the FK506-related ligands, the dispersive interactions make the dominant contribution to the binding free energy (∼20–30 kcal/mol).

The importance of dispersive interactions in driving the binding process can be understood from the relative density of the bulk relative to the protein. There is a larger number of atomic (nonhydrogen) van der Waals interaction centers per unit volume in the protein compared with liquid water. The transfer of a nonpolar ligand from the bulk to the binding site almost invariably yields a change of van der Waals dispersive interactions that favors association. Obviously, the favorable van der Waals interactions increase with the size of the ligand in general. These observations suggest that, to describe ligand binding with quantitative accuracy, one needs to account for the variations in the repulsive and attractive free energy contributions in the different environment of the bulk or the binding site. A similar observation has been made by Levy et al. (86).

Loss of conformational, translational, and orientational freedom

The net contribution from the translational free energy ΔΔG_t is ∼3 kcal/mol, though it goes up to 4.5 kcal/mol in the case of ligand 8 with a stronger restraint (Table 4). Since ΔΔG_t° ≈ −k_BT ln(ΔVC°), this would indicate that the center-of-mass of the bound ligand is fluctuating inside a microscopic volume ΔV on the order of ∼1 ų. For example, ΔΔG_t is estimated to be 4.6 kcal/mol using the fluctuations of the bound ligand in unbiased simulations in Eq. 10 in the case of ligand 8. Similarly, the loss of orientational freedom gives rise to a significantly unfavorable contribution. The net contribution from the rotational ΔΔG_r is ∼5 kcal/mol, which corresponds to a significant reduction of orientational freedom (accessible solid angle of rotation) ΔΩ from 8π². This was also previously noted by Swanson and McCammon (70). In the case of ligand 8 again, ΔΔG_r is estimated to be 5.0 kcal/mol using the fluctuations of the bound ligand in unbiased simulations in Eq. 11. Perhaps more surprising is the magnitude of the net contribution corresponding to the conformational restriction of the ligand upon binding, ΔΔG_c, which varies from 2 up to 6–7 kcal/mol depending on the ligand (Table 2). This is a very significant fraction of the standard binding free energy for those ligands.

The magnitude of the free energy contributions caused by the loss of conformational, translational, and orientational freedom has consequences for empirical implicit solvent scoring schemes attempting to estimate the ligand-protein binding free energy on the basis of fixed ligand-protein configurations. For example, MM/PBSA consists in averaging the results of PB calculations based on an ensemble of fixed snapshots generated by MD simulations with explicit solvent (66). What can be effectively generated by this procedure is an approximation to ΔΔG_int, the ligand-protein interaction free energy. This contribution most obviously favors binding. However, the remaining contributions, which are necessarily unfavorable to binding, must also be taken into account. To some extent, this may be achieved with the use of approximate expressions. For example, reliable estimates of the free energy contributions arising from the loss of translational and orientational degrees of freedom of the ligand may be obtained on the basis of fluctuation averages using Eqs. 10 and 11. Upon inspection, it seems likely that such approximation may be valid only for a fairly rigid ligand, or if a strong conformational restraining potential is applied to a flexible ligand. However, there is no straightforward estimator of ΔΔG_c. In the case of ligand 8, for example, the free energy required to conform the flexible ligand in the bulk to its bound state in FKBP12 (∼7 kcal/mol) is not correlated with the potential energy of the ligand molecule corresponding to the bound (83.27 kcal/mol) and free (84.73 kcal/mol) conformations (both relaxed with energy minimization). Designing an approximation to ΔΔG_c is very challenging because it is essentially dominated by a loss of conformational freedom of the ligand and not by a change of internal potential energy.

Accuracy and sensitivity to starting structure

Three sets of starting structures were used for the calculations. A first set of structures are x-ray crystallographic structures of FKBP12 with ligands 8, 9, and 20. A second set of structures are FKBP12 in complex with ligands 3 and 5, which were constructed from the crystal structure of ligand 9 (see Methods). A third set of structures are FKBP12 with all eight ligands provided by V. S. Pande and co-workers (personal communication, 2005); these docking models were equilibrated using MD for ∼200 ps with explicit solvent. For each ligand, the complete FEP/MD calculation was repeated at least three times (some up to five) starting from the beginning of the equilibration. The statistical precision of the calculated free energy is on the order of ∼1.0 kcal/mol, though the accuracy of the calculated value differs depending on the starting structure. The results summarized in Table 3 highlight the importance of the starting structure. For example, the results for ligand 8 are different if initiated from the crystallographic x-ray structure or from the MD equilibrated system of Pande, Shirts and co-workers (63,64). In contrast, ligand 5 appears to be particularly problematic. The ligand-protein complex was somewhat unstable during the equilibration, giving rise to more significant variations in the resulting binding free energy.

The present strategy based on biased sampling with restraining potentials does not require very long simulations as long as the starting structure is accurate and can remain stable in this neighborhood (within ∼1 Å). Bad or unstable initial structures start to drift during equilibration, which makes it difficult to design an optimal set of restraining potentials aimed at helping the sampling. In the familiar language of computational drug design, one might say that the present strategy is well suited to assign a value to a given ligand configuration (defined within ∼1 Å), i.e., for “scoring” a given ligand “pose”. The task of searching and finding the ligand pose, i.e., “docking”, is quite different and normally precedes scoring. Although docking by MD can be done, this is clearly not the most efficient approach to accomplish this task. Extensive FEP/MD calculations with very long trajectories amount essentially to accomplishing both the docking and the scoring tasks simultaneously. Ligand docking by extensive MD is certainly feasible, though accurate docking models may be generated at a lesser computational cost with heuristic methods. The concept of scoring a particular ligand pose from FEP/MD makes sense only if rapid interconversion to neighboring poses (assuming they exist) is prevented by energy barriers of several k_BT (i.e., they are essential different binding sites). If such condition is not met, then the true binding free energy must be obtained via a sampling over all the substate with proper weighting. While the present step-by-step formulation could be used advantageously with extensively long FEP/MD simulations, we believe that it is most useful when used in conjunction with accurate starting configurations, obtained either from x-ray crystallography or high-quality docking models.

CONCLUSION

The standard binding free energy of eight FK506-related ligands of FKBP12 was calculated using a FEP/MD simulation protocol incorporating the effect of full atomic flexibility and thermal fluctuations. The results are generally in good accord with experiments and the extensive calculations of Pande and co-workers (63) and Shirts (64). When the starting structure is taken from x-ray crystallography, the calculated binding free energy is usually in good agreement with the experimental results (within 2 kcal/mol) and the statistical error is small (∼1 kcal/mol). Given that the program and method used are significantly different from those used by Pande and co-workers (63), we consider the agreement satisfactory. On the other hand, if the initial complex structure is a modeled structure, the calculated binding free energy may be less precise. This highlights the importance of accurate docking to enable a successful rapid evaluation of the binding free energy with FEP/MD.

A number of features were implemented to enhance the accuracy of the results while reducing the overall computational cost of the calculations. First, the reversible work for the entire association/dissociation process was decomposed into eight sequential steps during which the ligand-surrounding interactions as well as various biasing potentials restraining the ligand are turned “on” and “off”. The usage of those biasing potentials decreases the size of the configurational space that needs to be explored, therefore reducing the sampling workload of the FEP/MD simulations. The advantage is noise reduction, which leads to a more rapid convergence of the computations. Second, a RMSD umbrella sampling PMF calculations was used to accurately sample the conformation of the ligand in the binding and in the bulk. Effectively, the RMSD restraining potential enables us to transform a flexible ligand into a relatively rigid molecule, which simplifies all the subsequent steps considerably. One may note that a similar RMSD potential could be easily extended to restrain a flexible protein receptor as well. Third, the convergence of the calculation of the nonbond interaction free energy contribution was improved by separating the LJ potential into a repulsive and dispersive free energy using WCA. This separation also allows a clear identification of the molecular components contributing favorably to the binding. Fourth, only a small number of atoms in the vicinity of the binding site were explicitly simulated with GSBP while the influence of the remaining atoms was incorporated implicitly. This allowed a significant reduction in the size of the simulated systems, from ∼25,000 to 2500 atoms.

Throughout the discussion, a number of observations were made concerning the physical meaning of various free energy contributions upon ligand binding, such as the loss of translational, orientational, and conformational freedom, as well as the changes in repulsive, dispersive, and electrostatic nonbonded interactions. Although the mathematical definition of all these contributions is unambiguous, it is important to recall that their precise numerical values depend on the choices of applied restraint potentials. Similarly, the free energy components arising from the separation of the nonbonded interactions (WCA-LJ and partial charge electrostatics) are well-defined, but nonetheless reflect a series of choices about hypothetical intermediate states. Ultimately, only the total absolute free energy is invariant and independent of all those choices. In trying to attribute a physical meaning to the various contributions, it is therefore important to keep these limitations in mind. Only a careful and judicious analysis of the various components can yield physically meaningful insight. The best is to utilize the free energy decomposition to highlight qualitative concepts, such as, for example, the general importance of the loss of translational and orientation freedom on the total binding free energy, the magnitude of the free energy cost to restrict the ligand into its bound conformation, and the relative change in the nonbonded interactions upon binding. For example, an important qualitative observation from the series of computations is that the dispersive interaction is an important driving force for complexation. In other words, isosteric nonpolar analogs of these ligands (without any partial charges) would still bind (assuming that their internal conformation would be unchanged). This observation arises naturally from the free energy decomposition used here to separate the various contributions to the nonbonded interactions (repulsion, dispersion, and electrostatics).

The step-by-step computational FEP/MD simulation protocol with restraining potential breaks down the complete calculation into many short MD simulations that are easy to distribute over independent compute nodes. This makes it possible to use trivially distributed computing resources for direct calculations of standard binding free energy. For each ligand system, ∼250 MD trajectories systems were generated, each taking ∼2–4 h using a single 1-GHz Pentium CPU. Thus, the total computational time to obtain the standard binding free energy of one ligand can be as little as 2–4 h, if 250 CPUs are available simultaneously. The various biasing restraints help reduce the noise and improve the convergence of the final results. At this point, it seems clear the ultimate limitations of calculated standard binding free energies is not the statistical precision that can be achieved. Whenever necessary, a higher precision could be obtained at reasonable computational cost simply by increasing the length and the number of simulations. Furthermore, it should be noted that while simulating a reduced GSBP atomic model may often be advantageous, such solvent boundary potentials remain approximate. If a better representation of the entire molecular system is warranted, the same step-by-step binding free energy formulation with restraint potentials could be used in extensive all-atom FEP/MD simulations with periodic boundary conditions. One area where there remains ample room for improvement concerns the atomic force fields. Without being overly pessimistic, it seems likely that no miraculous accuracy should be expected from simple nonpolarizable fixed-charges potential function (52). Quantitative accuracy (i.e., >0.5 kcal/mol) might only be possible by including the influence of induced polarization explicitly. With these advances in FEP/MD methodologies, it is clear that improved force fields could enable rapid predictive binding estimates of quantitative accuracy at a very reasonable computational cost for rational drug design.

APPENDIX A

In the expressions in Table A1, U₁ is the total potential energy of the system, and U₀ is the total potential energy of an intermediate state in which the ligand does not interact with its surrounding (protein and/or solvent). The conformational, translational, and orientational biasing potentials are u_c, u_t, and u_r respectively. Because the ligand molecule does not interact with its surrounding with potential U₀, the orientational factor F_r in Step 5 is given by

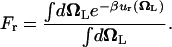(16)

where Ω_L are the three angles defining rigid body rotation of the ligand molecule (relative to the receptor); the volume element implicitly includes a Jacobian for the rotation angles. Similarly, the translational factor F_t in Step 6 is given by

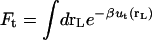(17)

(all other terms cancel out). The translational factor F_t, hence the binding constant K_b, has the dimension of volume (with a natural unit of ų in atomistic simulations). The standard equilibrium binding constant is K_b° and the standard binding free energy is ΔG°_bind. C° is the standard state concentration (equal to 1 M or 1/1661 Å⁻³).

TABLE A1.

Decomposition of the binding process in eight steps

Step	Process	Configurational integral	Contribution
1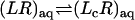
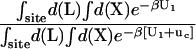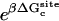2
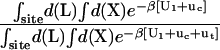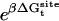3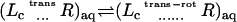
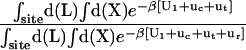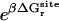4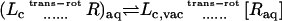
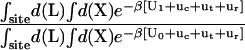5		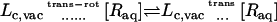	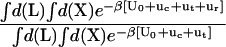Fr
6		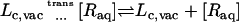	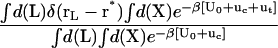Ft
7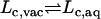
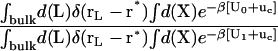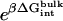8
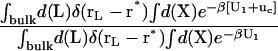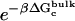Total

APPENDIX B

As used in Table B1, the units of energy and distance used in GROMACS are kJ/mol and nm, while they are kcal/mol and Å in CHARMM. The subscripts c and g (e.g., as in k_c and k_g) mean CHARMM and GROMACS, respectively. F(= 1/4.184kcal/kJ) is a conversion factor. In GROMACS format, Ryckaert-Bellemans (RB) dihedral energy can be expressed using the parameters k_n and φ_n (n = 0–5), which are converted from the parameters C_n as

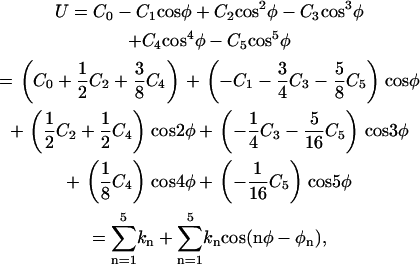(18)

where φ_n = 0 or 180°.

TABLE B1.

Conversion of AMBER force field from GROMACS to CHARMM format

		Conversion
GROMACS Energy	CHARMM Energy	para1	para2
Bond:	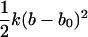k(b − b0)2	kc = (0.5/100)Fkg	bc = 10 bg
Angle:	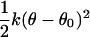k(θ − θ0)2	kc = 0.5 Fkg	θc = θg
NB:	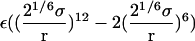	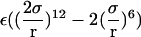εc = Fεg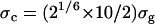
Dihe: k + kcos(nφ − φ0)	k + kcos(nφ − φ0)	kc = Fkg	φc = φg
RB Dihe:	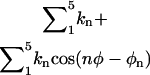	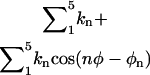kn, c = Fkn, g	φn, c = φn, g