DNA Hairpins: Fuel for Autonomous DNA Devices

Abstract

We present a study of the hybridization of complementary DNA hairpin loops, with particular reference to their use as fuel for autonomous DNA devices. The rate of spontaneous hybridization between complementary hairpins can be reduced by increasing the neck length or decreasing the loop length. Hairpins with larger loops rapidly form long-lived kissed complexes. Hairpin loops may be opened by strand displacement using an opening strand that contains the same sequence as half of the neck and a “toehold” complementary to a single-stranded domain adjacent to the neck. We find loop opening via an external toehold to be 10–100 times faster than via an internal toehold. We measure rates of loop opening by opening strands that are at least 1000 times faster than the spontaneous interaction between hairpins. We discuss suitable choices for loop, neck, and toehold length for hairpin loops to be used as fuel for autonomous DNA devices.

INTRODUCTION

Active devices constructed from DNA can use DNA hybridization as an energy source to drive changes in configuration, including stepwise movement down a track (1–5). These devices are not autonomous; they are driven around their operating cycle by sequential addition of “set” and “unset” strands. A chemically fueled device that operates autonomously must catalyze the reaction of its fuel: recent experiments that show autonomous operation of DNA devices have obtained energy by catalyzing the hydrolysis of ATP (6) or of the DNA backbone (7–9). Designs based on DNA or ATP hydrolysis require auxiliary enzymes (6,8) or incorporate one of a very limited class of catalytic deoxyribozymes (requiring a chimeric fuel containing at least one ribonucleotide) (7,9). In contrast, the use of DNA hybridization as an energy source is attractive because it is extremely flexible: many similar devices can be designed to operate independently using fuels with different base sequences. A long-lived fuel can be created by using secondary loop structure to hinder the hybridization of complementary DNA complexes. Hybridization of such a fuel can be catalyzed by using an invading oligonucleotide to open a loop (10). The design of an autonomous molecular motor made from DNA that is capable of extracting energy from a metastable DNA fuel is a current challenge in DNA nanotechnology.

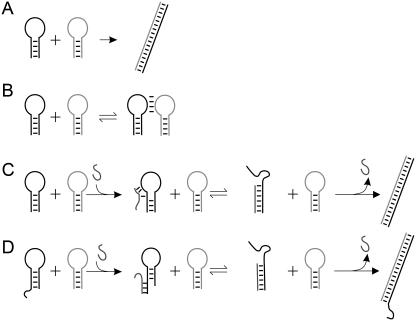
A system of two complementary DNA hairpin loops is a candidate fuel for an autonomous DNA motor. A hairpin loop forms from a single strand of DNA that contains two complementary neck domains separated by a loop domain. The reaction between two completely complementary hairpins (which have identical necks and complementary loop domains) to create a fully base-paired duplex is shown in Fig. 1 A. This reaction releases the energy stored in the unhybridized bases of the loop domains, which is of the order of 1.4 kcal mol⁻¹ per basepair at 20°C (11). Interaction between unpaired bases in the loop can also lead to the formation of a less stable “kissed” complex between unopened loops (12) (Fig. 1 B).

FIGURE 1.

Reactions of hairpin loops. (A) Hybridization of complementary hairpins. (B) Formation of a kissed complex by interaction of complementary loop domains. (C and D) Catalysis of hybridization by an opening strand capable of opening a hairpin by strand invasion initiated at an internal toehold (C) or an external toehold (D).

The topological constraint imposed by the closure of the loops can inhibit the hybridization reaction between complementary hairpins (10,12). At temperatures well below the melting temperature of the hairpins' necks the two-loop system can act as a long-lived fuel whose energy, stored in the unpaired bases of the complementary loops, can be released by catalyzing hybridization. One way to catalyze this interaction is to use an auxiliary “opening” strand (10) to force open the neck of a loop by strand invasion. This reaction is assisted thermodynamically and kinetically if the opening strand is given an additional “toehold” (1,13), consisting of a few (usually 3–10) bases complementary to unhybridized bases adjacent to the neck. The toehold can be located either inside the loop (“internal toehold,” Fig. 1 C) or at an overhang at the outer end of the neck (“external toehold,” Fig. 1 D). The catalytic cycle is completed when the opened loop hybridizes with its complement, displacing the catalyst. A similar system has been used to demonstrate a triggered amplification reaction (14) in which a loop-opening initiator triggers a cascade of hairpin-hairpin reactions.

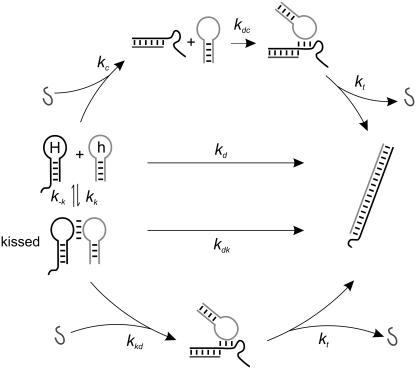
Reactions of a system of complementary hairpins and an opening strand are summarized in Fig. 2, which defines rate constants associated with the competing reaction pathways. Uncatalyzed reactions are shown in the center of the figure. An opening strand can catalyze the reaction between DNA hairpins by two pathways: opening a monomeric hairpin that, when opened, interacts more rapidly with its complement (upper); or interacting directly with a kissed complex (lower).

FIGURE 2.

Interactions between complementary hairpins, including catalysis of hybridization by an opening strand. (Middle) Spontaneous interactions between complementary hairpins: kissing, and complete hybridization to produce a fully basepaired duplex. (Upper) Hybridization between monomeric hairpins catalyzed by an opening strand. (Lower) Hybridization between kissed hairpins catalyzed by an opening strand. The catalyst shown initiates strand displacement by binding at an external toehold.

Most previous studies of DNA hairpins have used loop domains with repetitive base sequences. Poly-dA and poly-dT loops of up to 30 bases have been used to study the thermodynamics of hairpin loops (15,16), including stacking interactions between bases in the single-stranded loop domains (17–19), and hairpin closing rates. A hairpin with a repeated three-base motif forming the loop domain has been used to investigate the reaction of complementary hairpins to form an extended duplex via an intermediate kissing state (20). Interactions between RNA hairpins have been more extensively studied: kissing interactions between short complementary RNA loops are important in the stabilization of tertiary structure (21), in control of plasmid replication (22,23), and in dimerization of retroviral genomic RNAs (24,25).

Here we present a study of the interactions between DNA hairpins and opening strands that are depicted in Fig. 2. We study loop lengths of up to 40 bases: the longer the loop the more energy is released on hybridization with its complement and the greater the number of interactions with other components that can be encoded in the loop sequence. Nonrepetitive base sequences were used for loop, neck, and toehold domains. Use of nonrepetitive sequences is essential if systems incorporating more than one specific fuel-device interaction are to be constructed.

MATERIALS AND METHODS

Hairpin loops

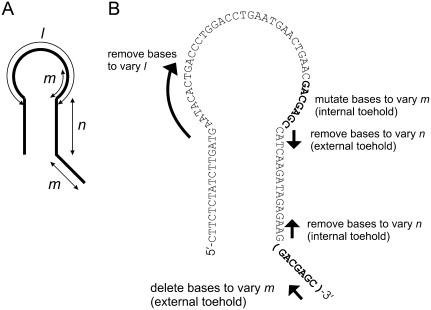
A basic hairpin, H, with a 40-base loop and a 16-basepair neck was designed by a process of random and by-hand mutation of a randomly generated starting sequence to minimize secondary structure predicted by MFOLD (26). Secondary structure was minimized both in the loop domain of the closed hairpin and in the open complex formed by hybridization of an opening strand to one of the neck domains. All other hairpins used were derived from H and its complement 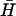by deletion or mutation of loop, neck, or toehold bases. Fig. 3 gives the sequence of hairpin H with a seven-base external toehold, and shows how it was adapted to create hairpins with shorter loop domains, necks, and toeholds.

FIGURE 3.

Hairpin description and design. (A) Definition of hairpin dimensions: loop domain length, l; neck length n; and toehold length, m (the toehold may be internal or external; see Fig. 1, C and D). (B) The sequence of hairpin H. The ways in which this sequence was adapted to generate hairpins with different values of l, m, and n are indicated.

To investigate the effect of neck and loop lengths on spontaneous hybridization rates (Fig. 4 A), 12- and 21-base loops were obtained by removing 28 and 19 bases, respectively, from the 5′ side of the loop domain of H and the complementary bases from the 3′ side of the loop domain of 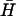. Seven-base necks were obtained by removing nine basepairs from the free ends of the necks of H and .

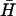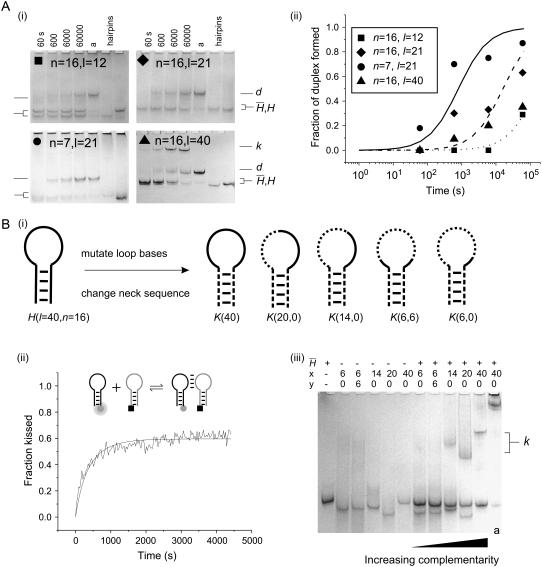
FIGURE 4.

Spontaneous interactions of complementary hairpins. (A i) Time-course PAGE analysis of the interactions between complementary pairs of hairpins with l-base loop domains and n-basepair necks. Controls: individual hairpins; a complementary hairpins annealed. Bands indicated are individual hairpins (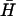, H), duplex (d), and kissed complex (k). (ii) Duplex formation as a function of time deduced from gel band intensities. The solid lines are calculated according to second-order reaction kinetics with rate constants 50 M⁻¹ s⁻¹ (dotted line), 500 M⁻¹ s⁻¹ (dashed line), and 10,000 M⁻¹ s⁻¹ (solid line). (B) The kissing interaction. (i) Designs of hairpins K used to investigate the kissing interaction. Regions complementary to hairpin 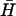are indicated by a solid black line, noncomplementary regions by a dashed line. (ii) Time dependence of the formation of a kissed complex, by hairpins with complementary 40-base loops and nonhomologous necks, derived from FRET data. The fitted line assumes reversible second-order reaction kinetics. The inset shows the positions of the dye labels. (iii) PAGE analysis of the strength of kissing interactions between hairpins with nonhomologous necks as a function of the degree of complementarity between their 40-base loops. Slower bands labeled k correspond to kissed complexes. The contents of lanes (hairpins K(x,y) and 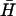) are indicated above. x and y are the dimensions of loop subdomains of K(x,y) that are complementary to 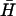. See text for descriptions of experiments, and Materials and Methods for experimental details.

For hairpin-opening experiments (Fig. 5), loop length, neck length, and toehold length were varied. Both internal and external toeholds were studied. One opening strand sequence was used for all experiments with an internal toehold and one for all experiments with an external toehold. External toeholds of different lengths were created by extending the 3′ end of H by up to seven bases. Hairpins with internal toeholds shorter than the maximum of seven bases allowed by the design of the opening strand were created by mutating the loop domain at the end of the toehold region further from the neck. m-base internal and external toeholds were designed to have similar binding strengths; for some toehold lengths they were identical. Some hairpins with an external toehold therefore had two sites at which the opening strand could bind, although only one of these could readily lead to strand displacement along the neck. A control measurement (see Supplementary Material) showed that hybridization between a hairpin and an opening strand initiated by means of a seven-base external toehold was unaffected by the presence of an identical internal toehold. Neck lengths for hairpins with external and internal toeholds were changed by deleting basepairs from the loop and free ends of the neck, respectively.

FIGURE 5.

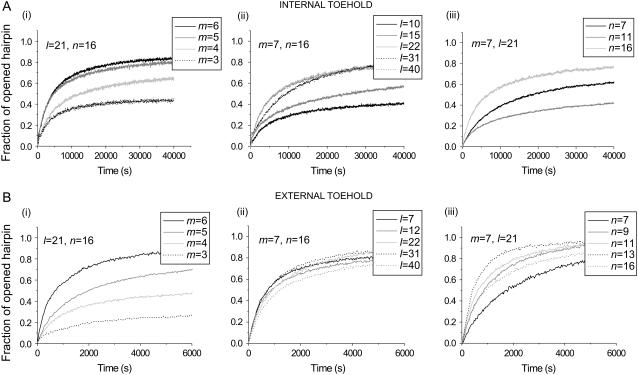
Opening of hairpin loops by opening strands with (A) internal and (B) external toeholds. (i) Toehold length m varied; loop length, l = 21 and neck length, n = 16, were fixed. (ii) Loop length l varied; m = 7 and n = 16 were fixed. (iii) Neck length n varied; m = 7 and l = 21 were fixed. Note the different scales on the time axes for A and B. See text for descriptions of experiments and Materials and Methods for experimental details.

Sequences of all oligonucleotides are given in Supplementary Material. Oligonucleotides were synthesized by Sigma-Genosys (Cambridge, UK) (fluorescently labeled hairpins and unlabeled hairpins, H and 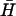, with 40-base loops); Eurogentec (Southampton, UK) (dual-labeled opening strands); and MWG (Ebersberg, Germany) (all other oligonucleotides).

Hybridization

The hybridization buffer used for all experiments was 0.1 M NaCl, 10 mM Tris·HCl/1mM EDTA, pH 8.0. Before use, hairpins were quenched by heating to 95°C at 1 μM concentration in this buffer, then cooling to 4°C over ∼60 s. Quenching avoids the formation of homodimers and larger complexes by hybridization of neck domains from different oligonucleotides.

Electrophoresis

Nondenaturing polyacrylamide gel electrophoresis (PAGE) was used. Gels containing 1× TAE (40 mM Tris, 19 mM acetic acid, and 1 mM EDTA, pH 8.0) and 15% 29:1 acrylamide:bis-acrylamide were run in 1× TAE buffer at 4°C. All reaction mixtures for gel experiments were prepared at room temperature with individual oligonucleotide concentrations of 0.1 μM unless otherwise stated. Timings shown for the time course experiment (Fig. 4 A) correspond to the approximate interval between mixing reactants and initiating electrophoresis. Gels were silver-stained and quantified as described in Supplementary Material.

Fluorescence

Fluorescence measurements were performed in 1.5 ml (Hellma, Southend on Sea, UK) cuvettes in a JY-Horiba (Tokyo, Japan) Fluoromax 3 fluorimeter. The cuvette temperature was maintained at 25°C by means of an external waterbath. As a consequence of the differing rates and extents of the reactions considered, different concentrations of reactants were used for different measurements. Small (of order 10 μl) volumes of reactants were added sequentially from stock solutions at high concentration and mixed by vigorous pipetting to achieve final concentrations for each oligonucleotide of 50 nM (Fig. 4 B ii), 7 nM (Fig. 5), and 100 nM (Fig. 6 A).

FIGURE 6.

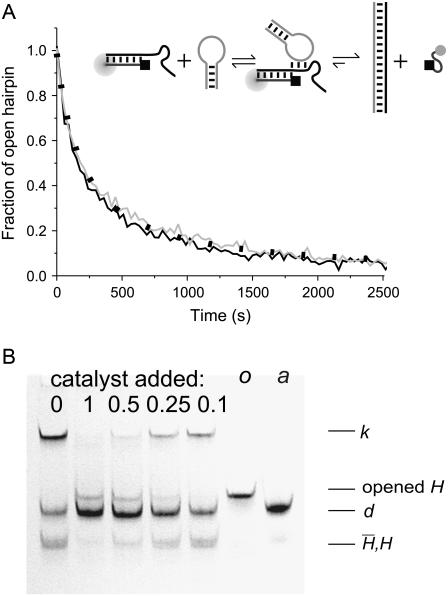
Catalysis of hairpin hybridization by an opening strand. (A) Displacement of an opening strand bound to hairpin H (l = 40, n = 16) by the complementary hairpin 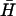. The schematic diagram shows the FRET labels on the opening strand used to observe the progress of the reaction. Black and gray lines show the time dependence of the reaction for opening strands with seven-base internal and external toeholds, respectively. The dots show a fit to the data assuming second-order kinetics with a rate constant of 5.1 × 10⁴ M⁻¹ s⁻¹. (B) Catalysis of the reaction between complementary hairpins H and 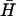(l = 40, n = 16) by an opening strand with a seven-base external toehold. Bands in the native polyacrylamide gel correspond to the reactants (individual hairpins 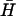, H and kissed complex k), the duplex product d, and the intermediate formed by the opening strand bound to H. Controls: o, annealed H and opening strand; a, annealed H and 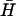. See text for descriptions of experiments and Materials and Methods for experimental details.

For Förster resonant energy transfer (FRET) (27), analysis of kissing kinetics (Fig. 4 B ii) hairpin K(40) was synthesized with a 5′ TET (tetrachlorofluorescein) fluorescent modification and hairpin 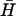with a 3′ BHQ1 dark quencher modification. TET (donor) fluorescence was excited at 520 nm and recorded at 539 nm (excitation and emission bandwidths 2 nm). Energy transfer from the directly excited donor to the acceptor (quencher) is enhanced when they are held within a few nanometers of each other in a kissed complex, resulting in a decrease in donor fluorescence. The TET fluorescence signal was assumed to depend linearly on the fraction of hairpins in kissed complexes: the initial fluorescence intensity from K(40) before addition of 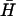, and the steady fluorescence intensity obtained on addition of a 40-fold excess of 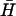, were taken to correspond to 0% and 100% kissing, respectively.

For FRET analysis of hairpin opening (Fig. 5), two opening strands with dual fluorescent labels 5′-FAM (6-carboxyfluorescein) and 3′-TAMRA (carboxytetramethylrhodamine) were used, one with a seven-base internal toehold and one with a seven-base external toehold. FAM (donor) fluorescence was excited at 495 nm and recorded at 519 nm (excitation and emission bandwidths 2 nm). The FAM fluorescence signal was assumed to depend linearly on the fraction of opening strands straightened by hybridization to the complementary section of H. The initial intensity from the opening strand, before addition of H, was measured. Reactions were allowed to run for >6000 s and >40,000 s for opening strands designed to bind to external and internal toeholds, respectively. The temperature of the water bath was then increased to 85°C, then cooled to 25°C over 1 h; then a control strand, identical to the portion of the hairpin to which the opening strand bound in the reaction, was added in 10-fold excess. The final fluorescence level reached after this addition was taken to correspond to complete hybridization of the opening strands.

For the measurement of the displacement of opening strand (Fig. 6 A), 0.5 μM dual-labeled opening strand with a seven-base external toehold was annealed with a stoichiometric amount of H. 30 μl of this annealed sample was added to the cuvette, giving a final concentration of each oligonucleotide of 100 nM. A stoichiometric amount of 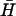was added to initiate the reaction. FAM fluorescence was monitored as described above. The initial fluorescence level was taken to correspond to 100% opening of hairpin H. The reaction was allowed to proceed for 3600 s and then annealed in situ as described above. The final fluorescence was taken to correspond to 0% opening of H.

RESULTS

Spontaneous duplex formation

The aim of this research program is to use the energy stored in the single-stranded loop domains of two complementary hairpins to drive a molecular motor, which will obtain energy by catalyzing hybridization (10). For this purpose it is important to design hairpins to minimize decay of the hairpin fuel by spontaneous duplex formation. Spontaneous interactions between complementary hairpins with different loop domains (l = 12, 21, and 40) and neck lengths (n = 7 and 16) are investigated in Fig. 4 A (see Materials and Methods for experimental details.)

Kinetics of duplex formation

Fig. 4 A i shows PAGE analysis of the time course of spontaneous hybridization of complementary hairpin pairs. Fig. 4 A ii shows the results of quantification of the intensities of hairpin and duplex bands in Fig. 4 A i. For hairpins with 12-base loops and a 16-basepair neck, duplex formation is only ∼20% complete after 60,000 s. We estimate that for this reaction the rate constant for spontaneous duplex formation is ∼50 M⁻¹ s⁻¹, ∼10⁵ times lower than for complementary oligonucleotides with no designed secondary structure (28). For hairpins with the same 16-basepair neck but longer 21-base loops, the reaction proceeds more quickly, but the half-time of the reaction is still ∼20,000 s. Shortening the neck causes a rapid increase in reaction rate: for a 21-base loop and seven-basepair neck the reaction half-time is reduced to ∼200 s.

Thermodynamics of duplex formation

The equilibrium state of stoichiometric mixtures (0.1 μM) of all complementary hairpin pairs tested was investigated by annealing the reactants (Fig. 4 A i, lane a). In all cases, annealing caused essentially complete conversion to the duplex, consistent with the large change in free energy associated with hybridization of the unpaired bases in the loops.

The kissing interaction

The most dramatic effect of increasing loop length is the formation of kissed complexes (12,29) held together by interactions between the loop domains of unopened hairpins (Fig. 1 B). Metastable kissed complexes, which migrate as a distinct band in a polyacrylamide gel, are observed for 40-base, but not 21- or 12-base, loops (Fig. 4 A i). The population of the kissed complex is not seen to diminish on the timescale of our experiment (60,000 s), suggesting that it cannot readily decay into the stable duplex. To study kissing without the complication of duplex formation, a series of hairpins, K, was designed with a new 16-basepair neck sequence that was designed to have little sequence homology with the neck of H (and 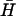). K(40) has a 40-base loop domain identical to that of H (i.e., completely complementary to that of 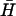). Hairpins K(x,y) have 40-base loop domains with reduced complementarity to 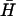(see Fig. 4 B i): the loop is identical to that of H for x,y bases at the 5′ and 3′ ends, respectively; the remaining (40-x-y) bases in the middle of the loop were designed to interact only weakly with 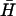. We have used FRET to measure the kinetics of kissing, and PAGE to measure the stability of the kissed state for pairs of hairpins with different degrees of complementarity.

Kissing kinetics

Fig. 4 B ii shows the kinetics of kissing between hairpins K(40) and 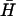, deduced from measurements of FRET between fluorophores conjugated to the ends of the necks. Kissing holds the dye labels within a few nanometers of each other, resulting in a change in the intensity of donor fluorescence (see Materials and Methods). K(40) and 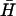have complementary 40-base loop domains that are the same as those of the fully complementary hairpin pair H, 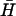: their kissing interaction is expected to be very similar to that between H and 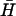, whose long-lived kissed complex was identified by PAGE (Fig. 4 A i). By fitting the time-dependent kissing curve shown in Fig. 4 B ii, we deduce a second-order rate constant for kissing between K(40) and 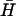of 3.2 (±0.4) × 10⁴ M⁻¹ s⁻¹ and a first-order dissociation constant for the kissed complex of 4.0 (±0.4) × 10⁻⁴ s⁻¹.

Kissing thermodynamics

Fig. 4 B iii shows interactions between hairpins with 40-base loop domains with varying degrees of complementarity and nonhomologous 16-basepair necks. Hairpins 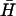and K(x,y) were mixed and incubated for 10 min at room temperature before loading onto the gel. Fig. 4 B iii demonstrates that kissing between hairpins with 40-base loops persists when the size of the complementary regions of the loop domains is reduced to 14 bases, but is not observed for pairs with only one or two six-base complementary regions positioned adjacent to the necks.

When hairpins K(40) and 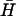are annealed (Fig. 4 B iii, lane a) multiple bands are observed. A pair of these loops can reduce its free energy by hybridization of the complementary 40-base loop domains, even at the cost of opening the neck domains and leaving them unhybridized. The free energy of this system can be reduced still further by hybridization of the neck domains from different pairs to form multimers. None of the other pairs of hairpins with less complementary loop domains form such heterodimeric complexes under the same reaction conditions (data not shown).

Opening hairpins

To make use of the energy released by hybridization of complementary hairpins to drive a free-running molecular machine, it is necessary for the machine to catalyze this reaction (10). In this section, we study the effects of loop length, neck length, and toehold length on the first step in the catalytic pathways shown in Fig. 2, the opening of the first hairpin by the catalytic opening strand.

Kinetics of opening

The kinetics and equilibria of opening reactions were investigated by measuring FRET between fluorophores conjugated to either end of the opening strand (see Supplementary Material): donor fluorescence increases when the opening strand is straightened by hybridization to the complementary domain of hairpin H. Fig. 5 shows the kinetics of hybridization between stoichiometric mixtures of an opening strand and its target hairpin. Fig. 5, A and B, shows results for opening strands with internal and external toeholds, respectively. Parameters that are varied are (i) toehold length, m; (ii) loop length, l; and (iii) neck length, n.

The most striking result is that, for all pairs of otherwise comparable reactions, opening rates are between one and two orders of magnitude faster with an external toehold (Fig. 5 B) than with an internal toehold (Fig. 5 A; note the different time scales in A and B). For a fixed seven-base external toehold and 16-basepair neck (Fig. 5 B ii), the opening rate (measured as either the initial reaction rate or the inverse reaction half-time) was approximately independent of loop length in the range l = 7–40. For the same toehold positioned internally, the opening rate was ∼10× slower for larger loops l = 21–40 and decreased sharply as the length of the loop was shortened from 21 to 15 and 10 bases. For a 10-base loop domain, the opening rate is two orders of magnitude slower with an internal toehold than with an external toehold.

Reaction rates do not change monotonically with neck length (Fig. 5, A iii and B iii). The variation in rate for both internal and external toeholds for neck lengths in the range 7–16 is small compared to the difference in rate between internal and external toeholds.

Thermodynamics of opened hairpins

The equilibrium constant of the hairpin/opening strand system was determined by comparing the steady-state donor fluorescence signal from the dual-labeled opening strand with the signal measured when all opening strands were hybridized (see Materials and Methods). The length of the toehold was varied from six to three bases. As expected, the equilibrium constant for hybridization of an opening strand to its target hairpin depends on the length of the toehold region (which is unhybridized in the initial state), but equilibrium constants for internal and external toeholds of the same length are approximately equal. Under the reaction conditions of Fig. 5, the reaction goes to near-completion for a six-base toehold, but only to 40% completion for a three-base toehold (see Table 1). The free energy of the reaction between opening strand and hairpin is the sum of the free energy of hybridization of the additional basepairs formed in the toehold region, 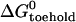and the free energy change associated with removing the constraint that the ends of the loop domain are held together, 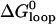. We can use the nearest-neighbor model (11) to estimate 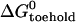. From the known reactant concentrations and measured equilibrium constant we can then deduce the loop free energy (which depends on the length of the loop (15,31,32)). Corresponding estimates of the loop free energy at 25°C for the 21-base loop with a 16-basepair neck, obtained by consideration of the equilibria of reactions with a range of opening strands, are shown in Table 1.

TABLE 1.

Free energy changes for hybridization between a hairpin (l = 21, n = 16) and opening strands with different toeholds

Toehold length, position	Fraction hybridized*	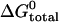(kcal mol−1)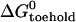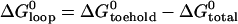†	(kcal mol−1)‡	(kcal mol−1)
5, e	0.88	−13.9	−8.2	5.7
4, e	0.67	−12.4	−6.8	5.6
3, e	0.38	−11.3	−4.6	6.7
5, i	0.86	−13.5	−8.9	4.6
4, i	0.73	−12.7	−6.7	6.0
3, i	0.47	−11.7	−5.3	6.4

^*The fraction hybridized is deduced from steady-state donor fluorescence from a dual-labeled opening strand.

^†Corresponds to the measured equilibrium constant.

^‡Calculated using nearest-neighbor model (11).

The average of our estimates of ΔG_loop is 5.8 ± 0.7 kcal mol⁻¹, in good agreement with that calculated in Kuznetsov et al. (15). This is of similar magnitude to the free energy related to hybridization of a three- or four-base toehold. It is a significant factor to consider when designing a DNA device powered by hairpins.

Displacement of opening strand by complementary hairpin

The final step in the catalysis of hairpin hybridization shown in Fig. 2 is the reaction of the opened hairpin with its complement, displacing the catalytic opening strand. FRET was used to monitor this reaction for complementary hairpins H, 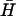, with l = 40, n = 16, and a dual-labeled opening strand with a seven-base external toehold (Fig. 6 A). As the reaction proceeds, the opening strand is displaced from H: the conjugated fluorophores are, on average, closer in the random coil configuration of the displaced strand, leading to a decrease in donor fluorescence. Hairpin 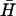was added to a preannealed mixture of H and the catalyst. The time dependence of the reaction can be fitted by assuming second-order reaction kinetics with a rate constant of 6.2 (±0.4) × 10⁴ M⁻¹ s⁻¹ for the internal opening strand, and 5.1 (±0.4) × 10⁴ M⁻¹ s⁻¹ for the external opening strand. These rate constants are close to those measured for hairpin opening using an opening strand with an internal toehold (Fig. 5 A).

Catalysis

Fig. 6 B shows the catalytic effect of adding different amounts of the same opening strand (seven-base external toehold) to the reaction between 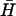and H. All three oligonucleotides were mixed in hybridization buffer at room temperature and were left for 60 min before PAGE analysis. The presence of the opening strand causes a significant increase in the concentration of the H 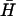duplex product and a corresponding reduction in the concentrations of the reactants, both monomeric hairpins and kissed complex. The catalyst achieves almost complete conversion of the hairpins to duplex when present at a half-stoichiometric concentration, and has a clear effect on the reaction at 10% stoichiometry, demonstrating catalytic turnover. A band corresponding to a low concentration of the intermediate complex consisting of the catalyst bound to an opened hairpin is seen for higher catalyst concentrations.

DISCUSSION

Spontaneous hybridization of complementary hairpins

Our measurements show that an increase in neck length is associated with a strong decrease in spontaneous reaction rate (Fig. 4 A). This is as expected: it is the closure of the loop by hybridization of the neck domains that provides the topological hindrance to hybridization between complementary loops. Hairpins with a sufficiently long neck form duplex only slowly, and could be used to provide energy over a period of many hours. Hybridization of unpaired bases contributes approximately 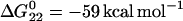and −20 kcal mol⁻¹, respectively, to the overall free-energy change for complete hybridization of the complementary pairs of hairpins with 40-base and 12-base loop domains (11). It is this free energy that is available to drive a molecular device capable of catalyzing the hybridization reaction.

Kissing

The formation of a kissed complex (Fig. 4 A i, and B) has previously been noted. Seelig et al. (29) observed the existence of a long-lived kissed complex formed by two-strand DNA loops with complementary 40-base loop domains. Bois et al. (12) also observed kissing between complementary DNA hairpins with 20-base loop domains and 10-basepair necks. We find that the rate constant for kissing (k_k = 3 × 10⁴ M⁻¹ s⁻¹) is an order of magnitude lower than that for hybridization of complementary 10-base oligonucleotides with no strong secondary structure (28). It is similar to that measured for kissing of six-base RNA loops (23). This rate constant is consistent with the rapid formation of kissed complexes between H and 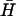seen in Fig. 4 A i. Using the measured rate constant for the kissing interaction, an approximate value for the rate constant for direct hybridization between H and 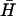of k_d = 3 × 10³ M⁻¹ s⁻¹ may be inferred from the time-dependent concentrations of hairpins, kissed complex, and duplex deduced from Fig. 4 A i. This is an order of magnitude lower than the rate constant for kissing: kissing can be the fastest spontaneous interaction between hairpins.

The ratio between the fitted rate constants for kissing and dissociation of K(40) and 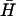, Fig. 4 B ii, corresponds to a free energy change 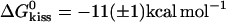, which is approximately equal to the free energy of hybridization for a 10-basepair duplex (11). This provides a rough estimate of the number of bases that interact in the kissed complex. The measurements of Weixlbaumer et al. (30) suggest that this may be an overestimate: they found that the free energy change on kissing of RNA hairpins with nine-base loop domains is 4 kcal mol⁻¹ more negative than the calculated free energy for hybridization of nine-base oligonucleotides with the same sequences as the loops.

Loop opening by a catalytic opening strand

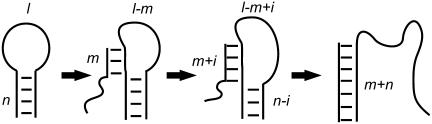
We attribute the large differences between the rates of opening reactions initiated at internal and external toeholds (Fig. 5) to the difference between the intermediate states in the branch migration process by which the catalyst opens the neck of the hairpin. For hybridization initiated at an external toehold the configuration of the bases displaced by the opening strand is relatively unconstrained: the displaced portion of the neck is free at one end and anchored only at the branch point. When hybridization is initiated at an internal toehold, however, the displaced bases join the loop domain (see Fig. 7): after migration of the branch point through i basepairs of the neck, the loop has length l − m + i bases with its ends held m + i basepairs from each other. The decrease in entropy of the loop region associated with this conformation can be estimated using the semiflexible polymer model (31,32): for hairpins with n = 16 and m = 7, the free-energy penalty as branch migration approaches completion is calculated to be ∼1.4 kcal mol⁻¹ for a 40-base loop and ∼3.5 kcal mol⁻¹ for a 15-base loop. This is an additional activation energy for loop opening by means of an internal toehold: the corresponding Arrhenius factors are 0.1 and 0.003, respectively, of the right order of magnitude to explain the observed reduction in opening rates associated with use of an internal toehold.

FIGURE 7.

Reaction of a catalytic opening strand with an internal toehold of length m with a hairpin of loop length l and neck length n.

Reaction time courses deduced from FRET data (Fig. 5 B) for external opening reactions with toehold length m ≥ 6 are fitted well by assuming second-order kinetics (see Supplementary Material), consistent with the interpretation that the rate-limiting step is the initial association of the catalyst and the hairpin, and that the random walk of the branch point between the neck of the hairpin and the catalyst, leading to neck opening, is relatively rapid. The rate constants for these reactions are in the range 10⁴–10⁵ M⁻¹ s⁻¹. Reaction time courses deduced from FRET data for external opening reactions with m ≤ 5, and for all internal opening reactions, do not fit well to second-order kinetics. This may be at least partly caused by the presence of a significant population of intermediate states (states in which the opening strand and hairpin have interacted but the hairpin is not fully opened). Donor fluorescence from such states is expected to be intermediate between fluorescence from fully bound and unbound opening strands, with the consequence that our assumption that the donor fluorescence intensity depends linearly on the fraction of open hairpins breaks down.

Modeling reaction kinetics

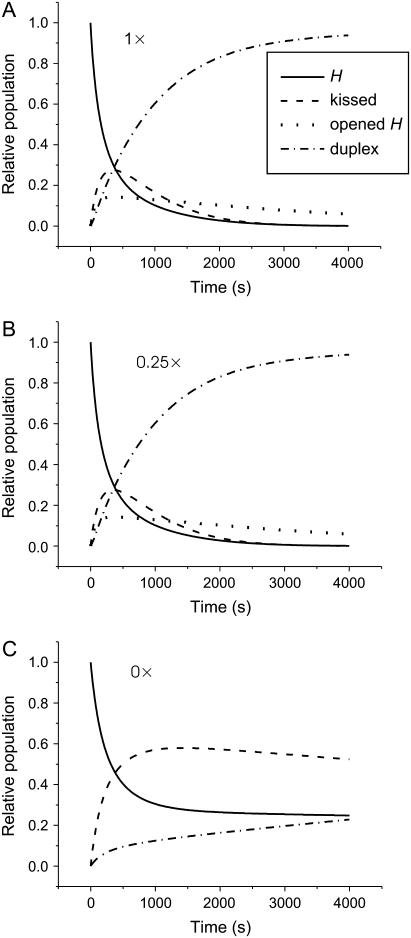
The measurements described above allow us to determine rate constants for most of the processes shown in Fig. 2. Rate constants are tabulated in Table 2. The equilibrium between monomeric hairpins and kissed complex under our experimental conditions made it difficult to isolate some rate constants. We have assumed that the direct conversion of kissed complex to duplex is negligible on the timescale of our experiments (12,29), and that the rate constant for interaction of the catalytic opening strand with a kissed complex is the same as that for interaction with a monomeric hairpin. Using these rate constants we can calculate the time evolution of a system of hairpins in the presence of different amounts of catalyst. Fig. 8 shows the results of such a calculation for the system investigated by PAGE in Fig. 6 B (hairpins H, 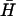, with l = 40, n = 16; catalytic opening strand with m = 7 external toehold).

TABLE 2.

Rate constants used to calculate reaction time course

Rate constant	Process	Value	Figure or assumption
kk	Kissing (association)	3 × 104 M−1 s−1	Fit to data shown in Fig. 4 B ii
k−k	Kissing (dissociation)	4 × 10−4 s−1	Fit to data shown in Fig. 4 B ii
kdk	Duplex from kissed	0 s−1	Measured to be slow*
kd	Direct duplex formation	5 × 103 M−1 s−1	Inferred from Fig. 4 A ii†
kc	Opening of hairpin loop by Opening strand	105 M−1 s−1	Fit to data shown in Fig. 5 B iii (Supplementary Material)
kdc	Reaction of opened hairpin with complementary hairpin, displacing opening strand	5 × 104 M−1 s−1	Fit to data shown in Fig. 6 A
kkd	Opening of hairpin loop in kissed complex by opening strand	105 M−1 s−1	Same as kc‡
kt	Resolution of three-strand complex (opening strand and hairpins) to form a duplex and free opening strand	(10 s−1)	Fast§

For a graphic depiction of the evolution of this system of hairpins, see Fig. 8.

^*Bois et al. (12) observe no decay of a kissed complex formed from complementary hairpins with a 20-base loop to duplex over 15,000 s. Seelig et al. (29) measure the decay of a kissed complex of two-strand loops to form a duplex and infer a rate constant of 1 × 10⁻⁶ s⁻¹ . The kissed complex is the dominant species at 6000 s and 60,000 s in the reaction studied in Fig. 4 A i, consistent with a rate constant for formation of duplex from the kissed complex k_dk ≪ 10⁻⁵ s⁻¹.

^†An approximate value for the rate constant for direct duplex formation may be inferred from the time-dependent concentrations of hairpins, kissed complex, and duplex that are deduced from Fig. 4 A i, and from the measured rate constant for the kissing interaction.

^‡It is assumed that kissing, which involves interaction between loop domains, does not significantly slow the hybridization of an opening strand initiated at an external toehold.

^§The displacement of the opening strand from an opened hairpin by hybridization of the complementary hairpin (Fig. 6 A) is fitted well by assuming second-order kinetics, consistent with the assumption that resolution of the three-oligonucleotide intermediate complex is rapid compared to association.

FIGURE 8.

Calculated evolution of a system of complementary hairpins H and 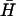(l = 40, n = 16, reactant concentration 0.1 μM) in the presence of 1×, 0.25×, and 0× catalytic opening strand with a seven-base external toehold.

Results of this calculation, shown in Fig. 8, are consistent with the PAGE analysis of hairpin hybridization catalyzed by an opening strand (Fig. 6 B). With no catalyst present, the dominant reaction is the association of monomeric hairpins to form the kissed complex (c.f. Fig. 4). In the presence of the catalyst the rate of duplex formation is dramatically increased. Catalysis of duplex formation causes rapid depletion of the populations of monomeric and kissed hairpins, so in the presence of the catalyst the initial increase in concentration of the kissed complex is transient.

Implications for DNA-powered devices

Interactions between hairpins intended as fuel for an autonomous molecular machine may be controlled through hairpin design. Long necks may be used to reduce the rate of spontaneous duplex formation. Shorter loop domains may be used to avoid the formation of stable kissed complexes, although reducing the loop length also reduces both the energy released by hybridization and the number of independent interactions that can be encoded within the loop domain. The connection between kissing and the duplex formation rate should be investigated further. Transient kissing might facilitate the spontaneous formation of a completely hybridized duplex; however, if the activation barrier to further interaction were too high, formation of a long-lived kissed complex could impede duplex formation. Although the simplest approach to the design of a hairpin fuel would be to avoid kissing, a kissed complex of complementary hairpins could be used as a one-component fuel (12,29).

Catalytic loop-opening via an external toehold is considerably faster than via an internal toehold, an obvious advantage for powering a device. However, a catalytic opening strand with an external toehold is not completely displaced by hybridization of the opened hairpin with its complement: it must dissociate from the toehold spontaneously. Transient interaction between the catalyst and the exposed toehold domains of hybridized hairpins reduces its availability to catalyze hybridization of another pair of hairpins. Use of a toehold with a melting temperature well below the reaction temperature reduces this problem, but also reduces the fractional population of opened hairpins. Use of an internal toehold avoids interaction between catalyst and duplex product altogether.

CONCLUSIONS

Spontaneous hybridization between complementary DNA hairpins is slow compared to the hybridization of complementary oligonucleotides with no secondary structure and slow compared to the loop-opening reaction between a hairpin and an opening strand. The rate of spontaneous duplex formation between hairpins may be reduced by decreasing loop length and by increasing neck length.

Hybridization between complementary DNA hairpins can be catalyzed by an opening strand capable of forcing open the neck of a hairpin loop by strand invasion. Loop opening removes the topological constraint that impedes spontaneous hybridization. Loop opening by a catalyst possessing an external toehold is 10–100 times faster than loop opening from an internal toehold. We attribute this difference between rates to an entropic activation barrier associated with the configuration of intermediate states formed as a catalyst bound at an internal toehold invades the neck.

Our results confirm that a system of complementary hairpin loops is suitable for use as a metastable fuel for free-running DNA devices capable of catalyzing their hybridization.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.