Pressure Tuning of the Morphology of Heterogeneous Lipid Vesicles: A Two-Photon-Excitation Fluorescence Microscopy Study

Abstract

We used a technique that allows us to visualize local and morphological changes of the membrane of more component giant unilamellar vesicles due to high pressure perturbation. Under these conditions, thermally induced processes are largely suppressed, and the bending rigidity and line tension are influenced by pressure-induced changes in lipid molecular packing and shape only. We studied the effect of pressure on the lateral organization and morphology of the model raft system DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine)/sphingomyelin/cholesterol as well as of the fluid mixture POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine)/DLPC (1,2-dilauroyl-sn-glycero-3-phosphocholine) by two-photon excitation fluorescence microscopy. The pressure-dependent experiments were carried out using a sample cell made from a thin fused silica capillary. The use of Laurdan as fluorescence label allowed us to also follow the lipid phase state by calculating the generalized polarization (GP) values of the vesicles and extracting their average value. During the compression cycle, a reduction in the volume of the vesicles is observed, accompanied by an increase of the average GP value, indicating an increasingly tighter packing of the lipids. Interestingly, the two systems studied show phenomena of budding and fission, and these at surprisingly low pressures of 200–300 bar. Moreover, these budding processes are not directly related to phase transitions to an overall ordered conformational state of the lipid membrane, which occur at much higher pressures. The topological changes of the lipid vesicles are irreversible and exhibit a different behavior depending on whether the pressure is increased or decreased. The results are discussed in light of the various contributions to the free energy functional of lipid vesicles. Finally, the biological relevance of these studies is highlighted.

INTRODUCTION

The full thermodynamic understanding of any system depends on the measurement of changes caused by variation in the thermodynamic variables temperature and pressure. Whereas temperature studies of biochemical systems, such as proteins and biomembranes, are rather easy to perform, pressure-dependent studies, while technically more difficult, have been initiated only in recent years to yield a more detailed physicochemical understanding of these systems (1–5). However, high hydrostatic pressure has also been used because high pressure is an important feature of certain natural membrane environments, for example, for understanding the physiology of deep sea organisms, the sensitivity of excitable cell membranes to pressure (high pressure nervous syndrome), and the antagonistic effect of pressure to anesthetic action (1–7). Furthermore, studies of pressure effects on biochemical systems often led to the discovery of new structures and phases and helped to understand the mechanisms underlying structural and phase transformations of these systems (3,5,8–10).

In this work, we focused on pressure effects on heterogeneous lipid vesicles. There is increasing evidence that biological membranes are heterogeneous with liquid-ordered (l_o) domains, so-called “rafts”, consisting of lipids that have saturated tails, including the naturally occurring glycosphingolipids and sphingomyelin (SM) as well as fatty acids (11–16). The long and saturated acyl chains in sphingolipids should allow cholesterol (Chol) to become tightly intercalated with such lipids, organizing an l_o phase, whereas unsaturated phospholipids are loosely packed and form a disordered or liquid-crystalline phase (l_d). The study of such raft-type domains in vitro through coexisting lipid phases in giant unilamellar vesicle (GUV) membranes containing three-component mixtures of saturated lipids, unsaturated lipids, and Chol was revealed to be a good method to directly observe micron-scale domains by fluorescence microscopy (17–21). Among different artificial membranes, GUVs are particularly good models of cell membranes due to their similarity to cells in terms of their dimensions (10–100 μm), radius of curvature, and lamellarity. Moreover, they can be visualized individually under the microscope, allowing one to study the properties of the membrane locally. This microscopy method allows us also to study the membrane under pressure (22).

A further important point of interest in membrane research concerns morphological transitions of fluid lipid vesicles, in particular in relation to budding. The formation of small membrane structures (vesicles or tubules) is required for most inter- and intracellular transport processes in biological cells and it allow us to hypothesize that every time a vesicle or tubule buds from a membrane, there is some sorting of the lipid components (23,24). In recent years, in a series of theoretical calculations, the morphological changes of lipid vesicles induced by temperature, composition fluctuations, osmotic stress, or local membrane asymmetry have been studied (25–35). The sites of vesicle or tubule budding are often regions of high curvature, and the shape of the lipid molecules can affect their ability to be accommodated in these regions of high curvature. This shape dependence could provide an efficient mechanism for lipid sorting. The l_o and l_d domains themselves generally have some curvature preferences, with l_o domains favoring flat parts of the membrane, and l_d domains being better able to accommodate curved regions (30,31).

The current theoretical understanding of the morphology and the morphology transformations of lipid vesicles is based on the important notion of bending elasticity. A large variety of vesicle shapes which minimize the bending energy has been found for certain physical parameters such as the enclosed volume and the area of the vesicle (26–29). A relevant quantity for a change in shape is the variation of the equilibrium area difference of the two monolayers, ΔA₀, leading to an additional, so called area-difference elasticity free energy contribution being proportional to (κ /A·D²)·(ΔA − ΔA₀)², where ΔA is the actual area difference, and D is the distance between the neutral surfaces of the two monolayers, i.e., roughly half the bilayer thickness (26,27). ΔA₀ is expected to be sensitively dependent on several factors including temperature and pressure. Because the thermal expansivity of a lipid bilayer is large compared to that of water, the vesicle area changes more rapidly with temperature than the vesicle volume, and hence the area/volume ratio increases with increasing temperature, which may then lead to various shape transformations. For example, if the outer monolayer expands more than the inner one, the additional area accumulated in this outer layer will cause budding since the formation of buds increases the area difference. Likewise, a stronger increase of the area of the inner monolayer may induce a transition to discotyes and stomatocytes.

Shape transformations are also predicted to arise in vesicles consisting of bilayers with different components due to different mechanisms (30–35). If, for example, two components form domains, the line energy associated with these domain boundaries can be reduced by budding of such a domain. Also, even if the membrane is in a one-phase region, a temperature-induced budding process may lead to a curvature-induced phase segregation since, in general, the two components couple differently to the local curvatures. In phase-segregated membranes, the free energy of the membrane consists essentially of the curvature energy of the domains and the line energy of the domain interfaces. As far as the edge energy is concerned, the line energy may be reduced by budding until it vanishes for a completely separated vesicle. But on the other hand, the curvature energy increases concomitantly. Generally, the energy functional contains contributions arising from bending resistance, line tension, and lateral tension (which is negligible for fluid membranes). The first term, the bending energy F_b of a symmetric lipid membrane, has components arising from mean curvature (first term) and Gaussian curvature (second term) and is summed over every domain i of the vesicle (31–34):

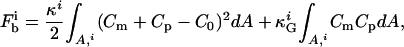(1)

where, κ, κ_G, C_m, and C_p are the mean and Gaussian bending rigidities and principal curvatures along the meridians and parallels, respectively, and the integrals are extended over all domain areas i. C₀ is a curvature preference (spontaneous curvature), which may be assumed to be constant within a domain, but can in general vary locally. The second term in Eq. 1 determines the vesicle shape only if 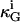values differ between domains i.

In multicomponent systems, there is a contribution from the line tension λ of the domain boundaries:

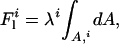(2)

which has been proposed to control membrane deformation, budding, and fission (27,32). Generally, the tendency toward budding is proportional to Lλκ ⁻¹, where L is the radius of the domain in the limit of flatness, λ is the line tension of the domain interface, and κ is the bending rigidity of the membrane. Hence, the tendency toward budding depends on domain size, line tension, and membrane stiffness, and all these parameters are expected to depend on temperature and pressure.

In this work, we studied the effect of pressure on individual GUVs formed by the three-component canonical lipid raft mixture DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine)/SM/Chol (33:33:33), as well as by the fluid mixture POPC/DLPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine/1,2-dilauroyl-sn-glycero-3-phosphocholine) (50:50). As fluorescent probe, we chose the amphiphilic fluorophore 6-dodecanoyl-2-dimethyl-amino-naphtalene (Laurdan), which is able to report on phase transitions and phase coexistence in lipid systems (36–38). We monitored single GUVs upon pressurization using the Laurdan intensity images and the Laurdan generalized polarization (GP) function, which provides information about the lipid phase state. In this study, pressure offers a very powerful means to perturb the physical conditions of the lipid bilayers (lipid order parameter, packing, sorting) without changing the thermal energy, as is done in temperature-dependent studies, and therefore can be used to tune and investigate the physics of the interactions of molecules contained in the lipid bilayer. Many studies have been performed in the past to study the response of multilamellar lipid vesicles to pressure using small-angle scattering techniques, calorimetry, NMR, fluorescence, and Fourier transform infrared spectroscopy to pressure (1–5,8,39,40). However, no high pressure studies have been conducted on individual heterogeneous lipid vesicles of this kind so far.

MATERIALS AND METHODS

Materials and sample preparation

DOPC, DLPC, POPC, and SM (brain, porcine) were purchased from Avanti Polar Lipids (Birmingham, AL), and Chol from Sigma-Aldrich (Deisenhofen, Germany). The chemicals were used without further purification.

Fluorescence microscopy and high pressure cell

Vesicle preparation

Laurdan (6-dodecanoyl-2-dimethylamino-naphthalene) was obtained from Molecular Probes (Eugene, OR). Stock solutions of phospholipids and Chol were prepared in a solution of chloroform/methanol 4:1 (v/v). The concentration of the lipid stock solutions composed of DOPC/SM/Chol and POPC/DLPC was 0.2 mg/mL. For preparing GUVs, we followed the electroformation method developed by Angelova et al. (41). To grow the GUVs, a special temperature-controlled chamber was used, which was described previously (42). The following steps were used to prepare the GUVs: 1), 2-μL of the lipid solution was spread on each platinum (Pt) wire of the electroformation chamber under a stream of N₂. To remove residues of the organic solvent, the samples were lyophilized for 1 h; and 2), to add the aqueous solvent (using Millipore water, 17.5 MΩ.cm) into the chamber, the bottom part of the chamber was sealed with a coverslip. The water was previously heated to 65°C and then sufficient water was added to cover the Pt wires. After this step, the Pt wires were connected to a function generator (Hewlett-Packard, Santa Clara, CA), and a low frequency alternating current (AC) field (sinusoidal wave function with a frequency of 10 Hz and an amplitude of 2 V) was applied for 90 min.

After vesicle formation, the AC field was turned off and the liquid sample was loaded into a fused silica microcapillary (Polymicro, Phoenix, AZ) of cylindrical geometry, with an outer diameter of 360 μm and an inner diameter of 50 μm, by applying suction on one end of the open capillary after connecting it to a syringe, while the other end was in contact with the sample. The capillary serves as a high pressure vessel, being able to hold pressures up to ∼3 kbar. Once the sample is loaded, the free end of the capillary is sealed. We sealed one end of the capillary by touching the very extreme of the capillary with the flame of a blowtorch, which fuses the silica end together. We typically left the last centimeter of the capillary void of sample, so that the heat is not in direct contact with the sample solution, which is sufficient as the thermal conductivity of fused silica is low. The other end of the capillary, which is inserted in an ∼400-μm hole drilled in a modified aluminum pressure plug and secured with epoxy glue, was connected to commercially available pressure tubing (HIP, Erie, PA). The pressure plug fits the receptacle of the coupling unit, which provides the high pressure connection between the capillary and the pressure tubing. The pressure tubing was connected with a home-built pressure generator, which uses ethanol as the pressure-transmitting medium. A manually operated piston screw pump (HIP 37-5.75-60) was used to generate hydrostatic pressure. A standard pressure gauge (HIP 6PG75) was connected to the pump for determining the pressure of the system. The overall compression and decompression cycles, where measurements were carried out, covered a pressure range of ∼1–3000 bar (typically in steps of 50–100 bar) and a time range of ∼2–3 h.

Experimental setup

The two-photon excitation microscopy experiments were performed at the Laboratory for Fluorescence Dynamics (University of Illinois at Urbana-Champaign). The high photon densities required for two-photon absorption were achieved by focusing a high peak power laser light source on a diffraction-limited spot through a high numerical aperture objective. Therefore, in the areas above and below the focal plane, two-photon absorption does not occur because of insufficient photon flux. This allows a sectioning effect without the use of emission pinholes as in confocal microscopy. Another advantage of two-photon excitation is the low extent of photobleaching and photodamage above and below the focal plane. For our experiments, we used a scanning two-photon fluorescence microscope (43,44). For the Laurdan GP experiments, we used a procedure similar to that previously described (45,46). We used a 63× immersion objective (Zeiss, Homldale, NJ) with a numerical aperture of 0.4. A titanium-sapphire laser (Mira 900; Coherent, Palo Alto, CA) pumped by a frequency-doubled Nd:vanadate laser was used as excitation light source. The excitation wavelength was set at 780 nm. The laser was guided by a galvanometer-driven x-y scanner (Cambridge Technology, Watertown, MA) to achieve beam scanning in both the x and y directions. The scanning rate was controlled by the input signal from a frequency synthesizer (Hewlett-Packard), and a frame rate of 25 s was used to acquire the images (256 × 256 pixels). To change the polarization of the laser light from linear to circular, a quarter wave plate (CVI LaserCorporation, Albuquerque, NM) was placed after the polarizer. The fluorescence emission was observed through a broad band-pass filter from 350 to 600 nm (BG39 filter; Chroma Technology, Brattleboro, VT). For measuring Laurdan GP values, two additional optical band-pass filters with 46-nm width and centered at 446 nm and 499 nm (Ealing Electro-Optics, Holliston, MA) were used to collect fluorescence in the blue and green regions of Laurdan's emission spectrum, respectively. A miniature photomultiplier (R5600-P; Hamamatsu, Brigdewater, NJ) was used for light detection in the photon-counting mode. A home-built card in a personal computer acquired the counts. GP values were corrected for the different transmission properties of the optical filters by using a solution of Laurdan in dimethyl sulfoxide.

Generalized polarization function

The Laurdan emission spectrum is sensitive to the degree of water penetration in the membrane and therefore to the degree of packing of the lipids in the membrane. The emission spectrum of Laurdan is blue in the lipid gel (ordered) phase, whereas in the l_d (fluid) phase it moves during the excited-state lifetime from the blue to the green (38,46). To quantify the emission spectral changes, the excitation GP function was defined analogously to the fluorescence polarization function as GP = (I_B − I_R)/(I_B + I_R), where I_B and I_R correspond to the intensities at the blue and red edges of the emission spectrum, respectively, for a given excitation wavelength.

RESULTS

The model raft system DOPC/SM/Chol (33:33:33)

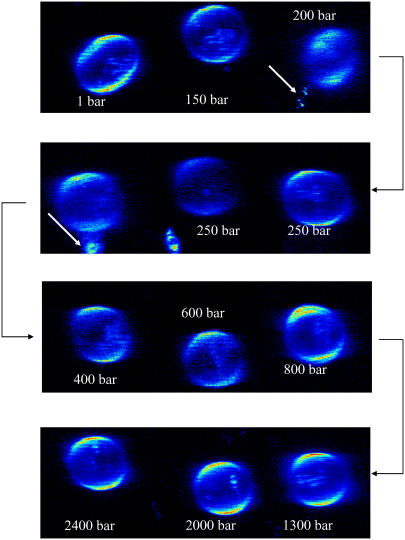
Pressure-dependent two-photon excited fluorescence microscopy experiments with GUVs containing DOPC, SM, and Chol at levels of 33 mol %, visualized by the membrane fluorophore Laurdan, were carried out at pressures from 1 to 2700 bar. Fig. 1 shows GUVs of the lipid mixture DOPC/SM/Chol (33:33:33) at selected pressures for T = 20°C. For this strongly heterogeneous lipid system exhibiting l_d and l_o domain coexistence, budding and fission of lipid material occurs upon pressurization. The white arrows in Fig. 1 indicate conditions where budding of small vesicles and fission of lipid material occurs. Budding is mostly observed at pressures of ∼200–300 bar, in the pressure range in which the lipid system reaches a significantly more ordered conformational structure but does not yet reach an all-ordered state (see below).

FIGURE 1.

Two-photon excitation fluorescence intensity images of a Laurdan-labeled GUV (of ∼30-μm diameter) composed of DOPC/SM/Chol (33:33:33) at selected pressures (T = 20°C). The GP images were taken at the top of the vesicle. The white arrows indicate conditions where budding of small vesicles and loss of lipid material occur.

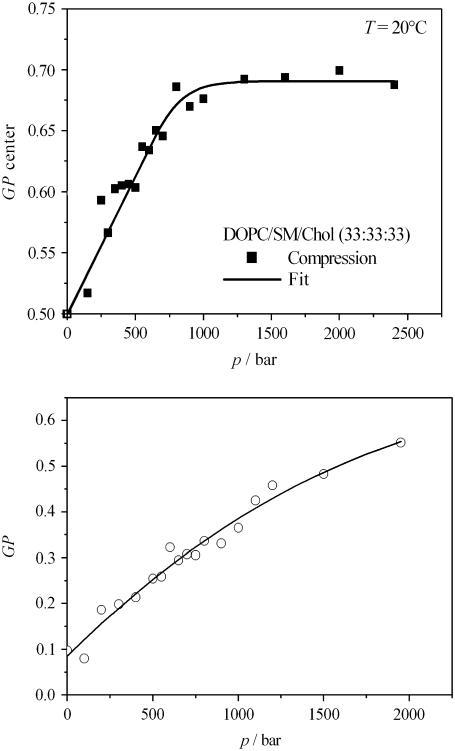
By Laurdan fluorescence spectroscopy, we also determined the average GP value of unilamellar vesicles of the system. Upon increasing the pressure, a significant increase in average GP value (GP center) of the lipid vesicles is detected, which levels off around 1000 bar for T = 20°C (Fig. 2 a); i.e., upon pressurization at room temperature (20°C), an overall (liquid- and solid-) ordered membrane state with high ordering of their acyl chains is reached at pressures of ∼1 kbar, only.

FIGURE 2.

(a) Average GP value (GP center) of the lipid mixture DOPC/SM/Chol (33:33:33) in excess water as a function of pressure during a compression cycle at T = 20°C. (b) Average GP value of the lipid mixture POPC/DLPC (50:50) in excess water as a function of pressure during a compression cycle at T = 20°C.

The POPC/DLPC (50:50) lipid mixture

During the compression cycle from 1 bar up to 2000 bar at 50–100 bar intervals at T = 20°C, the GUVs composed of POPC/DLPC (50:50) maintain their spherical shape. By increasing the pressure, the average GP value increases steadily (Fig. 2 b), indicating an overall tighter packing of the lipid chains of the mixture, which are in a fluid-like state at ambient pressure conditions and T = 20°C. At 2000 bar, the GP reaches a value of 0.55 (Fig. 2 b). A plateau has not been reached, however; i.e., the system is not completely in a conformationally ordered state yet, which is in accord with high-pressure small-angle x-ray scattering (SAXS) data (data not shown), which reveal that a phase transition to an ordered phase of the lipid system is reached above ∼2 kbar, only.

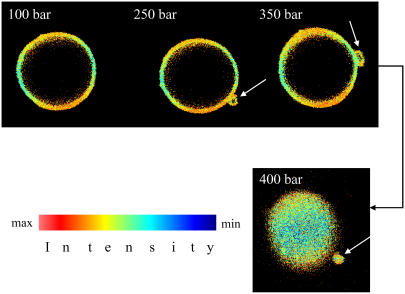
Selected examples of two-photon excited high pressure microscopy images are presented in Fig. 3. As can be clearly seen in the figure, budding of lipid vesicles is initiated upon pressurization. Until 200 bar, the GUVs retain their shape. Further increase of pressure by ∼50 bar leads to the growth of a bud, which develops upon further pressurization, becoming a small vesicle that finally disconnects from the parent vesicle at ∼400 bar.

FIGURE 3.

Selected two-photon excitation fluorescence intensity images of Laurdan-labeled GUVs of the system POPC/DLPC (50:50) at T = 20°C taken during the compression cycle. At 250 bar, a bud develops, which grows upon further pressurization. At ∼400 bar, fission occurs. The white arrows indicate budding and fission processes. The GP images are taken at the equatorial section for the pressures at 100, 250, and 350 bar and at the top of the GUV for 400 bar. The variations in GP values are here due to the imperfect circular polarization of the excitation light.

Upon subsequent release of the pressure from 2000 to 1 bar, a different scenario is observed: The vesicle shows a sequence of topological changes, from spherical to ellipsoidal to polygonal (Fig. 4). The morphological transformations are accompanied by dynamic fluctuations of the membrane surface. A shape transition from a spherical to an ellipsoidal shape occurs at ∼1400 bar. At that pressure, pronounced regions with different GP values are induced. In particular at the edges of the vesicles surfaces, higher GP values (i.e., regions of higher conformational order) are observed. An invagination of small vesicles is observed at that pressure as well. Upon further decompression, at ∼1100 bar, the vesicle shape becomes completely unstable and the membrane surface fluctuates steadily, transiently passing pear-like and dumbbell-like shapes. This phenomenon is accompanied by loss of membrane material (Fig. 4). Finally, smaller, polygon-like shaped vesicles appear at low pressures.

FIGURE 4.

Selected two-photon excitation fluorescence intensity images of Laurdan-labeled GUVs of the system POPC/DLPC (50:50) at T = 20°C taken during the decompression cycle from 2 kbar to 1 bar. The white arrows at 1100 bar indicate conditions where budding of small vesicles and pinching-off of lipid material occur. As the pressure is released, the GUVs start wobbling. Another interesting observation is that the GP is not homogeneous throughout the vesicle anymore.

DISCUSSION AND CONCLUSIONS

Pressure-dependent experiments on lipid vesicles of the mixtures POPC/DLPC (50:50) and DOPC/SM/Chol (33:33:33) were carried out from 1 bar up to ∼3000 bar using two-photon excitation fluorescence microscopy. The ability to visualize individual vesicles during the compression and decompression cycles enabled us to study the changes in fluidity, phase state, and topology of the membrane vesicles on a local scale. This type of information is generally lost in steady-state bulk measurements, which are the result of an ensemble average over many vesicles. By observing the GP values locally, we can also relate the curvature and topology of the membrane with its fluidity and phase state.

As discussed above, the shape of a lipid vesicle is largely determined by the minimum bending energy (26,27,32,34). As a consequence, the shape is given by the volume/area ratio of the vesicle, the spontaneous curvature, and the area difference of the two apposing monolayers, which are expected to be sensitively temperature and pressure dependent. In phase-segregated membranes, a further energy term becomes important, the line energy of the domain interfaces. As far as the line energy is concerned only, a flat circular disk does not represent the state of lowest energy since the length of the edge can be further reduced if the domains form a bud. If the line tension λ becomes too high, the neck of the bud may narrow down and lead to fission of daughter vesicles, generally of a different lipid composition (30–32). Temperature- and pressure-induced changes in lipid conformation, phase state, and domain coexistence regions are expected to affect the local bending energy as well as the line energy and hence shape of the lipid vesicle. Both factors are expected to be highly correlated in multiple component lipid vesicles.

In our systems studied, budding or even multiple budding and pinching-off of small vesicles has been observed upon pressurization of more component GUVs at surprisingly low pressures of only a few hundred bars. During the compression cycle, a reduction in the volume of the vesicles is observed, accompanied by an increase of the average GP value, indicating an increasingly tighter packing of the lipids. The change in volume of the lipid vesicles is greater than the change in volume due to the compression of water (the change of volume for water is ∼5% at 1000 bar only). From this we conclude that water must be expelled from the GUVs during the compression. Only at a pressure of ∼1000 bar, the lipid raft mixture DOPC/SM/Chol (33:33:33) reaches an overall ordered conformational state at T = 20°C. The POPC/DLPC (50:50) vesicles undergo a phase transition to a pressure-induced fluid-gel coexisting region at pressures above ∼2 kbar for T = 20°C, which would be in accord with the p,T phase diagrams of POPC and DLPC multilamellar vesicles (5). The two systems studied show phenomena of budding and fission already at much lower pressures of 200–300 bar, however. The budding process is therefore not directly related to phase transitions to an overall ordered conformational state of the lipid membrane; it rather requires a significant overall increase of pressure-induced conformational order, only. As discussed above, such budding could generally be expected to occur to decrease a pressure-induced rise of the line tension between domains on the one hand (Eq. 2), but it may also occur if the area-difference energy contribution (see Introduction) increases, which may be expected upon pressurization when the vesicle volume decreases. The latter scenario might play a dominant role in the case of the homogeneous lipid mixture POPC/DLPC (50:50). Budding owing to a pressure-induced increase of the line tension (as less disordered, flexible lipid molecules are present which could adsorb at the domain interfaces to keep the line tension low) is likely to be the case for the model raft mixture DOPC/SM/Chol (33:33:33), which, under ambient pressure conditions, is in an already rather ordered conformational state. A pressure-induced increase of differential compressibilities of the two apposing monolayers leading to budding could play an important role in these heterogeneous membranes as well, however.

The topological changes of the lipid vesicles may exhibit a different behavior, depending on whether the pressure is increased or decreased. Upon decreasing the pressure, the lipid mixture POPC/DLPC (50:50) shows quite drastic changes in the morphology of the GUVs. Spherical-ellipsoidal-polygonal shape transitions occur, accompanied by fluctuations of the membrane surface and fission of lipid material. On the contrary, the three-component lipid raft mixture containing 33 mol % Chol has a higher conformational order and rigidity and maintains an essentially spherical-ellipsoidal shape. In (liquid- or solid-) ordered phases, the total volume and surface area occupied by the lipids in the membrane is reduced and water is expelled from the membrane. Hence, in the case of vesicles, upon compression or decompression, a change in the surface area will cause a change in the volume of the entire vesicle. However, unless the internal vesicle volume can adapt to the changed surface area by expelling the internal water or by imbibing external bulk water, the membrane will be under stress. These processes can probably be easily achieved only in the compression direction, where sufficient water permeability of the membrane is possible. Probably, it does not hold true for the decompression cycles anymore, where water is less likely able to penetrate and pass the membrane sufficiently rapidly. If the initial pressure is high and the pressure is decreased up to values where the membrane will became significantly more fluid, the surface area will markedly increase. If the internal volume remains the same, then the shape of the vesicle must change, breaking the spherical topology of the vesicle. The vesicle abruptly loosens its tension and becomes flabby as observed in the POPC/DLPC vesicles. This change from the spherical shape will produce regions of different curvature and hence GP values. We can see that high curvature radii tend to have higher GP values. These phenomena are transient since water will eventually leak through the membrane.

Interestingly, in the pressure range of 1–2 kbar, ceasing of membrane protein function in natural membrane environments has been observed for a variety of systems (1,2,4,47–49), which might be correlated with the membrane matrix reaching a physiologically unacceptable overall ordered state at these pressures. As has been demonstrated above, this might also be due to pressure-induced morphological changes of the membrane.

The stage is now well set to also use the two-photon excited fluorescence microscopy method in studying the behavior of membrane proteins and lipid-protein interactions under pressure and, finally, of natural membranes and live cells.