Analysis Method for Measuring Submicroscopic Distances with Blinking Quantum Dots

Abstract

A method is described that takes advantage of the intermittency (“blinking”) in the fluorescence of quantum dots (QDs) to measure absolute positions of closely spaced QDs. The concept is that even if two QDs are separated by only tens of nanometers, the position of each QD is resolvable if the point spread function of each can be imaged independently of the other. In the case of QDs, this is possible if each QD separately blinks completely on and off during a time-lapse sequence. To demonstrate the principle of this method, time-lapse sequences of single blinking QDs were acquired and the centroids of the point spread functions determined. Images of the blinking QDs were then overlapped in software, pixel by pixel, generating a range of submicroscopic distances between QD pairs. Methods were developed for analyzing the overlapped time sequences of the QD pairs so that the positions of the QDs and the distances between them could be determined without prior knowledge of the single QD positions. We subsequently used this method to measure the end-to-end length of a 122-basepair double-stranded DNA fragment.

INTRODUCTION

Almost all biological processes underlying biological function involve at some point biochemical interactions occurring at or near cell membranes (including both plasma and intracellular membranes). Three examples include viral entry into cells during the initial stages of cell infection (1), receptors that initiate cellular response after extracellular ligand binding by phosphorylation of intracellular tyrosine residues (2), and the currently poorly understood role of lipid microdomains, sometimes called lipid rafts, in membrane function (3). These cases are stated only as examples; the challenge of characterizing membrane-associated biomolecular interactions is quite general, spanning most areas of biology.

To fully understand membrane-associated biochemical interactions, measurements must ultimately be carried out on live, intact cells. At present, the preferred method for examining biomolecular behavior on live cells is optical and, in particular, fluorescence microscopy. However, optical microscopy in the classical sense is limited by optical resolution (≈250 nm in the visible region of the spectrum) and many membrane-associated molecular events occur not on this spatial scale but on a scale more related to typical biomolecular sizes (≤10 nm). Thus, there is an urgent need for the development of new, more nuanced optical microscopy methods that can probe biomolecular interactions at submicroscopic resolution.

Several previous works have demonstrated that, with new approaches, fluorescence microscopy can indeed operate at distances well below the optical resolution of a microscope. Förster resonance energy transfer (FRET) has been used extensively for measuring direct molecular interactions or, when combined with single-molecule detection, for studying conformational changes and folding of a variety of biopolymers (4,5). However, FRET is typically limited by low signals and to distances <10 nm. A complementary method that uses plasmon coupling between single silver and gold nanoparticles to monitor the distance between these nanoparticles, and at separations up to 70 nm, has recently been described (6). However, it is difficult to obtain absolute distance measurements with either this method or FRET. Other methods include the use of evanescent illumination (7,8), metallic structures (9,10), stimulated emission depletion (11), near-field scanning optical microscopy (12), supercritical angle fluorescence (13,14), and micro- or nanofluidic channels (15).

A variety of single-molecule techniques that rely on curve fitting to the point spread function (PSF) of the microscope, and that use either gold particles or fluorescent dyes or proteins, have also been developed. These methods are typically capable of detecting the positions of stationary (and sometimes mobile) single molecules with an accuracy of only ∼10 nm; however, the positions of nearby molecules separated by these small distances cannot be readily resolved (16–18). Methods for resolving two nearby molecules that are separated by distances greater than the upper limit of FRET (<10 nm) but <∼100 nm have relied on dual-color colocalization experiments using spectrally separated fluorescent dyes, proteins, or nanoparticles such as fluorescent beads or quantum dots (QDs) (19,20). In these methods, the PSF for each molecule is acquired and fit separately and the results are superimposed after correcting for chromatic aberrations. In addition to the need to correct for chromatic aberrations, which typically limits the resolution, this method also generally suffers from the need for multiple excitation and emission combinations and highly customized equipment.

In an innovative approach, two different groups have also recently described a monochromatic method, which takes advantage of photobleaching to determine the centroid positions of single molecules that are separated by only tens of nanometers (21,22). In the first of these works, the spatial centroids of two nearby single fluorescent molecules were determined by global fitting of the PSF immediately before and after photobleaching (21). In the second work, time-lapse sequences of clustered single fluorescent molecules for which incremental photobleaching steps occurred, were observed until only a single fluorescent molecule remained unbleached (22). The sequence was subsequently analyzed by fitting the images iteratively, starting with the data acquired with only a single molecule on, continuing with the data acquired when two single molecules were simultaneously on, and repeating the process until the spatial centroids of all molecules were determined (22). Both of these studies reported precisions of only a few nanometers, but the time resolution was low (≤1 s).

In addition to the challenge of developing methods in optical microscopy that can overcome the classical diffraction limit, another limitation has been that fluorophores of organic origin undergo photobleaching. Photobleaching manifests itself, in the simplest interpretation, as a maximum number of photons that can be detected before fluorophore decomposition to an irreversible, nonfluorescent state; this sets an upper limit to the length of time that a single fluorophore may be observed. This seemingly universal problem with organic fluorophores has limited fluorescence microscopy for decades, although it has been taken advantage of in the works described above (21,22). Conventional fluorophores are typically also limited by their brightness, which serves to set limits on the spatial and temporal resolution with which the centroid of a single fluorophore may be located. A simple theoretical relation between the spatial precision with which a single fluorophore may be located and the total number of collected photons has been described (17).

QDs are small, inorganic nanoparticles that are very photostable, are brighter than conventional dye and protein fluorophores, are excitable over a broad wavelength range stretching from the ultraviolet up to slightly less than their emission peak, and have narrow, size-tunable emission bands (23–25). QDs do, however, exhibit an intermittency (“blinking”) phenomenon in which they undergo transitions between “on” states, where the dots are fluorescent, and “off” states, where they are not fluorescent. This blinking phenomenon has been shown to be influenced by several factors, including the excitation intensity (26), and to be suppressible in the presence of reducing agents such as dithiothreitol and β-mercaptoethanol (27). QDs have been used at the single-molecule level to study the diffusion of glycine receptors into synapses (28), the activation and internalization of EGF receptors (29), and the in vitro sliding of actin filaments (30).

In the work described here, we present a method that takes advantage of QD blinking to determine absolute positions and to measure distances between two closely spaced QDs. The concept is that even if two QDs are separated by only tens of nanometers, the position of each QD is resolvable if the PSF of each can be imaged separately from that of the other. For QDs, this is the case if each QD independently blinks during a time-lapse sequence. In contrast to methods that use photobleaching to distinguish between overlapping PSFs, the QD blinking phenomena is reversible and can potentially be used to monitor distances between two QDs over very long periods of time. The greater brightness of QDs, as compared to conventional fluorophores, further enables a spatial precision of at least 10 nm at a sampling frequency of 30 Hz. We show that this method can be used to obtain a measurement for the end-to-end length of a 122-basepair (bp) double-stranded (ds) DNA fragment that is consistent with the theoretically expected length for this size DNA fragment.

MATERIALS AND METHODS

Quantum dots

Streptavidin-conjugated QDs emitting at 605 nm were acquired from Quantum Dot Corp. (Hayward, CA; www.qdots.com). To keep the overall QD size minimized, we used QD conjugates which had the streptavidin conjugated directly to the water-stabilizing copolymer of octylamine and polyacrylic acid (31–33). These QDs, which are available as part of the Qtracker Cell Labeling Kits, have been reported to have a diameter of ∼15 nm (33). Specimens were prepared by applying 65 μl of a 200-pM solution of streptavidin QDs in 50 mM sodium borate, pH 8.2, supplemented with 1% bovine serum albumin, to a sample chamber consisting of a 22 × 22-mm No. 1 1/2 glass coverslip, two strips of doubly adhesive tape and a 3 × 1-in glass slide. QDs were allowed to adhere for 10 min, after which samples were extensively washed with 50 mM sodium borate, pH 8.2.

Purification and biotinylation of 122-bp dsDNA fragment

The 122-bp dsDNA fragment was generated by cutting the EGFP-N1 vector from Clontech (Mountain View, CA) with the restriction enzyme Bgl I from New England BioLabs (Ipswich, MA). This generated four distinct DNA fragments of lengths 2291, 2249, 122, and 71 bp. The cut DNA was run on an agarose gel and the 122-bp fragment was purified using the QIAquick Gel Extraction kit (QIAgen, Valencia, CA) The 122-bp dsDNA fragments were biotinylated with a biotin 3′ End DNA Labeling Kit (Pierce, Rockville, IL). Successful biotinylation was ensured by a dot blot (data not shown). Excess free biotin nucleotides were removed by performing a second round of agarose gel electrophoresis and subsequent purification of the biotinylated 122-bp dsDNA. Purified biotinylated 122-bp dsDNA fragments were appropriately diluted and mixed with 200 pM 605 nm streptavidin QDs in 50 mM sodium borate, pH 8.2, also containing 1% BSA. This solution was incubated for 15 min at room temperature before use. Imaging specimens were prepared as described above.

Imaging

QDs were imaged as diffraction-limited spots by use of an Olympus IX81 microscope, a 100W Hg arc lamp, a cooled intensified Stanford Photonics XR/MEGA-10Z ICCD (Stanford Photonics, Stanford, CA; www.stanfordphotonics.com), a 535/50 nm excitation bandpass and a 610/75 nm emission bandpass (Chroma, Brattleboro, VT; www.chroma.com). Images were acquired at 30 Hz with a 60×, 1.4 NA microscope objective plus an additional 1.6× magnification element that was placed in the Optivar. The projected pixel size on the camera was determined to be 108 × 108 nm. Differences in the fluorescence illumination intensity across the field of view were minimized by limiting image acquisition to a centered region of interest of roughly 400 × 400 pixels. The illumination intensity across this region was confirmed to vary by <10% as determined by the intensity values of an image of a uniformly fluorescent thin film (data not shown).

RESULTS

Identification of single quantum dots

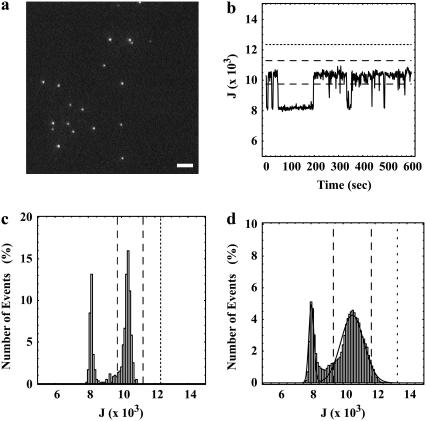
Fig. 1 a shows a typical image of deposited QDs. As shown in the supporting information (Movie 1), the dots visibly converted between fluorescent and nonfluorescent states as observed at 30 Hz over 600 frames.

FIGURE 1.

Identification of single QDs. (a) A single image from a 600-frame sequence acquired at 30 Hz of QDs immobilized on a glass coverslip (scale bar, 4 μm). The full time sequence, which illustrates the observed QD blinking, is shown as a movie in Supplementary Material. (b) The integrated peak intensities, J (Eq. 1), of single blinking QDs typically showed distinct fluctuations as a function of time. (c) Histograms constructed from the 600 integrated peak intensities, J, for single QDs also typically showed distinct “on” and “off” states. (d) Cumulative histogram of the integrated intensities derived from data for the 14 out of 26 diffraction-limited peaks in an image sequence (of which one frame is shown in a) that were firmly identified as single QDs (8400 points) and the best fit to the sum of two 1D Gaussians (Eq. 2 with q = 1). In b–d, the dashed line corresponds to the integrated peak intensities, J = J₁ ± 1.64σ₁, indicative of a single QD being in the “on” state, and the dotted line corresponds to the integrated peak intensity, J = J₁ ± 3.89σ₁, indicative of more than one QD being in the “on” state. In c and d, the leftmost peak arises from background (J₀).

An algorithm that automatically identified single QDs in an image sequence was constructed based on the following principles: QDs display discrete “on” and “off” fluorescence intensity states; a single QD exhibits only one “on” intensity state; and the magnitude of the “on” intensity state of a QD is constant over time and reproducible among all QDs. This algorithm served to reject, among other cases, dots that were coincidentally deposited on the surface close to one another, dots that were close to the edge of the imaged regions of interest, nonspecifically bound dot clusters, and dot clusters that may have been present in the preparations obtained from the manufacturer.

In the algorithm, first, peak positions of diffraction-limited spots were identified by generating a composite image consisting of the brightest-intensity pixel values in an image sequence and by using the “Analyze Particles” function in ImageJ (http://rsb.info.nih.gov/ij/). This maximum intensity projection of an entire image sequence represents the intensity at which each diffraction-limited spot was maximally on. A list containing the positions of all peaks and the entire set of raw data was imported into Mathematica (www.wolfram.com) for subsequent analysis. Imported peak positions were corrected to coincide with the brightest pixel of each identified peak.

Second, using the corrected peak positions, the integrated number of counts for each peak in each image frame was calculated by adding the pixel values over an 11 × 11-pixel region of interest centered on the determined peak position, i.e.,

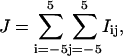(1)

where J denotes the integrated number of counts, I_ij denotes the counts detected at pixel position (i,j), and the maximum counts were observed at pixels i = 0 and j = 0. The integrated peak intensities were plotted as a function of image frame and examined as a function of time for each peak (Fig. 1 b). Histograms of the integrated intensities for each peak were also generated and examined (Fig. 1 c). In most cases, discrete intensity levels were observed that were indicative of single QDs blinking “on” and “off” as a function of time.

Third, to identify single QDs and to determine the range in the intensities of the “on” states, a histogram of the integrated peak intensities, J, was composed (data not shown). This histogram was obtained by examining six time sequences of images, each containing 600 frames. The bin width was 100 counts. The data set contained 231 peaks identified by ImageJ, and therefore 138,600 points. The constructed histogram was fit to the sum of three 1D Gaussians, i.e.,

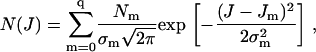(2)

with q = 2. In Eq. 2, J₀, J₁, and J₂ denote mean integrated counts; σ₀, σ₁, and σ₂ denote distribution widths; N₀, N₁, and N₂ denote numbers of events; and “0” denotes the background state, “1” denotes the state in which a single dot is fluorescing, and “2” denotes the state in which two dots are fluorescing. In this fit, all variables except for the indicator J were free parameters.

Fourth, the data set was refined by excluding all peaks that had <5% of the frames in their time sequences with integrated intensities, J, greater than J₀ + 2.58σ₀ (n = 21), indicating that the time sequence was composed primarily of frames with background intensities. Peaks with >5% of the frames in their time sequences with integrated intensities greater than J₁ + 1.64σ₁ (n = 44), indicating overlapping QDs, were also excluded. Further refinement was carried out by fitting the histogram of the remaining 166 peaks to the sum of two 1D Gaussians (Eq. 2 with q = 1) and by rejecting all peaks that had <10% of the frames in their time sequences with an integrated peak intensity, J, within J₁ ± 1.64σ₁, indicating single fluorescing QDs (n = 47). Thus, 119 peaks remained out of the original 231.

Finally, the cumulative histogram of the integrated intensities of the remaining 119 peaks was fit to Eq. 2 with q = 1 to establish the means and standard deviations of the “on” and “off” integrated intensities for single QDs (data not shown). These fitted values were found to be 8020 ± 160 events for the “off” state and 10,580 ± 720 events for the “on” state. The mean background-corrected integrated intensity of a single fluorescing QD, under the imaging conditions that were used, was determined arithmetically from these fitted parameters to be 2560 ± 740.

Spatial mapping of single QDs

Subsequent analysis, in preparation for modeling QD pairs, was limited to a single time sequence, one frame of which is shown in Fig. 1 a. In this sequence, 14 out of 26 diffraction-limited spots were identified as single QDs using the criteria described above. The best fit of the histogram of the integrated intensities of these 14 peaks to Eq. 2 with q = 1 established the means and standard deviations of the “on” and “off” intensity states for single QDs in this set (Fig. 1 d). The fitted values for this time sequence were found to be in agreement with the values determined for the other five time sequences, and were J₀ ± σ₀ = 7980 ± 120 for the “off” state and J₁ ± σ₁ = 10,520 ± 470 for the “single on” state. These parameters were used in the subsequent selection of frames to be analyzed for subpixel positions.

The spatial centroids of identified single QDs in the chosen sequence were determined by taking regions of interest (11 × 11 pixels) surrounding each diffraction-limited spot. For each peak, frames having integrated intensities within J₁ ± 1.64σ₁, indicating that the dot was in the “on” state, were selected for further analysis. Different peaks (denoted by index k) thus contained different numbers, N_k, of analyzed frames (denoted below by index p). Single QDs were in their “on” state for an average of N_k = 403 ± 159 out of 600 total frames (67 ± 27% of total time in the “on” state), with a range of 57 (10% of time in “on” state) to 539 (90% of time in “on” state) frames. In some cases, only sequential frames were analyzed; in other cases, all retained frames for a given dot were analyzed (see below).

The counts found in pixel (i,j) for the kth dot and the pth frame, 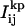, were fit to the PSF of the microscope, which is commonly approximated by a 2D spatial Gaussian (17,21,22); i.e.,

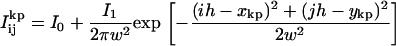(3)

In Eq. 3, I₀ is the mean intensity per pixel of the “off” state, I₁ is related to the maximum background-corrected pixel intensity of the “on” state, w is the PSF width, h = 108 nm is the pixel width, and the coordinate is the spatial centroid. For curve-fitting to Eq. 3, all variables were free parameters for each dot (k) and each frame (p), except for the pixel size, h, and the pixel position indicators -5 ≤ i,j ≤ 5.

For each dot, the mean position (denoted by coordinates 〈x〉 and 〈y〉) and the standard deviations of the position coordinates (denoted by 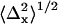and 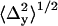), were calculated as

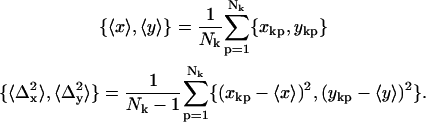(4)

Note that the index (k) has been omitted from the left sides of Eq. 4 and that in subsequent discussion it should be understood that all analyses were carried out with the values of these parameters corresponding to the appropriate time sequence. Fits that resulted in positions {x_kp, y_kp} which deviated from the arithmetic mean of all fitted points by more than an expected confidence level (1 − (4N_k)⁻¹) given by the actual number of fitted frames were rejected. The total number of analyzed frames for the 14 identified single QDs that met all criteria was 5599. The PSF width, averaged over these frames, was w = 170 ± 13 nm, consistent with expectations for conventional optical resolution.

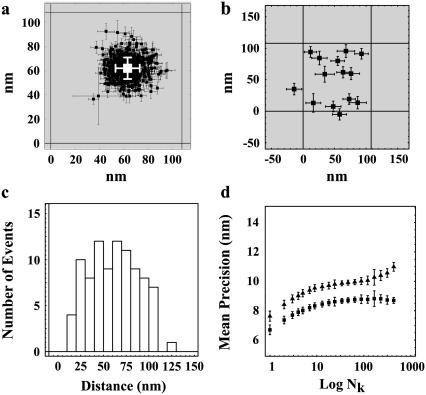
A representative distribution of centroids {x_kp, y_kp} for a single QD is shown in Fig. 2 a along with the average position {〈x〉,〈y〉}. The average positions for the 14 selected single QDs were randomly distributed around the center pixel as expected (Fig. 2 b). The known distances of separation for the 91 dot pairs, calculated from the single dot positions, ranged from 13 ± 17 nm to 121 ± 16 nm (Fig. 2 c). The precisions with which single QDs could be positioned were found to depend on the number of sequential frames that were analyzed for a given dot (Fig. 2 d). The average values for all QDs ranged from 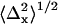= 7.6 ± 6.1 nm for adjacent frames to 12 ± 1.6 nm for all retained frames along the x axis; and 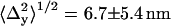for adjacent frames to 8.9 ± 0.9 nm for all retained frames along the y axis. The discrepancy of larger standard deviations of the centroid values along the x axis as opposed to the y axis is likely in part due to the greater stage drift observed along the x axis (1.0 ± 0.5 nm/s) compared to the y axis (−0.3 ± 0.2 nm/s) during the measurement.

FIGURE 2.

Spatial mapping of single QDs. (a) Representative plot of the fitted spatial centroids (± asymptotic standard error) of a single QD for all image frames (394 out of 600) that had integrated peak intensities within J₁ ± 1.64σ₁, indicative of a single QD, and the mean fitted position (white) of the single QD superimposed on the approximate pixel array of our optical system (pixel size, 108 nm). (b) Mean spatial centroids of 14 single QDs identified in Fig. 1 a superimposed on the approximate pixel array of our imaging system (pixel size, 108 nm) were randomly distributed. (c) Separation distances between all 91 possible pairs of QD ranged from 13 to 121 nm. (d) Mean precisions (± SE) (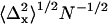, 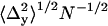) for mapping a single QD along the x (triangles) and y (squares) axes increased as a function of the number (N_k) of sequential frames that were averaged.

Spatial mapping of two simulated nearby QDs by blinking

The accuracy with which the centroid positions of two nearby QDs could be resolved by blinking was determined by overlapping all possible combinations of the previously characterized 14 single QDs from the first time sequence into a total of 91 QD pairs. In doing so, regions of interest (11 × 11 pixels) surrounding the diffraction-limited spots of each QD pair, for each time frame, were added pixel by pixel to generate 91 new time sequences. The time sequences of overlapped QD pairs were analyzed to obtain the positions of the single dots and the distances between them, without prior knowledge of the original single dot positions, as described in this section.

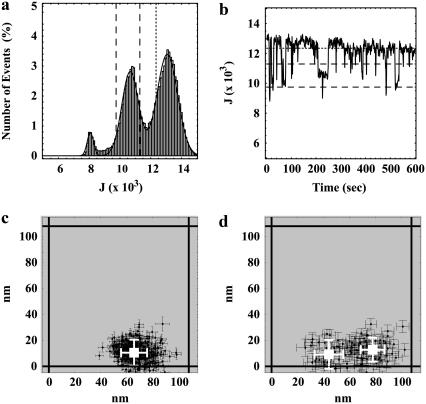
For each frame (p) of the time sequences of all dot pairs (k,ℓ), integrated peak intensities, denoted by J^kℓp, were calculated by adding the pixel values over the modified 11 × 11-pixel regions of interest, as defined above (Eq. 1). A count value of 7980 (J₀; see above) was subtracted from the integrated peak values to correct for the background intensity of one of the two added frames. A histogram of the integrated peak intensities was generated by arranging the 91 × 600 = 54,600 values of J^kℓp into 100-count bins (Fig. 3 a). Discrete intensity levels were again observed, indicative of two superimposed QDs blinking “on” and “off” as a function of time. The best fit of the histogram to Eq. 2 with q = 2 gave J₀ ± σ₀ = 8070 ± 210 for the “off” state, J₁ ± σ₁ = 10,670 ± 540 for the “single on” state, and J₂ ± σ₂ = 13,080 ± 670 for the “simultaneous on” state. Thus, the mean integrated intensities above background of the “single on” and the “simultaneous on” states were 2590 ± 580 and 5010 ± 700, respectively, or an overall mean intensity for single fluorescing QDs of 2500 ± 520, consistent with expectations. Fig. 3 b shows the time fluctuations in J^kℓp for a typical overlapped sequence.

FIGURE 3.

Spatial mapping of QD pairs. (a) A histogram of the integrated intensities per frame, J, of all 91 pairs of QDs shows three distinct intensity states. The number of points used to generate the plot was 91 × 600 = 54,600. The solid line shows the best fit to the sum of three 1D Gaussians (Eq. 2 with q = 2). (b–d) Representative example of a QD pair with a separation distance of 39 ± 18 nm. (b) The integrated peak intensities, J, of the QD pair as a function of time show intensity levels corresponding to all three states. (c) Fitted spatial centroids (± asymptotic standard error) of the QD pair when both QDs are simultaneously “on” give a single mean fitted position (white). (d) Fitted spatial centroids (± asymptotic standard error) of the QD pair when the QDs are separately “on” give two separate fitted mean QD positions (white). In a and b, the dashed line corresponds to the integrated peak intensities, J = J₁ ± 1.64σ₁, indicative of a single QD being in the “on” state, and the dotted line corresponds to the integrated peak intensity, J = J₁ + 3.89σ₁, indicating that more than a single QD is in the “on” state. The fitted distance of separation in this case was found to be 34 ± 14 nm, whereas the errors in the fitted positions of the two QDs were found to be 9 ± 17 nm and 4 ± 16 nm.

Using criteria similar to those established for single QDs, all frames from all dot pairs that had integrated peak intensities, J^kℓp, within J₁ ± 1.64σ₁, indicative of only one of the two QDs being in the “on” state, were identified. For each frame p in each sequence (k,ℓ), the pixel counts 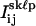were fit to Eq. 3. All variables except for i, j, and h were free parameters; i.e., the mean intensity per pixel of the “off” state, I₀, the parameter related to the maximum pixel intensity of the “on” state, I₁, the PSF width, w, and the centroid coordinates x_skℓp and y_skℓp. In addition, all frames with a value of J^kℓp > J₁ + 3.89σ₁, indicative of both QDs being in their “on” state simultaneously, were identified. Alternatively, in rare cases where <10 frames met the “simultaneous on” state criterion, the 10 frames that had the greatest values of J^kℓp were identified. The pixel counts 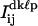from these frames were also fit to Eq. 3, with free parameters I₀, I₁, w, x_dkℓp, and y_dkℓp.

For both “single on” and “simultaneous on” sets, frames that had fitted centroid positions outside of the 95% confidence level of the mean or that (very rarely) had standard errors in the centroid position returned from the fit of zero or >50 nm were removed from the data set. The retained frames corresponded to overlapped QDs in the “single on” state for an average of 188 ± 131 out of 600 total frames (31 ± 22% of total time) with a range of 24 frames (4.0% of time) to 448 (75% of time). Retained frames for the “simultaneous on” state had an average of 293 ± 167 out of 600 frames (49 ± 28% of time) with a range of 10 (1.7% of time) to 507 (85% of time). From the retained frames, the following eight average values for each overlapped time sequence (k,ℓ) were calculated for use in subsequent analysis:

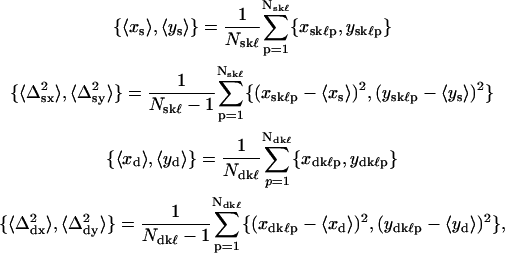(5)

where N_skℓ and N_dkℓ were the number of “single on” and “double on” retained frames for a given sequence (k,ℓ). Note that the indices (k, ℓ) have been omitted from the left sides of Eq. 5 and that in subsequent discussion it should be understood that all analyses were carried out with the values of these parameters corresponding to the appropriate time sequence.

Previously determined centroid coordinates of frames (p) corresponding to the “simultaneous on” state {x_dkℓp,y_dkℓp} for each overlapped sequence (k,ℓ) were used to assemble 2D spatial histograms, D_ij, with a bin width of s = 20 nm (Fig. 3 c). These “double on” histograms were fit to

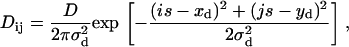(6)

with the bin width s fixed at its known value and with free parameters D, x_d, y_d, and σ_d. The starting conditions for the fit of these “double on” histograms to Eq. 6 were 〈x_d〉, 〈y_d〉, and σ_d = 15 nm (see Eq. 5). The fits to Eq. 6, which are less sensitive to outliers than are the calculated mean values from Eq. 5, generated best-fit values of the free parameters, denoted by 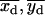, and 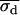for each time sequence.

In principle, the centroids from frames designated as arising from the “single on” state from the overlapped time sequence of a given dot pair should correspond to the sum of two 2D spatial Gaussians with the two centroids equal to the positions of the two dots. This concept is the central tenet of the work described here. Thus, 2D spatial histograms, denoted as S_ij, of the previously determined centroid coordinates {x_skℓp,y_skℓp}were constructed from all retained “single on” frames (p) in each of the 91 overlapped sequences, with a bin width of s = 20 nm (Fig. 3 d). The histograms were fit to

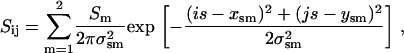(7)

with s fixed at its known value and with all other variables as free parameters except for the position indices i and j. Two fits for each dot pair were carried out. The starting conditions for these fits were determined from the “simultaneous on” centroids obtained by analysis with Eq. 6 and the “single on” standard deviations determined from Eq. 5 (see Appendix A). The results of the fit with the lower χ² value were retained for subsequent analysis and are denoted as 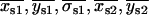, and .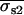

In the simplest case, for a given dot pair, the best-fit centroid position for the “simultaneous on” state {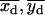} (Eq. 6) should be roughly positioned in the center of, and equidistant from, the two best-fit centroid positions of the “single on” state, {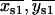} and {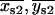} (Eq. 7). For many dot pairs, this condition was satisfied, but for some it was not. Therefore, two “special case” refinements were included in the algorithm (see Appendix B).

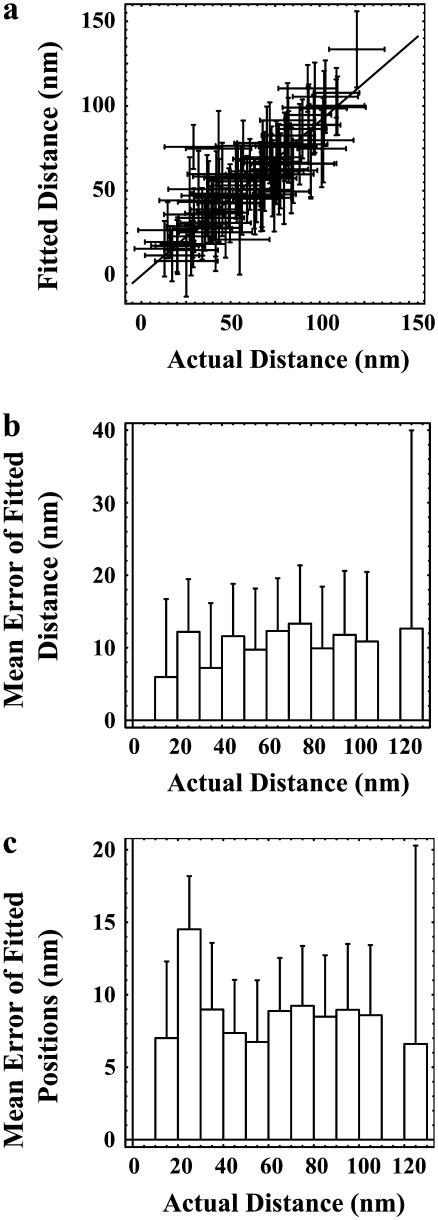
The accuracy with which the individual positions of two superimposed QDs could be resolved by blinking was evaluated by comparing the fitted distances of separation between pairs of QDs to the calculated distances determined from the centroid positions of each single QD, and by comparing the fitted centroid position of each single QD to its previously determined centroid position. A plot of the fitted distance versus the actual distance of separation was well fit by a straight line with a slope of 0.91 ± 0.02 (R² = 0.94) (Fig. 4 a). This result indicates that spatial information can be extracted with good accuracy over the entire distance range that was studied. (However, the algorithm does slightly underestimate the distances by ∼10%). The mean error of the fitted distance of separation was determined to be 11 ± 3 nm (n = 91) where the range of values is shown in Fig. 4 b. The mean error of recovered positions of superimposed QDs was determined to be 9 ± 1 nm (n = 182), where the range of values is shown in Fig. 4 c.

FIGURE 4.

Accuracy of spatial mapping of QD pairs. (a) The fitted distance of separation plotted versus the actual calculated distance of separation was well fit to a line with a slope of 0.91 ± 0.02 (R² = 0.94). (b and c) Mean accuracy of the fitted distances (91 points) and positions (182 points), respectively, as a function of the actual distance of separation with 10 nm bins (91 points). The number of data points for each distance is shown in Fig. 2 c.

Measuring end-to-end length of 122-bp dsDNA

Having determined that we can accurately find the positions of two simulated nearby QDs, we next applied our analysis to a set of images of QDs that had been preincubated with a biotinylated 122-bp-dsDNA fragment. This DNA fragment is shorter than the persistence length of DNA of ∼150 basepairs and hence should have an approximate length of 42 nm (122 bp × 3.4 Å/bp DNA). These measurements were done at low QD densities to minimize the occurrence of random two-QD aggregates.

New intensity criteria were established as before for 176 peaks (105,600 points) and the resulting intensity histogram was fit to Eq. 2 with q = 2. This resulted in mean integrated peak intensities and distribution widths (J_m ± σ_m) of 5510 ± 140, 7060 ± 760, and 9680 ± 680, respectively. All points that had >10% of frames with an integrated intensity greater than J₁ + 1.64σ₁ but <10% of frames greater than J₂ + 1.64σ₂ were identified as representing two closely spaced QDs. For the set analyzed, 25 out of 176 peaks were identified as representing two closely spaced QDs.

Using criteria similar to those established for determining the centroid positions of two nearby overlapped QDs, all frames that had integrated peak intensities, J^kℓp, within J₁ ± 1.64σ₁, indicative of only one of the two QDs being in the “on” state, were identified. For each frame p in each sequence (k,ℓ), the pixel counts 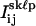were fit to Eq. 3, as before. In addition, all frames with a value of J^kℓp within J₂ ± 1.64σ₂, indicative of both QDs being in their “on” state simultaneously, were identified. The pixel counts 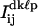from these frames were also fit to Eq. 3, as before. For the purposes of this analysis, stage drift was corrected for by first identifying the single QD in a particular image sequence that had the most number of frames in the “on” state over the largest range of frames. The centroid coordinates of these single QDs were then determined as before and the resulting values as a function of the frame numbers were curve fit to a second-order polynomial. The resulting fitting parameters were then used to correct for drift for that particular image sequence. The average fitted centroid coordinates of each of two nearby spaced QDs were then determined from these drift-corrected values as before using Eqs. 5–7.

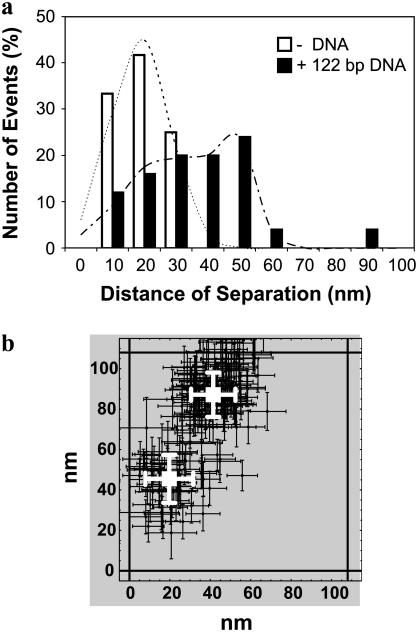
The final results from the analysis of peaks identified as representing two nearby overlapped QDs with or without 122-bp dsDNA are shown in Fig. 5 a. These results are complicated by the presence of QD aggregates even in the absence of cross-linking DNA. However, in all instances observed, at the low QD densities used, the distances of separation without DNA ranged from only a few nanometers to <30 nm. These distances are all consistent with one of two types of QD aggregates: one in which two separate QD cores are contained within the same water stabilizing polymeric coating and one in which two separately water stabilized QDs have aggregated. We determined the mean and standard deviation of the distance of separation in the absence of DNA to be 19 ± 13 nm by curve-fitting the histogram of observed distances to a single 1D spatial Gaussian (Eq. 2 with q = 1). In the presence of 122-bp dsDNA, we observed additional aggregates with a greater distance of separation. In this case, we determined the mean and standard deviation of the distances of separation of the aggregates to be 27 ± 19 nm and 48 ± 9 nm by curve-fitting the histogram of observed distances of separation to the sum of two spatial 1D Gaussians (Eq. 2 with q = 2). A typical example of the larger aggregates in the presence of DNA is shown in Fig. 5 b.

FIGURE 5.

End-to-end distance of 122-bp dsDNA. (a) A histogram of the frequency of events of the distance of separation between two nearby QDs with 10-nm bins. The observed distances of separation in the absence of DNA (open bars; N = 12) are <30 nm, whereas several of the observed distances of separation in the presence of DNA (solid bars; N = 24) are >30 nm. We determined the mean and standard deviation of the distance of separation in the absence of DNA to be 19 ± 13 nm (R² = 0.97) by curve-fitting the observed distance distribution to a single 1D spatial Gaussian (dashed lines). We determined the means and standard deviations of the aggregates in the presence of DNA to be 27 ± 19 nm and 48 ± 9 nm (R² = 0.96) by curve-fitting the observed distance distribution to the sum of two 1D spatial Gaussians (dot-dashed line). (b) A typical example of a QD aggregate in the presence of 122-bp dsDNA. These two nearby QDs were found to be separated by 47 ± 16 nm.

DISCUSSION

We have introduced a monochromatic single-molecule fluorescence imaging method that can accurately determine absolute positions of and distances between two QDs to within tens of nanometers. This method takes advantage of QD blinking to separately image each single QD and the overlapping QD pair to determine subpixel positions of each QD. We have shown that with the imaging conditions used, we can map a single stationary QD with a precision of ∼10 nm over a sequence of 600 frames acquired at 30 Hz. We have further shown that we can determine the positions of each separate QD in a QD pair and measure the distance between pairs of QDs to a mean accuracy of ∼10 nm over a range of distances stretching from 15 to 120 nm. Because the minimum distance of separation that could physically occur is the diameter of single QDs, which has been reported to be ∼15 nm (34), this approach could in theory be used to measure distances that exceed the minimum separation distances by just a few nanometers. The validity of this method for measuring actual distances on nanometer-size scales was confirmed by measuring the end-to-end length of a 122-bp-dsDNA fragment to be 48 ± 9 nm (mean ± SD). This distance is slightly greater than the theoretical persistence length of a DNA fragment of this size. This slight discrepancy is likely a result of the added size that QDs themselves add to the length measurement. In addition, these measurements are currently further restricted by the presence of spontaneous QD aggregates. These aggregates effectively limit length measurements by this method to those >∼30 nm.

In the ideal case for this method, an acquired time sequence of a blinking QD pair should contain multiple image frames of the PSF of each single QD and the centroids of each QD should be spatially separated. In practice, however, we observed a number of overlapped time sequences in which a majority of the frames that were indicative of a single QD “on” state arose from only one of the two QDs. In addition, there was frequently overlap between the two fitted centroids from “single on” frames which sometimes resulted in the two positions for the single QDs not adequately framing the “double on” centroid. In both cases, however, we found that the positions of each single QD in a QD pair could be accurately determined by using the fitted mean spatial centroid of the “double on” frames, both as a starting point for fitting the “single on” frames and as a reference point to which the fitted spatial centroids of single QDs could be compared to and adjusted if necessary (see Appendix B). Even in cases where we only obtained fitted spatial centroids for one of the two QDs in a QD pair, we could accurately determine the position of each QD by also using the fitted mean spatial centroid of the overlapping QDs. Hence, to use this analysis method to accurately map each single QD in a QD pair, the image time sequence should at a minimum contain either frames where each QD is on separately or frames where only a single QD is on, as well as frames where both QDs are on simultaneously.

The approach of using the integrated peak intensities to identify frames that represent single QDs or overlapping QDs and then fitting the results separately should also work for larger QD aggregates. For example, in the case of a QD aggregate consisting of three overlapping QDs, frames representing one, two, and three QDs in their “on” states would have to be identified and fit separately. The mean position for the case where all three QDs are simultaneously in their “on” states would then be determined and used as a starting point to locate the three possible positions in the case where two QDs are simultaneously in their “on” states. These positions would then be used to locate the positions of the three single QDs that made up the aggregate.

If the problem with the presence of spontaneous QD aggregates can be solved, this method of using QD blinking to determine distances between pairs of QDs has several advantages over alternative techniques. First of all, use of QDs is not limited by photobleaching, hence enabling long-time studies of distance measurements, as compared to techniques that rely on conventional fluorophores. QDs are also much brighter than conventional fluorophores, which allows for higher sampling rates and at a higher spatial resolution than would be the case with conventional fluorophores. Worth noting is that the use of blinking to determine submicroscopic distances is not necessarily limited to QDs, as organic fluorophores also exhibit intermittency in their fluorescence emission. Particularly interesting is the possible use of molecular optical switches, which can be controllably and reversibly converted between fluorescent and nonfluorescent states (34).

Additionally, the described method has the potential for characterizing submicroscopic clusters such as putative membrane lipid microdomains or rafts in live cells at a resolution that approaches that of transmission electron microscopy (3). In studies of submicroscopic clusters on living cell membranes, however, the lifetime of the clusters must be at least twice that of the sampling acquisition rate and ideally much longer. This method could also potentially be used to study biopolymer reorganization by monitoring the time course of deviations in the absolute distance between two adjacent QDs that had been attached to the biopolymer of interest. This method would likely require the immobilization of one QD and, hence, one end of the biopolymer, with the other end of the biopolymer remaining mobile. The caveat of studying biopolymer reorganization by this method, however, is that for a conformational change to be quantifiable, the distance between the two QDs has to deviate by >10 nm. In either case, the use of QDs would potentially allow one to study the time course of aggregation or reorganization over length scales ranging from micrometers down to just 10 nm, and over long periods of time.

Finally, we point out that another group has recently and independently developed a QD fluctuating analysis method for spatially separating adjacent QDs (35). The two approaches differ primarily by the method by which the subpixel positions of adjacent QDs are resolved. In the approach by Lidke et al. (35), independent component analysis was used to decompose an entire image sequence of two closely spaced, immobile, intensity fluctuating QDs into two separate single images of each fluctuating QD. The subpixel positions of the resulting images of single QDs were subsequently obtained by use of standard single-particle localization techniques. It is important to note that in the approach by Lidke et al., only QD intensity fluctuations, rather than discrete on-off blinking, are required. The disadvantage, however is that the independent component analysis approach is not amendable for mapping changes in QD positions over time. In contrast, in our approach, the discrete on-off blinking is required. We fit all image frames in an image sequence that meets a certain established fluorescence intensity criteria to Eq. 3. Although in this work we have applied this analysis technique to measure distances of separation between stationary QDs, this is not a requirement. In principle, our approach can be extended to using QD blinking to obtain spatial dynamics by monitoring changes in subpixel positions over time rather than averaging positions as was done here. Using this approach, it may be possible to obtain spatial dynamics about a variety of biologically relevant processes, including measuring the folding or unfolding of large biopolymers, as well as for obtaining size measurements of transient cell signaling clusters in the plasma membrane of live cells. In addition, in contrast to the earlier method, we observe discrete QD peak intensities that can be used to predict the number of QDs present in a QD aggregate. It is possible that this difference relates to the particular QDs that were used. In our case, we have used QDs emitting at 605 nm (QD605), whereas in the previous example, QDs emitting at 655 nm (QD655) were used (35). It has been our experience that the QD605s are far more likely to be in their “on” intensity state than the QD655s (data not shown). Although this may be detrimental to the eventual rate at which one can measure distances of separation by QD blinking, the greater stability of QD605s are more likely to lead to establishment of discrete intensity states.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX A: STARTING CONDITIONS FOR FITTING TO EQ. 7

The starting conditions for these fits were determined from the “simultaneous on” centroids obtained by analysis with Eq. 6 and the “single on” standard deviations determined from Eq. 5. In the first fit of S_ij to Eq. 7, the starting conditions were

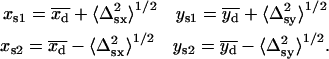(A1)

In the second fit, the starting conditions were

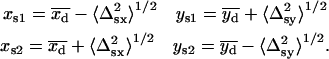(A2)

These conditions correspond to dots placed approximately at {+45°,−135°} or {−45°,+135°} relative to the “double on” centroid. In future work, investigating a wider range of starting conditions for fits to Eq. 7 might improve the overall results of the data analysis procedure.

APPENDIX B: SPECIAL CASE REFINEMENTS OF FITTED POSITIONS

First, the best-fit centroid positions for each dot pair were examined. If both 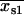and 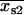were greater than 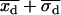or less than 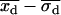, or if both 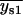and 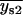were greater than 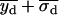or less than 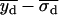, the centroids for the two “single on” states did not adequately frame the centroid of the “double on” state. In this case, only one of the two fitted “single on” centroid positions was retained and the second dot was assumed to be positioned at an equal, but opposite, distance from the retained single dot centroid relative to the centroid of the “double on” state. The decision about which of the two single QD centroid positions to retain was based on the best-fit amplitudes of the terms in Eq. 7, as well as the distances between the single QD positions and the position of the overlapping QDs. These distances were calculated as

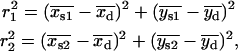(B1)

and compared to an arbitrary cut-off value of r = 10 nm. If r₁ > r and r₂ < r, the centroid position {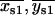} was retained; similarly, if r₂ > r and r₁ < r, the centroid position {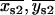} was retained. If both r₁ > r and r₂ > r, the centroid for the peak with the larger amplitude was retained. No correction was made in cases where both r₁ and r₂ were <r.

A second refinement was made for cases where 1), neither of the arithmetic mean positions 〈x_s〉 and 〈y_s〉 of the “single on” states were within one standard deviation of the arithmetic mean position for the “simultaneous on” state {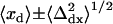,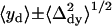}; 2), one, but not the other, of the two fitted mean positions {{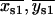}, {}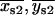} were within one standard deviation of the fitted “simultaneous on” state position {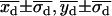}; and 3), the arithmetic mean standard deviations, 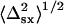and 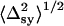were >20 nm. In these cases, the fitted mean position of single QDs that fell outside of one standard deviation of the fitted mean centroid position of the overlapping QDs was retained and used to calculate the mean centroid position of the other single QD arithmetically as before.

These two refinements identified and corrected cases where one, but not the other, of the fitted mean positions of single QDs was with some certainty coincident with the fitted mean position of the overlapping QDs. This complication typically occurred when there were very few fitted points for one out of the two overlapping QDs or when one of the two QDs was primarily in either the “off” or “on” state. In addition, in cases where both single QDs were dimmer than the mean intensity of all single QDs, there may have been a significant contribution of simultaneous “on” states to the frames that were identified as those representing only a single QD in the “on” state. This artifactual inclusion of “simultaneous on” frames in the “single on” set could also have occurred for frames where both QDs were in their “on” states for only a fraction of the image acquisition time. Such misassignments can lead to an additional peak in the 3D histogram that is generated from all fitted points (Eq. 2 with q = 2 (Fig. 3 a)).