Abstract
The transition between the B and Z conformations of double-helical deoxyribonucleic acid (DNA) belongs to the most complex and elusive conformational changes occurring in biomolecules. Since the accidental discovery of the left-handed Z-DNA form in the late 1970s, research on this DNA morphology has been engaged in resolving questions relative to its stability, occurrence, and function in biological processes. While the occurrence of Z-DNA in vivo is now widely recognized and the major factors influencing its thermodynamical stability are largely understood, the intricate conformational changes that take place during the B-to-Z transition are still unknown at the atomic level. In this article, we report simulations of this transition for the 3′-(CGCGCG)-5′ hexamer duplex using targeted molecular dynamics with the GROMOS96 force field in explicit water under different ionic-strength conditions. The results suggest that for this oligomer length and sequence, the transition mechanism involves: 1), a stretched intermediate conformation, which provides a simple solution to the important sterical constraints involved in this transition; 2), the transient disruption of Watson-Crick hydrogen-bond pairing, partly compensated energetically by an increase in the number of solute-solvent hydrogen bonds; and 3), an asynchronous flipping of the bases compatible with a zipperlike progression mechanism.
INTRODUCTION
The transition between the B and Z conformations of double-helical deoxyribonucleic acid (DNA) belongs to the most complex and elusive conformational changes occurring in biomolecules. Since the accidental discovery of the left-handed Z-DNA form in the late 1970s (1), numerous experimental studies have investigated the relative stability of this DNA form, the influence of environmental factors on this stability, and the possible role of Z-DNA conformations in biological processes (2). As a result of this research, the occurrence of Z-DNA in vivo is now widely recognized, and the major thermodynamic factors influencing its stability are well understood. Yet, the conformational pathway(s) followed during the interconversion between B- and Z-DNA remain experimentally unknown at the atomic level.
Under physiological (low-salt) conditions, DNA preferentially adopts B or A conformations (along with ∼20 sequence-dependent variations of these two forms (3–5)), characterized by Watson-Crick basepairing, anti orientation of the nucleotide bases, and a right-handed helicity (3,6). The A-DNA conformation is the one favored under low hydration or moderately high ionic-strength conditions, while the B-DNA conformation is preferred otherwise.
However, already in 1972, Pohl and Jovin (7) were able to observe an almost complete inversion of the ultraviolet circular dichroism (CD) spectrum of poly(GC) double-helical oligonucleotides upon addition of large amounts of salt (e.g., 4 m NaCl). The explanation for this effect was provided by the subsequent determination of the corresponding three-dimensional structure through x-ray diffraction (1,8), resulting in a left-handed helicity with an alternating anti (pyrimidine) and syn (purine) orientation of the nucleotide bases together with Watson-Crick basepairing (1). Due to the particular zigzag pattern adopted by the sugar-phosphate backbone, this new DNA form was termed Z-DNA. Apart from the inverted helicity, the Z-DNA structure is more compact along the double-helical axis (compared to the B form), with an average of one additional basepair per turn (3). As a consequence, the successive negatively-charged phosphate groups along the backbone reside on average closer to each other. At low ionic strengths, the resulting increase in electrostatic repulsion significantly destabilizes the Z form relative to the B form, even if the stacking interactions are expected to be more favorable in the Z-DNA conformation (9). Upon increasing the ionic strength, however, counterions provide more efficient electrostatic screening, and the relative stabilities of the two forms may be inverted (10). Indeed, it is now widely accepted that the dominant contribution to the free energy difference between the two forms is due to electrostatic interactions (11–15). The structural difference between the B- and Z-DNA conformations also leads to a different stacking pattern of the nucleotide bases. While the B-DNA conformation permits a continuous π-stacking of successive bases, the stacking in Z-DNA involves discontinuous series of four-base clusters along each of the two strands (16).
Besides the ionic strength, the relative stabilities of the B- and Z-DNA forms are influenced by the nature of the (local) nucleotide sequence and the temperature. The Z-DNA conformation appears to be favored by sequences of repeating AT or CG doublets along one strand or in supercoiled DNA (17). Furthermore, due to its lower conformational entropy (compared to B-DNA), the relative stability of the Z-DNA conformation generally decreases upon raising the temperature (18). This property, together with the intrinsic differences in π-stacking patterns between the two DNA forms (9), has recently been exploited in the design of a nanothermometer (19). The design of a nanomechanical motor device based on the B-to-Z transition has also been proposed (20,21) (under the basic assumption that the DNA unwinds during the transition), as well as that of a temperature-dependent reversible biomolecular switch (22).
Since the discovery of Z-DNA, much attention has been focused on the detection of Z-DNA in vivo and on the possible biological function of this particular DNA morphology (2,23–26). Because Z-DNA is intrinsically unstable under physiological conditions, this research is inherently difficult. However, it is now recognized that Z-DNA is not just a chemical oddity, but does occur in vivo (27). It is, for instance, formed transiently behind a moving RNA polymerase, stabilized by the negative supercoiling in the wake of the enzyme (28–31). In addition, there is growing evidence that Z-DNA segments or junctions may play a role in gene expression (16), recombination (32–34) and regulation (35–37), or in destructive effects of terminal differentiation (38), and that Z-DNA stability may be enhanced by etiological factors related with Alzheimer's disease (39,40).
Despite all these advances, one of the main unanswered questions remains how the very large conformational change associated with the B-to-Z transition actually takes place at the atomic level (41). Apart from the inversion of the helicity, the most striking conformational change occurring during the transition is the 180° rotation of the nucleotide bases with respect to their initial positions. The rotational mechanism involved during the transition appears to differ for the purine and pyrimidine bases. In the B-DNA conformation, the nucleotide base χ-angle of both nucleotide types, defined as the torsional angle O4′-C1′-N1-C2 (pyrimidine) or O4′-C1′-N9-C4 (purine), is in anti orientation, i.e., in the range 180 ± 90°. This orientation is required for the formation of canonical Watson-Crick hydrogen bonds, and bases with a syn orientation (0 ± 90°) in B-DNA serve as an indicator for a distortion of the double helix due to basepair opening or the presence of mismatched basepairs (3,42). However, in Z-DNA, purine bases generally adopt a syn conformation, i.e., they must rotate with respect to their associated deoxyribose unit along the B-to-Z transition pathway. In contrast, pyrimidine bases remain in anti orientation within Z-DNA due to steric constraints (3,42,43). Therefore, to keep the Watson-Crick basepairing intact, the whole pyrimidine nucleotide (including the sugar) needs to rotate, which places the deoxyribose 5′-carbon atom before the 3′-oxygen in terms of projection along the helix axis (with the 3′-end of the strand on the left and the 5′-end on the right), introducing a local half-twist in the backbone (44). This feature is commonly referred to as the chain-sense paradox, because the chain sense (3′ → 5′ or 5′ → 3′) becomes locally inverted (44).
Four main hypotheses have been formulated concerning the mechanism of the B-to-Z transition.
The first hypothesis (known as the Wang model) suggests that the transition involves basepair opening before the rotation of the nucleotide bases and of the backbone dihedral angles (1,7,10,45,46).
The second hypothesis (known as the Harvey model) postulates that the transition consists of a series of nondisruptive transfiguration steps (correlated rotations of the base and backbone dihedral angles) permitting a transition without disruption of the Watson-Crick hydrogen bonds (44,47–49).
A third hypothesis assumes a transition through an intermediate (A-type) conformation without disruption of Watson-Crick hydrogen bonds and without sterical interference (50,51).
The fourth hypothesis was formulated recently (52), based on the first crystallographic structure of a B-Z DNA junction (cocrystallized with an enzyme). In this structure, two basepairs are flipped out of the duplex between the two DNA forms (analogous to B-DNA structures cocrystallized with DNA editing enzymes such as methyltransferases (53)). Based on this observation, the authors suggested that the B-to-Z transition may be accomplished by sequentially extruding basepairs from the duplex, permitting their free rotation by 180°, before reentrance at their original positions (in contrast to the Wang model, where base rotation is assumed to occur within the double-helix core).
Since the B-to-Z transition is known to be highly cooperative, it is not unreasonable to assume the involvement of domain formation during the interconversion (54), especially when long sequences are considered (e.g., negative supercoiling effects in plasmids). The transition pathway(s) may therefore also depend on the length and nature of the DNA sequence, as well as on the detailed experimental conditions. This view is in principle contained in the zipper model (55), where after an initial high-barrier nucleation step resulting in a short Z-DNA segment enclosed between two B-Z junctions, the junctions migrate in opposing directions as the intervening basepairs flip and the backbone winds in the left-handed direction to form Z-DNA. The zipper model is in principle compatible with any of the four above-mentioned hypotheses for the actual base-flipping mechanism.
To determine or rule out possible mechanisms, it is necessary to acquire time-resolved information at the atomic level, either by experiment or through computer simulations, which is in both cases highly nontrivial. On the one hand, experimental techniques typically used to probe the structure of (bio-)molecular systems at atomic resolution, such as x-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy, offer limited information in the context of dynamical structural changes. On the other hand, computer simulation methods, such as explicit-solvent molecular dynamics (MD) simulations based on empirical force fields, are currently limited to timescales of the order of 10–100 ns for oligonucleotides (56). This is clearly insufficient to investigate the B-to-Z transition by straightforward MD, since this transition occurs on a timescale of seconds to minutes (either induced by the addition of salt (7,10) or of a Z-DNA stabilizing protein (57)), with energy barriers up to hundreds of kJ × mol−1 (7,46,57,58). Furthermore, computational methods commonly used to improve the sampling along a transition pathway (e.g., umbrella sampling (59,60)) are not applicable here, because the reaction coordinate for the transition is unknown. Traditional free energy perturbation methods (61–64) are also out of question due to the large structural dissimilarity between the two conformations, so that only the effect of base modifications on the relative stability of Z-DNA (compared to B-DNA) can be investigated (65,66). Given these difficulties together with the inherent structural complexity of the transition, theoretical studies have so far mostly relied on simplified models, which commonly use a coarse-grained representation of the oligomer and model the solvent via a mean-field approach. Examples of such models are the Soumpasis potential-of-mean-force approach (67) and others (12,14,68–74), which are able to reproduce reasonably well the experimental free energy difference and its dependency on the charge, size, and concentration of the counterions (73). However, simplified representations of this kind cannot give detailed insight on the transition pathway(s) at the atomic level.
Recently, simulations at atomistic resolution were applied using the approach of the stochastic difference equation with length of Elber et al. (75) to investigate the B-to-Z transition of the 3′-(CGCGCG)-5′ duplex. The results suggested yet another model for the B-to-Z transition pathway (76,77). In these simulations, the transition was observed to occur through an unwinding and overstretching of the oligomer, where the stretched conformation (increased terminal separation) could be viewed as an explicit intermediate structure for the transition (stretched-intermediate model). The main strength of the proposed model is that it provides a simple solution for the need to overcome very large sterical constraints to achieve the rotation of the nucleotide bases (purines) or sugar units (pyrimidines) during the transition. Conceptually, this suggested mechanism is related to the previously postulated mode of longitudinal breathing (44), which assumes that local backbone (longitudinal) stretching facilitates the flipping mechanism. The authors also proposed an experimental verification of the suggested mechanism by means of a fluorescence resonance energy transfer experiment (78) through the addition of two dyes at the oligomer termini. A decrease in the fluorescence signal during the transition would indicate an increase in the average dye separation and thus, provide evidence for the proposed stretching mechanism. However, three questions remain open with respect to the applied computational methodology and simulation setup. First, despite the conceptual elegance of variational methods based on minimizing the classical action integral, it is not clear whether the observed transition pathway has any physical significance at room temperature (since it corresponds in principle to a zero-temperature pathway). Second, the approach does not treat solvent molecules explicitly, but through a generalized-Born implicit (mean-field) solvation model (79). While the performance of the generalized Born approach has been excellent for some systems, in particular for studies on peptide folding (80) (with some notable exceptions (81,82)), its validity remains questionable in the context of DNA simulations, due to the key role of specific solute-solvent interactions (83–90). Third, the above simulations were undertaken in the absence of explicit counterions, and did not permit the investigation of ionic-strength effects on the transition.
Any computational approach to investigate the B-to-Z transition pathway currently requires the application of special methods for bridging of the timescale gap between simulation and experiment. However, this should be done by imposing as little constraint as possible on the dynamics of the system. A simple approach to this purpose is targeted molecular dynamics (TMD) (91–94). This algorithm allows for the description of a progressive conformational change between a starting and a target structure, by linearly decreasing the (mass-weighted) root-mean-square deviation (RMSD) in atomic position between the current structure and the target one (RMSD constraint) along the simulation. By performing the transformation reasonably slowly, the system should ideally remain at equilibrium with respect to all degrees of freedom orthogonal to the RMSD constraint. Thus, the sampled conformational pathway should provide a reasonable first guess to the true transition pathway, under the assumption that this true pathway involves a monotonic decrease of the RMSD to the target structure. In addition, the free energy difference between the initial and final states may be estimated by integrating the constraint force along the forced transition pathway (59), in a way analogous to the slow-growth protocol (59,61,95). Finally, this approach is easily combined with an explicit representation of the solvent molecules and counterions, allowing for a realistic modeling of solvation and ionic-strength effects.
The main goal of the present work is to:
Find a plausible transition pathway for the B-to-Z transition using TMD with explicit solvation and counterion representation.
Reassess the results of the recent theoretical studies (76,77), suggesting a stretched-intermediate model for this transition.
Investigate the impact of ionic strength on the stability of the B-and Z-DNA forms and on the transition pathway.
To this purpose, MD and TMD simulations are carried out for the double-helical hexanucleotide 3′-(CGCGCG)-5′ in water. The self-complementary (CGCGCG)2 duplex (melting temperature: Tm ≈ 320 K (96)) has been investigated previously in a number of experimental and theoretical studies (1,97–102), and is known to show a high propensity to form Z-DNA due to the presence of CG repeats (103). Six independent MD simulations at room temperature involve the hexamer duplex starting from either the B or the Z conformation, and either without counterions, with a neutralizing amount of sodium counterions, or with an excess amount (4 m) of sodium and chloride counterions. In addition, three independent TMD simulations of the B-to-Z transition (starting from the B conformation) are performed under the same temperature and ionic-strength conditions.
THEORY
Computational details
All simulations were performed using a modified version of the GROMOS96 program (104,105) together with the GROMOS96 45A4 force field for DNA (106) and the SPC water model (107). For the six MD simulations, a modeled B-DNA or Z-DNA hexamer duplex with sequence 3′-(CGCGCG)-5′ and net charge −10e was solvated in a cubic box of dimension 5 · 5 · 5 nm3 with explicit water molecules at a density of 1 g × cm−3, resulting in a total of 4111 (B-DNA) or 4102 (Z-DNA) solvent molecules. For each conformer, one system was simulated in the absence of counterions, one system with a neutralizing amount of 10 sodium ions and one system with an amount of sodium and chloride counterions corresponding to a 4-molal solution (for an overall neutral system). The initial ion locations were selected by successively replacing water molecules with sodium counterions at the positions of lowest electrostatic potential or with chloride ions at the positions of highest electrostatic potential (sodium and chloride ions were inserted in alternation), while obeying an ion-ion exclusion distance of 0.35 nm. Since the modeled B- and Z-DNA structures do not exactly correspond to stable energy minima in the GROMOS96 force field (106), the starting and target structures for the three TMD simulations were chosen as the equilibrated structures of the corresponding MD simulations with a neutralizing amount of counterions after 1 ns. The simulation conditions and codes employed in this article are summarized in Table 1 for the nine simulations.
TABLE 1.
Summary of the simulated systems and simulation conditions
| Simulation | Method | Water | Na+ | Cl− | I [m] |
|---|---|---|---|---|---|
| B0 | MD | 4111 | — | — | 0.00 |
| BN | MD | 4101 | 10 | — | 0.07 |
| BE | MD | 3593 | 264 | 254 | 4.00 |
| Z0 | MD | 4102 | — | — | 0.00 |
| ZN | MD | 4092 | 10 | — | 0.07 |
| ZE | MD | 3584 | 264 | 254 | 0.07 |
| BZ0 | TMD | 4111 | — | — | 0.00 |
| BZN | TMD | 4101 | 10 | — | 0.07 |
| BZE | TMD | 3593 | 264 | 254 | 4.00 |
The codes used in this article to refer to specific simulations are indicated (the letter B or Z denotes the starting conformation; BZ denotes a B-to-Z transition simulation; 0 denotes the absence of counterions; N denotes a neutralizing amount of counterions; and E denotes an excess of counterions). The ionic strength I of the solution is also reported (calculated for the counterions only, in molal units).
Electrostatic interactions were evaluated using a twin-range cutoff approach (with short- and long-range cutoff distances of 0.8 and 1.4 nm, respectively), a pair-list update frequency of five timesteps, and a Barker-Watts reaction-field correction (108,109) for the omitted interactions beyond the long-range cutoff distance (the relative permittivity of the medium outside the cutoff sphere was set to 66.6 (110)). Although lattice-sum methods (e.g., Ewald, P3M, or PME) are often quoted as the proper remedy to the numerous problems associated with straight-cutoff truncation of electrostatic interactions (111–118), the reaction-field scheme also appears to provide excellent (and often qualitatively similar) results (106,115,119). Furthermore, the application of lattice-sum methods in explicit-solvent simulations of solutions may lead (at least in some cases) to periodicity-induced artifacts (120–126).
All simulations were carried out at constant volume and at a constant temperature of 280.15 K (40 K below the melting temperature of the hexamer (96) to avoid any possible denaturation), maintained by weak-coupling to a heat bath (127) using a coupling time of 0.1 ps. For equilibration, the MD simulations were slowly heated up over a period of 0.1 ns while applying a position-restraining potential with a force constant of 2.5 · 104 kJ × mol−1 · nm−2 on all solute atoms, so as to relax the surrounding solvent molecules. Bond lengths were constrained by application of the SHAKE procedure (128) using a relative geometric tolerance of 10−4. A timestep of 2 or 1 fs was used to integrate the equations of motion for the MD and TMD simulations, respectively. The system center-of-mass motion was removed every 5000 time steps to prevent the buildup of center of mass velocity. All MD and TMD simulations were carried out for 2 ns.
For the calculation of the RMSD constraint forces (implemented analogously to the SHAKE algorithm (128) via a Lagrange multiplier approach), the same relative geometric tolerance of 10−4 was used. Since the bond-length (SHAKE) and RMSD (TMD) constraints may interfere with each other during a given integration timestep, the two protocols were iterated sequentially until convergence was reached for both. The atoms considered for the RMSD constraint were the NT = 84 heavy atoms of the 12 nucleotide bases, which should capture the largest conformational change during the B-to-Z transition. At every integration timestep, the target structure was superimposed onto the current structure by means of a (mass-weighted) translational and rotational least-squares fit (129) involving the NT atoms, followed by a calculation of the (mass-weighted) RMSD value (R), as
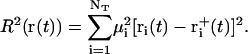 |
(1) |
Here, ri is the Cartesian coordinate vector of atom i in the current structure, 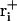 the corresponding coordinate vector in the target structure after fitting onto r, and
the corresponding coordinate vector in the target structure after fitting onto r, and 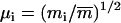 , with mi being the mass of atom i and
, with mi being the mass of atom i and 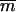 the average atomic mass of the NT atoms. The use of mass-weighted coordinates for the least-squares fitting and RMSD calculation results in a constraint force exempt of any overall translational and rotational component (94). The constraint to be satisfied by the coordinates at any timestep is written as
the average atomic mass of the NT atoms. The use of mass-weighted coordinates for the least-squares fitting and RMSD calculation results in a constraint force exempt of any overall translational and rotational component (94). The constraint to be satisfied by the coordinates at any timestep is written as
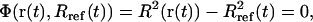 |
(2) |
where Rref is the reference value for the (mass-weighted) RMSD enforced at this timestep. This constraint, amplified by a Lagrange multiplier λ, is added to the physical (unconstrained) potential energy Vuc, i.e.,
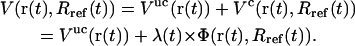 |
(3) |
The corresponding constraint force 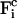 on each atom reads
on each atom reads
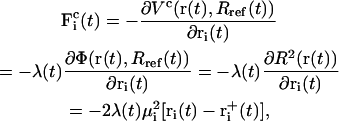 |
(4) |
where λ denotes the common Lagrange multiplier determining the strength of the constraint force at the given timestep. In the case of the leap-frog integrator the coordinates are propagated in time as
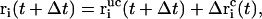 |
(5) |
with
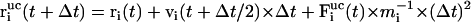 |
(6) |
and
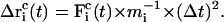 |
(7) |
Here, Δt is the integration timestep, 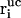 , vi, and
, vi, and 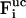 denote the free-flight coordinate, velocity, and unconstrained force associated with atom i and
denote the free-flight coordinate, velocity, and unconstrained force associated with atom i and 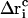 corresponds to the coordinate shift required to enforce the constraint at time t + Δt. An expression for the Lagrange multiplier λ(t) is obtained by inserting Eqs, 1, 4, 5, and 7 into Eq. 2 for r(t + Δt). This leads to the quadratic equation
corresponds to the coordinate shift required to enforce the constraint at time t + Δt. An expression for the Lagrange multiplier λ(t) is obtained by inserting Eqs, 1, 4, 5, and 7 into Eq. 2 for r(t + Δt). This leads to the quadratic equation
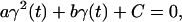 |
(8) |
with
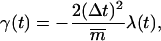 |
(9) |
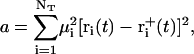 |
(10) |
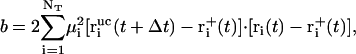 |
(11) |
and
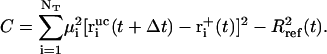 |
(12) |
To obtain a quasi-continuous trajectory, the solution of Eq. 8 with the lowest absolute value has to be taken throughout the simulation (92). The corresponding coordinate shift 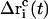 to be applied to each atom i may then be calculated at each timestep as
to be applied to each atom i may then be calculated at each timestep as
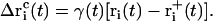 |
(13) |
Over the course of the TMD simulation, the RMSD distance Rref(t) to be satisfied is linearly reduced from an initial RMSD difference RBZ = 0.55 nm between the B- and Z-form down to zero, via a constant decrease ΔRref = 2.75 · 10−7 nm at each timestep Δt = 1 fs, which corresponds to a total simulation time of 2 ns.
The (Helmholtz) free-energy profile A(R) along the transition pathway defined by the RMSD reaction coordinate may be determined by application of the thermodynamic integration formula (130)
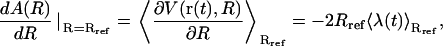 |
(14) |
where 〈…〉R denotes ensemble averaging at a specified value R of the RMSD and the second equality follows from Eqs. 2 and 3. Using a slow-growth approximation (59), this profile may be evaluated numerically as (94)
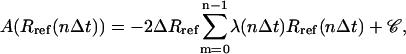 |
(15) |
where the constant 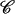 is chosen here to enforce A(RBZ) = 0, i.e., the zero of the profile is set to the B-DNA conformation.
is chosen here to enforce A(RBZ) = 0, i.e., the zero of the profile is set to the B-DNA conformation.
Due to the use of a mass-weighted RMSD as reaction coordinate, the configurational probability distribution is not affected by metric-tensor effects (94,131,132), and Eq. 15 becomes exact in the limit of an infinitesimally slow variation of Rref. However, due to the use of a polar coordinate system, the free energy profile A(R) may appear biased toward high R-values because the Cartesian coordinate volume associated with a given value of R decreases with R (94,133). In particular, A(R) diverges to infinity when R tends toward zero (i.e., by the end of the simulation). This effect can be viewed as arising from an entropic contribution related to the restriction of the accessible Cartesian volume upon decreasing R.
The analysis of the simulations was performed in terms of the following basic properties:
The time-series of the all-atom (non-mass-weighted) RMSD value with respect to the starting structure (as well as to the target structure for the TMD simulations).
The root-mean-square fluctuations (RMSFs) of atomic positions, excluding a total equilibration time of 0.2 ns.
The time evolution of the interstrand and oligomer to water hydrogen bonds, defining the presence of a hydrogen bond D-H···A by a H···A distance smaller than 0.25 nm and a D-H···A angle larger than 135°.
In addition, the rotation of the nucleotide bases during the TMD simulations was monitored through the time-series of the χ-dihedral angle around the sugar-base bond, defined by the atoms O4-C1′-N1-C2 (cytidine) and O4′-C1′-N9-C4 (guanosine). Because the cytidine bases do not rotate around the χ-dihedral angle during the transition (see Introduction), it is useful to monitor an alternate internal coordinate that is also sensitive to the rotation of the whole nucleotide. This was done by following the time-series of the angle η between the plane of the nucleotide base in the current configuration and the corresponding plane in the starting structure (after an all-atom non-mass-weighted translational and rotational least-squares fit of the two structures).
The ultraviolet (UV) absorbance (and in particular CD spectra in the UV range) are known to serve as a sensitive indicator of DNA conformation (134). Nucleic acids exhibit a strong π → π* transition in the far UV, due to the aromaticity of the bases, as well as an n → π* transition at longer wavelengths. The CD spectra of B- and Z-DNA show distinct differences, the hallmark for Z-DNA being an intense negative band at ∼195 nm (7). It is possible to estimate the rotational-strength R10 of a 0 → 1 transition based on a specific system configuration from ab initio calculations, as the imaginary part of the scalar product of the corresponding electronic μ and magnetic m transition dipole moments R10 = Im{μ01 · m10}. However, this calculation requires knowledge of the wavefunction for the ground- and excited states, which is computationally intractable for the present system (292 atoms). An alternative approach is to describe the ground and excited states at various wavelengths by monopole sets, and to construct a Hamiltonian matrix from which eigenvalues, eigenfunctions, and ultimately μ01 and m10 can be estimated (135,136). Such monopole sets for the two types of nucleotide bases considered here were derived by fitting to the direction and magnitudes of experimentally obtained transition dipole moments as described earlier (134). This approach was applied to calculate far-UV CD spectra based on selected configurations sampled during the present TMD simulations. The molar CD signal at a given wavelength λ, ΔE(λ), represents the difference in absorption between left- and right-circularly polarized light, reported in units of M−1×cm−1. It may be calculated from the rotational-strength as 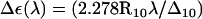 , where Δ10 is the half-bandwidth for the given 0 → 1 transition and R10 is expressed in the same units as ΔE(λ). In any monopole approximation, charge transfer effects, which can be of importance in the longer wavelength regions of DNA spectra, cannot be accounted for. In the far-UV region below 200 nm, however, these effects should be negligible.
, where Δ10 is the half-bandwidth for the given 0 → 1 transition and R10 is expressed in the same units as ΔE(λ). In any monopole approximation, charge transfer effects, which can be of importance in the longer wavelength regions of DNA spectra, cannot be accounted for. In the far-UV region below 200 nm, however, these effects should be negligible.
RESULTS
MD simulations of B- and Z-DNA
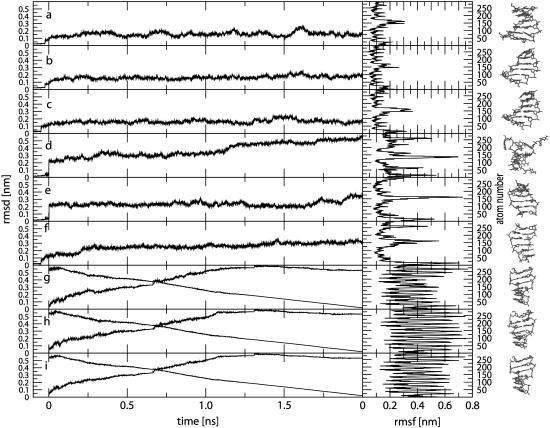
The time-series of the all-atom (non-mass-weighted) RMSD values from the starting structure are shown in Fig. 1, a–f, together with corresponding RMSF values for the MD simulations starting from B- or Z-DNA under different ionic-strength conditions. The RMSD values for all simulations starting from B-DNA exhibit maximum deviations of 0.15–0.20 nm, and reach these plateau values after ∼0.5 ns. For the simulations starting from Z-DNA, the system without counterions is clearly unstable and loses its double-helical structure almost immediately, reaching an RMSD value of ∼0.50 nm after 2 ns. Due to the large repulsive electrostatic interactions within the Z-DNA backbone, this behavior is not surprising. In contrast, the two Z-DNA systems with explicit counterions are stable, and show maximum deviations of 0.25–0.30 nm.
FIGURE 1.
Time-series of the all-atom (non-mass-weighted) RMSD values from the initial (model) structure (including the 0.1 ns equilibration time; from −0.1 to 0.0 ns) together with the corresponding RMSF values (excluding a total of 0.2 ns equilibration time) for the MD simulations starting from B- or Z-DNA and the TMD simulations of the B-to-Z transition under different ionic-strength conditions. For the TMD simulations, the RMSD from the target (equilibrated) Z-DNA structure is also shown. The end structure of each simulation is shown on the right. Panel codes (see Table 1) correspond to a, B0; b, BN; c, BE; d, Z0; e, ZN; f, ZE; g, BZ0; h, BZN; and i, BZE.
The RMSF values for the simulations starting from B-DNA are all in the range 0.1–0.2 nm, except for the more mobile nucleotides at the oligomer termini (strand 1: atoms 1–21 (1C) and 120–146 (6G); strand 2: atoms 147–167 (7C) and 266–292 (12G)). In comparison, the simulations starting from Z-DNA show significantly larger fluctuations, the highest RMSF values corresponding again to the terminal nucleotides. Overall, the trajectories for five of the six systems (with the exception of the Z-DNA simulation without counterions) are stable and lead to structures with no dramatic distortions. This suggests that (on the present simulation timescale) the use of a reaction-field corrected cutoff-truncation method for handling the electrostatic interactions should not necessarily be regarded as inferior to the application of lattice-sum methods in the context of DNA simulations (119,137,138).
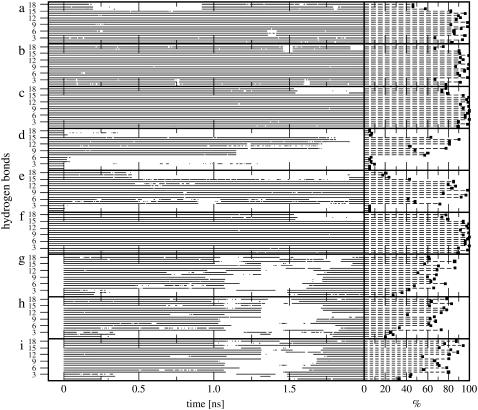
The analysis of the interstrand hydrogen-bonding patterns during these six MD simulations is reported in Fig. 2, a–f, and Table 2. For the sequence considered, a total of 18 canonical Watson-Crick (WC) hydrogen-bond pairs are possible (Table 2). The simulations starting from B-DNA exhibit a high occurrence of canonical hydrogen bonds under all conditions, i.e., these simulations conserve the initial WC basepairing pattern to a high extent. For the central basepairs, these hydrogen bonds are typically present over 85–100% of the simulation time. Their occurrence may be reduced in the strand termini due to increased mobility (see RMSF in Fig. 1, a–c) and more effective competition with hydrogen bonds to water molecules. Note also that the overall occurrence of canonical hydrogen bonds slightly increases upon increasing the ionic strength of the solution. For the simulations starting from Z-DNA, the system without counterions is characterized by a progressive disruption of the canonical hydrogen-bonding pattern, confirming the result of the RMSD analysis (Fig. 1 d). The hydrogen-bonding pattern is better preserved for the system with a neutralizing set of counterions, and essentially stable for the simulation with an excess of counterions. The increase in ionic strength leads to a decrease in the repulsive electrostatic interactions between backbone phosphate groups, which in turn results in a stabilization of the Z-DNA conformation, in agreement with independent experimental (7,10) and theoretical (73) results.
FIGURE 2.
Time-series (including the 0.1 ns equilibration time; from −0.1 to 0.0 ns) and occurrences (excluding a total of 0.2 ns equilibration time) of the 18 canonical Watson-Crick (WC) hydrogen bonds for the MD simulations starting from B- or Z-DNA and the TMD simulations of the B-to-Z transition under different ionic-strength conditions. The numbering of WC hydrogen bonds refers to Table 2, which also reports the corresponding occurrences in numbers. Panel codes (see Table 1) correspond to a, B0; b, BN; c, BE; d, Z0; e, ZN; f, ZE; g, BZ0; h, BZN; and i, BZE.
TABLE 2.
Possible Watson-Crick (WC) hydrogen bonds for the 3′-(CGCGCG)-5′ hexamer duplex and their occurrences (percentage of the simulation time where the hydrogen bond is present; excluding a total of 0.2 ns equilibration time) in the different simulations (see Fig. 2)
| Number | Strand 1–Strand 2 | B0 | BN | BE | Z0 | ZN | ZE | BZ0 | BZN | BZE |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1C (N4) → 12G (O6) | 83.2 | 77.4 | 89.0 | 4.8 | 4.8 | 89.0 | 27.5 | 19.9 | 32.8 |
| 2 | 1C (N3) ← 12G (N1) | 93.3 | 91.9 | 97.9 | 5.0 | 5.2 | 94.7 | 35.5 | 27.0 | 43.8 |
| 3 | 1C (O2) ← 12G (N2) | 67.0 | 67.3 | 89.2 | 9.5 | 5.1 | 86.7 | 42.5 | 25.0 | 44.4 |
| 4 | 2G (N1) → 11 C (N3) | 95.5 | 98.1 | 99.7 | 6.1 | 71.6 | 99.9 | 65.7 | 73.0 | 79.9 |
| 5 | 2G (N2) → 11C (O2) | 85.3 | 90.8 | 95.8 | 5.1 | 48.2 | 88.9 | 47.8 | 33.4 | 56.3 |
| 6 | 2G (O6) ← 11C (N4) | 85.1 | 88.9 | 95.9 | 6.2 | 41.7 | 75.5 | 76.8 | 63.3 | 78.2 |
| 7 | 3C (N4) → 10G (O6) | 92.2 | 95.0 | 97.7 | 57.1 | 92.2 | 95.9 | 62.9 | 61.2 | 71.2 |
| 8 | 3C (N3) ← 10G (N1) | 98.1 | 98.3 | 99.6 | 60.3 | 96.5 | 99.0 | 66.2 | 67.7 | 69.6 |
| 9 | 3C (O2) ← 10G (N2) | 82.1 | 86.7 | 93.7 | 47.9 | 75.0 | 90.8 | 60.0 | 62.4 | 66.8 |
| 10 | 4G (N1) → 9C (N3) | 98.0 | 99.4 | 99.2 | 77.8 | 98.0 | 99.4 | 68.2 | 66.3 | 80.1 |
| 11 | 4G (N2) → 9C (O2) | 87.2 | 90.7 | 91.2 | 43.3 | 83.1 | 91.4 | 50.7 | 40.9 | 55.1 |
| 12 | 4G (O6) ← 9C (N4) | 91.6 | 94.2 | 98.3 | 80.6 | 86.9 | 94.6 | 69.3 | 73.2 | 80.5 |
| 13 | 5C (N4) → 8G (O6) | 89.4 | 91.2 | 97.1 | 81.0 | 79.4 | 94.7 | 85.8 | 78.2 | 88.5 |
| 14 | 5C (N3) ← 8G (N1) | 96.1 | 99.1 | 99.0 | 89.9 | 84.9 | 98.9 | 70.5 | 75.8 | 82.3 |
| 15 | 5C (O2) ← 8G (N2) | 82.3 | 90.5 | 93.9 | 63.3 | 42.9 | 90.1 | 57.2 | 62.0 | 71.3 |
| 16 | 6G (N1) → 7C (N3) | 57.8 | 89.9 | 79.3 | 6.1 | 23.6 | 87.6 | 85.8 | 83.0 | 93.8 |
| 17 | 6G (N2) → 7C (O2) | 46.0 | 66.9 | 73.6 | 6.7 | 17.4 | 81.8 | 62.0 | 64.0 | 76.2 |
| 18 | 6G (O6) ← 7C (N4) | 46.3 | 75.2 | 77.3 | 4.9 | 20.4 | 77.0 | 60.9 | 78.0 | 87.6 |
The arrows indicate the donor-to-acceptor direction. The residue number, residue type, atom name, and atom are listed for the donors and acceptors involved in the respective strands. The atom names correspond to the latest GROMOS96 force field for nucleic acids (106). The simulation codes refer to Table 1.
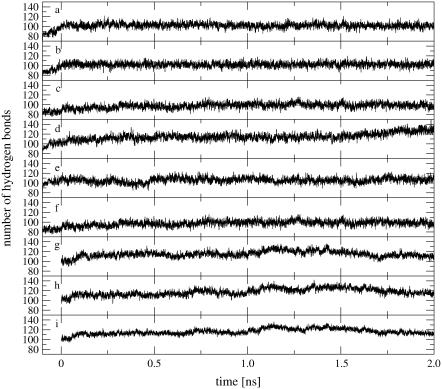
The time-series of the total number of oligomer to solvent hydrogen bonds is shown in Fig. 3, a–f, for the six MD simulations. In all cases, the number of solute-solvent hydrogen bonds expectedly increases during the equilibration period. The total numbers of hydrogen bonds converge to mean values and standard deviations (excluding a total of 0.2 ns equilibration time) of 102.1 ± 5.0 (B0), 102.2 ± 4.9 (BN), 93.5 ± 6.9 (BE), 114.9 ± 6.7 (Z0), 105.6 ± 5.8 (ZN), and 95.3 ± 6.3 (ZE). The disruption of the double-helical structure during the Z-DNA simulation without counterions is accompanied by a significant increase in the number of solute-solvent hydrogen bonds. For both DNA forms, the simulations with an excess amount of counterions show fewer solute-solvent hydrogen bonds compared to those with no or a minimal amount of counterions, an observation compatible with the corresponding higher occurrence of interstrand hydrogen bonds (Fig. 2, a–f, and Table 2).
FIGURE 3.
Time-series of the total number of oligomer to solvent hydrogen bonds (including the 0.1 ns equilibration time; from−0.1 to 0.0 ns) for the MD simulations starting from B- or Z-DNA and the TMD simulations of the B-to-Z transition under different ionic-strength conditions. Panel codes (see Table 1) correspond to a, B0; b, BN; c, BE; d, Z0; e, ZN; f, ZE; g, BZ0; h, BZN; and i, BZE.
TMD simulations of the B-to-Z DNA transition
The time-series of the all-atom (non-mass-weighted) RMSD values with respect to both the initial (model) B-DNA and the target (equilibrated) Z-DNA conformations are displayed in Fig. 1, g–i, together with corresponding RMSF values for the TMD simulations of the B-to-Z transition under different ionic-strength conditions. Along the three simulations, the RMSD value with respect to the target (Z-DNA) structure progressively decreases (with no major differences in the profile between the three simulations) and reaches a common value of 0.003 nm after 2 ns. Note that the decrease in this quantity is not exactly monotonic and linear, because the TMD constraint involves a mass-weighted RMSD calculated for a subset of atoms (atoms of the bases) rather than the all-atom non-mass-weighted RMSD value monitored here. The corresponding RMSD values with respect to the starting (B-DNA) structure do not evolve symmetrically with the values calculated with respect to the target structure. The two RMSD curves intersect at ∼0.7 ns, i.e., the simulations are progressing more rapidly away from the B-DNA form than they are moving toward the Z-DNA form. Due to the large conformational change involved in these simulations, the corresponding RMSF values averaged over the course of the transition are very high (because they account not only for the structural fluctuations but also for the overall structural change).
The analysis of the interstrand hydrogen-bonding patterns during these three TMD simulations is reported in Fig. 2, g–i, and Table 2. A major disruption of WC hydrogen bonds occurs after ∼1 ns upon leaving the initial B-DNA conformation. However, after an additional time period of ∼0.5 ns, most hydrogen bonds are recovered and maintained up to reaching the target Z-DNA conformation. Note that this transient disruption of WC hydrogen bonds is not accompanied by major distortions of the basepairing geometries (in particular, the flipping-out of bases into solution reported in the crystallographic structure of a B-Z junction (52), is never observed in the present simulations). There is no obvious difference with regard to the time evolution of the hydrogen-bonding pattern under different ionic-strength conditions.
The time-series of the total number of oligomer to solvent hydrogen bonds is shown in Fig. 3, g–i, for the three TMD simulations. These time-series show a significant increase between 1.0 and 1.5 ns, coinciding with the transient disruption of interstrand WC hydrogen bonds (Fig. 2, g–i). This suggests that the energetic cost involved in the transient breakdown of intrasolute hydrogen bonds is partly compensated by a concomitant increase in solute-solvent hydrogen-bonding. The total number of hydrogen bonds are characterized by mean values and standard deviations (excluding a total of 0.2 ns equilibration time) of 114.7 ± 6.6 (B0), 117.2 ± 7.5 (BZN), and 120.91 ± 6.1 (BZE). These average values are systematically higher than values in the corresponding MD simulations starting from either B- or Z-DNA. However, in contrast to the observations made in the context of these MD simulations, the number of solute-solvent hydrogen bonds is larger at higher ionic strength.
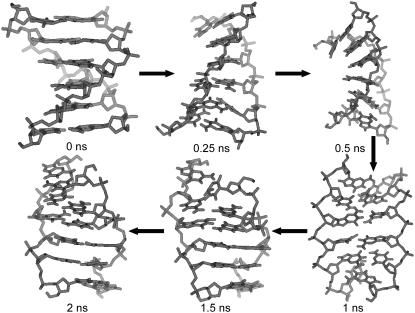
The transition pathway emerging from the TMD simulation with a neutralizing amount of counterions is illustrated in Fig. 4. Along the transition, the oligomer starts to partially unwind (first 0.25 ns), then undergoes a slight bending (0.25–0.5 ns) until reaching an extended or stretched conformation after ∼1 ns. The end-to-end distance of this stretched conformation at 1 ns (defined here as the average of the 1C-6G and 7C-12G phosphate atom distances of both strands) is 2.39 nm, to be compared with the corresponding values of 2.09 nm and 2.12 nm for the equilibrated B- and Z-DNA structures, respectively, corresponding to a stretching by ∼13.5%. At this time point, the nucleotide bases start to lose their canonical interstrand hydrogen bonds (Fig. 2, g–i) at the benefit of solute-solvent hydrogen bonding (Fig. 3, g–i), and begin to flip. After ∼1.5 ns, the WC hydrogen-bond pairing is entirely restored and the final Z-DNA conformation is progressively reached. The two other simulations (without and with an excess of counterions) follow a very similar pathway (not shown). The passage through a stretched configuration seems natural, because it facilitates the base-flipping process by allowing the nucleotide bases to occupy more space and enables the formation of the (local) chain-sense paradox. The transition pathway observed in the present explicit-solvent TMD simulations is in good qualitative agreement with the recent findings of Lim et al. (76,77), based on the simulation of a least-action path using an implicit solvent model.
FIGURE 4.
Structure snapshots along the B-to-Z DNA transition pathway observed in the TMD simulation with a neutralizing amount of counterions (duration of 2 ns). The two other simulations (without and with an excess of counterions) follow a very similar pathway (not shown).
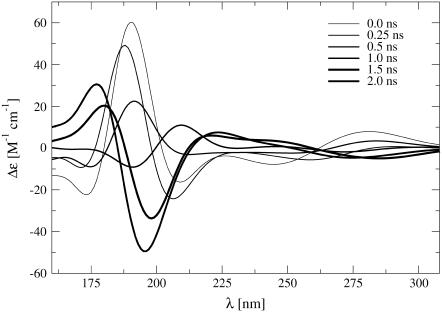
The CD spectra calculated for the configurations displayed in Fig. 4 are shown in Fig. 5. It is important to stress that experimental CD spectra characterize an ensemble of conformations rather than an individual structure (139). Nevertheless, the calculated single-structure spectra can be interpreted in a qualitative way. The individual structures along the pathway followed by the TMD simulation give rise to a spectral evolution, which is in good agreement with the experimentally observed signal inversion at 195 nm (7), i.e., the emergence of the spectral trademark of the Z-DNA configuration. The continuous progression of the band inversion over the course of the transition is also compatible with the experimental evolution observed in time-resolved measurements (7).
FIGURE 5.
CD spectra calculated for structure snapshots along the B-to-Z DNA transition pathway observed in the TMD simulation with a neutralizing amount of counterions (duration of 2 ns; illustrated in Fig. 4). Successive spectra along the transition are indicated by lines of increasing thickness. The calculated molar CD signal Δε(λ) = εL(λ) – εR(λ) at a given wavelength λ, where εL and εR are the extinction coefficients for left- and right-circularly polarized light, is displayed. The two other TMD simulations (without and with an excess of counterions) give rise to a similar spectral evolution (data not shown).
While the observed pathway is qualitatively similar for the three TMD simulations irrespective of the ionic-strength conditions, it is of interest to investigate possible differences in the flipping behavior of the nucleotides and bases. As pointed out previously (see Introduction), the rotational mechanism for the two types of nucleotide bases is formally different. While guanine rotates around the deoxyribose-base χ-angle by 180°, changing orientation from anti to syn, the cytosine bases remain in anti orientation and the flipping is accomplished through a rotation of the whole nucleoside involving the angle η. The corresponding χ- and η-angle values of the starting (equilibrated) B-DNA and target (equilibrated) Z-DNA conformations of the TMD simulations are reported in Table 3.
TABLE 3.
Values of the nucleotide-base dihedral angles χ and of the angles η between the planes of the nucleotide relative to the initial (equilibrated) B-DNA structure (after least-squares-fit superposition), reported for the starting (equilibrated) B-DNA and target (equilibrated) Z-DNA conformations of the TMD simulations
| Conformation | 1C | 2G | 3C | 4G | 5C | 6G | 7C | 8G | 9C | 10G | 11C | 12G |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| χ (B) | 246.7 | 248.9 | 255.6 | 245.0 | 230.0 | 258.9 | 242.0 | 241.4 | 231.2 | 240.7 | 244.2 | 245.1 |
| χ (Z) | 215.8 | 78.4 | 198.5 | 71.9 | 217.5 | 80.8 | 214.5 | 78.6 | 198.1 | 71.5 | 218.3 | 74.3 |
| η (B) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| η (Z) | 148.7 | 154.3 | 152.2 | 151.4 | 155.3 | 150.1 | 150.4 | 151.0 | 152.1 | 153.1 | 152.0 | 151.9 |
Values are given in degrees.
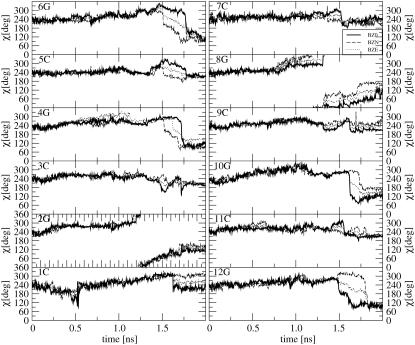
The time-series of the nucleotide-base χ-angles are displayed in Fig. 6 for the three TMD simulations. For all simulations, the χ-angle values of the target Z-DNA structure (Table 3) are reached after 2 ns, i.e., all bases adopt the expected syn (guanine) or anti (cytosine) orientations with respect to the deoxyribose sugar moiety. The evolution of the χ-angle appears to be very similar in the three TMD simulations. The guanosine bases are distributed into two groups, i.e., those for which the rotation occurs gradually through an increase in χ (so-called high-anti path; 2G, 8G) and those for which rotation occurs in a stepwise fashion through a decrease in χ (4G, 6G, 10G, 12G). Although the cytosine bases paired with a given guanosine do not flip, all of them show significant variations in their χ-angle during the time in which their partner guanosine flips.
FIGURE 6.
Time-series of the nucleotide-base dihedral angle χ (around the sugar-base bond) during the TMD simulations of the B-to-Z transition under different ionic-strength conditions (BZ0, solid line; BZN, dashed line; and BZE, dotted line; see Table 1 for the simulation codes).
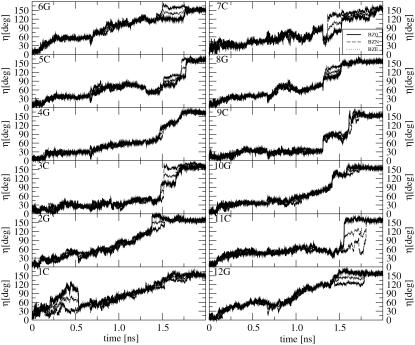
The time-series of the angle η between the nucleotide-base plane in the current and starting (B-DNA) structure (after least-squares-fit superimposition) are displayed in Fig. 7 for the three TMD simulations. Due to possible ambiguities related to the fitting procedure, the results may only be interpreted in a qualitative fashion. The flipping of the cytosine bases, mediated by the rotation of the corresponding deoxyribose moiety, is evident here. Here also, the bases are roughly distributed into two groups, i.e., those showing gradual rotation (1C, 2G, 6G, 12G) and those flipping more suddenly at a later stage of the transition (3C, 4G, 5C, 7C, 8G, 9C, 10G, 11C).
FIGURE 7.
Time-series of the angle η between the planes of the nucleotide bases in the current and initial (equilibrated) B-DNA structure (after least-squares-fit superimposition) during the TMD simulations of the B-to-Z transition under different ionic-strength conditions (BZ0, solid line; BZN, dashed line; BZE, dotted line; see Table 1 for the simulation codes).
Based on the information contained in Figs. 6 and 7, as well as on a visual inspection of the trajectories, it is possible to determine a flipping sequence for the different bases. Rotation begins gradually at the oligonucleotide termini through the basepairs 1C, 12G and 6G, 7C. This is expected since the sterical constraints are less severe for terminal pairs in a free oligonucleotide (note that this observation does not hold for an equivalent oligonucleotide stretch within a longer DNA segment, so that the flipping mechanism may possibly differ in this case). The flipping then progresses over time in direction 6G → 1C in strand 1 and 7C → 12G in strand 2, whereby bases 3C, 2G and 11C rotate the latest. In other words, the flipping process progresses in direction 5′ → 3′ along strand 1, and 3′ → 5′ along strand 2. This kind of propagation mechanism may be viewed as a (cooperative) zipperlike transition (55).
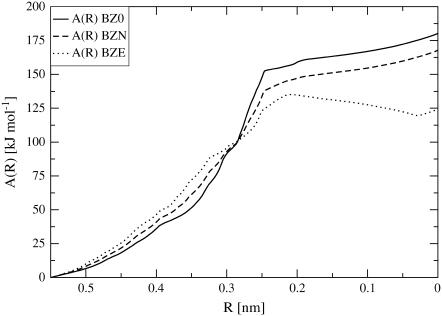
The free energy profiles A(R) calculated from the integral of the constraint force over the sampled pathways, are shown in Fig. 8 for the three TMD simulations under different ionic-strength conditions. The free energy profiles for the three simulations exhibit the same sigmoidal shape, with a transition point at R ∼ 0.25 nm (i.e., after ∼1 ns simulation time), which corresponds to the stretched intermediate conformation in Fig. 4. Only the simulation with an excess of counterions shows a clear minimum for low values of the reaction coordinate, suggesting again that the Z-DNA conformation is intrinsically unstable under lower ionic-strength conditions. The observation that the A(R) value for Z-DNA is higher compared to B-DNA, even at high salt concentration, can have two origins:
A distortion of the profile at low R due to the use of a “polar” reaction coordinate (low R values are associated with more restricted regions of configurational space compared to high R values, which can be viewed as an artificial entropy reduction upon decreasing R).
An energetical bias in the molecular model employed (force field), which has been refined against experimental data predominantly in the context of the A- and B-DNA forms (106).
FIGURE 8.
Free energy profile A(R), Eq. 15, where R is the (mass-weighted) nucleotide-base RMSD from the Z-DNA structure, Eq. 1, along the transition path followed during the three TMD simulations of the B-to-Z transition under different ionic-strength conditions.
On the other hand, the barrier for the transition is estimated to be ∼125–150 kJ × mol−1, which is of the same order of magnitude as reported literature values for the activation energy of this process (159 kJ × mol−1 (57)).
CONCLUSIONS
The goal of this study was to investigate the stability of the B- and Z-DNA conformations under different ionic-strength conditions and the mechanism of the B-to-Z DNA transition using MD and TMD simulations with an explicit representation of the solvent and counterions. The impact of the ionic strength on the stability of the Z-DNA conformation was clearly visible in the MD simulations, the latter form being only marginally stable with a neutralizing amount and stable with an excess amount (4 m) of counterions. The transition pathway observed during the TMD simulations (under all ionic-strength conditions) agrees qualitatively with the result of a recent theoretical study of the same oligomer (76,77) using a different computational methodology and an implicit-solvation model. The main features are the formation of a stretched (∼13.5%) intermediate configuration followed by a transient disruption of canonical hydrogen bonds, partly compensated energetically by a concomitant increase in the number of solute-solvent hydrogen bonds, and concluded by reformation of Watson-Crick hydrogen bonds and relaxation to the final Z-DNA structure. Two of the six guanine bases (2G, 8G) were found to undergo rotation about the deoxyribose χ-angle (to the syn orientation) via the high-anti pathway. The flipping process was found to progress along the 5′ → 3′ direction in strand 1, and along the 3′ → 5′ direction in strand 2, in accordance with a zipperlike progression mechanism (55). The stretched intermediate configuration was found to approximately coincide with the maximum of the corresponding free energy curve. The fundamental assumption underlying the realism of the mechanism suggested by the present TMD simulations is that the relaxation of the degrees of freedom orthogonal to the RMSD reaction coordinate (for which the TMD speed-up is of the order of 1010 compared to experiment) occurs on the subnanosecond timescale. Although there is currently no way to prove the validity of this assumption, the suggested pathway appears physically plausible, because it is compatible with the sterical constraints involved in fully flipping the bases (guanosine) and the deoxyribose-moieties (cytosine) during the transition, and provides a simple solution to the chain-sense paradox. This transition pathway also appears to be qualitatively insensitive to the ionic-strength conditions. However, the Z-DNA conformation only corresponds to a (shallow) free-energy minimum (along the profile) for the simulation under high ionic-strength conditions.
References
- 1.Wang, A. H., G. J. Quigley, F. J. Kolpak, J. L. Crawford, J. H. van Boom, G. van der Marel, and A. Rich. 1979. Molecular structure of a left-handed double helical DNA fragment at atomic resolution. Nature. 282:680–686. [DOI] [PubMed] [Google Scholar]
- 2.Rich, A., and Z. Shuguang. 2003. Z-DNA: the long road to biological function. Nature Rev. Gen. 4:566–573. [DOI] [PubMed] [Google Scholar]
- 3.Saenger, W. 1984. Principles of Nucleic Acid Structure. Springer Verlag, New York.
- 4.Wells, R., and S. Harvey, editors. 1989. Unusual DNA Structures. Springer, New York.
- 5.Ghosh, A., and M. Bansal. 2003. A glossary of DNA structures from A to Z. Acta Crystallogr. D. 59:620–626. [DOI] [PubMed] [Google Scholar]
- 6.Watson, J. D., and F. H. C. Crick. 1953. Molecular structure of nucleic acids—a structure for deoxyribose nucleic acid. Nature. 171:737–738. [DOI] [PubMed] [Google Scholar]
- 7.Pohl, F. M., and T. M. Jovin. 1972. Salt-induced co-operative conformational change of a synthetic DNA: equilibrium and kinetic studies with poly(dG-dC). J. Mol. Biol. 67:375–396. [DOI] [PubMed] [Google Scholar]
- 8.Ho, P. S., and B. H. M. Mooers. 1997. Z-DNA crystallography. Biopolymers. 44:65–90. [DOI] [PubMed] [Google Scholar]
- 9.Sponer, J., H. A. Gabb, J. Leszczynski, and P. Hobza. 1997. Base-base and deoxyribose-base stacking interactions in B-DNA and Z-DNA: a quantum-chemical study. Biophys. J. 73:76–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pohl, F. M. 1983. Salt-induced transition between two double-helical forms of oligo(DC-DG). Cold Spring Harb. Symp. Quant. Biol. 47:113–117. [DOI] [PubMed] [Google Scholar]
- 11.Kollman, P. A., P. K. Weiner, and A. Dearing. 1981. Theoretical studies of the structure and energies of basepaired nucleotides and the dissociation kinetics of a proflavine-dinucleotide complex. Ann. N. Y. Acad. Sci. 367:250–268. [DOI] [PubMed] [Google Scholar]
- 12.Gueron, M., and J. P. Demaret. 1992. A simple explanation of the B-to-Z transition of DNA. Proc. Natl. Acad. Sci. USA. 89:5740–5743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Misra, V. K., and B. Honig. 1996. The electrostatic contribution to the B-to-Z transition of DNA. Biochemistry. 35:1115–1124. [DOI] [PubMed] [Google Scholar]
- 14.Gueron, M., J. P. Demaret, and M. Filoche. 2000. A unified theory of the B-Z transition of DNA in high and low concentrations of multivalent ions. Biophys. J. 78:1070–1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Demaret, J. P., and M. Gueron. 2000. The sensitivity of the B-Z transition of DNA to multivalent cations in high and low concentrations: a unified electrostatic interpretation. J. Biomol. Struct. Dyn. S2:377–382. [Google Scholar]
- 16.Rich, A., A. Nordheim, and A. H. Wang. 1984. The chemistry and biology of left-handed Z-DNA. Annu. Rev. Biochem. 53:791–846. [DOI] [PubMed] [Google Scholar]
- 17.Haniford, D. B., and D. E. Pulleyblank. 1983. The in vivo occurrence of Z DNA. J. Biomol. Struct. Dyn. 1:593–609. [DOI] [PubMed] [Google Scholar]
- 18.Sugiyama, H., K. Kawai, A. Matsunaga, K. Fujimoto, I. Saito, H. Robinson, and A. H. Wang. 1996. Synthesis, structure and thermodynamic properties of 8-methylguanine-containing oligonucleotides: Z-DNA under physiological salt conditions. Nucleic Acids Res. 24:1272–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tashiro, R., and H. Sugiyama. 2003. A nanothermometer based on the different π-stackings of B- and Z-DNA. Ang. Chem. Intl. Ed. 42:6018–6020. [DOI] [PubMed] [Google Scholar]
- 20.Mao, C., W. Sun, Z. Shen, and N. C. Seeman. 1999. A nanomechanical device based on the B-Z transition of DNA. Nature. 397:144–146. [DOI] [PubMed] [Google Scholar]
- 21.Seeman, N. C., and A. M. Belcher. 2002. Emulating biology: building nanostructures from the bottom up. Proc. Natl. Acad. Sci. USA. 99:6451–6455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tashiro, R., and H. Sugiyama. 2005. Biomolecule-based switching devices that respond inversely to thermal stimuli. J. Am. Chem. Soc. 127:2094–2097. [DOI] [PubMed] [Google Scholar]
- 23.Rich, A. 1996. The biology of left-handed Z-DNA. J. Biol. Chem. 271:11595–11598. [DOI] [PubMed] [Google Scholar]
- 24.Stollar, B. D. 1997. Why the difference between B-DNA and Z-DNA? Lupus. 6:327–328. [DOI] [PubMed] [Google Scholar]
- 25.Belmont, P., J. F. Constant, and M. Demeunynck. 2001. Nucleic acid conformation diversity: from structure to function and regulation. Chem. Soc. Rev. 30:70–81. [Google Scholar]
- 26.Gagna, C. E., and W. C. Lambert. 2003. The halting arrival of left-handed Z-DNA. Med. Hypotheses. 60:418–423. [DOI] [PubMed] [Google Scholar]
- 27.Kim, Y. G., K. Lowenhaupt, D. Y. Oh, K. K. Kim, and A. Rich. 2004. Evidence that Vaccinia virulence factor ER binds to Z-DNA in vivo: implications for development of a therapy for poxvirus infection. Proc. Natl. Acad. Sci. USA. 101:1514–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu, L. F., and J. C. Wang. 1987. Supercoiling of the DNA template during transcription. Proc. Natl. Acad. Sci. USA. 84:7024–7027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wittig, B., T. Dorbic, and A. Rich. 1991. Transcription is associated with Z-DNA formation in metabolically active permeabilized mammalian cell nuclei. Proc. Natl. Acad. Sci. USA. 88:2259–2263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wittig, B., S. Wolfl, T. Dorbic, W. Vahrson, and A. Rich. 1992. Transcription of human c-Myc in permeabilized nuclei is associated with formation of Z-DNA in three discrete regions of the gene. EMBO J. 11:4653–4663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cerna, A., A. Cuadrado, N. Jouve, S. M. D. de la Espina, and C. de la Torre. 2004. Z-DNA, a new in situ marker for transcription. Eur. J. Histochem. 48:49–55. [PubMed] [Google Scholar]
- 32.Kmiec, E. B., K. J. Angelides, and W. K. Holloman. 1985. Left-handed DNA and the synaptic pairing reaction promoted by Ustilago rec1 protein. Cell. 40:139–145. [DOI] [PubMed] [Google Scholar]
- 33.Blaho, J. A., and R. D. Wells. 1987. Left-handed Z-DNA binding by the recA protein of Escherichia coli. J. Biol. Chem. 262:6082–6088. [PubMed] [Google Scholar]
- 34.Jaworski, A., W. T. Hsieh, J. A. Blaho, J. E. Larson, and R. D. Wells. 1987. Left-handed DNA in vivo. Science. 238:773–777. [DOI] [PubMed] [Google Scholar]
- 35.Schwartz, T., M. A. Rould, K. Lowenhaupt, A. Herbert, and A. Rich. 1999. Crystal structure of the Z-α domain of the human editing enzyme ADAR1 bound to left-handed Z-DNA. Science. 284:1841–1845. [DOI] [PubMed] [Google Scholar]
- 36.Oh, D. Y., Y. G. Kim, and A. Rich. 2002. Z-DNA-binding proteins can act as potent effectors of gene expression in vivo. Proc. Natl. Acad. Sci. USA. 99:16666–16671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Champ, P. C., S. Maurice, J. M. Vargason, T. Camp, and P. S. Ho. 2004. Distributions of Z-DNA and nuclear factor I in human chromosome 22: a model for coupled transcriptional regulation. Nucleic Acids Res. 32:6501–6510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gagna, C. E., H. R. Kuo, and W. C. Lambert. 1999. Terminal differentiation and left-handed Z-DNA: a review. Cell Biol. Int. 23:1–5. [DOI] [PubMed] [Google Scholar]
- 39.Suram, A., L. K. S. Rao, K. S. Latha, and M. A. Viswamitra. 2002. First evidence to show the topological change of DNA from B-DNA to Z-DNA conformation in the hippocampus of Alzheimer's brain. Neuromol. Med. 2:289–297. [DOI] [PubMed] [Google Scholar]
- 40.Hegde, M. L., S. Anitha, K. S. Latha, M. S. Mustak, R. Stein, R. Ravid, and K. S. J. Rao. 2004. First evidence for helical transitions in supercoiled DNA by amyloid β-peptide (1–42) and aluminum—a new insight in understanding Alzheimer's disease. J. Mol. Neurosci. 22:19–31. [DOI] [PubMed] [Google Scholar]
- 41.Jovin, T. M., D. M. Soumpasis, and L. P. McIntosh. 1987. The transition between B-DNA and Z-DNA. Annu. Rev. Phys. Chem. 38:521–560. [Google Scholar]
- 42.Voet, D., and J. G. Voet. 1995. Biochemistry, 2nd Ed. Wiley, New York.
- 43.Haschemeyer, A. E., and A. Rich. 1967. Nucleoside conformations—an analysis of steric barriers to rotation about the glycosidic bond. J. Mol. Biol. 27:369–384. [DOI] [PubMed] [Google Scholar]
- 44.Harvey, S. C. 1983. DNA structural dynamics: longitudinal breathing as a possible mechanics for the B ↔ Z transition. Nucleic Acids Res. 11:4867–4878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Goto, S. 1984. Characterization of intermediate conformational states in the B reversible Z transitions of poly(DG-DC)·POLY(DG-DC). Biopolymers. 23:2211–2222. [DOI] [PubMed] [Google Scholar]
- 46.Manzini, G., L. E. Xodo, F. Quadrifoglio, J. H. van Boom, and G. A. van der Marel. 1987. dC-dG alternating oligonucleotides: thermodynamic and kinetic aspects of the B-Z transformation. J. Biomol. Struct. Dyn. 4:651–662. [DOI] [PubMed] [Google Scholar]
- 47.Olson, W. K. 1981. Understanding the Motions of DNA. In Biomolecular Stereodynamics. R. H. Sarma and M. H. Sarma, editors. Adenine, New York. 327–343.
- 48.Sundaralingam, M., and E. Westhof. 1981. Structural motifs of the nucleotidyl unit and the handedness of polynucleotide helices. Int. J. Quantum Chem. (Suppl. 8):287–306.
- 49.Chaires, J. B., and J. M. Sturtevant. 1988. Thermodynamics of the B to Z transition in poly(DGDC). Biopolymers. 27:1375–1387. [DOI] [PubMed] [Google Scholar]
- 50.Saenger, W., and U. Heinemann. 1989. Raison d'être and structural model for the B-Z transition of poly d(G-C)·poly d(G-C). FEBS Lett. 257:223–227. [DOI] [PubMed] [Google Scholar]
- 51.Ivanov, V., K. Grzeskowiak, and G. Zocchi. 2003. Evidence for an intermediate state in the B-to-Z transition of DNA. J. Phys. Chem. B. 107:12847–12850. [Google Scholar]
- 52.Ha, S. C., K. Lowenhaupt, Y.-G. Kim, K. K. Kim, and A. Rich. 2005. Crystal structure of a junction between B-DNA and Z-DNA reveals two extruded bases. Nature. 437:1183–1186. [DOI] [PubMed] [Google Scholar]
- 53.Klimasauskas, S., S. Kumar, R. J. Roberts, and X. Cheng. 1994. Hhal methyltransferase flips its target base out of the DNA helix. Cell. 76:357–369. [DOI] [PubMed] [Google Scholar]
- 54.Chen, Y. Z., and E. W. Prohofsky. 1994. Nonlinear effects and thermal expansion as expressed in self-consistent phonon calculations on the temperature dependence of a phase change: application to the B to Z conformation change in DNA. Phys. Rev. E. 49:3444–3451. [DOI] [PubMed] [Google Scholar]
- 55.Ho, P. S. 1994. The non-B-DNA structure of d(CA/TG)n does not differ from that of Z-DNA. Proc. Natl. Acad. Sci. USA. 91:9549–9553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Cheatham, T. E., and M. A. Young. 2000. Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers. 56:232–256. [DOI] [PubMed] [Google Scholar]
- 57.Brown, B. A., K. Lowenhaupt, C. M. Wilbert, E. B. Hanlon, and A. Rich. 2000. The Z-α domain of the editing enzyme dsRNA adenosine deaminase binds left-handed Z-RNA as well as Z-DNA. Proc. Natl. Acad. Sci. USA. 97:13532–13536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.van Lier, J. J. C., M. T. Smits, and H. M. Buck. 1983. B-Z Transition in methylated DNA—a quantum-chemical study. Eur. J. Biochem. 132:55–62. [DOI] [PubMed] [Google Scholar]
- 59.van Gunsteren, W. F., T. C. Beutler, F. Fraternali, P. M. King, A. E. Mark, and P. E. Smith. 1993. Computation of free energy in practice: choice of approximations and accuracy limiting factors. In Computer Simulation of Biomolecular Systems, Theoretical and Experimental Applications, Vol. 2. W. F. van Gunsteren, P. K. Weiner, and A. J. Wilkinson, editors. ESCOM Science Publishers, Leiden, The Netherlands. 267–314.
- 60.Beutler, T. C., and W. F. van Gunsteren. 1994. The computation of a potential of mean force: choice of the biasing potential in the umbrella sampling technique. J. Chem. Phys. 100:1492–1497. [Google Scholar]
- 61.Mezei, M., and D. L. Beveridge. 1986. Free energy simulations. Ann. Acad. Sci. NY. 482:1–23. [DOI] [PubMed] [Google Scholar]
- 62.Kollman, P. 1993. Free energy calculations: applications to chemical and biochemical phenomena. Chem. Rev. 93:2395–2417. [Google Scholar]
- 63.Radmer, R. J., and P. A. Kollman. 1997. Free energy calculation methods: a theoretical and empirical comparison of numerical errors and a new method for qualitative estimates of free energy changes. J. Comput. Chem. 18:902–919. [Google Scholar]
- 64.Mark, A. E. 1998. Free energy perturbation calculations. In Encyclopedia of Computational Chemistry, Vol. 2. P. von Rague Schleyer, editor. John Wiley and Sons, New York. 1070–1083.
- 65.Dang, L. X., D. A. Pearlman, and P. A. Kollman. 1990. Why do A·T basepairs inhibit Z-DNA formation? Proc. Natl. Acad. Sci. USA. 87:4630–4634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Pearlman, D. A., and P. A. Kollman. 1990. The calculated free energy effects of 5-Methyl Cytosine on the B to Z transition in DNA. Biopolymers. 29:1193–1209. [DOI] [PubMed] [Google Scholar]
- 67.Soumpasis, D. M. 1984. Statistical mechanics of the B → Z transition of DNA: contribution of diffuse ionic interactions. Proc. Natl. Acad. Sci. USA. 81:5116–5120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Fenley, M. O., G. S. Manning, and W. K. Olson. 1990. A numerical counterion condensation analysis of the B-Z transition of DNA. Biopolymers. 30:1205–1213. [DOI] [PubMed] [Google Scholar]
- 69.Montoro, J. C. G., and J. L. F. Abascal. 1996. A method for the computer simulation of the free-energy difference in conformational changes of polyelectrolytes. Application to the B- to Z-DNA transition. Europhys. Lett. 34:471–476. [Google Scholar]
- 70.Montoro, J. C. G., and J. L. F. Abascal. 1997. The free energy difference between simple models of B- and Z-DNA: computer simulation and theoretical predictions. J. Chem. Phys. 106:8239–8253. [Google Scholar]
- 71.Zhou, H., Y. Zhang, and Z.-C. Ou-Yang. 2000. Elastic property of single double-stranded DNA molecules: theoretical study and comparison with experiments. Phys. Rev. E. 62:1045–1058. [DOI] [PubMed] [Google Scholar]
- 72.Abascal, J. L. F., and J. C. G. Montoro. 2000. Computer simulation results for the free-energy difference between B-DNA and Z-DNA. J. Phys. Cond. Mat. 12:A327–A332. [Google Scholar]
- 73.Abascal, J. L. F., and J. C. G. Montoro. 2004. Computer simulation of the thermodynamics of the B-Z-DNA transition: effect of the ionic size and charge. Mol. Phys. 102:2141–2148. [Google Scholar]
- 74.Dong, R. X., and X. L. Yan. 2004. The theoretical study of the effects of salt on structure transition of B-DNA to Z-DNA. Acta Sinica Physica. 53:4414–4419. [Google Scholar]
- 75.Elber, R., A. Ghosh, and A. Cardenas. 2002. Long time dynamics of complex systems. Acc. Chem. Res. 35:396–403. [DOI] [PubMed] [Google Scholar]
- 76.Lim, W., and Y. P. Feng. 2005. The stretched intermediate model of B-Z DNA transition. Biophys. J. 88:1593–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lim, W., and Y. P. Feng. 2005. Applying the stochastic difference equation to DNA conformational transitions: a study of B-Z and B-A DNA transitions. Biopolymers. 78:107–120. [DOI] [PubMed] [Google Scholar]
- 78.Jares-Erijman, E. A., and T. M. Jovin. 1996. Determination of DNA helical handedness by fluorescence resonance energy transfer. J. Mol. Biol. 257:597–617. [DOI] [PubMed] [Google Scholar]
- 79.Ghosh, A., C. S. Rapp, and R. A. Friesner. 1998. A generalized Born model based on a surface integral formulation. J. Phys. Chem. B. 102:10983–10990. [Google Scholar]
- 80.Gnanakaran, S., H. Nymeyer, J. Portman, K. Y. Sanbonmatsu, and A. E. Garcia. 2003. Peptide folding simulations. Curr. Opin. Struct. Biol. 13:168–174. [DOI] [PubMed] [Google Scholar]
- 81.Zhou, R. H., and B. J. Berne. 2002. Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water? Proc. Natl. Acad. Sci. USA. 99:12777–12782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zhou, R. H., G. Krilov, and B. J. Berne. 2004. Comment on “Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water?” The Poisson-Boltzmann equation. J. Phys. Chem. B. 108:7528–7530. [Google Scholar]
- 83.Song, M. Y., S. Kim, and M. S. Jhon. 1988. A theoretical study on the hydration of B-and Z-DNA double helices. J. Mol. Struct. 179:427–437. [Google Scholar]
- 84.Chalikian, T. V., A. P. Sarvazyan, G. E. Plum, and K. J. Breslauer. 1994. Influence of base composition, base sequence, and duplex structure on DNA hydration: apparent molar volumes and apparent molar adiabatic compressibilities of synthetic and natural DNA duplexes at 25°C. Biochemistry. 33:2394–2401. [DOI] [PubMed] [Google Scholar]
- 85.Schneider, B., and H. M. Berman. 1995. Hydration of the DNA bases is local. Biophys. J. 69:2661–2669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Feig, M., and B. M. Pettitt. 1998. A molecular simulation picture of DNA hydration around A- and B-DNA. Biopolymers. 48:199–209. [DOI] [PubMed] [Google Scholar]
- 87.Schneider, B., K. Patel, and H. M. Berman. 1998. Hydration of the phosphate group in double-helical DNA. Biophys. J. 75:2422–2434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Barciszewski, J., J. Jurczak, S. Porowski, T. Specht, and V. A. Erdmann. 1999. The role of water structure in conformational changes of nucleic acids in ambient and high-pressure conditions. Eur. J. Biochem. 260:293–307. [DOI] [PubMed] [Google Scholar]
- 89.Kang, N. S., K. T. No, and M. S. Jhon. 2003. A study of the hydrogen-bonded network around the left-handed and right-handed DNA in an ionic solution. Mol. Sim. 29:83–89. [Google Scholar]
- 90.Pal, S. K., and A. H. Zewail. 2004. Dynamics of water in biological recognition. Chem. Rev. 104:2099–2123. [DOI] [PubMed] [Google Scholar]
- 91.Schlitter, J., M. Engels, P. Krüger, E. Jacoby, and A. Wollmer. 1993. Targeted molecular dynamics simulation of conformational change—application to the T ↔ R transition in insulin. Mol. Sim. 10:291–309. [Google Scholar]
- 92.Schlitter, J., M. Engels, and P. Krüger. 1994. Targeted molecular dynamics—a new approach for searching pathways of conformational transitions. J. Mol. Graph. 12:84–89. [DOI] [PubMed] [Google Scholar]
- 93.Díaz, J. F., B. Wroblowski, J. Schlitter, and Y. Engelborghs. 1997. Calculation of pathways for the conformational transition between the GTP- and GDP-bound states of the Ha-ras-p21 protein: calculations with explicit solvent simulations and comparison with calculations in vacuum. Proteins Struct. Funct. Genet. 28:434–451. [PubMed] [Google Scholar]
- 94.Schlitter, J., W. Swegat, and T. Mülders. 2001. Distance-type reaction coordinates for modeling activated processes. J. Mol. Model. (Online). 7:171–177. [Google Scholar]
- 95.Zwanzig, R. W. 1954. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 22:1420–1426. [Google Scholar]
- 96.Rosemeyer, H., and F. Seela. 2002. Modified purine nucleosides as dangling ends of DNA duplexes: the effect of the nucleobase polarizability on stacking interactions. J. Chem. Soc., Perkin Trans. 2. 4:746–750. [Google Scholar]
- 97.Wang, A. H. J., G. J. Quigley, F. J. Kolpak, G. van der Marel, J. H. van Boom, and A. Rich. 1981. Left-handed double helical DNA—variations in the backbone conformation. Science. 211:171–176. [DOI] [PubMed] [Google Scholar]
- 98.Gessner, R. V., G. J. Quigley, A. H. J. Wang, G. A. van der Marel, and A. Rich. 1985. Structural basis for stabilization of Z-DNA by cobalt hexamine and magnesium cations. Biochemistry. 24:237–240. [DOI] [PubMed] [Google Scholar]
- 99.Ho, P. S., C. A. Frederick, D. Saal, A. H. J. Wang, and A. Rich. 1987. The interactions of ruthenium hexamine with Z-DNA—crystal-structure of a Ru(NH3)3+(6) salt of d(CGCGCG) at 1.2 Å resolution. J. Biomol. Struct. Dyn. 4:521–534. [DOI] [PubMed] [Google Scholar]
- 100.Gessner, R. V., C. A. Rederick, G. J. Quigley, A. Rich, and A. H. J. Wang. 1989. The molecular structure of the left-handed Z-DNA double helix at 1.0-Å atomic resolution. Geometry, conformation, and ionic interactions of d(CGCGCG). J. Biol. Chem. 264:7921–7935. [DOI] [PubMed] [Google Scholar]
- 101.Norberg, J., and L. Nilsson. 1996. Glass transition in DNA from molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 93:10173–10176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Malinina, L., V. Tereshko, E. Ivanova, J. A. Subirana, V. Zarytova, and Y. Nekrasov. 1998. Structural variability and new intermolecular interactions of Z-DNA in crystals of d(pCpGpCpGpCpG). Biophys. J. 74:2482–2490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ho, P. S., M. J. Ellison, G. J. Quigley, and A. Rich. 1986. A computer aided thermodynamic approach for predicting the formation of Z-DNA in naturally occurring sequences. EMBO J. 5:2737–2744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.van Gunsteren, W. F., S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott, and I. G. Tironi. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Vdf Hochschulverlag AG an der ETH Zürich, Zürich, Switzerland.
- 105.Scott, W. R. P., P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Krüger, and W. F. van Gunsteren. 1999. The GROMOS biomolecular simulation program package. J. Phys. Chem. A. 103:3596–3607. [Google Scholar]
- 106.Soares, T. A., P. H. Hünenberger, M. A. Kastenholz, V. Kräutler, T. Lenz, R. D. Lins, C. Oostenbrink, and W. F. van Gunsteren. 2005. An improved nucleic-acid parameter set for the GROMOS force field. J. Comput. Chem. 26:725–737. [DOI] [PubMed] [Google Scholar]
- 107.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. Reidel, Dordrecht, The Netherlands. 331–342.
- 108.Barker, J. A., and R. O. Watts. 1973. Monte Carlo studies of the dielectric properties of water-like models. Mol. Phys. 26:789–792. [Google Scholar]
- 109.Tironi, I. G., R. Sperb, P. E. Smith, and W. F. van Gunsteren. 1995. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 102:5451–5459. [Google Scholar]
- 110.Glättli, A., X. Daura, and W. F. van Gunsteren. 2002. Derivation of an improved simple point charge model for liquid water: SPC/A and SPC/L. J. Chem. Phys. 116:9811–9828. [Google Scholar]
- 111.Madura, J. D., and B. M. Pettitt. 1988. Effect of truncating long-range interactions in aqueous ionic solution simulations. Chem. Phys. Lett. 150:105–108. [Google Scholar]
- 112.Schreiber, H., and O. Steinhauser. 1992. Molecular dynamics studies of solvated polypeptides: why the cut-off scheme does not work. Chem. Phys. 168:75–89. [Google Scholar]
- 113.Schreiber, H., and O. Steinhauser. 1992. Cutoff size does strongly influence molecular dynamics results on solvated polypeptides. Biochemistry. 31:5856–5860. [DOI] [PubMed] [Google Scholar]
- 114.Smith, P. E., and W. F. van Gunsteren. 1993. Methods for the evaluation of long range electrostatic forces in computer simulations of molecular systems. In Computer Simulation of Biomolecular Systems, Vol. 2. Theoretical and Experimental Applications. P. K. van Gunsteren, W. F. and Weiner, and A. J. Wilkinson, editors. ESCOM Science Publishers, Leiden, The Netherlands. 182–212.
- 115.Norberg, J., and L. Nilsson. 2000. On the truncation of long-range electrostatic interactions in DNA. Biophys. J. 79:1537–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Patra, M., M. Karttunen, M. T. Hyvonen, E. Falck, P. Lindqvist, and I. Vattulainen. 2003. Molecular dynamics simulations of lipid bilayers: major artifacts due to truncating electrostatic interactions. Biophys. J. 84:3636–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Yonetani, Y. 2005. A severe artifact in simulation of liquid water using a long cut-off length: appearance of a strange layer structure. Chem. Phys. Lett. 406:49–53. [Google Scholar]
- 118.van der Spoel, D., and P. J. van Maaren. 2006. The origin of layer structure artifacts in simulations of liquid water. J. Chem. Theor. Comput. 2:1–11. [DOI] [PubMed] [Google Scholar]
- 119.Nina, M., and T. Simonson. 2002. Molecular dynamics of the tRNAAla acceptor stem: comparison between continuum reaction field and particle-mesh Ewald electrostatic treatments. J. Phys. Chem. B. 106:3696–3705. [Google Scholar]
- 120.Luty, B. A., and W. F. van Gunsteren. 1996. Calculating electrostatic interactions using the particle-particle particle-mesh method with nonperiodic long-range interactions. J. Phys. Chem. 100:2581–2587. [Google Scholar]
- 121.Hünenberger, P. H., and J. A. McCammon. 1999. Ewald artifacts in computer simulations of ionic solvation and ion-ion interaction: a continuum electrostatics study. J. Chem. Phys. 110:1856–1872. [Google Scholar]
- 122.Hünenberger, P. H., and J. A. McCammon. 1999. Effect of artificial periodicity in simulations of biomolecules under Ewald boundary conditions: a continuum electrostatics study. Biophys. Chem. 78:69–88. [DOI] [PubMed] [Google Scholar]
- 123.Weber, W., P. H. Hünenberger, and J. A. McCammon. 2000. Molecular dynamics simulations of a polyalanine octapeptide under Ewald boundary conditions: influence of artificial periodicity on peptide conformation. J. Phys. Chem. B. 104:3668–3675. [Google Scholar]
- 124.Boresch, S., and O. Steinhauser. 2001. The dielectric self-consistent field method. I. Highways, byways, and illustrative results. J. Chem. Phys. 115:10780–10792. [Google Scholar]
- 125.Boresch, S., and O. Steinhauser. 2001. The dielectric self-consistent field method. II. Application to the study of finite range effects. J. Chem. Phys. 115:10793–10807. [Google Scholar]
- 126.Kastenholz, M. A., and P. H. Hünenberger. 2004. Influence of artificial periodicity and ionic strength in molecular dynamics simulations of charged biomolecules employing lattice-sum methods. J. Phys. Chem. B. 108:774–788. [Google Scholar]
- 127.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 128.Ryckaert, J.-P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 129.McLachlan, A. D. 1979. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 128:49–79. [DOI] [PubMed] [Google Scholar]
- 130.Kirkwood, J. G. 1935. Statistical mechanics of fluid mixtures. J. Chem. Phys. 3:300–313. [Google Scholar]
- 131.Fixman, M. 1974. Classical statistical mechanics of constraints: a theorem and application to polymers. Proc. Natl. Acad. Sci. USA. 71:3050–3053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.van Gunsteren, W. F., and M. Karplus. 1982. Effect of constraints on the dynamics of macromolecules. Macromolecules. 15:1528–1544. [Google Scholar]
- 133.Markwick, P. R. L., N. L. Doltsinis, and D. Marx. 2005. Targeted CarÐParrinello molecular dynamics: elucidating double proton transfer in formic acid dimer. J. Chem. Phys. 122:054112. [DOI] [PubMed] [Google Scholar]
- 134.Williams, A. L. J., C. Cheong, I. J. Tinoco, and L. B. Clark. 1986. Vacuum ultraviolet circular dichroism as an indicator of helical handedness in nucleic acids. Nucleic Acids Res. 14:6649–6659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Bayley, P. M., E. B. Nielsen, and J. A. Schellman. 1969. Rotatory properties of molecules containing two peptide groups—theory. J. Phys. Chem. 73:228–243. [DOI] [PubMed] [Google Scholar]
- 136.Madison, V., and J. Schellman. 1972. Optical activity of polypeptides and proteins. Biopolymers. 11:1041–1076. [DOI] [PubMed] [Google Scholar]
- 137.Lee, H., T. A. Darden, and L. G. Pedersen. 1995. Molecular dynamics simulation studies of a high resolution Z-DNA crystal. J. Chem. Phys. 102:3830–3834. [Google Scholar]
- 138.Hünenberger, P. H. 1999. Lattice-sum methods for computing electrostatic interactions in molecular simulations. In Simulation and Theory of Electrostatic Interactions in Solution: Computational Chemistry, Biophysics, and Aqueous Solution. G. Hummer, and L. R. Pratt, editors. American Institute of Physics, New York. 17–83.
- 139.Glättli, A., X. Daura, D. Seebach, and W. F. van Gunsteren. 2002. Can one derive the conformational preference of a β-peptide from its CD spectrum? J. Am. Chem. Soc. 124:12972–12978. [DOI] [PubMed] [Google Scholar]