Abstract
Determining the relationships among and divergence times for the major eukaryotic lineages remains one of the most important and controversial outstanding problems in evolutionary biology. The sequencing and phylogenetic analyses of ribosomal RNA (rRNA) genes led to the first nearly comprehensive phylogenies of eukaryotes in the late 1980s, and supported a view where cellular complexity was acquired during the divergence of extant unicellular eukaryote lineages. More recently, however, refinements in analytical methods coupled with the availability of many additional genes for phylogenetic analysis showed that much of the deep structure of early rRNA trees was artefactual. Recent phylogenetic analyses of a multiple genes and the discovery of important molecular and ultrastructural phylogenetic characters have resolved eukaryotic diversity into six major hypothetical groups. Yet relationships among these groups remain poorly understood because of saturation of sequence changes on the billion-year time-scale, possible rapid radiations of major lineages, phylogenetic artefacts and endosymbiotic or lateral gene transfer among eukaryotes.
Estimating the divergence dates between the major eukaryote lineages using molecular analyses is even more difficult than phylogenetic estimation. Error in such analyses comes from a myriad of sources including: (i) calibration fossil dates, (ii) the assumed phylogenetic tree, (iii) the nucleotide or amino acid substitution model, (iv) substitution number (branch length) estimates, (v) the model of how rates of evolution change over the tree, (vi) error inherent in the time estimates for a given model and (vii) how multiple gene data are treated. By reanalysing datasets from recently published molecular clock studies, we show that when errors from these various sources are properly accounted for, the confidence intervals on inferred dates can be very large. Furthermore, estimated dates of divergence vary hugely depending on the methods used and their assumptions. Accurate dating of divergence times among the major eukaryote lineages will require a robust tree of eukaryotes, a much richer Proterozoic fossil record of microbial eukaryotes assignable to extant groups for calibration, more sophisticated relaxed molecular clock methods and many more genes sampled from the full diversity of microbial eukaryotes.
Keywords: eukaryotes, protists, molecular phylogenetics, molecular clock, systematics, superkingdoms
I would not say that the future is necessarily less predictable than the past. I think the past was not predictable when it started. (Donald Rumsfeld)
1. Eukaryote molecular phylogenetics—past and present
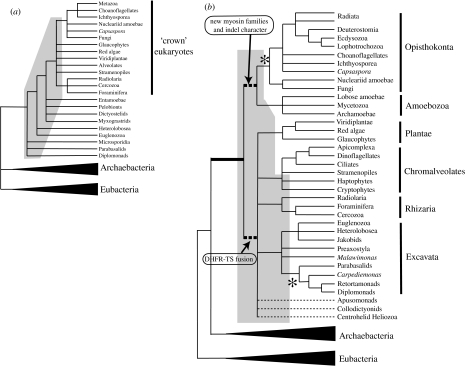
Large-scale eukaryote systematics was revolutionized with the development of small subunit (SSU) and large subunit (LSU) ribosomal RNA (rRNA) phylogenetics in the late 1970s and early 1980s (Sogin 1991), challenging earlier ideas about deep eukaryote phylogeny (Whittaker 1969; Taylor 1978). The broad picture of eukaryote evolution based on rRNA analyses ca 1991 (Sogin 1991) indicated an early divergence for several mitochondrion-lacking eukaryote lineages (diplomonads, parabasalids and microsporidia) followed by a ladder-like sequential divergence of a variety of protist lineages culminating in a so-called ‘crown’ radiation of many of the more familiar multicellular and unicellular groups (figure 1a). Ribosomal RNA analyses have yielded many important insights into deep eukaryote phylogeny including the sisterhood of metazoa and fungi (Wainwright et al. 1993), confirmation of the alveolate protist assemblage (ciliates, dinoflagellates and apicomplexa; Wolters 1991), and the discovery of the Cercozoa, a heterogeneous group of flagellates, algae and amoebae (Cavalier-Smith & Chao 2003). Unfortunately, other aspects of early rRNA phylogenies have misled many inferences about early eukaryote evolution over the past two decades. In particular the ‘crown’ versus ‘base’ distinction evident in most rRNA phylogenies (shaded grey in figure 1a) appears to be a methodological artefact that does not hold up once more sophisticated methods are applied and better taxonomic sampling is used (Philippe & Germot 2000; Simpson et al. 2002). It was on the basis of these analyses that amitochondriate protistan lineages such as diplomonads (e.g. Giardia), parabasalids (e.g. Trichomonas) and microsporidia (e.g. Encephalitozoon) became widely known as ‘early-branching’ eukaryotes whose cellular and genomic characteristics might represent an ancestral state for all eukaryotes (Sogin 1991). However, currently neither phylogenetics, discussed below, nor comparisons of cellular and genomic properties across eukaryotic diversity (see Embley 2006, this volume) provide compelling evidence for an early-branching status of these or any other eukaryote lineages.
Figure 1.
Alternative views of the tree of eukaryotes. (a) The topology typically recovered in rRNA phylogenies in the 1990s (Sogin 1991; Cavalier-Smith & Chao 1996). Multifurcations indicate poorly supported branches or different branching orders depending on the taxonomic sampling. The grey-shaded region of the tree indicates the part of the rRNA tree that is likely artefactual, resulting from long-branch attraction (LBA). Note that the late-branching position of the Foraminifera is shown as recovered in later rRNA analyses (Nikolaev et al. 2004). (b) A hypothetical phylogeny indicating the six major supergroups of eukaryotes (see Simpson & Roger (2004) and Keeling et al. (2005) for recent reviews). Dotted branches indicate lineages that do not clearly fall within any of the major groups. The placement of the root of the tree of eukaryotes is indicated by dihydrofolate reductase (DHFR)–thymidylate synthase (TS) fusion data (Stechmann & Cavalier-Smith 2002) and myosin gene family data (Richards & Cavalier-Smith 2005). Alternative positions for the root (Arisue et al. 2005) are indicated by asterisks. The grey shaded region depicts the parts of this hypothetical tree of eukaryotes that are not strongly recovered (with greater than 85% bootstrap support) in published single or multiple gene phylogenies (e.g. Hampl et al. 2005; Simpson et al. 2006).
2. Towards a consensus hypothesis of eukaryote relationships
During the 1990s, a number of protein genes were developed as alternative phylogenetic markers that began to lead to a different picture of early eukaryote evolution (Baldauf et al. 2000). Now, with the availability of large amounts of genomic data from diverse eukaryotes, more sophisticated phylogenetic methods coupled with improved understanding of unicellular eukaryotic diversity, a consensus hypothesis of the major ‘super-groups’ of eukaryotes is emerging. In this view, most known eukaryotes, can be placed into one of six major clades (figure 1b). The evidence for these groups ranges from improved taxonomic sampling in rRNA analyses (Rhizaria; Nikolaev et al. 2004), through phylogenies based on multiple nuclear and/or mitochondrial proteins (Amoebozoa, Arisue et al. 2002; Bapteste et al. 2002; Plantae, Rodriguez-Ezpeleta et al. 2005), gene replacement events (Chromalveolates; Fast et al. 2001; Patron et al. 2004) to ultrastructural synapomorphies (Excavata; Simpson 2003). It should be noted that the evidence is not strong for many of these groups and only a few of them are recovered in phylogenetic analyses of multiple genes with strong bootstrap support (figure 1b).
3. Rooting the tree of eukaryotes
One of the most controversial issues surrounding this new hypothesis of eukaryote diversity concerns the placement of the root. Here again, difficulties abound because the major groups are sometimes not well resolved and outgroup rooting of the eukaryote lineage with prokaryotic orthologs is fraught with phylogenetic artefacts (discussed later). An alternative method for rooting the eukaryote tree is to use characters such as gene fusions, insertion/deletion characters and the presence or absence of particular genes. For instance, Stechmann & Cavalier-Smith (2002) found that a fusion of the dihydrofolate reductase (DHFR) and thymidylate synthase (TS) genes was present in a number of eukaryote lineages they called the ‘bikonts’ but was apparently absent in Opisthokonts, Amoebozoa and in prokaryote outgroups. Later they pointed to a pyrimidine biosynthetic gene fusion that united the Opisthokonts and Amoebozoa (‘unikonts’) that, when considered in combination with the DHFR–TS data, suggested that the eukaryote root falls between bikonts and unikonts (Stechmann & Cavalier-Smith 2003b). However, the latter fusion has recently been detected in a putative bikont organism (Cyanidioschyzon, a red alga; Arisue et al. 2005), casting doubt on the original interpretation. This positioning of the root has most recently found support from analyses of myosin families; several specific myosin types as well as a single amino acid insertion in a myosin class II head domain appear to be unique to unikonts (Richards & Cavalier-Smith 2005; figure 1b).
However, these data are by no means conclusive. The DHFR–TS fusion has only been detected so far in a small selection of bikont taxa, with the inference of it being a synapomorphy based on other phylogenetic hypotheses that are themselves not definitively proven. For instance, it seems likely that these genes are lacking entirely in organisms such as diplomonads and parabasalids, and inferences that the fusion is ancestral to them can only be made if they form a clade with other DHFR–TS fusion-containing excavates (e.g. Euglenozoa), a relationship that, so far, remains unsupported by molecular phylogenies (Simpson et al. 2006). It is also possible that this gene fusion has occurred multiple times in evolution, or has spread horizontally by lateral gene transfer (LGT; Andersson 2005). In either case, it would no longer be considered a reliable phylogenetic marker.
The myosin data are also open to alternative interpretations. Many myosin gene families are completely undetectable in some genomes despite the fact that they were almost certainly present ancestrally in these lineages (Richards & Cavalier-Smith 2005). Therefore, the presence of the proposed new myosin sub-family genes in some, but not all, unikonts and the apparent absence of them in bikonts could be explained by loss or accelerated divergence in the latter organisms. Finally, while the insertion character in the myosin class II head domain is supportive of unikonts, single insertion/deletion events are weak characters, being subject to both frequent reversals and parallelisms (Bapteste & Philippe 2002).
4. Difficulties in inferring the deepest branches in the tree of eukaryotes
Although the general outlines of the scheme shown in figure 1b are becoming widely accepted as a working hypothesis for eukaryote phylogeny, four of the six major groups are not robustly recovered (i.e. with bootstrap support greater than 85%) by phylogenies of taxonomically well-sampled single or multiple concatenated genes. Furthermore, no molecular phylogenetic analysis published to date recovers this placement of the root on the tree. In fact, a recent study indicates this placement is significantly excluded on the basis of 22 protein-coding genes (Arisue et al. 2005), with two alternative root positions suggested (asterisks in figure 1b). Broadly speaking, the problems in recovering the deepest branches in the tree of eukaryotes using molecular phylogenetics stem from three sources: phylogenetic artefacts, lack of resolution and gene replacements from endosymbionts or other sources (LGT).
5. Phylogenetic artefacts
Phylogenetic artefacts (systematic error or bias) most commonly occur when the model of evolution is an inadequate description of the molecular evolutionary process (model misspecification). In this situation, if two or more distantly related sequences that form long branches in the phylogeny are separated by relatively short branches, the longest branches may artefactually group together; a phenomenon known as ‘long-branch attraction’ (LBA; Felsenstein 1978; Susko et al. 2004). This problem is particularly acute in rRNA analyses because the branch leading to the prokaryote outgroup sequences is extremely long and there is huge variation in the average rate of evolution in different eukaryotic lineages (Philippe & Germot 2000). Thus, the most divergent lineages typically emerge as the deepest-branching eukaryotes in the tree, clustering with the long branch leading to the prokaryote homologues. In rRNA trees, the most divergent lineages include the Foraminifera (Pawlowski et al. 1997), Microsporidia, Parabasalia and the diplomonads (Sogin 1991; figure 1a).
The example of the Microsporidia has been particularly well studied recently. This group of obligate intracellular parasites emerged deeply in trees of several molecules including SSU rRNA, LSU rRNA, elongation factor-1alpha (EF-1α) and EF-2 (reviewed in Keeling & McFadden (1998)). However, analyses during the 1990s of many other protein-coding genes showed a strikingly different position for Microsporidia as sister to, or included within, the Fungi (Keeling & McFadden 1998; Hirt et al. 1999; Baldauf et al. 2000). The latter position is now widely accepted to be correct. Recent analyses have given some insight into the nature of the phylogenetic artefacts at work. The LBA artefact is most pronounced when the substitution model used fits the data poorly. For instance, accommodating for among-site rate variation (ASRV) by removal of fast-evolving or constant sites or use of a gamma ASRV model dramatically reduces statistical support for the basal position of Microsporidia in SSU, LSU, EF-1α and EF-2 phylogenies (Hirt et al. 1999; Philippe & Germot 2000; Inagaki et al. 2004). Indeed, under these analytical conditions, for some unrooted EF-2 and LSU rRNA analyses, a Microsporidia+Fungi relationship becomes optimal, although poorly supported (Hirt et al. 1999; Van de Peer et al. 2000). For SSU rRNA, a fungal phylogenetic signal in microsporidian sequences has recently been recovered in unrooted likelihood-based analyses with improved taxonomic sampling combined with a sophisticated iterative procedure to model ASRV (Fischer & Palmer 2005).
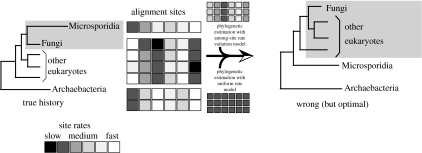
However, accounting for ASRV is only part of the story. The rate of evolution at a site can also change over the tree, a phenomenon that has been referred to as either ‘covarion-like’ evolution, heterotachy (Philippe et al. 2005) or across-tree-site rate variation (XTSRV; Inagaki et al. 2004). Ribosomal RNA genes and elongation factors of eukaryotes and prokaryotes have been shown to have significantly different rates at sites (Philippe & Germot 2000; Inagaki et al. 2004). In the case of EF-1α, eukaryotic sequences are typically more constrained and have more slowly evolving sites than Archaebacteria (Inagaki et al. 2004). Curiously, it appears that the rates-across-sites distribution in microsporidian homologues more closely resembles that of the Archaebacteria, especially with respect to fast-evolving sites. The affinity of the Microsporidia for the archaebacterial outgroup sequences disappears as sites with changes in rates across the Archaebacteria–eukaryote split are removed, indicating they are the source of the artefact (figure 2). Artefacts caused by heterotachy (XTSRV) have also been observed for other datasets (Lockhart et al. 2006) and this kind of model misspecification has recently been intensively investigated in a number of theoretical studies (Kolaczkowski & Thornton 2004; Susko et al. 2004; Spencer et al. 2005).
Figure 2.
Changing among-site rate variation (ASRV) distributions in EF-1α homologues cause Microsporidia to artefactually branch at the base of eukaryotes (Inagaki et al. 2004). The ASRV distribution (indicated by shaded boxes) of microsporidian sequences is more similar to the archaebacterial sequences, possibly because of parallel loss of constraints at sites that are functionally conserved in other eukaryotes. Under these conditions, phylogenetic methods that assume equal rates at sites or a simple ASRV distribution artefactually recover the Microsporidia as branching basally to other eukaryotes, grouping with the archaebacterial outgroup.
Another example concerns the Foraminifera, whose deeply branching position among eukaryotes in initial rRNA analyses (Pawlowski et al. 1996), has also been shown to be an LBA artefact by recent analyses of rRNAs with better taxonomic sampling (Nikolaev et al. 2004), protein phylogenies (Keeling 2001) and insertion-deletion characters (Archibald et al. 2003).
The case for an artefactually deep-branching position of diplomonads and parabasalids has been more difficult to prove. There is little doubt that these sequences tend to form much longer branches in phylogenies than most later-branching taxa, but an alternative phylogenetic position is not strongly supported by molecular data. Ultrastructural considerations strongly suggest a link between these taxa and other heterotrophic flagellates collectively called the Excavata (Simpson 2003). Some of these lineages, such as the jakobid flagellates, are less divergent and do not branch basally with diplomonads and parabasalids in rooted rRNA analyses (Simpson et al. 2002). Thus, if the Excavata are a clade, as suggested on ultrastructural grounds (shown in figure 1b), then the rooted rRNA analyses are likely misplacing the extremely long-branched diplomonads and parabasalids. Indeed, in rRNA analyses with diplomonads excluded, Carpediemonas membranifera (a short-branched sister lineage of diplomonads) emerges in the unresolved ‘crown’ region of the eukaryote tree, as do the parabasalid sequences (Simpson et al. 2002).
Philippe & Germot (2000) have shown that the crown versus base structure of the LSU and SSU rRNA trees all but dissolves when ASRV and XTSRV are taken into account. This is consistent with a general pattern that is observed for rooted phylogenies of eukaryotes for a number of single genes. Paralogue- or outgroup-rooted single gene phylogenies vary in which lineage is the deepest branching among eukaryotes, and the lineages that happen to be the fastest-evolving tend to branch basally. If the fastest-evolving sites are progressively removed from these datasets, the deep branching order among eukaryotes collapses (Philippe et al. 2000). Rather than retaining deep phylogenetic signal, it is more likely that these fast-evolving sites are most strongly affected by saturation as well as shifts in the molecular evolutionary process over time such as changes in the equilibrium nucleotide or amino acid composition (Foster & Hickey 1999). These and possibly other forms of model misspecification, when combined with the elevated rates of evolution in some eukaryote sequences, contribute to the LBA of these lineages to the outgroup.
6. Lack of resolution: saturation or a ‘big bang’ radiation?
Once the artefactual signal is removed, deep phylogenies of eukaryotes are usually left with little to no support for the branching order among major groups (Philippe et al. 2000; Stechmann & Cavalier-Smith 2003a; Arisue et al. 2005; Hampl et al. 2005; Harper et al. 2005; Simpson et al. 2006). This lack of resolution could result from rapid cladogenetic diversification of the major eukaryote lineages in a short period of time (the so-called ‘big-bang’ hypothesis; Philippe et al. 2000) or saturation of sequence changes on the billion-year timescale, or both. One might question how saturation might have erased the signal for the deepest branches of the eukaryote tree given that eukaryotes as a whole are often strongly resolved as monophyletic; how can some younger branches be unrecoverable due to saturation, whereas older ones are easily resolved? There are several reasons why this might be so. First, the branches separating the major eukaryote lineages may correspond to a much shorter time period than the separation of eukaryotes and prokaryotes; thus there are fewer changes in fewer sites supporting the former branches than the latter that could more easily be masked by saturation. Second, as different sites in molecules change at different rates, it is possible that the intra-eukaryote divergences occur in a region of the tree where the fast-evolving sites are saturated, yet slower-evolving sites did not accrue many phylogenetically informative changes. Finally, and most importantly, functional shifts in proteins that occurred at the prokaryote–eukaryote transition (discussed earlier) have created new functionally constrained ‘invariant’ sites in the eukaryote homologues (corresponding to either variable or differently constrained sites in prokaryotes) yielding a ‘fossilized’ eukaryotic signature in these proteins (Inagaki et al. 2004). Subsequently, then, during the diversification of eukaryotes, rapidly evolving sites could easily saturate, but these invariable sites would always remain fixed, or nearly so, and clearly separate prokaryote from eukaryote orthologues.
One last point regarding saturation deserves consideration. Intuitively, one might think that the presence of saturated sites in a sequence might only increase the ‘random noise’ in the data eroding support for branches, but would not bias the phylogenetic estimate. However, extreme saturation of some sites in a single sequence may introduce an LBA or long-branch-repels bias (depending on the proportion of saturated sites) that could give the misleading appearance of resolution in the tree (Susko et al. 2005). In this case, the bias shrinks with additional data. However, if two distantly related sequences share some saturated sites in common, they can be attracted to one another artificially, a bias that will worsen with sequence length. Thus, even with a large amount of data, an incorrect topology could be inferred with strong statistical support, regardless of the phylogenetic method employed and even if the correct substitution model is used. This, in part, could explain why the most highly divergent eukaryote sequences often tend to cluster with outgroup sequences, appearing as ‘early-branching’ lineages.
In any case, it will be rather difficult to disentangle the effects of saturation from a possible ‘big bang’ radiation of eukaryotes with molecular data alone. More robust fossil-calibrated molecular clock analyses (discussed later) and better understanding of how the Proterozoic microfossil record (Buick & Knoll 1999) and biomarker data (Brocks et al. 1999) relates to the emergence of extant eukaryotic lineages will be required.
7. Is phylogenomics the answer?
Theoretically, scaling up the amount of data analysed to include as many genes as possible should in principle provide better resolution in deep phylogenies. In agreement with this, several major groups of eukaryotes including the Opisthokonts (Philippe et al. 2004), the Conosa (Bapteste et al. 2002) (a subgroup of the Amoebozoa) and the Plantae (Rodriguez-Ezpeleta et al. 2005) have all recently been demonstrated to be monophyletic with strong statistical support by analyses of more than one hundred genes. Unfortunately, more data are not a panacea; while random phylogenetic error is quenched by added data, systematic error from model misspecification can be exacerbated, leading phylogenetic methods to converge on the incorrect tree with strong apparent statistical support (Phillips et al. 2004). This is illustrated by a recent study of the phylogenetic position of Microsporidia and cryptomonad nucleomorphs using more than one hundred genes (Brinkmann et al. 2005). Using the full datasets, these taxa always artefactually branched basally among eukaryotes. When genes were sorted according to the degree of divergence of the microsporidian or nucleomorph homologues relative to other sequences, and the most divergent orthologues from these taxa were progressively replaced with missing data, the bootstrap support shifted from strong for the basal positions (with no data removed) to strong support for their correct positions. This result is in agreement with another study (Thomarat et al. 2004) that showed that the basal versus fungal position of Microsporidia in single gene phylogenies was correlated with the high versus low rates of evolution respectively for the microsporidian homologues.
Furthermore, phylogenomic analysis is not simply phylogenetic analysis writ large; modelling the evolution of multiple gene data deserves careful attention. For example, a given lineage can be slowly evolving for some genes, whereas for other genes it may be fast evolving. If these genes are simply concatenated and analysed, then the branch lengths and ASRV parameters that are estimated will be averages that poorly describe each of the genes individually, yielding model misspecification that can lead to phylogenetic artefacts. Solutions that have been explored include estimating separate branch length and ASRV parameters for each gene (‘separate analysis’) or assuming that branch lengths from each gene are proportional to one another (Pupko et al. 2002; Bevan et al. 2005). These approaches have been shown to yield significantly better fits to real data and, in a number of cases, have yielded significantly different, and more reliable, phylogenetic estimates (Ruiz-Trillo et al. 2004; Bevan et al. 2005; Simpson et al. 2006). However, in other cases using the ‘separate’ versus concatenated approaches appears to make little difference (Brinkmann et al. 2005). For these analyses, other forms of model misspecification likely contribute to the LBA problems observed.
8. Endosymbiotic and lateral gene transfer
Finally, a widely overlooked potential confounding factor for estimating deep eukaryote phylogeny is endosymbiotic gene transfers and LGTs. LGT appears to be rampant among prokaryotic genomes (Gogarten et al. 2002), but the situation in eukaryotes is less well understood due to the relative paucity of full genome sequences from diverse eukaryotic microbes. A significant contribution of genes via endosymbiotic gene transfer from chloroplasts or mitochondria to eukaryotic nuclear genomes has been known for quite a while, and recent evidence suggests that it may be quantitatively more important than previously realized (Martin et al. 2002; Esser et al. 2004). Furthermore, the history of photosynthetic eukaryotes is littered with secondary and tertiary endosymbioses of plastid-containing eukaryotes that could have contributed large numbers of genes to their host lineages (Archibald 2005). Evidence is also accumulating for LGT from non-organellar sources in eukaryotic genomes. Although most reports are of prokaryote-derived genes in protists, some eukaryote-to-eukaryote transfer events have been demonstrated (see Andersson et al. (2005) for a review). Therefore, because LGT and endosymbiotic gene transfer could affect some genes in multiple gene analyses, it is important to test for phylogenetic congruence between the gene families. Several smaller multigene analyses (Hampl et al. 2005; Simpson et al. 2006) have examined this issue and found that different phylogenetic estimates can be obtained when genes conflicting with the bulk phylogenetic signal are removed. However, it is unclear at this point whether these conflicting signals are due to phylogenetic artefacts or eukaryote-to-eukaryote gene transfers. In the phylogenomic analyses by Brinkmann et al. (2005), apparently none of the individual genes showed clear signs of transfer between lineages.
9. Distinguishing between alternative explanations for conflicting phylogenetic signals
We have discussed both methodological and biological causes for conflicting phylogenetic signals in different genes. An obvious question, then, is how to tell which of these causes is responsible for a given case of incongruence. A general approach is to first investigate the datasets and their phylogenies for obvious signs of artefacts such as long branches on phylogenies and violations of the assumptions of the phylogenetic models. Model fitting using a variety of sophisticated substitution models should be performed prior to analysis and the impact of different models on the branching orders recovered and their bootstrap support should be investigated. Phenomena such as heterotachy, changing amino acid composition over the tree, coevolution between sites, and site-specific substitution processes have yet to be adequately modeled in most phylogenetic estimation software; but some of them can be assessed by statistical tests (Susko et al. 2002; Tillier & Lui 2003; Foster 2004; Lartillot & Philippe 2004). Unfortunately, there are likely many other ways in which real data deviate from phylogenetic models, for which we have inadequate tests, and whose impact on phylogenetic estimation is currently unknown.
If the aberrant branching pattern is not associated with obvious model violations and long-branching taxa, but is strongly supported by statistical topology tests or bootstrap analysis, then biological explanations such as: LGT, recombination between orthologues from different species or gene duplication (paralogy) and differential loss can be considered. These explanations can sometimes be further bolstered or refuted by the presence of insertion/deletion characters in the alignment, shared extra protein domains and improved taxonomic sampling (Andersson 2005).
In any case, neither artefacts nor biological causes for phylogenetic incongruence should be proposed simply as ad hoc explanations of the data. It is important to treat them as alternative hypotheses that should be tested by gathering more data and applying rigorous statistical methods.
10. Dating ancient divergences with molecular clocks
It should be clear from the foregoing discussion that the recovery of the phylogenetic relationships among the major eukaryote groups is extremely challenging. Yet this task pales in comparison with the difficulties that are encountered in dating these divergences using molecular clock methods for several reasons. First, estimates of divergence dates are only meaningful if the phylogeny they are based upon is correct in the first place. For instance, the date of the last common ancestor of extant eukaryotes cannot be estimated unless we know for certain where the root of the eukaryote tree lies. Second, molecular dating requires not only a correct tree, but also accurate models of how substitutions accrue in the genes under consideration over billion-year time-scales as well as how the rates of these substitutions have changed over the tree of life. Finally, it is necessary to calibrate the evolutionary process against dates of divergence from the fossil record that have error of several sorts associated with them including the error inherent in the dating of the associated geological strata and a systematic bias due to the fact that the true divergence date must be older than the first appearance of the descendant taxa in the fossil record (Hedges & Kumar 2004). Clearly, there are many assumptions underlying molecular clock dating and hence there are many potential sources of error.
The difficulties intrinsic to the dating of ancient divergences using molecular data are reflected in the disparities of date estimates for ancient divergences obtained to date. For instance, the divergence date estimates for the prokaryote–eukaryote divergence vary by roughly twofold ranging from ca 2200 million years ago (Myr ago; Feng et al. 1997) to 3970 Myr ago (Hedges et al. 2001). Estimates for the earliest divergence among extant eukaryote lineages vary by a similar factor with a recent study by Douzery et al. (2004) suggesting eukaryotes first diverged ca 1100 Myr ago, whereas Hedges et al. (2004) recovered ca 2300 Myr ago for this divergence time. Why are these estimates so different? In the latter case, one reason (of several) for the discrepancies is the different phylogenies of eukaryotes assumed by the two studies. However, other factors likely contribute to these apparently different age estimates including the different molecular clock methods employed and underestimated error. In the following sections, we explore the various sources of bias and error that are inherent in molecular clock dating studies of ancient divergences, beyond the acknowledged problem of generating accurate phylogenies.
11. Molecular dating of deep eukaryote divergences—some test cases
We have chosen to examine in detail two recently published datasets. The first dataset (abbreviated PB) was assembled by Peterson and Butterfield (Peterson & Butterfield 2005) and consists of seven genes, six nuclear and one mitochondrial, containing 2052 aligned amino acid sites. Their goal was to date the origin of the Eumetazoan groups and correlate putative changes in metazoan organization with changes in the surrounding microbial ecosystems implied by the microfossil record. The second dataset comes from a study of the origin and diversification of the major eukaryote lineages (Douzery et al. 2004). This dataset (abbreviated DZ) is much larger, consisting of a concatenated alignment of 129 protein genes containing a total of 30 399 amino acid sites sampled from a wide range of eukaryotes. Using sequence alignments and fixed topologies from the PB and DZ studies, the variation in date estimates and confidence intervals were assessed by investigating the impact of: the substitution model employed, the molecular dating method used, the way in which fossil date constraints were imposed, the uncertainty in branch length estimates, the prior assumptions, and the way in which multiple gene data were treated.
12. Properties and assumptions of the methods
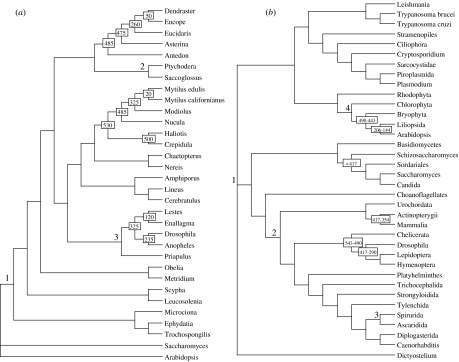
In all analyses described below, the topology of the phylogenetic trees in the original published studies were treated as correct and fixed, and the impact of various sources of error on the date estimates of a few select nodes were investigated (figure 3). Fossil dates used for calibration were also taken from the original studies and are shown on specific nodes in the trees in figure 3. We chose to examine four different molecular clock methods whose assumptions and optimality criteria are detailed in table 1.
Figure 3.
Assumed topologies for molecular clock studies. (a) Topology used by Peterson–Butterfield (PB) in their analyses (Peterson & Butterfield 2005). (b) Topology from the Douzery (DZ) dataset (Douzery et al. 2004). The nodes under examination in the current study are labelled by the large numbers. Boxed numbers indicate fossil dated (in millions of years) constrained nodes taken from the original studies.
Table 1.
Summary of molecular clock methods used and their assumptions.
| method | assumptions |
|---|---|
| Langley–Fitch (r8s) | strict molecular clock |
| substitutions over branches follow Poisson process with fixed rate on different branches | |
| branch lengths=observed no. of substitutions | |
| NPRS (r8s) | relaxed molecular clock |
| rates, r, change gradually over a fixed tree additive penalty function: a | |
| logarithmic penalty function: | |
| choose dates and rates to minimize P | |
| penalized likelihood (r8s) | rates change gradually over a fixed tree |
| substitutions over branches follow Poisson process with different rates on different branches | |
| rate penalty, P, as above | |
| choose dates and rates to maximize lnL−νP, where L is the likelihood, P is as defined above and ν is a penalty coefficient | |
| Bayesian (Multidivtime) | likelihood function approximated by multivariate normal distribution centred on the ML estimate |
| log-normal rate model with E[rd]=rpa | |
| more deviation from parental rates expected over longer time periods | |
| prior distributions on the age of the tree and parameters of the log-normal model | |
| rates and dates derived from mean of their posterior probability distribution |
rd and rp are the rates of the daughter and parental nodes, respectively.
The Langley–Fitch method (LF) is a ‘strict’ molecular clock method that requires the rate of substitution to be fixed over the tree (Langley & Fitch 1974), an extremely restrictive assumption. By contrast, the non-parametric rate smoothing (NPRS; Sanderson 1997), penalized likelihood (PL; Sanderson 2002) and the Bayesian log-normal method (Kishino et al. 2001) are all ‘relaxed’ molecular clock methods that allow the rates of evolution to change over the tree in a smooth manner. The latter methods are more realistic, but require many additional assumptions on how exactly rates vary over the tree (table 1). These and other methods have been recently reviewed by Welch & Bromham (2005).
Two programs that implement these methods were used for the estimation of ages and confidence intervals. For the LF, NPRS and PL methods the program r8s version 1.7 was used (Sanderson 2003). We also used the Bayesian relaxed clock method implemented in the Multidistribute package (ESTbranches/Multidivtime5b; Kishino et al. 2001).
13. The impact of the substitution model on branch length estimates
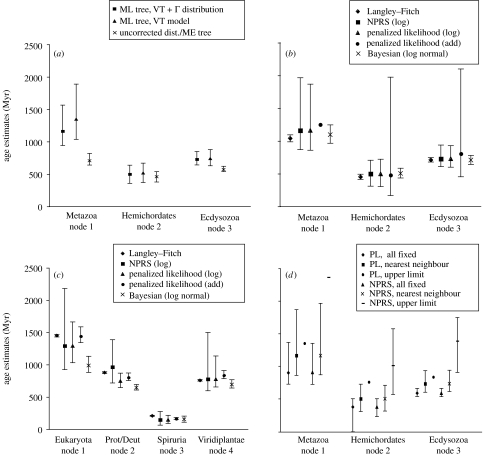
To get age estimates, Peterson & Butterfield (2005) used the LF method with a fixed tree with branch lengths generated by uncorrected distance/minimum evolution (ME) analysis as well as maximum-likelihood (ML) distance with complex models such as the VT model of amino acid change coupled with a gamma model for ASRV (the VT+Γ model). They argued that the simplest method (uncorrected-distances/ME) gave estimates that were most congruent with the fossil record and, therefore, should be preferred to more complex models. We have repeated these analyses for the PB dataset and the resulting age estimates and confidence intervals are shown in figure 4a for the PL method. A huge discrepancy is found between the uncorrected distance/ME based-estimates and the model-based ML methods, with the differences most pronounced for the deepest node. The uncorrected-distance/ME analysis indicates that the primary divergence within the metazoa occurred 639–818 Myr ago, a much more recent age than the estimates from the ML methods that indicate divergence times of 1162 Myr (VT+Γ) and 1346 Myr (VT), with confidence intervals spanning 620 Myr and 840 Myr, respectively.
Figure 4.
(a) Variation in age estimates and confidence intervals for the PB dataset under differing models of substitution. The trees and branch lengths were optimized by ML using Tree-Puzzle 5.2 (Schmidt et al. 2002) under the VT model (Müller et al. 2002) assuming equal rates or assuming a gamma distribution for ASRV (VT+Γ), or in PAUP* (Swofford 2000) using uncorrected distances and minimum evolution (ME). Age estimates and confidence intervals were generated using r8s (Sanderson 2003) under penalized likelihood (PL) with a logarithmic penalty with cross-validation optimization of the penalty coefficient. (b) Variation in age estimates under different molecular clock methods for the PB dataset. (c) Variation in age estimates under different molecular clock methods for the DZ dataset. Age estimates were generated for LF, NPRS and PL models in r8s using a tree with ML branch lengths using the VT+Γ model for the PB dataset and the Whelan and Goldman plus gamma (WAG+Γ) model (Whelan & Goldman 2001) for the DZ dataset. Bayesian estimates were generated using EST branches and Multidivtime5b (Kishino et al. 2001). (d) The effect of different schemes for constraining fossil dates on age estimates and confidence intervals. The branch lengths used were generated by ML with the VT+Γ model. Ages were generated in r8s employing either the NPRS or PL methods with a logarithmic penalty. Constraint models were either (i) all nodes fixed to the corresponding fossil date (‘all fixed’), (ii) nodes set with fossil dates as a minimum age and 1500 Myr as a maximum (‘upper limit’) or (iii) nodes set with their fossil dates as a minimum age and the corresponding fossil dates of the parent node age as a maximum (‘nearest-neighbour’). Cross-validation optimization of the PL penalty coefficient was not employed for analyses shown in (b), (c) and (d).
The discrepancy in the age estimates is not unexpected because the uncorrected distance/ME branch lengths of a tree are guaranteed to be underestimates of the true branch lengths as they ignore multiple substitutions and ASRV. This underestimation should get much worse in deeper portions of the tree, as multiple substitutions accrue (Susko et al. 2004). Although it is virtually certain that this is a poor approximation of the evolutionary process, it is difficult to assess this statistically, as the uncorrected distance does not derive from a Markov model of sequence change. However, Peterson and Butterfield claim that uncorrected distance/ME branch lengths were very similar to those from a Poisson-corrected distance model (Peterson & Butterfield 2005). Therefore, as a proxy for uncorrected distance/ME, the relative fit of the Poisson model can be compared with the more complex models—the VT model and the VT+Γ model—using likelihood ratio (LR) tests (Huelsenbeck & Rannala 1997). Likelihood ratio tests strongly reject the Poisson model in favour of the VT model (here we have approximated the degrees of freedom for the LR of Poisson versus VT, by the degrees of freedom for the LR of Poisson versus a fitted-GTR model, yielding a conservative test). The VT model, in turn, is soundly rejected in favour of the VT+Γ model (table 2).
Table 2.
Results of likelihood ratio tests for the Peterson–Butterfield (2005) dataset under different models.
| model comparison | Δln(L) | d.f. | p-value |
|---|---|---|---|
| Poisson versus VT a | 4353.48 | 210 | <0.0001 |
| VT versus VT+Γ | 3733.52 | 1,0b | <0.0001 |
| VT+Γ clock versus VT+Γ no clock | 191.50 | 30 | <0.0001 |
| VT+Γ equal bls versus VT+Γ individual bls | 2076.68 | 372 | <0.0001 |
Although the Poisson model is not nested within the VT model, this likelihood ratio test is based on approximating the degrees of freedom by those appropriate for a Poisson versus a fitted-GTR model comparison (see the text for a justification of this procedure).
VT model corresponds to VT+Γ, where α=∞, a boundary of the parameter space. The likelihood ratio under the null hypothesis is thus 0.5χ2d.f.=1+0.5χ2d.f.=0.
These tests indicate that the VT+Γ model is a much better description of the process that generated data than the simpler models and therefore the branch length estimates, and hence time estimates and confidence intervals, should be more accurate, provided they are not biased due to some other unaccounted form of model misspecification. One source of bias that is likely present in these analyses is caused by the failure to model the different evolutionary dynamics of the different genes in the dataset (discussed further in §17).
14. The impact of different molecular dating methods
We assessed the divergence date estimates of several nodes in the PB (figure 4b) and the DZ (figure 4c) datasets yielded by the strict molecular clock (LF), the NPRS, the PL and the Bayesian/log-normal methods.
Interestingly, for the PB dataset, the age estimates for the various nodes given by these methods all fall in a similar range (figure 4b). For the DZ dataset, there is a wider range for ages estimates with the Bayesian method giving the youngest ages for eukaryotes (986 Myr ago) and the LF method yielding the oldest (1448 Myr ago). The largest difference between methods is in the size of the confidence/credible intervals for age estimates. Under the LF method, confidence intervals are consistently much smaller than any of the relaxed clock models. PL and NPRS methods give the widest confidence intervals even for relatively shallow nodes (i.e. spanning more than 1700 Myr in some cases—see node 2, figure 4b), while the Bayesian analysis gave medium-sized credible intervals.
We used a variety of rigorous methods to try to choose between the alternative molecular clock dating methods. First, we tested whether a ‘strict’ molecular clock model can be statistically rejected using LR tests of model fit (table 2). Our results indicate that it can be soundly rejected indicating that the LF model can be excluded from further consideration in favour of the relaxed molecular clock methods.
For the relaxed clock procedures implemented in r8s, it is possible to estimate ages under either a logarithmic or additive penalty for the NPRS and PL methods (see table 1). It is clear that additive penalties tend to yield age estimates that are consistently older (figure 4b,c). Additionally, the confidence intervals determined under additive penalties were significantly larger than those under logarithmic penalties, in some cases spanning more than ca 1500 Myr, although on occasion the search for confidence intervals in r8s failed entirely for unknown reasons (e.g. figure 4b, node 1). Under NPRS with additive penalties, some of the deeper nodes on the PB dataset reached ages older than the estimated age of the Earth (data not shown)! We assessed the relative fit of these penalty functions to the data using a method called cross-validation, whereby portions of the tree are randomly removed from the estimation and rates are predicted and compared to the original estimates (Sanderson 2002). The PL method with the logarithmic penalty consistently had the smallest cross-validation error and is therefore optimal. Note that for the PL model, the penalty coefficient (table 1) used was chosen to minimize cross-validation error.
Unfortunately, it is not straightforward to directly compare the fit of the model used in the Bayesian analysis with PL. Recent simulation studies do suggest that the PL method tends to overestimate small rates and underestimate large rates, whereas the Bayesian method with the log-normal model does not show an obvious bias (Ho et al. 2005). This could mean the relatively younger date estimates yielded by Bayesian approach are more trustable. However, it is hard to assess the relative reliability of the large confidence intervals on dates from PL with log-rate penalties as compared to the medium-sized credible intervals of the Bayesian method. The differences likely lie in the different assumptions made by these methods, the validity of which is largely unknown. One point to note is that the Bayesian method employs a multivariate normal approximation to the likelihood function that will yield overly narrow credible intervals if the true likelihood function were multimodal. Whether or not the likelihood function is multimodal for real data should be tested in the future.
15. Constraining fossil calibration dates
There is considerable controversy over how to incorporate fossil dates into molecular clock analyses and specifically how to incorporate various sources of error into date constraints (Graur & Martin 2004; Hedges & Kumar 2004; Reisz & Muller 2004). Here, we used three different methods of applying the same set of fossil constraints to the PB dataset. The first method was to simply fix the nodes corresponding to the fossil divergence dates, as was done by Peterson & Butterfield (2005). However, it has been argued that fossil dates should be considered more as minimum bounds rather than central values in an error distribution (Hedges & Kumar 2004). Therefore, as an extreme alternative, we constrained the same nodes with the fossil date as the minimum age and 1500 Myr ago as a maximum age (‘upper limit’ constraints). Finally, we constrained the nodes with the fossil date as the minimum age and, where applicable, used the minimum age of the parent node as a maximum age (‘nearest-neighbour’ constraints).
These different methods gave drastically different estimates and confidence intervals, indicating that the controversies over the application of age constraints are well founded. Under fixed constraints, age estimates were younger and confidence intervals were smaller than under nearest-neighbour or the upper limit constraints (figure 4d), regardless of the method employed. Setting the maximum age of the nodes to 1500 Myr ago skewed the estimates toward the upper bound, giving extremely old age estimates for nodes deeper than the constraints, an effect that was most evident with the NPRS method. Under fixed age constraints NPRS gave 902 Myr ago for the earliest divergence within metazoa, whereas for upper limit constraints it gave an absurd estimate of 2365 Myr ago for the same node (figure 4d, node 1). With both NPRS and PL, the upper limit constraint method prevented r8s from estimating confidence intervals. As the nearest-neighbour constraints method gave age estimates in between the two extremes, and appears to be a logical method for constraining nodes, we chose to use this method with the PL/log-penalty method for the remainder of the analyses.
16. Accounting for error in branch length estimates
The LF and PL methods make the fundamental assumptions that the branch lengths from the input tree are observed counts of substitutions that are outcomes of a Poisson substitution process (table 1). These assumptions are grossly incorrect. As discussed earlier, for the PB dataset, a Poisson process can be soundly rejected in favour of more complex models of amino acid substitution (e.g. VT+Γ model). Furthermore, the branch lengths from the ML tree input into these methods are not direct observations (counts), they are model-based estimates, and, as such, they are associated with error. Unfortunately, the impact of the violation of the Poisson process on the PL calculations cannot be easily investigated using r8s. However, the importance of the estimation error associated with the branch lengths can be assessed through bootstrap analysis.
We compared the confidence intervals of the single ML tree with the confidence intervals derived from 100 trees with bootstrap re-estimated branch lengths (figure 5a). Bootstrap 95% confidence intervals were consistently larger—on average by ca 200 Myr for the three nodes tested—than the confidence intervals generated using the ML topology alone (the latter are based on the curvature of the likelihood surface). This confirms our suspicion that the error associated with branch length estimates is significant and should be taken into account by bootstrapping in LF-, NPRS- and PL-based analyses.
Figure 5.
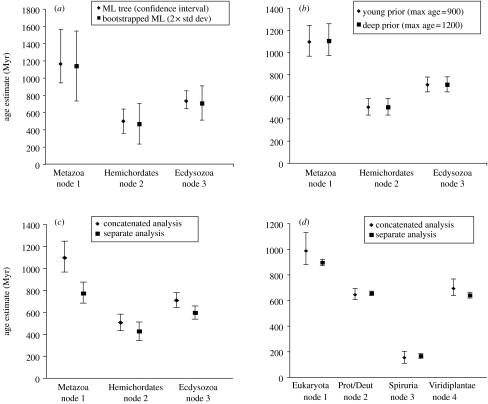
(a) Effect of bootstrapping on confidence intervals under penalized likelihood with a logarithmic penalty with cross-validation optimization of the penalty coefficient. 100 bootstraps of the PB dataset ML tree were generated using Puzzleboot (http://www.tree-puzzle.de) and Tree-Puzzle 5.2. In r8s, confidence intervals were generated for the single tree and the 100 bootstraps. Standard deviations from the bootstrapped trees were also obtained for the nodes of interest. (b) Effect of different priors under Bayesian analysis with Multidivtime5b. Two different prior distributions centred around two different root-to-tip age estimates were used and the posterior mean age estimates for nodes and their 95% credible intervals are shown. (c,d) Age estimates for datasets treated as a single large concatenate of genes or as ‘separate’ loci (Thorne & Kishino 2002). Estimates and 95% credible intervals for the PB dataset (c) and the DZ dataset (d) under these conditions are shown.
17. Priors and treatment of multiple gene data in Bayesian analyses
The Bayesian method used here estimates the posterior probability of dates of nodes and rates on branches conditional on a fixed tree topology, rate of evolution model parameters, and the fossil-date constrained nodes. This posterior distribution is a function of the likelihood of the data given the tree and model parameters and a number of prior probability distributions on rates and dates (Kishino et al. 2001). One of the priors that must be set by the user is the mean age of the tree from tip to root. If the data strongly discriminate between alternative dates and rates, then the likelihood function should dominate the shapes of the posterior distributions, otherwise the priors will dominate. We analysed the PB dataset under two different sets of priors: one with an estimated root to tip age of 900 Myr, and one with an age of 1200 Myr. A difference in the prior of 300 Myr hardly changed the age estimates or the 95% credible intervals at all (figure 5b), indicating that the posterior distribution of the divergence time estimates is little affected by the prior distribution on the age of the root node.
Another important aspect of relaxed clock analyses is how multiple gene data are treated. As discussed earlier, it is common in phylogenetic analysis of multiple gene data to simply concatenate genes together into one large alignment and treat this as if it were a single gene (e.g. Douzery et al. 2004; Blair & Hedges 2005; Peterson & Butterfield 2005). However, as with phylogenetic estimation, a concatenated gene approach is undesirable if the rates of evolution of particular lineages vary over different genes. Fortunately, Thorne & Kishino (2002) have recently implemented separate analyses in their Multidivtime program so the impact of concatenated versus separate analysis can be directly assessed. For the PB dataset, the separate analysis had a drastic effect on the date estimates—all of the nodes were estimated to be significantly younger than in the concatenated approach (figure 5c). This effect was most pronounced for the deepest node the age of which moved from 1095 Myr ago (concatenated) to 770 Myr ago (separate). Interestingly, this estimate is much closer to the original date preferred by Peterson & Butterfield (2005) on the basis of the fossil record. The impact of concatenated versus separate analysis on the DZ dataset was qualitatively quite different. The date estimates coming from the two methods were quite similar, although for the deepest node (the root of eukaryotes), the separate analysis gave an age of eukaryotes of 895 Myr ago, which is roughly 90 Myr younger than the concatenated analysis. The more dramatic impact was on the credible intervals; they were much narrower in the separate versus the concatenated analysis (figure 5d). The reasons for these effects are not obvious but may be related to the number of generations of the Monte Carlo Markov Chain procedure required to ensure convergence (i.e. the much larger parameter space of the separate analysis likely requires many more generations to be run than were possible here due to computational limitations). However, it is possible to test whether modelling the genes as separate versus concatenated is statistically justified. An LR test indicates that for both PB (table 2) and the DZ datasets (not shown), by treating the genes separately a statistically significant improvement in model fit is achieved.
18. The prokaryote–eukaryote divergence—pushing molecular dating too far?
Unfortunately, the difficulties in inferring the divergence time between prokaryotes and eukaryotes are likely to be even worse than dating the divergences among major eukaryote groups. A major reason for this is that, for many proteins conserved between eukaryotes and Archaebacteria (the nearest prokaryotic relatives of eukaryotes), there have been large functional shifts that have occurred during this evolutionary transition. For instance, there is good evidence that major site rate shifts have occurred between prokaryotes and eukaryotes in genes involved in translation including SSU rRNA, LSU rRNA and EF-1α owing to changing constraints on these molecules in prokaryotes versus eukaryotes (Philippe & Germot 2000; Inagaki et al. 2004) and the complexification of the translational apparatus in eukaryotes (Aravind & Koonin 2000). Similarly, Hedges et al. (2001) in their molecular clock analyses of prokaryotes and eukaryotes noted that estimates of the gamma shape parameter governing ASRV systematically became larger with increasing phylogenetic depth, a phenomenon that indicates that the rates at sites are changing over the tree (see appendix A.2 in Gu 1999).
Such rate shifts across the prokaryote–eukaryote divide cause several problems for molecular dating. First, a single gamma distribution for ASRV no longer correctly models how rates are evolving over the tree, and any method that estimates the numbers of substitutions along branches based on this assumption will be violated—this applies to all of the relaxed molecular clock methods currently available. However, the problem is worse than simple model misspecification. Consider a simple case of two sequences with an unknown distance (branch length) between them and an unknown ASRV distribution along the sequences. For simple models (e.g. the Poisson model), it is mathematically impossible to simultaneously obtain a unique ML estimate of the distance and the shape of the ASRV distribution for this pair of sequences (E. Susko & M. Steel 2005, personal communication). Similarly, for two subtrees (for example, Archaebacteria and eukaryotes) with different ASRV distributions separated by a central branch b with a third ASRV distribution, it will be impossible to estimate the latter distribution and the length of b simultaneously. In reality, the substitution process is more complex than a Poisson model and the rate distribution on the central branch is not totally uncorrelated with the ARSV distributions of the two subtrees. However, this argument suggests that, at the very least, it will be rather difficult to get an accurate estimate of the number of changes between Archaebacteria and eukaryotes in the presence of significant ASRV shifts across this split.
In addition, functional shifts in proteins between Archaebacteria and eukaryotes indicate that along this branch the rate of evolution was not constant—there was likely a period of accelerated evolution due to positive selection for a different function. This is illustrated by the extreme functional and, consequently, sequence divergence between paralogues such as α- and β-tubulin, which, if a strict molecular clock is assumed, must have duplicated prior to the origin of the Earth (Doolittle 1992)! Clearly, periodic accelerations in rates during functional divergence violate the relaxed molecular clock assumption of smoothly changing rates over the tree (table 1) and will make inferring the age of the split a significant challenge.
Finally, there continues to be a debate over the quantity and quality of the genetic contribution to eukaryotes from the archaebacterial versus eubacterial lineages. Almost a decade ago, it was shown that dating the divergence between eukaryote and prokaryotes depended heavily on determining which genes in eukaryotes were of ‘endosymbiotic’ (i.e. from the mitochondrial or chloroplast eubacterial endosymbionts) versus nucleocytoplasmic (archaebacterial-related) origin (Doolittle et al. 1996; Feng et al. 1997). This problem has become even more acute in the past few years, as the majority of genes in some eukaryote genomes appear to more similar to eubacterial than archaebacterial orthologues, calling into question their assumed nucleocytoplasmic origins (Esser et al. 2004). Obviously, the origins of the eukaryote homologues included in multiple-gene datasets need to be clearly established before any progress can be made in molecular dating analyses of the prokaryote–eukaryote divergence.
19. Concluding remarks
Much progress has been made over the past few years in determining the deep structure of the tree of eukaryotes (figure 1b) and we can anticipate more progress towards this goal as genomic data from the full diversity of eukaryotes become available and phylogenomic methods are refined. However, it will be difficult to make similar progress in determining the times of diversification of the major eukaryote lineages using relaxed molecular clock analysis alone. A key problem is that neither the position of the root of the eukaryote tree nor the monophyly of some of the major eukaryotic taxa has been definitively established. In addition, most of the fossil calibration points that are currently used for molecular dating of major eukaryote groups correspond to relatively recent Phanerozoic divergences (Hedges et al. 2004; Peterson & Butterfield 2005), whereas the deepest divergences in the eukaryote tree are probably anywhere from 2 to 10 times as old. The large confidence intervals we have observed indicate the error from extrapolation is likely to be quite significant. Once a robust tree of eukaryotes becomes available, a better way forward will be to improve the sampling of Proterozoic microfossils that correspond to a wide variety of extant eukaryote taxa (e.g. the vase-shape microfossils (Porter et al. 2003) or Bangiomorpha (Butterfield et al. 1990)) and to use a multitude of these to calibrate large multigene molecular clock analyses. Furthermore, there are many assumptions underlying current relaxed molecular clock methods that have yet to be rigorously tested by simulation and by using real data, where divergence times are already known. Properly accounting for error in such analyses is of paramount importance so as to avoid confusing and apparently conflicting results from different methods and datasets. Our analyses have touched on a few sources of error and bias, but there are a myriad of other significant sources we did not examine, such as the accuracy of the phylogenetic tree used, the error in fossil assignments and dates (Graur & Martin 2004; Reisz & Muller 2004), and the realism of the rate of evolution models (Aris-Brosou & Yang 2003; Ho et al. 2005; Welch et al. 2005).
Finally, it is important to remember that there are inherent limits to any methodology. It is absurd to think that our current relatively simple stochastic substitution models and models of the rate of evolution over the tree of life adequately describe the process of molecular evolution over billions of years of evolution. Yet, how much more complex and realistic can these models be made, given that there is only a finite amount of data available from which their parameters can be estimated? In the case of the prokaryote–eukaryote split, it is possible—even likely—that molecular clock dating analyses cannot, in isolation, determine these ancient divergence times with any certainty. Even so, we should not give up trying to use them in conjunction with geochemical and paeleontological data to provide better resolution than is currently available.
Acknowledgments
We would like to thank Ed Susko, Mike Steel, Yuji Inagaki and the members of the Statistical and Evolutionary Bioinformatics group at Dalhousie University for helpful discussions and insights. Thanks are due also to Katherine Dunn and Jessica Leigh for help with the Multidistribute package; John Archibald, Iñaki Ruiz-Trillo, Matt Spencer, Alastair Simpson and an anonymous reviewer for helpful comments on the manuscript. We thank Yuji Inagaki and Iñaki Ruiz-Trillo for creating figure 2. This work was supported by Discovery grant #227085-2005 from the Natural Sciences and Engineering Research Council (NSERC) and grant MOP-62809 from the Canadian Institutes of Health Research (CIHR) awarded to A.J.R. L.A.H. is supported by an NSERC and a Killam graduate scholarship. A.J.R. is supported by a fellowship from the Alfred P. Sloan Foundation, a Peter Lougheed/CIHR New Investigator fellowship and the Canadian Institute for Advanced Research Program in Evolutionary Biology. We would also like to acknowledge Donald Rumsfeld for making bizarre and quotable statements.
Footnotes
One contribution of 14 to a Discussion Meeting Issue ‘Major steps in cell evolution’.
References
- Andersson J.O. Lateral gene transfer in eukaryotes. Cell. Mol. Life Sci. 2005;62:1182–1197. doi: 10.1007/s00018-005-4539-z. 10.1007/s00018-005-4539-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson J.O, Sarchfield S.W, Roger A.J. Gene transfers from Nanoarchaeota to an ancestor of diplomonads and parabasalids. Mol. Biol. Evol. 2005;22:85–90. doi: 10.1093/molbev/msh254. 10.1093/molbev/msh254 [DOI] [PubMed] [Google Scholar]
- Aravind L, Koonin E.V. Eukaryotic-specific domains in translation initiation factors: implications for translation regulation and evolution of the translation system. Genome Res. 2000;10:1172–1184. doi: 10.1101/gr.10.8.1172. 10.1101/gr.10.8.1172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archibald J.M. Jumping genes and shrinking genomes—probing the evolution of eukaryotic photosynthesis with genomics. IUBMB Life. 2005;57:539–547. doi: 10.1080/15216540500167732. [DOI] [PubMed] [Google Scholar]
- Archibald J.M, Longet D, Pawlowski J, Keeling P.J. A novel polyubiquitin structure in Cercozoa and Foraminifera: evidence for a new eukaryotic supergroup. Mol. Biol. Evol. 2003;20:62–66. doi: 10.1093/molbev/msg006. 10.1093/molbev/msg006 [DOI] [PubMed] [Google Scholar]
- Aris-Brosou S, Yang Z. Bayesian models of episodic evolution support a Late Precambrian explosive diversification of the Metazoa. Mol. Biol. Evol. 2003;20:1947–1954. doi: 10.1093/molbev/msg226. 10.1093/molbev/msg226 [DOI] [PubMed] [Google Scholar]
- Arisue N, Hashimoto T, Lee J.A, Moore D.V, Gordon P, Sensen C.W, Gaasterland T, Hasegawa M, Müller M. The phylogenetic position of the pelobiont Mastigamoeba balamuthi based on sequences of rDNA and translation elongation factors EF-1alpha and EF-2. J. Eukaryot. Microbiol. 2002;49:1–10. doi: 10.1111/j.1550-7408.2002.tb00332.x. 10.1111/j.1550-7408.2002.tb00332.x [DOI] [PubMed] [Google Scholar]
- Arisue N, Hasegawa M, Hashimoto T. Root of the Eukaryota tree as inferred from combined maximum likelihood analyses of multiple molecular sequence data. Mol. Biol. Evol. 2005;22:409–420. doi: 10.1093/molbev/msi023. 10.1093/molbev/msi023 [DOI] [PubMed] [Google Scholar]
- Baldauf S.L, Roger A.J, Wenk-Siefert I, Doolittle W.F. A kingdom-level phylogeny of eukaryotes based on combined protein data. Science. 2000;290:972–977. doi: 10.1126/science.290.5493.972. 10.1126/science.290.5493.972 [DOI] [PubMed] [Google Scholar]
- Bapteste E, Philippe H. The potential value of indels as phylogenetic markers: position of trichomonads as a case study. Mol. Biol. Evol. 2002;19:972–977. doi: 10.1093/oxfordjournals.molbev.a004156. [DOI] [PubMed] [Google Scholar]
- Bapteste E, et al. The analysis of 100 genes supports the grouping of three highly divergent amoebae: Dictyostelium, Entamoeba, and Mastigamoeba. Proc. Natl Acad. Sci. USA. 2002;99:1414–1419. doi: 10.1073/pnas.032662799. 10.1073/pnas.032662799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan R.B, Lang B.F, Bryant D. Calculating the evolutionary rates of different genes: a fast, accurate estimator with applications to maximum likelihood phylogenetic analysis. Syst. Biol. 2005;54:900–915. doi: 10.1080/10635150500354829. 10.1080/10635150500354829 [DOI] [PubMed] [Google Scholar]
- Blair J.E, Hedges S.B. Molecular clocks do not support the Cambrian explosion. Mol. Biol. Evol. 2005;22:387–390. doi: 10.1093/molbev/msi039. 10.1093/molbev/msi039 [DOI] [PubMed] [Google Scholar]
- Brinkmann H, van der Giezen M, Zhou Y, Poncelin de Raucourt G, Philippe H. An empirical assessment of long-branch attraction artifacts in deep eukaryotic phylogenomics. Syst. Biol. 2005;54:743–757. doi: 10.1080/10635150500234609. [DOI] [PubMed] [Google Scholar]
- Brocks J.J, Logan G.A, Buick R, Summons R.E. Archean molecular fossils and the early rise of eukaryotes. Science. 1999;285:1033–1036. doi: 10.1126/science.285.5430.1033. 10.1126/science.285.5430.1033 [DOI] [PubMed] [Google Scholar]
- Buick R, Knoll A.H. Acritarchs and microfossils from the Mesoproterozoic Bangemall Group, northwestern Australia. J. Paleontol. 1999;73:744–764. doi: 10.1017/s0022336000040634. [DOI] [PubMed] [Google Scholar]
- Butterfield N.J, Knoll A.H, Swett K. A bangiophyte red alga from the Proterozoic of arctic Canada. Science. 1990;250:104–107. doi: 10.1126/science.11538072. [DOI] [PubMed] [Google Scholar]
- Cavalier-Smith T, Chao E.E. Molecular phylogeny of the free-living archezoan Trepomonas agilis and the nature of the first eukaryote. J. Mol. Evol. 1996;43:551–562. doi: 10.1007/BF02202103. 10.1007/BF02202103 [DOI] [PubMed] [Google Scholar]
- Cavalier-Smith T, Chao E.E. Phylogeny and classification of phylum Cercozoa (Protozoa) Protist. 2003;154:341–358. doi: 10.1078/143446103322454112. 10.1078/143446103322454112 [DOI] [PubMed] [Google Scholar]
- Doolittle R.F. Stein and Moore Award address. Reconstructing history with amino acid sequences. Protein Sci. 1992;1:191–200. doi: 10.1002/pro.5560010201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doolittle R.F, Feng D.F, Tsang S, Cho G, Little E. Determining the divergence times of the major kingdoms of living organisms with a protein clock. Science. 1996;271:470–477. doi: 10.1126/science.271.5248.470. [DOI] [PubMed] [Google Scholar]
- Douzery E.J, Snell E.A, Bapteste E, Delsuc F, Philippe H. The timing of eukaryotic evolution: does a relaxed molecular clock reconcile proteins and fossils? Proc. Natl Acad. Sci. USA. 2004;101:15 386–15 391. doi: 10.1073/pnas.0403984101. 10.1073/pnas.0403984101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Embley T.M. Multiple secondary origins of the anaerobic lifestyle in eukaryotes. Phil. Trans. R. Soc. B. 2006;361:1055–1067. doi: 10.1098/rstb.2006.1844. 10.1098/rstb.2006.1844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esser C, et al. A genome phylogeny for mitochondria among alpha-proteobacteria and a predominantly eubacterial ancestry of yeast nuclear genes. Mol. Biol. Evol. 2004;21:1643–1660. doi: 10.1093/molbev/msh160. 10.1093/molbev/msh160 [DOI] [PubMed] [Google Scholar]
- Fast N.M, Kissinger J.C, Roos D.S, Keeling P.J. Nuclear-encoded, plastid-targeted genes suggest a single common origin for apicomplexan and dinoflagellate plastids. Mol. Biol. Evol. 2001;18:418–426. doi: 10.1093/oxfordjournals.molbev.a003818. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Cases in which parsimony or compatibility methods will be positively misleading. Syst. Zool. 1978;27:401–410. [Google Scholar]
- Feng D.-F, Cho G, Doolittle R.F. Determining divergence times with a protein clock: update and reevaluation. Proc. Natl Acad. Sci. USA. 1997;94:13 028–13 033. doi: 10.1073/pnas.94.24.13028. 10.1073/pnas.94.24.13028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer W.M, Palmer J.D. Evidence from small-subunit ribosomal RNA sequences for a fungal origin of Microsporidia. Mol. Phylogenet. Evol. 2005;36:606–622. doi: 10.1016/j.ympev.2005.03.031. 10.1016/j.ympev.2005.03.031 [DOI] [PubMed] [Google Scholar]
- Foster P.G. Modeling compositional heterogeneity. Syst. Biol. 2004;53:485–495. doi: 10.1080/10635150490445779. 10.1080/10635150490445779 [DOI] [PubMed] [Google Scholar]
- Foster P.G, Hickey D.A. Compositional bias may affect both DNA-based and protein-based phylogenetic reconstructions. J. Mol. Evol. 1999;48:284–290. doi: 10.1007/pl00006471. 10.1007/PL00006471 [DOI] [PubMed] [Google Scholar]
- Gogarten J.P, Doolittle W.F, Lawrence J.G. Prokaryotic evolution in light of gene transfer. Mol. Biol. Evol. 2002;19:2226–2238. doi: 10.1093/oxfordjournals.molbev.a004046. [DOI] [PubMed] [Google Scholar]
- Graur D, Martin W. Reading the entrails of chickens: molecular timescales of evolution and the illusion of precision. Trends Genet. 2004;20:80–86. doi: 10.1016/j.tig.2003.12.003. 10.1016/j.tig.2003.12.003 [DOI] [PubMed] [Google Scholar]
- Gu X. Statistical methods for testing functional divergence after gene duplication. Mol. Biol. Evol. 1999;16:1664–1674. doi: 10.1093/oxfordjournals.molbev.a026080. [DOI] [PubMed] [Google Scholar]
- Hampl V, Horner D.S, Dyal P, Kulda J, Flegr J, Foster P.G, Embley T.M. Inference of the phylogenetic position of oxymonads based on nine genes: support for metamonada and excavata. Mol. Biol. Evol. 2005;22:2508–2518. doi: 10.1093/molbev/msi245. 10.1093/molbev/msi245 [DOI] [PubMed] [Google Scholar]
- Harper J.T, Waanders E, Keeling P.J. On the monophyly of chromalveolates using a six-protein phylogeny of eukaryotes. Int. J. Syst. Evol. Microbiol. 2005;55:487–496. doi: 10.1099/ijs.0.63216-0. 10.1099/ijs.0.63216-0 [DOI] [PubMed] [Google Scholar]
- Hedges S.B, Kumar S. Precision of molecular time estimates. Trends Genet. 2004;20:242–247. doi: 10.1016/j.tig.2004.03.004. 10.1016/j.tig.2004.03.004 [DOI] [PubMed] [Google Scholar]
- Hedges S.B, Chen H, Kumar S, Wang D.Y, Thompson A.S, Watanabe H. A genomic timescale for the origin of eukaryotes. BMC Evol. Biol. 2001;1:4. doi: 10.1186/1471-2148-1-4. 10.1186/1471-2148-1-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedges S.B, Blair J.E, Venturi M.L, Shoe J.L. A molecular timescale of eukaryote evolution and the rise of complex multicellular life. BMC Evol. Biol. 2004;4:2. doi: 10.1186/1471-2148-4-2. 10.1186/1471-2148-4-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirt R.P, Logsdon J.M, Healy B, Dorey M.W, Doolittle W.F, Embley T.M. Microsporidia are related to fungi: evidence from the largest subunit of RNA polymerase II and other proteins. Proc. Natl Acad. Sci. USA. 1999;96:580–585. doi: 10.1073/pnas.96.2.580. 10.1073/pnas.96.2.580 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho S.Y, Phillips M.J, Drummond A.J, Cooper A. Accuracy of rate estimation using relaxed-clock models with a critical focus on the early metazoan radiation. Mol. Biol. Evol. 2005;22:1355–1363. doi: 10.1093/molbev/msi125. 10.1093/molbev/msi125 [DOI] [PubMed] [Google Scholar]
- Huelsenbeck J.P, Rannala B. Phylogenetic methods come of age: testing hypotheses in an evolutionary context. Science. 1997;276:227–232. doi: 10.1126/science.276.5310.227. 10.1126/science.276.5310.227 [DOI] [PubMed] [Google Scholar]
- Inagaki Y, Susko E, Fast N.M, Roger A.J. Covarion shifts cause a long-branch attraction artifact that unites microsporidia and archaebacteria in EF-1a phylogenies. Mol. Biol. Evol. 2004;21:1340–1349. doi: 10.1093/molbev/msh130. 10.1093/molbev/msh130 [DOI] [PubMed] [Google Scholar]
- Keeling P.J. Foraminifera and Cercozoa are related in actin phylogeny: two orphans find a home? Mol. Biol. Evol. 2001;18:1551–1557. doi: 10.1093/oxfordjournals.molbev.a003941. [DOI] [PubMed] [Google Scholar]
- Keeling P.J, McFadden G.I. Origins of microsporidia. Trends Microbiol. 1998;6:19–23. doi: 10.1016/S0966-842X(97)01185-2. 10.1016/S0966-842X(97)01185-2 [DOI] [PubMed] [Google Scholar]
- Keeling P.J, Burger G, Durnford D.G, Lang B.F, Lee R.W, Pearlman R.E, Roger A.J, Gray M.W. The tree of eukaryotes. Trends Ecol. Evol. 2005;20:670–676. doi: 10.1016/j.tree.2005.09.005. 10.1016/j.tree.2005.09.005 [DOI] [PubMed] [Google Scholar]
- Kishino H, Thorne J.L, Bruno W.J. Performance of a divergence time estimation method under a probabilistic model of rate evolution. Mol. Biol. Evol. 2001;18:352–361. doi: 10.1093/oxfordjournals.molbev.a003811. [DOI] [PubMed] [Google Scholar]
- Kolaczkowski B, Thornton J.W. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature. 2004;431:980–984. doi: 10.1038/nature02917. 10.1038/nature02917 [DOI] [PubMed] [Google Scholar]
- Langley C.H, Fitch W.M. An examination of the constancy of the rate of molecular evolution. J. Mol. Evol. 1974;3:161–177. doi: 10.1007/BF01797451. 10.1007/BF01797451 [DOI] [PubMed] [Google Scholar]
- Lartillot N, Philippe H. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol. Biol. Evol. 2004;21:1095–1109. doi: 10.1093/molbev/msh112. 10.1093/molbev/msh112 [DOI] [PubMed] [Google Scholar]
- Lockhart P, Novis P, Milligan B.G, Riden J, Rambaut A, Larkum T. Heterotachy and tree building: a case study with plastids and eubacteria. Mol. Biol. Evol. 2006;23:40–45. doi: 10.1093/molbev/msj005. 10.1093/molbev/msj005 [DOI] [PubMed] [Google Scholar]
- Martin W, et al. Evolutionary analysis of Arabidopsis, cyanobacterial, and chloroplast genomes reveals plastid phylogeny and thousands of cyanobacterial genes in the nucleus. Proc. Natl Acad. Sci. USA. 2002;99:12 246–12 251. doi: 10.1073/pnas.182432999. 10.1073/pnas.182432999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller T, Spang R, Vingron M. Estimating amino acid substitution models: a comparison of Dayhoff's estimator, the resolvent approach and a maximum likelihood method. Mol. Biol. Evol. 2002;19:8–13. doi: 10.1093/oxfordjournals.molbev.a003985. [DOI] [PubMed] [Google Scholar]
- Nikolaev S.I, Berney C, Fahrni J.F, Bolivar I, Polet S, Mylnikov A.P, Aleshin V.V, Petrov N.B, Pawlowski J. The twilight of Heliozoa and rise of Rhizaria, an emerging supergroup of amoeboid eukaryotes. Proc. Natl Acad. Sci. USA. 2004;101:8066–8071. doi: 10.1073/pnas.0308602101. 10.1073/pnas.0308602101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patron N.J, Rogers M.B, Keeling P.J. Gene replacement of fructose-1,6-bisphosphate aldolase supports the hypothesis of a single photosynthetic ancestor of chromalveolates. Eukaryot. Cell. 2004;3:1169–1175. doi: 10.1128/EC.3.5.1169-1175.2004. 10.1128/EC.3.5.1169-1175.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawlowski J, Bolivar I, Fahrni J.F, Cavalier-Smith T, Gouy M. Early origin of foraminifera suggested by SSU rRNA gene sequences. Mol. Biol. Evol. 1996;13:445–450. doi: 10.1093/oxfordjournals.molbev.a025605. [DOI] [PubMed] [Google Scholar]
- Pawlowski J, Bolivar I, Fahrni J.F, de Vargas C, Gouy M, Zannetti L. Extreme differences in rates of molecular evolution of foraminifera revealed by comparison of ribosomal DNA sequences and the fossil record. Mol. Biol. Evol. 1997;14:498–505. doi: 10.1093/oxfordjournals.molbev.a025786. [DOI] [PubMed] [Google Scholar]
- Peterson K.J, Butterfield N.J. Origin of the Eumetazoa: testing ecological predictions of molecular clocks against the Proterozoic fossil record. Proc. Natl Acad. Sci. USA. 2005;102:9547–9552. doi: 10.1073/pnas.0503660102. 10.1073/pnas.0503660102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H, Germot A. Phylogeny of eukaryotes based on ribosomal RNA: long-branch attraction and models of sequence evolution. Mol. Biol. Evol. 2000;17:830–834. doi: 10.1093/oxfordjournals.molbev.a026362. [DOI] [PubMed] [Google Scholar]
- Philippe H, Lopez P, Brinkmann H, Budin K, Germot A, Laurent J, Moreira D, Müller M, Le Guyader H. Early-branching or fast-evolving eukaryotes? An answer based on slowly evolving positions. Proc. R. Soc. B. 2000;267:1213–1221. doi: 10.1098/rspb.2000.1130. 10.1098/rspb.2000.1130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H, Snell E.A, Bapteste E, Lopez P, Holland P.W.H, Casane D. Phylogenomics of eukaryotes: impact of missing data on large alignments. Mol. Biol. Evol. 2004;21:1740–1752. doi: 10.1093/molbev/msh182. 10.1093/molbev/msh182 [DOI] [PubMed] [Google Scholar]
- Philippe H, Zhou Y, Brinkmann H, Rodrigue N, Delsuc F. Heterotachy and long-branch attraction in phylogenetics. BMC Evol. Biol. 2005;5:50. doi: 10.1186/1471-2148-5-50. 10.1186/1471-2148-5-50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips M.J, Delsuc F, Penny D. Genome-scale phylogeny and the detection of systematic biases. Mol. Biol. Evol. 2004;21:1455–1458. doi: 10.1093/molbev/msh137. 10.1093/molbev/msh137 [DOI] [PubMed] [Google Scholar]
- Porter S.M, Meisterfeld R, Knoll A.H. Vase-shaped microfossils from the Neoproterozoic Chuar Group, Grand Canyon: a classification guided by modern testate amoebae. J. Paleontol. 2003;77:409–429. [Google Scholar]
- Pupko T, Huchon D, Cao Y, Okada N, Hasegawa M. Combining multiple data sets in a likelihood analysis: which models are the best? Mol. Biol. Evol. 2002;19:2294–2307. doi: 10.1093/oxfordjournals.molbev.a004053. [DOI] [PubMed] [Google Scholar]
- Reisz R.R, Muller J. The comparative method for evaluating fossil calibration dates: a reply to Hedges and Kumar. Trends Genet. 2004;20:596–597. doi: 10.1016/j.tig.2004.09.004. 10.1016/j.tig.2004.09.004 [DOI] [PubMed] [Google Scholar]
- Richards T.A, Cavalier-Smith T. Myosin domain evolution and the primary divergence of eukaryotes. Nature. 2005;436:1113–1118. doi: 10.1038/nature03949. 10.1038/nature03949 [DOI] [PubMed] [Google Scholar]
- Rodriguez-Ezpeleta N, Brinkmann H, Burey S.C, Roure B, Burger G, Löffelhardt W, Bohnert H.J, Philippe H, Lang B.F. Monophyly of primary photosynthetic eukaryotes: green plants, red algae, and glaucophytes. Curr. Biol. 2005;15:1325–1330. doi: 10.1016/j.cub.2005.06.040. 10.1016/j.cub.2005.06.040 [DOI] [PubMed] [Google Scholar]
- Ruiz-Trillo I, Inagaki Y, Davis L.A, Sperstad S, Landfald B, Roger A.J. Capsaspora owczarzaki is an independent opisthokont lineage. Curr. Biol. 2004;14:946–947. doi: 10.1016/j.cub.2004.10.037. 10.1016/j.cub.2004.10.037 [DOI] [PubMed] [Google Scholar]
- Sanderson M.J. A nonparametric approach to estimating divergence times in the absence of rate constancy. Mol. Biol. Evol. 1997;14:1218–1231. [Google Scholar]
- Sanderson M.J. Estimating absolute rates of molecular evolution and divergence times: a penalised likelihood approach. Mol. Biol. Evol. 2002;19:101–109. doi: 10.1093/oxfordjournals.molbev.a003974. [DOI] [PubMed] [Google Scholar]
- Sanderson M.J. r8s: inferring absolute rates of molecular evolution and divergence times in the absence of a molecular clock. Bioinformatics. 2003;19:301–302. doi: 10.1093/bioinformatics/19.2.301. 10.1093/bioinformatics/19.2.301 [DOI] [PubMed] [Google Scholar]
- Schmidt H.A, Strimmer K, Vingron M, von Haeseler A. TREE-PUZZLE: maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics. 2002;18:502–504. doi: 10.1093/bioinformatics/18.3.502. 10.1093/bioinformatics/18.3.502 [DOI] [PubMed] [Google Scholar]
- Simpson A.G.B. Cytoskeletal organisation, phylogenetic affinities and systematics in the contentious taxon Excavata (Eukaryota) Int. J. Syst. Evol. Microbiol. 2003;53:1759–1777. doi: 10.1099/ijs.0.02578-0. 10.1099/ijs.0.02578-0 [DOI] [PubMed] [Google Scholar]
- Simpson A.G.B, Roger A.J. The real ‘kingdoms’ of eukaryotes. Curr. Biol. 2004;14:R693–R696. doi: 10.1016/j.cub.2004.08.038. 10.1016/j.cub.2004.08.038 [DOI] [PubMed] [Google Scholar]
- Simpson A.G.B, Roger A.J, Silberman J.D, Leipe D, Edgcomb V.P, Jermiin L.S, Patterson D.J, Sogin M.L. Evolutionary history of ‘early diverging’ eukaryotes: the excavate taxon Carpediemonas is closely related to Giardia. Mol. Biol. Evol. 2002;19:1782–1791. doi: 10.1093/oxfordjournals.molbev.a004000. [DOI] [PubMed] [Google Scholar]
- Simpson A.G.B, Inagaki Y, Roger A.J. Comprehensive multi-gene phylogenies of excavate protists reveal the evolutionary positions of ‘primitive’ eukaryotes. Mol. Biol. Evol. 2006;23:615–625. doi: 10.1093/molbev/msj068. [DOI] [PubMed] [Google Scholar]
- Sogin M.L. Early evolution and the origin of eukaryotes. Curr. Opin. Genet. Dev. 1991;1:457–463. doi: 10.1016/s0959-437x(05)80192-3. 10.1016/S0959-437X(05)80192-3 [DOI] [PubMed] [Google Scholar]
- Spencer M, Susko E, Roger A.J. Likelihood, parsimony, and heterogeneous evolution. Mol. Biol. Evol. 2005;22:1161–1164. doi: 10.1093/molbev/msi123. 10.1093/molbev/msi123 [DOI] [PubMed] [Google Scholar]
- Stechmann A, Cavalier-Smith T. Rooting the eukaryote tree by using a derived gene fusion. Science. 2002;297:89–91. doi: 10.1126/science.1071196. 10.1126/science.1071196 [DOI] [PubMed] [Google Scholar]
- Stechmann A, Cavalier-Smith T. Phylogenetic analysis of eukaryotes using heat-shock protein Hsp90. J. Mol. Evol. 2003a;57:408–419. doi: 10.1007/s00239-003-2490-x. 10.1007/s00239-003-2490-x [DOI] [PubMed] [Google Scholar]
- Stechmann A, Cavalier-Smith T. The root of the eukaryote tree pinpointed. Curr. Biol. 2003b;13:R665–R666. doi: 10.1016/s0960-9822(03)00602-x. 10.1016/S0960-9822(03)00602-X [DOI] [PubMed] [Google Scholar]
- Susko E, Inagaki Y, Field C, Holder M.E, Roger A.J. Testing for differences in rates-across-sites distributions in phylogenetic subtrees. Mol. Biol. Evol. 2002;19:1514–1523. doi: 10.1093/oxfordjournals.molbev.a004214. [DOI] [PubMed] [Google Scholar]
- Susko E, Inagaki Y, Roger A.J. On inconsistency of the neighbor-joining, least squares, and minimum evolution estimation when substitution processes are incorrectly modeled. Mol. Biol. Evol. 2004;21:1629–1642. doi: 10.1093/molbev/msh159. 10.1093/molbev/msh159 [DOI] [PubMed] [Google Scholar]
- Susko E, Spencer M, Roger A.J. Biases in phylogenetic estimation can be caused by random sequence segments. J. Mol. Evol. 2005;61:351–359. doi: 10.1007/s00239-004-0352-9. 10.1007/s00239-004-0352-9 [DOI] [PubMed] [Google Scholar]
- Swofford D.L. Sinauer Associates; Sunderland, MA: 2000. PAUP*, Phylogenetic Analysis Using Parsimony (*and other methods), version 4. [Google Scholar]
- Taylor F.J.R. Problems in the development of an explicit hypothetical phylogeny of the lower eukaryotes. Biosystems. 1978;10:67–89. doi: 10.1016/0303-2647(78)90031-x. 10.1016/0303-2647(78)90031-X [DOI] [PubMed] [Google Scholar]
- Thomarat F, Vivares C.P, Gouy M. Phylogenetic analysis of the complete genome sequence of Encephalitozoon cuniculi supports the fungal origin of microsporidia and reveals a high frequency of fast-evolving genes. J. Mol. Evol. 2004;59:780–791. doi: 10.1007/s00239-004-2673-0. 10.1007/s00239-004-2673-0 [DOI] [PubMed] [Google Scholar]
- Thorne J.L, Kishino H. Divergence time and evolutionary rate estimation with multilocus data. Syst. Biol. 2002;51:689–702. doi: 10.1080/10635150290102456. 10.1080/10635150290102456 [DOI] [PubMed] [Google Scholar]
- Tillier E.R, Lui T.W. Using multiple interdependency to separate functional from phylogenetic correlations in protein alignments. Bioinformatics. 2003;19:750–755. doi: 10.1093/bioinformatics/btg072. 10.1093/bioinformatics/btg072 [DOI] [PubMed] [Google Scholar]
- Van de Peer Y, Ben Ali A, Meyer A. Microsporidia: accumulating molecular evidence that a group of amitochondriate and suspectedly primitive eukaryotes are just curious fungi. Gene. 2000;246:1–8. doi: 10.1016/s0378-1119(00)00063-9. 10.1016/S0378-1119(00)00063-9 [DOI] [PubMed] [Google Scholar]
- Wainwright P.O, HInkle G, Sogin M.L, Stickel S.K. Monophyletic origins of the metazoa: an evolutionary link with fungi. Science. 1993;260:340–342. doi: 10.1126/science.8469985. [DOI] [PubMed] [Google Scholar]
- Welch J.J, Bromham L. Molecular dating when rates vary. Trends Ecol. Evol. 2005;20:320–327. doi: 10.1016/j.tree.2005.02.007. 10.1016/j.tree.2005.02.007 [DOI] [PubMed] [Google Scholar]
- Welch J.J, Fontanillas E, Bromham L. Molecular dates for the “cambrian explosion”: the influence of prior assumptions. Syst. Biol. 2005;54:672–678. doi: 10.1080/10635150590947212. 10.1080/10635150590947212 [DOI] [PubMed] [Google Scholar]
- Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol. Biol. Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- Whittaker R.H. New concepts of kingdoms of organisms. Science. 1969;163:150–160. doi: 10.1126/science.163.3863.150. [DOI] [PubMed] [Google Scholar]
- Wolters J. The troublesome parasites: molecular and morphological evidence that apicomplexa belong to the dinoflagellate-ciliate clade. Biosystems. 1991;25:75–83. doi: 10.1016/0303-2647(91)90014-c. 10.1016/0303-2647(91)90014-C [DOI] [PubMed] [Google Scholar]