Digital particle image velocimetry measurements of the downwash distribution of a desert locust Schistocerca gregaria

Abstract

Actuator disc models of insect flight are concerned solely with the rate of momentum transfer to the air that passes through the disc. These simple models assume that an even pressure is applied across the disc, resulting in a uniform downwash distribution. However, a correction factor, k, is often included to correct for the difference in efficiency between the assumed even downwash distribution, and the real downwash distribution. In the absence of any empirical measurements of the downwash distribution behind a real insect, the values of k used in the literature have been necessarily speculative. Direct measurement of this efficiency factor is now possible, and could be used to compare the relative efficiencies of insect flight across the Class. Here, we use Digital Particle Image Velocimetry to measure the instantaneous downwash distribution, mid-downstroke, of a tethered desert locust (Schistocerca gregaria). By integrating the downwash distribution, we are thereby able to provide the first direct empirical measurement of k for an insect. The measured value of k=1.12 corresponds reasonably well with that predicted by previous theoretical studies.

1. Introduction

To date, several estimates have been made of the aerodynamic force production of flying insects by regarding their stroke plane as an actuator disc, which is considered ‘pulsed’ if the upstroke is inactive (Rayner 1979; Ellington 1984a,b). Actuator disc models, derived from propeller theory, are concerned solely with the vertical momentum imparted to the air flowing through the disc, and therefore can disregard detail of wing kinematics, wing shape, and the specific details of the wing's interaction with the air. This has been a useful simplification but suffers from many limiting assumptions, including the most basic one that the disc imparts a uniform downward acceleration to the fluid across its entire area. Only ideal (i.e. theoretical) propellers or wings have uniform downwash distributions. Real propellers have a specific non-uniformity in downwash across the disc, which is caused by several factors. These include losses due to wingtip vortices, wing root vortices, possible reductions in downwash close to the hub, and variations in downwash due to changes in wing twist or planform. Deviations from a uniform downwash velocity profile cause inefficiency. The force generated by the actuator disc equals the rate of change of momentum of the air accelerated through the disc, given by mv/t during hover (where m is the mass of air being accelerated to a velocity, v, in unit time, t). A uniformly loaded actuator disc accelerates the entire mass of air swept by the wings to a uniform velocity. Any other loading distribution giving the same total change in momentum must require higher velocities over some part of the disc, but in the actuator disc model the kinetic energy lost to the wake is given by mv²/2. Because of the v² term, kinetic energy losses due to these higher velocities are more detrimental than any benefits from lower velocities elsewhere on the disc. A uniform downwash across the disc, therefore, provides the lowest kinetic energy lost to the wake for a given force production, and the highest efficiency.

To compensate for the inefficiency caused by an uneven application of pressure, a correction factor, k, is used to modify existing actuator disc models: k is defined as the ratio of actual induced power to ideal induced power for a given thrust. Hence, for an ideal actuator disc, k=1, while any departure from ideal efficiency gives k>1. Without any specific knowledge of the downwash distribution across the wing disc of any insect, values of k>1 have been selected so as to fit the difference between the ideal power required for any given thrust, and estimates of the induced power which is actually required to produce that thrust (based on muscle masses, muscle efficiencies and metabolic rates—e.g. Dudley & Ellington 1990). Fundamentally, however, k is a correction factor for the departure of the actual downwash velocity profile from the ideal, uniform profile, and is therefore amenable to direct aerodynamic measurement using Digital Particle Image Velocimetry (DPIV). Here, we present the first downwash velocity profile data measured directly from a flying tethered insect and use it to provide a direct empirical estimate of k for a desert locust.

2. Material and methods

Desert locusts, Schistocerca gregaria Forskål, were obtained from a captive bred population, and selected for physical characteristics indicative of health (good wing condition, strong free-flight ability, etc.). Data presented here were collected during a 2 h bout of flight from a single male individual weighing 1.21 g, with a hindwing length of 49 mm and a thorax width of 14 mm. The locust was rigidly tethered in a wind tunnel at a body angle of 7° (the angle from the horizontal to the ventral surface of the thorax; for further details see Taylor & Thomas 2003), a value previously shown to stimulate tethered flight with lift balancing body weight (Weis-Fogh 1956a,b; Zarnack & Wortmann 1989; Wortmann & Zarnack 1993; Taylor & Thomas 2003), and also consistent with the body angles adopted by free-flying locusts in the wild (S. gregaria, Waloff 1972; Locusta migratoria, Baker et al. 1981). Tethering also allowed manipulation of the locust relative to the laser sheet such that DPIV could be used to measure the induced flow at a series of stations from the body centreline out along the wing. Measurements were performed in a low-speed, low-turbulence wind tunnel (1.0×0.5×0.5 m working section) at 3.50 m s⁻¹ under the same experimental conditions and using the same techniques as outlined in Bomphrey et al. (2005).

Two-dimensional DPIV uses a double-pulsed laser sheet to illuminate seeding particles in the plane of interest, and a digital camera to record an image pair from that plane (Adrian 1991). Cross-correlation techniques are then applied to sequential pairs of DPIV images across an interrogation region grid to obtain the statistically dominant particle movement at each grid point. From the particle displacements, an instantaneous velocity is obtained from each grid point to yield high-resolution planar instantaneous vector maps of flow velocity and vorticity. Seventy-three image pairs (limited by data storage) were recorded yielding 73 corresponding vector maps for each of nine positions along one wing. In the set-up used here, a JEM Hydrosonic 2000 seeder with ‘long lasting’ smoke fluid was used to produce seeding with a mean particle diameter of less than 10 μm. A pulsed New Wave Gemini Nd-YAG laser (120 mJ per 5 ns pulse), combined with plano-concave and plano-cylindrical lenses (focal lengths −50 and 75 mm) produced a 0.5 mm thick light sheet oriented vertically across the imaging area. The laser was synchronized with a double frame digital camera (Kodak ES1.0 digital CCD 1000² pixels) to record image pairs at 15 Hz (a little slower than the 19 Hz wingbeat frequency of the locust). The pulse separation interval was optimized at 120 μs for 3.50 m s⁻¹ freestream velocity, to retain sufficient seeding particles within the light sheet. The vertically aligned light sheet was centred in the working section of the wind tunnel and a racked traverse moved the insect mount perpendicular to the light sheet to illuminate various vertical and chordwise planes at stations across the wingspan. Dantec FlowManager software was used to control the camera and laser for DPIV data acquisition. DPIV images were processed using TSI UltraPIV Insight software incorporating the Hart Algorithm (Hart 2000).

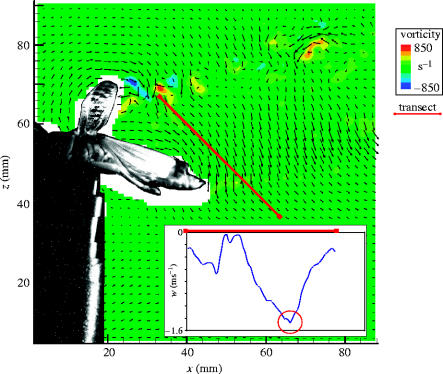
At each spanwise position, the peak value of downwash behind the hindwings (while they were horizontal) was measured as close to the trailing edge as possible without being affected by data dropout due to glare on the trailing edge. Here, the downwash will be defined as w, the velocity component parallel to the vertical axis, z, with z+ve being upwards, against gravity, g. The x-axis will be defined as that aligned with the freestream, and the y-axis as the third orthogonal axis. To ensure as accurate a measurement as possible, we took the peak downwash close to the trailing edge of the wing as representing the highest deflection of the flow as a result of the geometry and kinematics of that section of wing. In order to be confident of measuring the peak downwash, w was sampled in a transect approximately perpendicular to the path of the wing, centred on the trailing edge. For consistency frame-to-frame and wingbeat-to-wingbeat, the transect was set at an angle of 45° to the vertical—in other words, the transect was a line at 45° in the x–z plane, as illuminated by the laser sheet (figure 1). Measuring peak w within this transect should yield the peak downwash behind the trailing edge of the wing. The transect length was selected to be sufficient to record the peak w, and the decay away from that peak with distance along the transect—see inset of figure 1.

Figure 1.

Shows a typical DPIV vector map with the freestream subtracted and with every other vector (in both x- and z-directions) removed for clarity. The locust has been overlain for spatial reference. The red line indicates where the transect was measured within the plane. The plane itself was 25.5 mm from the centre of the disc, corresponding to approximately 0.5R. The inlay graph shows the vertical component of the locust-induced flow against the transect length. The red ring highlights the maximum downward flow velocity along that transect, and corresponding to one data point in the following analysis.

3. Analysis

Wings generate lift by imparting linear momentum to the fluid through which they pass. The lift developed is equal to the rate of flux of vertical momentum through a vertical (y–z) plane in the distant wake, far enough from the wing that the pressure equals that of the surrounding fluid. The induced velocity increases, and (for an even downwash) eventually doubles, as the pressure equilibrates downstream of the wing (Stepniewski & Keys 1984). Knowledge of the instantaneous downwash in the vicinity of the wing is, therefore, sufficient to determine the instantaneous lift if the mass flow characteristics of the wing are also known and it is assumed that the local downwash velocities double in the far wake.

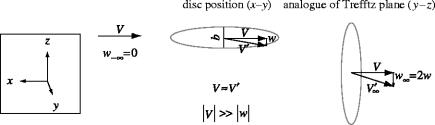
An actuator disc model for the case of horizontal flight has been proposed by Stepniewski & Keys (1984), and actuator disc models, in general, have since been adopted as a standard model by the animal flight community (e.g. Ellington 1984a,b; Chai et al. 1997). Beyond the fundamental simplifying assumptions common to all actuator disc theories, the model is formulated through a heuristic argument in which it is assumed that the horizontal actuator disc is rotated into the vertical plane far downstream of the wing (figure 2), equivalent to the Trefftz plane in classical wing theory (figure 2). The mass flow through the disc is, therefore, $\rho V\pi b^2/4$, where ρ is the density of the fluid, V is the freestream velocity and b is the span.

Figure 2.

Schematic representation of the actuator disc model in horizontal flight including the inherent assumptions. Where w is the downwash at the disc, V is the freestream velocity, V′ is the resultant velocity vector, the subscript, ∞, represents the far wake, and −∞ represents the volume of fluid before it has been affected by the disc. The disc exists in the x–y plane, but the far wake is measured in the y–z plane. Once rotated through 90° the plane in the far wake is analogous to the Trefftz plane of conventional wing theory.

It is well known that induced drag is minimized when the downwash velocity at the wing (w) is constant across the span (Munk 1921). Assuming an even downwash, the total lift on the wing is therefore

$$L=\rho \frac{\pi b^2}{2}Vw,$$ (3.1)

and the total induced power is simply

$$P_{\text{ideal}}=\rho \frac{\pi b^2}{2}V{w}^2.$$ (3.2)

These results are identical to the results of lifting line theory if an elliptic spanwise loading distribution is assumed. In this particular case, the potential flow in a vertical plane in the far wake is equivalent to that of a flat plate of the same span (b) as the wing moving downward with normal velocity 2w, and the potential flow solution for a flat plate shows that the apparent mass accelerated is equal to the mass of a circular cylinder of fluid having the plate's span as its diameter. The wing can, therefore, be thought of as deflecting a circular jet of diameter b downward with velocity 2w (Jones 1990), and the lifting line theory, therefore, arrives at the same results as Stepniewski & Keys' actuator disc model. This suggests that the exact area physically swept by the wings may not be of fundamental importance in determining the forces generated and the power required to do so, provided that the flow may be treated as potential and quasi-steady, and provided that the downwash is approximately even.

Lifting line theory gives different results if the downwash distribution is uneven, and the equivalence to the model of Stepneiwski & Keys is then lost. Nevertheless, for small deviations from an even downwash, we may reasonably assume that the wings still encounter a circular jet of diameter b, and we may continue to argue that the exact area physically swept by the wings is not of fundamental importance to the forces generated. In any case, assuming that the wings continue to impart momentum to a horizontal circular disc of diameter b moving horizontally with velocity V, the elemental contributions to lift and induced power across the span may be written

$$\text{d}L=2\rho Vw(y)\sqrt{b^2-4y^2}\text{d}y,$$ (3.3)

and

$$\text{d}P=2\rho V{w}^2(y)\sqrt{b^2-4y^2}\text{d}y,$$ (3.4)

respectively. Hence, if we know the actual downwash distribution w(y) by measurement, we may obtain the equivalent ideal downwash velocity w required for the same total lift by integrating equation (3.3) across the wing and equating the solution with equation (3.1):

$$w=\frac{4}{\pi b^2}{\int }_{-b/2}^{b/2}w(y)\sqrt{b^2-4y^2}\text{d}y.$$ (3.5)

Defining an efficiency factor $k=P/P_{\text{ideal}}$, we may calculate the efficiency of a given downwash distribution by integrating equation (3.4), dividing through by equation (3.2) and substituting in equation (3.5) to yield

$$k=\frac{\pi b^2}{4}\frac{{\int }_{-b/2}^{b/2}{w}^2(y)\sqrt{b^2-4y^2}\text{d}y}{{\left[{\int }_{-b/2}^{b/2}w(y)\sqrt{b^2-4y^2}\text{d}y\right]}^2}.$$ (3.6)

Finally, applying the transform

$$\theta =\frac{2y}{b}\pi ,$$ (3.7)

we may eliminate b to write equation (3.6) in the simpler form:

$$k=\frac{{\pi }^3}{2}\frac{{\int }_{-\pi }^{\pi }{w}^2(\theta )\sqrt{{\pi }^2-{\theta }^2}\text{d}\theta }{{\left[{\int }_{-\pi }^{\pi }w(\theta )\sqrt{{\pi }^2-{\theta }^2}\text{d}\theta \right]}^2}.$$ (3.8)

4. Results

The efficiency factor k may be evaluated by approximating the measured downwash data as an analytical function of spanwise coordinate θ. The empirical data were well approximated by a cosine series with three harmonics (figure 3a):

$$w(\theta )=\sum _{n=0}^3{a}_n\text{cos}(n\theta ),$$ (4.1)

which we fitted as a general linear model, using the ‘glmfit’ function in Matlab 7.0.4 (The MathWorks Inc. 2005). All of the fitted coefficients were highly significant (p<0.01) and the model explained 91% of the total variance in the downwash measurements (table 1).

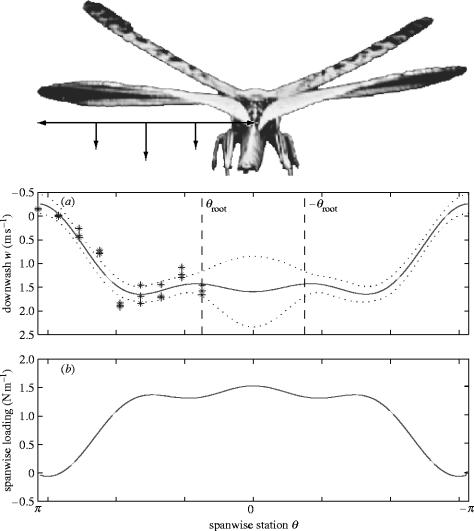
Figure 3.

(a) Measured downwash velocity and fitted downwash distribution behind the locust's wing. The solid line denotes the best fitting cosine series with three harmonics (equation 4.1). The dotted lines denote the upper and lower 95% confidence limits, and the vertical dashed lines denote the spanwise station (θ_root) of the most proximal downwash measurements. (b) Spanwise loading calculated for the fitted downwash distribution.

Table 1.

Fitted values and standard errors for the coefficients of the cosine series (equation 4.1) describing the downwash distribution immediately behind the locust's wing (n=30).

	fitted value	standard error
a0	1.16	0.07
a1	0.66	0.13
a2	−0.49	0.12
a3	0.27	0.09

The spanwise loading distribution, dL(y) (figure 3b), can be calculated by substituting the empirically fitted downwash distribution, w(θ), from equation (4.1) into equation (3.3), making use of the identity in equation (3.7). Integrating across the span gives an instantaneous total lift of 0.11 N, which is around 10 times the locust's body weight. Although, the instantaneous lift peaks at this point in the wingbeat, this estimate is clearly too high, and suggests that the model overestimates the total mass of fluid accelerated by the wings. Errors in the total apparent mass cancel in calculating the dimensionless efficiency factor k, however, and provided the relative mass of air accelerated at each spanwise station is reasonably approximated by the circular distribution assumed, the calculated value of k should also be reasonable.

In order to calculate the efficiency factor k, we integrated equation (3.8) numerically in Mathematica 5.1 (Wolfram Research Inc. 2004). This gave k=1.12 for the fitted values of the coefficients a_n in table 1. We then used the standard errors of the coefficients in table 1 to perform a Monte Carlo analysis on the error in our estimate of k, drawing 10 000 sets of values for the coefficients from t-distributed populations (d.f.=23), and evaluating equation (3.8) for each of the 10 000 sets. The resulting sample of estimates of k is plotted as a histogram of relative frequency in figure 4a. We then used the upper and lower 2.5 percentiles of this sample to construct a 95% confidence interval for k (1.07,1.22).

Figure 4.

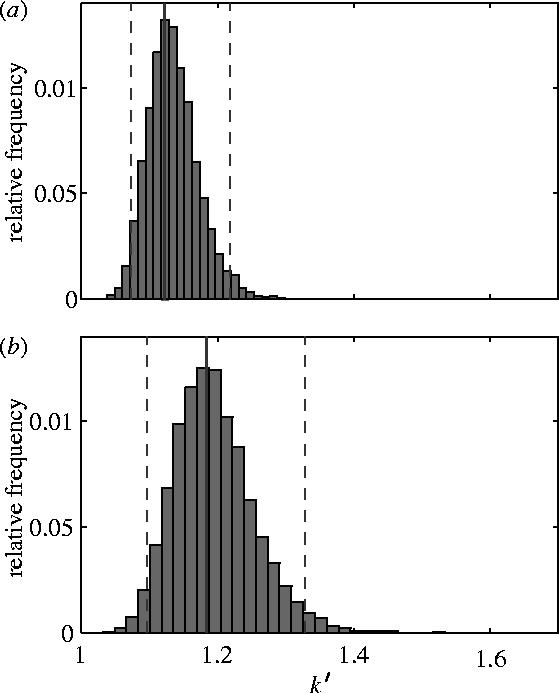
Histogram of relative frequency of estimates of (a) the efficiency factor k and (b) the modified efficiency factor k′ from a Monte Carlo analysis in which the values of the coefficients of the cosine series describing the downwash distribution were allowed to vary as samples from t-distributed populations based on the standard errors of the coefficients. The solid vertical line on each graph marks the best estimate of k or k′ based on the best fitting values of the coefficients; the dashed lines denote the upper and lower 2.5 percentiles, giving 95% confidence limits for k and k′.

It is clear from figure 3a that the confidence interval for the downwash distribution is rather wide in the region between the sagittal plane of the locust and the most proximal of the spanwise stations at which the downwash was measured. Since, we were prevented from obtaining information on the downwash in this region by the presence of the body, we decided to evaluate k over only the portion of the downwash distribution distal to the spanwise station of the most proximal downwash measurements (θ_root=0.748). This requires some adjustment to the integrals, and we therefore define a modified efficiency factor k′ evaluated over this interval as

$$k^{\prime }=\frac{{\int }_{{\theta }_{\text{root}}}^{\pi }\sqrt{{\pi }^2-{\theta }^2}\text{d}\theta {\int }_{{\theta }_{\text{root}}}^{\pi }{w}^2(\theta )\sqrt{{\pi }^2-{\theta }^2}\text{d}\theta }{{\left[{\int }_{{\theta }_{\text{root}}}^{\pi }w(\theta )\sqrt{{\pi }^2-{\theta }^2}\text{d}\theta \right]}^2},$$ (4.2)

given bi-lateral symmetry.

We repeated the procedure described above for calculating k and its error for k′, yielding a modified efficiency factor k′=1.18, with 95% confidence interval (1.10,1.33; figure 4b). Removing this central portion of the wing also yields a more reasonable estimate of the total instantaneous lift (0.07 N).

5. Discussion

The result of this experiment, k=1.12 or k′=1.18, is a little lower than estimates used in other studies (k=1.0–2.0 (depending on the vortex ring spacing parameter and the relative contributions of self-induced velocity to the total axial ring velocity) in fig. 7b of Ellington (1984a); k=1.2 in Spedding & Pennycuick (2001); k=1.2, following Ellington (1984a), in Usherwood & Ellington (2002)), suggesting that despite mechanical and evolutionary constraints locust wings are rather efficient, indeed, only 12–18% less than ideally efficient. It is a little higher than that estimated by Spedding (1987) for a gliding kestrel, where k=1.04. Spedding derived this figure from the ratio of the measured wingtip vortex spacing to that predicted for an elliptically loaded wing of the same span. The assumption of elliptical loading should cause Spedding's estimated value of k for a kestrel to be lower than our measurement of k for a locust, but the difference may also be due to the emarginated primary feathers of kestrels forming a staggered array of winglets; although k=1 is a minimum for planar wings, values of k<1 are possible for non-planar wings (e.g. through disruption of the wingtip vortex by winglets). The total instantaneous estimate for lift (up to 10 times bodyweight) is probably unrealistically high, yet this is not a limitation of this experiment because the errors included in the estimation of added mass cancel during calculation of k. That the figure is too high should perhaps act as a cautionary note to those pursuing the actuator disc model in order to determine total flight forces.

This experiment was limited in that it could only measure the downwash at one point through the wingbeat cycle of a tethered locust. A fuller account of the downwash, with its changing magnitude and distribution for a variety of insects, preferably in free-flight, is planned next to help provide a more realistic model of insect flight. If we are to measure and compare the differences between species, then a standard reference position is required to permit unambiguous comparisons. Here, we have selected the position with the wings held 180° apart (taking the larger pair of wings for functionally four-winged insects). This position has a number of advantages. First, it occurs in the middle of the wing stroke for almost all insects, so variations due to wing accelerations or rotations are unlikely to dominate the flows. Second, it maximizes wing span, easing problems of resolution. Third, because the wings are essentially horizontal at this point in the stroke modelling the flow is simplified. Variations in insect wing design are spectacular, but we know almost nothing about the aerodynamic effects of those variations, or the evolutionary selection pressures that have lead to them. A comparative DPIV approach of this nature would allow the definition of similarities in design, leading to groupings of aerodynamic solutions, which are conserved despite compromises enforced by other evolutionary selective pressures.

No insect wing can be ideally loaded: most insects have simple quasi-planar wing geometry (unlike birds with their branching, fingered wingtips), so aerodynamic inefficiencies are inevitable, thus increasing the required induced power to stay aloft, and consequently raising k to a value above the ideal of unity. Evolutionary biologists would like to discover whether the wings of each flying insect have at least a close to locally optimal design in terms of aerodynamics. Measuring the downwash distribution can provide new insights into insect wing design by revealing how the combination of aerodynamic mechanisms and wing architecture are employed to keep k as low as possible. It is not a surprise for a migratory species such as S. gregaria to maximize flight efficiency, and it would be of interest to compare this result with measurements from insects with differing flight morphologies.