Abstract
To analyse the evolutionary emergence of structural complexity in physical processes, we introduce a general, but tractable, model of objects that interact to produce new objects. Since the objects—ϵ-machines—have well-defined structural properties, we demonstrate that complexity in the resulting population dynamical system emerges on several distinct organizational scales during evolution—from individuals to nested levels of mutually self-sustaining interaction. The evolution to increased organization is dominated by the spontaneous creation of structural hierarchies and this, in turn, is facilitated by the innovation and maintenance of relatively low-complexity, but general individuals.
Keywords: self-organization, evolution, population dynamics, autocatalysis, structure, hierarchy
Long before the distinction between genetic information and functional molecules, there were objects that simply interacted and mutually transformed each other. Today, the functioning of life relies on macromolecules that are simultaneously encoded by stored information and also manipulate it. How did structured objects with the dual roles of information storage and transformation emerge from initially disorganized environments? Here, we introduce a class of models that allows us to explore this question, in a setting often referred to as pre-biotic evolution (Rasmussen et al. 2004). In contrast to prior work, we focus on the questions of what levels of structure and information processing can emerge and, specifically, what population dynamical mechanisms drive the transition from pre-biotic to biotic organization.
One of the key puzzles in this is to understand how systems produce structure that becomes substrate for future functioning and innovation. The spirit of our approach to this puzzle follows that suggested by Schrodinger (1967) and found in von Neumann's (1966) random self-assembly model. However, our model is more physical than chemical in the sense that we do not assume the existence of sophisticated chemical entities, such as macromolecules, nor do we even use chemical metaphors, such as information being stored in one-dimensional arrays—in aperiodic crystals, as Schrodinger presciently proposed. While ultimately interested in pre-biotic organization and its emergence, our focus is on what one might call pre-chemical evolution. As such, the following provides a first step to directly address how structural complexity and evolutionary population dynamics interact (Crutchfield 2001).
Here, we introduce a model of the emergence of organization and investigate it in a setting that, at one and the same time, provides a well-defined and quantitative notion of structure and is mathematically tractable. The goal is to develop predictive theories of the population dynamics of interacting, structured individuals and their collective organization. With a well-defined measure of structural complexity, one can precisely state the question of whether or not complexity has genuinely emerged over time in pre-biotic and pre-chemical processes. Additionally, with a predictive theory of the population dynamics, one can identify and analyse the (at some point evolutionary) mechanisms that lead to such increases (and to decreases) in structural complexity.
We create a well-stirred population—the finitary process soup—of initially random, finite ϵ-machines (Crutchfield & Young 1989) that interact and transform each other, making new ϵ-machines of differing structure and so of differing transformational properties. The initial random soup serves as a reference that, for reasons to become apparent below, has ‘null’ structural complexity, both in the individuals (on average) and across the population. Here, we consider the case of a process gas: objects, ϵ-machines and , are successively randomly paired (pan-mixia) and act on each other to create progeny: . No externally applied selection or variation is imposed.
An ϵ-machine consists of a set of causal states and transitions between them: , . We interpret the symbols labelling the transitions in the alphabet as consisting of two parts: an input symbol that determines which transition to take from a state and an output symbol which is emitted on taking that transition. ϵ-Machines have several key properties (Crutchfield & Young 1989): all of their recurrent states form a single strongly connected component. Their transitions are deterministic in the specific sense that a causal state together with the edge symbol-pair determines the successor state. And, is minimal: an ϵ-machine is the smallest causal representation of the transformation it implements. Two examples are shown in figure 1.
Figure 1.
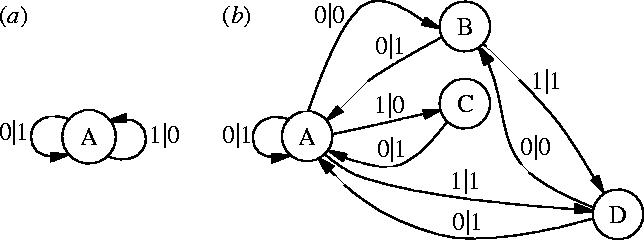
Two examples of ϵ-machines. Each consists of states (circles) and transitions (edges with labels input|output). (a) The ‘bit-flip’ ϵ-machine which, for example, takes in any binary string and produces a string of equal length in which 0s and 1s have been exchanged. It has statistical complexity zero: bits; it adds no new structure to ϵ-machines with which it interacts. (b) A typical four-state ϵ-machine found in one of the multistate finitary process soups mentioned in the text. Its statistical complexity is bits.
Due to these properties, one can quantify an ϵ-machine's structural complexity. To do this, we need the probability distribution over the states in , how often they are visited, and this is given by the normalized left eigenvector associated with eigenvalue 1 of the stochastic matrix . Denote this eigenvector, normalized in probability, by . An ϵ-machine's structural complexity is the amount of stored information:
| (1) | (1) |
When is finite, we say the ϵ-machine (or, more properly, the transformation it describes) is finitary.
Thus, unlike previous models—such as λ-expressions (Fontana 1991), machine instruction codes (Rasmussen et al. 1990; Ray 1991; Adami et al. 2000; Pargellis 2001), tags (Bagley et al. 1989) and cellular automata (Crutchfield & Mitchell 1995)—ϵ-machines allow one to readily measure the structural complexity and disorder of the transformations they specify. It is well known that algorithms do not even exist to measure these quantities for machine-language programs and λ-expressions, for example, since these are computation-universal models (Brookshear 1989). As our results demonstrate, these tractable aspects of ϵ-machines give important quantitative, interpretive and theoretical advantages over prior work on the pre-biotic evolutionary emergence of structural complexity. The finitary assumption is also consistent with the recent proposal that gene expression is implemented with finite-memory computational steps (Benenson et al. 2004).
We should emphasize that, in these finitary process soups and in contrast to prior work, ϵ-machines do not have two distinct modes of representation or functioning. The objects are only functions, in the prosaic mathematical sense. Thus, one benefit of this model of pre-biotic evolution is that there is no assumed distinction between gene and protein (von Neumann 1966; Schrodinger 1967), between data and program.1
Finitary process soups allow one to quantitatively analyse not only the structural complexity of individuals, but also the interaction between individual structure and population organization and dynamics in terms of how they store and process information and the causal architecture that supports these. Since this view of a system intrinsically computing applies both to individuals and to the population as a whole, we can identify the locus of a population's structural complexity. Is it largely the sum of the individuals' or largely embodied in the transformative relationships between individuals? Perhaps, it derives from some irreducible interaction between these levels.
The finitary process soup differs from early investigations in which finite-state machines were evolved using an explicit mutational operator (Fogel et al. 1966). Here, novelty derives directly from how the objects themselves are structured, since this determines how they transform each other. Equally important, survivability is determined by an individual's rate of reproduction—the original biological notion of fitness; there is no externally imposed fitness function. In this, the process soup is similar to the molecular evolution models of Eigen & Schuster (Schuster 1977).
A population P is a set of N individuals, each of which is an ϵ-machine. More compactly, one can also describe the population as a distribution of ϵ-machine types: , where n is the number of ϵ-machine types in the soup and is the number of individuals of type . A single replication is determined through compositions and replacements in a two-step sequence. First, construct ϵ-machine :
With probability , forming the composition from and randomly selected from the population and minimizing (Brookshear 1989).
With probability , generating a random .
Second, replace a randomly selected ϵ-machine, , with . is the rate of influx of new (random) ϵ-machines. When , the soup is a closed system. When , the soup is open, but consists of entirely random ϵ-machines and so is unstructured. The initial population —with —is similarly unstructured.
As a first step to detect population structure, we define the interaction network as the ϵ-machine compositions that have occurred in the population. For a population with n different types, is described by an matrix, the entries of which are the machine types returned by the compositions . We represent as a graph whose nodes are the machine types in the population and whose directed edges connect one node, say , to another, , when . The edges are labelled with the transforming machine . We also represent as a transition matrix , when .
The second step is to introduce a natural notion of organization that encompasses interaction and dynamic stability; we define a meta-machine as a set of ϵ-machines that is both closed and self-maintained under composition, i.e. is a meta-machine if and only if (i) , for all Ti, and (ii) for all , there exists Ti, , such that . This definition of self-maintenance captures Maturana et al.'s autopoiesis (Varela et al. 1974), Eigen & Schuster's hypercycles (Schuster 1977) and autocatalytic sets (Kauffman 1986; Fontana 1991). In a process soup, awash in fluctuations and change, a meta-machine is a type of organization that can be regarded as an autonomous and self-replicating entity. Note that, in this sense, the initial random soup is not organized. To the extent that interaction networks persist, they are meta-machines.
To measure the diversity of interactions in a population, we define the interaction network complexity as
| (2) | (2) |
where
| (3) | (3) |
and is a normalizing factor.
Finally, a machine type's frequency changes at each generation according to its interactions and is given by
| (4) | (4) |
where denotes the transpose of vector f and is a normalizing factor.
Let us now explore a base case: the population dynamics of one simple subset of ϵ-machines, those consisting of only a single state. This class is especially instructive since it is closed under composition: the composition of two single-state machines is itself a single-state machine. There are 15 single-state ϵ-machines; excluding the null machine. As a consequence, there are a finite number of possible interactions and this, in turn, greatly facilitates an initial analysis. Although a seemingly simple case, a population of these machines exhibits non-trivial dynamics and leads to several insights about populations not restricted to single-state ϵ-machines.
The first obvious evolutionary pressure driving the system is that governed by trivial self-reproduction (copying). ϵ-Machines with the ability to copy themselves (directly or indirectly) are favoured, possibly at other ϵ-machines' expense or in symbiosis with other ϵ-machines. The number of such self-reproducing machines grows in relation to the whole population, further increasing the probability of self-reproduction. Interaction networks that sustain this will emerge, consisting of cycles of cooperatively reproducing ϵ-machines. These are chains of composed mappings that form closed loops.
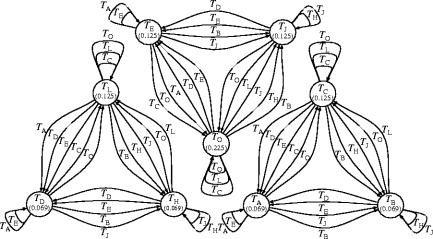
Figure 2 shows the dynamics of a population sampled from in a closed system of ϵ-machines. The figure shows that equation (4) predicts the simulations quite well. Out of the interactions between all possible ϵ-machines, the population settles down to a steady-state interaction network of nine ϵ-machines. Figure 3 shows this meta-machine. Note that the structural complexity of individual ϵ-machines is always zero: for single-state machines. Thus, the population's structural complexity is due solely to that coming from the network of interactions.
Figure 2.

Population dynamics starting with randomly sampled single-state ϵ-machines: fraction of ϵ-machine types as a function of time t (number of replications). Simulations (dashed lines) and theory, equation (4), (solid lines).
Figure 3.
Organization of the steady-state population—a single meta-machine : the interaction graph after replications, at the end of figure 2. For simplicity, the graph shows only -denoted interactions, not the complementary interactions. Therefore, the three components displayed are not separate; they are parts of a single connected interaction network. For example, ϵ-machine (lower-left node in left component) appears on edges in each of the other components. bits.
Note that the fluctuations of the simulation about the theoretical values at late times are due to finite-size population sampling. The deviations between theory and simulation at earlier times come from a slight difference in generational time-scale. The theory above assumes the entire population is updated synchronously and simultaneously, when individuals in the simulation individually and asynchronously replicate. This can be corrected for, but requires careful treatment, which will appear in a sequel.
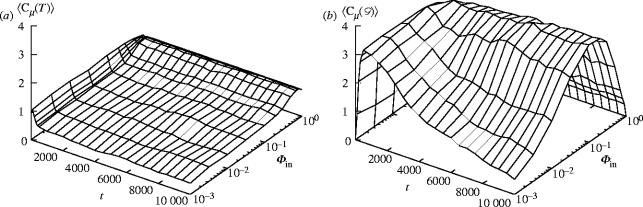
With ways to predict the population dynamics and to detect the emergence of structural complexity in the soup, we now turn to the evolution of unrestricted populations of multistate ϵ-machines. We summarize the results using the population-averaged ϵ-machine complexity and the run-averaged interaction network complexity as a function of time and influx rate (see figure 4). One observes an initial rapid construction of increasingly complex individuals and interaction networks. In the closed system , both of these reach a maximum and then decline to less complex steady states within a small subspace of possible structures. In fact, both structural complexities effectively vanish at this extreme. The closed system specializes, ages and eventually dies away. At the extreme of high influx , when the population looses the ability to store information, the network complexity vanishes and the individual complexity becomes that of a purely random sample of ϵ-machines.
Figure 4.
(a) Population-averaged ϵ-machine complexity (bits) and (b) run-averaged interaction network complexity (bits) versus time t and influx rate for a population of size N=100 averaged over 50 runs at each . Each run starts with a uniform sample of two-state ϵ-machines. For , the randomly introduced ϵ-machines come from a uniform sample of two-state ϵ-machines.
Away from these extremes, the evolution of the open systems' network complexity is maximized at an intermediate influx rate . Notably, the emergence of complex organizations occurs where individual ϵ-machine complexity is small. Survival, however, requires these individuals to participate in interaction networks and so to interact with a variety of other machines; they are generalists in this sense. At higher influx large is correlated with markedly less complex networks. These more complex machines are specialized and do not support robust complex interaction networks.
It turns out that the maximum network complexity grows slowly (linearly) with time. It is ultimately capped by the population size, since there is only so much structure that can be built with a finite number of components. More extensive investigations show that it grows in an unbounded way——indicating the possibility of reaching highly structured populations at large sizes.
Up to this point, we have discussed structural complexity that has emerged on two levels—the individual and the interaction of individuals. More extensive studies of the population dynamics, which will be reported elsewhere, reveal a higher level of organization in which meta-machines take on an autonomy and form their own networks of interaction. Thus, the finitary process soup exhibits the spontaneous emergence of several distinct scales of organization.
The finitary process soup demonstrates (i) that complexity of the entire system arises mainly from the transformative relationships between individuals and (ii) that those individuals tend to be non-complex and to implement general rather than specialized local functions. Thus, the population dynamics makes a trade-off: simpler individuals facilitate the emergence of global structure. Conversely, for a system to become complex, it is not necessary to evolve complex individuals. The results strongly suggest that replicative processes will use this particular strategy to build successively higher levels of structural complexity from the compositional (‘metabolic’) network of interacting finitary components. In this way, the finitary process soup evolves higher computational representations; they are not built-in or accessible at the outset.
The finitary process soup is a model of endogenous evolution. In particular, fitness is defined and measured in the biologically plausible way, as the rate of individual reproduction, and there is no externally imposed mutational operator. It is also a flexible model; we showed pan-mixia replication and will report on populations with spatial structure elsewhere. Moreover, it is extensible in a number of ways. Specifically, it is straightforward to couple in energetic and material costs of composition. This will allow one to analyse trade-offs between energetics, dynamics and organization. Finally, one of the key determinants of evolutionary dynamics is the structure of selection-neutral genotype networks (see Crutchfield 2001 and references therein). The neutral networks of ϵ-machines and of ϵ-machine networks can be directly probed.
We close with a few general comments. Given that organization in a population becomes hierarchical, we believe that powerful computational representations, when employed as the basic objects, are neither effectively used by nor necessary for natural evolutionary processes to produce complex organisms. We hypothesize that individuals with finitary computational capacity are appropriate models of molecular entities and transformations. From these, more sophisticated organizations and functions can be hierarchically assembled. This can only be tested by experiment, of course, but this will soon be possible.
It has been recently estimated that the genomes of many species consist of a surprisingly similar number of genes2 despite some being markedly more complex and diverse in their behaviours (Lynch & Conery 2003; Rat Genome Sequencing Project Consortium 2004). Moreover, many of those genes serve to maintain elementary functions and are shared across species. These observations accord with the evolutionary dynamics of the finitary process soup: global complexity is due to the emergence of higher level structures and this in turn is facilitated by the discovery and maintenance of relatively non-complex, but general objects. In both the genomic and finitary soup cases, one concludes that an evolving system's sophistication, complexity and functional diversity derive from its hierarchical organization.
Acknowledgements
This work is supported by Intel Corporation, core grants from the National Science and MacArthur Foundations and DARPA Agreement F30602-00-2-0583. O.G. was partially supported by the International Masters Programme in Complex Adaptive Systems.
Footnotes
One recovers the dichotomy by projecting onto (i) the sets that an ϵ-machine recognizes and generates and (ii) the mapping between these sets (Brookshear 1989).
Humans have only 30% more genes than the worm Caenorhabditis elegans; humans, mice and rats have nearly the same number.
References
- Adami C, Ofria C, Collier T.C. Proc. Natl Acad. Sci. USA. 2000;97:4463–4468. doi: 10.1073/pnas.97.9.4463. doi:10.1073/pnas.97.9.4463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagley R.J, Farmer J.D, Kauffman S.A, Packard N.H, Perelson A.S, Stadnyk I.M. BioSystems. 1989;23:113–138. doi: 10.1016/0303-2647(89)90016-6. doi:10.1016/0303-2647(89)90016-6 [DOI] [PubMed] [Google Scholar]
- Benenson Y, Gil B, Ben-Dor U, Adar R, Shapiro E. Nature. 2004;429:423–429. doi: 10.1038/nature02551. doi:10.1038/nature02551 [DOI] [PubMed] [Google Scholar]
- Brookshear J.G. Benjamin/Cummings; Redwood City, CA: 1989. Theory of computation. [Google Scholar]
- Crutchfield J.P. In: Evolutionary dynamics. Crutchfield J.P, Schuster P.K, editors. Oxford University Press; New York: 2001. pp. 101–134. [Google Scholar]
- Crutchfield J.P, Mitchell M. Proc. Natl Acad. Sci. USA. 1995;92:10 742–10 746. [Google Scholar]
- Crutchfield J.P, Young K. Phys. Rev. Lett. 1989;63:105–108. doi: 10.1103/PhysRevLett.63.105. doi:10.1103/PhysRevLett.63.105 [DOI] [PubMed] [Google Scholar]
- Fogel L.J, Owens A.J, Walsh M.J. Wiley; New York: 1966. Artificial intelligence through simulated evolution. [Google Scholar]
- Fontana W. In: Artificial life II. Langton C, et al., editors. Addison-Wesley; Redwood City, CA: 1991. pp. 159–209. [Google Scholar]
- Kauffman S.A. J. Theor. Biol. 1986;119:1–24. doi: 10.1016/s0022-5193(86)80047-9. [DOI] [PubMed] [Google Scholar]
- Lynch M, Conery J.S. Science. 2003;302:1401–1404. doi: 10.1126/science.1089370. doi:10.1126/science.1089370 [DOI] [PubMed] [Google Scholar]
- Pargellis A. Artif. Life. 2001;7:63–75. doi: 10.1162/106454601300328025. doi:10.1162/106454601300328025 [DOI] [PubMed] [Google Scholar]
- Rasmussen S, Knudsen C, Feldberg R, Hindsholm M. Physica D. 1990;75:1–3. [Google Scholar]
- Rasmussen S, Chen L, Deamer D, Krakauer D.C, Packard N.H, Stadler P.F, Bedau M.A. Science. 2004;303:963–965. doi: 10.1126/science.1093669. doi:10.1126/science.1093669 [DOI] [PubMed] [Google Scholar]
- Rat Genome Sequencing Project Consortium Nature. 2004;428:493–521. doi: 10.1038/nature02426. doi:10.1038/nature02426 [DOI] [PubMed] [Google Scholar]
- Ray T.S. In: Artificial life II. Langton C, et al., editors. Addison-Wesley; Redwood City, CA: 1991. pp. 371–408. [Google Scholar]
- Schrodinger E. Cambridge University Press; Cambridge, UK: 1967. What is life? and mind and matter. [Google Scholar]
- Schuster P.K. Naturwissenshaften. 1977;64:541–565. doi:10.1007/BF00450633 [Google Scholar]
- Varela F.J, Maturana H.R, Uribe R. BioSystems. 1974;5:187–196. doi: 10.1016/0303-2647(74)90031-8. doi:10.1016/0303-2647(74)90031-8 [DOI] [PubMed] [Google Scholar]
- von Neumann J. University of Illinois Press; Urbana, IL: 1966. Theory of self-reproducing automata. [Google Scholar]