Noise, cost and speed-accuracy trade-offs: decision-making in a decentralized system

Abstract

Many natural and artificial decision-making systems face decision problems where there is an inherent compromise between two or more objectives. One such common compromise is between the speed and accuracy of a decision. The ability to exploit the characteristics of a decision problem in order to vary between the extremes of making maximally rapid, or maximally accurate decisions, is a useful property of such systems. Colonies of the ant Temnothorax albipennis (formerly Leptothorax albipennis) are a paradigmatic decentralized decision-making system, and have been shown flexibly to compromise accuracy for speed when making decisions during house-hunting. During emigration, a colony must typically evaluate and choose between several possible alternative new nest sites of differing quality. In this paper, we examine this speed-accuracy trade-off through modelling, and conclude that noise and time-cost of assessing alternative choices are likely to be significant for T. albipennis. Noise and cost of such assessments are likely to mean that T. albipennis' decision-making mechanism is Pareto-optimal in one crucial regard; increasing the willingness of individuals to change their decisions cannot improve collective accuracy overall without impairing speed. We propose that a decentralized control algorithm based on this emigration behaviour may be derived for applications in engineering domains and specify the characteristics of the problems to which it should be suited, based on our new results.

Introduction

Speed-accuracy trade-offs are a common and often adaptive feature of decision-making in diverse organisms (Edwards 1965; Chittka et al. 2003). They can also be a useful characteristic of decision-making algorithms in artificial systems where there are varying time constraints on the algorithms' execution, and have led to the development of a class of algorithms known as ‘anytime algorithms’ (Dean & Boddy 1988). Anytime algorithms are those in which the quality of the solution generated increases the longer the algorithm runs; the algorithm can be made quickly to compute an approximate solution, or take longer to compute a better solution. There are typically two ways of achieving this, either pre-specifying an execution duration for the algorithm, or interrupting it during execution and taking the best solution found so far (Dean & Boddy 1988). In this paper, we study speed-accuracy trade-offs in the context of a natural decentralized decision-making system, in which components of the system must make local decisions using only local and uncertain information, leading to a system-level decision without the need for centralized control or global information. The ways in which natural selection has shaped such decentralized systems to deal elegantly with the problems posed by local information and uncertainty are fascinating, and worthy of our attention in their own right. They are also the potential source of interesting new artificial decision-making algorithms, suitable for application in the increasing number of engineering domains where decentralized control is required using only local and uncertain information (Bonabeau et al. 1999). In this paper, we investigate such a naturally occurring decentralized decision-making system, house-hunting in the ant Temnothorax albipennis, and identify the characteristics of decision problems to which it might be fruitfully applied.

When colonies of the ant T. albipennis select a new nest site, they employ an ingenious and sophisticated collective decision-making process (Mallon et al. 2001, Pratt et al. 2002, Franks et al. 2003a, Dornhaus et al. 2004). This process utilises a two-stage decision mechanism and positive feedbacks to achieve a consensus for the best of several alternatives, without central control. Individuals use only the local information that is available to them; no individual coordinates the process by collating incoming information on the alternatives available, and not all colony members need directly compare alternatives (Mallon et al. 2001). Of particular interest is the observation that colonies of T. albipennis are able adaptively to compromise between the accuracy of their decision and the speed with which it is reached, according to the urgency of the decision; good conditions allow slow, carefully considered selections, while bad conditions require quick choices which may be less accurate (Franks et al. 2003a). This elegantly flexible and decentralized decision-making mechanism, that works reliably using only local information, motivated us to study its characteristics and consider its application in engineering domains.

House-hunting in T. albipennis

Temnothorax albipennis is an ant species with small workers (about 3 mm long) and small colonies (less than 400 workers). The workers are monomorphic and colonies have a single, singly mated queen (see Partridge et al. 1997). Colonies can be found nesting in extremely thin crevices in rocks, typically occupying an area of a few square centimetres. As they live in such small flat nests, they can easily be cultured and experimented with in the laboratory (Franks et al. 2002, 2003a,b).The rocks they inhabit in nature are typically rather unstable and friable. Colonies of the ant T. albipennis periodically need to emigrate from their current nest site to a new one. Two typical reasons for such emigrations are that either the original nest site has been rendered uninhabitable, perhaps being destroyed by a larger animal, or the colony's numbers have grown such that the current nest site is no longer large enough. The details of this emigration process have been elucidated by experimental observation (Mallon et al. 2001; Pratt et al. 2002; Franks et al. 2003a; Dornhaus et al. 2004) as follows. When an emigration begins, scout ants from the colony leave the original nest site and search for potential new nest sites in the vicinity. On finding a potential site, a scout will assess several criteria, such as internal area (Mallon & Franks 2000), structural integrity, darkness, etc. and integrate these different criteria into a single quality measurement (Franks et al. 2003b). This measure translates into a time-delay before recruitment that is inversely proportional to the perceived quality of the site. After delaying, the scout will recruit other scouts to assess the same site and these in turn recruit others, thus providing a kind of multiple ‘second opinion’. When a scout recruits to a potential site, she initially recruits via a slow process known as ‘tandem running’, in which the scout leads another ant to the site, maintaining physical contact throughout. However, if a scout enters a potential site and discovers that it contains a sufficient number of ants from the same colony, she will change her subsequent recruitment mode to a process known as ‘social carrying’. Social carrying involves the scout picking up another passive ant or brood item and carrying it; social carrying is approximately three times faster than tandem-running (Pratt et al. 2002). The number of nest mates that must be in a potential site to trigger social carrying is known as the ‘quorum threshold’. The quorum threshold is a key control device in the colony's decision-making process, allowing the colony to achieve slow but accurate decisions, or fast but less accurate decisions, by having a high or low quorum threshold, respectively. Low quorum thresholds mean that scouts begin social carrying earlier, leading to more individualistic decision-making, while high thresholds mean that scouts take longer to begin social carrying, allowing them to recruit many other scouts to give their verdict on a site's quality. Colonies respond adaptively to the urgency of their emigration by varying the quorum threshold appropriately (Franks et al. 2003a). Colonies use low quorum thresholds and hence fast, more error prone decisions when their original nest has been destroyed, or they find themselves in a harsh environment. However, colonies use high quorum thresholds to achieve slower, more accurate decisions when there is no urgency, for example when the original nest site is intact and they are simply searching for a superior nest site (Dornhaus et al. 2004).

Speed-accuracy trade-offs in problems and decisions

A speed-accuracy trade-off is not in itself a desirable feature of a decision-making process. It would, of course, be preferable to be able to make highly accurate decisions in the minimum time possible. Rather, a speed-accuracy trade-off is usually inherent in the combination of the decision problem and the sensory and cognitive apparatus with which the decision-making system is equipped.1 In this case, the problem can be understood as exhibiting a Pareto-front; a region in the performance space in which the performance according to one metric (speed or accuracy) cannot be improved without the performance according to the other metric (accuracy or speed) deteriorating (figure 1). If such a trade-off is inherent in the problem, such as in online decision problems in which information accrues over time (Wald & Wolfowitz 1948), then it is likely to be beneficial if the decision-making mechanism can exploit it, and vary its strategy according to the circumstances of the decision.

Figure 1.

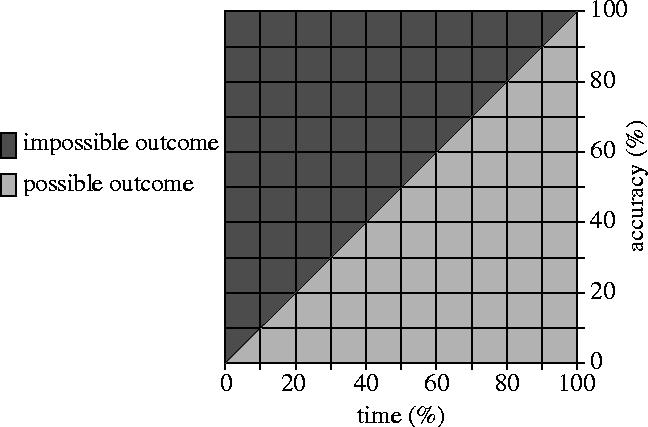
The performance of the decision-making system can move flexibly along the Pareto-front (the interface between the light-shaded and dark-shaded regions) that the decision problem exhibits. The characteristics of the decision problem mean that it is not possible to go beyond (above) this Pareto-front into the dark-shaded region; only combinations of decision time and accuracy in the light-shaded region on or below the line are possible. Thus, from any point on the diagonal, it is not possible to improve the speed performance without the accuracy performance deteriorating, and vice-versa. By moving along the Pareto-front, the decision-making system is able to trade speed for accuracy and vice-versa, according to the circumstances of the decision.

A flexible decision-making mechanism, then, is one that is able to change its performance along this Pareto-front so that performance in one regard is sacrificed for a corresponding increase in performance in another regard, and vice-versa, as circumstance dictates. In environments where varying time constraints are imposed on decision-making, it is clear that a flexible decision-making mechanism that can make quick, but less accurate decisions or slow, accurate decisions will be at an advantage compared to an inflexible decision-making mechanism that can only make slow, accurate decisions or, conversely, to a different inflexible mechanism that can make only quick, inaccurate decisions. House-hunting in T. albipennis is just such a flexible decision-making mechanism.

An initial model of ant house-hunting

We are interested in modelling the emigration process described above in order to investigate its speed-accuracy trade-off in more detail. In particular, we wish to identify the characteristics of the emigration problem itself that force the house-hunting algorithm, used by T. albipennis, to choose between fast decisions and accurate decisions. Pratt et al. (2002) made a first attempt at modelling the decision-making mechanism used in emigrations by T. albipennis. They model the decision-making process as a system of ordinary differential equations (ODEs), specifying the rates of change of populations of ants that are either inactive in the original nest site, assessing a particular potential nest site, or recruiting to a particular potential nest site. While this model has since been superseded by a more sophisticated and extensively verified model (Pratt et al. in press), by virtue of its simplicity the ODE model provides us with a useful starting point in our investigations. The ODE model, reproduced in appendix A, captures the two-stage recruitment process used by T. albipennis, and the variable quorum threshold which provides the means for colonies to vary the speed and accuracy of their decisions. Using the parameters from Pratt et al. (2002), measured by observing real emigrations, we can see that their simple model also captures the speed-accuracy trade-off exhibited by T. albipennis (figure 2a), despite not being formulated explicitly for this purpose. Figure 2a shows that as the quorum threshold used increases the accuracy increases, but similarly the time taken to complete the emigration also increases. When modelling only the evacuation phase of the emigration, as done in the Pratt et al. model, we measure decision accuracy as proportion of colony members in the superior site. This is a sensible measure as, apart from times of the year when colonies split into more than one nest (Partridge et al. 1997), the colony will ultimately have to be reunified in a single nest site. This will incur an energetic and time-cost as ants and brood items are moved from one site to the other to be reunited with the colony, and may also increase exposure to predators. Therefore, our accuracy measure is closely related to that used in the original biological experiments, namely frequency of recruitment to the inferior nest site (Franks et al. 2003a). Our accuracy measure also gives us a range of possible accuracies for a given emigration rather than simply indicating if the colony chose the superior site, the inferior site, or split between them.

Figure 2.

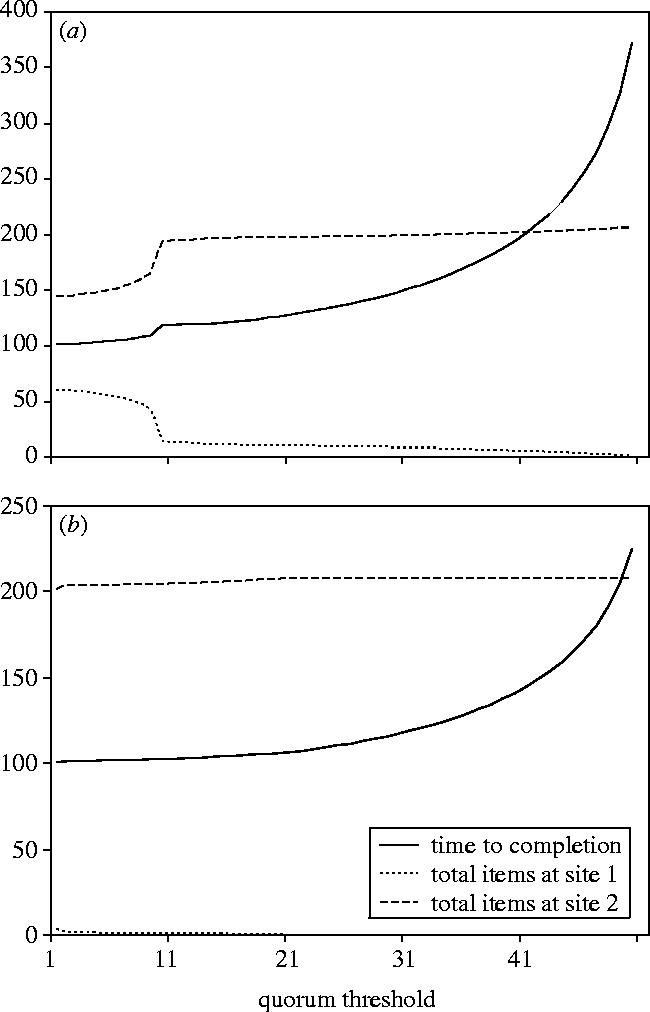
(a) Output from a mathematical model of house-hunting in T. albipennis parameterized to replicate their speed-accuracy trade-off. The graph shows the decision time (time until the original nest site is empty) and accuracy (items ending up at site 2, the superior site) achieved with different quorum thresholds (results from the model presented in Pratt et al. (2002)). (b) Output from the same mathematical model (Pratt et al. 2002) with the same parameters used to generate figure 2, but with the switching rate, ρ₁₂, from the inferior to superior nest site increased from 0.008 to 0.06. The result of this change is that the speed-accuracy trade-off observed in figure 2 disappears; minimal quorum size leads to almost perfectly accurate decisions without any corresponding increase in decision time, and decision time becomes less influenced by quorum threshold used.

We investigated this model and found that it is extremely sensitive to one particular parameter, ρ₁₂, the rate at which ant scouts switch from assessing or recruiting for the inferior nest site to assessing or recruiting for the superior nest site. Increasing ρ₁₂ from 0.008 to 0.06 results in an almost perfectly accurate decision being reached with the minimum quorum threshold of 1, with no corresponding increase in the time taken to reach the decision (figure 2b). In other words, purely individual decision-making by individual ant scouts leads to a near perfect decision, and in the minimum time possible.

While this result may seem surprising initially, consideration of the model quickly leads to the following explanation. A key feature of the model is the assumption, based on observations, that ρ₂₁=0; in other words that ants switch from the inferior site to the superior site, but not from the superior site to the inferior site. As there is no explicit cost associated with switching, looking at equation (A 3) we quickly see that, in the limit of ρ₁₂=∞, the model collapses from a two-choice decision problem into a single-choice decision problem, because scouts considering the inferior alternative inevitably switch to the superior site immediately.

Thus, while the model is able to recreate the speed-accuracy trade-off observed in nest site selection by T. albipennis, rather than explaining it the model actually predicts that the colonies should be able to achieve almost perfect decisions in minimal time without the need for a speed-accuracy trade-off. We hypothesize that real ants do not make such accurate yet rapid decisions because their preference switching rate, ρ₁₂, is too low.

Perhaps, the most obvious explanation for why the real ants do not exhibit a higher switching rate is that there are physical constraints on the ants that lead to an upper bound for it; the physical distance between alternative sites and the rates at which scouts considering an inferior site encounter scouts recruiting for a superior site might limit ρ₁₂. Note, however, that in the accurate yet rapid decisions possible in our model below, half of the colony's scouts will evaluate both potential new nest sites; as discovery of equidistant nest sites is equiprobable, on average half of the scouting ants will visit the inferior site first. If a decision is to be completely accurate, these scouts must not carry nest mates to the inferior site, but must subsequently also evaluate the second, superior site, and confine their recruitment to that.

Experimental data indicate that this level of dual comparisons is feasible for real colonies, suggesting that a limited switching rate may not be the only explanation for the ants' observed performance. Mallon et al. (2001) report three emigrations in which 86, 46 and 32% of recruiters visited both potential sites. We propose, therefore, that two other factors may play an important role. These factors are the degree of noise and the time-cost inherent in assessing alternative nest sites, hereafter referred to as assessment noise and assessment cost, respectively.

By disallowing mistakes in which an ant scout switches its allegiance from a superior site to an inferior site, the original model assumes that individual scouts are perfect assessors. However, given the evidence that individual scouts assess, for example, floor-area with a considerable variance (Mallon & Franks 2000), such an assumption seems unrealistic. The parameterization of ρ₂₁=0 in the Pratt et al. (2002) model was based on experimental observations that scouts did not switch their preference from superior to inferior site; however, two important points must be made in this regard. First, the switching rate ρ₁₂=0 was used in the Pratt et al. model both for ants assessing a site, and ants recruiting to a site; subsequent re-examination of the data has, however, shown that erroneous switching from the superior site to the inferior site did occur among assessors in the experiments used to parameterize the model (Planqué et al. in preparation). Second, the difference in nest designs used in the experiment had been tuned such that the ants expressed a statistically significant preference (Mallon et al. 2001). In situations where differences in quality are less distinct, it seems reasonable to expect switching from superior to inferior site by scouts to be more likely.

Additionally, while the assessment cost of considering alternative sites can be implicitly included in the original model by limiting the rate at which scouts can switch from one alternative to the other, by not explicitly separating out this aspect of the decision-making process it is not possible to investigate the effect of assessment cost on the behaviour of the decision-making system independent of switching rate. In order to investigate the effect of assessment noise and assessment cost on the decision-making process, we therefore designed a more sophisticated model of house-hunting in T. albipennis.

An extended model of house-hunting

Our model of the nest site selection process in T. albipennis, which we call the Ant House-Hunting Algorithm (AH-HA) model, is an individual-based model. Our choice of this modelling strategy is supported by Pratt et al.'s (in press) demonstration of the sufficiency of individual rules to reproduce the global behaviour observed in colonies of T. albipennis. An individual-based model differs from the kind of mathematical model originally used by Pratt et al. (2002), which describes the collective behaviour of the system from the top down, in terms of rates of change of numbers of ants in different states. Rather, an individual-based model explicitly describes the states, behaviours and interactions of individually modelled ants and proceeds from the bottom up to determine the overall system behaviour. This provides us with two main benefits. First, in any system with a small number of interacting components, such as ant scouts in our example, allowing infinitesimal changes in the number of components in any state and hence, in effect, assuming an infinite population is rather unrealistic. Indeed, explicitly representing the discrete components and their interactions can lead to qualitatively different dynamics and reveal system-level behaviours that must be explicitly incorporated into an equation-based model (e.g. Wilson 1998; Marshall & Rowe 2003). Second, using an individual-based approach will make the transition from model to algorithm much easier. Our intention is to derive and apply a decentralized algorithm for engineering domains. In many such domains continuous simultaneous sampling of alternatives is either impractical or too costly in time or money. These domains will, in practice, require discrete sampling, and a strategy for efficient allocation of parallel trials to the available alternatives. Temnothorax albipennis realizes such a strategy through individual scouts assessing alternatives and then recruiting other scouts to do the same. The use of an individual-based approach, rather than the continuum approach used in the Pratt et al. (2002) model, allows a more faithful replication of this behaviour. This modelled behaviour should in turn map easily onto the kinds of engineering domains described above, with minimal deviation from the conditions under which it operates in T. albipennis, and under which it is expected to perform optimally.

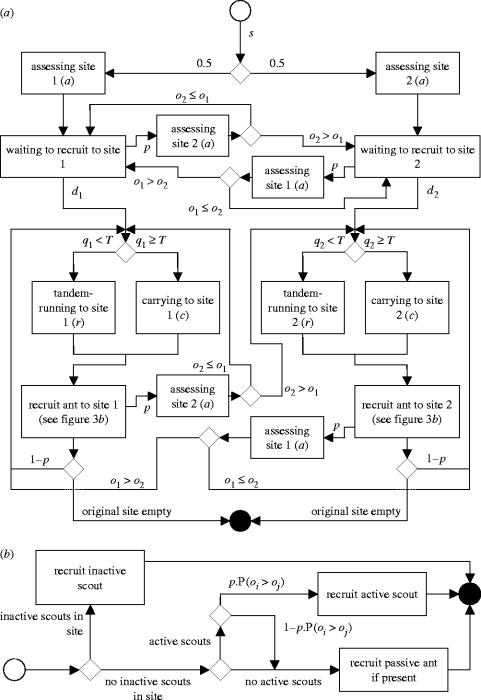
Figure 3 describes the behaviour of the model using a state transition diagram for ant scouts (figure 3a), and a decision diagram for which ants are recruited by ant scouts (figure 3b).

Figure 3.

(a) State transition diagram for ant scouts in the AH-HA model. The number of time-steps spent in a state is indicated where applicable, and conditions or (per-time-step) probabilities are associated with arrows between states. o_i refers to a scout's most recent assessment of site i's quality, subject to noise. This diagram is symmetric for sites 1 and 2. (b) Recruitment strategy diagram for ant scouts recruiting from a site in the AH-HA model. The colony is divided into scouts, which may recruit others, and passive ants, which may not. Scouts are classified as active if they are recruiting other ants to their preferred nest site, and inactive otherwise. Conditions or probabilities are associated with decision arrows. Here, o_i is the recruiting scout's most recent assessment of its preferred site's quality (site i), subject to noise, while o_j is the potential recruit's most recent assessment of its preferred site's quality (site j, where it is possible that i=j), again subject to noise.

Ant scouts start off in their current nest, which they leave and start searching for a new nest site with a certain probability s. On leaving her nest, a scout will discover each of the alternative sites available with equal probability, as they are equidistant from the scout's original nest. The scout will then assess the site, which incurs an assessment cost of a time-steps. On concluding this assessment, the scout will have observed the quality of the site. As there is potential assessment noise, the scout will not necessarily have an exact assessment of the site's quality; rather, the scout's observation o_i on site i will be a sample from a normal distribution with mean Q_i (site i's actual quality) and standard deviation σ (the noise inherent in the assessment process). The scout will then delay before she begins recruiting, by setting the per-time-step probability d_i with which she begins recruiting to be proportional to the observed quality of the site, such that

$$d_i=\{\begin{array}{cc}\frac{o_i}{Q_{\text{max}}}& \text{if}{o}_i\le Q_{\text{max}},\\ 1& \text{otherwise},\end{array}$$ (5.1)

where Q_max is a limit on the maximum quality that a nest can be perceived as having. The geometric distribution of latencies realized by this method is analogous to the survivorship curves measured by Mallon et al. (2001) for recruiters in emigration experiments. During this waiting period, the scout will at each time-step have the opportunity to consider the alternative nest site with probability p. If the scout does consider the alternative nest site she spends a time-steps doing this, then changes her preference if the quality of her observation of the alternative site exceeds the quality of her observation of her current choice of site. Over all scouts, switches from site i to site j will occur at a rate proportional to P(o_j>o_i), i.e. the probability that a sample of the quality of site j exceeds a sample of the quality of site i. This probability can be calculated based on the variance and means of the two distributions from which nest site quality samples are drawn. If the scout does not change her preference then she resumes waiting before beginning to recruit.

Once a scout begins recruiting, she first determines which recruitment method to use, tandem-running or social carrying, by assessing the quorum size q_i in her preferred nest site. The scout compares this assessed quorum size against a quorum threshold, T, which is context sensitive. The quorum threshold is low if there is an urgent need to emigrate, and high otherwise. If this assessed quorum exceeds the quorum threshold, social carrying is used; otherwise tandem-running is used. Social carrying takes c time-steps to complete, while tandem-running takes r time-steps, with social carrying being three times quicker than tandem-running (i.e. r=3c). At the conclusion of such a recruitment act a scout selects an ant to recruit according to the criteria described in figure 3b. Inactive scouts in the origin nest are sought first, then active but willing scouts that are recruiting for a different site, then if no willing scouts are available, passive ants and brood items in the origin nest. Willingness of an active scout is probabilistic, and is determined by the preference switching probability p, with 0 indicating complete unwillingness on average and 1 indicating complete willingness. A willing scout is selected from the population of all active scouts and will be recruited regardless of her current activity. For example, if a willing scout is currently carrying out a recruitment act, she will suspend this activity while being recruited in turn and assessing the new nest site, then resume her original recruitment if she perceives the new nest site to be inferior to her current preference. This departure from biological plausibility is necessary to capture the zero assessment cost assumption of the Pratt et al. model (2002). If after a recruitment act the recruiting scout's origin nest site is empty she becomes inactive in her preferred nest, then may subsequently become active again with probability s, and explore for alternatives from her new home site. In this case the only available alternative will be the other nest site the colony is considering, as the colony's original nest site is considered uninhabitable. If, however, ants remain in the scout's origin nest, she will again consider an alternative nest site with probability p, and again spend a time-steps assessing the alternative. After this assessment is completed, she will switch her preference if the observation of the alternative site's quality is greater than the observation of her currently preferred nest site, i.e. with probability P(o_j>o_i) across all scouts. If the scout does not consider an alternative site, or considers but rejects an alternative site, she recruits again from her origin nest site to her currently preferred nest site. A scout may assess the same site several times during the course of an emigration, in which case her perception of the site's quality will be that given by her most recent assessment of it.

The same switching probability p is used by both assessing scouts and recruiting scouts, however the less frequent opportunities for recruiters to switch (after each recruitment act) will result in assessors switching more frequently than recruiters. This is in agreement with the results of Planqué et al.'s (in preparation) analysis of Mallon et al.'s (2001) data. The results of allowing switching probabilities for assessors and recruiters to differ shall be explored in Planqué et al.

Recruited scouts spend a time-steps assessing the quality of the site they have been recruited to, at the conclusion of which they have an observation o_i of the site's quality. If the scout was recruited by social carrying she then becomes inactive in the new nest site, as carried ants are not considered able to learn the route to a nest site (Franks et al. 2003a). The carried scout may subsequently become active from there with per-time-step probability s. If the scout was recruited by tandem running and had no previous preferred site she will delay according to the quality she perceives the site to have (equation (5.1)), just as if she had discovered it independently herself, before recruiting other nest mates to her new preference. If, on the other hand, the scout was recruited by tandem running, but was already engaged in recruiting to her preferred nest site, she will compare her last assessment of her preferred site's quality with her assessment of the new site's quality. She will then switch the target of her recruitment efforts to the new site if she perceives it to be of higher quality, i.e. if o_j>o_i, where site i is the scout's current preference and site j is the new site.

In addition to ant scouts, passive ants are also modelled. These are simply moved between sites by scout ants in the event that no inactive scouts or active scouts that are willing to be recruited are found.

On each simulated time-step, the model sequentially updates the state of each ant according to its current state and activity. As there is no bias associated with update ordering in the model, this ordering is fixed throughout the model's execution. The full program code for the model is available in the Electronic Appendix.

Experimental design

An experiment was designed to investigate the speed-accuracy trade-off in decision-making using the AH-HA model, and the effects of assessment noise and assessment cost on it. The experiment was designed to mimic that used by Mallon et al. (2001) with real ant colonies, namely a choice experiment between two alternatives of differing quality, both equidistant from the colony's original nest. Parameters for the experiment were configured to match the data reported by Mallon et al. (2001) and used by Pratt et al. (2002) for their original model. Three parameters were systematically varied and results collected for each combination: time-cost of nest assessments (assessment cost), standard deviation of noise inherent in nest assessments (assessment noise), and probability of considering an alternative nest site while recruiting or waiting to recruit to a nest site (preference switching probability). The main results of interest were the accuracy of the decision, defined as the number of ants in the superior nest site at the end of the emigration, and the time taken to complete the emigration. The emigration was considered to be over when the original nest site was empty and all recruitment acts from the original nest site had been completed.

Analysis of results

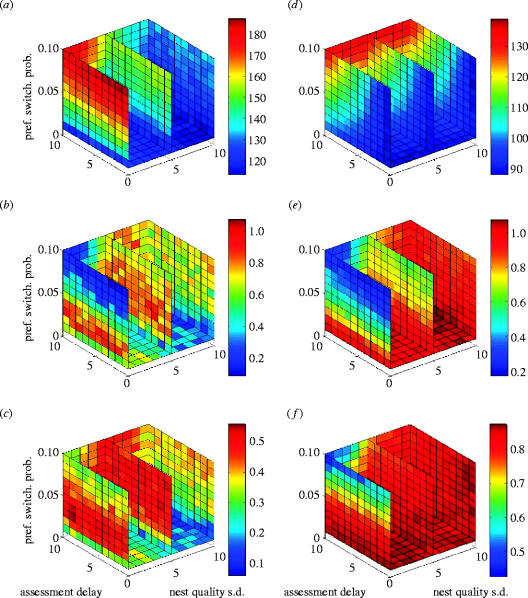
As detailed in appendix B, for every combination of assessment cost, assessment noise, and preference switching probability, non-parametric linear regressions of decision time and decision accuracy on quorum threshold were performed. As we varied three parameters, we present the results of the analyses in three dimensions, with one parameter along each axis, and using colour to represent the result of interest. We plot only representative slices through the parameter space for clarity. This is done in figure 4 for the slope and rank correlation coefficient of the regression line, both for decision time dependent on quorum threshold, and for decision accuracy dependent on quorum threshold. Figure 4 also shows the mean decision time and decision accuracy at quorum threshold 1, as this is a more accurate measure of the decision time and decision accuracy with minimum quorum threshold than the computed intercept from the linear regression. With a quorum threshold of 1, decision-making is purely individualistic, and leads to the fastest, least accurate collective decisions (Franks et al. 2003a)

Figure 4.

Results of systematically varying preference switching probability, assessment cost and assessment noise in the AH-HA model. Plots demonstrate the effect of varying these three parameters on the speed-accuracy trade-off, by showing statistics for speed dependent on quorum threshold, and accuracy dependent on quorum threshold: (a) mean accuracy for minimum quorum threshold (T=1); (b) slope of line of best fit for accuracy; (c) rank correlation coefficient (r_s) of accuracy with quorum threshold; (d) mean speed for minimum quorum threshold (T=1); (e) slope of line of best fit for speed; (f) rank correlation coefficient (r_s) of speed with quorum threshold.

The results from the AH-HA model with no assessment cost or assessment noise agree with those of the Pratt et al. (2002) model. As can be seen from figure 4a, with assessment cost and noise equal to 0 and as preference switching probability (p) is increased from 0.008, the mean accuracy achieved with the minimum quorum threshold (T) of 1 rapidly approaches 90% (at p=0.1, 188±11 ants out of 208 ants in the colony ended the emigration in the superior nest site; quadratic regression of decision accuracy on p at T=1: accuracy=117.044+1373.34p−6808.35p², p<0.001, r=0.80, n=1100). Under the same conditions, as can be seen from figure 4d, there is no significant increase in the time taken to reach these decisions with the minimum quorum threshold of 1 (linear regression of decision time on p at T=1: p=0.87, r=0.0, n=1100).

We therefore return to the question of why ant scouts do not switch between alternative sites at a higher rate. If we do not consider the possibility of a physical constraint on the maximum switching rate, then as discussed before two obvious factors remain: assessment cost and assessment noise. We expect that the ants do not show a higher rate of preference switching because the effects of assessment noise or assessment cost mean that to do so would either improve accuracy only at the cost of speed, or vice-versa (i.e. their decision mechanism is Pareto-optimal with respect to switching rate). This indeed appears to be the case; by reference to figure 4 the effects of assessment noise and assessment cost on the decision-making system of AH-HA can be observed as follows (full three-dimensional plots are available in the Electronic Appendix).

With no assessment noise and cost

As previously discussed, increasing the preference switching probability (p) from 0.008 to 0.1 increases accuracy to approximately 90% using the minimum quorum threshold (T) 1 (figure 4a–c), with no statistically significant increase in the decision time (figure 4d). At the same time, the quorum threshold's effect on the decision time is reduced with increasing switching probability (non-parametric linear regression slope of decision time decreases from approximately 1 to 0.2 as p increases from 0.008 to 0.1, figure 4e,f; general linear model of decision time versus T and p: p<0.001, n=2200). As noted above, these observations align with results from the Pratt et al. (2002) model.

Increasing assessment noise

Increasing assessment noise (σ) reduces the benefits to accuracy associated with increasing the preference switching probability p (slope of linear regression on p of decision accuracy, i.e. number of ants ending in superior site, at T=1 decreases by over four-fifths, from 638 to 118, as σ increases from 0 to 10, figure 4a–c; general linear model of decision accuracy versus p and σ: p<0.001, n=2200). Additionally, increasing assessment noise tends to preserve the effect of quorum threshold on decision time even as p increases (figure 4d–f). By itself, increased assessment noise does not mean the ants' decision-making system is Pareto-optimal with regard to switching probability, but it does significantly reduce the benefit of increased switching probability, while preserving the system's speed-accuracy trade-off under increased switching probability.

Increasing assessment cost

Increasing assessment cost (a) tends to increase the sensitivity of the decision time to the preference switching probability p, meaning that under increasing costs the same elevated probability p will lead to progressively slower and slower decisions (slope of linear regression on p of decision time at T=1 increases from less than 0 to 385 as a increases from 0 to 10, figure 4d; general linear model of decision time versus p and a: p<0.001, n=2200). The relationship between quorum threshold and decision time is apparently not affected by assessment cost (figure 4e,f), nor is the relationship between quorum threshold and decision accuracy (figure 4a–c).

By itself, increased assessment cost does not preserve the speed-accuracy trade-off in the ants' decision-making system as switching probability increases. However, increased assessment cost does put the system on or close to the Pareto-front, where increased switching probability cannot improve decision accuracy without sacrificing decision speed.

Discussion

From the results described above, it is clear that assessment noise and assessment cost are crucially important for the performance of the decentralized decision-making system modelled. Without them, an artificial speed-accuracy trade-off exists, which can be eliminated by increasing the preference switching probability with no negative performance effects. With them, increasing the preference switching probability does not eliminate the trade-off, or does so only at the expense of general performance.

Decentralized decision-making in T. albipennis

It is undeniable that nest assessment by scouts of T. albipennis must have a time-cost associated with it, as physical exploration of a potential site is required (Mallon & Franks 2000, Franks et al. 2003b), as well as the time-cost to travel to and from the site being assessed. It is also highly likely that there is some noise associated with this assessment process, due to the mechanisms the scouts employ to evaluate criteria such as internal area (Mallon & Franks 2000; Mugford et al. 2001). Indeed, as Mugford et al. show, the variance in assessing internal area of a nest site is quite high, even if the mean assessed area is very close to the actual area. Both our model and the original model by Pratt et al. (2002) predict that a higher rate of switching between nest sites by scouts would vastly improve the accuracy of decisions reached, with no associated cost in terms of time taken to reach these decisions. The models predict that the colony should be able to make these highly accurate and quick collective decisions using the minimum quorum threshold of 1. Note that decisions made with a quorum threshold of 1 are the fastest possible in the models as we parameterized them; slope of decision time on quorum threshold is always positive in figure 4e, while decision time increases monotonically with quorum threshold in figure 2. Thus, with increased switching rate, quorum threshold ceases to play a useful role in mediating between speed and accuracy of decision-making, and colony performance on both measures will be optimized if the scouts use a purely individualistic decision-making strategy, i.e. a quorum threshold of 1. It is gratifying that the two different models, one based on differential equations, and one on discrete simulation of individuals, should agree on these points, and increases our confidence in the predictions.

The question of why T. albipennis scouts do not therefore exhibit a higher rate of switching between alternative sites finds a possible answer by noting that introducing assessment noise mitigates the benefits of higher switching rates for decision accuracy, while the introduction of assessment cost means that higher switching rates lead to slower decisions. With moderate levels of assessment noise, moderate assessment costs, or a combination of the two, it seems that the decentralized decision-making mechanism employed by T. albipennis is likely to be Pareto-optimal with regard to switching rate. That is, the decision-making mechanism is unable to improve accuracy of decisions without sacrificing speed, or vice-versa. Independently, Pratt and colleagues have also noted the importance of assessment cost and quorum size for the speed and accuracy of colonies' decision-making (S. Pratt, personal communication, February 17th 2005).

Mugford et al. (2001) have already demonstrated how variance of assessment noise can be assessed for T. albipennis, and some data have also been collected on assessment cost (Mallon & Franks 2000). While the data already collected are insufficiently detailed to determine exactly the ants' location in the parameter space of the model, further experimental work could address this question. Additionally, as mentioned before, other considerations may limit the rate at which scouts switch between alternative sites; the physical constraint of nests some distance apart may prevent a higher switching-rate, or the ants' decision-making process may be tuned to work efficiently on scenarios in which more than two alternative nest sites are available. Experimentation on T. albipennis and the AH-HA model should help resolve these issues. For T. albipennis, a new experiment based on that of Mallon et al. (2001) but with the two alternative nest sites placed directly next to each other should give scope for higher switching rates to be realized if they are beneficial. For AH-HA, an extension of the experiments presented here to three or more nests might show other cases where there is no benefit to a higher preference switching probability; for example in situations with a large number of alternative choices, where a lower switching probability might allow collective agreement on one, sub-optimal, choice, while a higher switching probability might result in a failure to reach collective agreement (cf. Hutchinson 2004).

Decentralized decision-making in artificial systems

As already mentioned, one of our motivations for studying the collective decision-making system of T. albipennis is to try to derive a decentralized algorithm suitable for use in artificial systems where it would be advantageous to be able to make faster, less accurate decisions, or slower, more accurate decisions as circumstances dictate. House-hunting by T. albipennis can be thought of as a decentralized anytime algorithm (Dean & Boddy 1988), for which execution time is pre-specified by setting the quorum threshold used by individual scouts. Conceivably, the same behaviour might also function as an anytime algorithm that can be interrupted at any time and return its best solution so far, if scouts can dynamically reduce the quorum threshold they are using in response to new environmental stimuli, such as a cue indicating the presence of a predator (Franks et al. 2003a). That the algorithm can work in a decentralized manner, without the need for centralized control, suggests that it would be suitable for use in distributed environments, or on problems where a centralized solution bottleneck limits the scale of problems that may be tackled. The investigation into the AH-HA model of collective decision-making in T. albipennis, presented here, allows us to specify further aspects of a decision problem that would make it particularly suitable for AH-HA. Specifically, if evaluation of possible solutions is noisy and costs time, this will lead to an inherent speed-accuracy trade-off which can be exploited by the algorithm.

It is important to compare any new approach to a problem with existing approaches, and biologically inspired approaches are no exception. One such existing approach is a decentralized stochastic search algorithm called Stochastic Diffusion Search (SDS) (Bishop 1989). As noted by Meyer et al. (2003), SDS has some similarities with nest site selection by T. albipennis, and therefore with AH-HA by extension. However, SDS lacks a key feature of AH-HA, the variable quorum threshold, which allows the algorithm flexibly to compromise speed of decisions for accuracy of decisions. More traditional statistical approaches are known for noisy decision problems, such as the provably optimal sequential probability ratio test (Wald & Wolfowitz 1948) for discriminating between two alternative hypotheses, which specifies when to stop integrating further evidence in order to achieve a given error rate. If simultaneous sampling of alternatives were possible, this strategy would be applicable to the decision problem presented in this paper, with assessment noise but without assessment cost, and in this case would be preferred over our algorithm. Considering more than two alternatives complicates matters, but would still admit solution by an asymptotically optimal strategy (Dragalin et al. 1999). When house-hunting, T. albipennis is faced with a decision problem requiring a strategy for the allocation of noisy assessments over the available alternative nest sites. This scenario bears a close resemblance to a bandit problem, where a reward-maximising strategy is used to allocate trials to different alternatives of varying, but uncertain, reward. However, the introduction of an assessment cost for switching trials between alternatives renders the optimal solution of bandit problems infeasible (Banks & Sundaram 1994; Jun 2004). It is worth emphasising, then, that the cost of assessing alternatives is thus likely to be the most important factor in making the optimal strategy for solving a decision problem hard to find. For such problems, it is justifiable to look for novel strategies, and the decision strategy used by T. albipennis is worthy of interest.

An algorithm derived from this decision strategy should be most suitable for decision problems that would benefit from a speed-accuracy trade-off, where assessment of the available alternatives is time consuming and noisy, and where the problem is decentralized in nature, or where the algorithm would scale better to larger problem instances if a decentralized approach were taken. Of these characteristics, the most important is likely to be assessment cost, due to the problems it poses for optimal solutions of bandit problems. Two possible application areas for the algorithm might be decentralized process migration and load-balancing in distributed computing environments (Foster & Kesselman 2003), and parallel genetic algorithms with noisy and expensive fitness functions (Stender 1993). In trying to deal with such uncertain and costly environments in a decentralized manner, we think that the millions of years of evolution that have shaped such behaviours as nest selection in T. albipennis will provide us with efficient new approaches.

Appendix A

The Pratt et al. (2002) model describes rates of change of populations of ants that are either inactive in the original nest site (S), assessing a particular nest site (A_i), or recruiting to a particular nest site (R_i). The number of ants in each population changes as follows:

$$\frac{\text{d}S}{\text{d}t}=-\sum _{j=1}^M{\mu }_{j}S-\sum _{j=1}^M{\lambda }_{j}I(R_j,S),$$ (A1)

where μ_i is the per capita discovery rate for site i, λ_i is the per capita rate at which recruiters lead ants to a site i, and the function I, given in equation (A 4) below, implements a switching rule such that active recruiters are only recruited to a site if the number of ants recruiting for it is below the quorum threshold T.

$$\frac{\text{d}{A}_i}{\text{d}t}={\mu }_{i}S+{\lambda }_{i}I(R_i,S)+\sum _{j\ne i}({\rho }_{ji}{A}_j-{\rho }_{ij}{A}_i)-k_i{A}_i,$$ (A2)

where ρ_ij and ρ_ji are the rates at which scouts switch the target of their recruitment efforts from site i to j and vice-versa, and k_i is the rate, proportional to site quality, at which scouts stop assessing a site and begin recruiting to it.

$$\frac{\text{d}{R}_i}{\text{d}t}=k_i{A}_i+\sum _{j\ne i}({\rho }_{ji}{R}_j-{\rho }_{ij}{R}_i),$$ (A 3)

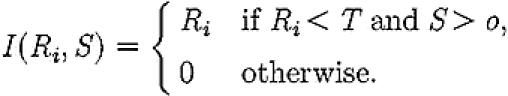
$$I(R_i,S)=\{\begin{array}{ll}{R}_i\hfill & \text{if}{R}_i<T\text{and}S>o,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (A 4)

The model is completed by also considering the population P_i of passive ants and brood items at site i

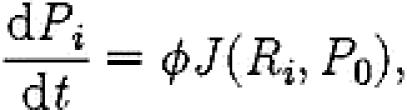
$$\frac{\text{d}{P}_i}{\text{d}t}=\phi J(R_i,P_0),$$ (A5)

where P₀ is the number of passive ants at the old nest site, φ gives the per capita rate of transport and the function J confines transport to sites where a quorum of T recruiters has been reached:

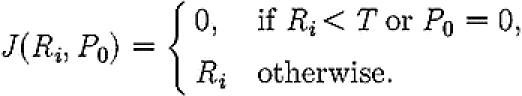
$$J(R_i,P_0)=\{\begin{array}{ll}0,\hfill & \text{if}{R}_i<T\text{or}{P}_0=0,\hfill \\ R_i\hfill & \text{otherwise}.\hfill \end{array}$$ (A6)

Appendix B

Experimental design

Parameters for the Ant House-Hunting Algorithm (AH-HA) were set to be comparable to those used in the Pratt et al. (2002) model as follows: colony size=208, number of scouts=52, tandem run speed=5, social carry speed=15, start scouting probability (s)=0.026, distances between nests=150, inferior nest quality (Q₁)=15, superior nest quality (Q₂)=20, maximum nest quality (Q_max)=1000. The combinations of distances and speeds gave time to recruit by tandem running (r)=30 and time to recruit by carrying (c)=10. With these parameter values, one time-step in the AH-HA model corresponds to 1 min in a real emigration. Preference switching (p) probability was varied over the following values: 0.008, 0.0172, 0.0264, 0.0356, 0.0448, 0.054, 0.0632, 0.0724, 0.0816, 0.0908 and 0.1. Nest assessment cost (a) and standard deviation of nest assessment noise (σ) were both varied in the range 0–10, in increments of 1. For each combination of these parameters, the quorum threshold (T) used in the decision-making was varied over the following values: 1, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50. One hundred replicates were performed at each quorum threshold. Full program code for the mode is available in the electronic supplementary material.

Analysis

To estimate the effect of quorum threshold on decision time and accuracy with minimal assumptions on the nature of the relationships, non-parametric linear regression was calculated using Theil's incomplete method (Theil 1950) and rank correlation coefficients were calculated using Spearman's rank correlation. For more accurate investigation of decision time and accuracy under minimum quorum threshold, means of these results for quorum threshold 1 were calculated, rather than intercepts of the linear regression. Full program code for conducting the analysis is provided in the electronic supplementary material.

Supplementary Material

Noise, cost and speed-accuracy trade-offs: decision making in a decentralised system