A hierarchical approach to protein molecular evolution

Abstract

Biological diversity has evolved despite the essentially infinite complexity of protein sequence space. We present a hierarchical approach to the efficient searching of this space and quantify the evolutionary potential of our approach with Monte Carlo simulations. These simulations demonstrate that nonhomologous juxtaposition of encoded structure is the rate-limiting step in the production of new tertiary protein folds. Nonhomologous “swapping” of low-energy secondary structures increased the binding constant of a simulated protein by ≈10⁷ relative to base substitution alone. Applications of our approach include the generation of new protein folds and modeling the molecular evolution of disease.

The exponential complexity of protein space limits evolution by means of DNA base substitution alone and remains a major challenge to many quantitative treatments of evolution. Random assembly and base substitution are ideally suited for searching local regions of polypeptide space, as demonstrated experimentally by the isolation of large numbers of stable structures from random encoded peptide libraries (1–3) and the rapid improvement of function seen in molecular evolutions of synthetic antibodies (4–6). However, in vitro homologous recombination experiments, termed DNA shuffling, have already demonstrated the limitations of protein evolution by means of base substitution alone (7–11). Indeed, a complete hierarchy of natural mutational events composed of rearrangements, deletions, horizontal transfers (12), transpositions (13), and other nonhomologous juxtapositions, in addition to base substitution and homologous recombination, is required for the rapid generation of protein diversity.

Modern neo-Darwinism and neutral evolutionary treatments, therefore, fail to explain satisfactorily the generation of the diversity of life found on our planet. Yet most theoretical treatments of evolution consider only the limited point-mutation events that form the basis of these theories. Similarly, methods of experimental protein evolution are generally limited to point mutation and DNA shuffling. Genetic studies, on the other hand, have indicated the importance of dramatic DNA swapping events in natural evolution (12, 14–18).

We address here, from a theoretical point of view, the question of how protein space can be searched efficiently and thoroughly, either in the laboratory or in Nature. We demonstrate that point mutation alone is incapable of evolving systems with substantially new protein folds. We demonstrate further that even the DNA shuffling approach is incapable of evolving substantially new protein folds. Our Monte Carlo simulations demonstrate that nonhomologous DNA “swapping” of low-energy structures is a key step in searching protein space.

More generally, our simulations demonstrate that the efficient search of large regions of protein space requires a hierarchy of genetic events, each encoding higher-order structural substitutions. We show how the complex protein function landscape can be navigated with these moves. We conclude that analogous moves have driven the evolution of protein diversity found in Nature. We suggest that our moves, which appear to be experimentally feasible, would make an interesting addition to the techniques of molecular biotechnology. Applications of our approach include improvement of current molecular evolution techniques, generation of nonnatural protein folds, and modeling the molecular evolution of disease.

The Generalized Block NK Model.

We performed model Monte Carlo simulations to quantify and optimize hierarchical protein space searching by genetic means. Molecular evolution strategies were simulated by using an energy function as selection criterion. The energy function is a generalization of the NK (19–21) and block NK (22) models. Our energy function takes into account the spontaneous generation of convergent secondary structures by means of the interactions of amino acid side chains as well as the interactions between secondary structures within proteins. In addition, we include a contribution to model binding to a substrate. This approach assigns a unique energy value to each evolving protein sequence. This model, while a simplified description of real proteins, captures much of the thermodynamics of protein folding and ligand binding. This generalized NK model contains several parameters, and a reasonable determination of these parameters is what allows the model to compare successfully with experiment. The combined ability to fold and bind substrate is what we seek to optimize; that is, the direction of our protein evolution will be based on this energy function.

The specific energy function used as the selection criterion in our molecular simulations is

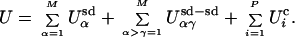1

This energy function is composed of three parts: secondary structural subdomain energies (U^sd), subdomain–subdomain interaction energies (U^sd−sd), and chemical binding energies (U^c). Each of these three energy terms is weighted equally, and each has a magnitude near unity for a random sequence of amino acids. In this NK-based simulation, each different type of amino acid behaves as a completely different chemical entity; therefore, only five chemically distinct amino classes are considered (e.g., negative, positive, polar, hydrophobic, and other). Simplified amino acid alphabets not only are capable of producing functional proteins (23, 24) but also may have been used in the primitive genetic code (25, 26). Simulated proteins have M = 10 secondary structural subdomains of N = 10 amino acids in length. They belong to one of L = 5 different types (e.g., helices, strands, loops, turns, and others). This gives L different (U^sd) energy functions of the NK form (19–22).

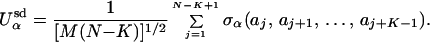2

We consider Q = 5 different chemical classes of amino acids with K = 4 interactions (21). The quenched unit-normal random number σ_α in Eq. 2 is different for each value of its argument for each of the L classes. This random form mimics the complicated amino acid side chain interactions within a given secondary structure. The energy of interaction between secondary structures is given by

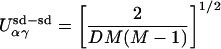3

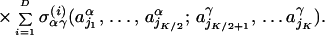We set the number of interactions between secondary structures at D = 6. Here the unit-normal weight, σ_αγ ⁽ⁱ⁾, and the interacting amino acids, {j₁, … , j_K}, are selected at random for each interaction (i, α, γ). The chemical binding energy of each amino acid is given by

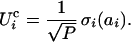4

The contributing amino acid, i, and the unit-normal weight of the binding, σ_i, are chosen at random. We assume P = 5 amino acids contribute directly to the binding event, as in a typical pharmacophore.

Simulation Protocol.

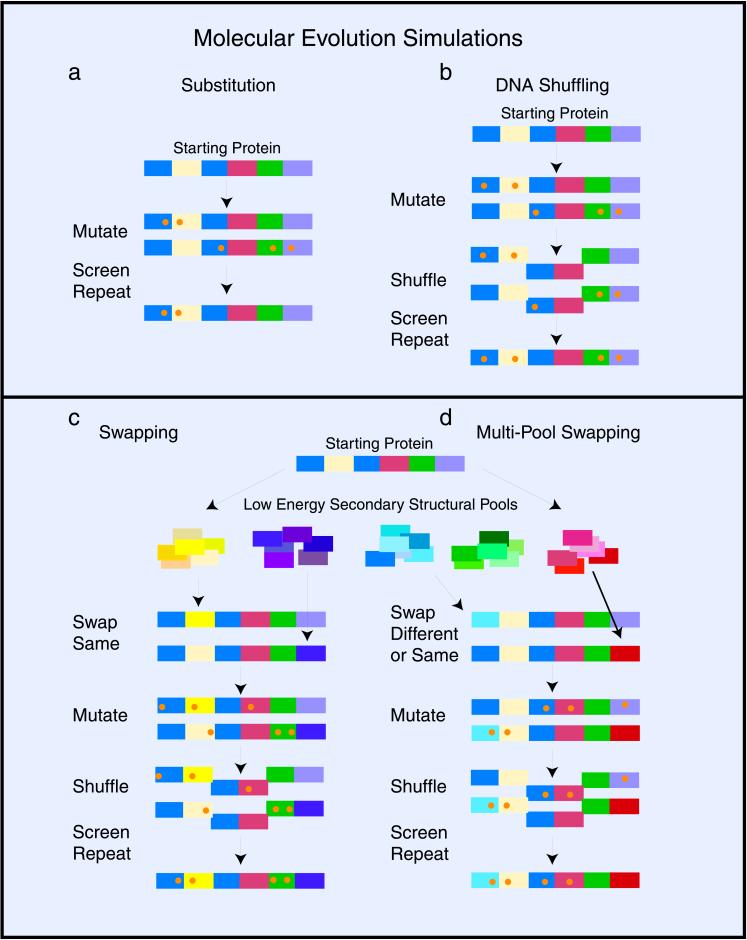
In each simulated mutagenesis, we started with 10,000 copies of a 100 amino acid polypeptide sequence. We determined that it was optimal to keep the 10% best (lowest-energy) protein sequences after selection and then amplify these back up to a total of 10,000 copies before the process was repeated. In each experiment, 100 rounds of mutagenesis and selection were performed because of the relatively low optimal rates of base substitution and DNA swapping. To obtain a base line for searching fold space, we simulated molecular evolution by means of simple mutagenesis (see Fig. 1a). Simulated evolutions by amino acid substitution lead to significantly improved protein energies. These evolutions always terminated at local energy minima, however (see Table 1). This trapping is because of the difficulty of combining the large numbers of individual highly correlated substitutions necessary to generate new protein folds. Increasing the screening stringency in later rounds did not improve the binding constants of simulated proteins, most likely because of the lack of additional selection criteria such as growth rates. Although we directly simulated only nonconservative mutations, conservative and synonymous neutral mutations are not excluded and could be taken into account in a more detailed treatment. Indeed, our optimized average mutation rate of one amino acid substitution/sequence per round is equivalent to roughly one to six random base substitutions per round.

Figure 1.

Schematic diagram of the simulated molecular evolution protocols. (a) Simulation of molecular evolution by means of base substitution (substitutions are represented by orange dots). (b) Simulated DNA shuffling showing the optimal fragmentation length of two subdomains. (c) The hierarchical optimization of local space searching: the 250 different sequences in each of the five pools (e.g., helices, strands, turns, loops, and others) are schematically represented by different shades of the same color. (d) The multipool swapping model for searching vast regions of tertiary fold space is essentially the same as in the Fig. 1c, except that now sequences from all five different structural pools can be swapped into any subdomain. Multipool swapping allows for the formation of new tertiary structures by changing the type of secondary structure at any position along the protein.

Table 1.

Results of Monte Carlo simulation of the evolution protocols

Evolution method	Starting energy	Evolved energy	Achieved binding constant
Amino acid substitution	−17.00	−23.18	1
DNA shuffling	−17.00	−23.83	100
Swapping	0	−24.52	1.47  ×  104
Mixing	0	−24.88	1.81  ×  105
Multipool swapping	0	−25.40*	8.80  ×  106*

The starting polypeptide energy of −17.00 comes from a protein-like sequence (minimized U^sd), and 0 comes from a random initial sequence of amino acids. The evolved energies and binding constants are median values. The binding constants are calculated as ae^−bU, where a and b are constants determined by normalizing the binding constants achieved by point mutation and shuffling to 1 and 100, respectively. 

^*Note that the energies and binding constants achieved by means of multipool swapping represent typical best-evolved protein folds. 

Simulated DNA Shuffling.

DNA shuffling improves the search of local fold space by means of a random yet correlated combination of homologous coding fragments that contain limited numbers of beneficial amino acid substitutions. As in experimental evolutions (7–10), the simulated shuffling improved protein function significantly better than did point mutation alone (see Table 1 and Fig. 1b). However, local barriers in the energy function also limit molecular evolution by way of DNA shuffling. For example, when we increased our screen size to 20,000 proteins per round, we saw no further improvement in the final evolved energies. Interestingly, our optimal simulated DNA shuffling length of 20 amino acids (60 bases) is nearly identical to fragment lengths used in experimental protocols (8).

Single-Pool Swapping.

In Nature, local protein space can be searched rapidly by the directed recombination of encoded domains from multigene pools. A prominent example is the creation of the primary antibody repertoire in an adaptive immune system. We generalized these events by simulating the swapping of amino acid fragments from five different structural pools representing helices, strands, loops, turns, and others (see Fig. 1c). During the swapping step, subdomains were randomly replaced with members of the same secondary structural pools with an optimal probability of 0.01 per subdomain per round. We limited the simulated evolution of the primary fold by maintaining the linear order of swapped secondary structure types. The addition of the swapping move was so powerful that we were able to achieve binding constants two orders of magnitude higher than in shuffling simulations (see Table 1). Significantly, these improved binding constants were achieved starting with 10–20 times less minimized structural subdomain material.

Parallel Experiments.

Parallel tempering is a powerful statistical method that often allows a system to escape local energy minima (27). This method simulates simultaneously several systems at different temperatures, allowing systems at adjacent temperatures to swap configurations. The swapping between high- and low-temperature systems allows for an effective searching of configuration space. In Nature as well, it is known that genes, gene fragments, and gene operons are transferred between species of different evolutionary complexity (i.e., at different “temperatures”). By analogy, we simulated limited population mixing among parallel swapping experiments by randomly exchanging evolving proteins at an optimal probability of 0.001 per protein per round. These mixing simulations optimized local space searching and achieved binding constants ≈10⁵ higher than did base substitution alone (see Table 1). Improved function is caused, in part, by the increased number of events in parallel experiments. Indeed, mixing may occur in Nature when the evolutionary target function changes with time. That is, in a dynamic environment with multiple selective pressures, mixing would be especially effective when the rate of evolution of an isolated population is slower than the rate of environmental change. Recently, it has been demonstrated that the mixing and DNA shuffling of orthologous proteins resulted in rapid and dramatic increases in recombinant protein function (8). It has also been argued recently that spatial heterogeneity in drug concentration (a form of “spatial parallel tempering”) facilitates the evolution of drug resistance (28).

Multipool Swapping.

The effective navigation of protein space requires the discovery and selection of tertiary structures. To model the large-scale search of this space, we began with random polypeptide sequences and repeated our swapping protocol, but now allowed secondary structures from all five different pools to swap in at every position (see Fig. 1d). This multipool swapping approach evolved proteins with binding constants ≈10⁷ better than did amino acid substitution of a protein-like starting sequence (see Table 1). This evolution was accomplished by the random yet correlated juxtaposition of different types of low-energy secondary structures. This approach dramatically improved specific ligand binding while efficiently discovering new tertiary structures (see Fig. 2). Optimization of the rate of these hierarchical molecular evolutionary moves, including relaxation of the selection criteria, enabled the protein to evolve despite the high rate of failure for these dramatic swapping moves. Interestingly, of all the molecular evolutionary processes that we modeled, only multipool swapping demonstrated chaotic behavior in repetitive simulations. This chaotic behavior was likely because of the discovery of different model folds that varied in their inherent ability to serve as scaffolds for ligand-specific binding.

Figure 2.

Schematic diagram representing a portion of the high-dimensional protein composition space. The three-dimensional energy landscape of Protein Fold 1 (green) is shown in cutaway. The arcs with arrowheads represent the ability of a given molecular evolution process to change the composition and so to traverse the increasingly large barriers in the energy function. The smallest arc (light yellow) represents the ability to evolve improved fold function by means of point mutation. Then in increasing order: DNA shuffling (dark yellow), swapping (orange), and mixing (red). Finally, our multipool swapping model allows an evolving system to move (purple arc) to a different energy landscape representing a new tertiary fold (bottom). With this model, functional tertiary fold space has a large yet manageable number of dimensions. That is, in 100 amino acids we assume 10 secondary structures of 5 types (we balance rare forms with the predominance of strands and helices) roughly yielding the potential for ≈10⁷ basic tertiary folds in Nature. Clearly, organization into secondary structural classes represents a dramatic reduction in the realized complexity of sequence space (e.g., versus 300 bases of open reading frame DNA, ≈10¹⁷⁰, or 100 amino acids with a 20-letter or 5-letter genetic code, ≈10¹³⁰ or ≈10⁷⁰, respectively).

Possible Experimental Implementations.

The search of large regions of protein space should identify new folds and functions that would be of great value to basic, industrial, and medical research. Our multipool searching protocol could be attempted experimentally within present constraints (≈10⁴–10¹⁵ recombinants, depending on the screening or selection method). One possibility is the combination of DNA shuffling with synthetic splicing libraries (29) that contain representative pools of native low-energy structures encoded within multiple (≈10) short exons. Alternatively, it should be possible to generate multiple libraries of synthetic oligonucleotide pools (30, 31) encoding numerous specific secondary and subdomain structures. Asymmetric complementary encoded linkers with embedded restriction sites would make the assembly, shuffling, and swapping steps possible.

Parallels with Natural Evolution.

During the course of any evolutionary process, proteins become trapped in local energy minima. Dramatic moves, such as swaps and juxtapositions, are needed to break out of these regions. Dramatic moves are usually deleterious, however. The evolutionary success of these events depends on population size, generation time, mutation rate, population mixing, selective pressure or freedom, such as successful genome duplications or the establishment of set-aside cells (32), and the mechanisms that transfer low-energy encoded structural domains.

In Nature, mechanisms have evolved to increase the probabilities of successful exchanges. Viruses and transposons, for example, have evolved large-scale integration mechanisms, while terminal variable diversity joining segment recombination is effective despite >50% in-frame failures. Whereas random swapping of genomic DNA is unlikely to lead to useful protein products at a high rate, a possible scenario is that exon shuffling generated the primordial fold diversity (14–16). This hypothesis is bolstered by the correlation between splice junction location and boundaries of encoded structural domains. Alternatively, if splicing was not primitive, random swapping by horizontal transfer, rearrangement, recombination, deletion, and insertion could have led to high in-frame success rates if primitive genomes had high densities of coding domains and reading frames, as in certain prokaryotes and mitochondria.

Three dramatic examples of use of swapping by Nature are particularly notable. The first is the development of antibiotic resistance. It was originally thought that no bacteria would become resistant to penicillin because of the many point mutations required for resistance. Resistance occurred, however, within several years. It is now known that this resistance occurred through the swapping of pieces of DNA between evolving bacteria (17, 18). Multidrug resistance is a major current health-care problem. The creation of the primary antibody repertoire in vertebrates is another example of DNA swapping (of genes, gene segments, or pseudogenes). Finally, the evolution of Escherichia coli from Salmonella occurred exclusively by DNA swapping (12). Indeed, none of the phenotypic differences between these two species is caused by point mutation. Moreover, even the observed rate of evolution caused by DNA swapping, 31,000 bases/million years, is higher than that caused by point mutation, 22,000 bases/million years. That is, even though a DNA swapping event is less likely to be tolerated than is a point mutation, the more dramatic nature of the swapping event leads to a higher overall rate of evolution. This is exactly the behavior we observed in our simulations.

Summary.

DNA base substitution, in the context of the genetic code, is ideally suited for the generation, diversification, and optimization of local protein space (25, 33). However, the difficulty of making the transition from one productive tertiary fold to another limits evolution by means of base substitution and homologous recombination alone (Fig. 2, light and dark-yellow arrows, respectively). Nonhomologous DNA recombination, rearrangement, and insertion allow for the combinatorial creation of productive tertiary folds by way of the novel juxtaposition of suitable encoded structures. The efficient search of high-dimensional fold space depends on the spontaneous generation and convergence of secondary structure and the hierarchical range of DNA mutation events present in our model (Figs. 1d and 2, purple arrow). Starting with very small pools of low-energy secondary structures, we evolved new protein folds with specific binding constants ≈10⁷ higher than those optimized by base substitution alone. More generally, it seems likely that organization into higher-order fundamental units such as nucleic acids, the genetic code, secondary and tertiary structure, cellular compartmentalization, cell types, and germ layers allows systems to escape complexity barriers and potentiates explosions in diversity.

Qualitative changes in protein space such as those modeled here allow viruses, parasites, bacteria, and cancers to evade the immune system, vaccines, antibiotics, and therapeutics. The successful design of vaccines and drugs must anticipate the evolutionary potential of both local and large space searching by pathogens in response to therapeutic and immune selection. The addition of disease-specific constraints to our Monte Carlo simulations should be a promising approach for predicting pathogen plasticity. Experimental implementation of our hierarchical protocol should be a powerful approach to the discovery of new therapeutics. Infectious agents will continue to evolve unless we can force them down the road to extinction.