The topomer-sampling model of protein folding

Abstract

Clearly, a protein cannot sample all of its conformations (e.g., ≈3¹⁰⁰ ≈ 10⁴⁸ for a 100 residue protein) on an in vivo folding timescale (<1 s). To investigate how the conformational dynamics of a protein can accommodate subsecond folding time scales, we introduce the concept of the native topomer, which is the set of all structures similar to the native structure (obtainable from the native structure through local backbone coordinate transformations that do not disrupt the covalent bonding of the peptide backbone). We have developed a computational procedure for estimating the number of distinct topomers required to span all conformations (compact and semicompact) for a polypeptide of a given length. For 100 residues, we find ≈3 × 10⁷ distinct topomers. Based on the distance calculated between different topomers, we estimate that a 100-residue polypeptide diffusively samples one topomer every ≈3 ns. Hence, a 100-residue protein can find its native topomer by random sampling in just ≈100 ms. These results suggest that subsecond folding of modest-sized, single-domain proteins can be accomplished by a two-stage process of (i) topomer diffusion: random, diffusive sampling of the 3 × 10⁷ distinct topomers to find the native topomer (≈0.1 s), followed by (ii) intratopomer ordering: nonrandom, local conformational rearrangements within the native topomer to settle into the precise native state.

The question, “How do proteins fold?” (1), has puzzled researchers for decades. Based on a very simple calculation, Levinthal (2) estimated that an average-sized protein would require longer than the age of the universe to sample every state [for example, if there are three possible conformations for each residue (3), a 100-residue protein would have ≈3¹⁰⁰ ≈ 10⁴⁸ distinct backbone conformations, which would require ≈10³⁰ years to sample every state]. Because proteins of this length can fold on a millisecond timescale, they clearly sample only an infinitesimal fraction of their possible conformations. It was originally assumed that proteins overcome this Levinthal Paradox by following a directed folding pathway (4) that drastically reduces the number of structures that must be sampled. Currently, however, it is generally acknowledged that proteins need not follow a single pathway to fold on a millisecond timescale. Just as a water droplet can follow many different trajectories while descending from the top of a ceramic funnel, a folding energy landscape shaped like a funnel (5) can have numerous folding pathways leading to a properly folded state at the base of the funnel. This suggests that proteins fold along an ensemble of pathways with the folding time scale determined by the ruggedness (kinetic barriers) and slope of the folding energy landscape [see ref. 6 for an excellent review of the “new view” of protein folding (7, 8)].

In considering the nature of the dynamics of an ensemble of folding protein conformations, we find it useful to introduce the concept of a topomer. A topomer is the set of structures that are obtainable from a specific structure through local backbone coordinate transformations that do not disrupt the covalent bonding of the peptide backbone. Thus, the native topomer is the set of near-native structures for a protein. In this paper, we present the generic protein (GP) computational procedure to estimate the number of disjoint topomers required to span all possible compact and semicompact conformations for an N-residue polypeptide. For 100 residues, we find ≈3 × 10⁷ disjoint topomers. This procedure also leads to an estimate of the distance between neighboring topomers. By combining this distance with an experimentally determined protein intrachain diffusion constant, we estimate that a 100-residue polypeptide undergoing random, diffusive motion samples one topomer every ≈3 ns. This suggests that a 100-residue protein can find its native topomer (the topomer containing the native conformation) by random sampling in ≈100 ms. This is comparable to the experimentally observed timescale required for a denatured protein domain to reestablish its native structure. These results suggest that, for a 100-residue protein (an average sized protein domain), the folding from a denatured form can proceed in a two stage folding process consisting of (i) topomer diffusion: random, diffusive sampling to find the native topomer, followed by (ii) intratopomer ordering: nonrandom, local conformational changes within the native topomer to find the unique native state.

Our results suggest that the topomer diffusion step requires ≈100 ms for a 100-residue protein. We expect that the time required for intratopomer ordering may be more rapid than the topomer diffusion stage, leading to a cooperative, two-state folding mechanism (9, 10), or comparable to the topomer diffusion stage, leading to multistate folding kinetics.

METHODS

We wanted to estimate the number of disjoint topomers required to span all possible compact and semicompact conformations for a polypeptide of length N. To do this, we used the GP Direct Monte Carlo procedure described below to generate large ensembles of self-avoiding protein conformations. We compared each conformation to a test set of ≈20 dissimilar native protein structures of length N and determined whether it was topomeric to any of the test proteins. This process was continued until we had generated at least one topomeric match to each and every one of the ≈20 test proteins. The number of conformations generated at this point was a measure of the total number of disjoint topomers for an N-residue polypeptide.

Definition of a Topomer.

We define two protein conformations to be topomeric if they have the same backbone topology (11): that is, if one conformation is obtainable from the other through local backbone coordinate transformations that (i) do not require cooperative movements between nonlocal residues and (ii) do not disrupt the overall compactness of the structure or covalent bonding of the peptide backbone.

We define a topomer as the set of all conformations topomeric to a particular conformation. Thus, a topomer is a bundle of conformations sharing the same backbone topology. The native topomer for a protein consists of all conformations topomeric to the native conformation. We present below a simple algorithm to test whether two conformations are topomeric.

The Native Protein Test Sets.

The native test proteins were compiled from the CATH protein domain database (http://www.biochem.ucl.ac.uk/bsm/cath) (12). To have at least 20 test structures for each protein length N, we included longer structures truncated at the carboxyl terminus. For example, our test set for N = 45 consists of residues 1–45 from available protein structures with lengths of 45–49. In instances in which the coordinate file contained more than one set of coordinates for a given structure, we used the first set. The 22 proteins in the test set for N = 100 are listed here by their Protein Data Bank or CATH domain classification name: 1aaj, 1ab2, 1acx, 1bet, 1 cmbA, 1etc, 1fd2, 1fkb, 1fus, 1hks, 1hrc, 1ltsD, 1onc, 1pal, 1put, 1thx, 1tlk, 1ycc, 2atcB, 2cdv, 2imn, and 2pna. The complete list for each N is available at http://www.wag.caltech.edu/home/derek/gp.

GP Direct Monte Carlo Method.

The GP direct Monte Carlo method uses the continuous configurational Boltzmann biased Direct Monte Carlo (13) procedure in conjunction with a protein representation in which (i) six (φ,ψ) backbone torsion pair choices (14) are allowed for each residue [the torsion about the peptide bond is fixed at 180°, and all bonds and angles have fixed standard values (15)], and (ii) a simple 12–6 Lennard-Jones potential is used to account for both the excluded volume and the cohesion of each residue (identical for all amino acids).

A GP conformation is constructed by adding residues one-by-one (alternating right and left) to a single residue-starting fragment located at the center of the protein sequence. During buildup, the probability of selecting one of the six (φ,ψ) candidates is given by

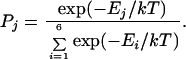1

The addition energy, E_i, of a single residue is given by the summation of its pair-wise interaction energies with each residue in the polypeptide fragment. For all amino acids, the energy of a residue pair is

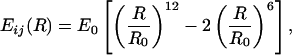2

where R₀ = 5.5 Å, E₀ = 0.15 kcal/mol, and R is the distance between the α-carbon of each residue. Here, i and j includes all pairs within a cutoff of 10 Å but excluding nearest and next-nearest neighbors in the sequence. Energetically favorable addition steps are replicated by a factor m = int[(z_i/〈z_i〉)/(z_{i − 1}/ 〈z_{i − 1}〉)], where z_i = exp(−E_i/kT) and 〈z_i〉 denotes the average value of z at residue i over all generated chains, according to the continuous configurational Boltzmann biased (13) procedure.

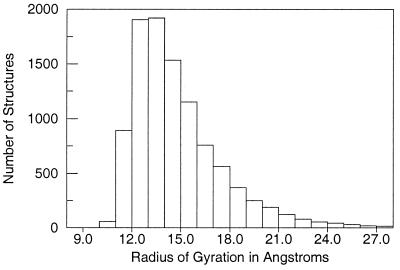
The parameter values R₀ = 5.5 Å and E₀ = 0.15 kcal/mol were selected because they yield an ensemble of generic folds with about the same distribution for the radius of gyration found in the Protein Data Bank. For the GP ensemble of 100-residue conformations, half have a radius of gyration between 12 and 15 Å (Fig. 1), the observed range for the radius of gyration for 100-residue globular proteins (16). The GP ensemble has 10% more compact than 12 Å whereas the remaining 40% are less compact than 15 Å. Thus, the GP procedure rapidly generates a diverse ensemble of compact and semicompact protein chains with realistic peptide backbone geometries [>10⁶ conformations for a 50-residue protein are generated in one day on a single processor Silicon Graphics (Mountain View, CA) R10000 workstation]. Because no information about sequence identity is included in the GP energy expression, the GP ensemble is a generic, sequence-independent set of self-avoiding polypeptide conformations.

Figure 1.

Radius of gyration histogram for 10,000 100-residue structures generated by the GP method. Compact globular protein structures 100 residues in length typically have a radius of gyration between 12 and 15 Å (16). One-half of the GP structures are within this range, with only 10% of the GP structures more compact.

Determining the Number of Distinct Topologies for an N-Residue Polypeptide.

We determined the number of distinct topologies for an N-residue polypeptide by calculating how many GP structures must be generated to obtain a topomeric match to each of ≈20 dissimilar native test proteins of length N. As each GP structure was generated, we calculated its α-carbon root-mean-squared (CMRS) deviation (17) from each structure in the native protein test set. Every GP structure with a relatively low CRMS to any of the test structures was saved along with the point at which it was generated. Thus, after generating a large ensemble of GP structures, we retained a small subset of structures (typically 100) with a low CRMS difference to each native test structure. (It was necessary to save many structures for subsequent analysis because a low CRMS difference does not necessarily imply that two structures are topomeric.)

From the retained sets of structures, we used the Native Topomer Test Procedure to verify which structures (if any) were topomeric to each native test structure. First, each candidate GP backbone was optimally superimposed onto the corresponding native test structure. Next, each α-carbon in the candidate GP backbone was tethered with a harmonic constraint [using a force constant of 5 (kcal/mol)/A²] to the coordinates of the same α-carbon in the native test structure. Conjugate gradient minimization (200 steps) then was performed on the constrained GP backbone [using Dreiding (15) force-field parameters]. During minimization, each α-carbon in the GP structure attempts to follow a direct, noncooperative trajectory toward the corresponding native α-carbon. Topology differences are easily observed by the inability of the GP structure to minimize to the native coordinates, because the force-field parameters do not permit covalent bond breakage in the peptide backbone. Using this automated method, it is possible to determine quite quickly whether a retained GP structure is topomeric to the corresponding native test structure. Note that the Native Topomer Test Procedure is simply a computational test to determine whether two structures are topomeric. This procedure does not accurately simulate how a protein finds its precise native state once it has found its native topomer. However, the test procedure minimization trajectories followed by the GP structures to their corresponding native states are useful for visualizing the conformational differences that two topomeric structures may possess. QuickTime movies of the minimization trajectories for all 277 native test structures are available at http://www.wag.caltech.edu/home/derek/gp.

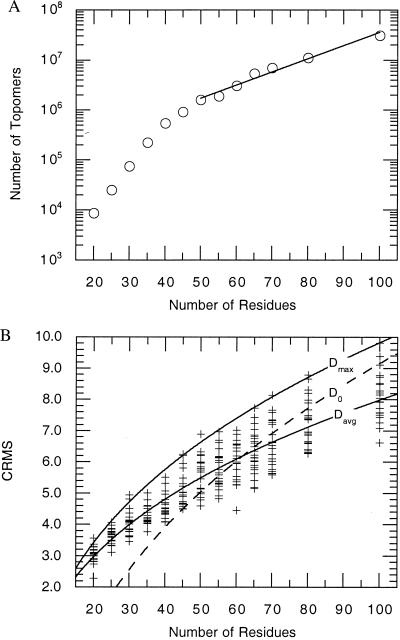
The GP algorithm does not include any mechanism to prevent the generation of more than one structure for each topology. Thus, by the point at which all 22 test proteins had been matched for the N = 100 calculation, we had found an average of ≈5 matches for each test protein. This suggests that our measurement slightly overestimates the number of distinct topologies. On the other hand, the use of a finite number (≈20) of test systems may underestimate the number of GP structures required to generate a topomeric match to topologies more complex than any of the test proteins. We expect that these factors balance each other. The calculated number of topomers (Fig. 2A) increases monotonically with the number of residues despite completely independent choices of the native protein test sets. This suggests that the estimate has systematic inaccuracies well less than an order of magnitude.

Figure 2.

(A) The number of disjoint topomers estimated for an N-residue polypeptide. Beyond N = 50, the number of topomers, S_N, scales as S_N = (83936) × (1.0624)^N. For N = 100, the number of topomers is ≈(1.19)^N. (B) The CRMS between each of the 277 native test conformations and their topomeric matches from the generic structure sets. The dashed line in the figure represents a previously developed average threshold for topological similarity developed by Maiorov and Crippen (11). They found that two N-residue structures are topologically similar when their CRMS is below the threshold, D₀ = a + b (N)^1/3, where a = −10.82 ± 0.37 and b = 4.31 ± 0.08. For N ≥ 50, the CRMS values we obtained from topomeric matches correlate well with the Maiorov-Crippen D₀ threshold for topological similarity. Fitting a similar functional form to the average and maximum of our CRMS data for topomeric conformations yields D_avg (a = −4.12 ± 0.24; b = 2.61 ± 0.06) and D_max (a = −5.62 ± 0.40; b = 3.33 ± 0.11), respectively.

RESULTS AND DISCUSSION

Total Number of Topomers.

Fig. 2A shows the number of topomers estimated for polypeptides of length 20–100. For N = 55–100, the number of topomers scales as (1.06)^N, even though the number of distinct conformation states scales at least as fast as 3^N. For N = 100, we find ≈3 × 10⁷ topomers, a large number, but vastly smaller than 3¹⁰⁰ ≈ 10⁴⁸. Visual comparisons between some of the test structures and the topomeric GP structures are shown in Fig. 3.

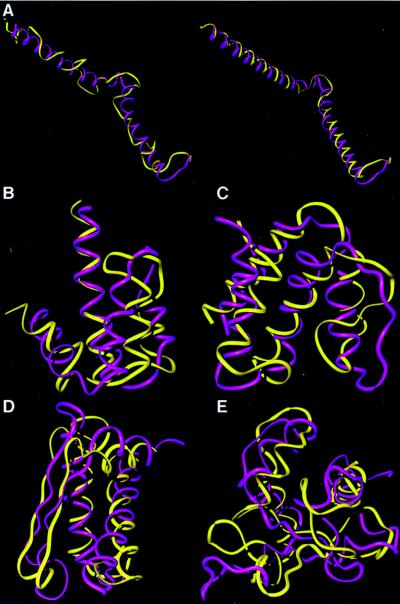
Figure 3.

Comparisons of the native conformations (purple) with their topomeric counterparts from the generic structure sets (yellow). To facilitate viewing, the local geometry of each generic conformation has been refined to incorporate native helix and β-strand segments while preserving the tertiary fold topology. This refinement is demonstrated in a, where the generic structure (left, in yellow) is refined by using the native helix assignment (right, in yellow). (a) The 65-residue segment from the NMR determined structure of the proteolytic fragment from Bacteriorhodopsin (44) (1bct). This example is one of many semicompact test folds that was topomerically matched by a GP structure. Thus, our estimate considers semicompact as well as compact topomers. (b) A 65-residue Porcine C5a_desArg (1c5a) (45). (c) An 80-residue fragment from acyl-CoA binding protein (1aca) (46). (d) An 80-residue segment from domain four of the N-terminal domain of 70-kDa heat-shock cognate protein (1hpm04) (47). (e) A 100-residue segment from heat shock transcription factor (1hks) (48).

Estimates of Folding Times.

Next, we estimated how long it would take a protein to randomly sample all of its compact and semi-compact topomers. Fig. 2B shows the CRMS between each of the 277 conformations in the native protein test sets and its topomeric match in the ensemble of GP structures. For 100 residues, there is a maximal CRMS distance of 9.8 Å between each native test protein and its topomeric conformation in the GP set. This indicates that the greatest distance between any two conformations in the same topomer is ≈9.8 Å CRMS. Thus, any two conformations more than ≈9.8 Å CRMS from each other are necessarily members of different topomers. Hence, the maximum distance between neighboring yet disjoint topomers is ≈9.8 Å CRMS. To estimate the sampling timescale, we used the three-dimensional Einstein diffusion equation,

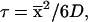3

where 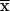is the CRMS between neighboring, disjoint topomers, D is the diffusion coefficient, and τ is the topomer-sampling time. Eaton and coworkers (18) determined that D ≈ 5 × 10⁻⁷ cm²/s for extensive intrachain protein motion in cytochrome c folding. Using this value for D in Eq. 3 with 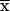= 9.8 Å suggests that the topomer-sampling time for N = 100 is τ ≈ 3.2 ns. Given ≈3 × 10⁷ topomers and an average topomer-sampling rate of one topomer every ≈3.2 ns, we estimated that a 100-residue protein can randomly sample all compact and semicompact topomers in ≈100 ms.

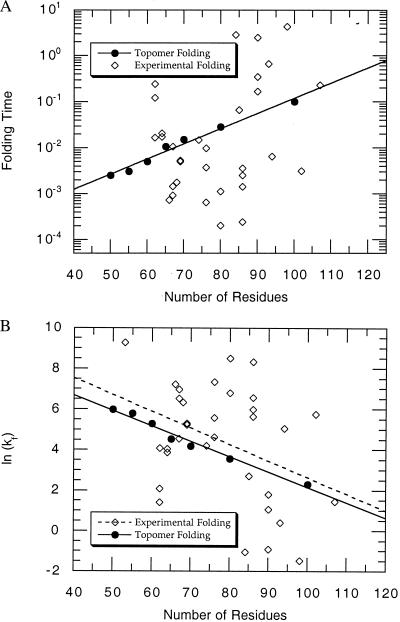
Similar estimates for other N (using the maximum CRMS for each N in Fig. 2B and the number of topomers for each N in Fig. 2A) lead to the plot in Fig. 4A. In this plot, the solid circles represent the time estimated for a polypeptide to randomly sample all of its topomers (for N = 50, 55, 60, 65, 70, 80, and 100), and the solid line is the exponential fit through these points.

Figure 4.

(A) The dark circles represent the estimated time in seconds for a polypeptide of length N to randomly sample all of its topomers. This is based on the results in Fig. 2 A and B combined with Eq. 3 by using the experimentally derived diffusion constant, D = 5 × 10⁻⁷ cm²/s. The solid line is the best fit to these first principles predicted topomer sampling times. It leads to a topomer sampling folding time, t_fold(seconds) = (5.98 × 10⁻⁵) × (1.079)^N. The open diamond points are 32 experimentally determined folding timescales (time = 1/k_f) for single domain proteins <120 residues in length compiled in Table 1 of a recent review be S. E. Jackson (19). The predicted topomer-sampling model timescale (10⁻³–10⁰ s) correlates well with the experimentally determined folding times. (B) The timescale data in A replotted as the natural log of the intrinsic folding rate, ln(k_f). The dashed line is the best exponential fit through the experimental folding rate points. The P value for this fit is P = 0.082, suggesting that there is only a 1 in 12 chance that a correlation with this significant a slope would appear by chance. Thus, the topomer sampling model (solid line) predicts the correct magnitude and length dependence (slope) for the folding rates of two-state folding proteins without using any adjustable parameters.

It is interesting to compare the folding timescales predicted by the topomer-sampling model with experimentally determined folding times. The open diamond points in Fig. 4A represent 32 experimentally determined folding times [time = 1/k_f (intrinsic folding rate)] for single domain, two-state folding proteins compiled in Table 1 of a recent review by S. E. Jackson (19). The predicted topomer-sampling model timescale (10⁻³–10⁰ s) correlates well with the experimentally determined folding times. Note that the correct folding timescale is achieved in our model without using any tunable parameters (the topomer folding timescale is determined directly from the number of topomers, the distance between topomers, and an experimentally determined intrachain diffusion constant). [Table 1 in ref. 19 contains 38 folding rates for small, monomeric proteins that fold with two-state kinetics. Six of these rates were considered unsuitable for this plot and were excluded: λ-repressor (native helix stabilizing mutations), Arc repressor (two domains connected by a linker), Villin 14T (>120 residues), and the three cytochrome c variants (heme-containing).]

In Fig. 4B, we replot the timescale data in Fig. 4A as the natural log of the intrinsic folding rate, ln(k_f). Experimental folding times can vary by three orders of magnitude for proteins of similar length [even for homologous sequences (20)], suggesting that factors independent of protein length [such as topological complexity (21) and sequence mutation] drastically affect the rate of protein folding. However, we expect that these factors average out over the different proteins in the experimental data set. Hence, the best exponential fit through these experimental points (the dashed line in Fig. 4B) is a reasonable estimate of the length-dependent part of the protein folding timescale. The P value for this fit is P = 0.082, implying that there is only a 1 in 12 chance that a correlation with this significant a slope would appear by chance (see ref. 21 for a detailed explanation of P values in this context). Remarkably, the predicted topomer-sampling timescale (solid-line) and the apparent length-dependent part of the experimental folding timescale (dashed line) are in excellent agreement. Thus, the topomer sampling model (solid line) predicts the correct magnitude and length dependence (slope) for the folding rates of two-state folding proteins without using any adjustable parameters.

Folding Mechanisms.

Our results suggest that an average sized protein domain can find its native topology without any mechanisms to simplify the conformational search (22, 23). Thus, the topomer-sampling model is fundamentally different from folding models that insist that regions of correctly folded structure form during the early stages of protein folding, before a structure with the native topology has been sampled. The topomer-sampling model suggests that the condensation of specific native contacts (24) is not required to simplify the search for the native topomer. Furthermore, the topomer-sampling model suggests that early nucleation of native secondary structure (25, 26) is not essential for an average-sized domain to fold. Indeed, the 86-amino acid reduced HIV-1 Tat (trans-activator) protein (27) folds on a biologically relevant time frame to a structure with a well defined core yet possesses no secondary structure or disulfide bonds.

For large protein domains (longer than ≈120 residues), our results imply that some type of early nucleation or condensation mechanism is required for the native topomer to be found in <1 s (Fig. 4A). Indeed, we expect that, for many large proteins (especially those with high helical content), such mechanisms greatly expedite the search for the native topology and lead to folding rates that are faster than those found in small proteins (because small proteins may not require early nucleation or condensation mechanisms to fold, such mechanisms may not have evolved in short sequences to the degree that they have in long ones). Experiments have shown that native-like secondary structure is found in the kinetic folding intermediates of many larger proteins (28) and in fragments excised from proteins (29, 30). Such moderate local structural biases probably help large domains find the native topology by reducing the complexity of the search for the native topomer. These biases certainly help proteins of all sizes find their precise native conformation once they have found the native topomer.

The Folding Landscape.

To this point, we have treated the energy landscape outside the native topomer as flat, yet rugged, like a golf course (31). However, calorimetric studies (32) and experiments using the hydrophobic fluorescent probe ANS (33) show that a significant portion of the nonpolar surface area that is buried in the native state is also buried in partially folded structures. Thus, the hydrophobic effect operates on the protein long before the protein has found its native topology, and conformations with poor solvation energies (34) are not sampled during the search for the native topomer.

However, the fact that a protein only samples conformations with favorable solvation energies need not drastically limit the number of topologies searched. Two structures within the same topomer can have very different solvation energies because small perturbations in the backbone conformation can drastically affect the orientation of the side chains with respect to the interior of the overall fold. Thus, one can easily construct a conformation that is topomeric to the native structure such that the nonpolar sidechains are directed away from the core and the polar sidechains are buried in the interior. Conversely, most compact and semicompact topomers contain conformations such that the nonpolar sidechains are properly directed into the interior and the polar sidechains extend into the solvent. A protein will tend to sample good solvation energy structures within each topomer.

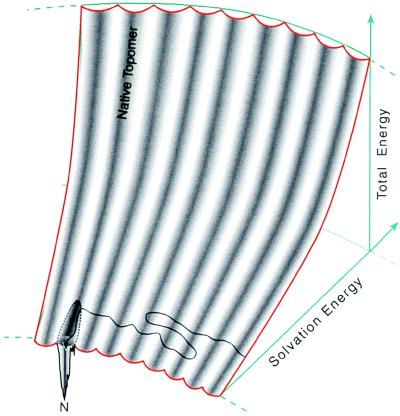
Fig. 5 presents a diagram for the folding energy landscape that simultaneously illustrates these ideas about the variability of solvation energies and the similarity of conformation states within a single topomer. The folding energy landscape is shaped like the seating in the Rose Bowl. The total energy is given by the height of the stadium. Conformations with poor solvation energy are situated far away from the playing field whereas conformations with favorable solvation energies are situated close to the field. The conformations within one topomer are distributed in a single, columnar section in the stadium (the complete energy landscape for a 100-residue polypeptide contains 3 × 10⁷ topomer columns). Thus, each topomer contains conformations with both very poor and very favorable solvation energies. As a protein folds, it samples different topomers by randomly sampling the favorable solvation energy states. When the protein samples a conformation in the native topomer, the native funnel directs the protein to its unique native structure.

Figure 5.

A representation of the folding energy landscape suggested by the topomer-sampling model. This diagram indicates that structures within the same topomer have a variety of solvation energies (shown along the radial axis). The landscape is shaped like the seating in the Rose Bowl. The total energy is given by the height in the stadium. Conformations with poor solvation energy are situated far from the playing field whereas conformations with favorable solvation energies are situated close to the field. The conformations within a single topomer are distributed in a single, columnar section of the stadium. For a 100-residue polypeptide, the complete folding energy landscape contains 3 × 10⁷ such topomer columns. On this topomer folding diagram, the topomer-sampling model of protein folding is a meandering trajectory (black line with arrowhead) that travels from topomer to topomer, sampling only favorable solvation energy conformations within each topomer. When the protein samples a conformation within its native topomer, specific favorable hydrogen bonding and core packing interactions (represented by a funnel within the native topomer) direct the protein to its unique native structure (N). We show this funnel connected to only a part of the space spanned by the native topomer to indicate that only the favorable solvation energy structures in the native topomer are near the native funnel. Thus, mutations that affect the solvation properties of a protein can drastically affect the time required for a protein to find its native funnel (see text). On this diagram, an early folding nucleation event decreases the number of topomer columns that must be sampled, thereby decreasing the folding rate (by whatever fraction of the total number of topomers is eliminated).

In the topomer-sampling model, even though an average-sized protein is assured of randomly sampling some conformation in the native topomer, there is no guarantee that this conformation will be within the clutches of the native folding funnel. We believe that the hydrophobic effect plays a key role in ensuring that, when a protein samples a conformation in the native topomer, its sidechain and hydrogen bond donor orientations will be appropriate for a cooperative collapse to the native state.

In the complete absence of a hydrophobic effect, the solvation energy dimension of the folding energy landscape collapses (Fig. 5), so that the folding energy landscape becomes a flat, rugged surface. In such a scenario, the line representing the protein folding trajectory is not confined to the lower levels of a stadium-like surface but is allowed to wander over an entire flat landscape, precluding the protein from finding the native folding funnel on a tractable timescale. In this manner, we expect that disruptions in the solvation properties of a protein (by changing the solvent or making sequence mutations) will drastically influence the time it takes to find the native funnel and consequently will have a large effect on the overall folding rate. Consistent with this, numerous experiments have demonstrated that there is a strong correlation between protein folding rates and protein stability across differing solvent conditions (35) and that stability is a significant determinant of the relative kinetics of homologous proteins (20, 36, 37).

Our estimate of the folding timescale as the time it takes to randomly sample all compact and semicompact topomers assumes that each topomer contains one or more conformations of favorable solvation energy and that each topomer is sampled as the protein moves between favorable solvation energy conformations. Barron and coworkers (38, 39) have recently used Raman optical activity experiments to show that residues in disordered regions in molten globule states “flicker” between the allowed regions of the Ramachandran plot at rates of ≈10¹²⋅s⁻¹. This suggests that local polypeptide chain dynamics can accommodate very fast equilibration to low solvation energy conformations without disturbing the tertiary topology. We have not yet evaluated the solvation energy for all possible conformations of a 100-residue polypeptide. Hence, we do not yet know how many topomers do not contain any conformations with favorable solvation energies. However, we believe that it is not a significant fraction (probably less than a factor of 100) because our assumption that all semicompact and compact topomers are sampled correlates well with experimental folding rate data.

CONCLUSION

We find that partitioning conformation space into sets of topologically equivalent conformations (topomers) allows us to understand how proteins can fold to native structures on a subsecond timescale. Our results suggest that average-sized protein domains (<120 residues) can fold by a two-step process: (i) topomer diffusion: a random, diffusive search for a conformation with the native topology (≈0.1 s for 100 residues), followed by (ii) intratopomer ordering: a nonrandom, “funneled” local conformational search for the precise native state.

Thus, early protein folding can be a highly dynamic, diffusive process. This highly dynamic mechanism for folding is consistent with recent experiments showing that the rate of protein folding strongly depends on the viscosity of the solvent (40–42). Resolving the exact details of these early folding processes requires monitoring protein folding in the microsecond time regime.

This dynamic picture of early protein folding is also consistent with the phenomenon of prions (43), proteins that apparently have more than one stable conformation. The topomer-sampling model suggests that numerous non-native topologies are explored before the native topology is sampled. It is quite conceivable that there could be more than one topology containing a funnel with the correct properties to yield a kinetically trapped folded state. Evidently, evolution has selected for protein sequences that have only one such funnel and hence fold to a singular native state at biological temperatures.

ABBREVIATIONS

GP

generic protein

CMRS

α-carbon root-mean-squared deviation