Molecular model of muscle contraction

Abstract

A quantitative stochastic model of the mechanochemical cycle of myosin, the protein that drives muscle contraction, is proposed. It is based on three premises: (i) the myosin head incorporates a lever arm, whose equilibrium position adjusts as each of the products of ATP hydrolysis dissociates from the nucleotide pocket; (ii) the chemical reaction rates are modified according to the work done in moving the arm; and (iii) the compliance of myosin’s elastic element is designed to permit many molecules to work together efficiently. The model has a minimal number of parameters and provides an explanation, at the molecular level, of many of the mechanical and thermodynamic properties of steadily shortening muscle. In particular, the inflexion in the force–velocity curve at a force approaching the isometric load is reproduced. Moreover, the model indicates that when large numbers of myosin molecules act collectively, their chemical cycles can be synchronized, and that this leads to stepwise motion of the thin filament. The oscillatory transient response of muscle to abrupt changes of load is interpreted in this light.

While the sliding-filament theory of muscle contraction (1, 2) is universally accepted, the detailed mechanism of transduction of chemical energy, derived from ATP hydrolysis, into mechanical work remains the object of intense research. In vitro motility assays have established that the relative motion of thick and thin filaments in the sarcomere is generated by myosin heads (3), which undergo an actin-activated ATPase cycle during which they form transient crossbridges between the filaments. How are the mechanical properties of muscle related to the structure and the biochemical kinetics of myosin? To what extent can the dynamics of sarcomere shortening be ascribed to events at the molecular level?

This issue is explored here in the context of a model of the mechanochemical cycle of myosin, based on the “swinging lever arm” hypothesis (4)—a refinement of the swinging crossbridge picture (5, 6) that has been prompted by recent structural studies (7). I investigate how an ensemble of motor proteins generates sliding between a single pair of filaments, under conditions in which an external force opposes the motion, and report a striking correspondence with a number of features that are familiar from experiments on muscle. The Fenn effect and A.V. Hill’s characteristic relation (8) between force and velocity are reproduced, and so are the deviations from Hill’s law that have been detected in single muscle fibers (9). Most significantly, the model displays a transition from smooth sliding to stepwise motion at high load, because of the synchronization of the power strokes of a large fraction of the myosin molecules.

Structural Properties of Myosin, Chemical Kinetics, and Their Interrelation.

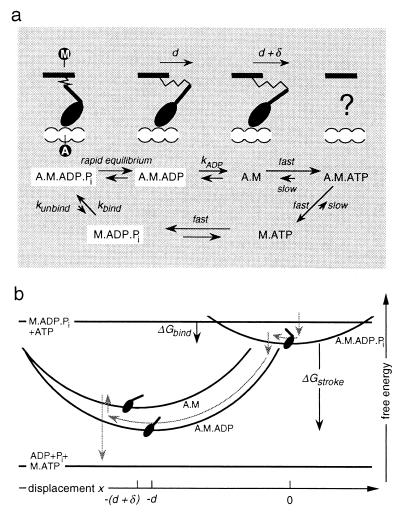
The model is illustrated in Fig. 1. Each myosin molecule is anchored in the thick filament, and its head binds stereospecifically to sites on the thin filament. The head contains a lever arm that amplifies any small change in conformation that occurs when different ligands bind at, or dissociate from, the nucleotide binding site. The resulting movement of the distal end of the arm is accommodated, in the first instance, by the compliance of an elastic element within the neck of the molecule. The elastic force subsequently causes relative motion of the two filaments, which permits the element to relax. The affinity of the head for the actin filament is regulated by the hydrolysis cycle, according to the Lymn–Taylor scheme (10). Myosin with bound ATP has a low affinity for actin, but the “primed” head, which is the product of ATP splitting, binds readily. Once the head is attached, the rapid release of P_i provokes a major rotation, or “power stroke,” of the lever arm. Subsequently, ADP dissociates only slowly, giving rise to a change of conformation of (as yet) unspecified size. This event is immediately followed by the binding of ATP, which destabilizes the actomyosin interaction and causes the head to detach, thereby completing the cycle.

Figure 1.

(a) Biochemical cycle of myosin, showing the conformation of the head domain that corresponds to each chemical state. M labels the point of attachment of the head to the thick filament and A labels the binding site on the thin filament. Because of the fast reactions, only the three states boxed in white are populated to a significant degree. Note that there are variations of this reaction scheme that do not substantially change the model; e.g., the binding rate could be limited by the rate at which M⋅ADP⋅P_i is created by hydrolysis of M⋅ATP. (b) Because of the linear elastic element in the myosin neck, the free energy of attached states varies quadratically with the displacement x of A relative to M (the elastic strain of A·M·ADP⋅P_i is taken to be zero at x = 0). The gray arrows indicate the typical reaction pathway of a myosin molecule when the thin filament is propelled by an ensemble of motor proteins.

A crucial aspect of myosin action is the way in which mechanical forces affect its chemistry. Thermodynamic arguments constrain the strain-dependence of the reaction rates, as remarked by A. F. Huxley and R. M. Simmons (11) for the power-stroke transition and formally stated by T. L. Hill (12) for the entire cycle. The ratio of forward and reverse rate constants between any two states is determined by the free energy difference. If this is a function of the strain, as it will be if one or both of the states are attached to actin, then at least one of the rate constants must be strain dependent. The functional form of the dependencies, however, is undetermined. A rational approach to this problem, taken here, is to adopt Kramers’ theory of chemical reactions (13), in which the rate depends exponentially on the free energy required to attain a transition state. Because the free energy barrier is modified by changes in the elastic energy concomitant with conformational changes, the strain dependence of reaction rates is determined by three parameters that specify the structural properties of the molecule: the spring constant K; the distance d that the distal point of the lever advances when executing the power stroke; and the additional distance δ moved by the lever on ADP release. It is worth emphasizing that this approach provides more exacting theoretical constraints than previous models (14–17), which include rate constants that are arbitrary functions of the strain. In essence, I argue that structural changes alone are responsible for strain dependence, and that such changes are inevitable for each reaction that involves an alteration of ligand. A similar rigorous approach has been taken by Smith and Geeves (18).

Expressions for Reaction Rates.

To simplify computation, it is assumed that only one head of a given myosin (M) molecule is active at any instant. Further, it is supposed that a head can bind to any point on the thin filament, rather than at discrete binding sites, and that the filaments are inextensible. The following assumptions are made about the rates of the six chemical reactions shown in Fig. 1a. (i) Hydrolysis of detached M⋅ATP is fast. (ii) The overall rate of binding of M⋅ADP⋅P_i to actin (A) is constant and is given by k_bind. But because the elastic element of the detached molecule fluctuates thermally, the probability that, on binding, the displacement x between A and M is x₀ is proportional to exp(−[1/2]Kx ₀ ² /k_BT), and consequently the binding rate varies with x₀. Here, T is the absolute temperature and k_B is the Boltzmann constant. The reverse reaction occurs at constant rate k_unbind. (iii) The P_i release reaction, which is accompanied by a large (negative) change in chemical free energy ΔG_stroke, is rapid. Consequently, the two states A⋅M⋅ADP⋅P_i and A⋅M⋅ADP are in dynamic equilibrium, and it suffices to specify the ratio of forward and reverse rates, rather than both separately. At a given instant, the relative probability of the two states is P_A.M.ADP(x)/P_A.M.ADP.Pi(x) = exp(−(ΔG_stroke + ΔE)/k_BT), where ΔE = [1/2] Kd(2x + d) is the change in elastic energy concomitant with the power stroke. (iv) On ADP release, the strain energy changes by ΔE = Kδ(x + d) + constant, which alters the free energy barrier of the reaction so that k_ADP = k_ADP⁰ exp(−Kδ(x + d)/k_BT). Here, k_ADP⁰ is the rate of ADP release when the elastic element is relaxed. (v) The reverse rate (assumed constant) is much slower than ATP binding, which is sufficiently rapid that any strain dependence due to a conformational change is irrelevant. (vi) ATP-mediated detachment is very fast and the reverse reaction is slow enough to be neglected.

As indicated in Fig. 1, the model effectively reduces to a three-state one, involving transitions between one detached and two attached states. The above formulae, which are consistent with Kramers’ theory, completely specify the strain dependence of transition rates between these states.

Stochastic Motion Generated by an Ensemble of Myosin Molecules.

Although apparently a dynamical process, the relative motion of a pair of rigid filaments, generated by an ensemble of N ≈ 100 motor proteins, may be treated as a problem of mechanical equilibrium that is continually being adjusted as chemical reactions occur. This is because the viscous relaxation time of the system is very rapid compared with the typical time between reaction events; whenever the chemical state of one head is altered, the filaments quickly shift position to maintain the equality of the sum of the forces acting in the ensemble of crossbridges and the (constant) load.† Simulation of this stochastic process is straightforward if a record is kept of the state and the strain of each myosin molecule. It involves the repetition of five steps: (i) Evaluate the mean time τ until the next attachment/detachment event; (ii) determine the time step by drawing a random variable from an exponential distribution with mean τ; (iii) choose, with probability proportional to the respective rates of the different events, which myosin molecule was involved and which transition occurred; (iv) change the state of the myosin head accordingly and readjust the mechanical equilibrium; (v) reequilibrate the power-stroke transition of all of the bound heads. This procedure permits the calculation of the sliding velocity as a function of the force opposing the motion. The form of the force–velocity relation is determined by four dimensionless combinations of the model parameters: the energy ratios ɛ₁ =  [1/2] Kd²/ΔG_stroke   and ɛ₂ = Kdδ/k_BT, which govern, respectively, the strain dependencies of the power stroke and of ADP release; and the ratios of rate constants, γ₁ = k_ADP⁰/k_bind and γ₂ = k_unbind/k_bind, which determine the proportion of heads that are bound to the thin filament at a given moment. The magnitudes of force and velocity are scaled by the “unitary” values, F_unit = Kd and v_unit = dk_bind.

Regulation of the Number of Bound Heads According to the Load.

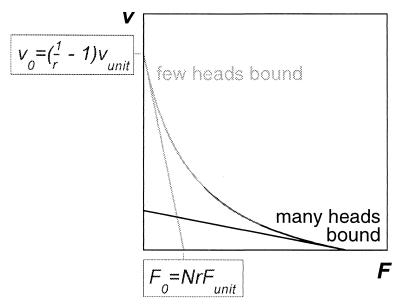
To understand how the values of the dimensionless parameters affect the motor performance, consider first the hypothetical case in which the molecular energy supply is unlimited and the conformational change on ADP release is negligible, so that ɛ₁ and ɛ₂ are both zero, although K and d are finite. Then the reaction rates are strain independent and the mean fraction r of myosin molecules with a head bound to the thin filament is independent of load, r = 1/(1 + γ₁). Moreover, the equilibrium between A⋅M⋅ADP⋅P_i and A⋅M⋅ADP is overwhelmingly in favor of A⋅M⋅ADP, so that the latter is effectively the only attached state. In this case, the velocity decreases linearly with the applied force (19), falling from v₀ = γ₁v_unit = ([1/r] − 1)v_unit at F = 0, to zero at a stall force F₀ = Nr F_unit (see Fig. 2). Clearly, the unloaded speed can be maximized by choosing small r, or alternatively the stall force can be maximized by choosing r close to unity. Good performance at both tasks would be preferable, and myosin has presumably evolved to achieve this. What is needed is a mechanism to ensure that the proportion of bound heads increases from a low value at zero load to a high value when a strong force is applied. A conformational change on ADP release produces precisely the desired effect, provided that it moves the lever in the same direction as the power stroke. Then, the rate of ADP release and subsequent ATP-induced detachment increases as the elastic element relaxes: if sliding is permitted, detachment occurs more rapidly, and the fraction of bound heads falls; if sliding is blocked so that the crossbridges remain strained, detachment slows and the proportion of heads bound to the thin filament rises. The result is a concave force–velocity relation, whose curvature is controlled by the parameter ɛ₂.

Figure 2.

The force–velocity relation is linear if the reaction rates are independent of the load, with a slope that depends on the fraction of myosins with a head bound to the thin filament. If the proportion of time that a head spends in a bound state is regulated by the load and increases monotonically from a low value to a value close to unity as the load is augmented, a force–velocity relation similar to Hill’s characteristic relation is obtained.

Optimization of the Mechanical Efficiency.

In the above case, it is possible to obtain an indefinitely high force by suitably increasing the spring stiffness. A finite energy supply limits this possibility because, when ɛ₁ > 1, P_i release is disfavored and the power stroke is inhibited. Because those heads that are bound to the thin filament, but that have not performed a power stroke, do not generate force, the tail of the force–velocity curve is cut off, and the stall force drops below the value Nr F_unit. Thus it is clear that the molecule would be an ineffective motor either if the spring were too compliant (because the unitary force would be weak), or if it were too stiff (because the power stroke would fail). I postulate that the myosin molecule has evolved so that its elastic constant is that which maximizes the peak mechanical efficiency. Solution of the model indicates that the peak work performed per ATP molecule split is maximal when ɛ₁ ≈ 1.3, for a wide range of choices of other parameters. The fact that ɛ₁ is greater than unity—i.e., that the chemical energy is insufficient to power the stroke from the zero-strain state—is notable. It means that, for the majority of myosin molecules, the power stroke does not follow binding immediately but is delayed until the filament has been propelled through a short distance by the action of other heads (see Fig. 1b). This delay has a number of important consequences, discussed below, which have not been anticipated because existing crossbridge models (15–18) have not examined the regime ɛ₁ > 1.

Force–Velocity Relation and Load-Dependent ATPase Rate: Comparison with Mechanical and Thermodynamic Properties of Muscle.

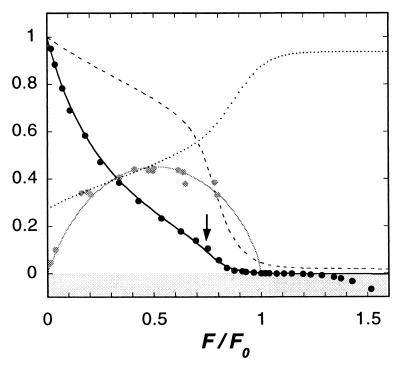
With ɛ₁ fixed at this optimal value, the other three dimensionless parameters were varied to reproduce the force–velocity relation of muscle. Fig. 3 shows the result of a fit to Edman’s accurate data (9), measured from a single fiber of a frog muscle. The values used were ɛ₂ = 1.6, γ₁ = 2, and γ₂ = 0.05 (which corresponds to ΔG_bind = −3 k_BT). The resulting zero-load velocity is v₀ = 4.1 v_unit, and the stall force is F₀ = 0.23 NF_unit. The maximum rate of ATP splitting is V₀ = 0.7 Nk_bind.

Figure 3.

Variation with load F of: the sliding velocity v/v₀ (black line); the average fraction r of myosin molecules with a bound head (dotted line); and the ATP splitting rate V/V₀ (dashed line). Parameter values as cited in the text. Also shown, the mechanical efficiency when ΔG_stroke = −15 k_BT (gray line). Black circles are Edman’s experimental measurements of velocity (Fig. 7 of ref. 9). Gray circles are Hill’s experimental measurements of mechanical efficiency (27). These results are the time-averaged velocity of an indefinitely long thin filament being propelled by a thick filament comprising N = 150 myosin molecules (total number of chemical reaction events = 10⁸).

A conspicuous feature, remarked by Edman and arrowed in Fig. 3, is the break in the curve at F/F₀ ≈ 0.75. The model provides an explanation, which differs from that which has been proposed previously (20). As mentioned above, when ɛ₁ > 1, a newly attached head typically executes its power stroke only after the filaments have slid through a displacement equal to a small fraction of d. At loads approaching the stalling force, the velocity is so low that the probability that a myosin head performs its power stroke, before it unbinds again, is diminished significantly. Because the lack of power strokes, in turn, reduces the rate of sliding, the consequence is a sharp decline in velocity with increasing load. The response of muscle to stretching is a smooth continuation of this process. At negative sliding velocities, only a tiny fraction of heads perform a power stroke; the majority undergo a simple reversible cycle, binding and unbinding as M⋅ADP⋅P_i. On average, each head remains bound for duration 1/k_unbind, during which time its strain decreases from zero to −v/k_unbind, so a crossbridge exerts mean force −Kv/2k_unbind. Thus the force–velocity relation in this region is linear: v/v_unit = −2γ₂ F/NF_unit. The effect is akin to a high viscous friction. The progressive yield above F/F₀ = 1.3 is not reproduced by the model, although it can be understood (21) to be a consequence of heads getting ripped off at forces slightly exceeding F_unit, as has been observed experimentally (22).

The variation with load of the average proportion of myosins with a head bound to the thin filament, shown in Fig. 3, is consistent with measurements of muscle stiffness (23), which rises from about 20% of rigor stiffness at zero load to 70% in isometric conditions.‡ The increase in the ATP splitting rate with sliding velocity is also broadly compatible with the fact that muscle generates heat more rapidly the faster it shortens (8) (the Fenn effect). Note that at negative velocities, very little ATP is consumed, since few power-stroke cycles are completed; this is consistent with the observation that during slow stretching, cross-bridges can develop high tension without splitting ATP (26). Note also that peak efficiency is attained at a velocity that corresponds to the filaments sliding, on average, through displacement d during the time that a head is bound; in this way, the strain generated by the power stroke is typically just relaxed at detachment, and little energy is wasted stretching the elastic elements to negative strains.

Values of the Physical Parameters: Comparison with Measurements Made on Single Myosin Molecules and on Muscle Fibers.

The peak mechanical efficiency (ratio of work to enthalpy change) of frog muscle is measured to be about 45% (27). Assuming the enthalpy change per molecule of ATP split is ΔH_ATP = −20 k_BT, as measured (28), an estimate of the values of the structural parameters can be obtained. As shown in Fig. 3, the observed efficiency is matched when ΔG_stroke = −15 k_BT. Various pairs of values of the stroke size and the spring constant are then compatible with ɛ₁ = 1.3, with the most plausible range being d = 5–17 nm and corresponding K = 5 − 0.5 pN/nm. In what follows, the values d = 11 nm and K = 1.3 pN/nm are chosen; the value of ɛ₂ then implies δ = 0.5 nm, so the conformational change on ADP release is very modest indeed. These figures are in accord with independent estimates from a variety of sources. Tension transients in muscle are indicative of a 10- to 12-nm crossbridge motion (11, 29). Moreover, populations of events centered at 11 nm have been recorded in experiments that use optical tweezers to measure the step displacements generated by single myosin molecules (30, 31) [but note that other authors have reported smaller (32) or larger (33) steps]. Direct measurement of myosin elasticity (22) yields an average value K = 0.6 pN/nm; however, because of the unknown series compliance in the links used to hold the molecules in position,§ the highest observed value K = 1.2 pN/nm (22) may be a more reliable estimate. A study in which a paramagnetic probe was used to detect the conformational change of the head of skeletal myosin on ADP release concluded that the movement of the lever arm is smaller than the resolution of the technique (i.e., δ < 1 nm) (34).‖

The above values of the structural parameters also yield reasonable figures for whole muscle. Because there are N = 150 myosin molecules per half-thick filament, and the thick filament density is 5 × 10¹⁴ m⁻², the estimate of the isometric force obtained from the model is 2.5 × 10⁵ Nm⁻², which is close to the value typically measured. The experimental value of the speed of shortening at zero load, v₀ = 1.8 μm/s per half-sarcomere (at 0°C) (9) can be fitted by setting k_bind = 40 s⁻¹, in which case the ATPase rate at zero load is 30 s⁻¹ per myosin head. This is two times faster than the maximum ATPase rate measured in shortening muscle (36). But if heads are torn off at forces exceeding F_unit (22), the rate of ATP splitting is diminished at fast shortening speeds, and agreement with the experimental data is improved (unpublished data).

Biochemical Synchronization, Stepwise Motion, and Their Relation to the Isotonic Transient Response.

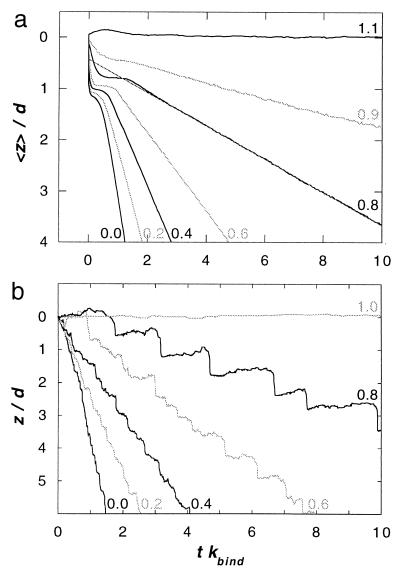
Many clues to the mechanism of muscular contraction have been obtained by studying the transient response of fibers to sudden changes in conditions. One striking characteristic is the damped oscillatory response to a step change of load (37). As shown in Fig. 4a, this behavior is reproduced by the model when the average motion of many filament pairs, each sliding independently, is computed. The initial response consists of an abrupt displacement, followed by a pause whose duration diminishes as the size of the force step increases. The dynamics of individual filaments on the time-scale of the chemical reactions provides insight into how the collective action of the motor proteins produces this effect. Fig. 4b shows the time course of the relative displacement of a single pair of filaments at various values of a steady opposing force. A clear transition in behavior is apparent: at low load, the motion is smooth, but at high load the thin filament advances in discrete steps. As illustrated in Fig. 5, the stepwise movement is due to the synchronization of the power strokes of the myosin molecules. At first sight, this is surprising, because the individual molecules are undergoing chemical reactions with stochastic kinetics. Coordination arises, despite this randomness, because when one head changes chemical state, the strain that is generated is communicated by means of the rigid thin filament to all of the other attached heads, thereby regulating their biochemistry.

Figure 4.

(a) Average displacement <z> of the thin filament subsequent to an abrupt change of load, from F₀ to F, at time t = 0. The transient response is averaged over 4,000 pairs of filaments, each linked by N = 150 myosin molecules. Curves are labeled by the value of F/F₀. (b) Trace of the displacement z of a single thin filament, propelled by N = 150 myosin molecules, at various values of a steady load F. Curves are labeled by the value of F/F₀.

Figure 5.

(a) Sequence of snapshots of N = 30 motor proteins propelling a thin filament (lower white rod) toward the left at zero load. Myosin heads are colored according to their chemical state: red = detached, orange = A⋅M⋅ADP⋅P_i (primed head), green = A⋅M⋅ADP (post-power stroke head). Elastic elements are shown in yellow. The time interval between stills is 0.4/k_bind. (b) Same, with the motion opposed by load F/F₀ = 0.8. The arrows indicate two instants at which the power strokes of a large fraction of the heads occur almost simultaneously. For clarity of presentation, this figure was prepared by using a slightly modified model that incorporates discrete binding sites, separated by intervals of 5.5 nm on the thin filament. Discrete and continuum models yield almost identical results.

Crucial, once again, is the condition ɛ₁ > 1; the power stroke does not immediately follow binding and, at high load, many of the attached heads are waiting in the “primed” state A⋅M⋅ADP⋅P_i. If one of these heads executes its power stroke, the thin filament will advance, thereby reducing the strain on all of the other attached heads and enhancing the probability that each one of them performs its own power stroke. Because of this positive feedback, a single chemical event is sufficient to tip the balance and provoke a cascade of power-stroke transitions. The thin filament jerks forward, accompanied by a burst of P_i release. The subsequent ATP-mediated detachment of positively strained crossbridges then causes the thin filament to move slowly in reverse (see Fig. 5b), diminishing the likelihood of further power-stroke transitions. A pause ensues, until a sufficient number of new crossbridges have been created to precipitate another cascade. Because of this dynamics, the trace of the thin filament position has a distinctive saw-tooth profile. At each jump, the filament moves forward a distance of order d, but the subsequent retraction is further at higher load so that the overall distance advanced per step decreases with increasing load. The step duration is of the order of the cycle time, 1/k_bind, and increases as the load approaches the stalling force. Although steps become less frequent as the load increases, it is worth remarking that occasional steps do occur even when the average velocity is zero. So the state F = F₀ is not a stationary one.

Returning to the isotonic transient response (Fig. 4a), the oscillatory behavior is caused by a gradual loss of correlation of the stepwise motion of different filaments, subsequent to an initial synchronization of the myosin power strokes imposed by the abrupt change in force. Although such an interpretation has been suggested before (38), stepwise motion during isotonic shortening seemed difficult to reconcile with stochastic crossbridge kinetics. In the present model, biochemical coordination arises naturally when the load is close to the stalling force. Thus, the damped oscillation is most marked after a small step decrease in load. The measured oscillation can be more pronounced than the simulated one (39), however, so some additional mechanism may be involved.

When evaluating the relevance of these results to muscle, it should be noted that the presence of steps does not rely on large fluctuations in force or displacement, because the number of motor proteins is small, nor on the assumption that the binding sites on the thin filament are continuous. Rather, it follows from the fact that, at high load, the probability distributions of the various states are not stationary, but evolve with time in a quasi-periodic way.¶ Thus, stepwise motion could potentially be coordinated throughout a sarcomere, in which hundreds of filament pairs are coupled in parallel. The range over which myosin heads cooperate would be limited by filament compliance.

Transient Response to Sudden Change of Length.

Step-length perturbation studies of muscle fibers (11, 29) have played a pivotal role in the development of theories of contraction, so it is important to verify that this model is consistent with experimental data. When an isometrically contracting fiber is subjected to a sudden change of length, the tension drops almost instantaneously, then regains its original value on a time-scale comparable to the period of the myosin cycle. But a proportion of the initial change in tension is recovered much more rapidly. The extreme value of the tension during the step, T₁, and the value after completion of the early recovery, T₂, depend in a characteristic way on the size of the step. This transient response is thought to be indicative of conformational changes of the bound heads, which occur with greater rapidity than detachment and attachment.

Fig. 6 presents the results of a simplified simulation that relates to experiments in which single muscle fibers were subjected to sudden length changes as they were contracting at various speeds (23). The calculated curves of T₁ and T₂ agree qualitatively with the experimental data, and the quantitative discrepancies are consistent with the neglect of filament compliance. It has been argued previously that the T₂ curve would show a region of negative slope if the power stroke is larger than the distance between binding sites on the thin filament (40). But this argument supposes that all sarcomeres respond in an equivalent fashion, a simplification which is appropriate in the context of models that assume that, during uniform contraction, there is a steady-state probability distribution of myosin states (14–18). An important feature of the present model is that, when the load is close to the stalling force, no such steady state exists. Amongst different half-sarcomeres, there are large variations in both the number and the conformation of bound myosin heads. As a consequence, significant sliding occurs during the rapid transient; some half-sarcomeres shorten, while others lengthen. Because of this readjustment, relatively few power-stroke transitions occur** and T₂ does not rise above the isometric tension.

Figure 6.

Transient tension in a model fiber after a step-change in length of Δz per filament pair. The “fiber” consisted of a series of filament pairs, joined end-to-end to mimic 50 sarcomeres. Initially the fiber was contracting under load such that the average sliding velocity between filaments was v. It was assumed that the sudden step change of length caused an equal shortening of each filament pair. In response, bound heads adjusted the chemical equilibrium of the power stroke reaction A⋅M⋅ADP⋅P_i ⇌ A⋅M⋅ADP. Filaments were permitted to slide relative to one another to maintain a uniform tension in the fiber, but the ends of the fiber were held fixed. T₁ is the tension immediately after the step, before any power-stroke transitions have taken place. T₂ is the tension attained once the power-stroke transition of all of the bound heads has been reequilibrated.

Summary.

This molecular model of muscle contraction has been built on three pillars: the hypothesis that the myosin head incorporates a swinging lever arm; a physical argument for the strain dependencies of the chemical rates; and the notion that the myosin molecule has evolved to operate efficiently in muscle. Some important new insights emerge from a synthesis of these concepts. Because the lever arm amplifies any slight conformational change that occurs at the nucleotide binding site, motion of the distal end of the arm is inevitable when each of the products of ATP splitting is released. Detailed balance then implies that the associated chemical rates are necessarily strain dependent, and myosin can use this property to advantage. The small structural change on ADP release provides a means to regulate the proportion of heads bound to the thin filament, so that additional motors are recruited at higher loads. The large rotation of the lever arm on P_i release provides the main power stroke. For this transition, the premise that myosin’s elastic element has been selected to optimize the collective efficiency of motors leads to a surprising result: the change in chemical free energy is insufficient to power the stroke of an individual head. Thus a myosin molecule operates poorly on its own. Myosin is a cooperative protein and each molecule requires the help of others to work effectively. There are three observable consequences, which are interrelated: the abrupt decline in velocity as the stall load is approached; biochemical synchronization and stepwise motion; and the oscillatory transient response to a step change of load.

The model contains inevitable simplifications but has the merit of containing few parameters, each of which corresponds to a physical quantity that can be measured independently. This permits theoretical predictions to be confronted with the experimental results of motility assays. Can stepwise motion be detected when an individual myofilament interacts with an actin filament? How does the force–velocity relation of myosin molecules with genetically modified heads (42) depend on the structural parameters? Such experiments will provide a more rigorous test of a model of myosin action that, despite its simplicity, captures the essential features of muscle contraction.

ABBREVIATIONS

M

myosin

A

actin